A molecular descriptor of a shallow potential energy surface for the ground state to achieve narrowband thermally activated delayed fluorescence emission†
Received
2nd December 2023
, Accepted 4th January 2024
First published on 5th January 2024
Abstract
Narrowband thermally activated delayed fluorescence (TADF) molecules have extensive applications in optoelectronics, biomedicine, and energy. The full-width at half-maximum (FWHM) holds significant importance in assessing the luminescence efficiency and color purity of TADF molecules. The goal is to achieve efficient and stable TADF emissions by regulating and optimizing the FWHM. However, a bridge from the basic physical parameters (such as geometric structure and reorganization energy) to the macroscopic properties (delayed fluorescence, efficiency, and color purity) is needed and it is highly necessary and urgent to explore the internal mechanisms that influence FWHM. Herein, first-principles calculations coupled with the thermal vibration correlation function (TVCF) theory were performed to study the energy consumption processes of the excited states for the three TADF molecules (2,3-POA, 2,3-DPA, and 2,3-CZ) with different donors; inner physical parameters affecting the FWHM were detected. By analyzing the basic geometric and electronic structures as well as the transition properties and reorganization energies, three main findings in modulating FWHM were obtained, namely a large local excitation (LE) proportion in the first singlet excited state is advantageous in reducing FWHM, a donor group with weak electron-donating ability is beneficial for achieving narrowband emission, and small reorganization energies for the ground state are favorable for reducing FWHM. Thus, wise molecular design strategies to achieve efficient narrowband TADF emission are theoretically proven and proposed. We hope that these results will promote an in-depth understanding of FWHM and accelerate the development of high color purity TADF emitters.
1. Introduction
In recent years, with the thriving development of thermally activated delayed fluorescence (TADF) materials, the research interest in TADF molecules has rapidly escalated.1–5 TADF molecules have become a research hotspot in organic light-emitting diodes (OLEDs) due to their advantages of 100% internal quantum efficiency and the absence of precious metals.6–10 Although the efficiency of TADF molecules has greatly improved, high color purity remains a key issue that needs to be addressed.11–17 Organic luminescence molecules typically exhibit strong vibrational relaxation (with rates ranging from 1012 to 1015 s−1) and strong vibrational coupling between the excited state and ground state; as a result, their emission spectra are relatively broad, and developing narrowband TADF molecules is a longstanding challenge in the field of electroluminescence.18–24
Researchers have made great efforts in this field. For the first time, Duan et al. reported a series of efficient green-emitting multi-resonance induced thermally activated delayed fluorescence (MR-TADF) materials by amplifying the influence of the skeleton and peripheral units. Peripheral units with electron-deficient characteristics could significantly reduce the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energy gap while maintaining color purity. Thus, an MR-TADF emitter with a photoluminescence quantum yield of over 90% and a full-width at half-maximum (FWHM) of 25 nm was developed.25 Woo et al. synthesized a series of green fluorescence moieties based on a tetra-azaacene core by introducing nitrile substituents at different positions. Corresponding results showed that the molecular structure of organic fluorescence moieties could be modulated by adjusting the structure and position of the substituents, thereby suppressing the narrowband emission from the ν0–n (n = 1, 2, 3…) vibrational transition.26 Zhang and Adachi proposed an ultrapure green emitter of 11,16,28,33,39-pentakis(2-methylprop-2-yl)-19,36-dibora-1,7,24-triazatridecacyclo[21.19.2.12,6.17,18.124,35.020,43.019,47.036,44.031,45.014,46.08,13.037,42.025,30]heptatetraconta-2(3),4,6(47),8(9),10,12,14(15),16,18(46),20(43),21,23(44),25(26),27,29,31(45),32,34,37(42),38,40-henicosaene (DBTN-2) based on organic boron with a highly twisted fused π-conjugated molecular design. This design concept significantly reduced the relaxation energy between the excited state and the ground state geometries, resulting in an FWHM of only 20 nm.27 Lee and colleagues improved the rigidity, and resonance strength, suppressed molecular bending and twisting, and destabilized the HOMO energy by intramolecular cyclization in the carbonyl/N resonant core. This resulted in the formation of a deep blue emitter with a peak wavelength of 440 nm and an ultranarrow bandwidth of 16 nm.28 In addition, Wu et al. performed a detailed theoretical analysis of the recombination energy that characterizes the vibrational coupling strength, elucidating the color purity changes of B, O-doped polycyclic aromatic compounds with MR-TADF. The computational results showed that changes in the bond length played a major role in the recombination energy of these highly conjugated aromatic molecules, and the source of the large recombination energy could be explained from the perspective of molecular orbitals;29 researchers have also made significant efforts to improve the color purity of TADF molecules.30–35
However, there is still a lack of theoretical research on the internal physical factors of FWHM, which hinders a true understanding of the internal mechanisms for improving color purity of luminescence molecules. Therefore, we believe that a time-saving and effective strategy is to fundamentally understand the influencing factors of FWHM through theoretical analyses.
Recently, Zheng et al. effectively synthesized TADF conjugates of carbazole/carbonyl through the addition and cyclization reaction of cyanide with carbazole. The attachment of auxiliary donors (including carbazole, diphenylamine, and phenolazine) to the carbazole/carbonyl backbone further shifted their emissions from blue to yellow-green. It is worth mentioning that a pure blue OLED with a peripheral carbazole-attached emission layer had a maximum external quantum efficiency (EQEmax) of 22.3% and FWHM of 48 nm.36 Based on this point, detailed theoretical calculations and analyses were performed for these three molecules (shown in Fig. 1), the energy consumption processes of excited states are fully revealed, and the influence of the donor groups on the FWHM of vibrational resolved TADF spectra is illustrated. The results show that molecules with charge transfer (CT) states exhibit larger FWHM, while molecules with hybridized local charge-transfer (HLCT) states have smaller FWHM. Moreover, the relationship between FWHM and reorganization energy is explored, and low reorganization energies contribute to the reduction in FWHM. Additionally, the electron-donating ability of the donor group affects the spectral broadening, with weaker abilities resulting in narrower spectra. Thus, a wise strategy to achieve narrowband thermally activated delayed fluorescence emission by constructing a shallow potential energy surface for the ground state is theoretically proved and proposed.
 |
| | Fig. 1 Molecular structures and PCM models (in toluene) of 2,3-POA, 2,3-DPA, and 2,3-CZ. The atomic numbers are also being displayed in the figure. | |
2. Theoretical derivations from FWHM to PES for the ground state
Let us start by reviewing the Golden rule expression for the molar absorptivity of the transition from the r state to the p state. Neglecting the coordinate dependence of the optical dipole matrix element, the molar absorbance εν, denoted by −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I/I0 = ενML, is defined as the ratio of the incident light intensity (I0) to the transmitted light intensity (I) multiplied by the molar concentration (M) of the solute and the path length (L).
I/I0 = ενML, is defined as the ratio of the incident light intensity (I0) to the transmitted light intensity (I) multiplied by the molar concentration (M) of the solute and the path length (L).
Next, we turn to the quantum expression. In the Golden rule expression for the electron-transfer rate constant and that for absorbance εν/ν or fluorescence fν/ν3 quantum expression when the Condon approximation is introduced:37,38
| |  | (1) |
There into:
| | | hν ≤ Epm − Ern + ΔE0rp ≤ h(ν + δν) | (2) |
Epm and
Ern represent the
mth and
nth energy levels of the p and r electronic states, respectively, measured relative to their respective lowest states considering nuclear motion.
ψpn and
ψrm are the wave functions for the nuclear motion on the p and r surfaces, respectively. Δ
E0rp represents the adiabatic energy difference between the r-state and p-state. Similarly, for the fluorescence spectrum of the transition from the p-state to the r-state, the probability of emitting photons in the frequency range per unit time (
ν,
ν +
δν) is denoted as
fνδν:
| |  | (3) |
In (1)Ca is given by:39
| |  | (4) |
where

denote Avogadro's number divided by 10
3,
μrp represent the transition dipole matrix element for the r → p transition.
n,
c, and
Qr denote the refractive index of the medium, the velocity of light, and the partition function of the system when the solute is in the r electronic state.
Similarly,
| | | Cf = 64π4n|μrp|2/ehc3Qp | (5) |
where
Qp denotes the partition function of the entire system with the solute in the p electronic state.
Expanding eqn (1) yields:
| |  | (6) |
where |〈
φrn|
φpm〉|
2 is the Franck–Condon factor for the vibrational mode, and
pn(
T) is the equilibrium probability of the solute in the
n vibrational level of the electronic state r.
Gsr(
x) is the equilibrium solvation free energy for the r-state. In the case of weak electronic coupling between the r-state and p-state:
40| |  | (7) |
| |  | (8) |
where

is the reorganization energy on the electronic r-state. Combining
eqn (7) and (8) yields:
| |  | (9) |
Finally, the expression for the FWHM of the fluorescence spectrum is:
| | Wf ≃ 2[(λriℏωr + 2λ0kBT + 2λikBTkr/kp)(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)]1/2 2)]1/2 | (10) |
where
λri is the “vibrational reorganization parameter”. ℏ
ωr is the spacing of energy levels in the r states.
λ0 is a second solvent contribution.
kr/
kp denotes the ratio of the force constant in the equilibrium solvation-free energy of r and p states. It is evident from the abovementioned equations that nuclear motion wavefunctions can influence the reorganization energy of lower energy states, thereby affecting the FWHM of the emission spectrum. Moreover, considering the TADF process that we are investigating, we believe that the reorganization energy of the S
0 state has a significant impact on the FWHM.
Based on the total spontaneous emission rate:41,42
| |  | (11) |
Considering radiation occurring between two electronic states and under the adiabatic approximation with Pr = Pr(T) taken as the Boltzmann distribution, eqn (11) can be written as:
| | 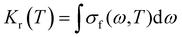 | (12) |
where:
| |  | (13) |
σf(
ω,
T) represent the differential radiation rate. |
ψrνr〉 and |
ψpνp〉 represent the Born–Oppenheimer adiabatic states. From
eqn (11)–(13), it is also evident that the nuclear motion wavefunction has an impact on the spontaneous emission rate. It is well known that the nuclear motion wavefunction and the potential energy surface mutually influence each other. The shape and parameters of the potential energy surface affect the form and energy level distribution of the nuclear motion wavefunction, whereas the form and energy level distribution of the nuclear motion wavefunction, in turn, affect the shape of the potential energy surface. This interaction allows the potential-energy surface and the nuclear motion wavefunction to jointly describe the molecular structure and dynamics in quantum chemistry. Based on the above, we can come to the following conceptions:
Based on the aforementioned analyses, we now explain this issue using a more easily understandable approach. As is commonly known, the energy value of a system corresponds to the molecular geometric structures, and the energy values at different nuclear coordinates together form the potential energy surface (PES). Therefore, PES serves as a pivotal means for investigating the internal mechanisms of molecules.43–48 According to Marcus's theory, λ1 and λ2 represent the different reorganization energies (shown in Fig. 2(a)). If we express the abscissa of the spectrum as energy E, the absorption and emission spectra of the organic luminescence molecules are illustrated in Fig. 2(b). It is evident that the broadening of the absorption spectrum is primarily associated with λ1 on the S1 PES, while the broadening of the emission spectrum is mainly influenced by λ2 on the S0 PES. Therefore, the relationships between FWHM and PES for the ground state are established, and our subsequent discussion primarily focuses on the S0 PES.48–58
 |
| | Fig. 2 (a) Potential energy surfaces of the S0 and S1 states and (b) schematic representation of the absorption and emission spectra. | |
3. Computational details
To better describe the photophysical properties of TADF molecules in the liquid phase, a PCM computational model was established.59–62 Additionally, the excited-state properties are highly sensitive to the choice of functional. In addressing this issue, different functionals such as B3LYP, BMK, M062X, PBE0, and WB97XD were employed to calculate the emission wavelengths in the liquid phase, and the results are presented in Table 1. It is observed that the PBE0 functional exhibited excellent agreement with the experimental values for all the studied molecules. Therefore, our subsequent calculations were performed based on the PBE0 functional coupled with the 6-31g(d) basis set. In the calculations, both the ground state and excited state geometric and electronic data were obtained using the density functional theory (DFT) and time-dependent density functional theory (TD-DFT) methods, respectively. All the above-mentioned calculations were carried out using the Gaussian16 package.63 In order to investigate the excited state energy consumption processes of these TADF molecules, the radiative decay rate (kr) was calculated based on Einstein's spontaneous emission equation with the expression of kr = −E2f/1.499 s−1. The non-radiative decay rate (knr) is determined using the thermal vibration correlation function (TVCF) theory method, obtained through the MOMAP program, with a Lorentzian broadening width of 100 cm−1.64 Furthermore, the spin–orbit coupling (SOC) constants were calculated using the Dalton 2013 program,65 based on fully optimized geometric and electronic data. In addition, the normal mode analyses for reorganization energies were performed using the DUSHIN package.66 The vibrational resolved TADF spectra are simulated using the TVCF spectral theory implemented in the MOMAP program. All these related equations and processes can be found in Peng, Shuai, Cui, Ma, Bai, and our works.67–70 Besides, the vibration-mode mixing effect can be taken into account as 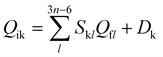 . Here, S is the Duschinsky rotation matrix representing the mixing of normal modes in the initial and final states and the vector Dk is the displacement along the normal mode k. All these parameters and reorganization energies can be projected onto the internal coordinates using Reimers’ algorithm.71,72
. Here, S is the Duschinsky rotation matrix representing the mixing of normal modes in the initial and final states and the vector Dk is the displacement along the normal mode k. All these parameters and reorganization energies can be projected onto the internal coordinates using Reimers’ algorithm.71,72
Table 1 Emission wavelengths (nm) of S1 calculated by different functionals for 2,3-CZ, 2,3-DPA and 2,3-POA in toluene
|
|
B3LYP |
BMK |
M062X |
PBE0 |
WB97XD |
Expa |
|
Emission peak at room temperature measured in toluene (5.0 × 10−5 m).
|
| S1 |
2,3-CZ |
470.81 |
395.93 |
371.66 |
443.10 |
359.93 |
449 |
| 2,3-DPA |
524.29 |
431.87 |
402.38 |
492.00 |
391.78 |
496 |
| 2,3-POA |
649.73 |
493.58 |
431.86 |
598.02 |
399.75 |
547 |
4. Results and discussion
4.1. Impact of donor groups on FWHM
Firstly, as depicted in Fig. 3, we calculated the spectral full width at half maximum of the three molecules by setting FWHM = 150 cm−1, resulting in values of 92 nm, 50 nm, and 38 nm. We then compared our calculated values with the corresponding experimental data obtained from ref. 36, which were 92 nm, 57 nm, and 36 nm, respectively. A close correspondence between our calculated and experimental values is evident. By analyzing the data, we observed that the 2,3-POA molecule has the largest FWHM (96 nm), followed by the 2,3-DPA molecule with an FWHM of 52 nm, while the 2,3-CZ molecule exhibited the smallest FWHM, measuring 40 nm. This indicates that the different donor groups could generate significant influence on FWHM. Later, we calculated the absorption spectra of the three molecules in toluene, and the corresponding results are shown in Fig. S1 (ESI†). The results reveal distinct absorption peaks at different wavelengths for each molecule. Specifically, 2,3-POA exhibits an absorption peak at 494 nm, 2,3-DPA at 454 nm, and 2,3-CZ at 418 nm. Moreover, to provide a better understanding of their photophysical properties, we conducted a molecular frontier orbital analysis. The energy and distribution of the orbitals are depicted in Fig. S2–S4 (ESI†). It is evident that the S0 and S1 states of the investigated molecule were primarily governed by the transition of the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). Similarly, the T1 state of 2,3-POA was also dominated by the HOMO → LUMO transition. The T2 state of 2,3-DPA is predominantly influenced by the HOMO−1 → LUMO transition (68.9%), in addition to the transitions involving HOMO → LUMO (11.3%) and HOMO−8 → LUMO (4.4%). The T3 state of 2,3-CZ is mainly influenced by the HOMO−1 → LUMO transition (44.2%), along with the transitions involving HOMO → LUMO (22.8%), HOMO−2 → LUMO (8.5%), and HOMO−7 → LUMO (8.9%).
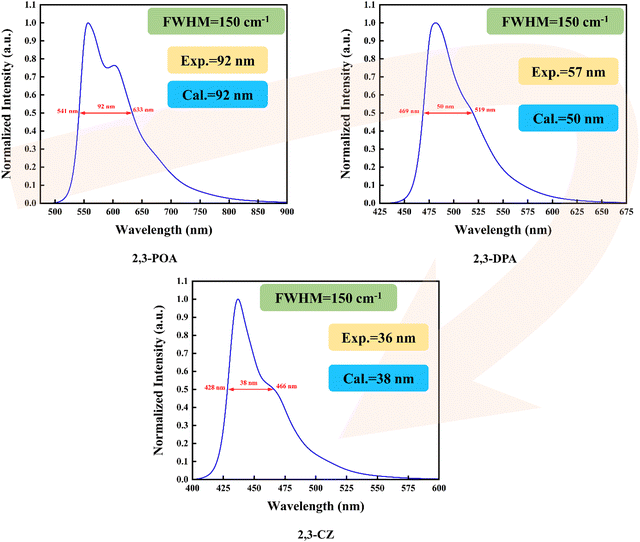 |
| | Fig. 3 Calculated phosphorescence spectra in toluene at room temperature. | |
In order to elucidate the reasons behind these differences, we first analyzed the electronic structures of the three molecules, which revealed the impact of different donor groups on the transition properties. The natural transition orbitals (NTOs) of the S1 state for the three molecules are illustrated in Fig. 4. Here, we know that the S1 state of 2,3-POA exhibits a typical CT feature with the LE (local excitation) proportion of 21.31%, which corresponds to a larger FWHM. On the other hand, 2,3-DPA and 2,3-CZ displayed typical HLCT features, with LE proportions of 40.96% and 47.66%, respectively, resulting in smaller FWHM. Based on this, we hypothesize that a large LE proportion in the S1 state is advantageous in reducing FWHM, 2,3-DPA, and 2,3-CZ with HLCT features favoring to possess small FWHM values (52 nm and 40 nm, respectively) compared with that of 2,3-POA (96 nm). At the same time, we performed analysis of the T-state NTOs, as depicted in Fig. 4. The findings demonstrated that the T1 state of 2,3-POA corresponded to a CT state, the T2 state of 2,3-DPA corresponded to an HLCT state, and the T3 state of 2,3-CZ also corresponded to an HLCT state, exhibiting similarities with the transition properties of the S1 state. Notably, the S1 state of 2,3-POA exhibited a 21.31% from LE proportion, whereas the T1 state displayed a 31.21% LE proportion, indicating a difference of 9.90%. Similarly, the S1 state of 2,3-DPA manifested a 40.96% LE proportion, while the T2 state exhibited a 59.75% LE proportion, signifying a difference of 18.79%. Likewise, the S1 state of 2,3-CZ showcased a 47.66% LE proportion, whereas, the T3 state revealed a 65.60% LE proportion, indicating a difference of 17.94%. Based on these observations, it can be inferred that the S1 and T1 states of 2,3-POA exhibited the smallest SOC, whereas the SOC between the S1 and T2 states of 2,3-DPA, and between the S1 and T3 states of 2,3-CZ, were of similar magnitudes.
 |
| | Fig. 4 Natural transition orbitals (NTOs) of the S1 state for 2,3-POA, 2,3-DPA, and 2,3-CZ, as well as T1 state for 2,3-POA, T2 state for 2,3-DPA, and T3 state for 2,3-CZ in toluene. | |
Furthermore, as mentioned in Section 2, the FWHM is closely related to the reorganization energy of the ground state. Ideally, eliminating all vibrational transitions except for the main emission peak is desirable; however, due to the redistribution of charges in the S1 state, it is not possible to completely restrict structural changes. Therefore, the molecular design of narrowband emitting TADF molecules requires smaller reorganization energies. Similarly, we speculate that 2,3-CZ has the smallest reorganization energy. Based on this point, we analyzed the reorganization energies of the three molecules, and the corresponding results are shown in Fig. 5. As we speculated, the reorganization energy of 2,3-POA is the highest with large contributions from high-frequency modes. Therefore, we believe that changes in the bond length significantly contribute to the reorganization energy. Moreover, the reorganization energy of 2,3-DPA is smaller, while the reorganization energy corresponding to the same high-frequency modes remains larger. As for 2,3-CZ, the reorganization energy is the smallest. Hence, we conclude that small reorganization energies are advantageous in reducing FWHM. Subsequently, we analyzed the contributions from bond length, bond angle, and dihedral angle to the reorganization energy, and the corresponding results are shown in Fig. S5 (ESI†) and the calculated data are summarized in Table 2. We find that for all three molecules, bond lengths contribute the most, accounting for 62%, 47%, and 53%, respectively. Furthermore, to reveal the effect of different donor groups on reorganization energies, reorganization energy contributions from the bond length in the donors of 2,3-POA, 2,3-DPA, and 2,3-CZ were analyzed, and the corresponding results are shown in Table S1 (ESI†). We know that the bond lengths between atoms 17 and 24 as well as between atoms 17 and 25, exhibited significant contributions.
 |
| | Fig. 5 Calculated reorganization energies versus the normal mode frequencies for 2,3-POA, 2,3-DPA, and 2,3-CZ in toluene, respectively. Representative vibration modes are shown as insets. | |
Table 2 Reorganization energies (cm−1) for 2,3-POA, 2,3-DPA and 2,3-CZ from the bond length, bond angle and dihedral angle in toluene, respectively
|
|
Reorganization energy (cm−1) |
| Bond length |
Bond angle |
Dihedral angle |
Total |
| 2,3-POA |
1216.28 |
497.85 |
247.47 |
1961.60 |
| 2,3-DPA |
649.32 |
442.55 |
293.17 |
1385.04 |
| 2,3-CZ |
719.31 |
316.44 |
321.68 |
1357.43 |
Based on this issue, we calculated the potential energy curves for the bond lengths between atoms 17–24 and 17–25 for the three molecules, corresponding results are shown in Fig. 6 and 7, respectively. As mentioned earlier, the FWHM is closely related to the reorganization energy on the S0 potential energy surface. Therefore, we focus on the S0 potential energy surface. From Fig. 6, we can see that 2,3-POA has the largest variation in reorganization energies attributed to changes in the bond length (λ2) value of 0.014 eV, followed by 2,3-DPA with 0.005 eV, and 2,3-CZ has the smallest λ2 value of 0.003 eV. Similarly, from Fig. 7, a similar pattern is determined with λ2 values of 0.011 eV, 0.002 eV, and 0.001 eV for 2,3-POA, 2,3-DPA, and 2,3-CZ, respectively. This result perfectly corresponds to the previously mentioned pattern of FWHM. Therefore, we conclude that the emission spectral broadening of these three molecules is primarily related to the variation in the bond lengths of the donor groups. In addition, we conducted simultaneous potential energy surface scans for the bond lengths between the 17th and 24th atoms, as well as between the 17th and 25th atoms, in the S0, S1, and T1 states of the three molecules, and the obtained results are shown in Fig. S6 (ESI†). The findings demonstrate that all three molecules exhibit a single minimum energy configuration across the S0, S1, and T1 states, and no additional structures are discovered.
 |
| | Fig. 6 Potential energy curve of bond length between atom 17 and atom 24 for 2,3-POA, 2,3-DPA, and 2,3-CZ in toluene. | |
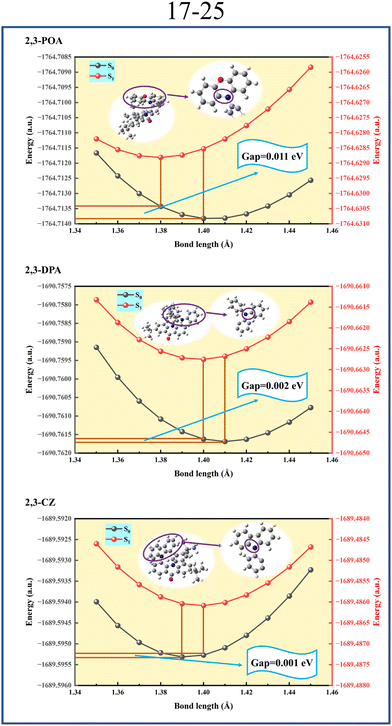 |
| | Fig. 7 Potential energy curve of bond length between atom 17 and atom 25 for 2,3-POA, 2,3-DPA, and 2,3-CZ in toluene. | |
In addition, if there is little or no nuclear displacement between the ground state and the excited state, indicating the same configurations, the 0–0 transition dominates, as depicted in Fig. S9(b) (ESI†). Conversely, if there is a significant nuclear displacement, signifying a large configuration difference, the scenario illustrated in Fig. S9(a) (ESI†) emerges, where the 0–0 transition deviates from the highest peak. Furthermore, the larger the deviation, the greater the configuration difference between the two states. Based on this, we employ FCclasses3 to calculate the vibrational resolved spectra of the three molecules and annotate the distance between the 0–0 transition and the highest peak, as shown in Fig. 8. The figure reveals that the discrepancy between the 0–0 transition and the highest peak is 9.51 nm for 2,3-POA, 8.6 nm for 2,3-DPA, and 3.96 nm for 2,3-CZ. Consequently, we posit that smaller nuclear displacement corresponds to a smaller FWHM, aligning with the conclusion obtained from Scheme 1.
 |
| | Fig. 8 Emission spectra of the sample are shown, with the vibrational levels represented by C1–C7. The spectra are fitted using a Lorentzian function with a HWHM of 0.036 eV. | |
 |
| | Scheme 1 Relationship between the basic physical parameters and FWHM. | |
Subsequently, we focussed on the effect of different donor groups, and the interfragment charge transfer (IFCT) of the electrons between the acceptor and donor was calculated. The obtained data are listed in Table 3. The results showed that 2,3-POA exhibited the strongest electron-donating ability (0.92998), while 2,3-DPA had a weaker electron-donating ability (0.68018), and 2,3-CZ had the weakest electron-donating ability (0.48306).
Table 3 Interfragment charge transfer (IFCT) of electrons between acceptor (A) and donor (D)
|
|
A → D |
D → A |
Net D → A |
| 2,3-POA |
0.00053 |
0.93052 |
0.92998 |
| 2,3-DPA |
0.00393 |
0.68411 |
0.68018 |
| 2,3-CZ |
0.00409 |
0.48714 |
0.48306 |
Thus, based on these analyses, we conclude that a donor group with weaker electron-donating ability is more favorable for achieving a narrower spectral broadening in TADF emission. Moreover, a wise strategy to achieve narrowband emission by constructing a shallow potential energy surface for the ground state is theoretically proved and proposed.
4.2. Excited state dynamics of the TADF molecules
To investigate the TADF properties of these three molecules, the geometric and electronic structures of the ground and excited states were fully optimized, and the corresponding energy landscapes are shown in Fig. S7 (ESI†). Results indicate that 2,3-POA had a small energy difference between its S1 and T1 states, measuring 0.06 eV. Similarly, 2,3-DPA has a small energy difference between its S1 and T2 states, measuring 0.01 eV, while 2,3-CZ has a small energy difference between its S1 and T3 states, measuring 0.03 eV. We then conducted vertical excitation energy calculations for 2,3-CZ, as illustrated in Fig. S8 (ESI†). The S1 state exhibits a vertical excitation energy of 3.13 eV, whereas the T1, T2, T3, and T4 states possess energies of 2.68 eV, 2.91 eV, 3.11 eV, and 3.25 eV, respectively. It is evident that the energy of the T3 state is lower than that of the S1 state, while the energy of the T4 state is higher. Therefore, the related SOC constants, intersystem crossing (ISC), and reverse intersystem crossing (RISC) rates were calculated, and the corresponding results are shown in Table 4. The dominant SOC constants of 0.06 cm−1, 0.77 cm−1, and 0.77 cm−1 are determined for 2,3-POA, 2,3-DPA, and 2,3-CZ, respectively. Thus, the measured RISC rates are also promising with 2.65 × 105 s−1, 2.94 × 108 s−1, and 5.24 × 106 s−1, respectively. Thus, these findings demonstrate the favorable TADF properties of 2,3-POA, 2,3-DPA, and 2,3-CZ, as evidenced by their small energy differences between the relevant states, significant SOC constants, and efficient RISC rates.
Table 4 Calculated ISC and RISC processes and SOC constants (cm−1) among S1, T1, T2 and T3 for 2,3-POA, 2,3-DPA and 2,3-CZ in toluene
| 2,3-POA |
〈S1|Ĥso|T1〉 |
k
ISC(S1→T1) (s−1) |
k
RISC(T1→S1) (s−1) |
| 0.06 |
1.64 × 106 |
2.65 × 105 |
| 2,3-DPA |
〈S1|Ĥso|T2〉 |
k
ISC(S1→T2) (s−1) |
k
RISC(T2→S1) (s−1) |
| 0.77 |
9.30 × 107 |
2.94 × 108 |
| 2,3-CZ |
〈S1|Ĥso|T3〉 |
k
ISC(S1→T3) (s−1) |
k
RISC(T3→S1) (s−1) |
| 0.77 |
1.60 × 108 |
5.24 × 106 |
Furthermore, to investigate the energy consumption process, the transition dipole moments, oscillator strengths, and radiative and non-radiative decay rates of the three molecules were theoretically calculated, all these results are listed in Table 5. We know that 2,3-POA exhibits the smallest transition dipole moment of 0.87 Debye, while 2,3-DPA possesses a larger value of 2.22 Debye, and 2,3-CZ has the highest transition dipole moment of 2.69 Debye. The oscillator strengths followed a similar pattern, measuring 0.006, 0.047, and 0.077, respectively. Based on these values, we can anticipate the trends in radiative decay rates, which are also confirmed by the calculations. Specifically, 2,3-POA exhibited the lowest radiative rate of 1.10 × 106 s−1 and 2,3-CZ demonstrated the highest rate of 2.62 × 107 s−1. Additionally, 2,3-CZ displayed a relatively lower non-radiative decay rate of 5.72 × 107 s−1. Consequently, we conclude that 2,3-CZ exhibits a higher luminescence efficiency. As such, the analysis of the transition dipole moments, oscillator strengths, and radiative, and non-radiative decay rates revealed distinct characteristics among the three molecules. Specifically, 2,3-POA demonstrates the smallest transition dipole moment and radiative decay rate, while 2,3-CZ exhibits the largest transition dipole moment and relatively lower non-radiative decay rate, indicating its superior luminescence efficiency.
Table 5 Rate constants of radiative and non-radiative from S1 to S0 as well as transition dipole moment (μ) and oscillator strength (f) of S1 for all studied molecules in toluene
|
|
μ (Debye) |
f
|
k
r (s−1) |
k
nr (s−1) |
| 2,3-POA |
0.87 |
0.006 |
1.10 × 106 |
2.58 × 107 |
| 2,3-DPA |
2.22 |
0.047 |
1.30 × 107 |
5.89 × 107 |
| 2,3-CZ |
2.69 |
0.077 |
2.62 × 107 |
5.72 × 107 |
5. Conclusions
In summary, the impact of the donor groups on the FWHM of the vibrational resolved spectra was theoretically studied for the three TADF molecules (2,3-POA, 2,3-DPA, and 2,3-CZ), excited state energy consumption processes were revealed and an efficient strategy to modulate FWHM was proposed. The results showed that 2,3-POA had the largest FWHM of 96 nm, while 2,3-CZ had the smallest FWHM of 40 nm. By analyzing the electronic structures and transition properties, we found that a large LE proportion in the S1 state is advantageous in reducing the FWHM and that a donor group with weaker electron-donating ability is more favorable for achieving narrowband emission. By analyzing the geometric structures and reorganization energies, we know that small reorganization energies for the S0 state are beneficial for reducing the FWHM. Moreover, bond lengths (atoms 17–24 and 17–25) in the donor unit exhibited significant contributions to the reorganization energies and generated remarkable influence on the FWHM and TADF properties. In addition, excited state energy consumption processes are revealed by analyzing the radiative and non-radiative as well as ISC and RISC rates, and the superior TADF properties of 2,3-CZ were theoretically verified. Thus, a wise strategy to achieve narrowband TADF emission by constructing a shallow potential energy surface for the ground state was theoretically proven and proposed. Overall, these findings provide a theoretical perspective to realize mall FWHM and facilitate the development of efficient TADF emitters with high color purity.
Author contributions
Jiaqiang Zhao: writing – original draft; Huanling Liu: data curation; Jianzhong Fan: supervision; Qingfang Mu: writing – review and editing.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 62005199, 12204355, and 12274266) and the Natural Science Foundation of Shandong Province (grant no. ZR2020KF017, ZR2021LLZ011, ZR2020QA072 and ZR2020LLZ001). We thank Professor Yingli Niu for his great help in the usage of MOMAP.
References
- J. Huo, S. Xiao, Y. Wu, M. Li, H. Tong, H. Shi, D. Ma and B. Z. Tang, Molecular engineering of blue diphenylsulfone-based emitter with aggregation-enhanced emission and thermally activated delayed fluorescence characteristics: impairing intermolecular electron-exchange interactions using steric hindrance, Chem. Eng. J., 2023, 452, 1385–8947 CrossRef.
- Y. Shi, H. Ma, Z. Sun, W. Zhao, G. Sun and Q. Peng, Optimal Dihedral Angle in Twisted Donor–Acceptor Organic Emitters for Maximized Thermally Activated Delayed Fluorescence, Angew. Chem., Int. Ed., 2022, 61, e202213463 CrossRef CAS PubMed.
- X.-K. Chen, D. Kim and J.-L. Brédas, Thermally Activated Delayed Fluorescence (TADF) Path toward Efficient Electroluminescence in Purely Organic Materials: Molecular Level Insight, Acc. Chem. Res., 2018, 51(9), 2215–2224 CrossRef CAS PubMed.
- Y. Wada, K. Shizu and H. Kaji, Molecular Vibration Accelerates Charge Transfer Emission in a Highly Twisted Blue Thermally Activated Delayed Fluorescence Material, J. Phys. Chem. A, 2021, 125(21), 4534–4539 CrossRef CAS PubMed.
- Y. Im, M. Kim, Y. J. Cho, J.-A. Seo, K. S. Yook and J. Y. Lee, Molecular Design Strategy of Organic Thermally Activated Delayed Fluorescence Emitters, Chem. Mater., 2017, 29(5), 1946–1963 CrossRef CAS.
-
K. Wang, X.-C. Fan, D.-D. Zhang, Y. Tsuchiya, L. Mei, Y.-Z. Shi, M. Tanaka, Z. Lin, Y.-T. Lee, Y. Xie, Y.-Y. Pan, X. Zhang, W. Liu, G.-L. Dai, J.-X. Chen, B. Wu, J. Zhong, J.-Y. Yuan, C.-J. Zheng, J. Yu, A. K.-Y. Jen, X.-K. Chen, C.-S. Lee, C. Adachi and X.-H. Zhang, Intermolecular pi-pi-packing-induced thermally activated delayed fluorescence: a novel pathway toward luminescence efficiency of nearly 100%, ChemRxiv, 2023, preprint DOI:10.26434/chemrxiv-2023-wxk36-v2.
- F.-H. Yu, X.-F. Song, G.-H. Liu, X. Chang, K. Li, Y. Wang, G. Cui and Y. Chen, Highly Efficient Au(I) Alkynyl Emitters: Thermally Activated Delayed Fluorescence and Solution-Processed OLEDs, Chem. – Eur. J., 2022, 28, e202202439 CrossRef CAS PubMed.
- Y. Xiao, H. Wang, Z. Xie, M. Shen, R. Huang, Y. Miao, G. Liu, T. Yu and W. Huang, NIR TADF emitters and OLEDs: challenges, progress, and perspectives, Chem. Sci., 2022, 13, 8906–8923 RSC.
- L. Xue, B. Cui, S. Xie and S. Yin, Influence of the Length of the Donor–Acceptor Bridge on Thermally Activated Delayed Fluorescence, J. Phys. Chem. Lett., 2019, 10(2), 302–308 CrossRef CAS PubMed.
- S. Lin, Q. Ou, Y. Wang, Q. Peng and Z. Shuai, Aggregation-Enhanced Thermally Activated Delayed Fluorescence Efficiency for Two-Coordinate Carbene–Metal–Amide Complexes: A QM/MM Study, J. Phys. Chem. Lett., 2021, 12(11), 2944–2953 CrossRef CAS PubMed.
- Y.-J. Yu, F.-M. Liu, X.-Y. Meng, L.-Y. Ding, L.-S. Liao and Z.-Q. Jiang, Carbonyl-Containing Thermally Activated Delayed Fluorescence Emitters for Narrow-Band Electroluminescence, Chem. – Eur. J., 2023, 29, e202202628 CrossRef CAS PubMed.
- J. Liu, Y. Geng, D. Li, H. Yao, Z. Huo, Y. Li, K. Zhang, S. Zhu, H. Wei, W. Xu, J. Jiang and B. Yang, Deep Red Emissive Carbonized Polymer Dots with Unprecedented Narrow Full Width at Half Maximum, Adv. Mater., 2020, 32, 1906641 CrossRef CAS PubMed.
- C. Lv, X. Wang, Q. Zhang and Y. Zhang, Narrowband emission: organic thermally-activated
delayed fluorescence materials and underlying mechanisms, Mater. Chem. Front., 2023, 7, 2809–2827 RSC.
- J. Chen, X. Xiao, S. Li, Y. Duan, G. Wang, Y. Liao, Q. Peng, H. Fu, H. Geng and Z. Shuai, A Novel Strategy toward Thermally Activated Delayed Fluorescence from a Locally Excited State, J. Phys. Chem. Lett., 2022, 13(11), 2653–2660 CrossRef CAS PubMed.
- B. C. Garain, S. Das and S. K. Pati, Delineating Conformation Control in the Photophysical Behaviour of a Molecular Donor–Acceptor–Donor Triad, ChemPhysChem, 2021, 22, 2297 CrossRef CAS PubMed.
- Z. Xiong, W. Gong, P. Xu, M. Jiang, X. Cai, Y. Zhu, X. Ping, H. Feng, H. Ma and Z. Qian, Reexamining the heavy-atom-effect: The universal heavy-atom-induced fluorescence enhancement principle for through-space conjugated AIEgens, Chem. Eng. J., 2023, 451(4), 1385–8947 Search PubMed.
- J. Li, M. Zhang, T. Li, D. Guo, T. Tian and H. Zhang, Realization of switching between TADF and HLCT emissions through modulation of the intramolecular charge transfer character, J. Mater. Chem. C, 2022, 10, 13124–13136 RSC.
- H. Tasaki, S. Shikita, I. S. Park and T. Yasuda, Ester-functionalized thermally activated delayed fluorescence materials, J. Mater. Chem. C, 2022, 10, 4574–4578 RSC.
- H. J. Kim and T. Yasuda, Narrowband Emissive Thermally Activated Delayed Fluorescence Materials, Adv. Opt. Mater., 2022, 10, 2201714 CrossRef CAS.
- M. Xie, M. Sun, S. Xue and W. Yang, Recent progress of blue fluorescent organic light-emitting diodes with narrow full width at half maximum, Dyes Pigm., 2023, 208, 0143–7208 Search PubMed.
- H. Wu, Y.-Z. Shi, K. Wang, J. Yu and X.-H. Zhang, Conformational isomeric thermally activated delayed fluorescence (TADF) emitters: mechanism, applications, and perspectives, Phys. Chem. Chem. Phys., 2023, 25, 2729–2741 RSC.
- H. Wu, X.-C. Fan, H. Wang, F. Huang, X. Xiong, Y.-Z. Shi, K. Wang, J. Yu and X.-H. Zhang, Conformational isomerization: A novel mechanism to realize the AIE-TADF behaviors, Aggregate, 2023, 4, e243 CrossRef CAS.
- M. Hasan, A. Shukla, M. Mamada, C. Adachi, S.-C. Lo and E. B. Namdas, Correlating Exciton Dynamics of Thermally Activated Delayed-Fluorescence Emitters to Efficiency Roll-Off in OLEDs, Phys. Rev. Appl., 2022, 18, 054082 CrossRef CAS.
- C. Zhao, F. Zhao, K. Wang, H. Yu, T. Huang, R. Wang, C. Zhang, B. Hu and L. Duan, Stabilization of Blue Emitters with Thermally Activated Delayed Fluorescence by the Steric Effect: A Case Study by means of Magnetic Field Effects, Phys. Rev. Appl., 2020, 14, 034059 CrossRef CAS.
- Y. Zhang, D. Zhang, J. Wei, Z. Liu, Y. Lu and L. Duan, Multi-Resonance Induced Thermally Activated Delayed Fluorophores for Narrowband Green OLEDs, Angew. Chem., Int. Ed., 2019, 58, 16912 CrossRef CAS PubMed.
- J. M. Ha, H. B. Shin, J. F. Joung, W. J. Chung, J.-E. Jeong, S. Kim, S. H. Hur, S.-Y. Bae, J.-Y. Kim, J. Y. Lee, S. Park and H. Y. Woo, Rational Molecular Design of Azaacene-Based Narrowband Green-Emitting Fluorophores: Modulation of Spectral Bandwidth and Vibronic Transitions, ACS Appl. Mater. Interfaces, 2021, 13(22), 26227–26236 CrossRef CAS PubMed.
- X.-C. Fan, K. Wang, Y.-Z. Shi, Y.-C. Cheng, Y.-T. Lee, J. Yu, X.-K. Chen, C. Adachi and X.-H. Zhang, Ultrapure green organic light-emitting diodes based
on highly distorted fused π-conjugated molecular design, Nat. Photonics, 2023, 17, 280–285 CrossRef CAS.
- C. Cao, J.-H. Tan, Z.-L. Zhu, J.-D. Lin, H.-J. Tan, H. Chen, Y. Yuan, M.-K. Tse, W.-C. Chen and C.-S. Lee, Intramolecular Cyclization: A Convenient Strategy to Realize Efficient BT.2020 Blue Multi-Resonance Emitter for Organic Light-Emitting Diodes, Angew. Chem., Int. Ed., 2023, 135, e202215226 CrossRef.
- W. Cai, C. Zhong and D.-Y. Wu, Achieving high color purity in multi-resonance thermally activated delayed fluorescence emitters through a substitution-driven design strategy, Mater. Chem. Front., 2023, 7, 3762–3773 RSC.
- Z. Huang, H. Xie, J. Miao, Y. Wei, Y. Zou, T. Hua, X. Cao and C. Yang, Charge Transfer Excited State Promoted Multiple Resonance Delayed Fluorescence Emitter for High-Performance Narrowband Electroluminescence, J. Am. Chem. Soc., 2023, 145(23), 12550–12560 CrossRef CAS PubMed.
- Y. Gu, X. Sun, M. Wu and K. Wang, Pressure-shortened delayed fluorescence lifetime of solid-state thermally activated delayed fluorescent 4CzIPN: the structure evolution, Phys. Chem. Chem. Phys., 2023, 25, 17264–17268 RSC.
- J. Liu, Y. Zhu, T. Tsuboi, C. Deng, W. Lou, D. Wang, T. Liu and Q. Zhang, Toward a BT.2020 green emitter through a combined multiple resonance effect and multi-lock strategy, Nat. Commun., 2022, 13, 4876 CrossRef CAS PubMed.
- X. Cai, J. Xue, C. Li, B. Liang, A. Ying, Y. Tan, S. Gong and Y. Wang, Achieving 37.1% Green Electroluminescent Efficiency and 0.09 eV Full Width at Half Maximum Based on a Ternary Boron–Oxygen–Nitrogen Embedded Polycyclic Aromatic System, Angew. Chem., Int. Ed., 2022, 61, e202200337 CrossRef CAS PubMed.
- C.-Y. Chan, Y.-T. Lee, M. Mamada, K. Goushi, Y. Tsuchiya, H. Nakanotani and C. Adachi, Carbazole-2-carbonitrile as an acceptor in deep-blue thermally activated delayed fluorescence emitters for narrowing charge-transfer emissions, Chem. Sci., 2022, 13, 7821–7828 RSC.
- I. S. Park, K. Matsuo, N. Aizawa and T. Yasuda, High-Performance Dibenzoheteraborin-Based Thermally Activated Delayed Fluorescence Emitters: Molecular Architectonics for Concurrently Achieving Narrowband Emission and Efficient Triplet–Singlet Spin Conversion, Adv. Funct. Mater., 2018, 28, 1802031 CrossRef.
- X.-F. Luo, F.-L. Li, J.-W. Zou, Q. Zou, J. Su, M.-X. Mao and Y.-X. Zheng, A Series of Fused Carbazole/Carbonyl Based Blue to Yellow-Green Thermally Activated Delayed Fluorescence Materials for Efficient Organic Light-Emitting Diodes, Adv. Opt. Mater., 2021, 9, 2100784 CrossRef CAS.
-
T. Förster, Fluoreszenz Organischer Verbindungen, Vandenhoeck & Ruprecht, Göttingen, 1951 Search PubMed.
-
N. Mataga and T. Kubata, Molecular Interactions and Electronic Spectra, M. Dekker, New York, 1970 Search PubMed.
- R. A. Marcus, Relation between charge transfer absorption and fluorescence spectra and the inverted region, J. Phys. Chem., 1989, 93(8), 3078–3086 CrossRef CAS.
- R. A. Marcus, Nonadiabatic processes involving quantum-like and classical-like coordinates with applications to nonadiabatic electron transfers, J. Phys. Chem., 1984, 81(10), 4494–4500 CrossRef CAS.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules, J. Phys. Chem. A, 2010, 114(30), 7817–7831 CrossRef CAS PubMed.
- Y. Niu, Q. Peng and Z. Shuai, Promoting-mode free formalism for excited state radiationless decay process with Duschinsky rotation effect, Sci. China, Ser. B: Chem., 2008, 51(12), 1153–1158 CrossRef CAS.
- B. Zee, Y. Li, G.-J. A. H. Wetzelaer and P. W. M. Blom, Triplet-Polaron-Annihilation-Induced Degradation of Organic Light-Emitting Diodes Based on Thermally Activated Delayed Fluorescence, Phys. Rev. Appl., 2022, 18(6), 064002 CrossRef.
- Y. Ning, X. Zhao, F. Wu, Y. Wu, J. Chen, F. Wei, H. Wang, X. Chen and Z. Xiong, Charge-Transfer Dynamics in OLEDs with Coexisting Electroplex and Exciton States, Phys. Rev. Appl., 2023, 19(6), 064055 CrossRef CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Relating the open-circuit voltage to interface molecular properties of donor:acceptor bulk heterojunction solar cells, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(12), 125204 CrossRef.
- K. Bergmann, R. Hojo and Z. M. Hudson, Uncovering the Mechanism of Thermally Activated Delayed Fluorescence in Coplanar Emitters Using Potential Energy Surface Analysis, J. Phys. Chem. Lett., 2023, 14(2), 310–317 CrossRef CAS PubMed.
- M. Kurt, H. Yurtseven, A. Kurt and S. Aksoy, Calculation of the infrared frequency and the damping constant (full width at half maximum) for metal organic frameworks, Chin. Phys. B, 2019, 28(6), 066401 CrossRef CAS.
- Y. Zhang, D. Zhang, T. Huang, A. J. Gillett, Y. Liu, D. Hu, L. Cui, Z. Bin, G. Li, J. Wei and L. Duan, Multi-Resonance Deep-Red Emitters with Shallow Potential-Energy Surfaces to Surpass Energy-Gap Law, Angew. Chem., Int. Ed., 2021, 60(37), 20498–20503 CrossRef CAS PubMed.
- K. Zhang, F. Yang, Y. Zhang, Y. Ma, J. Fan, J. Fan, C.-K. Wang and L. Lin, Highly Efficient Near-Infrared Thermally Activated Delayed Fluorescence Molecules via Acceptor Tuning: Theoretical Molecular Design and Experimental Verification, J. Phys. Chem. Lett., 2021, 12(7), 1893–1903 CrossRef CAS PubMed.
- S. Kundu, P. P. Roy, G. R. Fleming and N. Makri, Franck–Condon and Herzberg–Teller Signatures in Molecular Absorption and Emission Spectra, J. Phys. Chem. B, 2022, 126(15), 2899–2911 CrossRef CAS PubMed.
- F. F. Kong, X. J. Tian, Y. Zhang, Y. J. Yu, S. H. Jing, Y. Zhang, G. J. Tian, Y. Luo, J. L. Yang, Z. C. Dong and J. G. Hou, Probing intramolecular vibronic coupling through vibronic-state imaging, Nat. Commun., 2021, 12(1), 1280 CrossRef CAS PubMed.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg-Teller effect: The Qx band of porphyrin as a case study, J. Chem. Phys., 2008, 128(22), 24311 CrossRef PubMed.
- W. Cai, H. Zhang, X. Yan, A. Zhao, R. He, M. Li, Q. Meng and W. Shen, What accounts for the color purity of tetradentate Pt complexes? A computational analysis, Phys. Chem. Chem. Phys., 2019, 21(15), 8073–8080 RSC.
- X. K. Chen, V. Coropceanu and J. L. Brédas, Assessing the nature of the charge-transfer electronic states in organic solar cells, Nat. Commun., 2018, 9(1), 5295 CrossRef CAS PubMed.
- J. P. Menzel, H. J. de Groot and F. Buda, Photoinduced electron transfer in donor-acceptor complexes: Isotope effect and dynamic symmetry breaking, J. Phys. Chem. Lett., 2019, 10(21), 6504–6511 CrossRef CAS PubMed.
- Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Structural changes accompanying intramolecular electron transfer: focus on twisted intramolecular charge-transfer states and structures, Chem. Rev., 2003, 103, 3899–4032 CrossRef PubMed.
- K. Zhang, X. Zhang, J. Fan, Y. Song, J. Fan, C.-K. Wang and L. Lin, Novel Deep Red Thermally Activated Delayed Fluorescence Molecule with Aggregation-Induced Emission Enhancement: Theoretical Design and Experimental Validation, J. Phys. Chem. Lett., 2022, 13, 4711–4720 CrossRef CAS PubMed.
- S. A. Ahmad, J. Eng and T. J. Penfold, Rapid predictions of the colour purity of luminescent
organic molecules, J. Mater. Chem. C, 2022, 10(12), 4785–4794 RSC.
- Y. Song, B. Li, S. Liu, M. Qin, Y. Gao, K. Zhang, L. Lin, C.-K. Wang and J. Fan, Structure–property relationship study of blue thermally activated delayed fluorescence molecules with different donor and position substitutions: theoretical perspective and molecular design, J. Mater. Chem. C, 2022, 10(12), 4723–4736 RSC.
- H. Zou, Y. Ma, H. Liu, Q. Mu, K. Zhang, Y. Song, L. Lin, C.-K. Wang and J. Fan, A QM/MM study on through space charge transfer-based thermally activated delayed fluorescence molecules in the solid state, J. Mater. Chem. C, 2022, 10(2), 517–531 RSC.
- H. Liu, K. Zhang, H. Zou, Q. Mu, X. Wang, Y. Song, L. Lin, C.-K. Wang and J. Fan, A theoretical perspective of the relationship between the structures and luminescence properties of red thermally activated delayed fluorescence molecules, Phys. Chem. Chem. Phys., 2022, 24(8), 17140–17154 RSC.
- H. Zou, H. Liu, Q. Mu, K. Zhang, Y. Song, L. Lin, Y. Xu, C.-K. Wang and J. Fan, Theoretical perspective for substitution effect on luminescent properties of through space charge transfer-based thermally activated delayed fluorescence molecules, Spectrochim. Acta, Part A, 2023, 285, 121899 CrossRef CAS PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. WilliamsYoung, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, 2016 Search PubMed.
- Y. Niu, W. Li, Q. Peng, H. Geng, Y. Yi, L. Wang, G. Nan, D. Wang and Z. Shuai, MOlecular MAterials Property Prediction Package (MOMAP) 1.0: a software package for predicting the luminescent properties and mobility of organic functional materials, Mol. Phys., 2018, 116, 1078–1090 CrossRef CAS.
-
A. Dalton, Molecular electronic structure program, https://daltonprogram.org Search PubMed.
- J. R. Reimers, A Practical Method for the use of Curvilinear Coordinates in Calculations of Normal-Mode-Projected Displacements and Duschinsky Rotation Matrices for Large Molecules, J. Chem. Phys., 2001, 115(20), 9103–9109 CrossRef CAS.
- Q. Peng, H. Ma and Z. Shuai, Theory of Long-Lived Room-Temperature Phosphorescence in Organic Aggregates, Acc. Chem. Res., 2021, 54(4), 940–949 CrossRef CAS PubMed.
- H. Ma, Q. Peng, Z. An, W. Huang and Z. Shuai, Efficient and Long-Lived Room-Temperature Organic Phosphorescence: Theoretical Descriptors for Molecular Designs, J. Am. Chem. Soc., 2019, 141(2), 1010–1015 CrossRef CAS PubMed.
- Z. W. Li, L. Y. Peng, X. F. Song, W. K. Chen, Y. J. Gao, W. H. Fang and G. Cui, Room-Temperature Phosphorescence and Thermally Activated Delayed Fluorescence in the Pd Complex: Mechanism and Dual Upconversion Channels, J. Phys. Chem. Lett., 2021, 12(25), 5944–5950 CrossRef CAS PubMed.
- Q. Mu, K. Zhang, H. Zou, H. Liu, Y. Song, C.-K. Wang, L. Lin and J. Fan, Theoretical insights into room temperature phosphorescence emission with anti-Kasha behavior in aggregate, Dyes Pigm., 2022, 205, 110560 CrossRef CAS.
- J. R. Reimers, A Practical Method for the Use of Curvilinear Coordinates in Calculations of Normal-Mode-Projected Displacements and Duschinsky Rotation Matrices for Large Molecules, J. Chem. Phys., 2001, 115, 9103–9109 CrossRef CAS.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *b and
Qingfang
Mu
*b
*b and
Qingfang
Mu
*b

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I/I0 = ενML, is defined as the ratio of the incident light intensity (I0) to the transmitted light intensity (I) multiplied by the molar concentration (M) of the solute and the path length (L).
I/I0 = ενML, is defined as the ratio of the incident light intensity (I0) to the transmitted light intensity (I) multiplied by the molar concentration (M) of the solute and the path length (L).



 denote Avogadro's number divided by 103, μrp represent the transition dipole matrix element for the r → p transition. n, c, and Qr denote the refractive index of the medium, the velocity of light, and the partition function of the system when the solute is in the r electronic state.
denote Avogadro's number divided by 103, μrp represent the transition dipole matrix element for the r → p transition. n, c, and Qr denote the refractive index of the medium, the velocity of light, and the partition function of the system when the solute is in the r electronic state.



 is the reorganization energy on the electronic r-state. Combining eqn (7) and (8) yields:
is the reorganization energy on the electronic r-state. Combining eqn (7) and (8) yields:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)]1/2
2)]1/2
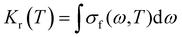


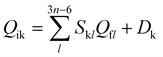 . Here, S is the Duschinsky rotation matrix representing the mixing of normal modes in the initial and final states and the vector Dk is the displacement along the normal mode k. All these parameters and reorganization energies can be projected onto the internal coordinates using Reimers’ algorithm.71,72
. Here, S is the Duschinsky rotation matrix representing the mixing of normal modes in the initial and final states and the vector Dk is the displacement along the normal mode k. All these parameters and reorganization energies can be projected onto the internal coordinates using Reimers’ algorithm.71,72







