Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical structural and spectroscopic characterization of peroxyacetic acid (CH3–CO–OOH): study of the far infrared region†
Sinda
Brahem
abc,
Dorsaf
Missaoui
abc,
Ounaies
Yazidi
a,
Faouzi
Najar
 a and
María Luisa
Senent
a and
María Luisa
Senent
 *bc
*bc
aLaboratoire de Spectroscopie Atomique Moléculaire et Applications, Faculté des Sciences de Tunis, Université de Tunis El Manar, 2092, Tunisia
bDepartamento de Química y Física Teóricas, Instituto de Estructura de la Materia, IEM-CSIC, Serrano 121, Madrid 28006, Spain
cUnidad Asociada GIFMAN, CSIC-UHU, Spain. E-mail: ml.senent@csic.es
First published on 27th March 2024
Abstract
Peroxyacetic acid, a non-rigid oxygenated organic molecule which acts in the atmosphere as a reservoir of HOX and ROX radicals, is studied using highly correlated ab initio methods with the aim of its spectroscopic characterization in the gas phase. The study focuses on the far infrared region providing reliable rovibrational parameters such as energy levels and splittings. The molecule presents three conformers that inter-convert by internal rotation, drawing a potential energy surface of 12 minima. One of them shows prominent stability due to the formation of one weak intramolecular bond between the hydrogen atom of the hydroperoxy group and the oxygen atom of the carbonyl group. For the three minimum energy structures, rotational constants and centrifugal distortion constants are provided. It may be expected that the most stable conformer is the only one contributing to the spectral features in further measurements at low temperature. In this structure, the methyl torsional barrier has been found to be very low, V3 = 88.6 cm−1 producing a splitting of 2.262 cm−1 for the ground vibrational state. The study confirms that the ν20 torsional mode interacts strongly with the other two torsional modes ν19 and ν21, but slightly with the remaining vibrations. Then, a variational procedure in three dimensions allows the exploration of the low-frequency modes. The methyl torsional fundamental ν21 was found to be 49.1 cm−1 (Ai) and 33.4 cm−1 (E). The fundamentals of ν20 (C–O bond torsion) and ν19 (OH torsion) have been computed to be 216.7 cm−1 (A2) and 218.5 cm−1 (E) and 393.6 cm−1 (A2) and 394.1 cm−1. Since non-rigidity can have effects on the reactivity due to the conformer interconversion, and transitions involving low-lying levels can be observed with many spectroscopic techniques, this work can help kinetic studies and assignments of further spectroscopic studies needed for the detection in the gas phase of trace molecules.
1. Introduction
Organic peroxides represent oxygenated organic molecules (OOMs) that can act as reservoirs of the HOX and ROX radicals in the atmosphere.1,2 They are receiving much research attention due to their potential role in enhancing tropospheric oxidation capacity1–3 as well as early phases of secondary aerosol formation.4 Organic peroxides generally form in the atmosphere via OH mediated oxidation of saturated and unsaturated hydrocarbons.5,6 They have a significant impact on air quality and human health.7 The toxic effects of oxygen species in atmospheric aerosols on human health have been emphasized,8 motivating their detection in urban areas.9–11Gas-phase OOMs can contribute substantially to the growth of newly formed particles.9 Recent reviews attend to the relevance of OOM peroxides in the chemistry of the atmosphere.12,13 OOMs are emitted into the atmosphere from natural and anthropogenic sources, and they are formed in the atmosphere as oxidation products of all hydrocarbons present in the atmosphere.12 Low-volatility multifunctional oxygenated organic compounds condense onto existing atmospheric particles and hence increase the organic fraction content of secondary organic aerosols.12 Noziere et al.13 reviewed the different techniques available today to characterize atmospheric organic compounds. They analyzed the efficiency of rovibrational spectroscopy for the trace molecule identification.
The subgroup of peroxycarboxylic acids (RCO–OOH) is considered as important intermediates in the oxidation of volatile organic compounds.14 The simple and abundant one, peroxyacetic acid (peracetic acid, PAA, CH3CO–OOH), is a colorless liquid with melting and boiling points of 0.1 °C and 105 °C, respectively. It has been widely detected in the terrestrial atmosphere.15 It has been shown that the local photochemical production was the major source of PAA, and its concentration increased with increasing temperature, solar radiation and ozone but decreased with increasing NOx (NO and NO2), CO, SO2, and relative humidity.15 PAA is considered to be the third most common urban peroxide after hydrogen peroxide and methyl hydroperoxide. It contributes to the oxidation of SO2 and HSO3 in the atmosphere.16 Its dissociation has been studied by UV laser photolysis in the gas phase producing CH3 + CO2 + OH.17
PAA concentrations have been detected in plumes from biomass burning.18 PAA can be formed in the atmosphere through the reactions of H2O or HO2 with free radicals such as CH3CO–OO, or through the reaction of O3 with acetic acid.19 The photolysis of biacetyl in aqueous aerosols, fogs, and clouds produces PAA.20 PAA competes with the formation of peroxyacyl nitrate (PAN = CH3CO–OONO2), a peroxyacetic acid-nitronium ion complex playing a vital role in the global distribution of tropospheric ozone.21
The aim of this work is to perform spectroscopic characterization of PAA for which extremely limited spectroscopic experimental and theoretical information are available. The first spectroscopic studies occurred in the fifties. In 1952, Giguère et al.22 published the infrared spectrum of performic and peracetic acids focusing on the effect of the intramolecular hydrogen bond on the band positions and stabilities and comparing the spectra with those of formic acid and acetic acid. They provide band center positions in the vapor phase in the region between 3570 cm−1 and 648 cm−1. Based on their observations, they concluded that a stable five-membered ring conformer, resulting from the formation of an intramolecular hydrogen bond between the carbonyl oxygen and the hydrogen of the hydroxyl group, represents the predominant structure.
Later, Cugley et al.23 recorded the infrared spectrum in Ar and N2 matrices of PAA and three deuterated varieties, CH3CO–OOD, CD3CO–OOD and CD3CO–OOD, at 4 K. The observed vibrational bands were assigned to the most stable PAA geometry stabilized by the intramolecular H-bond, previously reported by Giguere et al.22 They provide force constants and thermodynamic functions. In another publication, Cugley et al.24 analyzed the microwave spectrum of CH3CO–OOH and CH3CO–OOD in the gas phase, in the range from 12 to 40 GHz. They estimated the methyl torsional barrier to be very low (V3 = 76.70 (45) cm−1). From the Stark effect, the dipole moment components were determined to be μa = 2.294(3) D, μb = 0.650(4) D and μ = 2.384(5) D.23 The three rotational constants were estimated to be A0 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.95 MHz, B0 = 4275.06 MHz and C0 = 3122.64 MHz.23
814.95 MHz, B0 = 4275.06 MHz and C0 = 3122.64 MHz.23
The effect of the weak intramolecular hydrogen bond on the OH stretching transitions in peroxyformic acid and peroxyacetic acid was studied by Hazra et Sinha.25,26 The vapor phase absorption spectra and the integrated band intensities of the OH stretching fundamental, as well as first and second overtones (2νOH and 3νOH) of peroxyacetic acid (PAA) were measured using a combination of FT-IR and photoacoustic spectroscopy.26 The authors compared theoretical calculations at the MP2 and CCSD levels of theory with the observations and found strong disagreements between the measured and calculated integrated absorption cross sections of the 1νOH, 2νOH and 3νOH.26
Peroxyacetic acid has been the object of various theoretical works.27–29 The proton affinity has been computed using ab initio methods by Miller and Francisco.30 These authors, with the goal of better understanding the proton affinity of PAN,31 provide a systematic investigation of the structure, harmonic force field, and proton affinity31 using Density Functional Theory and MP2 and QCISD ab initio methods.
The present paper aims at the spectroscopic characterization of PAA with a special mention to the Far Infrared region. We search for very accurate molecular properties that can help the interpretation of further investigations. The calculations of the equilibrium structures and potential energy surface are performed using highly correlated ab initio methods and procedures previously tested in studies of alike molecules.32–35 Given the lack of previous research, most of our findings are predictions that cannot be compared with the existing experimental data. In these cases, the goal is to obtain new spectroscopic data that might help the interpretation of far-infrared measurements and the assignment of rotational and rovibrational spectra. For the far infrared region, we employed a variational procedure in three dimensions whose independent variables are the internal rotations responsible for the inter-conversion of the minima. This allows very low energy levels to be obtained and their torsional subcomponents that can be involved in transitions observable using different spectroscopic techniques in different spectral regions.
Identification of trace molecules in the atmosphere through rovibrational spectroscopy requires a previous laboratory characterization. In the case of non-rigid species, assignments of the measurements are complex. A previous theoretical study describing the FIR region can help further experimental work. The conformational analysis can help kinetic studies.
2. Results and discussion
2.1. Electronic structure calculations
The structural parameters related to the minimum-energy structures of PAA were computed using explicitly correlated coupled cluster theory with single and double substitutions augmented by a perturbative treatment of triple excitations (CCSD(T)-F12b)36,37 as it is implemented in Molpro38 version 2022 and selecting the default options. A correlation consistent basis set, cc-pCVTZ-F12 (denoted by CVTZ-F12 in this paper), optimized for accurately describing core–core and core-valence correlation effects with explicitly correlated F12 method, was employed.39Two different pathways were used to obtain spectroscopic parameters: (a) vibrational second-order perturbation theory (VPT2)40 implemented in the Gaussian version C.0141 which starting point are anharmonic force fields computed using second-order Möller–Plesset theory (MP2)42 and the aug-cc-pVTZ basis set (denoted by AVTZ in this paper);43 (b) a variational procedure of reduced dimensionality designed for the study of the far infrared (FIR) spectra of non-rigid molecules.44–46 In this case, the starting point is a three-dimensional potential energy surface computed with CCSD(T)-F12b/CVTZ-F12.
2.2. The structure of peroxyacetic acid
The PAA molecule is a non-rigid molecule where three internal rotations, the methyl group torsion (θ), the torsion of the C–O single bond (α), and the hydroxyl group torsion (β) interconvert the equilibrium geometries. Fig. 1 can help to understand the torsional coordinates and the labelling of the atoms. The three torsional coordinates can be defined as a linear combination of curvilinear internal coordinates: | (1) |
Table 1 summarizes the distinctive properties of the three PAA conformers: the CCSD(T)-F12b/AVTZ-F12 structural parameters and relative energies E, the equilibrium rotational constants, and the MP2/AVTZ components of the dipole moment with respect to the primary axis system which are compared with the experimental values of Cugley et al.24 The E energies were vibrationally corrected to obtain EZPVE (see Fig. 2) considering the anharmonic zero-point vibrational energies (ZPVE), which were computed with MP2/AVTZ. Energies and structural parameters are provided in the ESI† (see Table S1).
| Cc | Ct | Ttg | Cc | Ct | Ttg | ||
|---|---|---|---|---|---|---|---|
| Equilibrium structural parameters (distances, in Å, angles, in degrees) | |||||||
| C2C1 | 1.4940 | 1.5023 | 1.4955 | H7C2C1 | 111.4 | 108.2 | 107.6 |
| O3C1 | 1.3465 | 1.3632 | 1.3734 | H8C2C1 | 108.4 | 108.2 | 110.4 |
| O4C1 | 1.2061 | 1.1921 | 1.1952 | H9C2C1 | 108.4 | 112.1 | 110.3 |
| O5O3 | 1.4347 | 1.4460 | 1.4506 | O4C1C2O3 | 180.0 | 180.0 | 179.2 |
| H6O5 | 0.9806 | 0.9645 | 0.9639 | O5O3C1C2 | 180.0 | 180.0 | −0.30 |
| H7C2 | 1.0850 | 1.0871 | 1.0840 | H6O5O3C1 | −0.0 | 180.0 | 221.3 |
| H8C2 | 1.0872 | 1.0871 | 1.0872 | H7C2C1O3 | −0.0 | 121.4 | 182.4 |
| H9C2 | 1.0872 | 1.0852 | 1.0871 | H8C2C1H7 | 121.3 | 121.3 | 120.9 |
| O3C1C2 | 111.1 | 108.6 | 117.7 | H9C2C1H7 | −121.3 | −121.3 | −120.6 |
| O4C1C2 | 127.0 | 126.9 | 126.5 | ||||
| O5O3C1 | 110.4 | 108.7 | 111.0 | H6–O4 | 1.8511 | ||
| H6O5O3 | 100.0 | 97.6 | 98.6 | ||||
The Cc conformer (θ = 0°, α = 180°, β = 0°) exhibits notable stability due to the presence of an intramolecular hydrogen bond of 1.8511 Å between the oxygen atom of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the hydrogen atom of OH. As was previously observed,25,26,32 weak hydrogen bonds perturb the structural and spectroscopic properties of organic molecules. The excitation of the torsional modes causes the weak bond breaking, leading to the conformers Ct (θ = 0°, α = 180°, β = 180°) and Ttg (θ = −172.6°, α = −0.3°, β = −138.7°), which lie 1627.7 cm−1 and 2015.9 cm−1 above Cc, respectively. This explains why previous experimental studies focused on Cc neglecting the secondary minima. Additionally, the Ttg conformer is less stable than Ct due to non-bonding repulsions between the hydrogen atoms of OH and methyl group.
O and the hydrogen atom of OH. As was previously observed,25,26,32 weak hydrogen bonds perturb the structural and spectroscopic properties of organic molecules. The excitation of the torsional modes causes the weak bond breaking, leading to the conformers Ct (θ = 0°, α = 180°, β = 180°) and Ttg (θ = −172.6°, α = −0.3°, β = −138.7°), which lie 1627.7 cm−1 and 2015.9 cm−1 above Cc, respectively. This explains why previous experimental studies focused on Cc neglecting the secondary minima. Additionally, the Ttg conformer is less stable than Ct due to non-bonding repulsions between the hydrogen atoms of OH and methyl group.
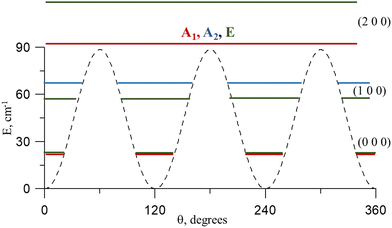
Torsional barriers are shown in Table 1. Fig. 3 shows the energy variation with the methyl torsional coordinate θ. The curves were computed by fixing α and β to their respective values in the three conformers, for which the V3 barriers are estimated to be 88.6 cm−1 (Cc), 33.4 cm−1 (Ct), and 624.2 cm−1 (Ttg). For the most stable conformer Cc, our computed parameters are in good agreement with the experimental data of Cugley et al.24 (V3 = 76.70(45) cm−1) derived from the assignment of the microwave spectrum. This value is half of what was calculated for the most stable conformer of acetic acid (V3 = 169.8 cm−1),46 which is also quite low. A quite complicated distribution of the low methyl torsional energy levels and their splittings can be expected.
 | ||
| Fig. 3 V 3 methyl torsional barriers computed using CCSD(T)-F12b/CVTZ-F12. Energies are given relative to the Cc global minimum. | ||
As was first computed for methyl isocyanate (V3 = 16.2 cm−1)47 and trans-methyl formate (V3 = 26 cm−1),48 the V3 barrier of the Ct conformer is so low that the methyl group torsion can be understood as a free internal rotation. In the Ttg conformer, the interaction between the methyl and OH groups increase the parameters to a magnitude similar to that of several sulfur analogs of methyl hydroperoxide, showing V3 barriers of 685.52 cm−1 (CH3–O–S–H), 696.6 cm−1 (CH3–S–O–H), and 584.3 cm−1 (CH3S–S–H).49
The two profiles in Fig. 4 represent the variation in energy with respect to the α coordinate (C–O bond torsion). These were computed by fixing the θ and β angles at θ = 0° and β = 0° or 180°. The profile corresponding to β = 180° represents a minimum energy pathway for the Ct → Ttg interconversion, which is restricted by a barrier of VCO (β = 180°) estimated to be 4875 cm−1. The barrier VCO (β = 0°) has been estimated to be 8707 cm−1.
 | ||
| Fig. 4 One-dimensional potential energy surfaces V(α, β = 0°, θ = 0°) and V(α, β = 180°, θ = 0°). Energies are given relative to the Cc global minimum. | ||
The profiles in Fig. 5 represent the energy variation with the β coordinate (OH torsion), while the remaining coordinates were frozen; in A, θ = 0° and α = 180° correspond to the values of these angles in the Cc and Ct conformers, and in B, θ = 180° and α = 0° correspond to the Ttg region of the ground electronic state potential energy surface. While the interconversion of Cc → Ct is restricted by a relatively high value (∼1896 cm−1), the reverse process Ct → Cc shows a quite low value (∼150 cm−1) that justifies why Ct is not observed. Some of these values allow the comparison with acetic acid, where the cis geometry is 1883 cm−1 over the favor trans-conformation and the T → C process is restricted by a barrier of 4432 cm−1.46
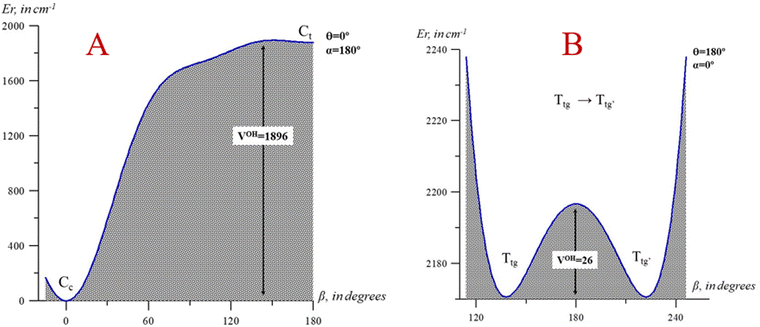 | ||
| Fig. 5 One-dimensional cuts of the 3D-PES depending on the β coordinate (OH torsion). (A) V(β, θ = 0°, α = 180°); (B) V(β, θ = 180°, α = 0°). Energies are given relative to the Cc global minimum. | ||
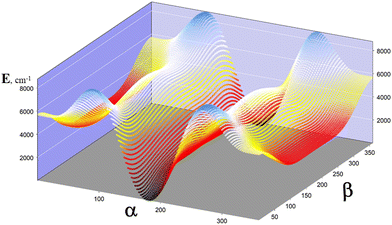
As evident, the two profiles of Fig. 5, A and B, are extremely different. In B, β varies from 120° to 240° to emphasize the very low barrier of the Ttg → Ttg′ process, although V(β) reaches 4739 cm−1 at β = 0°. This occurs because the C–O and OH torsional modes are strongly coupled. This study reveals that the three torsions interact and are not separable. Additionally, the methyl group torsion and the C–O torsion are not negligible. Fig. 6 represents a two-dimensional potential energy surface that depends on α and β. The anisotropy of this figure highlights the relevance of the torsional coupling between these two torsional motions.
2.3. VPT2 vibrational analysis
For the 21 vibrational modes, the fundamental frequencies were obtained from the vibrational energies computed using the equation: | (2) |
In Table 2, they are summarized and compared with experimental data in the case of Cc for which these data are available. Unfortunately, the experimental data of Table 2 were measured in Ar matrices.23 It must be pointed out that the VPT2 theory predicts significant shifts due to Fermi resonances in the transitions emphasized in bold. To perform the test of Fermi resonances, we have built and diagonalized a large matrix composed of all singly excited states, doubly excited states (within a single vibrational mode) and 1 + 1 combinations, together with all off-diagonal Fermi coupling matrix elements by diagonalizing a matrix which has been built with the energy levels corresponding to excitations of one or two vibrational modes (diagonal terms) and the cubic force field (out-diagonal terms).
| Mode | Assign.b | Cc (Cs) | Ct (Cs) | Ttg(C1) | |||
|---|---|---|---|---|---|---|---|
| Calc. | Calc.′ | Exp.c | Calc. | Calc. | |||
| a Emphasized in black, the frequencies for which displacements by Fermi resonances can be relevant. b st = stretching; b = bending; w = wagging; tor = torsion. c Measured in the Ar matrix;23 the experimental frequencies are those selected by the authors used in the force constant calculation. d Harmonic fundamentals, ω. | |||||||
| A′ | A | ||||||
| 1 | OH-st | 3284 | 3317 | 3282 | 3597 | 3596 | |
| 2 | CH3-st | 3074 | 3033 | 3025 | 3070 | 3079 | |
| 3005 | |||||||
| 2995 | |||||||
| 3 | CH3-st | 2992 | 2962 | 2981 | 2991 | ||
| 4 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-st O-st |
1763 | 1769 | 1767 | 1809 | 1797 | |
| 5 | CH3-b | 1459 | 1460 | 1439 | 1456 | 1445 | |
| 6 | HOO-b | 1443 | 1447 | 1364 | 1374 | ||
| 7 | CH3-b | 1371 | 1371 | 1369 | 1363 | 1351 | |
| 8 | C–O-st | 1235 | 1242 | 1234.3 | 1184 | 1204 | |
| 9 | HCC-b | 1011 | 1009 | 940 | 996 | 994 | |
| 10 | C–O-st | 965 | 955 | 865 | 928 | 927 | |
| 11 | HCC-b | 868 | 874 | 827 | 785 | ||
| 12 | C–C-st | 647 | 644 | 618.8 | 625 | 556 | |
| 13 | OCO-b | 430 | 432 | 449 | 415 | 487 | |
| 14 | OOC-b | 318 | 319 | 318.5 | 296 | 325 | |
| A′′ | |||||||
| 15 | CH3-st | 3057 | 3018 | 3055 | A | 3048 | |
| 16 | CH3-b | 1448 | 1438 | 1452 | 1436 | ||
| 17 | CH3-b | 1040 | 1037 | 1040 | 1038 | 1042 | |
| 18 | CH3-b | 617 | 615 | 646.5 | 589 | 546 | |
| 19 | OH-tor | 428 | 419 | 422 | 92d | 26 | |
| 20 | C–O tor | 220 | 213 | 195 | 154 | ||
| 21 | CH3-tor | 52 | 61 | 63 | 175 | ||
The presence of an intermolecular hydrogen bond in the Cc conformer is indicated by the OH stretching fundamental, which band center was computed at 3285 cm−1 (MP2) and 3317 cm−1 (CCSD(T)-F12 + MP2) and observed at 3282 cm−1,23 below the corresponding bands of Ct (3597 cm−1) and the one for Ttg (3596 cm−1).
The band center of 2νOH and 3νOH bands of Cc peroxyacetic acid have been measured using a combination of FT-IR and photoacoustic spectroscopy26 at 6315 cm−1 and 9037 cm−1, respectively26 whereas our computations place them at 2νOH = 6346 cm−1 and 3νOH = 9185 cm−1 (MP2). Furthermore, VPT2 place the 2νOH overtone at 8031 cm−1 and 7030 cm−1, in Ct and Ttg, respectively.
The weak intramolecular bond has an important effect on the OH-torsional fundamental, ν19, computed to be 428 cm−1 (MP2) and to be 419 cm−1 (CCSD(T9-F12 + MP2) in Cc and to be ∼92 and 26 cm−1 in Ct and Ttg, respectively. The mode ν19 was observed by Cugley et al.23 at 422 cm−1 in the Ar matrix.
Unfortunately, the comparison between computation and the available experimental data for the torsional modes23 is difficult, mainly because the corresponding band observed in Ar matrices is expected to be displaced to higher frequencies with respect to the measurements in the gas phase which are unavailable. For this reason, to obtain reliable results, we opted for a variational procedure instead of the VPT2 theory, which is developed specifically for semi-rigid species.
Table 2 displays the harmonic fundamental ω19 = 92 cm−1 instead of ν19 for which the MP2/AVTZ value is unrealistic due to the shape of the potential energy surface in the region of Ct that favours the Ct → Cc interconversion (see the A-profile of Fig. 5) and introduces errors in the computations of fourth-order numerical derivatives and the anharmonic force field.
2.4. Ground vibrational state: rotational and centrifugal distortion constants
The vibrational ground state rotational constants reported in Table 3 were calculated from the CCSD(T)-F12b equilibrium rotational constants using the following equation:| B0 = Be(CCSD(T)-F12b/CVTZ-F12) + ΔBvib(MP2)/AVTZ | (3) |
| Cc | Ct | Ttg | ||
|---|---|---|---|---|
| Calc. | Exp23 | Calc. | Calc. | |
| In MHZ | ||||
| A 0 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821.92 821.92 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.95 814.95 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535.79 535.79 |
9263.06 |
| B 0 | 4276.17 | 4275.06 | 4173.37 | 4529.61 |
| C 0 | 3125.52 | 3122.64 | 3051.14 | 3106.31 |
| In KHz | ||||
| Δ J | 760.959 | 800.013 | 870.364 | |
| Δ K | 673.708 | 170.200 | 200.167 | |
| Δ JK | 391.100 | 892.416 | 463.298 | |
| δ J | 206.666 | 214.054 | 255.165 | |
| δ K | −947.367 | 656.527 | 304.396 | |
| In Hz | ||||
| ϕ J | 0.4883 | 0.6246 | −0.1239 | |
| ϕ K | −0.1353 | −0.1830 | 0.2724 | |
| ϕ JK | −0.8139 | −0.7126 | 0.2170 | |
| ϕ KJ | 0.1174 | 0.9239 | −0.1364 | |
| ϕ J | 0.4892 | 0.5053 | 0.2051 | |
| ϕ K | −0.4072 | −0.3733 | 0.2865 | |
| ϕ JK | −0.5334 | −0.8744 | 0.2046 | |
To our knowledge, experimental rotational constants are only available for the preferred conformer (Cc) whose stability is prominent. For this structure, the agreement between the theoretical and experimental rotational constants is excellent. The computed parameters A0 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821.92 MHz, B0 = 4276.17 MHz and C0 = 3125.52 MHz compare well with those of Cugley et al.,24A0 = 10
821.92 MHz, B0 = 4276.17 MHz and C0 = 3125.52 MHz compare well with those of Cugley et al.,24A0 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.95 MHz, B0 = 4275.06 MHz, C0 = 3122.64 MHz), derived from microwave spectroscopy. Dissimilarities ΔB0 = |BExp − BCalc| are very small (ΔA0 ∼ 7 MHz, ΔB0 ∼ 1 MHz and ΔC0 ∼ 3 MHz). Divergences coincide with previous studies of other molecules such as methyl glyoxal or methyl vinyl ketone, performed at the same level of theory.34
814.95 MHz, B0 = 4275.06 MHz, C0 = 3122.64 MHz), derived from microwave spectroscopy. Dissimilarities ΔB0 = |BExp − BCalc| are very small (ΔA0 ∼ 7 MHz, ΔB0 ∼ 1 MHz and ΔC0 ∼ 3 MHz). Divergences coincide with previous studies of other molecules such as methyl glyoxal or methyl vinyl ketone, performed at the same level of theory.34
The MP2/AVTZ force field was used to compute the quartic and sextic centrifugal distortion constants shown in Table 3. They are parameters of the Watson asymmetrically reduced Hamiltonian (IIIr representation).50
2.5. The Far Infrared region
Searching for an accurate description of the Far Infrared region, the low-lying vibrational energy levels that correspond to the three internal rotations were computed by solving a three-dimensional Hamiltonian which obeys the formula:44–46 | (4) |
Here, qi, qj = θ, α, β. This Hamiltonian was defined by considering the predictions of the test of resonances described in previous sections which confirm the separability of the torsional modes with respect to the remaining vibrations. In eqn (4), Bqiqj and Veff represent the kinetic energy parameters44 and the vibrationally corrected effective potential defined as the sum of three contributions:
| Veff(θ,α,β) = V(θ,α,β) + V′(θ,α,β) + VZPVE(θ,α,β) | (5) |
Here, V(θ,α,β) represents the ab initio three-dimensional potential energy surface, and V′(θ,α,β) and VZPVE(θ,α,β) represent the Podolsky pseudopotential and the zero-point vibrational energy correction, respectively.
The ab initio three-dimensional potential energy surface, V(θ,α,β), was constructed using the total electronic energies of 156 geometries selected for different values of H7C2C1O3 (0°, 180°, and ±90°), O5O3C1C2 (0°, 30°, 60°, 90°, 120°, 150°, 180°) and H6O5O3C1 (0°, ±30°, ±60°, ±90°, ±120°, ±150°, 180°) dihedral angles. In all the geometries, 3Na-9 internal coordinates (Na = number of atoms) were allowed to be relaxed at the MP2/AVTZ level of theory. The 156 structures are provided in the ESI† (see Table S4). Energies were computed in CCSD(T)-F12b/CVTZ-F12 single point computations on the 156 geometries. The zero-point vibrational correction VZPVE(θ,α,β) was computed at the MP2/AVTZ level of theory within the harmonic approximation.51 This approximation has been tested in previous papers for which experimental data measured in the gas phase are available. Generally, its consideration improves the computed frequencies. In the case of PAA, if the vibrational correction is considered, the fundamental levels displace ∼0.5 cm−1 (methyl torsion), ∼1 cm−1 (C–O bond torsion) and ∼−6 cm−1 (OH torsion). V′(θ, α, β) adds a negligible correction of the 3D-PES.
A triple Fourier series transforming as the totally symmetric representation of the G12 Molecular Symmetry Group (MSG)33 was selected to represent analytically the effective potential:
 | (6) |
The 156 vibrationally corrected energies were fitted to obtain the 132 coefficients which are provided in the ESI† (see Table S2). The parameters of the linear fit reached σ = 0.82 × 10−4 and R2 = 0.9999; the coefficients of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3θ
3θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3α (121.356 cm−1) and sin
3α (121.356 cm−1) and sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3θ
3θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3α (−138.752 cm−1) denote important resonances between the methyl and the C–O bond torsions although those describing the interaction between the methyl and the OH torsion (terms type cos
3α (−138.752 cm−1) denote important resonances between the methyl and the C–O bond torsions although those describing the interaction between the methyl and the OH torsion (terms type cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3θ
3θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kβ) are quite small. Contributing coefficients describing the interactions between the CC-bond and the OH torsions are obtained (i.e. 976.139 cos
Kβ) are quite small. Contributing coefficients describing the interactions between the CC-bond and the OH torsions are obtained (i.e. 976.139 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3α
3α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3β).
3β).
Analytical expressions containing 132 terms and formally identical to eqn (6) were employed for the fitting of the kinetic energy parameters, Bqiqj. The expansion coefficients are provided in the ESI† (see Table S3). The most contributed ones are the ACCC000 coefficients determined to be A000(Bθθ) = 5.6243 cm−1, A000(Bαα) = 1.5428 cm−1, A000(Bββ) = 20.0919 cm−1, A000(Bθα) = −0.1618 cm−1, A000(Bθβ) = 0.0009 cm−1, and A000(Bαβ) = −0.7741 cm−1.
The Hamiltonian of eqn (4) was solved variationally using symmetry adapted Fourier series. Since the stability of the Cc conformer is prominent, all the low energies below 600 cm−1 can be assigned to this minimum. The energies of Table 4 are classified using three quanta ν21ν20ν19 and the representations of the G6 subgroup of G12. Due to tunnelling effects in the methyl torsion barriers, the energy levels split into three components, one non-degenerated Ai (i = 1, 2) and one twofold degenerate E. The energies are compared with results obtained using VPT2 and with one-dimensional calculations performed by solving one-dimensional Hamiltonians depending on θ, α or β,
 | (7) |
| ν 21 ν 20 ν 19 | Variational | VPT2 | ν 21 ν 20 ν 9 | Variational | VPT2 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 3D | 1D | 3D | 1D | ||||||
| 0 0 0 | A1 | 0 | 0 | 0 | ν 13 (A′) | ||||
| E | 2.262 | 2.102 | |||||||
| 1 0 0 | A2 | 49.082 | 55.421 | 51.8 | 0 2 0 | A1 | 429.798 | 354.402 | 437.5 |
| E | 35.676 | 39.544 | 60.5 | E | 437.135 | 422.8 | |||
| 2 0 0 | A1 | 73.105 | 73.166 | 104.5 | 1 0 1 | A1 | 440.798 | 474.3 | |
| E | 99.917 | 103.556 | 121.9 | E | 426.397 | 474.2 | |||
| 3 0 0 | A2 | 202.581 | 214.643 | 158.1 | 4 0 0 | A2 | 462.825 | 468.992 | — |
| A1 | 201.735 | 215.111 | 212.6 | A1 | 473.365 | 468.414 | |||
| E | 146.831 | 153.32 | 184.2 | E | 532.722 | 372.529 | |||
| E | 265.487 | 288 | 247.4 | E | 594.882 | 575.625 | |||
| 0 1 0 | A2 | 216.673 | 177.883 | 220 | 2 0 1 | A2 | 463.636 | ||
| E | 220.721 | 212.6 | E | 490.757 | |||||
| 1 1 0 | A1 | 268.17 | 259.3 | 3ν21ν14 (A′′) | 470.7 | ||||
| E | 324.459 | 260.6 | 498.6 | ||||||
| 2 1 0 | A2 | 288.912 | 299.5 | ν 21 ν 13 (A′′) | 482.5 | ||||
| E | 329.151 | 309.5 | 493.5 | ||||||
| ν 14 (A′) | 317.5 | 1 2 0 | A2 | 499.658 | 464.3 | ||||
| 319.3 | E | 463.172 | 458.3 | ||||||
| 3 1 0 | A2 | 387.325 | 340.6 | 2 2 0 | A1 | 510.99 | 492 | ||
| A1 | 388.021 | 359.3 | E | 517.926 | 494.7 | ||||
| E | 393.656 | 3 2 0 | A1 | 580.606 | |||||
| E | 450.894 | A2 | 581.063 | ||||||
| ν 21 ν 14 (A′′) | 367.7 | E | 598.993 | ||||||
| 378.2 | |||||||||
| 2ν21ν14 (A′) | 418.7 | E | >600 | ||||||
| 437.9 | |||||||||
| 0 0 1 | A2 | 393.635 | 372.367 | 428.1 | 3 0 1 | A2 | 591.438 | 569.3 | |
| E | 396.325 | A1 | 592.926 | ||||||
| E | 537.52 | ||||||||
| E | 607.952 | ||||||||
| 3D-ZPVE | 335.392 | ||||||||
The first excited energy (0 1 0) for the ν20 mode (C–O bond torsion) has been found to be 216.673 cm−1 (A2) and 220.721 cm−1 (E). These values are in good agreement with the VPT2 energy (220.0/212.6 cm−1) but over the 1D-energy computed variationally (177.883 cm−1). These results confirm that ν20 interacts strongly with the other two torsional modes, but slightly with the remaining vibrations, which were considered in the VPT2 model and neglected in the 3D-model.
The first excited energy (0 0 1) corresponding to the ν19 mode (OH torsion) has been computed to be 393.635 cm−1 (A2) and 396.325 cm−1 (E) below the experimental value by Cugley et al.23 (422 cm−1) measured in the Ar matrix. Unfortunately, available experimental data is not sufficient for a complete comparison, but in general, measurements with this technique produce different frequencies than the gas phase measurements specially for LAMs. The one-dimensional energy value (372.367 cm−1) is much lower than the three-dimensional one, as it was obtained for the C–O torsional fundamental.
The two overtones 2ν21 (2 0 0), 2ν20 (0 2 0), and 2ν19 (0 0 2) have been computed to be 73.105 cm−1 (A1) and 99.917 cm−1 (E), and 429.798 cm−1 (A2) and 437.135 cm−1 (E), respectively. 2ν19 (0 0 2) lies over 600 cm−1.
In a first approximation and for very low temperatures, it may be inferred that the methyl internal rotation is the unique mode that can be treated in one dimension as usually done in assignments of experimental microwave spectra, where the employed effective Hamiltonians depend on a single or (at much) two large amplitude motions.
3. Conclusions
This study aims to provide a theoretical description of the structural spectroscopic properties of PAA. This species, for which there is a lack of previous information, represents an OOM present in urban areas. Like other peroxides, it contributes to increasing the oxidation capacity of the troposphere. The results can help further experimental studies required by the atmosphere chemistry research.A detailed search for equilibrium structures performed with CCSD(T)-F12b revealed three conformers, Cc, Ct, and Ttg. The Cc conformer exhibits notable stability due to the presence of an intramolecular hydrogen bond of 1.8511 Å between the oxygen atom of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the hydrogen atom of OH. The excitation of the three torsional modes causes the breaking of the weak bond, leading to the conformers Ct and Ttg at 1627.7 cm−1 and 2015.9 cm−1 above Cc, respectively. The fact that both structures are neglected in previous experimental studies is sufficiently justified by the computed relative stabilities and the shape of the potential energy surface. The computed barriers restricting the conformer interconversion can help further kinetic studies.
O and the hydrogen atom of OH. The excitation of the three torsional modes causes the breaking of the weak bond, leading to the conformers Ct and Ttg at 1627.7 cm−1 and 2015.9 cm−1 above Cc, respectively. The fact that both structures are neglected in previous experimental studies is sufficiently justified by the computed relative stabilities and the shape of the potential energy surface. The computed barriers restricting the conformer interconversion can help further kinetic studies.
The Cc ground vibrational state rotational constants have been computed to be A0 = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821.92 MHz, B0 = 4276. 17 MHz and C0 = 3125. 52 MHz at a few MHz of the available experimental data. These parameters can help to understand the accuracy of the employed methodology.
821.92 MHz, B0 = 4276. 17 MHz and C0 = 3125. 52 MHz at a few MHz of the available experimental data. These parameters can help to understand the accuracy of the employed methodology.
This work provides molecular properties that can help to advance experimental spectroscopic research of PAA. We consider that the distribution of levels that we provide can rarely be obtained by experimental techniques, although their knowledge is necessary for a proper interpretation of measurements. We have obtained low-energy levels which transitions can be observed using many experimental techniques. We emphasize the part of the work describing the distribution of vibrational energies and their splittings in the potential energy surface because this distribution cannot be understood without the employment of theoretical techniques based on highly correlated ab initio methods.
In Cc, the methyl torsional barrier has been found to be very low, V3 = 88.6 cm−1 producing a splitting of 2.262 cm−1 for the ground vibrational state. The distributions of the 3D-energy levels corresponding to low vibrational excitations of the methyl torsional mode, are anarchic, specially for the E energies. The fundamentals for the ν21 (methyl torsion), ν20 (C–O bond torsion) and ν19 (OH torsion) have been computed to be 49.1 cm−1 (Ai), 33.4 cm−1 (E), 216.7 cm−1 (A2) and 218.5 cm−1 (E) and 393.6 cm−1 (A2) and 394.1 cm−1, respectively.
The VPT2 full-dimensional vibrational analysis predicts that Fermi resonances between low-lying torsional energy levels and other vibrations are very weak. This confirms the validity of the 3D variational model used for the study of the FIR spectrum and confirms that the addition of more independent coordinates is not necessary for computing low energies. It has to be considered that in the employed vibrational theory, the interactions between the 3 independent coordinates and the remaining 3Na-6-3 coordinates are partially considered when they are allowed to be relaxed in all the 156 selected geometries employed to construct the PES and when the ZPVE correction is added.
However, the variational study confirms that the ν20 torsional mode interacts strongly with the other two torsional modes ν19 and ν21. In a first approximation and for very low temperatures, the methyl internal rotation is the unique mode that can be treated in one dimension as usually done in assignments of microwave spectra. In many cases, the effective Hamiltonians defined for the study of the rotational structure depend on a single or (at much) two large amplitude motions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 872081”. This research was supported by the Agencia Estatal de Investigación of Spain through the grant PID2020-112887GB-I00/AEI/10.13039/501100011033. The author acknowledges the CTI (CSIC) and CESGA and the “Red Española de Computación” for the grant RES-AECT-2022-3-0006 for computing facilities. S. B. and D. M. acknowledge the “Conseil National de la Recherche Scientifique de Tunis” for the exchange grants in 2022 and 2023.References
- C. E. Reeves and S. A. Penkett, Chem. Rev., 2003, 103, 5199 CrossRef CAS PubMed.
- F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg and T. F. Mentel, et al. , Chem. Rev., 2019, 119, 3472 CrossRef CAS PubMed.
- J. G. Calvert, A. Lazrus, G. L. Kok, B. G. Heikes, J. G. Walega, J. Lind and C. A. Cantrell, Nature, 1985, 317, 27 CrossRef CAS.
- M. Krapf, I. E. Haddad, E. A. Bruns, U. Molteni, K. R. Daellenbach, A. S. H. Prévot, U. B. Baltensperger and J. Dommen, Chem, 2016, 1, 603 CAS.
- J. D. Crounse, K. A. McKinney, A. J. Kwan and P. O. Wennberg, Anal. Chem., 2006, 78, 6726 CrossRef CAS PubMed.
- P. O. Wennberg, T. F. Hanisco, L. Jaegle, D. J. Jacob, E. J. Hintsa, E. J. Lanzendorf, J. G. Anderson, R.-S. Gao, E. R. Keim and S. G. Donnelly, et al. , Science, 1998, 279, 49 CrossRef CAS PubMed.
- M. Qin, Z. Chen, H. Shen, H. Li, H. Wu and Y. Wang, Atmos. Environ., 2018, 183, 144 CrossRef CAS.
- S. J. Fuller, F. P. H. Wragg, J. Nutter and M. Kalberer, Atmos. Environ., 2014, 92, 97 CrossRef CAS.
- X. Qiao, C. Yan, X. Li, Y. Guo, Y. Rujing, D. Chenjuan, L. Chang, N. Wei, W. Mingyi and C. Runlong, et al. , Environ. Sci. Technol., 2021, 55, 13646 CrossRef CAS PubMed.
- Y. Wang, P. Clusius, C. Yan, K. Dällenbach, R. Yin, M. Wang, X. C. He, C. Biwu and L. Yiqun, et al. , Environ. Sci. Technol., 2022, 56, 770 CrossRef CAS PubMed.
- X. Cheng, Y. J. Li, Y. Zheng, K. Liao, T. Zhu, C. Ye, X. Qiu, K. T. Koenig, Y. Ge and Q. Chen, EGUsphere, 2023 Search PubMed.
- A. Mellouki, T. J. Wallington and J. Chen, Chem. Rev., 2015, 115, 3984 CrossRef CAS PubMed.
- B. Nozière, M. Kalberer, M. Claeys, J. Allan, B. D’Anna, S. Decesari, E. Finessi, M. Glasius, I. Grgic and J. F. Hamilton, et al. , Chem. Rev., 2015, 115, 3919 CrossRef PubMed.
- H. Wu, Y. Wang, H. Li, L. Huang, D. Huang, H. Shen, Y. Xing and Z. Chen, Atmos. Environ., 2017, 164, 61 CrossRef CAS.
- X. Zhang, Z. M. Chen, S. Z. He, W. Hua, Y. Zhao and J. L. Li, Atmos. Chem. Phys., 2010, 10, 737 CrossRef CAS.
- J. A. Lind, A. L. Lazrus and G. L. Kok, J. Geophys. Res., 1987, 92, 4171 CrossRef CAS.
- B. K. Keller, M. D. Wojcik and T. R. Fletcher, J. Photochem. Photobiol., A, 2008, 195, 10 CrossRef CAS.
- R. J. Yokelson, J. D. Crounse, P. F. DeCarlo, T. Karl, S. Urbanski, E. Atlas, T. Campos, Y. Shinozuka, V. Kapustin and A. D. Clarke, et al. , Atmos. Chem. Phys., 2009, 9, 5785 CrossRef CAS.
- F. A. F. Winiberg, T. J. Dillon, S. C. Orr, C. B. M. Groß, I. Bejan, C. A. Brumby, M. J. Evans, S. C. Smith, D. E. Heard and P. W. Seakins, Atmos. Chem. Phys., 2016, 16, 4023 CrossRef CAS.
- B. C. Faust, K. Powell, C. J. Rao and C. Anastasio, Atmos. Environ., 1997, 31, 497 CrossRef CAS.
- H. B. Singh, L. J. Salas and W. Viezee, Nature, 1986, 321, 588 CrossRef CAS PubMed.
- P. A. Giguère and A. W. Olmos, Can. J. Chem., 1952, 30, 821 CrossRef.
- J. Cugley, R. Meyer and H. S. H. Günthard, Chem. Phys., 1976, 18, 281 CrossRef CAS.
- J. A. Cugley, W. Bossert, A. Bauder and H. S. H. Günthard, Chem. Phys., 1976, 16, 229 CrossRef CAS.
- M. K. Hazra and A. Sinha, J. Phys. Chem. A, 2011, 115, 5294 CrossRef CAS PubMed.
- M. K. Hazra, X. Kuang and A. Sinha, J. Phys. Chem. A, 2012, 116, 5784 CrossRef CAS PubMed.
- R. Benassi and F. Taddei, THEOCHEM, 1994, 303, 83 CrossRef.
- S. L. Khursan and V. L. Antonovsky, Russ. Chem. Bull., 2003, 52, 1908 CrossRef CAS.
- C. H. Langley and E. A. Noe, THEOCHEM, 2004, 682, 215 CrossRef CAS.
- C. E. Miller and J. S. Francisco, J. Phys. Chem. A, 2004, 108, 2930 CrossRef CAS.
- C. E. Miller and J. S. Francisco, J. Phys. Chem. A, 2001, 105, 750 CrossRef CAS.
- R. Boussesi, M. L. Senent and N. Jaïdane, J. Chem. Phys., 2016, 144, 164110 CrossRef PubMed.
- R. Boussesi and M. L. Senent, Phys. Chem. Chem. Phys., 2020, 22, 23785 RSC.
- I. Toumia, S. Dalbouha, M. M. Al-Mogren, O. Yazidia, N. Jaïdane, M. Carvajal and M. L. Senent, J. Phys. Chem. A, 2022, 126, 7230 CrossRef PubMed.
- M. Salah, K. Marachi, N. Komiha and M. L. Senent, Theoretical spectroscopic study of isopropyl alcohol (CH3–CHOH–CH3), Astrophys. J., 2024, 963, 143 CrossRef.
- T. B. Adler, G. Knizia and H. J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H. J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, et al., MOLPRO, version 2022, a package of ab initio programs, see https://www.molpro.net.
- J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108 CrossRef PubMed.
- V. Barone, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., GAUSSIAN 16, Revision C.01, 2016 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- R. A. Kendall, T. H. Dunning, Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- M. L. Senent, Chem. Phys. Lett., 1998, 296, 299 CrossRef CAS.
- M. L. Senent, J. Mol. Spectrosc., 1998, 191, 265 CrossRef CAS PubMed.
- M. L. Senent, Mol. Phys., 2001, 99, 1311 CrossRef CAS.
- S. Dalbouha, M. L. Senent, N. Komiha and R. Domínguez-Gómez, J. Chem. Phys., 2016, 145, 124309 CrossRef CAS PubMed.
- M. L. Senent, M. Villa, F. J. Meléndez and R. Domínguez-Gómez, Astrophys. J., 2005, 627, 567 CrossRef CAS.
- S. Dalbouha, M. L. Senent and N. Komiha, J. Chem. Phys., 2015, 142, 074304 CrossRef CAS PubMed.
- J. K. G. Watson, J. Chem. Phys., 1968, 48, 4517 CrossRef CAS.
- A. G. Császár, V. Szalay and M. L. Senent, J. Chem. Phys., 2004, 120, 1203 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05783f |
| This journal is © the Owner Societies 2024 |