Insights on adsorption of pyocyanin in montmorillonite using molecular dynamics simulation

Abstract

Pyocyanin is an important virulence factor in the resistance of Pseudomonas aeruginosa to antibiotics. Pyocyanin is a planar three ring aromatic molecule that occurs as zwitterionic (PYO) or protonated species (PYOH⁺). Our earlier studies have shown that montmorillonite, through adsorption and transformation, can inactivate both PYO and PYOH⁺ in the interlayer space. The objective of this study was to elucidate the interaction mechanisms between montmorillonite and the adsorbed pyocyanin and to characterize the structure of the pyocyanin–montmorillonite complex via molecular dynamics (MD) simulations. The MD simulations were performed for the complexes of hydrated Na-montmorillonite (HM) with (i) neutral pyocyanin (HMP) and (ii) protonated pyocyanin (HMPH); and dehydrated Na-montmorillonite (DM) with (iii) neutral pyocyanin (DMP) and (iv) protonated pyocyanin (DMPH). The simulations indicated that in dry conditions, both PYO and PYOH⁺ were well-ordered in the midplane of the interlayer of montmorillonite, with the three aromatic rings almost parallel to the basal surface and sandwiched in-between basal surface-adsorbed Na⁺ planes. In humid conditions, the pyocyanin and Na⁺ were solvated in the interlayer space and the pyocyanin was less ordered compared to dehydrated models. Ion–dipole interaction (Na–O) was the dominant interaction for the dehydrated complexes DMPH and DMP but the interaction was stronger in the latter. The Na–O ion–dipole interaction remained the dominant interaction in hydrated HMP while in HMPH, water outcompeted PYOH⁺ for Na⁺ resulting in water–Na interaction being the dominant interaction. These results revealed the arrangement of the two species of pyocyanin in the interlayer spaces of montmorillonite and the mechanism of interaction between the pyocyanin and montmorillonite.

---

1. Introduction

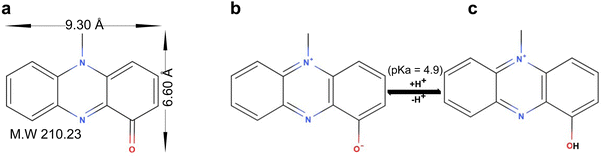
Pyocyanin (C₁₃H₁₀N₂O) is one of the redox-active tricyclic phenazines produced as a virulence factor by the drug-resistant Pseudomonas aeruginosa through a series of complex gene-mediated steps.^1,2 Pyocyanin has a pK_a of 4.9 and exists as protonated species (PYOH⁺) at pH < pK_a or neutral zwitterionic species (PYO) at pH > pK_a (Fig. 1). Pyocyanin facilitates the recalcitrance and resistance of P. aeruginosa to antibiotics by killing and inhibiting the growth of competing microbes,^3,4 suppression of host immune system,⁵ and formation of biofilms.^6–8 In view of the importance of pyocyanin in the pathogenicity of P. aeruginosa, the inactivation/deactivation of the molecule or the modulation of pyocyanin production was proposed as an alternative approach to disarming the pathogen.^9,10 Indeed, the inactivation of virulence factors (including pyocyanin) by adsorption has been shown to attenuate the cytotoxicity of the pathogen by neutralizing virulence factors, and transcriptionally suppress virulence gene expression.^11,12

Fig. 1 Model of (a) pyocyanin and its (b) zwitterionic and (c) protonated species.

Our earlier study showed that clay minerals (Na-montmorillonite and sepiolite) adsorbed pyocyanin and probably transformed pyocyanin in the interlayer of the montmorillonite and in the tunnel of sepiolite.¹³ For Na-montmorillonite, at pH < pK_a, the mechanism of adsorption is by ion-exchange of interlayer cation by PYOH⁺. At pH > pK_a, there are two types of adsorption mechanism which was mainly dictated by the type of interlayer cations.¹⁴ Mechanism I – protonation of a fraction of the neutral pyocyanin (i.e., xPYO + (x − y)H⁺ → yPYO + (x − y)PYOH⁺) followed by incomplete ion-exchange of PYOH⁺ for interlayer cation while mechanism II – the diffusion and the adsorption of the zwitterionic PYO in interlayer of montmorillonite with little to no protonation. Mechanism I was mostly observed in alkali and alkali earth-montmorillonite while mechanism II was dominant on Cu²⁺- and Mn²⁺-montmorillonite.¹⁴

These studies demonstrated that clay minerals can combat P. aeruginosa infections by pyocyanin adsorption and also elucidate the influence of smectite properties (type of interlayer cation, layer charge density, and source of layer charge) and the speciation of pyocyanin on the adsorption of pyocyanin.^13,14 Yet, little is known about the details of pyocyanin–montmorillonite bonding/interaction at the molecular level. More specifically, the arrangement of pyocyanin in the interlayer of montmorillonite and the interaction between pyocyanin and exchangeable cations, water molecules, and the siloxane surfaces of the mineral. An understanding of the interaction is important in the selection and improvement (modification) of smectites as pyocyanin adsorbent/degrader and in the design of functional nanomaterials to serve similar purposes.

As a result of the complexity of clay minerals, experimental approach is often insufficient to convincingly elucidate the dynamics and bonding mechanism between adsorbed organics and smectites components – especially involving basal surfaces, interlayer cations and solvation water. On the other hand, molecular simulation approaches – molecular dynamics (MD) and density functional theory (DFT) – when guided and constrained by experimental data can aid the understanding of the energy, structure, and dynamics of hydrated and dehydrated smectite and organic–smectite systems.

With respect to organic–smectite complexes, MD simulations have been an important tool in understanding the structure, dynamics, interactions, and interfacial energetics of these complex systems.^15–20 Using MD simulation, this present study investigated the interactions of pyocyanin with the cations and water molecules in the interlayer space of montmorillonite to provide a molecular scale insight into the interaction mechanism in dehydrated and hydrated montmorillonite–pyocyanin systems. The specific objectives of the current study were to characterize the structures of pyocyanin–montmorillonite complexes and investigate the interaction mechanisms in pyocyanin–montmorillonite complexes.

2. Methods

Initial structures of the montmorillonite and pyocyanin were constructed with BIOVIA Materials Studio (MS) 2018; all the MD simulations were performed with the LAMMPS code; structure output files were visualized in OVITO and MS; and post analysis was either computed on the fly in LAMMPS or using in-house Python scripts.^21–23

2.1 Pristine dehydrated and hydrated montmorillonite

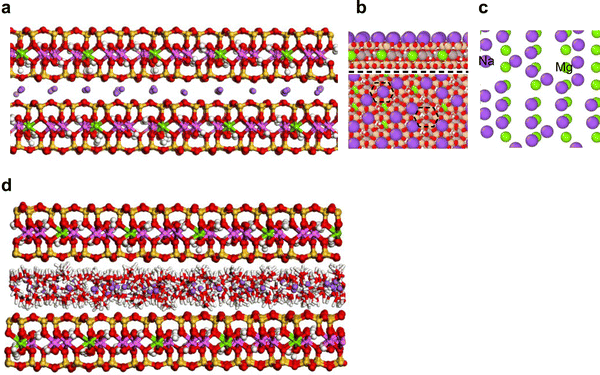
A unit cell of montmorillonite with layer charge of −1e was built from an orthogonal unit cell of pyrophyllite.²⁴ The charge deficit was balanced with one Na⁺ placed in a 3.153 Å slab (i.e., interlayer space) built above the siloxane surface. The unit cell (NaSi₈Al₃MgO₂₀(OH)₄) has cell parameters of 5.160, 8.966, and 12.50 Å, along the a, b, and c-axis, respectively. The model was expanded (16a × 10b × 4c) to create an 82.56 × 89.66 × 50 Å supercell. This represents the dehydrated Na-montmorillonite (DM, Fig. 2(a)). To construct hydrated Na-montmorillonite, 4800 water molecules were dispersed in the interlayer of DM (i.e., 1200 H₂O/interlayer). The H₂O/Na⁺, H₂O/(unit cell) and water content in the supercell were of 7.5, 7.5 and ∼180 mg H₂O g_clay⁻¹, respectively. The model was referred to as HM (Fig. 2(b)). This large amount of water was considered because the forcefield employed in this study renders the smectite structure metastable for smectite structures of this large size, high charge density, and low hydration. To circumvent this issue we added enough water to the interlayer to hydrate all cations thus discouraging electrostatic attraction between interlayer cations and the basal surface.

Fig. 2 An abridged (2 × 5 × 2) starting structure for (a) dehydrated montmorillonite, (b) hydrated montmorillonite, (c) dehydrated pyocyanin–montmorillonite, and (d) hydrated pyocyanin–montmorillonite along yz. The atom coloring scheme is as follows: Na = purple; O = red; Mg = green; Si = orange; C = grey; N = blue; H = white.

2.2 Arrangement of pyocyanin in the interlayer of montmorillonite

The X-ray diffractograms of pyocyanin–montmorillonite complexes have shown that only a single layer of pyocyanin can be adsorbed in the interlayer of montmorillonite^13,14 but the arrangement of pyocyanin was not clear. To determine the most thermodynamically favourable arrangement of pyocyanin in the interlayer of montmorillonite, three possible arrangements (tail-to-head, head-to-head, and random) were investigated using a 2 × 5 × 2 montmorilonite supercell (see Fig. S1, ESI†). Results indicated there was no significant difference in the potential energy or crystallographic parameters for the three arrangements (see Table S1, ESI†). Consequently, the random arrangement was adopted.

2.3 Dehydrated and hydrated PYOH⁺–montmorillonite

In accordance with the results from X-ray energy dispersive spectroscopy,^13,14 half of the interlayer Na⁺ in DM was randomly replaced with PYOH⁺ to represent the cation exchange mechanism (mechanism I) of pyocyanin adsorption. This structure represented the dehydrated protonated PYOH⁺–Na-montmorillonite complex and denoted as DMPH (Fig. 2(c)). Then, each interlayer of DMPH was saturated with (i) 4000 water molecules (i.e., 1000 water/interlayer) to represent the hydrated PYOH⁺–Na-montmorillonite complexes (HMPH, see Fig. 2(d)).

2.4 Dehydrated and hydrated PYO–montmorillonite

To depict mechanism II, the PYOH⁺ molecules in both DMPH and HMPH were deprotonated followed by the addition of Na⁺ to maintain a neutral model. The resulting structures correspond to the dehydrated and hydrated PYO–montmorillonite and denoted as DMP and HMP, respectively.

2.5 Forcefields

The forcefield parameters for water and pyocyanin were taken from the flexible SPC water model and consistent valence forcefield (CVFF), respectively.^25,26 The forcefield parameters for Na-montmorillonite were taken from Clayff^27,28 with slight modification to the parameter for Na⁺ and bridging oxygen.²⁹ This modification was necessary to avoid the unrealistic attraction of Na⁺ deep into the ditrigonal cavity of dehydrated montmorillonite as observed in previous simulation studies.^30–32 See Tables S2–S4 (ESI†) and Fig. 3 for a summary of the assigned forcefield parameters for the non-bonded and bonded terms in Na-montmorillonite and pyocyanin structure.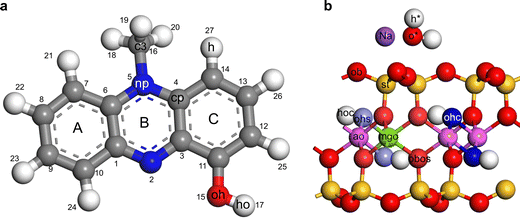

Fig. 3 Forcefield assignment for (a) protonated pyocyanin and (b) Na-montmorillonite. For neutral pyocyanin the ho was deleted while the oh was reassigned as o′ (see Tables S2–S4 for a summary of the assigned forcefield parameters, ESI†).

2.6 Simulation

Using the LAMMPS software package, MD simulations were performed with 3D periodic boundary conditions. The energy of the non-bonded component was computed according to eqn (S1.2)–(S1.4) (ESI†). The distance and energy interaction parameters for the non-bonded atoms was computed using the Lorentz–Berthelot combination rules.³³ A 10.0 Å real-space cut-off was used for short-range interactions, and the particle–particle particle–mesh algorithm (PPPM) was used to compute long-range interactions at an accuracy of 1.0 × 10⁻⁴.³⁴

Using a time step of 1 fs, MD simulations were sequentially performed using the microcanonical NVE ensemble (constant number of atoms N, constant volume V, and constant energy E), the canonical NVT ensemble (constant temperature T), and the isothermal–isobaric NPT ensemble (constant pressure P). Temperature and pressure were controlled using a Nosé–Hoover thermostat and barostat.³⁵

As indicated in the MD simulation protocols (Fig. 4), an energy minimization was first performed for the models using conjugate gradient algorithm³⁶ followed by MD equilibration (NVE) of the models at 300 K for 1 ns. Two NVT runs were each conducted at 300 K for 2 ns while damping (relaxing) the temperature at 100 timestep. The first NVT (NVT1) was performed to maintain a stable temperature prior to the second NVT run (NVT2). Following the NVT ensemble simulation, two NPT runs were each performed at 1 atm and 300 K for 2 ns. The first NPT (NPT1) was performed to equilibrate the system while the second NPT (NPT2) was used to compute thermodynamic properties, trajectories, d-spacings every 100 fs and radial distribution functions (RDF) as an average of every 100 fs. Atomic density profiles (ADP) were computed from the atomic trajectories.

Fig. 4 A schematic of the MD simulation protocol.

2.7 Radial distribution function (RDF)

The radial distribution function, g(r), is a description of the changes in density as a function of distance from a reference point. The RDF is estimated as the probability of finding an atom A from at a distance r from an atom B and can be calculated:³³where ρ is the density and dn_r is a function that computes the number of atoms within a shell of thickness d_r. Pairwise distances were computed for: Na–Na, Na–ob, Na–obos, Na–o*, h*–ob, Na–oh, oh–ob, c3–ob, and oh–o* (see Fig. 3). The RDF was calculated from a histogram obtained by binning the pairwise distances in 300 bins from 0.0 to 10.0 Å.

2.8 Atomic density profiles (ADP)

The ADP along the z-axis (i.e., 00l) was computed as the distance between an atom and a reference atom (basal oxygen “ob” in this case). The coordinates were extracted from the trajectory files of the second NPT run of the simulation and 400 bins were used to compute histograms. The computed densities were normalized to densities per layer by stipulating a maximum|cut-off|value for the distance between an atom and the reference atom (ob, see Fig. 3(b)).

3. Results and discussion

3.1 Basal spacings

3.1.1 Dehydrated (DM) and hydrated (HM) Na-montmorillonite. At the end of the second NPT MD simulation, the d₀₀₁-spacing of DM collapsed from 12.5 Å to 9.82 Å (Table 1). This layer distance is in agreement with experimentally observed 9.60–9.75 Å d₀₀₁-spacing of dehydrated Na-montmorillonite^14,37 and agrees with previous MD simulation.²⁹ The structure of HM has a larger d₀₀₁-spacing compared to DM due to hydration of the interlayer space (Fig. 5(d) and Table 1).

Table 1 Experimental and calculated d-spacings (Å)

	Unit cell parameters
	a (Å)	b (Å)	c (Å)	c′ (Å)		α, β, γ
Note: the a, b, and c dimensions are per unit cell; c′ = experimentally observed dimension in vacuum (*), at 200 °C (†) or at 65% relative humidity (**) conditions. The † and ** are from Fashina and Deng^13,14 and * is under atmosphere of nitrogen (see Fig. S2, ESI).
Start	5.16	8.97	12.5			90
DM	5.18 ± 0.02	9.00 ± 0.02	9.82 ± 0.02	9.73*	9.75^†	90
HM	5.18 ± 0.02	8.98 ± 0.02	14.14 ± 0.05	12.70**		90
DMPH	5.19 ± 0.02	9.00 ± 0.02	13.02 ± 0.03	12.54*	12.48^†	90
HMPH	5.19 ± 0.02	8.98 ± 0.02	16.21 ± 0.06	12.70**		90
DMP	5.19 ± 0.02	9.01 ± 0.02	13.34 ± 0.06	12.54*	12.48^†	90
HMP	5.19 ± 0.02	8.98 ± 0.02	16.38 ± 0.06	12.70**		90

---

Fig. 5 Snapshots after NPT run showing (a) mid-plane adsorbed Na⁺ (yz), (b) adsorption of Na⁺ just above the ditrigonal hole (yz, top) and distribution of Na⁺ in the ditrigonal holes (xy, bottom), (c) distribution of Na⁺ relative to the site of substitution (xy) in dehydrated Na-montmorillonite and (d) structure of hydrated Na-montmorillonite.

3.1.2 Dehydrated (DMPH) and hydrated (HMPH) PYOH⁺–montmorillonite. The d₀₀₁-spacing of the DMPH was 13.02 Å with intercalation of the protonated pyocyanin. This is equivalent to an interlayer space of about 3.7 Å (Table 1). This difference between the predicted and the experimentally observed interlayer spacing being ∼0.50 Å (Table 1). The d₀₀₁-spacing of the HMPH increased to 16.21 Å which is equivalent to about 6.91 Å interlayer space (Table 1). This value is about 3.5 Å higher than the experimentally observed value (Table 1) probably because the experimental XRD was acquired as air-dried films at 60–70% humidity. The large water content used in these simulations was necessary to observe the pyocyanin–montmorillonite interactions in the expanded interlayer.

3.1.3 Dehydrated (DMP) and hydrated (HMP) PYO–montmorillonite. The d₀₀₁-spacing of the DMP was 13.34 Å which is equivalent to interlayer space of about 4.00 Å (Table 1 and Fig. 10). The difference between the predicted and the experimentally observed interlayer space being ∼0.85 Å (Table 1). Similar to HMPH, the d₀₀₁-spacing for the equilibrated HMP simulation increased to 16.38 Å which is equivalent to an interlayer space of about 7.0 Å. The deviation from experiments stemmed from the high-water content in the starting models as noted above.

3.2 Atomic density profile – structure and arrangement

3.2.1 Dehydrated (DM) and hydrated (HM) Na-montmorillonite. In DM, the Na⁺ was adsorbed midplane in the interlayer at about 1.70 Å from the basal oxygens (Fig. 5(a) and 6(a)). This favours electrostatic interaction between Na and basal oxygens. The Na⁺ are randomly distributed directly above the ditrigonal cavity and the distribution is not determined by the site of isomorphous substitution (Fig. 5(b) and (c)). A small peak for Na⁺ also is observed close to the basal surface which is indicative of surface adsorption. In HM, the Na⁺ ions were solvated midplane in the interlayer at 3.75 Å from the basal oxygens of the siloxane surface (Fig. 6(b)) corresponding to outer-sphere surface complexes. The o* peaks – 2.6 Å (sharp peak) and 1.98 Å (small shoulder) from the basal oxygen which corresponds to two layers (2W) of water in the interlayer. Similar observation was made for a Na-montmorillonite with similar charge and water content as this study.³⁸ The h* peaks occur at about 1.6 Å and 2.95 Å from the basal oxygens (Fig. 6(b)) corresponding to first layer (1L) and second layer (2L) of waters in the interlayer.

Fig. 6 Atomic density profile of (a) dehydrated and (b) hydrated Na-montmorillonite.

3.2.2 Dehydrated PYOH⁺–montmorillonite (DMPH). The structure of the dehydrated complex is such that Na⁺ are adsorbed close to the ditrigonal cavities of the clay surface while a plane of PYOH⁺ molecules is oriented subparallel to the surface and sandwiched (midplane) between surface-adsorbed Na⁺ planes. This is similar to the orientation of phenazine on the surface of aluminium oxide.³⁹ To minimize repulsion, each ho of the PYOH⁺ points away from the Na⁺ (Fig. 7(a) and (b)). The ho is observed at ∼1.70 Å while the oh is ∼2.60 Å from the basal ob (Fig. 8(a)). This suggests electrostatic interaction between the ho and the negatively charged basal ob. The ho and oh peaks being on either basal surface, despite midplane arrangement of PYOH⁺, is due to electrostatic interaction between ho and basal ob. The N peak was a single, narrow, and symmetrical peak at about 3.20 Å from the basal surface. This suggests one layer of well-ordered PYOH⁺ molecules in the midplane of the interlayer. Based on the full width at half maximum (FWHM) of the N peak, the angle of tilt of the pyrazine ring (ring B, Fig. 3(a)) is estimated to be less than 15°. The split of the C (i.e., c3) around the N peak indicates that c3 points towards basal ob at about 2.90 Å from the basal plane. Assuming a bond distance of 1 Å and angle of 109.5° between c3 and H, the distance between the methyl H and basal oxygen is about 2.0 Å. This suggests that the H of the methyl group could be closely interacting with the basal oxygens by H-bonding. Perhaps, this H-bonding and the ho–ob electrostatic interaction caused the observed slight slanting of PYOH⁺.

Fig. 7 Snapshot of the MD simulation of PYOH⁺ (a) and (b) in the interlayer (yz) and (c) on the basal surface (xz) of dehydrated PYOH⁺–Na-montmorillonite. The atom coloring scheme is as follows: Na = purple; O = red; Mg = green; Si = orange; C = grey; N = blue; H = white, H of OH pyocyanin = black.

Fig. 8 Atomic density profile of (a) dehydrated PYOH⁺–Na-montmorillonite, (b) hydrated PYOH⁺–Na-montmorillonite, (c) dehydrated PYO–Na-montmorillonite, and (d) hydrated PYO–Na-montmorillonite.

Unlike the structure of DM, most of the Na⁺ in DMPH were adsorbed closer to the clay surface (Fig. 8(a)). This strong adsorption suggests (i) strong repulsion between charged PYOH⁺ and Na⁺ or (ii) that the inorganic cation has a strong preference for the clay surface when PYOH⁺ is adsorbed. The former is supported by the fact that the protonated end of PYOH⁺ always points away from adsorbed Na⁺ and towards the edge of the ditrigonal cavity unoccupied by Na⁺ (Fig. 7(c)). This arrangement exposed both oh and N to interact with Na⁺ (i.e. ion–dipole interactions).

3.2.3 Hydrated PYOH⁺–montmorillonite (HMPH). In contrast to DMPH, the Na⁺ in HMPH were mostly solvated in the middle of the interlayer (Fig. 9). The Na⁺ ions were at 3.19 to 3.87 Å from the basal ob of the clay (Fig. 8(b) and Table S4, ESI†). The slight splitting of the Na⁺ peak is indicative of two layers of Na⁺ in contrast to HM where one layer of Na⁺ was solvated in the midplane.

Fig. 9 Snapshot of the MD simulation of protonated pyocyanin (a) and (b) in the interlayer (yz) and (c) on the basal surface (xz) of hydrated Na-montmorillonite. The atom coloring scheme is as follows: Na = purple; O = red; Mg = green; Si = orange; C = grey; N = blue; H = white, H of OH pyocyanin = black. Water not shown on image “a” for clarity.

The o* and h* each has two peaks (a sharp and a broad peak) on opposite sides of the interlayer indicating two layers of water solvating two layers of Na⁺. The 1L was the dominant with peaks at 2.65 Å (o*) and 1.63 Å (h*) from the basal surface while the 2L has peaks at 1.93 Å (o*) and 2.81 Å (h*) from the basal ob. The 2L of water has the H-atoms pointed towards the basal surface and allows water to mainly interact with the (i) basal surface of the clay (i.e., ob–h*) by H-bonding and (ii) with the interlayer Na⁺ ions (i.e., o*–Na) by ion–dipole. The 1L of water has the H-atoms pointed inwards towards the interlayer allowing water to interact mainly with PYOH⁺ (o*–ho) or form a network of H-bonding (o*–h*) with the 2L of water.

The oh/ho have two peaks on opposite sides of the interlayer and are at similar distance to the basal surface as o* and h* (Table S4, ESI† and Fig. 8(b)). The splitting of the oh and ho is indicative of two possible orientations/configurations of the oh/ho atoms on the single layer of PYOH⁺. The first configuration has the oh and ho at 2.52 and 1.63 Å from the basal ob, respectively. The second configuration of PYOH⁺ has the oh and ho at 1.93 and 2.81 Å from the basal surface, respectively. As evident by the weak small peak, the first configuration is the dominant.

The dominant configuration allows the proton to interact (i) with basal ob (i.e., ho–ob) via inner sphere complexation or electrostatic interaction and (ii) with both configurations of water (i.e., ho–o*) via H-bonding. The oxygen (i.e., oh) of the dominant configuration can also interact with the interlayer Na⁺ (i.e., oh–Na) through ion–dipole at distance of 1.35 and 0.67 Å for the farthest and nearest Na from the basal ob, respectively. The second and weaker oh/ho configuration interacts (i) with water (i.e., ho–o* and oh–h*) through H-bonding at a distance of 0.88 Å and, (ii) interlayer Na⁺ (i.e., oh–Na) through ion–dipole of length 1.94 and 1.26 Å for the farthest and nearest Na from the basal ob, respectively. This suggests that the dominant oh/ho configuration allows stronger interaction with the basal surface and interlayer components while the second oh/ho configuration is mostly solvated—water bridged.

The split two N peaks on each side of the basal surface represents the two types of N in tilted pyrazine ring of PYOH⁺ rather than different configurations of the pyrazine ring. This statement is corroborated by the c (i.e., c3) peak which showed no splitting on each side of the interlayer. If indeed the split N peaks represented two different configurations, the c3 should show similar split. The distance of both N and c3 peak from basal ob suggest that the N peaks at 3.87 and 3.19 Å correspond to methyl substituted N (atom 5 on Fig. 3(a)) and unsubstituted N (atom 2 on Fig. 3(a)), respectively. The unsubstituted N of the pyrazine ring is about 0.40 Å from the h* suggesting interaction with water. Similar to this MD study, experimental results indicate that H-bonded phenazine–water and pyrazine–water complexes were possible through the unsubstituted N in the pyrazine ring.^40,41 Along the z-axis, the two Na⁺ and two N peaks were at the same distance from the basal surface. We propose that the Na⁺ farthest from the basal surface could interact with the unsubstituted N. Such ion–dipole interaction might contribute to the stabilization of the PYOH⁺–montmorillonite complex.

The C (c3) peak was 2.65 Å from the basal surface. Factoring the C–H bond, the length of the methyl H from the surface can be estimated to be about 1.75 Å. This is similar to the 2.0 Å estimated for the DMPH. Hence, as in under dry conditions, PYOH⁺ could be interacting with the basal surfaces through the methyl group (i.e., H-bonding).

In relation to Na⁺, the main configuration of o* was 1.07 and 0.84 Å from the two Na⁺ peaks indicating that both Na was well-solvated. The pyrazine ring is almost at the same height as the solvated Na⁺ which suggest that the solvation of the Na might disfavour the formation of direct Na–N ion–dipole in HMPH.

3.2.4 Dehydrated PYO–montmorillonite (DMP). The arrangement of PYO in DMP is similar to the arrangement in DMPH in that PYO molecules are adsorbed subparallel in the midplane and sandwiched between surface-adsorbed Na⁺ (Fig. 10(b) and 8(c)).

Fig. 10 Snapshot of the MD simulation of neutral pyocyanin (a) and (b) in the interlayer (yz) and (c) on the basal surface (xz) of dehydrated Na-montmorillonite. The atom coloring scheme is as follows: Na = purple; O = red; Mg = green; Si = orange; C = grey; N = blue; H = white.

The o′, N, and C (i.e., c3) are at ∼3.37 Å from the basal surface indicating that the rings of PYO remained planar in the midplane and parallel to the basal surface (Fig. 8(c) and Table S4, ESI†). Unlike in DMPH, the o′ atoms in PYO remained midplane because there is no proton being attracted to the basal surfaces. Similar to DMPH, the molecules of PYO are well-ordered midplane in the interlayer and the angle of tilt of the pyrazine ring (ring B, Fig. 3(a)) is estimated to be less than 15°. The C (i.e., c3) did not split (in contrast to DMPH) but was at a farther distance from the basal surfaces compared to the DMPH. Yet, a c3 distance of 3.37 Å from the basal surface means that the H atoms of the methyl group are at about 2.50 Å from the basal surface. This suggests H-bonding at a slightly longer distance compared to the 2.00 Å observed for DMPH.

Like what was observed in DMPH, most of the Na⁺ in DMP were adsorbed on the surface at 1.26 Å from the clay surface (Fig. 8(c) and Table S4, ESI†). This strong adsorption suggests that the earlier observed surface adsorption in DMPH might not be entirely due to the repulsion between the proton of PYOH⁺ and Na⁺. Rather, in dry conditions, Na⁺ ions have a higher affinity to be attracted to the basal surfaces of smectite. This arrangement exposes both o′ and N to Na⁺ at distance of 2.11 Å each. This suggests Na⁺–O and Na⁺–N ion–dipole interactions. The former being at longer distance in DMP compared to DMPH while the latter is at same distance in both DMPH and DMP.

3.2.5 Hydrated PYO–montmorillonite (HMP). The arrangement of water and Na⁺ in the interlayer and the distances from the basal ob were almost the same for both HMPH and HMP simulations (Table S4, ESI†). Therefore, the interpretation for the arrangements and interactions of water and Na⁺ in HMPH also holds for HMP. The main difference in the equilibrated structure of HMPH and HMP is in the arrangement of PYO and how it interacts with the clay component (Fig. 11).

Fig. 11 Snapshot of the MD simulation of neutral pyocyanin (a) and (b) in the interlayer (yz) and (c) on the basal surface (xz) of hydrated Na-montmorillonite. The atom coloring scheme is as follows: Na = purple; O = red; Mg = green; Si = orange; C = grey; N = blue; H = white. Water not shown on image “a” for clarity.

The dominant peak of o′ was at 4.87 Å from the basal ob and another small peak at 2.95 Å from the basal ob (Fig. 8(d)). The dominant peak was right in the middle of the interlayer suggesting that most PYO molecules were adsorbed in the midplane. The major o′ peaks were 1.07 and 1.90 Å from both Na⁺ suggesting an ion–dipole interaction. Hence, the ion–dipole interaction in DMP is shorter (0.54 and 1.20 Å) than in HMP (1.07 and 1.90 Å). The major o′ peak is about 2.20 Å from the major h* peak implying the possibility of H-bonding.

The C (i.e., c3) peak was 2.94 Å from the basal ob. The distance of the H-methyl from the surface ob can be estimated as 1.94 Å which is the same as the value observed for HMPH but lower than DMP. Hence, interaction between the H-methyl and the basal ob is more favourable under humid conditions.

3.3 Interlayer bonding between adsorbed pyocyanin and montmorillonite

Radial distribution functions, derived from the equilibrated MD simulations, help to better assess the relative strengths of atom–atom interactions.

3.3.1 Dehydrated and hydrated montmorillonite. the major interaction for equilibrated DM simulations: Na⁺–ob (basal) ≈ 3 Å, Na⁺–apical oxygen ≈ 4.75 Å, and Na⁺–Na⁺ repulsion ≈ 5.5 Å (Fig. 12(a)). In general, this indicates a strong interaction between Na and basal oxygens and strong repulsion between Na ions, respectively. For HM, the major interaction was the coordination of water molecules around Na⁺ at about 2.3 Å (i.e., Na⁺–O*) followed by another Na–water coordination peak ≈ 4.4 Å (Fig. 12(b)) representing the first and second layer of water, respectively. The Na⁺–Na⁺ repulsion also is reduced, compared to DM, due to the coordination of water molecules around Na⁺. These interactions of the montmorillonite layer and the interlayer components have been reported in previous studies.³⁸

Fig. 12 The radial distribution function of (a) dehydrated and (b) hydrated Na-montmorillonite.

3.3.2 Dehydrated PYOH⁺–montmorillonite. For the DMPH simulations, the major interactions followed the trend (Fig. 13(a)): ion–dipole between Na⁺ and the oh of pyocyanin at a distance of about 2.7 Å > electrostatic attraction between Na⁺ and basal oxygens at 2.85 Å > ion–dipole interaction between Na⁺ and N at ≈3 Å. Therefore, in dry conditions, the major mechanism of interaction between PYOH⁺ and exchange cations in montmorillonite was ion–dipole interaction. This interaction might not be stable because of the vibration of the hydroxyl group that could lead to the repulsion of the Na⁺. The ho–ob electrostatic interaction is discouraged, despite been suggested by the ADP, because of the repulsion of the proton by the surface adsorbed Na⁺. The ho–ob electrostatic interaction might be favorable in low-charged montmorillonite. Other interactions within the interlayer were between the basal oxygens and: the hydrogens of the methyl group (as suggested by the ob–c3 interaction at a distance of 3.75 Å) > the ho of pyocyanin (as suggested by the ob–oh interaction at a distance of 2.7 Å). Considering the length of the C–H bonds, the interaction between ob and H of methyl was less than 2.5 Å.

Fig. 13 The radial distribution function of PYOH⁺–montmorillonite in (a) dry condition, (b) humid condition, (c) PYO–montmorillonite in dry condition, and (d) humid condition.

3.3.3 Hydrated PYOH⁺–montmorillonite. Similar to HM, the dominant interaction in the interlayer of HMPH is coordination of Na⁺ by water molecules at a distance of 2.35 Å > H-bonding between pyocyanin (oh) and water as suggested by the oh–o* coordination at a distance of about 2.6 Å (Fig. 13(b)). Other interactions include Na–oh ion–dipole interaction at about 2.6 Å, Na⁺–N ion–dipole interaction at about 3.05 Å, and water bridges between Na⁺ and OH (inset Fig. 13(b)). Hence, humidity condition influences the dominant interaction mechanism in PYOH⁺–montmorillonite. In dry condition, the Na⁺–oh ion–dipole interaction was dominant while under humid conditions, water outcompetes PYOH⁺ for Na⁺.

3.3.4 Dehydrated PYO–montmorillonite. Similar to DMPH results, the dominant interaction followed the trend (Fig. 13(c)): Na⁺–o′ ion–dipole of length ≈ 2.30 Å > Na⁺–ob electrostatic attraction ≈ 2.80 Å > Na⁺–N ion–dipole of length ≈ 2.80 Å. Hence, similar interaction mechanism dominated the interaction of montmorillonite and pyocyanin in dry conditions irrespective of the speciation of pyocyanin. The DMP structure is different from the DMPH in that: (i) the proportion of Na⁺–oxygen ion–dipole is at least three times higher in DMP partly because of the larger number of Na⁺ ions in the interlayer (ii) the coordination distance between Na⁺–oxygen is shorter (i.e., stronger) in DMP.

3.3.5 Hydrated PYO–montmorillonite. In contrast to HMPH, the dominant interaction were (Fig. 13(d)): ion–dipole Na–o′ 2.35 Å > coordination of Na⁺–o* ≈ 2.35 Å > H-bonding between water and pyocyanin as suggested by the 3.10 Å o*–o′. Other interactions include the 2.95 Å Na–N ion–dipole. Hence, humidity condition does not strongly influence the mechanism of interaction between PYO and montmorillonite. In both the humid and dry montmorillonite, the Na–o′ ion–dipole interaction was most favored. The observation that PYO can outcompete water for the interlayer cation further supports the observed stability of pyocyanin–montmorillonite complexes.¹⁴

4. Conclusion

This experiment-guided molecular simulation study investigated the interaction mechanism and the structure of protonated (PYOH⁺) and zwitterionic (PYO) pyocyanin in the interlayer of Na-montmorillonite in dry and humid conditions. Large-scale molecular dynamics simulations and accurate interatomic potentials were used to determine stable structures and configurations of pyocyanin species, water molecules, and counterions within the interlayer gallery of montmorillonite. With limited experimental and spectroscopic data for organic-clay systems, the molecular simulations provide key insights into the nature of atomic interactions in the interlayer of smectite minerals. Based on the equilibrated MD simulations, the following conclusions were reached:

(1) In dry condition, PYOH⁺ and PYO are well-ordered, oriented subparallel to the basal surface and situated between basal surface-adsorbed Na⁺.

(2) In humid conditions, Na⁺, PYOH⁺ and PYO are solvated near the midplane of the interlayer gallery and the pyocyanin molecules are less orderly arranged compared to MD results for the dry DMPH and DMP systems.

(3) The dominant interlayer bonding in DMPH is mainly a 2.7 Å ion–dipole between Na⁺ and the –OH of PYOH⁺ and, to a lesser degree, ion–dipole interaction between Na⁺ and N at a distance of about 3 Å. In DMP, these two interactions were also observed but occur at shorter distances of 2.30 Å (Na–OH) and 2.80 Å (Na–N). Hence, similar interaction mechanisms dominated the interaction of montmorillonite and pyocyanin in dry conditions irrespective of the speciation of pyocyanin.

(4) The dominant interlayer bonding in HMPH is between the Na⁺ and water. This bonding is at least an order of magnitude greater than the interaction between –OH of PYOH⁺ and water which suggests that PYOH⁺ cannot outcompete water for adsorption sites. Water bridged Na⁺ and PYOH interaction were also observed. In HMP, the dominant pair coordination was ion–dipole Na⁺–o′ at 2.35 Å and, to a lesser degree, H-bonding between water and PYO. The Na⁺–o′ coordination is more common compared to the coordination of water to Na⁺. Therefore, unlike PYOH⁺, the PYO molecules can outcompete water for the Na⁺ in the interlayer. There is on-going spectroscopic work to verify these mechanisms.

Overall, this molecular dynamics simulation study improved the understanding of the arrangement of pyocyanin species in the interlayer of montmorillonite and, provided insights into the main mechanisms of interaction in pyocyanin–montmorillonite complexes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the provision of supercomputing facilities and software by the Texas A&M University High Performance Research Computing (HPRC). The research was financially supported by the Department of Soil and Crop Sciences, Texas A&M University and the Joe and Martha Dixon Endowment. Thank you to Diane Uwacu for reviewing the codes used for post-processing of the MD results.

References

1. D. V. Mavrodi, R. F. Bonsall, S. M. Delaney, M. J. Soule, G. Phillips and L. S. Thomashow, Functional analysis of genes for biosynthesis of pyocyanin and phenazine-1-carboxamide from Pseudomonas aeruginosa PAO1, J. Bacteriol., 2001, 183, 6454–6465.
2. K. J. Reszka, Y. O’Malley, M. L. McCormick, G. M. Denning and B. E. Britigan, Oxidation of pyocyanin, a cytotoxic product from Pseudomonas aeruginosa, by microperoxidase 11 and hydrogen peroxide, Free Radical Biol. Med., 2004, 36, 1448–1459.
3. K. L. Tomlin, O. P. Coll and H. Ceri, Interspecies biofilms of Pseudomonas aeruginosa and Burkholderia cepacia, Can. J. Microbiol., 2001, 47, 949–954.
4. A. Price-Whelan, L. E. P. Dietrich and D. K. Newman, Nat. Chem. Biol., 2006, 2, 71–78.
5. J. B. Lyczak, C. L. Cannon and G. B. Pier, Clin. Microbiol. Rev., 2002, 15, 194–222.
6. T. Das and M. Manefield, Pyocyanin Promotes Extracellular DNA Release in Pseudomonas aeruginosa, PLoS One, 2012 DOI:10.1371/journal.pone.0046718.
7. T. Das, A. I. Ibugo, W. Klare and M. Manefield, Microbial Biofilms – Importance and Applications, InTech, 2016.
8. P. K. Taylor, A. T. Y. Yeung and R. E. W. Hancock, Antibiotic resistance in Pseudomonas aeruginosa biofilms: Towards the development of novel anti-biofilm therapies, J. Biotechnol., 2014, 191, 121–130.
9. K. C. Costa, M. Bergkessel, S. Saunders, J. Korlach and D. K. Newman, Enzymatic degradation of phenazines can generate energy and protect sensitive organisms from toxicity, mBio, 2015, 6(6), 10–1128.
10. J. Jabłońska, A. Augustyniak, K. Dubrowska and R. Rakoczy, The two faces of pyocyanin–why and how to steer its production?, World J. Microbiol. Biotechnol., 2023, 39, 103.
11. H. Hirakawa, A. Kimura, A. Takita, S. Chihara, K. Tanimoto and H. Tomita, Adsorption of extracellular proteases and pyocyanin produced by Pseudomonas aeruginosa using a macroporous magnesium oxide-templated carbon decreases cytotoxicity, Curr. Res. Microb. Sci., 2022, 3, 100160.
12. D. Wang, W. Johnston, S. Ching, B. Fashina and Y. Deng, in Poultry Science Asociation 2022 Latin America Scientific Conference, Parana, 2022.
13. B. Fashina and Y. Deng, Smectite, sepiolite, and palygorskite for inactivation of pyocyanin, a biotoxin produced by drug-resistant Pseudomonas aeruginosa, Microporous Mesoporous Mater., 2022, 331, 111668.
14. B. Fashina and Y. Deng, The effect of layer charge origin and density, type of interlayer cations, and occupancy of the octahedral sheet of smectites on the adsorption of pyocyanin, Appl. Clay Sci., 2023, 237, 106884.
15. J. A. Greathouse and R. T. Cygan, Water structure and aqueous uranyl(VI) adsorption equilibria onto external surfaces of beidellite, montmorillonite, and pyrophyllite: Results from molecular simulations, Environ. Sci. Technol., 2006, 40, 3865–3871.
16. V. Aggarwal, H. Li and B. J. Teppen, Triazine adsorption by saponite and beidellite clay minerals, Environ. Toxicol. Chem., 2006, 25, 392–399.
17. Q. Zhou, W. Shen, J. Zhu, R. Zhu, H. He, J. Zhou and P. Yuan, Structure and dynamic properties of water saturated CTMA-montmorillonite: molecular dynamics simulations, Appl. Clay Sci., 2014, 97–98, 62–71.
18. M. Maruthi Sena and M. Krishnan, Role of Cations in Adsorption of Supercritical Carbon Dioxide at Smectite Mineral-Water Interfaces: Molecular Dynamics and Adaptive Biasing Force Simulation Studies, J. Phys. Chem. C, 2019, 123, 1170–1184.
19. M. Szczerba, Y. Deng and M. Kowalik-Hyla, Molecular Modeling to Predict the Optimal Mineralogy of Smectites as Binders of Aflatoxin, Clays Clay Miner., 2022, 70(6), 824–836.
20. T. A. Ho, C. F. Jove-Colon and Y. Wang, Low hydrogen solubility in clay interlayers limits gas loss in hydrogen geological storage, Sustainable Energy Fuels, 2023, 7(14), 3232–3238.
21. D. S. Biovia, Material Studio, v. 08, San Diego Dassault Syst, 2018.
22. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19.
23. A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool, Model. Simul. Mater. Sci. Eng., 2009, 18, 15012.
24. J. H. Lee and S. Guggenheim, Single crystal X-ray refinement of pyrophyllite-1 Tc, Am. Mineral., 1981, 66, 350–357.
25. P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Structure and energetics of ligand binding to proteins: Escherichia coli dihydrofolate reductase-trimethoprim, a drug-receptor system, Proteins: Struct., Funct., Bioinf., 1988, 4, 31–47.
26. O. Teleman, B. Jönsson and S. Engström, A molecular dynamics simulation of a water model with intramolecular degrees of freedom, Mol. Phys., 1987, 60, 193–203.
27. R. T. Cygan, J.-J. Liang and A. G. Kalinichev, Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field, J. Phys. Chem. B, 2004, 108, 1255–1266.
28. R. T. Cygan, J. A. Greathouse and A. G. Kalinichev, Advances in Clayff Molecular Simulation of Layered and Nanoporous Materials and Their Aqueous Interfaces, J. Phys. Chem. C, 2021, 125, 17573–17589.
29. T. A. Ho, L. J. Criscenti and J. A. Greathouse, Revealing Transition States during the Hydration of Clay Minerals, J. Phys. Chem. Lett., 2019, 10, 3704–3709.
30. L. N. Lammers, I. C. Bourg, M. Okumura, K. Kolluri, G. Sposito and M. Machida, Molecular dynamics simulations of cesium adsorption on illite nanoparticles, J. Colloid Interface Sci., 2017, 490, 608–620.
31. S. L. Teich-McGoldrick, J. A. Greathouse, C. F. Jové-Colón and R. T. Cygan, Swelling Properties of Montmorillonite and Beidellite Clay Minerals from Molecular Simulation: Comparison of Temperature, Interlayer Cation, and Charge Location Effects, J. Phys. Chem. C, 2015, 119, 20880–20891.
32. J. A. Greathouse, D. B. Hart, G. M. Bowers, R. J. Kirkpatrick and R. T. Cygan, Molecular Simulation of Structure and Diffusion at Smectite-Water Interfaces: Using Expanded Clay Interlayers as Model Nanopores, J. Phys. Chem. C, 2015, 119, 17126–17136.
33. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017.
34. R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, 2021 DOI:10.1887/0852743920.
35. W. Shinoda, M. Shiga and M. Mikami, Rapid estimation of elastic constants by molecular dynamics simulation under constant stress, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103.
36. W. Ford, Krylov Subspace Methods, Numer. Linear Algebra Appl., 2015, 491–532.
37. Z. Malek, V. Balek, D. Garfinkel-Shweky and S. Yariv, The study of the dehydration and dehydroxylation of smectites by emanation thermal analysis, J. Therm. Anal., 1997, 48, 83–92.
38. L. Zhang, X. Lu, X. Liu, J. Zhou and H. Zhou, Hydration and mobility of interlayer ions of (Nax, Cay)-montmorillonite: A molecular dynamics study, J. Phys. Chem. C, 2014, 118, 29811–29821.
39. R. J. Graves and H. W. White, Study of the adsorption of acridine and phenazine on aluminum oxide using tunnelling spectroscopy, Spectrochim. Acta, Part A, 1987, 43, 107–118.
40. S. D. Choudhury and S. Basu, Interaction of phenazine with water and DNA bases, Spectrochim. Acta, Part A, 2005, 62, 736–739.
41. C. Marzzacco, Electronic spectra of the various hydrogen-bonded species of pyrazine in a mixed hydroxylic solvent, J. Am. Chem. Soc., 1973, 95, 1774–1777.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05762c

---