Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conformational preference of dipeptide zwitterions in aqueous solvents†
Francisco
Adasme-Carreño
 *ab,
Alvaro
Ochoa-Calle
*c,
Marcelo
Galván
*ab,
Alvaro
Ochoa-Calle
*c,
Marcelo
Galván
 c and
Joel
Ireta
c and
Joel
Ireta
 *c
*c
aCentro de Investigación de Estudios Avanzados del Maule (CIEAM), Vicerrectorá de Investigación y Postgrado Universidad Católica del Maule, Talca 3480112, Chile. E-mail: fadasme@ucm.cl
bLaboratorio de Bioinformática y Química Computacional (LBQC), Departamento de Medicina Traslacional, Facultad de Medicina, Universidad Católica del Maule, Talca 3480112, Chile
cDepartamento de Química, División de Ciencias Básicas e Ingeniería, Universidad Autónoma Metropolitana-Iztapalapa, Ciudad de México 09340, Mexico. E-mail: aochoagauge@gmail.com; iret@xanum.uam.mx
First published on 7th February 2024
Abstract
Proper description of solvent effects is challenging for theoretical methods, particularly if the solute is a zwitterion. Here, a series of theoretical procedures are used to determine the preferred solvated conformations of twelve hydrophobic dipeptides (Leu-Leu, Leu-Phe, Phe-Leu, Ile-Leu, Phe-Phe, Ala-Val, Val-Ala, Ala-Ile, Ile-Ala, Ile-Val, Val-Ile and Val-Val) in the zwitterionic state. First, the accuracy of density functional theory (DFT), combined with different implicit solvent models, for describing zwitterions in aqueous solvent is assessed by comparing the predicted against the experimental glycine tautomerization energy, i.e., the energetic difference between canonical and zwitterionic glycine in aqueous solvents. It is found that among the tested solvation schemes, the charge-asymmetric nonlocally determined local-electric solvation model (CANDLE) predicts an energetic difference in excellent agreement with the experimental value. Next, DFT-CANDLE is used to determine the most favorable solvated conformation for each of the investigated dipeptide zwitterions. The CANDLE-solvated structures are obtained by exploring the conformational space of each dipeptide zwitterion concatenating DFT calculations, in vacuum, with classical molecular dynamics simulations, in explicit solvents, and DFT calculations including explicit water molecules. It is found that the energetically most favorable conformations are similar to those of the dipeptide zwitterions in their respective crystal structures. Such structural agreement is indicative of the DFT-CANDLE accomplishment of the description of solvated zwitterions, and suggests that these biomolecules self-assemble as quasi-rigid objects.
1. Introduction
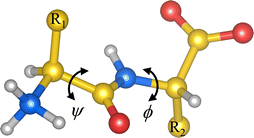
Under proper conditions, peptides as small as dipeptides (Fig. 1) self-assemble into ordered aggregates of different morphologies like piled layers, tubes, rods, hydrogels, etc.1–3 These aggregates are of great interest due to their resemblance to amyloid-like fibers,4,5 whose presence in human organs is associated with diseases like Alzheimer’'s and Parkinson's diseases.6 Peptide aggregates are also promising candidates for technological applications, owing to their remarkable electrical and mechanical properties.7–11 Understanding the self-assembly of such systems, at the molecular level, may thus be valuable for bottom-up design of bionanodevices10,12 and drug carriers,13 or for envisaging triggering factors of the amyloid fiber formation.All hydrophobic natural dipeptides have been crystallized (Fig. 2).14 Some of these dipeptides crystallize forming pores, and others do it as a set of layers.14 In these crystals, dipeptides assemble as zwitterions, i.e., with –NH3+ and –COO− as the capping groups (Fig. 1). In aqueous solvents, dipeptides prefer to be in the zwitterionic state too.15 Therefore, we would like to get insight into the influence that such locally charged but globally neutral state has on dipeptide conformations, which may be crucial along the self-assembly pathway of these systems. In this work, we use theoretical methods for investigating the influence of the zwitterionic state in the conformational preferences of two sets of hydrophobic natural dipeptides. Both sets of dipeptides crystallize forming pores. The set here named class V–A comprises the Ala-Val (AV), Val-Ala (VA), Ala-Ile (AI), Ile-Ala (IA), Ile-Val (IV), Val-Ile (VI) and Val-Val (VV) dipeptides, and the set labelled as class F–F includes the Phe-Phe (FF), Leu-Leu (LL), Leu-Phe (LF), Phe-Leu (FL) and Ile-Leu (IL). Determining peptide zwitterion conformations in solution is challenging using theoretical methods. This is primarily due to the inadequacy of the procedures commonly used for describing solvent effects, particularly in situations in which the solute is locally or globally charged.
Commonly, the non-zwitterionic N-acetyl-alanyl-N′-methylamide (Ac-Ala-NHMe) molecule is used to investigate peptide conformational preferences.16 Ac-Ala-NHMe is a capped peptide comprising two peptide bonds flanking a single side chain; hence, it is usually called dipeptide. The crystallized natural peptides mentioned above, however, are constituted by two amino-acid residues linked by one peptide bond. Thus these are named dipeptides too. Hereinafter the term dipeptide is used solely for referring to the latter systems. Dipeptide conformations are here characterized in terms of the ϕ and ψ torsional angles (Fig. 1), in the same way as these torsional angles are ordinarily used to describe the Ac-Ala-NHMe conformations.
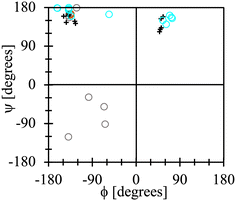
According to calculated Ramachandran maps for Ac-Ala-NHMe, i.e., plots of its potential energy surface (PES) in terms of ϕ and ψ, the most stable conformation in aqueous solvent is the so-called polyproline II conformation,17–22 outcome that has been confirmed using Raman optical activity experiments.23 If Ac-Ala-NHMe is considered to be in vacuum, the preferred conformation is predicted to be an extended one,24,25 a geometry similar to that of protein residues in strands forming β-sheets.26 The β-sheets are common protein backbone conformations characterized by ϕ, ψ mean values around −130°, 144° in antiparallel β-sheets and −122°, 137° in parallel β-sheets, respectively.27 Thus, either in aqueous solvent or in vacuum, Ac-Ala-NHMe prefers to adopt conformations that lie in the upper left quarter of the Ramachandran map (Fig. 3).28 Molecules containing glycine (Gly) instead of Ala behave similarly.15,29 The conformations of class V–A dipeptides in crystals grown in aqueous solutions are similar to those of a β-strand segment (Fig. 3). These conformations are characterized by ϕ, ψ dihedral angles with values around −137° and 155°, respectively.30 However, conformations of class F–F dipeptides in their crystals are quite different from those of the class V–A (Fig. 3). Conformations of class F–F dipeptides lie in the upper right quarter of the Ramachandran map and are characterized by a ϕ angle around 60°, and a ψ angle with values between 120° and 170° (Fig. 3).30
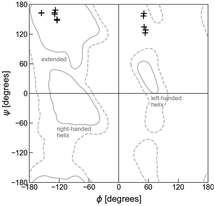 | ||
| Fig. 3 Ramachandran plot and dipeptide conformations in the crystals. The + symbols at the upper left quarter correspond to the V–A class conformations in the crystals (side chains in trans orientation). The + symbols at the upper right quarter correspond to the F–F class conformations in the crystals (side chains in cis orientation). Solid lines account for the 95% of residue conformations in protein crystals, and dashed lines for 99%.31 Apart from the extended conformations, that usually form part of β-sheets and polyproline II motifs, regions in which residue conformations correspond to right- and left-handed helices, other major backbone motifs of proteins, are also indicated. | ||
Despite the conformational differences described above, both classes of dipeptides, the F–F and V–A, crystallize as a bundle of tubes in aqueous solutions.32,33 In such crystal structures, however, class V–A dipeptides accommodate their side chains in a trans arrangement, while the class F–F dipeptides do it in a cis conformation, with respect to the peptide plane (Fig. 2). Consequently, the interior of the formed tubes is hydrophobic and narrow in class V–A crystals, whereas hydrophilic and wide in the class F–F ones. These crystal morphologies seem to be dictated by inter- and intra-peptide interactions, as well as by interactions with the solvent.34–37 For example, if the FF crystal is grown in methanol or tetrahydrofuran instead of water, the crystal structure changes as well as the FF conformation in it, which becomes similar to an extended one, like the arrangement of amino-acid residues in strand-forming β-sheets.35,37
To determine the conformational preferences of dipeptide zwitterions in aqueous solvent, we use density functional theory (DFT) calculations and classical molecular dynamics (MD) simulations, combined with explicit and implicit solvent models. As mentioned above, proper description of solvent effects is challenging for theoretical methods. Particularly if the solute is a zwitterion, since it is a neutral molecule possessing both positive and negative electrical charges. Therefore, care should be taken in selecting the solvent model for investigating such kinds of systems. If an implicit solvent model is chosen, it should describe equally well both the cationic and anionic environments coexisting in the same molecule. The latter is not the case for commonly used implicit solvent models.38 If an explicit solvent model is used, it should be considered that a minimum number of water molecules is required to stabilize the zwitterionic state of a peptide.39,40 Inclusion of explicit solvent in DFT calculations has been mostly done for investigating microsolvation effects on the conformation of peptides and their relative stability at 0 K.27,41,42 Implicit solvent models, however, can be used to estimate relative stabilities at room temperature, as these models are usually parameterized to estimate free energies. Here we use both solvent models together with DFT calculations to determine the optimal conformation of the zwitterions in solvent and implicit solvent to determine relative stabilities at room temperature.
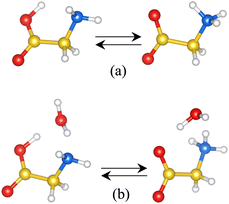
To choose a suitable implicit solvent model that adequately describes solvated dipeptide zwitterions, we first investigate the tautomerization reaction of Gly (Fig. 4). It is found that among the different implicit solvation models tested, the charge-asymmetric nonlocal determined local-electric (CANDLE) solvation model43 gives the best result for the free energy difference between the canonical and the zwitterionic state of Gly, as compared to the experimental value. Thus, geometries obtained for each dipeptide zwitterion, obtained combining MD simulations and DFT calculations, are solvated using CANDLE. In this manner, it is found that the most favorable conformation for dipeptide zwitterions in aqueous solution is quite similar to the conformation of the dipeptide in the corresponding crystal structure, and that the zwitterion–solvent interaction is fundamental in determining the preferred conformation of, primarily, the class F–F dipeptides. Furthermore, it is also found that the conventional continuum solvation model such as the integral equation formalism of the polarizable continuum model (PCM)44–46 predicts that only the V–A class dipeptides adopt conformations like these in their respective crystal structures. Lastly, it is argued that the obtained results help to understand the self-assembly mechanism of the investigated systems.
2. Methodology
2.1. Glycine tautomerization reaction
To select an adequate solvent model for describing solvated zwitterions, the energy associated with the Gly tautomerization reaction, ΔEtot (Fig. 4), is calculated at the DFT level of theory using the Perdew–Burke–Ernzerhof (PBE) approximation47 to the exchange–correlation functional, and the Grimme's D2 dispersion corrections.48 Several solvation models are tested: conventional continuum solvation models like PCM and the self-consistent reaction field solvation model (SMD),49 the self-consistent solvation models within the joint-density functional theory (JDFT),50 such as the PCM-like model proposed by Gunceler, Letchworth-Weaver, Sundararaman, Schwarz and Arias (GLSSA13),51 the spherically averaged liquid susceptibility ansatz (SaLSA),52 and CANDLE, a solvation model derived from SaLSA. The solvent is also described using classical DFT (CDFT) for fluids with a simplified free energy functional for liquid water.53 PCM and SMD are tested using the Gaussian 09 software54 with a 6-311+G(d,p) basis set. The other solvent models are used as implemented in the JDFTx code55 version 1.6.0, with the Garrity–Bennett–Vanderbilt library of ultrasoft pseudopotentials56 and a plane-waves basis set with an energy cutoff of 800 eV.2.2. Searching the lowest energy conformations for dipeptide zwitterions in aqueous solvent
The conformational space of the investigated dipeptides in the canonical state, i.e., with –NH2 and –COOH as capping groups, is explored to identify the allowed conformations in vacuum. The canonical state is used in this point of the study because it is known that the zwitterionic state is not stable in vacuum. The PES as a function of the torsion angles ϕ and ψ (Fig. 1) is calculated using PBE and the dispersion correction method reported by Tkatchenko and Scheffler (TS),57 as PBE-TS has been shown to properly describe peptide systems.11,30,58 Plane waves and pseudopotentials together with the projector augmented-wave method59,60 are used with an energy cutoff of 1100 eV. The dipeptide in vacuum is modeled using the supercell approach, where the unit cell is chosen large enough to avoid interactions with neighboring images. The Γ-point is employed for sampling the Brillouin zone. These DFT calculations are carried out with the Vienna ab initio simulation package (VASP).60,61The PES maps are obtained varying the torsion angles ϕ and ψ from −180° to 180° in twelve steps of 30° each, yielding a total of 144 distinct geometries. The latter are subjected to geometry optimization using the RMM-DIIS algorithm62 (or the conjugate gradient algorithm upon convergence issues) with a convergence criterion of a maximum force of 1.2 × 10−2 eV Å−1. The atoms defining ϕ and ψ are fixed and the others fully optimized. The positions for the fixed atoms are chosen such that bond distances and angles associated with them equal those of the optimal geometry of the fully extended conformation in vacuum. The optimal orientation of the carboxyl capping group is only evaluated for the FF dipeptide varying the N–C–C–O dihedral angle. The –COOH orientation with the lowest energy for each (ϕ, ψ) pair in FF is used in the initial geometry for all the other dipeptides. The full PES maps are generated using a cubic spline interpolation.
The structures connected to the minima thus obtained are further relaxed without constraints. Afterwards, these optimized canonical dipeptides are turned into zwitterions, solvated with explicit water molecules by inserting them into a pre-equilibrated cubic box of water molecules with a padding of 10 Å. For this the VMD software is used.63 The solvent is fully relaxed around the dipeptides using a classical MD equilibration protocol. The water molecules are first energetically minimized by 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps using the conjugate gradient and line search algorithm. The CHARMM36 force field64 with the CMAP correction is used to describe the dipeptides together with the TIP3P water model.65 The particle mesh Ewald algorithm66 is chosen to treat the electrostatic interactions under periodic boundary conditions, and the van der Waals forces are smoothly switched off between 9 and 10 Å. The minimization is followed by two 100 ps NVT and 500 ps NPT MD simulations. A 2 fs integration time step is used with the water covalent bonds restrained by the SETTLE algorithm.67 The r-RESPA algorithm68 is used to integrate the equations of motion, with non-bonded short-range forces computed every time step and a full electrostatic evaluation every five time-steps. The temperature is kept at 300 K using a Lanvegin thermostat with a damping coefficient of 2 ps−1. Pressure is kept at 1 atm by the Nose–Hoover Langevin piston method,69,70 with an oscillation period of 400 fs and a damping timescale of 300 fs. The dipeptide atoms are fixed at the initial coordinates. These calculations are performed using the NAMD v2.14 software.71
000 steps using the conjugate gradient and line search algorithm. The CHARMM36 force field64 with the CMAP correction is used to describe the dipeptides together with the TIP3P water model.65 The particle mesh Ewald algorithm66 is chosen to treat the electrostatic interactions under periodic boundary conditions, and the van der Waals forces are smoothly switched off between 9 and 10 Å. The minimization is followed by two 100 ps NVT and 500 ps NPT MD simulations. A 2 fs integration time step is used with the water covalent bonds restrained by the SETTLE algorithm.67 The r-RESPA algorithm68 is used to integrate the equations of motion, with non-bonded short-range forces computed every time step and a full electrostatic evaluation every five time-steps. The temperature is kept at 300 K using a Lanvegin thermostat with a damping coefficient of 2 ps−1. Pressure is kept at 1 atm by the Nose–Hoover Langevin piston method,69,70 with an oscillation period of 400 fs and a damping timescale of 300 fs. The dipeptide atoms are fixed at the initial coordinates. These calculations are performed using the NAMD v2.14 software.71
A single frame from the trajectory is selected for each dipeptide such that the backbone hydrogen bond (H-bond) acceptors and donors form an expected minimum number of hydrogen bonds; i.e., 3 for –NH3+ cap, 6 for –COO− cap, 2 for backbone –CO, and 1 for backbone –NH. Water molecules that do not interact with the dipeptide are removed. The microsolvated geometries are then geometry optimized with PBE-TS, first with the dipeptide atoms fixed to optimize the orientation of the water molecules, and next fully optimizing all the atomic coordinates. These calculations are carried out using VASP with the same parameters as those used in the PES calculations.
Finally, the optimized geometries for the microsolvated dipeptide zwitterions are solvated with the implicit solvent models CANDLE and PCM, and fully geometry optimized under each scheme. As is shown below, CANDLE is chosen owing to the adequate description of the Gly tautomerization reaction. PCM is also chosen for contrasting the CANDLE results against a commonly used solvation scheme. In this latter step microsolvation water molecules are not considered.
3. Results and discussion
3.1. Glycine tautomerization reaction
In aqueous solution, the canonical and zwitterionic Gly states coexist in chemical equilibrium. Measurements of the corresponding tautomerization free energy, ΔG, indicate that the zwitterionic state is more stable by 7.3 kcal mol−1 than the canonical one at a temperature of 298 K.72,73 These experimental results opened a theoretical discussion about the number of water molecules needed to stabilize the otherwise unstable Gly zwitterion,74–76 and whether implicit solvent models are able to stabilize the zwitterion over the canonical state. It has been suggested that an explicit water molecule should be added for predicting ΔG values close to the experimental one with implicit solvent models.77Starting from the geometries reported in ref. 77, we calculate the relative stability of zwitterionic Gly with respect to the canonical one, using the solvent models mentioned in the methodology section and two models for representing the solute: the non-assisted model (NAM), in which the solute is the bare Gly, and the assisted-model (AM) in which the solute is Gly plus a water molecule. Both, the canonical and zwitterionic Gly conformations here investigated are such that all heavy atoms lay in the same plane (Fig. 4). In the canonical glycine, the –OH group lays in the same plane as the heavy atoms, and it is located such that it can form a hydrogen bond with the –NH2 group (Fig. 4(a)). In the AM, the water molecule is located between the amine and carboxilate groups such that it forms hydrogen bonds with both groups either in the canonical and in the zwitterionic state (Fig. 4(b)). The solvated canonical and zwitterionic AM and NAM are fully optimized using each of the solvation schemes.
According to the results for ΔEtot listed in Table 1, all the solvation schemes predict the zwitterionic Gly as the energetically favorable tautomer in solution, either with NAM or AM. Except for PCM which only in combination with the AM forecasts the expected ordering. We compare ΔEtot directly against the experimental free energies as the implicit solvation schemes here used were parameterized to predict free solvation energies. Notably, ΔEtot calculated with CANDLE and the AM differ by less than 1 kcal mol−1 from the experimental tautomerization free energy, and CANDLE in combination with NAM predicts that only the zwitterionic state exists in aqueous solvent. Hence, to be able to calculate ΔEtot with CANDLE and the NAM we perform single-point calculations combining the PCM-optimized geometries with CANDLE. The latter is also done using the GLSSA13 and CDFT solvation schemes. Unexpectedly, all but one of the ΔEtot values calculated in this manner are in better agreement with the experimental value; e.g., we get a difference between experiment and theory of less than 0.1 kcal mol−1 solvating with CANDLE the PCM-optimized NAM. Nevertheless, the PCM-optimized NAM, solvated with the other solvation schemes, still underestimates the experimental value (in absolute value) by ∼2.5 kcal mol−1 (34%) or more. Conversely, all the solvation schemes improve the estimation of the tautomerization energy if the AM is used instead of the NAM. Except for CANDLE in combination with the PCM-optimized geometries. Yet, CANDLE together with the AM provides a better estimation of the tautomerization energy than the other solvation schemes combined with the AM. The appropriate performance of CANDLE is related to the fact that it is calibrated to describe solvation free energies at 298 K of negative and positive species with the same accuracy. For calibrating the CANDLE parameters a set of 346 free energies (240 of neutral molecules, 54 of cations and 55 of anions) obtained at 298 K was used, as reported in ref. 43, 78 and 79. Accordingly, for investigating the most stable conformation of the V–A and F–F dipeptides in aqueous solvent, we use PCM-optimized NAM geometries solvated with CANDLE, and further re-optimized under the CANDLE solvation scheme. The energies thus obtained are used for the conformational ordering described below. For comparison purposes we also report the energetic analysis obtained with PCM and the NAM, as PCM is a commonly used implicit solvation model.
3.2. Conformational search in vacuum
To determine the most stable conformations for the V–A and F–F classes of dipeptide zwitterions in solution, we first explore the conformational space for the corresponding canonical dipeptides in vacuum. For this, we calculate a PES in terms of (ϕ, ψ) for each of the investigated dipeptides using DFT-PBE/TS. These Ramachandran-like maps exhibit well-defined minima labelled according to the corresponding orientations of the side chains (either cis or trans with respect to the peptide bond plane), as shown in Fig. 5. The regions of low energy somewhat agree with the most-populated Ramachandran regions in proteins (gray lines), but the shape and location differ significantly, likely due to the structural differences among protein residues and the dipeptides studied here; i.e., a protein residue is more like Ac-Ala-NHMe. Dipeptide structures associated with the minima labelled as t and c, are similar to the trans and cis dipeptide conformations observed in their crystal structures. The (ϕ, ψ) angles corresponding to the actual dipeptide conformations in these crystals are marked by + symbols in the maps. As can be seen in Fig. 5, all the + marks lay inside the energy basins labelled with t or c, and in some cases the marks are at the basin minimum. The t minima are in the region that is associated with extended conformations such as β sheets in proteins. In contrast, the c minima are located in an area that is scarcely populated by protein residues and even considered to be an energetically prohibited region for a hard-spheres model of Ac-Ala-NHMe.80 For all the dipeptides at least two other well defined minima are found, in one of them dipeptides have their side chains in cis conformation (minima labelled as c′), and in the others in trans conformation (minima labelled as t′ or t′′ if a fifth minimum exist). The t′′ minima are shallow and appears only for AI, AV, FF and FL. Basins associated with the c′ minima are close to the Ramanchandran region connected to right-handed α-helices in proteins, and those associated with the t′ minima of the V–A dipeptide class to the left-handed α-helices. However, the corresponding basins to t′ and t′′ minima for the F–F class are in a region poorly populated in protein Ramachandran maps.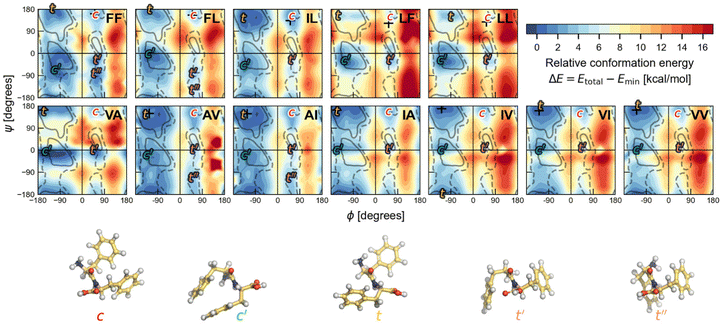 | ||
Fig. 5 Ramachandran PES of each the twelve investigated dipeptides in vacuum. Relative energies are referred to the lowest minimum at each PES. + symbols indicate the conformation observed in the corresponding crystals. The minimum position at each basin is labelled with t (in yellow) if the relative side chain orientation is trans, or with c (in red) if such orientation is cis. The labels 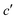 (in green), (in green), 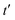 and and 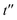 (both in pink) stand for minima connected to alternative cis and trans conformations not observed in dipeptide crystals. Solid lines account for 95% of proteins, and dashed lines for 99%.31 FF geometries at each of the minima found in the corresponding PES are shown at the bottom. Carbon atoms are colored in yellow, oxygen atoms in red, nitrogen atoms in blue, and hydrogen atoms in light gray. (both in pink) stand for minima connected to alternative cis and trans conformations not observed in dipeptide crystals. Solid lines account for 95% of proteins, and dashed lines for 99%.31 FF geometries at each of the minima found in the corresponding PES are shown at the bottom. Carbon atoms are colored in yellow, oxygen atoms in red, nitrogen atoms in blue, and hydrogen atoms in light gray. | ||
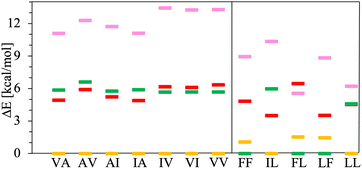
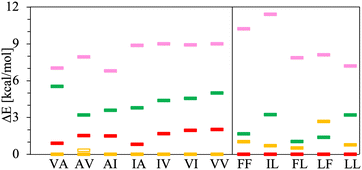
The chart in Fig. 6 shows the relative energies for the conformations connected to the minimum at each basin. These relative energies are referred with respect to the lowest one. All the lowest energy conformations of the V–A class dipeptides in vacuum belong to t basins, except for the V–A dipeptide whose lowest energy conformation is located in the corresponding c′ basin (Fig. 6). On the contrary, the lowest energy conformations of the F–F class belong to c′ basins, except for the IL dipeptide whose lowest energy conformation is located in the corresponding t basin. Notably, the energy difference between the t and the c′ minima is around 1 to 3 kcal mol−1 for all these canonical dipeptides in vacuum. Nevertheless, none of these dipeptides crystallize adopting a conformation connected to a c′ basin. In Fig. 6 are also depicted the relative energies for the canonical dipeptides in vacuum investigated by Gonzalez-Diaz et al.30 (the + symbols). As it can be seen, some of these conformations are lower in energy than the ones found here, although by less than 1 kcal mol−1. The discrepancy is attributed to the orientation of the –COOH capping group. Here it was only sampled for FF, but the ideal orientation may vary depending on the dipeptide and conformation. That may account for the inconsistencies found for VA and IL.
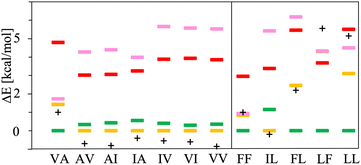 | ||
| Fig. 6 Relative energies, ΔE in kcal mol−1, of the canonical dipeptide conformations in vacuum connected to the t (in yellow), c (in red), t′ (in pink) and c′ (in green) minima along the potential energy surfaces shown in Fig. 5. The reference energy corresponds to the lowest energy conformation found in this work for each system. Left panel class V–A dipeptides. Right panel class F–F dipeptides. For LF, the energy of t and c conformations is the same, therefore a yellow mark is not distinguishable for this dipeptide. The + symbols stand for the ΔE values corresponding to the canonical gas-phase dipeptides reported in ref. 30. | ||
3.3. Conformations of dipeptide zwitterions in aqueous solvent
Next, solvation effects are assessed following two steps. First, it is evaluated if structures connected to the energy basins found for the canonical dipeptides in vacuum preserve their conformation upon transforming them into solvated zwitterions. For that, the structures connected to the minima of each basin are transformed into zwitterions, solvated with explicit solvent and subjected to a md simulation to properly distribute the water molecules around the dipeptide zwitterion (see the methodology section). Then, the solute with a microsolvation shell is extracted from the md trajectories. Such microsolvated dipeptide zwitterions are further fully geometry-optimized using DFT-PBE/TS. The number of water molecules in the microsolvation shells fluctuates between 8 and 13, depending on the dipeptide and the conformation (see Fig. S1 and S2 of the ESI†). The water molecules in the microsolvation shell are chosen such that the backbone amine and carbonyl groups, as well as the charged –NH3+ and –COO− capping groups, form all the expected H-bonds. We have found that after optimization, microsolvated dipeptide geometries change slightly (up to 20° for both ϕ and ψ) except for the AV and AI conformers belonging to the t′′ minima. Thus, for most of the dipeptide zwitterions the initial arrangement of their side chains (either trans or cis) is the same after optimization. For AV and AI, the structures connected to the t′′ minima turned the side chain position into cis upon optimization due to changes in ϕ and ψ around 40°. However, that change is not large enough for considering such structures as part of the c′ basins. Based on these results one can conclude that solvation and transformation to a zwitterionic state keep the structure in the energetic basin found for the canonical dipeptide in vacuum, and that the conformation, as measured with ϕ and ψ, changes little, i.e., charged endings in zwitterions do not have a sizable effect on the dipeptide conformation; however, as it is discussed below, they affect the energetic ordering.In the second step for evaluating the solvation effects, the microsolvation shell of the optimized dipeptide zwitterions is stripped out. Then, these are solvated with implicit solvent. In this step we have also considered other dipeptide conformations belonging to the t and c basins, namely the dipeptide zwitterions obtained from the conformations marked with + symbols in Fig. 5. All these structures are fully optimized considering the PCM implicit solvent. Next, the lowest energy conformations found at each basin are chosen for the energy comparison presented in Fig. 7. According to these results, all class V–A PCM-solvated dipeptide zwitterions and some of the class F–F (IL and LL) prefer to adopt a conformation belonging to the t basin. The other class F–F PCM-solvated dipeptide zwitterions prefer to adopt conformations belonging to the c′ basin. Lastly, the PCM-optimized structures are further optimized considering them solvated with the CANDLE implicit solvent model. The energy comparison of the lowest energy conformations found at each basin is presented in Fig. 8. For class V–A, all dipeptide zwitterions prefer to adopt conformations belonging to the t basin, as it is found using PCM. However, for class F–F, the outcome is different; all dipeptide zwitterions prefer to adopt conformations belonging to the c basin. Differences in the results obtained with PCM and CANDLE are also noticeable in the energetic ordering of the conformations belonging to the other basins. While CANDLE predicts that the second most stable conformation is around 1 to 2 kcal mol−1 above the most stable ones, PCM predicts differences ranging from 1 to 7 kcal mol−1. Moreover, CANDLE predicts that the two lowest energy conformations are connected either to basin t or basin c, except for LF that prefer basin c′ for the second lowest energy conformation, whereas PCM predicts that the two lowest energy conformations belong to basin t, c′ or c. Yet, both implicit solvation schemes predict that for all dipeptide zwitterions but one (solvated with PCM), the least stable conformation is the connected to the t′ basin.
It is noteworthy that the lowest energy conformations for all the dipeptide zwitterions solvated with CANDLE, except one, are alike to those observed in their corresponding crystal structures, as is illustrated by the Ramachandran-like plot depicted in Fig. 9. The exception is the conformation for the AV dipeptide, which still belongs to the t basin but with a ϕ angle differing about 100° with respect to the experimental value. For that structure, however, an alternative conformation is found in the t basin that is solely ∼0.3 kcal mol−1 higher in energy than the lowest one (see Fig. 8). This second structure has a ϕ angle that differs by less than 20° from the ϕ value for the dipeptide zwitterion in the crystal structure (brown open dot in Fig. 9).
According to the results presented above, the CANDLE solvation scheme is the one that predicts accurately the tautomerization free energy for glycine. Hence, one may assume that it also correctly describes class V–A and F–F dipeptide zwitterions in aqueous solvent. The latter is supported by our findings about the most stable dipeptide conformations in aqueous solvent, i.e., the CANDLE-solvated dipeptide zwitterions prefer conformations similar to the ones in their corresponding crystal structures.
These results suggest that along the self-assembling path for these systems, the dipeptide zwitterions behave like semi-rigid objects in aqueous solvents, changing little their backbone conformation and side chains relative orientations, thus avoiding large conformational changes that could prevent them from crystallizing in a reasonable time. Therefore, it can be suggested that diffusion and desolvation, but not the conformational changes, should play a major role in the self-assembly process of such systems.
4. Conclusions
In this work, we have presented evidence indicating that PBE plus van der Waals corrections, together with the implicit solvent CANDLE adequately describes zwitterions in aqueous solutions. Particularly, the ΔG of the tautomerization reaction of Gly in aqueous solvent is accurately predicted, and it is shown that the twelve dipeptide zwitterions resulting from combining Ala, Ile, Leu, Val and Phe hydrophobic amino acids adopt a conformation in aqueous solvent quite similar to that in their corresponding crystal structures. Therefore, it can be suggested that the process that leads to the formation of the corresponding crystal structures involves an assembly of semi rigid objects, which may ease the crystallization of such dipeptide zwitterions from aqueous solutions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank LANCAD and CONACTY for the computer time granted on the supercomputer Yoltla at the LSVP at UAM-Iztapalapa. J. I. acknowledges funding from CONACYT project A1-S-42775 and 1561802. F. A.-C. acknowledges funding from ANID FONDECYT Postdoctorado 2018 no. 3180193 and ANID Convocatoria Nacional Subvención a Instalación en la Academia, Convocatoria año 2021, Folio SA772100091.Notes and references
- C. H. Gorbitz, Chem. – Eur. J., 2007, 13, 1022–1031 CrossRef PubMed.
- C. Yuan, W. Ji, R. Xing, J. Li, E. Gazit and X. Yan, Nat. Rev. Chem., 2019, 3, 567–588 CrossRef CAS.
- M. Monti, E. Scarel, A. Hassanali, M. Stener and S. Marchesan, Chem. Commun., 2023, 59, 10948–10951 RSC.
- C. H. Goerbitz, Chem. Commun., 2006, 2332–2334 RSC.
- S. Brahmachari, Z. A. Arnon, A. Frydman-Marom, E. Gazit and L. Adler-Abramovich, ACS Nano, 2017, 11, 5960–5969 CrossRef CAS PubMed.
- D. Selkoe, Nature, 2003, 426, 900–904 CrossRef CAS PubMed.
- A. Kholkin, N. Amdursky, I. Bdikin, E. Gazit and G. Rosenman, ACS Nano, 2010, 4, 610–614 CrossRef CAS PubMed.
- Q. Li, Y. Jia, L. Dai, Y. Yang and J. Li, ACS Nano, 2015, 9, 2689–2695 CrossRef CAS PubMed.
- N. Kol, L. Adler-Abramovich, D. Barlam, R. Shneck, E. Gazit and I. Rousso, Nano Lett., 2005, 5, 1343–1346 CrossRef CAS PubMed.
- L. Adler-Abramovich and E. Gazit, Chem. Soc. Rev., 2014, 43, 6881–6893 RSC.
- J. M. del Campo and J. Ireta, Phys. Chem. Chem. Phys., 2021, 23, 11931–11936 RSC.
- J. G. Fernandez and S. Dritsas, Matter, 2020, 2, 1352–1355 CrossRef.
- S. Gupta, I. Singh, A. K. Sharma and P. Kumar, Front. Bioeng. Biotechnol., 2020, 8, 504 CrossRef PubMed.
- C. H. Gorbitz, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 311–318 CrossRef CAS PubMed.
- J. L. Alonso and J. C. Lopez, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, 2015, vol. 364, pp. 335–401 Search PubMed.
- J. Hermans, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3095–3096 CrossRef CAS PubMed.
- J. Carlos Campini, M. A. Aguilar and M. Elena Martina, J. Mol. Liq., 2022, 351, 118557 CrossRef.
- K. Cai, F. Du, J. Liu and T. Su, Spectrochim. Acta, Part A, 2015, 137, 701–710 CrossRef CAS PubMed.
- M. Feig, J. Chem. Theory Comput., 2008, 4, 1555–1564 CrossRef CAS PubMed.
- J. Rubio-Martinez, M. Santos Tomas and J. J. Perez, J. Mol. Graph. Model., 2017, 78, 118–128 CrossRef CAS PubMed.
- D. Chakraborty, A. Banerjee and D. J. Wales, J. Phys. Chem. B, 2021, 125, 5809–5822 CrossRef CAS PubMed.
- V. Mironov, Y. Alexeev, V. K. Mulligan and D. G. Fedorov, J. Comput. Chem., 2019, 40, 297–309 CrossRef CAS PubMed.
- V. Parchansky, J. Kapitan, J. Kaminsky, J. Sebestik and P. Bour, J. Phys. Chem. Lett., 2013, 4, 2763–2768 CrossRef CAS PubMed.
- R. Vargas, J. Garza, B. Hay and D. Dixon, J. Phys. Chem. A, 2002, 106, 3213–3218 CrossRef CAS.
- F. Carrascoza, S. Zaric and R. Silaghi-Dumitrescu, J. Mol. Graph. Model., 2014, 50, 125–133 CrossRef CAS PubMed.
- F. Adasme-Carreno, J. Caballero and J. Ireta, J. Chem. Inf. Model., 2021, 61, 1789–1800 CrossRef CAS PubMed.
- J. Ireta, J. Chem. Theory Comput., 2011, 7, 2630–2637 CrossRef CAS PubMed.
- C. Cabezas, M. Varela, V. Cortijo, A. I. Jimenez, I. Pena, A. M. Daly, J. C. Lopez, C. Cativiela and J. L. Alonso, Phys. Chem. Chem. Phys., 2013, 15, 2580–2585 RSC.
- C. M. Leavitt, K. B. Moore, III, P. L. Raston, J. Agarwal, G. H. Moody, C. C. Shirley, H. F. Schaefer, III and G. E. Douberly, J. Phys. Chem. A, 2014, 118, 9692–9700 CrossRef CAS PubMed.
- N. E. Gonzalez-Diaz, R. Lopez-Rendon and J. Ireta, J. Phys. Chem. C, 2019, 123, 2526–2532 CrossRef CAS.
- S. Lovell, I. Davis, W. Adrendall, P. de Bakker, J. Word, M. Prisant, J. Richardson and D. Richardson, Proteins, 2003, 50, 437–450 CrossRef CAS PubMed.
- C. Gorbitz, Chem. – Eur. J., 2001, 7, 5153–5159 CrossRef CAS PubMed.
- C. Gorbitz, New J. Chem., 2003, 27, 1789–1793 RSC.
- J. Wang, K. Liu, R. Xing and X. Yan, Chem. Soc. Rev., 2016, 45, 5589–5604 RSC.
- Z. Chaker, P. Chervy, Y. Boulard, S. Bressanelli, P. Retailleau, M. Paternostre and T. Charpentier, J. Phys. Chem. B, 2021, 125, 9454–9466 CrossRef CAS PubMed.
- E. Mayans and C. Alemán, Molecules, 2020, 25, 6037 CrossRef CAS PubMed.
- T. O. Mason, D. Y. Chirgadze, A. Levin, L. Adler-Abramovich, E. Gazit, T. P. J. Knowles and A. K. Buell, ACS Nano, 2014, 8, 1243–1253 CrossRef CAS PubMed.
- D. G. Fedorov, J. Chem. Theory Comput., 2019, 15, 5404–5416 CrossRef CAS PubMed.
- C. M. Aikens and M. S. Gordon, J. Am. Chem. Soc., 2006, 128, 12835–12850 CrossRef CAS PubMed.
- R. Tripathi, L. Durán Caballero, R. Pérez de Tudela, C. Hölzl and D. Marx, ACS Omega, 2021, 6, 12676–12683 CrossRef CAS PubMed.
- J. Ireta, Int. J. Quantum Chem., 2012, 112, 3612–3617 CrossRef CAS.
- J. Ireta, Theor. Chem. Acc., 2016, 135, 220 Search PubMed.
- R. Sundararaman and W. A. Goddard, III, J. Chem. Phys., 2015, 142, 064107 CrossRef PubMed.
- A. Fortunelli and J. Tomasi, Chem. Phys. Lett., 1994, 231, 34–39 CrossRef CAS.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. A. Petrosyan, J.-F. Briere, D. Roundy and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205105 CrossRef.
- D. Gunceler, K. Letchworth-Weaver, R. Sundararaman, K. A. Schwarz and T. A. Arias, Model. Simul. Mater. Sci. Eng., 2013, 21, 074005 CrossRef.
- R. Sundararaman, K. A. Schwarz, K. Letchworth-Weaver and T. A. Arias, J. Chem. Phys., 2015, 142, 054102 CrossRef PubMed.
- R. Sundararaman and T. Arias, Comput. Phys. Commun., 2014, 185, 818–825 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- R. Sundararaman, K. Letchworth-Weaver, K. A. Schwarz, D. Gunceler, Y. Ozhabes and T. Arias, SoftwareX, 2017, 6, 278–284 CrossRef PubMed.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- J. Nochebuena, A. Ramirez and J. Ireta, Int. J. Quantum Chem., 2015, 115, 1613–1620 CrossRef CAS.
- P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Huang and A. D. MacKerell Jr, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- J. C. Phillips, D. J. Hardy, J. D. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin and W. Jiang, et al. , J. Chem. Phys., 2020, 153, 044130 CrossRef CAS PubMed.
- J. T. Edsall and M. H. Blanchard, J. Am. Chem. Soc., 1933, 55, 2337–2353 CrossRef CAS.
- G. Wada, E. Tamura, M. Okina and M. Nakamura, Bull. Chem. Soc. Jpn., 1982, 55, 3064–3067 CrossRef CAS.
- J. H. Jensen and M. S. Gordon, J. Am. Chem. Soc., 1995, 117, 8159–8170 CrossRef CAS.
- Y. Ding and K. Krogh-Jespersen, J. Comput. Chem., 1996, 17, 338–349 CrossRef CAS.
- O. Rahaman, A. C. T. van Duin, W. A. Goddard and D. J. Doren, J. Phys. Chem. B, 2011, 115, 249–261 CrossRef CAS PubMed.
- W. Tang, C. Cai, S. Zhao and H. Liu, J. Phys. Chem. C, 2018, 122, 20745–20754 CrossRef CAS.
- O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 064102 CrossRef PubMed.
- C. Dupont, O. Andreussi and N. Marzari, J. Chem. Phys., 2013, 139, 214110 CrossRef CAS PubMed.
- G. N. Ramachandran, C. Ramakrishnan and V. Sasisekharan, J. Mol. Biol., 1963, 7, 95–99 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05742a |
| This journal is © the Owner Societies 2024 |