Open Access Article
Open Access ArticleDiversity of protonated mixed pyrene–water clusters investigated by collision induced dissociation†
Arya
M. Nair
ac,
Héloïse
Leboucher
 b,
Lorris
Toucouere
b,
Sébastien
Zamith
b,
Lorris
Toucouere
b,
Sébastien
Zamith
 *a,
Christine
Joblin
*a,
Christine
Joblin
 c,
Jean-Marc
L'Hermite
a,
Alexandre
Marciniak
c,
Jean-Marc
L'Hermite
a,
Alexandre
Marciniak
 a and
Aude
Simon
a and
Aude
Simon
 b
b
aLaboratoire Collisions Agrégats Réactivité (LCAR/FERMI), UMR5589, Université Toulouse III – Paul Sabatier and CNRS, 118 Route de Narbonne, F-31062 Toulouse, France. E-mail: sebastien.zamith@irsamc.ups-tlse.fr
bLaboratoire de Chimie et Physique Quantiques LCPQ/FERMI, Université Toulouse III – Paul Sabatier and CNRS, 118 Route de Narbonne, F-31062 Toulouse, France
cInstitut de Recherche en Astrophysique et Planétologie (IRAP), Université Toulouse III – Paul Sabatier, CNRS, CNES, 9 Avenue du Colonel Roche, F-31028 Toulouse, France
First published on 15th January 2024
Abstract
Protonated mixed pyrene–water clusters, (Py)m(H2O)nH+, where m = [1–3] and n = [1–10], are generated using a cryogenic molecular cluster source. Subsequently, the mass-selected mixed clusters undergo controlled collisions with rare gases, and the resulting fragmentation mass spectra are meticulously analyzed to discern distinct fragmentation channels. Notably, protonated water cluster fragments emerge for n ≥ 3, whereas they are absent for n = 1 and 2. The experimental results are complemented by theoretical calculations of structures and energetics for (Py)(H2O)nH+ with n = [1–4]. These calculations reveal a shift in proton localization, transitioning from the pyrene molecule for n = 1 and 2 to water molecules for n ≥ 3. The results support a formation scenario wherein water molecules attach to protonated pyrene PyH+ seeds, and, by extension, to (Py)2H+ and (Py)3H+ seeds. Various isomers are identified, corresponding to potential protonation sites on the pyrene molecule. Protonated polycyclic aromatic hydrocarbons are likely to be formed in cold, dense interstellar clouds and protoplanetary disks due to the high proton affinity of these species. Our findings show that the presence of protonated PAHs in these environments could lead to the formation of water clusters and mixed carbon–water nanograins, having a potential impact on the water cycle in regions of planet formation.
1 Introduction
One recent discovery in astrochemistry was the identification of abundant small aromatic molecules in the gas-phase in cold interstellar molecular clouds.1–5 This raises the question on how these species can form in low-density environments and at cold temperatures (10–30 K). Kaiser and Hansen6 have discussed possible mechanisms for the growth of polycyclic aromatic hydrocarbons (PAHs) in the gas-phase, highlighting those that may be effective in low-temperature environments. Molecular clouds are the sites where stars and planets are formed, so we expect these species to be part of the original matter of our solar system, and some of them to have been preserved in primitive solar system bodies such as comets and asteroids. In particular, small PAHs such as C16H10, fluoranthene and pyrene, together with phenanthrene (C14H10) are found to be the most abundant compounds in such primitive bodies.7–9Water is a crucial molecule in the physics and chemistry of star and planet formation, observed in both solid10 and gas11 phases. Recent observations of the HDO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratio suggest that water molecules in our solar system were inherited from cold chemistry in the presolar nebula.12 There are various pathways leading to H2O formation, both in the gas phase and solid phase.13 In dense, cold regions, H2O formation predominantly occurs on the surface of cold grains, evident through a strong H2O ice absorption band. In more diffuse regions, ion-neutral chemistry is the dominant route. In this network, a pivotal product is the hydronium ion, H3O+, formed either through a series of ion–molecule reactions or by protonation of H2O using abundant proton donors like H3+ and HCO+. The gas-phase formation of H2O is expected to result from recombination with electrons, a slow process in cold clouds, leading to H2O formation in a limited number of cases (≈ 15%).13
H2O ratio suggest that water molecules in our solar system were inherited from cold chemistry in the presolar nebula.12 There are various pathways leading to H2O formation, both in the gas phase and solid phase.13 In dense, cold regions, H2O formation predominantly occurs on the surface of cold grains, evident through a strong H2O ice absorption band. In more diffuse regions, ion-neutral chemistry is the dominant route. In this network, a pivotal product is the hydronium ion, H3O+, formed either through a series of ion–molecule reactions or by protonation of H2O using abundant proton donors like H3+ and HCO+. The gas-phase formation of H2O is expected to result from recombination with electrons, a slow process in cold clouds, leading to H2O formation in a limited number of cases (≈ 15%).13
In recent years, a large number of protonated molecules have been identified in dense clouds, revealing a pattern where the MH+/M ratio rises with increasing Proton Affinity (PA).14 A high PA increases the number of possible proton donors, particularly the abundant HCO+ and H3O+ species. This protonation chemistry results from the ion chemistry generated by the interaction of cosmic rays with molecules, resulting in the generation of UV photons and secondary electrons. Protonated PAHs have been the subject of several spectroscopic studies demonstrating the astrochemical significance of these compounds as carriers of both aromatic infrared bands and diffuse interstellar bands.15–19
Even though PAHs and H2O are both key species in cold, dense molecular clouds and regions of star- and planet-formation, their interaction in the gas phase has not been the subject of detailed studies. PAHs have high PAs,20 and they could be involved in proton transfer reactions. O. Dopfer and collaborators conducted the first experiments on protonated mixed PAH–water clusters.21 The authors demonstrated that in the case of naphthalene (Naph, C10H8), the proton is attached to Naph when one water molecule is present, but the proton is located on the water moiety for two water molecules.21 The study was extended to a larger number of H2O molecules, and the proton location was found to be related to PAs and solvation energies.22 In this experiment, infrared photodissociation spectroscopy served as a diagnostic to probe proton localization. Rotational and far-infrared spectroscopy were employed in a number of studies on neutral PAH–water clusters to characterize noncovalent intermolecular interactions involving aromatic rings and water. The investigation of mixed clusters of neutral acenaphthene (up to 3 units) and water (up to 3 units) revealed distinct features from pure acenaphthene clusters or pure water clusters, but no signs of PAH–water interactions were observed.23 In the case of phenanthrene–water and phenanthridine–water clusters, the presence of a nitrogen heteroatom was found to lock the water molecule to the nitrogen atom and preserve the overall quasi-planar geometry of the cluster with an increasing number of water molecules.24
We study here the structure of protonated mixed pyrene–water clusters produced using a cryogenic molecular cluster source.25 Building on prior research on protonated naphthalene–water clusters, we anticipate observing various scenarios of proton localization on either the aromatic or water cluster components.22,26 Isolating systems with one to three pyrene molecules and one to ten water molecules, we analyze their structure through collision induced dissociation (CID) with rare gas atoms. In a previous examination of protonated hydrated uracil clusters, we determined that the observed experimental fragmentation channels were indicative of the low-energy isomers' structure, emphasizing the CID method's utility in probing source-formed isomer structures.27,28 In this study, we identify different isomers of protonated pyrene–water complexes and discuss their structures using results from density functional theory. We also pinpoint preferred formation conditions triggered by ionized seeds, including protonated pyrene, and discuss potential astrophysical implications.
2 Methods
2.1 Experimental
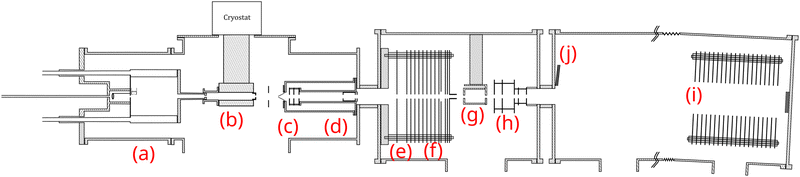
The molecular clusters (here mixed pyrene–water clusters) are produced in the gas aggregation source (Fig. 1(a) and 2). The source works on the principle of evaporation of molecules in an oven that are carried out by a helium flux mixed with water molecules in a cold environment where they clusterize. In the following we detail the technical elements of this source. The source consists of a double-walled chamber through which liquid nitrogen circulates. An oven filled with Py powder (Sigma Aldrich 96% purity) is located at the entrance of the source. The controlled temperature of the oven is varied between 298 to 338 K depending on the type of species of interest. A controlled flow of helium gas is introduced to the source which results in a pressure of about 1 mbar. Water vapor from a reservoir is introduced into the helium flux via a needle valve. The water molecules are carried by the helium flux into the source. Alternatively, water can also be introduced at the source exit, in the junction between the source and the thermalizer.
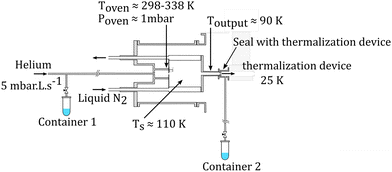 | ||
| Fig. 2 Schematics of the gas aggregation source. Water can be introduced either with the helium flux at the source entrance or at the source exit, just before the thermalization stage. | ||
An electron gun is located at the exit of the oven, consisting of a tungsten filament heated by a current of 2.4 A and biased at −150 eV. The electrons produced can ionize and potentially dissociate the molecular species that exit the oven. Although both Py vapor and water vapor are present in the oven, the formation of water–Py clusters at this stage is very unlikely due to the relatively high temperature in the oven. Even if some clustering occurs, they would most probably get dissociated upon ionization by electron impact at the exit of the oven. Therefore, the clustering and the growth process of the species happen after the ionization, in the coldest part of the source, the seeds for the cluster formation being ionic molecular species. The formation mechanisms of the produced species will be discussed in the next section, Section 2.1.2.
The charged clusters produced in the source are then brought to the thermalization stage by the helium carrier gas. The thermalization chamber (Fig. 1(b)) is cooled down to 25 K by a closed helium cryostat. At this stage the clusters are thermalized to 25 K by thousands of collisions with the helium carrier gas. After the thermalization, the ionized clusters are focused by an electrostatic lens to pass through a 1 mm skimmer and they are then transmitted to the first Wiley–McLaren acceleration region (WML 1, Fig. 1(c)).
The instrument can be operated in two modes. In the first mode, a regular time-of-flight mass spectrometry (TOF-MS) is performed to detect all the produced cationic clusters. In this mode, the mass filter, energy focusing, deceleration electrodes and the second Wiley–McLaren acceleration stage (WML 2) are grounded. The clusters are therefore accelerated using the Wiley–McLaren acceleration stage WML 1 and are directed towards the reflectron (Fig. 1(i)). Finally, they are detected using a dual Micro Channel Plate (MCP) detector which is biased at −10 kV. An example of this kind of mass spectrum obtained in this mode can be found in the following section (Fig. 3). This mode helps to optimize the conditions favourable for the production of the clusters of interest.
In the second mode, the species of interest are mass selected, energy focused and are decelerated. They then undergo collision induced dissociation (CID) with inert gases. In this mode, the species which are accelerated by the WML 1 enter the mass filter (Fig. 1(d)). A high voltage pulse is applied to the mass filter when the species of interest enter it and is shut down before they leave the filter. This helps in the elimination of the neighbouring masses. The mass selected clusters then enter the energy focusing region (Fig. 1(e)). In this region, faster clusters are ahead, and there is a linear relationship (to first order) between their kinetic energy and their position. By applying a pulsed high voltage, the kinetic energy dispersion is then almost compensated. The timing of the application of the pulsed voltages ensures that only species of interest are appropriately energy focused. The energy focused clusters are then decelerated by an electrostatic potential barrier (Fig. 1(f)). The potential is shut down at the end of the barrier, in the zero field region. The clusters then fly freely through the collision cell where they can undergo collision with the inert gas.
The mass selected clusters enter the collision cell through a 5 mm diameter hole. The collision cell is 5 cm long with an inner diameter of 2.5 cm and an exit hole of 6 mm diameter. Two 1 cm-diameter tubes are attached to the sides of this collision cell. One tube is used to introduce the collision gas into the cell, while the other is connected to two pressure gauges, an ionization gauge and a capacitive gauge, which simultaneously measure the pressure in the collision cell. The capacitive gauge is used to obtain absolute pressure values and to calibrate the ionization gauge. The latter is used to routinely record pressure, as it is less noisy than the capacitive gauge. The pressure given by the ionization gauge must be multiplied by a factor of 0.25, 1.2, 1.55 and 2.35 for neon, argon, krypton and xenon respectively, to obtain absolute values.
After passing through the collision cell, when the clusters reach WML 2 (Fig. 1(h)), pulsed high voltages are applied to direct them towards the reflectron. The ions are then detected by the MCPs (Fig. 1(j)), enabling TOF-MS analysis of the collision products.
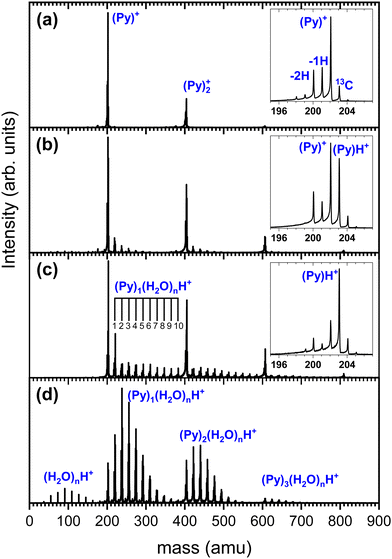
We show in Fig. 3 several TOF-MS obtained under different conditions. Fig. 3(a) displays a typical TOF-MS obtained in the absence of water. The inset in Fig. 3(a) shows that several sub-peaks are present, with the main contribution coming from the cationic pyrene, i.e. (C16H10)+ or (Py)+. This peak is accompanied on its right by the isotopologue (13CC15H10)+ due to the relatively high abundance of the 13C isotope. We note the presence of dehydrogenated (−1H and −2H) species probably produced by dissociative ionization in the source. A similar distribution of sub-peaks is observed for each complex with a number m of Py molecules. This distribution of peaks is typical of our gas aggregation source.30–32
In Fig. 3(b) we present a TOF-MS obtained by introducing a very small amount of water in the helium flux. The inset in Fig. 3(b) displays the distribution of peaks around the pyrene cation. Again, dehydrogenated species are present, but the most notable effect is the appearance of (Py)H+. Protonation occurs due to the injection of water in the gas aggregation source. In fact, when producing pure water clusters with the same source, only protonated water clusters are produced.25 We also observe the presence of mixed pyrene–water clusters, (Py)m(H2O)nH+, with species up to n = 5 for m = 1. Under these conditions, the amount of protonated pyrene is similar to the one of cationic pyrene.
As the amount of water introduced in the source is increased, the protonated pyrene peak gets more dominant and larger pyrene–water complexes are formed. Fig. 3(c) depicts an example of TOF-MS analysis of the species produced in the gas aggregation source when the amount of water introduced in the helium flow is increased. The dominating species in the mass spectrum are pure protonated Py clusters. Mixed clusters, in the form (Py)m(H2O)nH+ [m = 1–4 and n = 1–10], can be clearly seen in the mass spectrum.
At this stage, we can only speculate about the formation mechanism of the different species. Due to the larger interaction between ion-neutral over neutral–neutral species, we assume that the growth of clusters starts from ionic seeds. Upon electron impact ionization of water the main channels are the production of H2O˙+, OH+ and H+.33,34 The radical cation H2O˙+ is expected to efficiently give rise to proton transfer and produce (H3O)+.35 The production of protonated pyrene (PyH+), which becomes the dominant species in the presence of water, then most likely results from proton transfer from H3O+ to Py, Py + H3O+ → PyH+ + H2O, which is expected to be promoted by the high PA of Py.
Protonated mixed pyrene–water clusters can then be formed following two possible pathways, either from the (Py)H+ molecule or from protonated water clusters:
| (PyH)+ + H2O → (PyH+)(H2O) + H2O → ⋯ → (PyH+)(H2O)n | (1) |
| (H2O)nH+ + Py → (Py)1(H2O)nH+ | (2) |
A number of non-protonated mixed pyrene–water clusters were also observed suggesting that the Py cation (and its dehydrogenated counterparts) also serves as a seed and attaches both neutral pyrene and neutral water molecules.
In order to gain insight into the formation mechanisms, another way of producing the mixed pyrene–water clusters by adding water at the source exit is used. In this case, we start with conditions such as the ones of Fig. 3(b) in order to produce some (Py)mH+ seeds. These ion seeds propagate to the end of the source where interaction with neutral water molecules occurs, leading to water molecules attachment. We present in Fig. 3(d) an example of TOF-MS obtained under these conditions. One can see that the parent ions (protonated and cationic) are almost completely depleted whereas mixed pyrene–water clusters dominate the TOF-MS. Producing the clusters this way ensures that only the path given by 1 is in principle involved in the formation of (Py)m(H2O)nH+.
To obtain more details on the peaks, we show in Fig. 4 a zoomed in version around the (Py)1(H2O)1H+ complex obtained under the two cluster production methods. In Fig. 4(a), corresponding to the conditions of Fig. 3(c) of introducing water upstream, the main contribution arises from the protonated mixed species, (Py)1(H2O)1H+, accompanied on the right by its isotope peaks. We also note the presence of the (Py)1(H2O)1+ peak and the dehydrogenated (−1H and −2H) species that have attached a water molecule.
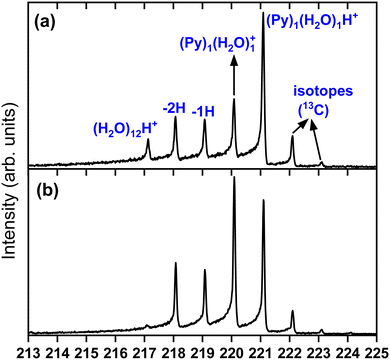 | ||
| Fig. 4 Zoomed in view around the (Py)1(H2O)1H+ species. (a) Panel (a) corresponds to Fig. 3(c) and panel (b) to Fig. 3(d). | ||
In Fig. 4(b) we present a zoomed in version around the (Py)1(H2O)1H+ complex obtained by introducing water downstream (Fig. 3(d)). The peak distribution is relatively similar to the one obtained by introducing water in the helium flow with the notable difference that the (Py)1(H2O)1+ peak is the dominant one now. This is of concern since this will lead to a non-negligible amount of isotopic contribution from (Py)1(H2O)n+ into the (Py)1(H2O)nH+ peaks. For instance, we estimate the amount of (13CC15H10)1(H2O)n+ to be about 20% of the peaks at the masses of (Py)1(H2O)nH+. For the TOF-MS of Fig. 4(a), this is when water is introduced upstream in the source, and this abundance goes down to 8%. For the (Py)2(H2O)nH+, the isotope contamination to peaks of interest goes up to 44% when water is introduced downstream whereas it is only 18% when it is introduced upstream.
Therefore, one advantage of introducing water upstream in the source is that protonated species are more dominant leading to less contamination due to 13C isotope.
However, as will be shown later, the CID of species produced with both methods give similar results, pointing towards a growth mechanism dominated by the attachment of water molecules onto ionized pyrene seeds such as (Py)mH+.
In the present study we will only study mixed pyrene–water clusters in their protonated form.
In this experiment, the mass selected clusters (Py)m(H2O)nH+ [m = 1–3, n = 1–10] undergo collisions with inert gases at a constant center of mass (COM) collision energy of 7.5 eV. The COM collision energy (ECOM) is calculated as:
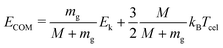 | (3) |
Several experiments have been performed with different collision gases. Depending on the collision gas and the clusters size, the laboratory frame kinetic energy is adjusted so that the center of mass collision energy remains the same.
The experiments were performed at relatively low pressures in order to maintain single collision conditions. For (Py)1(H2O)nH+ with argon, the working pressure is 8 × 10−5 mbar and the maximum cross section obtained corresponds to 90 Å2. This results in an average collision count of 0.09, with 96% of the total collisions being single collisions.
The data consist in TOF-MS acquired with (signal, Sk) and without (background, Bk) pressure in the collision cell. The acquisition is stopped when the parent ion reaches a given level. This sequence is repeated Nd = 11 times for each studied species. The quantities of interest, namely branching ratios (BRs) and fragmentation cross-sections σfrag (see next section), can be extracted in two ways. Either by first summing all Nd backgrounds 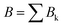 and signals
and signals 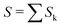 and then doing the subtraction S−B. The value of the BRs and σfrag are then obtained from the resulting summed mass spectrum. This gives the best signal to noise ratio but is sensitive if some drift occurs during the acquisition. For instance, the cluster size distribution may evolve slowly with time, leading to background peaks after mass selection that evolve from one acquisition to the other. To circumvent this, the backgrounds can also be subtracted individually, Si−Bi. In this case for each Nd, BRs and σfrag are obtained that are then averaged. Here, the signal to noise ratio is possibly degraded but the deduced quantities are less sensitive to possible long-term drifts during the acquisitions.
and then doing the subtraction S−B. The value of the BRs and σfrag are then obtained from the resulting summed mass spectrum. This gives the best signal to noise ratio but is sensitive if some drift occurs during the acquisition. For instance, the cluster size distribution may evolve slowly with time, leading to background peaks after mass selection that evolve from one acquisition to the other. To circumvent this, the backgrounds can also be subtracted individually, Si−Bi. In this case for each Nd, BRs and σfrag are obtained that are then averaged. Here, the signal to noise ratio is possibly degraded but the deduced quantities are less sensitive to possible long-term drifts during the acquisitions.
All data have been analysed with both methods and both give consistent results. From the second method, error bars representing one standard deviation can be deduced from the Nd repeated acquisitions. Furthermore, for some sizes the measurements have been repeated on different days under different source conditions. For simplicity, the error bars that could arise from possible drifts during the acquisition is called Δ1 and the one from acquisitions on different days are called Δ2 hereafter.
From such fragmentation mass spectra, one can deduce absolute fragmentation cross-sections and branching ratios. Absolute fragmentation cross-sections are obtained as:
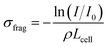 | (4) |
Branching ratios are calculated as:
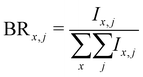 | (5) |
The parent cluster undergoes fragmentation by either losing water molecules or by losing both Py and water molecules. Our results will be mainly discussed in terms of these fragmentation channels. For the mixed cluster with only one Py, the loss of water molecules only ends up in the detection of (Py)1(H2O)xH+ fragments, with x = [0:n − 1]. The loss of both Py and water molecules ends up in the detection of protonated water clusters (H2O)xH+, with x = [2:n]. Here, we begin at x = 2 as we are unable to detect H3O+.
More generally, when starting with a parent cluster in the form (Py)m(H2O)nH+, we identify m + 1 fragmentation channels corresponding to fragments in the form (Py)k(H2O)x=0:n−1H+, with k = [0:m]. The branching ratios for these fragmentation channels are calculated as:
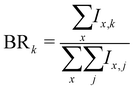 | (6) |
As an example, the branching ratio BR0 corresponds to the loss of all Py molecules and some of the water molecules. In other words, it corresponds to the detection of protonated water clusters. In the following sections we will refer to the fragmentation channels using BRk, with k being the number of Py molecules in the fragments.
An overview of the experiments performed is given in Table 1.
| Species | Collision gas | E COM (eV) | E k (eV) |
|---|---|---|---|
| (Py)1(H2O)nH+n = [1–10] | Neon | 7.5 | 90–151 |
| Argon | 7.5 | 49–79 | |
| (Py)1(H2O)nH+n = [1–10] | Argon | 15 | 98–158 |
| (Py)2(H2O)nH+n = [1–6] | Krypton | 7.5 | 45–53 |
| Argon | 7.5 | 87–103 | |
| Xenon | 7.5 | 32–37 | |
| (Py)3(H2O)nH+n = [2–5] | Xenon | 7.5 | 44–48 |
In the case of the Py monomer and dimer complexes, the experiments were repeated with different collision gases. Hence the mass ratios were varied which allowed us to check that deflection events induced by collision did not play a major role in our results. For instance, for the CID of (Py)1(H2O)nH+ with neon, deflections are negligible whereas in the case of argon deflections are expected to occur. However, both the cross-sections and the branching ratios obtained with neon and argon are very similar (see Fig. S1, ESI†). This indicates that the global effect of ion losses due to deflection is negligible here.
In the case of (Py)2(H2O)nH+, three collision gases—argon, krypton, and xenon—were employed for the CID. Notably, the obtained cross sections with these different gases exhibit variations. The cross section tends to decrease with the mass of the collision gas. This phenomenon can be attributed to deflections causing ion losses, thus reducing the apparent cross section. Furthermore, the choice of collision gas impacts the fragmentation patterns. For example, channels corresponding to the loss of all water molecules (that is the detection of (Py)1H+ and (Py)2H+) become relatively suppressed when heavier collision gases are used (see Fig. S2, ESI†). These channels likely represent the outcomes of the most energetic collisions, where deflections are more anticipated. Nevertheless, despite the presence of such effects, the branching ratios obtained with the three collision gases remain relatively similar (see Fig. S3, ESI†).
When going to light collision gases, the kinetic energy in the laboratory frame has to be increased significantly (around 100 eV, see Table 1). For such high kinetic energies, the mass selection is not as effective as for lower values. However, as can be seen from Fig. S3 ESI,† very similar results are obtained despite different collision gas being employed.
Experiments were also performed on (Py)1(H2O)nH+ with argon at a higher COM collision energy, namely 15 eV. Similar results were obtained for ECOM = 7.5 and 15 eV (see Fig. S4, ESI†).
For the (Py)3(H2O)nH+, experiments were only performed with xenon.
The experiments on (Py)1(H2O)nH+ and (Py)2(H2O)nH+ with argon and (Py)3(H2O)nH+ with xenon at ECOM = 7.5 eV are presented here. A comparison of the experiments with the other collision gases and at different collision energies is provided in the ESI.†
2.2 Theoretical
As an attempt to rationalize the experimental results, the structures and energetics of the most stable isomers of (Py)1(H2O)nH+, n = [1–4] were determined using a two-step procedure as in the article by Leboucher et al.36 We considered three initial protonation sites of [PyH]+ in order to determine the lowest energy isomers with the extra H atom on either the C1, C2 or C4 carbon (Fig. S11, ESI†). Briefly, for each stoichiometry, exploration of the potential energy surface (PES) was achieved using a Monte Carlo parallel tempering (MCPT) algorithm as implemented in the deMonNano code.37 Several starting points were tried, which differ by the relative positions of the water molecules with respect to the [PyH]+ monomer. The geometries of the PyH+ monomers and of the water molecules were kept frozen during the MCPT simulations.38 The parameters of the simulations were the same for all systems, i.e. simulations of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps were run for a geometrical sequence of 10 temperatures ranging from 40 K to 700 K. Only exchanges between sequential temperatures were authorized and tried every 10 steps. The displacement of an atom was accepted only if it was kept inside a sphere of 25 bohrs centered at the center of mass of the cluster. At each step, the energy was computed at the self-consistent-charge density functional based tight binding (SCC-DFTB)39 level of theory using an adapted Hamiltonian ensuring a good description of intermolecular interactions, which is a challenge for such systems.36 The isomers were then sorted by increasing energy order and the lowest energy one was locally optimized at the DFT level using the B3LYP-GD3 functional in conjunction with the d95V(d,p) basis set. For each cluster, full diagonalization of the mass weighted hessian matrix was achieved in order to check that they are minimum energy geometries and to compute the zero point energy (ZPE) corrections. The energetics were improved by single-point calculations increasing the basis set to aug-cc-pvtz. The final B3LYP-GD3/aug-cc-pvtz level of theory was used as it was shown to provide a good description of [(C10H8)H(H2O)1–2]+ clusters.22 DFT calculations were performed with the Gaussian16 suite of programs.40
000 steps were run for a geometrical sequence of 10 temperatures ranging from 40 K to 700 K. Only exchanges between sequential temperatures were authorized and tried every 10 steps. The displacement of an atom was accepted only if it was kept inside a sphere of 25 bohrs centered at the center of mass of the cluster. At each step, the energy was computed at the self-consistent-charge density functional based tight binding (SCC-DFTB)39 level of theory using an adapted Hamiltonian ensuring a good description of intermolecular interactions, which is a challenge for such systems.36 The isomers were then sorted by increasing energy order and the lowest energy one was locally optimized at the DFT level using the B3LYP-GD3 functional in conjunction with the d95V(d,p) basis set. For each cluster, full diagonalization of the mass weighted hessian matrix was achieved in order to check that they are minimum energy geometries and to compute the zero point energy (ZPE) corrections. The energetics were improved by single-point calculations increasing the basis set to aug-cc-pvtz. The final B3LYP-GD3/aug-cc-pvtz level of theory was used as it was shown to provide a good description of [(C10H8)H(H2O)1–2]+ clusters.22 DFT calculations were performed with the Gaussian16 suite of programs.40
3 Experimental results
3.1 CID of (Py)m(H2O)nH+, m = 1
In Fig. 6, the fragment distributions for the CID of (Py)1(H2O)nH+n = [1–10] with argon at 7.5 eV COM collision energy are displayed. The fragment intensities are obtained from the integration of the fragment peaks in the TOF-MS. The groups of red and black peaks correspond to the (Py)1(H2O)xH+ and (H2O)xH+ fragments, respectively.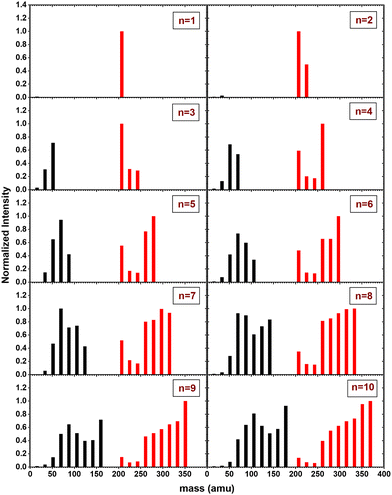 | ||
| Fig. 6 Mass distribution of the fragments obtained from CID experiment with (Py)1(H2O)nH+n = [1–10] colliding with argon at 7.5 eV COM collision energy. | ||
We observe that up to n = 2, almost no protonated water cluster fragments are detected. Indeed, for n = 1, the only observed fragment is (Py)1H+ and for n = 2 the only observed fragments are (Py)1H+ and (Py)1(H2O)1H+.
The significance of protonated water cluster peaks (depicted by black peaks) becomes pronounced starting from n = 3. As the parent cluster size increases, the distribution of protonated water fragments widens and shifts toward larger sizes. The evolution of the distribution progresses from a relatively smooth bell-like shape for n = 3 to 6, to a more structured distribution for the largest parent cluster sizes (n ≥ 7). The observed structure might be a signature of the statistical fragmentation occurring after collisional energy transfer and reflects the relative stability of the protonated water fragments.
For (Py)1(H2O)xH+ peaks (red peaks), (Py)1H+ is the dominant peak up to n = 3. For n ≥ 4, the PyH+ fragment is no longer dominant. We observe also that (Py)1(H2O)1H+ and (Py)1(H2O)2H+ are the least intense peaks in the fragment distribution. For sizes above n = 5, a plateau is appearing starting with the fragment (Py)1(H2O)3H+.
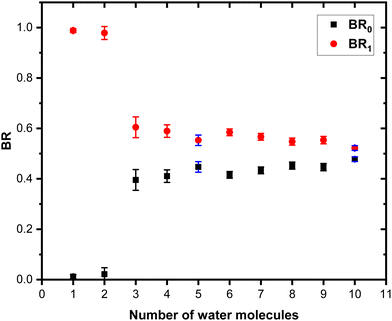
The grouped fragments (black and red peaks) allow defining the branching ratios BR1 and BR0 corresponding to the loss of water molecules only and the loss of both Py and water molecules, respectively.
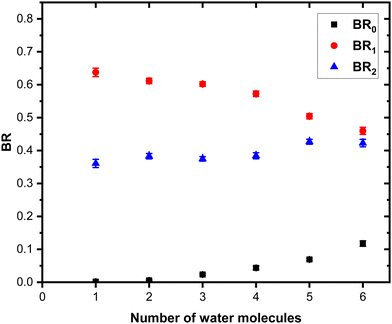
Fig. 7 shows these branching ratios plotted as a function of the number of water molecules attached to the Py molecule. For n ≤ 2, almost no protonated water fragments are observed and BR0 ≈ 0. A sudden change in the branching ratios arises at n = 3.
Indeed, from n = 3 up to n = 10, both types of fragments (black and red peaks) are detected, namely (H2O)xH+ and (Py)1(H2O)xH+. The corresponding branching ratios BR0 and BR1 are almost constant as a function of the number of water molecules. The branching ratio BR0 slowly evolves from 0.4 to 0.45. Conversely, BR1 goes from 0.6 to 0.55.
The experiment has also been repeated with argon at higher COM collision energy, namely 15 eV. It has also been performed with neon as collision gas at 7.5 eV COM collision energy. Both these experiments give very similar results as the one presented here (see Fig. S1 and S4 in the ESI† for the comparison).
We also performed the CID at 7.5 eV COM collision energy with argon for (Py)1(H2O)nH+ species produced by adding water at the source exit. A comparison of the branching ratios is provided in Fig. S7 of the ESI.† The branching ratios, once corrected for the isotope contamination of the parent peak are remarkably similar to the ones obtained for water added upstream.
3.2 CID of (Py)m(H2O)nH+, m = 2
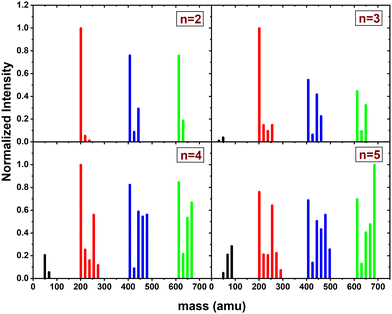
In this section, we present the results of the CID of (Py)2(H2O)nH+n = [1–6] with argon at 7.5 eV COM collision energy. A comparison of this experiment using krypton and xenon is given in Fig. S2 and S3 of the ESI.†Fig. 8 shows the distribution resulting from CID of (Py)2(H2O)nH+n = [1–6] with argon at 7.5 eV COM collision energy. The groups of black, red and blue peaks correspond to the detection of the different types of fragments (H2O)xH+, (Py)1(H2O)xH+ and (Py)2(H2O)xH+, respectively.
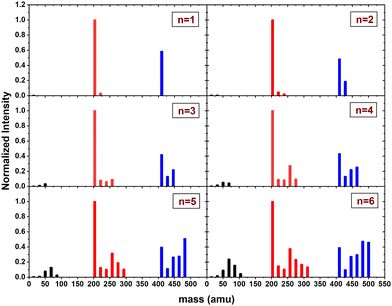 | ||
| Fig. 8 Normalized mass distributions of the fragments from the CID of (Py)2(H2O)nH+n = [1–6] colliding with argon at 7.5 eV COM collision energy. | ||
Protonated water clusters fragments (black peaks) are negligible for n = 1 and n = 2 water attached and start to appear clearly from n = 3 onward. The distributions of (H2O)xH+ peaks have a similar pattern as in the case of (Py)1(H2O)nH+ (see the black peaks in Fig. 6).
The (Py)2(H2O)xH+ fragment distribution (red peaks) is quite structured, with a low abundance of fragments and plateaus. For instance, the x = 1 fragment has a low abundance, followed by a plateau at x = 2–3 (visible from n = 3 to 6). As n increases, another plateau develops at x = 4–5. (Py)1H+ is clearly the dominant fragment. Similar to what we observed for the CID of Py1(H2O)nH+, the (Py)1(H2O)3H+ fragment shows up in the distribution and is relatively more intense than the neighbouring species from n = 4 onward.
For the water loss channels ((Py)2(H2O)xH+ fragments; blue peaks), (Py)2(H2O)1H+ appears to be the least intense in all cases.
Fig. 9 shows the branching ratios plotted as a function of the number of water molecules attached on the Py. The fragments are grouped into the three channels corresponding to the detection of pure protonated water fragments (BR0), (Py)1(H2O)xH+ fragments (BR1) and (Py)2(H2O)xH+ fragments (BR2). Contrary to the m = 1 case, no sudden change is observed in the branching ratios. Instead, we observe a slow rise of BR0 with n to a value of 0.1 at n = 6. BR1 is the dominant channel which decreases from 0.63 to 0.46. The branching ratio BR2 is almost constant with the number of water molecules attached.
These measurements have been repeated using krypton and xenon at 7.5 eV COM energy, and similar results have been obtained within the small differences due to deflections induced by heavier gas colliders (see the ESI† for details).
For some sizes we also performed the CID at 7.5 eV COM collision energy with argon for (Py)2(H2O)nH+ species produced by adding water at the source exit. A comparison of the branching ratios is provided in the ESI† (Fig. S8). The branching ratios, once corrected for the isotope contamination of the parent peak are in good agreement with the experiments carried out by adding water upstream.
3.3 CID of (Py)m(H2O)nH+, m = 3
The CID experiment on (Py)3(H2O)nH+ with xenon at 7.5 eV COM collision energy was performed for n = [2–5]. We could not start with n = 1 as the number of ions produced was too small to have enough signal after mass selection. This species was found to be less stable even in the fragmentation mass spectrum. We note that for (Py)3(H2O)nH+ the data quality is not as good as for (Py)1(H2O)nH+ and (Py)2(H2O)nH+. This is due to the lower number of parent ions produced and due to the presence of a relatively large background, especially for the (H2O)xH+ fragments.The mass distribution of the fragments resulting from the CID of (Py)3(H2O)nH+n = [2–5] upon collision with xenon at 7.5 eV COM collision energy is given in Fig. 10.
The (H2O)xH+ fragments (black peaks) are present only for n ≥ 3 but with a smaller intensity and remain as a rather minor channel as in the case of m = 2.
Regarding the other fragmentation channels for m = 3, namely (Py)1(H2O)xH+ (red peaks) and (Py)2(H2O)xH+ (blue peaks) we find similarities with the m = 1 and m = 2 cases. Namely, the (Py)1(H2O)3H+ shows up with a relatively high intensity as n increases. We also note that similar to the m = 2 case, the (Py)2(H2O)1H+ fragment has a low intensity.
Concerning the last fragmentation channel, (Py)3(H2O)xH+ (green peaks), we observe that the fragment (Py)3(H2O)1H+ is the least intense species among the neighbouring fragments.
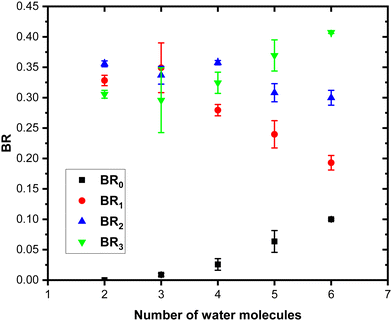
Fig. 11 shows the branching ratios plotted as a function of the number of water molecules in the complex, which correspond to the fragments (Py)3(H2O)xH+ (BR3), (Py)2(H2O)xH+ (BR2), (Py)1(H2O)xH+ (BR1) and (H2O)xH+ (BR0). We can observe that BR0 for n = 2–3 is almost negligible and is increasing slightly for n = 4–5 (note the large error bar for n = 5). BR1 is decreasing from 0.33 to 0.24 as a function of the number of water molecules attached. BR2 is nearly a constant up to n = 4 and is slightly decreasing for n = 5. BR3 is slowly increasing from 0.31 to 0.37.
4 Theoretical results
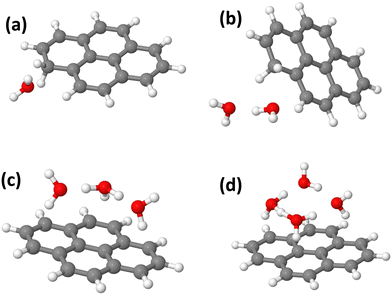
In this section, we present the structures, energetic and adiabatic dissociation energies of (Py)1(H2O)nH+, n = [1–4] for the three lowest energy isomers of protonated pyrene determined using the methodology described in Section 2.2. The lowest energy structures of (Py)1(H2O)nH+ are shown in Fig. 12.Structure determination was performed by assuming three different initial carbon sites (C1, C2 and C4, see Fig. S11 in the ESI† for the numbering convention) for the proton localization on the Py molecule. The structures of all the computed (Py)1(H2O)nH+ isomers (n = 1–4) are reported in Fig. S12–S23 in the ESI.† The relative energies of the corresponding structures are shown in Table 2.
| n | Isomer C1 | Isomer C2 | Isomer C4 |
|---|---|---|---|
| 0 | 0.0 | 0.61 | 0.45 |
| 1 | 0.0 | 0.57 | 0.42 |
| 2 | 0.01 | 0.0 | 0.42 |
| 3 | 0.62 | 0.0 | 0.71 |
| 4 | 0.78 | 0.0 | 0.72 |
In the absence of water, the lowest energy isomer is the one with the proton on C1, followed by the ones with the proton on C4 (+0.45 eV) and on C2 (+0.61 eV). These values are in extremely good agreement with the ones obtained by Chin and Lin41 and the DFT results by Bahou et al.42 who reported values of +0.44 and +0.61 eV respectively. By examining the electron density, the obtained structures are pointing towards a cationic hydrogenated Py rather than an appropriately protonated Py. Indeed, the charge appears to be delocalized over the whole Py molecule. Nevertheless, the electron density remains lower on the external H atoms, and especially where the extra H atom is present.
When a single water molecule is added, whatever the starting isomer for PyH+, the extra H atom remains located on the Py molecule. It can be understood due to the important PA difference between the two monomers. The water molecule has its oxygen pointing towards the location of the extra H atom site, due to the relatively lower electron density there. The lowest energy structure is obtained with the C1 isomer (Fig. 12(a)).
With two water molecules, two competing structures are present, arising from the C1 and C2 isomers. For C1, this corresponds to the PyH+ with two water molecules in the close vicinity of the extra H site (Fig. 12(b)). For C2, during the geometry optimization, there is a proton transfer to the water dimer. The proton is shared by the two water molecules lying on top of the Py plane. For isomer C4, the extra H atom remains on the Py molecule. It can be interpreted because the PAs of (H2O)2 and Isomer C2 have similar values (see Table 3).
| Isomer C1 | Isomer C2 | Isomer C4 | (H2O) | (H2O)2 | (H2O)3 | (H2O)4 | |
|---|---|---|---|---|---|---|---|
| PA | 9.19 | 8.57 | 8.74 | 7.06 | 8.44 | 9.07 | 9.38 |
Dissociation energies are calculated as the difference in energy (including ZPEs) of adjacent sizes for the same isomer family. The values are reported in Table 4.
| n | Isomer C1 | Isomer C2 | Isomer C4 |
|---|---|---|---|
| 1 | 0.26 | 0.31 | 0.29 |
| 2 | 0.30 | 0.88 | 0.31 |
| 3 | 0.22 | 0.83 | 0.54 |
| 4 | 0.34 | 0.50 | 0.49 |
With three water molecules, the lowest energy structure is found when starting with the C2 isomer. In the optimized structure, the proton is located on the water trimer (Fig. 12(c)). For the C1 and C4 isomers, the extra H atom remains on the cationic Py. Interestingly, in the case of the C4 isomer, the hydrogenated cycle becomes distorted and the oxygen atom of the central water monomer becomes close to the adjacent carbon atom of the dihydrogenated carbon of the same cycle (1.53 Å, see the ESI†).
Finally, adding four water molecules starting with the C2 isomer leads to the lowest energy structure where the proton has jumped to the water tetramer that lies on top of the Py plane (Fig. 12(d)). For the C1 isomer, the extra H atom remains on the cationic Py. Regarding isomer C4, the trend observed for n = 3 is strengthened as we observe the formation of a C–(OH) bond, (C–O distance of 1.47 Å) while the proton is transferred onto a kind of water trimer (see the structure in Fig. S23 of the ESI†).
In Table 3 are presented the PAs calculated at the DFT level for the three lowest isomers of the protonated pyrene and of cluster sizes for n = 1 to 4. The obtained values compare well with previously reported values (see Fig. S10 in the ESI† for a comparison of the PA from previous works).43–49 For isomer C1 the PA of pyrene becomes comparable to the one of the water cluster for n = 3. For isomers C2 and C4, the values become comparable for n = 2.
For n = 1, the dissociation energy for the loss of a neutral water molecule is around 0.3 eV for the three isomers. For n = 2, isomers C1 and C4 have similar dissociation energies around 0.3 eV. For C2, the binding energy is much higher at 0.88 eV. However, in this case, the difference in energy is calculated between a structure with the proton on the water dimer (n = 2) and one where the proton is on the Py molecule (n = 1).
For n = 3, when one considers the C2 isomer, the dissociation energy for the loss of a water molecule from the Py–water complex (0.83 eV) is similar to the one for the loss of a water molecule from the protonated water trimer (∼ 0.9 eV).47,50,51 Furthermore the structure of the protonated water trimer is rather similar with and without the interaction with the Py molecule. For the C1 isomer the binding energy is slightly smaller than the n = 1 case. For the isomer C4 the deduced binding energy is higher as it implies breaking of the C–OH bond.
For n = 4, the presence of the Py molecule strongly disturbs the native tetrahedral protonated water tetramer structure in both isomers C2 and C4. Both isomers have a similar binding energy of around 0.5 eV. For the C1 isomer this binding energy is again around 0.3 eV as it corresponds to the breaking of a single hydrogen bond in the neutral water network.
5 Discussion
The case of a cluster composed of a single pyrene unit with several water molecules (Py)1(H2O)nH+ is the one that can be scrutinized in the context of theoretical calculations. In this instance, the experimental results manifest a clear transition from n = 2 to n = 3, characterized by the appearance of protonated water cluster fragments at n = 3. This abrupt shift at n = 3 is ascribed to the direct dissociation of the initial structures of the isomers within the clusters.The theoretical structure calculations indicate that for n = 1, the lowest energy structures correspond to PyH+ with a neutral water molecule attached, regardless of the starting isomer (C1, C2, or C4). For n = 2, the C1 and C4 PyH+ isomers are predicted to form (PyH+)(H2O)n species, meaning that the proton remains located on the pyrene molecule. In the case of the C2 isomer for n = 2, a proton transfer towards the water molecules is observed during local optimization. For the C4 isomer, the proton transfer towards the water is predicted to occur for n = 4. In the case of the C1 isomer, the proton remains localized on pyrene at least up to n = 4. The observed behavior broadly aligns with the relative PAs of Py compared to the water clusters (see Table 3). However, it does not strictly adhere to this alignment, underscoring the importance of solvation processes.
We have shown that the mixed pyrene water-clusters are most likely produced by attaching neutral water molecules onto protonated pyrene seeds PyH+. If only the lowest energy C1 was produced in the source, then one would not expect to see the jump in the branching ratio at n = 3 since the C1 isomer would only lead to the formation of (PyH+)(H2O)n which would only produce (PyH+)(H2O)x fragments. This observation implies that there is a contribution from other PyH+ isomers (C2 and/or C4). Starting from n = 2, the C2 isomer would lead to the formation of (Py)(H2O)nH+ which fragments into (Py)(H2O)xH+ and (H2O)xH+. The same would happen with the C4 isomer but for n ≥ 4.
An argument in favor of an initial mixture of (Py)(H2O)nH+ and (PyH+)(H2O)n species is that for n ≥ 3 the BRs are almost constant. If the PyH+ C1, C2 and C4 isomers were present in a given proportion, then the addition of water to these seeds would lead to a constant proportion of (Py)(H2O)nH+ and (PyH+)(H2O)n species, and therefore to almost constant branching ratios as a function of the number of water molecules. We also note that there are four equivalent protonation sites for the C1 and C4 isomers and only 2 for the C2 one. Assuming that all protonation sites are equally probable would then give a probability of 60% of forming clusters with a proton transfer towards the water for n > 3. Given the fact that all isomers can contribute to the BR1 channel, independently of the fact that the proton is localized on Py or water, this simple counting brings us close to the actual experimentally observed branching ratios. Since the three isomers of PyH+ are located at different energies (C1 being the lowest in energy), this also implies that their formation is not governed by energetics but by kinetic parameters. This could also explain the discrepancy observed for isomer C2 at n = 2 between theory and experiment.
Upon collisional excitation, the energized mixed pyrene–water clusters experience fragmentation. This fragmentation can take place through either a statistical dissociation cascade, where neutral monomers dissociate one by one, allowing the system to rearrange before dissociation. The fragmentation pattern in this case is expected to reflect the relative stability of the fragments. Alternatively, fragmentation can occur in a direct manner, characterized by sudden dissociation with no significant time for system rearrangement. In the current experiment, both types of fragmentation are likely. Collisions occur with a distribution of impact parameters, where large impact parameters may result in statistically occurring fragmentation, while small impact parameters, such as head-on collisions, may lead to more direct fragmentation. The collision site on the mixed pyrene–water cluster could also play a significant role. Given the large size difference between the constituents, hitting the Py molecule is more likely, acting as an energy reservoir for later statistical dissociation. Conversely, if the water molecules are directly hit, a more direct dissociation of these units may be expected.
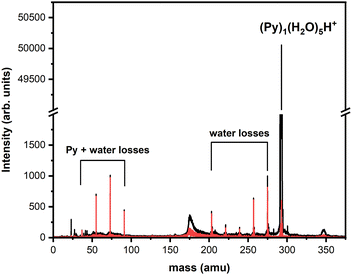
Looking at the fragment distributions for (Py)1(H2O)xH+ (Fig. 6), we note that the (Py)1(H2O)3H+ species appears to have higher abundances than the x = 1 and x = 2 fragments. This indicates that this cluster has a remarkable stability. For n = 3, the highest dissociation energy for the loss of a water molecule is obtained for isomer C2. We therefore assign the particular stability of the x = 3 cluster to the formation of a protonated water trimer on top of the pyrene molecule.
The production of protonated water cluster fragments (H2O)xH+ results from the loss of the neutral Py molecule. In the distribution, the fragment with x = n, corresponding to the sole loss of the neutral Py molecule, remains relatively intense for all sizes. This suggests that upon collision, the protonated water cluster remains relatively unperturbed, allowing it to survive the collision. We hypothesize that if the collision occurs onto the Py molecule, it absorbs most of the energy, becomes vibrationally excited, and detaches from the protonated water cluster.
The relative intensities of the (H2Ox)H+ fragments can be understood in terms of their dissociation energies. The dissociation energy of the protonated water clusters is 1.56 eV for x = 2, 0.92 for x = 3, and 0.78 for x = 4. It has a minimum around 0.37 eV for x = 5 and 6, stabilizing around 0.45 eV for larger sizes.47,50–53 The x = 4 fragment appears relatively intense for sizes n = 4–8. For the largest sizes n = 8, 9, the most intense protonated water fragment is the one with x = n, while the distribution of other fragments is centered around 5–6. Therefore, the fragment distribution in this case results from a sudden collision with the loss of pyrene, followed by sequential statistical losses of water monomers.
In conclusion, while the observed fragmentation pattern is an outcome of an average of various potential events, a meticulous analysis of the branching ratios and fragmentation patterns, in conjunction with theoretical predictions and possible formation mechanisms, allows us to identify potential structures for the protonated mixed pyrene–water clusters under investigation.
For a mixed cluster containing two pyrene units (m = 2), we observe a slow rise of the BR0 channel, accompanied by a slow decrease of BR1 whereas BR2 remains almost constant. This differs from the m = 1 case, where the branching ratios are almost constant for n ≥ 3.
The gradual change in BR0 may indicate a more gradual evolution in the prevalence of isomers where the proton becomes localized onto the water. For m = 2, there could still be a mixture of the C1, C2, and C4 PyH+ acting as a seed in the formation of (Py)2H+. Depending on the specific isomer involved in the resulting (Py)2H+ complex, we might anticipate varying degrees of charge delocalization across the pyrene units, leading to different scenarios for proton localization compared to the m = 1 case in the presence of water. These distinct charge configurations, combined with the larger spatial extension of (Py)2H+ compared to (Py)H+, are expected to reduce the likelihood of water clusters forming.
In the (Py)2(H2O)xH+ fragment channel (BR2), the fragmentation pattern appears to be sensitive to the relative stability of the fragments, suggesting a dissociation cascade in a statistical fashion ending up with the (Py)(PyH+) fragment. However, it can be seen that the (PyH+) fragment has the greatest abundance. This implies a complete dissociation of the (Py)2(H2O)nH+ species, namely the loss of all water molecules plus one neutral Py unit.
Assuming that the clusters originate from a (Py)(PyH+) stacked seed with neutral water molecules attached, collisions with small impact parameters are highly likely to occur on the plane of one of the stacked Py molecules. In such cases, collisional energy would efficiently transfer to the dissociative mode of the (Py)(PyH+), leading to the formation of (Py)1(H2O)xH+ fragments. Notably, the distribution of (Py)1(H2O)xH+ fragments reveals a higher abundance for x = 3, emphasizing the remarkable stability of this species. The fragmentation pattern for (Py)1(H2O)xH+ fragments mirrors the one observed for m = 1 (except for the elevated abundance of (PyH+)). Consequently, after the initial loss of one Py molecule, a similar fragmentation mechanism may occur as encountered for m = 1. This hypothesis aligns with the protonated water cluster fragments' distribution, as the distributions for m = 1 and m = 2 appear quite similar (illustrated for n = 6 in Fig. S6 of the ESI†).
The largest studied mixed cluster contains three pyrene units (m = 3). Similar to m = 2, BR0 slowly increases from n = 3–4 together with BR3 (BR2 for m = 2), whereas the other channels BR1 and BR2 decrease. This trend is consistent with a population of isomers on which the proton is localized on water. It is remarkable that in the three systems under investigation, for n = 1 and 2, we do not observe any protonated water fragments. This may point towards a general behaviour of these systems, where the PAs of the pyrene clusters remain larger than the PAs of the water monomer and dimer. This is probably dictated by the PA of the individual pyrene, which remains despite the clustering.
By comparing the fragment distributions for m = 1, 2 and 3 (see Fig. 6, 8 and 10), similarities can be observed. For instance, for (Py)1(H2O)xH+ fragments, the (Py)1(H2O)3H+ peak is relatively intense for n > 3 in all three cases. Regarding the (Py)2(H2O)xH+ fragments, the (Py)2(H2O)1H+ species is less abundant than the neighbouring ones for both m = 2 and m = 3. We note that the (Py)yH+ fragments have a relatively high intensity compared to the (Py)y(H2O)xH+ fragments: the binding energies between the pyrene molecules are higher than the water–pyrene cluster one.38 The (Py)3(H2O)1H+ species has a low intensity, which is a confirmation of its poor stability (its production was already quite inefficient in the source).
As m goes from 1 to 3, we probably have an evolution from a direct dissociation dominated fragmentation pattern to a more statistical-like fragmentation. For m = 1, the number of degrees of freedom goes from 84 to 129 when n goes from 1 to 6. For m = 2 (3), it evolves from 162 (246) to 207 (291) for the same n range. Therefore, one expects statistical dissociation to play a more important role here as more degrees of freedom are available for collision energy redistribution. A detailed molecular dynamics study of the CID of these systems would help to disentangle such an evolution and shed light on the fragmentation mechanisms.
6 Conclusions
In this study, we conducted collision-induced dissociation of (Py)m(H2O)nH+ for [m = 1–3, n = 1–10] at various collision energies (7.5 eV, 15 eV) using different collision gases. The use of a versatile gas aggregation source combined with CID enables the investigation of proton localization in mixed pyrene–water clusters.The growth of mixed pyrene–water clusters is found to occur on protonated pyrene molecules. The various potential protonation sites on pyrene result in different isomers.
For m = 1, we interpret the branching ratio and fragment distributions as reflecting the initial population of isomers due to direct dissociation. We observe that for n = 1 and 2, the proton is always localized onto the pyrene molecule. For n ≥ 3, there are cases in which the proton is transferred to the water network, leading to the observation of protonated water fragments. For m = 2 and 3, we also observe the appearance of protonated water cluster fragments for n ≥ 3 but for a more limited number of occurrences. In all cases, (Py)(H2O)3H+ appears to be remarkably stable.
This study presents opportunities for advancing astrochemical models, especially in situations where protonation reactions play a crucial role in ion-neutral chemistry, such as in cold molecular clouds and the inner regions of protoplanetary disks.54 PAHs, with their high proton affinities, may play a critical role in maintaining charge balance in these environments. Due to their charged nature, protonated PAHs could also act as nucleation seeds for water ice and mixed carbon–water nanograins. These systems could potentially contribute to the chemical evolution of PAHs in protoplanetary disks and play a role in planet formation. Several models aim to investigate the relationship between the spatial distribution of PAHs and the snowline, taking into account processes like PAH clustering and the condensation of PAHs onto ice mantles.55,56 Significant progress in this field is expected in the near future driven by the enhanced capabilities of advanced infrared observatories like the James Webb Space Telescope, as well as ground-based very large telescopes and interferometers.12,57,58
Author contributions
A. M. N.: formal analysis, investigation, validation, visualization, writing – original draft. H. L.: formal analysis, methodology, software, writing – review & editing. L. T.: methodology, software. S. Z.: conceptualization, formal analysis, investigation, methodology, validation, writing – review & editing. C. J.: conceptualization, formal analysis, resources, supervision, writing – review & editing, funding acquisition. J.-M. L.: resources, writing – review & editing. A. M.: investigation, formal analysis, writing – review & editing. A. S.: conceptualization, formal analysis, methodology, software, writing – review & editing. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work received support from the European Research Council under the European Union's Seventh Framework Programme ERC-2013-SyG, Grant Agreement No. 610256, NANOCOSMOS and from CNRS through the 80|Prime program (Project Nanoeau). This study has been (partially) supported through the EUR grant NanoX no. ANR-17-EURE-0009 in the framework of the “Programme des Investissements d'Avenir”. Aude Simon and Héloïse Leboucher thank the computing mesocenter CALMIP (“CALcul en MIdi Pyrénées”, UAR3667 of CNRS) for generous allocation of computer resources (project p17002).References
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS PubMed.
- J. Cernicharo, M. Agúndez, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 649, L15 CrossRef CAS PubMed.
- A. M. Burkhardt, K. Long Kelvin Lee, P. Bryan Changala, C. N. Shingledecker, I. R. Cooke, R. A. Loomis, H. Wei, S. B. Charnley, E. Herbst, M. C. McCarthy and B. A. McGuire, Astrophys. J., Lett., 2021, 913, L18 CrossRef CAS.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Science, 2021, 371, 1265–1269 CrossRef CAS PubMed.
- M. Agúndez, N. Marcelino, B. Tercero and J. Cernicharo, Astron. Astrophys., 2023, 677, L13 CrossRef.
- R. I. Kaiser and N. Hansen, J. Phys. Chem. A, 2021, 125, 3826–3840 CrossRef CAS PubMed.
- M. A. Sephton, Nat. Prod. Rep., 2002, 19, 292–311 RSC.
- H. Naraoka, Y. Takano, J. P. Dworkin, Y. Oba, K. Hamase, A. Furusho, N. O. Ogawa, M. Hashiguchi, K. Fukushima, D. Aoki, P. Schmitt-Kopplin, J. C. Aponte, E. T. Parker, D. P. Glavin, H. L. McLain, J. E. Elsila, H. V. Graham, J. M. Eiler, F.-R. Orthous-Daunay, C. Wolters, J. Isa, V. Vuitton, R. Thissen, S. Sakai, T. Yoshimura, T. Koga, N. Ohkouchi, Y. Chikaraishi, H. Sugahara, H. Mita, Y. Furukawa, N. Hertkorn, A. Ruf, H. Yurimoto, T. Nakamura, T. Noguchi, R. Okazaki, H. Yabuta, K. Sakamoto, S. Tachibana, H. C. Connolly, D. S. Lauretta, M. Abe, T. Yada, M. Nishimura, K. Yogata, A. Nakato, M. Yoshitake, A. Suzuki, A. Miyazaki, S. Furuya, K. Hatakeda, H. Soejima, Y. Hitomi, K. Kumagai, T. Usui, T. Hayashi, D. Yamamoto, R. Fukai, K. Kitazato, S. Sugita, N. Namiki, M. Arakawa, H. Ikeda, M. Ishiguro, N. Hirata, K. Wada, Y. Ishihara, R. Noguchi, T. Morota, N. Sakatani, K. Matsumoto, H. Senshu, R. Honda, E. Tatsumi, Y. Yokota, C. Honda, T. Michikami, M. Matsuoka, A. Miura, H. Noda, T. Yamada, K. Yoshihara, K. Kawahara, M. Ozaki, Y. I. Iijima, H. Yano, M. Hayakawa, T. Iwata, R. Tsukizaki, H. Sawada, S. Hosoda, K. Ogawa, C. Okamoto, N. Hirata, K. Shirai, Y. Shimaki, M. Yamada, T. Okada, Y. Yamamoto, H. Takeuchi, A. Fujii, Y. Takei, K. Yoshikawa, Y. Mimasu, G. Ono, N. Ogawa, S. Kikuchi, S. Nakazawa, F. Terui, S. Tanaka, T. Saiki, M. Yoshikawa, S. I. Watanabe and Y. Tsuda, Science, 2023, 379, eabn9033 CrossRef CAS PubMed.
- S. S. Zeichner, J. C. Aponte, S. Bhattacharjee, G. Dong, A. E. Hofmann, J. P. Dworkin, D. P. Glavin, J. E. Elsila, H. V. Graham, H. Naraoka, Y. Takano, S. Tachibana, A. T. Karp, K. Grice, A. I. Holman, K. H. Freeman, H. Yurimoto, T. Nakamura, T. Noguchi, R. Okazaki, H. Yabuta, K. Sakamoto, T. Yada, M. Nishimura, A. Nakato, A. Miyazaki, K. Yogata, M. Abe, T. Okada, T. Usui, M. Yoshikawa, T. Saiki, S. Tanaka, F. Terui, S. Nakazawa, S. I. Watanabe, Y. Tsuda, K. Hamase, K. Fukushima, D. Aoki, M. Hashiguchi, H. Mita, Y. Chikaraishi, N. Ohkouchi, N. O. Ogawa, S. Sakai, E. T. Parker, H. L. McLain, F.-R. Orthous-Daunay, V. Vuitton, C. Wolters, P. Schmitt-Kopplin, N. Hertkorn, R. Thissen, A. Ruf, J. Isa, Y. Oba, T. Koga, T. Yoshimura, D. Araoka, H. Sugahara, A. Furusho, Y. Furukawa, J. Aoki, K. Kano, S. I. M. Nomura, K. Sasaki, H. Sato, T. Yoshikawa, S. Tanaka, M. Morita, M. Onose, F. Kabashima, K. Fujishima, T. Yamazaki, Y. Kimura and J. M. Eiler, Science, 2023, 382, 1411–1416 CrossRef CAS PubMed.
- A. C. A. Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581 CrossRef CAS.
- E. F. van Dishoeck, L. E. Kristensen, J. C. Mottram, A. O. Benz, E. A. Bergin, P. Caselli, F. Herpin, M. R. Hogerheijde, D. Johnstone, R. Liseau, B. Nisini, M. Tafalla, F. F. S. van der Tak, F. Wyrowski, A. Baudry, M. Benedettini, P. Bjerkeli, G. A. Blake, J. Braine, S. Bruderer, S. Cabrit, J. Cernicharo, Y. Choi, A. Coutens, T. de Graauw, C. Dominik, D. Fedele, M. Fich, A. Fuente, K. Furuya, J. R. Goicoechea, D. Harsono, F. P. Helmich, G. J. Herczeg, T. Jacq, A. Karska, M. Kaufman, E. Keto, T. Lamberts, B. Larsson, S. Leurini, D. C. Lis, G. Melnick, D. Neufeld, L. Pagani, M. Persson, R. Shipman, V. Taquet, T. A. van Kempen, C. Walsh, S. F. Wampfler, U. Yldz and W. I. S. H. Team, Astron. Astrophys., 2021, 648, A24 CrossRef CAS.
- J. J. Tobin, M. L. R. van't Hoff, M. Leemker, E. F. van Dishoeck, T. Paneque-Carreño, K. Furuya, D. Harsono, M. V. Persson, L. I. Cleeves, P. D. Sheehan and L. Cieza, Nature, 2023, 615, 227–230 CrossRef CAS PubMed.
- E. F. van Dishoeck, E. Herbst and D. A. Neufeld, Chem. Rev., 2013, 113, 9043–9085 CrossRef CAS PubMed.
- M. Agúndez, C. Cabezas, N. Marcelino, R. Fuentetaja, B. Tercero, P. de Vicente and J. Cernicharo, Astron. Astrophys., 2022, 659, L9 CrossRef.
- A. Pathak and P. J. Sarre, Mon. Not. R. Astron. Soc.: Lett., 2008, 391, L10–L14 CrossRef.
- H. Knorke, J. Langer, J. Oomens and O. Dopfer, Astrophys. J., Lett., 2009, 706, L66–L70 CrossRef CAS.
- I. Alata, C. Dedonder, M. Broquier, E. Marceca and C. Jouvet, J. Am. Chem. Soc., 2010, 132, 17483–17489 CrossRef CAS PubMed.
- M. Bahou, P. Das, Y.-F. Lee, Y.-J. Wu and Y.-P. Lee, Phys. Chem. Chem. Phys., 2014, 16, 2200–2210 RSC.
- M. Tsuge, C.-Y. Tseng and Y.-P. Lee, Phys. Chem. Chem. Phys., 2018, 20, 5344–5358 RSC.
- D. H. Aue, M. Guidoni and L. Betowski, Int. J. Mass Spectrom., 2000, 201, 283–295 CrossRef CAS.
- I. Alata, M. Broquier, C. Dedonder-Lardeux, C. Jouvet, M. Kim, W. Y. Sohn, S.-S. Kim, H. Kang, M. Schütz, A. Patzer and O. Dopfer, J. Chem. Phys., 2011, 134, 074307 CrossRef PubMed.
- K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2020, 124, 1134–1151 CrossRef CAS PubMed.
- A. K. Lemmens, S. Gruet, A. L. Steber, J. Antony, S. Grimme, M. Schnell and A. M. Rijs, Phys. Chem. Chem. Phys., 2019, 21, 3414–3422 RSC.
- D. Loru, A. L. Steber, P. Pinacho, S. Gruet, B. Temelso, A. M. Rijs, C. Pérez and M. Schnell, Phys. Chem. Chem. Phys., 2021, 23, 9721–9732 RSC.
- I. Braud, S. Zamith and J.-M. L'Hermite, Rev. Sci. Instrum., 2017, 88, 043102 CrossRef CAS PubMed.
- I. Alata, M. Broquier, C. Dedonder-Lardeux, C. Jouvet, M. Kim, W. Y. Sohn, S.-S. Kim, H. Kang, M. Schütz, A. Patzer and O. Dopfer, J. Chem. Phys., 2011, 134, 074307 CrossRef PubMed.
- I. Braud, S. Zamith, J. Cuny, L. Zheng and J.-M. LHermite, J. Chem. Phys., 2019, 150, 014303 CrossRef PubMed.
- L. Zheng, J. Cuny, S. Zamith, J.-M. L'Hermite and M. Rapacioli, Phys. Chem. Chem. Phys., 2021, 23, 27404–27416 RSC.
- F. Chirot, S. Zamith, P. Labastie and J.-M. L'Hermite, Rev. Sci. Instrum., 2006, 77, 063108 CrossRef.
- S. Zamith, M.-C. Ji, J.-M. L'Hermite, C. Joblin, L. Dontot, M. Rapacioli and F. Spiegelman, J. Chem. Phys., 2019, 151, 194303 CrossRef PubMed.
- S. Zamith, J.-M. LHermite, L. Dontot, L. Zheng, M. Rapacioli, F. Spiegelman and C. Joblin, J. Chem. Phys., 2020, 153, 054311 CrossRef CAS PubMed.
- S. Zamith, A. Kassem, J.-M. LHermite and C. Joblin, J. Phys. Chem. A, 2022, 126, 3696–3707 CrossRef CAS PubMed.
- H. C. Straub, B. G. Lindsay, K. A. Smith and R. F. Stebbings, J. Chem. Phys., 1998, 108, 109–116 CrossRef CAS.
- M.-Y. Song, H. Cho, G. P. Karwasz, V. Kokoouline, Y. Nakamura, J. Tennyson, A. Faure, N. J. Mason and Y. Itikawa, J. Phys. Chem. Ref. Data, 2021, 50, 023103 CrossRef CAS.
- W. T. Huntress, Jr. and R. F. Pinizzotto Jr., J. Chem. Phys., 1973, 59, 4742–4756 CrossRef.
- H. Leboucher, A. Simon and M. Rapacioli, J. Chem. Phys., 2023, 158, 114308 CrossRef CAS PubMed.
- T. Heine, M. Rapacioli, S. Patchkovskii, J. Frenzel, A. Koster, P. Calaminici, H. A. Duarte, S. Escalante, R. Flores-Moreno, A. Goursot, J. Reveles, D. Salahub and A. Vela, 2023, deMonNano experiment, https://demon-nano.ups-tlse.fr/ Search PubMed.
- L. Dontot, F. Spiegelman and M. Rapacioli, J. Phys. Chem. A, 2019, 123, 9531–9543 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- C.-H. Chin and S. H. Lin, Phys. Chem. Chem. Phys., 2016, 18, 14569–14579 RSC.
- M. Bahou, Y.-J. Wu and Y.-P. Lee, J. Phys. Chem. Lett., 2013, 4, 1989–1993 CrossRef CAS PubMed.
- H.-P. Cheng, J. Phys. Chem. A, 1998, 102, 6201–6204 CrossRef CAS.
- T. Wròblewski, L. Ziemczonek and G. P. Karwasz, Czech. J. Phys., 2004, 54, C747 CrossRef.
- Y. Kawai, S. Yamaguchi, Y. Okada, K. Takeuchi, Y. Yamauchi, S. Ozawa and H. Nakai, Chem. Phys. Lett., 2003, 377, 69–73 CrossRef CAS.
- D. J. Goebbert and P. G. Wenthold, Eur. J. Mass Spectrom., 2004, 10, 837–845 CrossRef CAS PubMed.
- T. F. Magnera, D. E. David and J. Michl, Chem. Phys. Lett., 1991, 182, 363–370 CrossRef CAS.
- E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- M. Meot-Ner, J. Phys. Chem., 1980, 84, 2716–2723 CrossRef CAS.
- K. Hansen, P. U. Andersson and E. Uggerud, J. Chem. Phys., 2009, 131, 124303 CrossRef CAS PubMed.
- N. F. Dalleska, K. Honma and P. B. Armentrout, J. Am. Chem. Soc., 1993, 115, 12125–12131 CrossRef CAS.
- E. Bruzzie, R. Parajuli and A. J. Stace, Int. J. Mass Spectrom., 2013, 333, 1–7 CrossRef CAS.
- T. Wróblewski, L. Ziemczonek, E. Gazda and G. P. Karwasz, Radiat. Phys. Chem., 2003, 68, 313–318 CrossRef.
- T. Balduin, P. Woitke, U. G. Jørgensen, W. F. Thi and Y. Narita, Astron. Astrophys., 2023, 678, A192 CrossRef CAS.
- K. Lange, C. Dominik and A. G. G. M. Tielens, Astron. Astrophys., 2023, 674, A200 CrossRef CAS.
- J. Y. Seok and A. Li, Astrophys. J., 2016, 818, 2 CrossRef.
- I. Kamp, T. Henning, A. M. Arabhavi, G. Bettoni, V. Christiaens, D. Gasman, S. L. Grant, M. Morales-Calderón, B. Tabone and A. Abergel, et al. , Faraday Discuss., 2023, 245, 112–137 RSC.
- G. Yoffe, R. van Boekel, A. Li, L. B. F. M. Waters, K. Maaskant, R. Siebenmorgen, M. van den Ancker, D. J. M. P. dit de la Roche, B. Lopez, A. Matter, J. Varga, M. R. Hogerheijde, G. Weigelt, R. D. Oudmaijer, E. Pantin, M. R. Meyer, J. C. Augereau and T. Henning, Astron. Astrophys., 2023, 674, A57 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05734h |
| This journal is © the Owner Societies 2024 |