Open Access Article
Open Access ArticleVariational quantum eigensolver for closed-shell molecules with non-bosonic corrections
Kyungmin
Kim†
 a,
Sumin
Lim†
b,
Kyujin
Shin
a,
Sumin
Lim†
b,
Kyujin
Shin
 *c,
Gwonhak
Lee
d,
Yousung
Jung
*c,
Gwonhak
Lee
d,
Yousung
Jung
 e,
Woomin
Kyoung
e,
Woomin
Kyoung
 c,
June-Koo Kevin
Rhee
*dfg and
Young Min
Rhee
c,
June-Koo Kevin
Rhee
*dfg and
Young Min
Rhee
 *a
*a
aDepartment of Chemistry, KAIST, Daejeon, 34141, Republic of Korea. E-mail: ymrhee@kaist.ac.kr
bDepartment of Physics, KAIST, Daejeon, 34141, Republic of Korea
cMaterials Research & Engineering Center, CTO Division, Hyundai Motor Company, Uiwang 16082, Republic of Korea
dSchool of Electrical Engineering, KAIST, Daejeon, 34141, Republic of Korea. E-mail: rhee.jk@kaist.ac.kr
eDepartment of Chemical Engineering, Seoul National University, Seoul, 08826, Republic of Korea
fKAIST ITRC of Quantum Computing for AI, KAIST, Daejeon, 34141, Republic of Korea
gKAIST Institute for IT Convergence, KAIST, Daejeon, 34141, Republic of Korea
First published on 26th February 2024
Abstract
The realization of quantum advantage with noisy-intermediate-scale quantum (NISQ) machines has become one of the major challenges in computational sciences. Maintaining coherence of a physical system with more than ten qubits is a critical challenge that motivates research on compact system representations to reduce algorithm complexity. Toward this end, the variational quantum eigensolver (VQE) used to perform quantum simulations is considered to be one of the most promising algorithms for quantum chemistry in the NISQ era. We investigate reduced mapping of one spatial orbital to a single qubit to analyze the ground state energy in a way that the Pauli operators of qubits are mapped to the creation/annihilation of singlet pairs of electrons. To include the effect of non-bosonic (or non-paired) excitations, we introduce a simple correction scheme in the electron correlation model approximated by the geometrical mean of the bosonic (or paired) terms. Employing it in a VQE algorithm, we assess ground state energies of H2O, N2, and Li2O in good agreement with full configuration interaction (FCI) models respectively, using only 6, 8, and 12 qubits with quantum gate depths proportional to the squares of the qubit counts. With the adopted seniority-zero approximation that uses only one half of the qubit counts of a conventional VQE algorithm, we find that our non-bosonic correction method reaches reliable quantum chemistry simulations at least for the tested systems.
1 Introduction
The concept of quantum simulation using a quantum computer was first proposed by Feynman,1 from an insight that a coupled quantum state has the ability to efficiently and accurately simulate another quantum mechanical system. More than a decade later, the conjectured efficiency was confirmed by Lloyd.2 In the early developments, the phase estimation algorithm (PEA) proposed by Kitaev was adopted crucially,3 with experimental verification in a small qubit system such as a nuclear magnetic resonance (NMR) device.4 Among the many different possibilities of using quantum algorithms in solving real-world problems, efficiently solving electronic structure problems as suggested by Aspuru-Guzik et al.5 has drawn much attention. While quantum computers in the future are expected to outperform classical computers for some specific problems, in the viewpoint of scalability we currently only have few tens of noisy qubits as Preskill pointed out.6 The present devices are conventionally characterized as noisy-intermediate-scale quantum (NISQ) devices. Thus, demonstrating quantum superiority within this limitation is one of the major challenges.With this situation, the variational quantum eigensolver (VQE)7 has become likely the primary algorithm for performing quantum chemistry simulations. In the realm of the electronic structure theory, small molecules approximately having 10 electrons are simulated by quantum hardware,8–10 while systems that require 20–30 qubits have been calculated on models.11,12 Development of VQE algorithms to perform more efficient quantum simulations using NISQ hardware is being reported continuously.13,14
In electronic structure problems, obtaining the exact solution of the time-independent Schrödinger equation, i.e., full configuration interaction (FCI) energy, has a complexity close to O(N!) or exponential for practical purposes with the basis set size N. FCI calculations consider all possible electron configurations within the available orbital space beyond the Hartree–Fock (HF) determinant. A VQE approach initiates the post-HF calculation by mapping the N selected spin-orbitals to qubits and generates an ansatz that can be prepared by a system of unitary coupled cluster (UCC) gates or some other heuristic gates. This is followed by measuring the energy expectation value for the corresponding Pauli operators in the computational basis. VQE obtains an approximate value of the FCI energy with a polynomial complexity with respect to N, which is attained by adjusting the parameters of ansatz using the classical optimizer. Practically, however, as the numbers of qubits and gates of a noisy quantum computer increase, the fidelity starts to drop rapidly and the VQE algorithm does not achieve the desired accuracy. Therefore, in the NISQ era, constructing an efficient VQE algorithm that reduces the numbers of qubits and gates is one of the most significant approaches. In conventional VQE algorithms, a spin orbital is encoded by a single qubit by Jordan–Wigner15 or Bravyi–Kitaev16 transformation. For the closed-shell molecules, however, a seniority-zero approximation is routinely applied to reduce the total number of qubits required,17 which truncates the un-paired excitations in the VQE ansatz. An example of this approximation is doubly occupied configuration interaction (DOCI), where one includes all determinants only with doubly occupied orbitals. Because such pair-correlated methods can capture a significant portion of static correlations, previous studies18,19 focused on improving the missing dynamic correlations. From the viewpoint of the NISQ device, the pair-correlated approximation is promising since the number of qubits required to implement the ansatz can be reduced by a factor of two, because one qubit encodes a spatial orbital,17 not a spin-orbital. Indeed, some of the authors have recently demonstrated this advantage with trapped-ion quantum hardware with the orbital-optimized pair-correlated unitary pair coupled cluster double ansatz (oo-upCCD).20 Thus, designing a VQE algorithm that can recover the missing correlation energy of the pair-approximation will be important for the utility of a NISQ quantum computer.
Here, we propose a simple correction scheme for the orbital-optimized pair-correlated VQE simulation. Specifically, we first construct an ansatz by using exchange gates between the qubits corresponding to occupied and virtual spatial orbitals. The essence of this construct is the same as in the earlier studies listed above. The VQE optimization within the ansatz and then subsequent measurements provide information needed for further performing orbital optimizations,18,20 which we then perform with a classical algorithm. For handling electron correlations involving singly occupied orbitals besides the double excitations, we propose a simple non-bosonic correction based on the terms designed with the geometric means of the related bosonic excitation terms. The correction can be performed without using any quantum resource. We test the performance of our scheme by considering a series of molecular systems. Indeed, reasonable agreements with the FCI results are attained for all the tested systems, and the non-bosonic corrections in many cases are shown to be crucial in achieving the agreements. In fact, the non-bosonic correction scheme that we are proposing is computationally almost free yet improves greatly the practical accuracy of the paired-electron approximation.
2 Methods
In our construction, two electrons in one molecular orbital (MO) correspond to one qubit. Accordingly, when 2n electrons are contained in N MOs, the qubit ansatz is prepared as| |Ψ0〉 = |11…1100…00〉 | (1) |
 | ||
| Fig. 1 Ansatz preparation based on exchange-type gates, as suggested in ref. 21. | ||
Now, the final state can be translated into
 | (2) |
 | (3) |
 | (4) |
 | (5) |
The merge of the last two sums in the first line into the second line is for further convenience. The first sum is non-vanishing only if σ ≠ τ, and by introducing  and dp as the pair creation and annihilation operators with dp = apβapα and
and dp as the pair creation and annihilation operators with dp = apβapα and 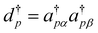 , we can easily get
, we can easily get
 | (6) |
By properly considering commutation relations, we can trivially reach
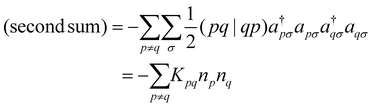 | (7) |
 | (8) |
Note that in the second sum, the condition of p ≠ q additionally reduced the summation over the spin indices. We also adopted Jpq and Kpq to respectively represent the Coulomb and the exchange integrals associated with p and q in compact forms, as well as the number operator  . With these, the working expression for the Hamiltonian is obtained as
. With these, the working expression for the Hamiltonian is obtained as
 | (9) |
While we can adopt the set of HF MOs for constructing this Hamiltonian, it will not be an ideal choice for obtaining the molecular energy. Therefore, we performed orbital optimizations toward minimizing 〈Ψ|H|Ψ〉 as in ref. 20.
Then, the total energy is calculated as
| E = 〈Ψ|H|Ψ〉 +EnB | (10) |
Although the analytic expression of EnB cannot be derived based on the information available with the pair excitations, its contribution may still be accounted for toward achieving more reliable energy calculations at least at a heuristic level. We propose to approximate it as
 | (11) |
This correction was devised with the following reasoning. First, among all missing unpaired configurations, the ones with two or four unpaired electrons (seniority 2 and 4) will contribute most.24 This is a reasonable assumption when we consider the terms that constitute low order correlation corrections. Also, such configurations can be generated by operating  (with omitted spin indices for brevity) on some doubly occupied configuration. We naturally expect that the largest non-bosonic contributions should be from 〈Φ0|H|Φrspq〉 = (pr||qs), when Φ0 is the HF ground state reference configuration. Thus, we argue that the energy contribution by an unpaired configuration will be proportional to the associated ERI, (pr||qs). To know the actual contribution, we need its proportionality constant (“amplitude”), but by construction we do not have that information. With a similar intuition in the spin-restricted ensemble-referenced Kohn–Sham (REKS) method,25 we assume that the open-shell contribution is related to the populations (occupation numbers in the REKS terminology) of two bosonic single determinant reference states. We accordingly reason that this unknown amplitude can be approximated by the geometric mean of the two contributions related to
(with omitted spin indices for brevity) on some doubly occupied configuration. We naturally expect that the largest non-bosonic contributions should be from 〈Φ0|H|Φrspq〉 = (pr||qs), when Φ0 is the HF ground state reference configuration. Thus, we argue that the energy contribution by an unpaired configuration will be proportional to the associated ERI, (pr||qs). To know the actual contribution, we need its proportionality constant (“amplitude”), but by construction we do not have that information. With a similar intuition in the spin-restricted ensemble-referenced Kohn–Sham (REKS) method,25 we assume that the open-shell contribution is related to the populations (occupation numbers in the REKS terminology) of two bosonic single determinant reference states. We accordingly reason that this unknown amplitude can be approximated by the geometric mean of the two contributions related to  and
and  , namely the portions of |Ψ〉 that have filled p (q) orbitals and empty r (s) orbitals. These will be the norms of
, namely the portions of |Ψ〉 that have filled p (q) orbitals and empty r (s) orbitals. These will be the norms of  and
and 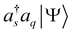 , leading to eqn (11). After a short algebra, we can also show that eqn (11) is equivalent to
, leading to eqn (11). After a short algebra, we can also show that eqn (11) is equivalent to
 | (12) |
In calculating this energy correction with EnB, we need a way of fixing the orbital signs, even though the energy calculated by the variational optimization before adding this correction is invariant to the choice of orbital signs. In this work, we aimed to adjust the signs such that the energy becomes as low as possible. In principle, we can test all different combinations of the signs of all orbitals, but doing so will require testing on ∼2N combinations with the number of orbitals N, which will be unacceptable. Thus, we have taken the following practical tactic. When the number of electron pairs is denoted as n, we started by arbitrarily fixing the signs of the n-th and the (n + 1)-th orbitals, which will correspond to the highest occupied and the lowest unoccupied orbitals with the HF picture. Of course, after the further orbital optimizations, the HF picture will not last any longer, but the indices inherited from the initial HF calculations still remain. With an index a fixed to a = (n + 1), we walked down the indices over {i = (n − 1),(n − 2),…,1} together with i+ = i + 1, and at each stage fixed the sign of the i-th orbital such that the electron-repulsion integral (i+a|ia) becomes positive. The same process was also taken for over {a = (n + 1),(n + 2),…,N} by considering (na−|na) with a− = (a − 1) and by walking up in the index space of a. For these procedures, we can possibly use indexes of canonical orbitals in defining i and a. However, doing so does not provide any connection between adjacent orbitals, and sometimes (i+a|ia) or (na−|na) is too close to zero, which renders the sign fixing process rather ill defined. Choosing a spatially best overlapping orbital as the neighboring one will be better in this regard, but orbitals are conventionally given with orthogonality intrinsically implemented and using overlap will not be a good tactic in this regard, either. Therefore, we adopted the one-electron matrix hpq to decide the proximity in orbitals. Namely, for any given orbital i, we chose i+ such that i+ was not considered before and hii+ was the maximum. The same could be applied for choosing a−. Apparently, the computational efforts for choosing the sequence of orbitals in this manner scale as ∼N2.
3 Results
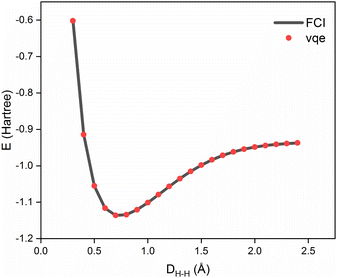
We first tested our VQE algorithm using H2 with the minimal basis set, STO-3G. Because of the symmetry constraint, this case with only two MOs does not involve any correlations with a non-bosonically excited configuration. Thus, it can serve as a baseline benchmark for our closed-shell quantum simulator algorithm. In terms of the number of qubits, only two were required while four qubits will be needed with the conventional Jordan–Wigner encoding for handling four spin-orbitals. Because there are only one occupied and one virtual orbitals in this case, one exchange gate with one mixing parameter was enough for VQE. The results at varying bond distances, in the range from 0.3 to 2.4 Å, are plotted in Fig. 2, together with the corresponding FCI and the HF results. One can clearly see that the VQE result with ∼105 shots is in excellent agreement with the FCI energies with nearly negligible errors of ≪ 1 milliHartree (mH), evidencing that our VQE algorithm is working properly.We next tested our scheme by computing the bond dissociation potential curves of a series of small molecules: H2O, LiH, N2, and Li2O, with the same STO-3G basis set and the same number of shots for obtaining the expectation values of the Pauli terms. The adopted computational resources for the molecules are listed in Table 1. In this work, we adopted a quantum simulator IBM-Qiskit,26 and thus with actual quantum hardware, the optimal numbers of shot averages will differ depending on the fidelity and the coherence time of the hardware.
| Molecule | H2 | LiH | H2O | N2 | Li2O |
|---|---|---|---|---|---|
| No. qubits (occ,vir) | 2 (1,1) | 3 (1,2) | 6 (4,2) | 8 (5,3) | 12 (4,8) |
| No. paramters (θia) | 1 | 2 | 8 | 15 | 32 |
| No. two-qubit-gates | 3 | 6 | 24 | 45 | 96 |
The first tested molecule, LiH, serves the purpose of checking how much correlation energy can be recovered with VEQ itself. In this case, there are six MOs with the STO-3G basis. VQE simulations were performed by a circuit consisting of six qubits, corresponding to two occupied and four virtual orbitals. The ground state energies were obtained in the Li–H distance range of 0.5 to 2.4 Å and are shown in Fig. 3. As shown in this figure, hereafter, we will designate the VQE energies based on HF orbitals with “vqe” and the ones after orbital optimizations with “oo-vqe”. When EnB in eqn 12 is added, of course, the energies will be respectively designated as “vqe-nB” and “oo-vqe-nB”. Both vqe and vqe-nB results show good agreement with FCI energy around the distance near the equilibrium separation. However, the errors become quite large at long separations, and orbital optimizations indeed cover this discrepancy rather nicely. This is expected as the spin-restricted HF orbitals should severely fail in such a case, and pair-correlation methods are known to perform well for handling the related nondynamical correlations.27 In any case, over the entire region, our pair-correlated VQE performs quite well after orbital optimization and EnB does not contribute much with LiH.
The next tested molecule, H2O, has seven MOs with the minimal basis set. Of the seven, oxygen 1s hardly participates in forming the bonds, and we excluded this core orbital from the VQE calculations via the frozen-core approximation. Hence, VQE was performed by mapping six MOs (four occupied and two virtual ones) to as many qubits. Thus, there were 8 parameters in applying the exchange gates between the occupied and virtual orbitals, with a total of 24 two-qubit gates. Fig. 4 shows how the molecular energy changes by varying the H–O bond length at a fixed H–O–H angle of 104.45 deg. From this figure, we can again see that the paired ansatz by itself (vqe) displays a significant deviation from the FCI result. Much of the discrepancy is fixed with the subsequent orbital optimization (oo-vqe), and the non-bosonic correction that we propose here almost correctly recovers from the remaining error, with the largest deviation from the FCI curve being barely noticeable from the figure. Interestingly, the non-bosonic correction without performing the orbital optimization (vqe-nB) also displays quite reliable agreement in this case.
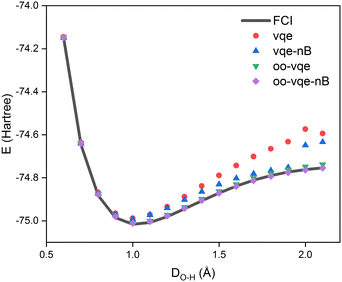 | ||
| Fig. 4 H2O ground state energies with differing O–H distances. The two bond lengths were kept identical to each other. | ||
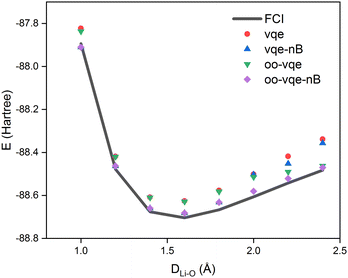
Now, let us move on to a larger system Li2O. Indeed, the molecule is practically related to the operation of Li–air batteries, and enabling quantum simulations of battery materials will be of significant industrial interest.11 Similarly to H2O, by applying the frozen core approximation for 1s orbitals, we were able to conduct VQE simulations with only 12 qubits. As they represented 4 occupied and 8 virtual orbitals, a total of 32 parameters matching with 96 two-qubit gates were needed. The ground state energies at varying Li–O bond distances are shown in Fig. 5. Compared to H2O, because more virtual orbitals are available, we can expect that the contribution of the non-bosonic excitations will be larger in this case. Indeed, from the figure, we can see that vqe or oo-vqe does not reproduce the FCI PES that well. Instead, oo-vqe-nB reproduces FCI results much better with errors smaller than ∼10 mH.
Now, let us consider the dissociation curve of N2 to further confirm the utility of our approach. In fact, N2 with its triple bond has been considered as one of the most difficult systems to model with electronic structure theories, and accordingly, it will act as a stringent test case for us. Not surprisingly, even the CCSD(T) method fails drastically in describing this triple bond dissociation because it is still a single-reference approach (Fig. 6). In contrast, our VQE results with the frozen core approximation reasonably reproduce the FCI results, with the equilibrium bond length and the entire energetic features being in good agreement. We note, however, that the energies at configurations stretched from the equilibrium geometry (RN−N ∼ 1.2 Å) display an error of 30–50 mH. We will defer commenting on this quantitative discrepancy to a later section, as a more detailed analysis about this mismatch will be covered in the Discussion section.
4 Discussion
In order to see how our method that separately treats bosonic and non-bosonic excitations constructs the electronic structure, with Li2O at 1.6 Å separation, we compared the populations of each excited configuration with FCI and VQE. The largest population among bosonically excited configurations was associated with the excitation involving the 7-th and the 13-th MOs (in the order of canonical orbital energies), with the FCI population of 0.11156. The same population from vqe can be compared as ∼0.11244, which is in close agreement with the FCI value. The second largest population, involving an excitation between the 6-th and the 12-th HF MOs, has essentially the same population with 0.11156 for FCI and 0.11142 for VQE. The third populations similarly compare favorably as 0.04982 and 0.04628. Therefore, FCI and our VQE scheme show very similar electronic structures.The situation with N2 was somewhat different. At its minimum energy geometry (∼1.2 Å), the contribution by a quadruple excitation term was quite important with FCI. Namely, a double pair excitation from the 6-th and the 7-th (occupied) MOs to the 8-th and the 9-th (virtual) MOs contributed by ∼30% as large as the most important bosonic double excitation (7-th → 9-th). Still, the population of the quadruply excited configuration was 0.05368 with FCI and 0.05373 with VQE, being in close agreement at the minimum energy geometry. However, when the molecule was stretched with its interatomic distance at 2.0 Å, the double pair excitation contributed even more importantly at the level of ∼75% of the 7-th → 9-th term and bore the second largest population. In this case, the corresponding VQE population was 0.35355 and showed a substantial discrepancy with respect to the FCI population of 0.26495. While our method could still accommodate excitations in pairs and thus the result was not too bad at the equilibrium geometry, it could not handle multiple-bond breaking with enough satisfaction. This is somewhat expected as the situation will likely increase the importance of pair-broken multiple excitations. Thus, our approach started to deviate from the exact answer in stretched geometries as higher excitations become more important. Of course, the fidelity of the simple correction with eqn (11) will also deviate. Thus, we note that treating a triple bond still remains a difficult problem.
We also wish to point out the effects and the limitations of our bosonic mapping and non-bosonic correction. It has been discussed that the bosonic mapping is a powerful tool and can qualitatively reproduce the dissociation curves of simple molecules.17 However, it is destined to underestimate the correlation energy because it only includes a subset of properly treated excitations. Interestingly, our non-bosonic correction mostly shows quite good agreement with exact answers at least for the single-bonded molecules, as exemplified with H2O and Li2O. In contrast, in the cases of molecules involving double or triple bonds, our correction term may not work that well. Indeed, in the case of N2 with a triple bond (Fig. 6), similar results were obtained whether the correction term was added or not. Even in such cases, however, our approach can still be considered meaningful in terms of reducing the required resources for simulations. Although several reports have shown that quantum unitary coupled cluster singles and doubles (UCCSD) can reproduce the dissociation curves of some small single-bonded molecules and even N2 within a few mH error,28–31 the required number of gates was about 104–105,28 which are still distant from the practical applicability with the currently available NISQ devices. It is also interesting to note that various symmetry-restricted versions of quantum UCCSD approaches show errors in the tens of mH regime.28 Our model actually provided curves with an at least similar level of errors, but with only the half number of qubits and tens of two-qubit gates. Indeed, our resource requirements will likely be much more reasonable with the presently available devices.
5 Conclusions
In summary, we have proposed a VQE quantum simulation method that uses a qubit to map a spatial MO in closed-shell molecules with a rather simple correction. The method requires only a half number of qubits compared to conventional Jordan–Wigner or Bravyi–Kitaev mapping based methods. Using the method, dissociation curves of LiH, H2O, and Li2O were obtained, demonstrating errors within ∼10 mH in comparison with FCI. The number of gates and optimization parameters are proportional to O(N2), which is significantly less than the more conventional O(N3) or O(N4) scaling22 and is reasonably accessible with actually available physical qubit systems. We wish that our method can be of help in further advancing techniques in the NISQ era that we have already entered.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Hyundai Motor Company (Hyundai-KAIST Joint Quantum Algorithm Research Project). We thank Dr Seung Hyun Hong and Dr Jongkook Lee at Hyundai Motor Company for enlightening discussions. We also thank Dr Luning Zhao and Dr Joshua Goings at IonQ as well as Prof. Jae Woo Park at Chungbuk National University for useful discussions.References
- R. P. Feynman, Int. J. Theor. Phys., 1982, 21, 467–488 CrossRef.
- S. Lloyd, Science, 1996, 273, 1073–1078 CrossRef CAS PubMed.
- A. Y. Kitaev, Quantum measurements and the Abelian Stabilizer Problem, arXiv, 1995, preprint, arXiv:quant-ph/9511026v1, DOI:10.48550/arXiv.quant-ph/9511026.
- J. Du, N. Xu, X. Peng, P. Wang, S. Wu and D. Lu, Phys. Rev. Lett., 2010, 104, 030502 CrossRef PubMed.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- J. Preskill, Quantum, 2018, 2, 79 CrossRef.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. Obrien, Nat. Commun., 2014, 5, 4213 CrossRef CAS.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242–246 CrossRef CAS PubMed.
- Z. Li, X. Liu, H. Wang, S. Ashhab, J. Cui, H. Chen, X. Peng and J. Du, Phys. Rev. Lett., 2019, 122, 090504 CrossRef CAS PubMed.
- Y. Nam, J.-S. Chen, N. C. Pisenti, K. Wright, C. Delaney, D. Maslov, K. R. Brown, S. Allen, J. M. Amini and J. Apisdorf, et al. , npj Quantum Inf., 2020, 6, 1–6 CrossRef.
- J. E. Rice, T. P. Gujarati, M. Motta, T. Y. Takeshita, E. Lee, J. Latone and J. M. Garcia, J. Chem. Phys., 2021, 154, 134115 CrossRef CAS.
- A. J. McCaskey, Z. P. Parks, J. Jakowski, S. V. Moore, T. D. Morris, T. S. Humble and R. C. Pooser, npj Quantum Inf., 2019, 5, 99 CrossRef.
- G. A. Quantum, et al. , Science, 2020, 369, 1084–1089 CrossRef PubMed.
- B. Foxen, C. Neill, A. Dunsworth, P. Roushan, B. Chiaro, A. Megrant, J. Kelly, Z. Chen, K. Satzinger and R. Barends, et al. , Phys. Rev. Lett., 2020, 125, 120504 CrossRef CAS PubMed.
- P. Jordan and E. P. Wigner, Z. Phys., 1928, 47, 14–75 Search PubMed.
- S. B. Bravyi and A. Y. Kitaev, Ann. Phys., 2002, 298, 210–226 CAS.
- V. E. Elfving, J. A. Gámez and C. Gogolin, Phys. Rev. A, 2021, 103, 032605 CrossRef CAS.
- T. Stein, T. M. Henderson and G. E. Scuseria, J. Chem. Phys., 2014, 140, 214113 CrossRef.
- M. Van Raemdonck, D. R. Alcoba, W. Poelmans, S. De Baerdemacker, A. Torre, L. Lain, G. E. Massaccesi, D. Van Neck and P. Bultinck, J. Chem. Phys., 2015, 143, 104106 CrossRef PubMed.
- L. Zhao, J. Goings, K. Wright, J. Nguyen, J. Kim, S. Johri, K. Shin, W. Kyoung, J. I. Fuks, J.-K. K. Rhee and Y. M. Rhee, npj Quantum Inf., 2023, 9, 60 CrossRef.
- P. K. Barkoutsos, J. F. Gonthier, I. Sokolov, N. Moll, G. Salis, A. Fuhrer, M. Ganzhorn, D. J. Egger, M. Troyer and A. Mezzacapo, et al. , Phys. Rev. A, 2018, 98, 022322 CrossRef CAS.
- P. Gokhale, O. Angiuli, Y. Ding, K. Gui, T. Tomesh, M. Suchara, M. Martonosi and F. T. Chong, IEEE Trans. Quantum Eng., 2020, 1, 1–24 Search PubMed.
- A. Szabo and N. S. Ostlund, Modern quantum chemistry: introduction to advanced electronic structure theory, Courier Corporation, 2012 Search PubMed.
- L. Bytautas, T. M. Henderson, C. A. Jimenez-Hoyos, J. K. Ellis and G. E. Scuseria, J. Chem. Phys., 2011, 135, 044119 CrossRef PubMed.
- M. Filatov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 146–167 CAS.
- Qiskit: Open-Source Quantum Development, https://www.qiskit.org/ Search PubMed.
- M. Ravi, A. Perera, Y. C. Park and R. J. Bartlett, J. Chem. Phys., 2023, 159, 094101 CrossRef CAS.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, J. Chem. Phys., 2020, 152, 124107 CrossRef CAS PubMed.
- J. A. Gomez, T. M. Henderson and G. E. Scuseria, J. Chem. Phys., 2016, 145, 134103 CrossRef PubMed.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2018, 15, 311–324 CrossRef.
- W. Mizukami, K. Mitarai, Y. O. Nakagawa, T. Yamamoto, T. Yan and Y. Ya Ohnishi, Phys. Rev. Res., 2020, 2, 033421 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work |
| This journal is © the Owner Societies 2024 |