Open Access Article
Open Access ArticleAnalysing the stability of He-filled hydrates: how many He atoms fit in the sII crystal?†
Raquel
Yanes-Rodríguez‡
 and
Rita
Prosmiti
and
Rita
Prosmiti
 *
*
Institute of Fundamental Physics (IFF-CSIC), CSIC, Serrano 123, 28006 Madrid, Spain. E-mail: rita@iff.csic.es; Tel: +34 915616800
First published on 1st December 2023
Abstract
Clathrate hydrates have the ability to encapsulate atoms and molecules within their cavities, and thus they could be potentially large storage capacity materials. The present work studies the multiple cage occupancy effects in the recently discovered He@sII crystal. On the basis of previous theoretical and experimental findings, the stability of He(1/1)@sII, He(1/4)@sII and He(2/4)@sII crystals was analysed in terms of structural, mechanical and energetic properties. For this purpose, first-principles DFT/DFT-D computations were performed by using both semi-local and non-local functionals, not only to elucidate which configuration is the most energetically favoured, but also to scrutinize the relevance of the long-range dispersion interactions in these kinds of compounds. We have encountered that dispersion interactions play a fundamental role in describing the underlying interactions, and different tendencies were observed depending on the choice of the functional. We found that PW86PBE-XDM shows the best performance, while the non-local functionals tested here were not able to correctly account for them. The present results reveal that the most stable configuration is the one presenting singly occupied D cages and tetrahedrally occupied H cages (He(1/4)@sII) in line with the experimental observation.
Clathrate hydrates and ice crystals are chemical inclusion compounds with the ability of encapsulating (guest) atoms and/or molecules in the spaces, cavities or channels formed in their own (host) structure.1–5 Both entities share the similarity of being made up of a host water network in which the guest species are entrapped, with the difference that in clathrate hydrates the guests occupy cavities of different sizes and shapes and in the ice structures they are arranged along channels.6–8
One of the guest species that has been seen to be able to enter both crystalline structures is the He atom. In 1988, Londono et al.9 experimentally identified a helium compound with a host lattice very similar to ice II, which would later be known as C1 (He@C1). This structure corresponded to the first helium hydrate9–11 and it was formed by applying He gas pressures of 0.28–0.48 GPa into deuterated water. Since then, unsuccessful attempts have been made to find the first helium clathrate hydrate, frequently resulting in ice-like structures. It was not until 2018 that this helium clathrate hydrate (He@sII) was finally synthesized.12 This achievement was possible thanks to previous experiments13,14 in which a new synthesis route was discovered, which consisted of removing guest atoms from filled structures. In this manner, they were able to synthesize He@sII by refilling empty ice XVI with He atoms. Apart from such He@hydrostructures, this small and weakly interacting atom exhibits a preference for other ice-like systems,15–18 such as hexagonal ice, He@Ih, and is also predicted to have the capacity of travelling through the channels of the recently discovered microporous material,14,19,20 ice XVII, giving rise to the He@C0 structure.21
Finally, another type of inclusion compound related to He, which may be a key point to understanding the layer structure and evolution of icy giant planets,22 is the He–water superionic complexes.23–26 These novel structures are composed of a solid oxygen lattice, with the He and H atoms freely moving and exhibiting liquid-like behaviour. This combination of solid–liquid features makes these compounds not only interesting from a fundamental point of view, but also due to their unique properties such as conductivity similar to that of metals.27
At this point, theoretical studies become essential, since they can provide new insights into the physicochemical properties and stability of these compounds that complement and facilitate future experiments.28–30 Indeed, numerous theoretical studies in the field of clathrate hydrates and ices have made use of a variety of computational methodologies and techniques,31–39 such as first-principles electronic structure methods, semi-empirical approaches, classical molecular mechanics and molecular dynamics or Monte Carlo simulations.40–44
In this vein, previous experimental and theoretical outcomes12,45,46 have predicted that the most likely arrangement of He atoms inside the sII structure is the one that contains 1 He atom in the small cages (D) and 4 He atoms in the large cages (H). We have already examined the multiple cage occupancy effects on the individual (D/H) and two-adjacent (DD/HH/DH) cages, finding that this prediction is fulfilled.47 However, we have also observed that the D cages can store 2 He atoms under more demanding T–P conditions. Similar discussions about cage occupancy in clathrate hydrates with other guest species have been found in the literature.38,48–52 Therefore, in tune with our earlier research,53–55 we aim to study the multiple cage occupancy effects in the crystalline systems through periodic DFT/DFT-D calculations. Thus, we can make a more direct comparison with the experimental outcomes, elucidating which He-filled configuration is more likely to form. In this way, we report structural, mechanical and energetic properties of three different He-filled configurations of the sII structures, namely He(1/1)@sII, He(1/4)@sII and He(2/4)@sII. Our focus is on examining the stability of each configuration and exploring whether the interactions within these systems, including the entire guest–guest, guest–host, and host–host interactions, are influenced by the presence of multiple He atoms within the cages.
1 Computational details
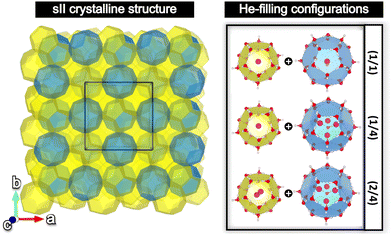
The sII cubic unit cell (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry) is formed by 136 water molecules arranged in 16 small 512 (or D) and 8 large 51264 (or H) cages (xy, where x designates the type of face (pentagonal, hexagonal), while y represents the number of those face types that compose the cage, e.g. 512 is a pentagonal dodecahedral cage). The empty crystal structure was taken from the 3D crystalline framework given in ref. 56, with the oxygen atom positions being extracted from the X-ray diffraction experiments, and the hydrogen atoms’ orientations being determined from TIP4P water model optimizations, satisfying both the ice rules and the net zero dipole moment for the unit cell configuration. Three different He-filled structures are also considered in order to explore the occupation effects: the (1/1) configuration with a total of 24 He atoms distributed in singly fully occupied D and H cages (H2O:He hydration number of 5.67), (1/4) configuration with a total of 48 He atoms arranged in singly and tetrahedrally fully occupied D and H cages (hydration number of 2.83), respectively, and the (2/4) configuration with a total of 64 He atoms disposed in doubly and tetrahedrally fully occupied D and H cages (hydration number of 2.13), respectively. The He atoms were located at the center of each cage, with the HeN (N = 2, 4) geometries being determined by PW86PBE/AVTZ optimizations in the individual D and H cages (see Fig. 1).47 Thus, the initial average He–He bond lengths are R = 2.36 Å for He2 inside D and R = 2.80 Å for He4 inside H.
m space group symmetry) is formed by 136 water molecules arranged in 16 small 512 (or D) and 8 large 51264 (or H) cages (xy, where x designates the type of face (pentagonal, hexagonal), while y represents the number of those face types that compose the cage, e.g. 512 is a pentagonal dodecahedral cage). The empty crystal structure was taken from the 3D crystalline framework given in ref. 56, with the oxygen atom positions being extracted from the X-ray diffraction experiments, and the hydrogen atoms’ orientations being determined from TIP4P water model optimizations, satisfying both the ice rules and the net zero dipole moment for the unit cell configuration. Three different He-filled structures are also considered in order to explore the occupation effects: the (1/1) configuration with a total of 24 He atoms distributed in singly fully occupied D and H cages (H2O:He hydration number of 5.67), (1/4) configuration with a total of 48 He atoms arranged in singly and tetrahedrally fully occupied D and H cages (hydration number of 2.83), respectively, and the (2/4) configuration with a total of 64 He atoms disposed in doubly and tetrahedrally fully occupied D and H cages (hydration number of 2.13), respectively. The He atoms were located at the center of each cage, with the HeN (N = 2, 4) geometries being determined by PW86PBE/AVTZ optimizations in the individual D and H cages (see Fig. 1).47 Thus, the initial average He–He bond lengths are R = 2.36 Å for He2 inside D and R = 2.80 Å for He4 inside H.
Electronic structure DFT calculations were performed for both the empty and He-filled structures, using the Quantum Espresso (QE) code.57–59 On the basis of previous reports,39,54,60,61 the accuracy of different DFT functionals on balance with the computational cost has been verified, and the PW86PBE funcional, as implemented in the LIBXC library62 of QE57–59 has been chosen. In order to account for the long-range London dispersion interactions, correction schemes are also considered. On the one hand, the exchange dipole moment (XDM) scheme63 as implemented in QE, and the D4 scheme as a postprocessing tool with the DFTD4 program64–67 are used. On the other hand, another alternative to solve this deficiency in the calculation of dispersion interactions is the use of non-local functionals which try to capture the effect of the long and intermediate van der Waals (vdW) forces on the energy,68 by adding a non-local term in the calculation of the exchange correlation energy. In this way, the vdW coefficients are themselves functionals of the electron density, thus improving the description of dispersion forces in comparison with local or semi-local functionals. Therefore, within this group of non-local functionals, the vdW-DF69 and vdW-DF270 were chosen for this work, as implemented in the QE software.57–59
The plane-wave pseudopotential approach within the projector-augmented-waves (PAW) method71 was employed using the standard PBE-based pseudopotentials supplied within QE. Moreover, the convergence of the energy cutoff for the plane-wave expansion of the wavefunctions, Ecut_wfc, and for the charge density, Ecut_rho, was checked, resulting in a selection of 360 Ry (4898 eV) for Ecut_wfc and 80 Ry (1088 eV) for the Ecut_rho. A Monkhorst–Pack 1 × 1 × 1 k-point grid72 in the reciprocal space was used per unit cell, while calculations for the isolated He and H2O molecules were performed at the Γ-point in a cubic simulation cell of volume 30 × 30 × 30 Å3, considering the Makov–Payne method73 of electrostatic interaction correction for these aperiodic systems. Geometry optimizations, with all atomic positions relaxed, were carried out using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton algorithm with convergence criterion for the components of energy and forces being smaller than 10−4 Ry (0.00136 eV) and 10−3 Ry bohr−1 (0.026 eV Å−1), respectively.
Three energetic terms are calculated in order to analyse the feasibility of the formation of these crystalline structures. The cohesive energy indicates the energy required to completely separate all the atoms in the crystal, thus quantifying the strength of the chemical bonds and interatomic forces. The cohesive energies per water molecule for the fully occupied HeN@sII structures were calculated as,
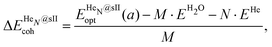 | (1) |
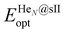 is the total energy of the fully occupied HeN @sII clathrate hydrate unit cell obtained by structural relaxation at each lattice constant a, EH2O and EHe are the total energies of the isolated ground-state H2O molecules and He atoms, respectively, M is the total number of water molecules (M = 136) and N corresponds to the total number of He atoms, that is, N = 24/48/64 for the (1/1), (1/4) and (2/4) configurations, respectively. With regards to the empty sII crystal, the cohesive energy is computed as,
is the total energy of the fully occupied HeN @sII clathrate hydrate unit cell obtained by structural relaxation at each lattice constant a, EH2O and EHe are the total energies of the isolated ground-state H2O molecules and He atoms, respectively, M is the total number of water molecules (M = 136) and N corresponds to the total number of He atoms, that is, N = 24/48/64 for the (1/1), (1/4) and (2/4) configurations, respectively. With regards to the empty sII crystal, the cohesive energy is computed as,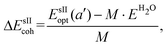 | (2) |
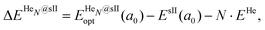 | (3) |
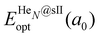 corresponds to the total energy of the fully occupied HeN@sII structure obtained by structural relaxation at the equilibrium lattice constant a0 and EsII(a0) is the total energy of the empty sII structure at the equilibrium lattice constant a0. This energetic quantity indicates the energy release associated with the incorporation of each He atom into the lattice. Finally, the energetic property that more precisely describes the stability of the system is the energy corresponding to the saturation of all the cages in the sII crystal, at a0, calculated as:
corresponds to the total energy of the fully occupied HeN@sII structure obtained by structural relaxation at the equilibrium lattice constant a0 and EsII(a0) is the total energy of the empty sII structure at the equilibrium lattice constant a0. This energetic quantity indicates the energy release associated with the incorporation of each He atom into the lattice. Finally, the energetic property that more precisely describes the stability of the system is the energy corresponding to the saturation of all the cages in the sII crystal, at a0, calculated as: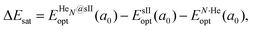 | (4) |
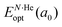 is the total energy resulting from the structural relaxation of the entire number of He atoms at the fixed equilibrium lattice constant a0. It provides an estimate of the overall energy gain realized when all the cages are occupied by the total number of He atoms.
is the total energy resulting from the structural relaxation of the entire number of He atoms at the fixed equilibrium lattice constant a0. It provides an estimate of the overall energy gain realized when all the cages are occupied by the total number of He atoms.
2 Results and discussion
Here we will analyse the effect of the multiple cage occupancy in the sII crystal and, consequently, the discovery of the most stable configuration. Previous experimental and theoretical outcomes have predicted that the small D cages can be occupied by just 1 He atom, whereas the large H cages can encapsulate up to 4 He atoms.12,45,46 However, we have recently verified that the D cages could also accommodate 2 He atoms at a higher energy cost under more demanding T–P conditions.47 Additionally, a similar behaviour has been observed for other small guests, such as hydrogen.74–77 Therefore, in order to shed more light on this matter, three different He-filled sII structures will be investigated in this work: He(1/1)@sII, He(1/4)@sII and He(2/4)@sII. The empty sII crystal will also be considered in order to check the influence of the He guests on the lattice.2.1 He-filling influence on structural and mechanical properties
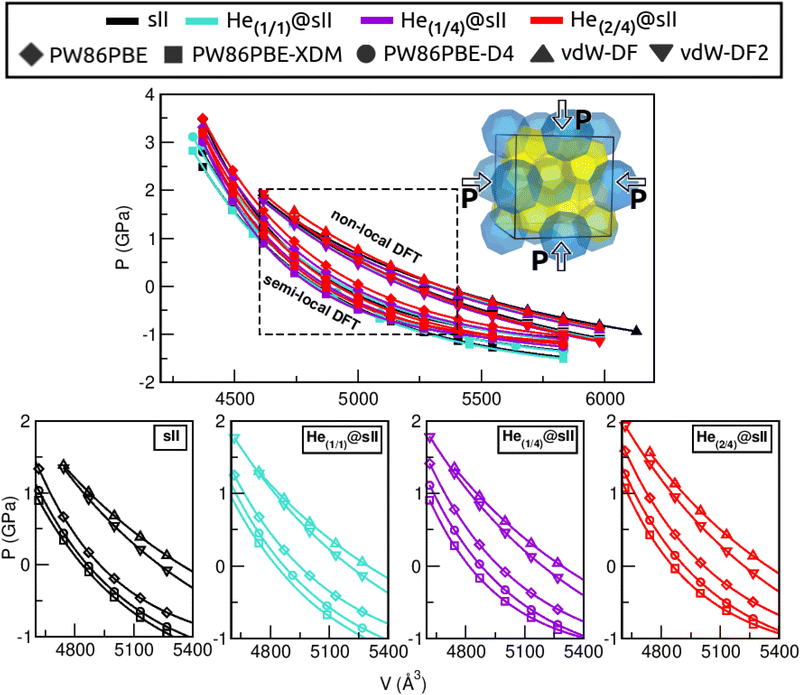
First of all, we performed full geometry optimizations on the empty and He-filled structures at different lattice constant, a, values using the PW86PBE (with and without dispersion corrections), vdW-DF and vdW-DF2 functionals. Total energies were computed and cohesive energies per water molecule were analysed as a function of a as shown in Fig. 2. Starting with the non-local DFT functionals, on the one hand, we observe a displacement of the lattice parameters calculated with both vdW-DF and vdW-DF2, resulting in larger a values. A similar behaviour has been reported for CH4,78 CO79 and N280 hydrates. This overestimation of the lattice parameters is due to the repulsive nature of the exchange–correlation part in the vdW-DF/vdW-DF2 functionals, which leads to an overestimation of the strength of the repulsive interactions between the atoms in the crystal lattice. Consequently, the atoms are pushed apart more than they would be in reality, resulting in overestimated lattice parameters and a less compact crystal than the actual structure. On the other hand, in connection with the previous comment, we see that the vdW-DF functional yields even higher cohesive energies than PW86PBE in the absence of dispersion corrections, while vdW-DF2 predicts energies which are in between those of PW86PBE and PW86PBE-D4. Focusing on the PW86PBE results, we see that, as expected, the application of dispersion corrections to the energy translates into lower DEcoh values, this effect is more pronounced with the XDM scheme. As for the energy predictions, there is no agreement between the different DFT/DFT-D approaches. Both the vdW-DF and vdW-DF2 predict that the He(2/4)@sII is the most energetically favoured configuration, closely followed by He(1/4)@sII, with the empty system being the least energetically favoured structure. For the PW86PBE-XDM functional, the He(1/4)@sII and the empty sII are the most and least energetically favoured structures, respectively. Finally, the PW86PBE and PW86PBE-D4 share the least energetically favoured system, the He(2/4)@sII one, while the He(1/1)@sII and He(1/4)@sII configurations are the most energetically favoured ones for the functional without and with dispersion correction, respectively.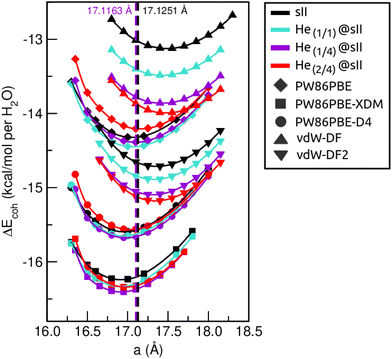 | ||
| Fig. 2 Cohesive energies, in kcal mol−1 per water molecule, of the empty sII and fully occupied He(1/1)@sII, He(1/4)@sII and He(2/4)@sII clathrate hydrate configurations, as a function of the lattice constant a in Å. The PW86PBE (with and without dispersion schemes) results related to sII and He(1/1)@sII structures are extracted from ref. 55. Solid lines correspond to the MEOS fits. Vertical dashed lines represent the experimental values found for the empty (black) and He-filled (violet) sII systems.12,13 | ||
The next step consists of calculating the equilibrium lattice constant, a0, by fitting the DFT/DFT-D total energy values to the Murnaghan equation of state (MEOS),81 which establishes a relationship between the energy and the volume of a system, such that
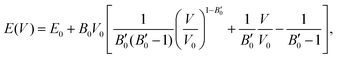 | (5) |
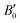 are the modulus of incompressibility and its first derivative with respect to the pressure, respectively, with V = a3. The resulting a0 values, together with the bulk moduli (bulk modulus, B0, and bulk modulus pressure derivative,
are the modulus of incompressibility and its first derivative with respect to the pressure, respectively, with V = a3. The resulting a0 values, together with the bulk moduli (bulk modulus, B0, and bulk modulus pressure derivative, 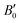 , at zero pressure), are listed in Table S1 of the ESI.† As expected, the non-local functionals provide larger a0 values, being specifically 2–3% larger than the PW86PBE ones (with and without dispersion schemes). When it comes to the lattice behaviour with increasing He filling, two distinct patterns emerge. For instance, in the case of PW86PBE and PW86PBE-D4, an increase in the equilibrium lattice parameter is observed as the He-filling rises. Conversely, this functional with the XDM dispersion correction, as well as the vdW-DF and vdW-DF2 approaches, predicts that as we move from the empty sII system to He(1/1)@sII and then to He(1/4)@sII, the lattice parameter gradually decreases. Surprisingly though, the He(2/4)@sII crystal exhibits an increase in a0, reaching values even higher than those of the empty structure. This observation is consistent with the experiment in which they report that a0 decreases from 17.0832 Å to 17.0763 Å as He-filling increases from a hydration number of 5.92 (∼23 He) to 4.56 (∼30 He) at 100 MPa and 80–120 K.12 This finding can be attributed to the enhancement of attractive vdW interactions between the host and guest molecules, which has been previously observed in another clathrate hydrate structure.82 It is the case of the sH system encapsulating different numbers of noble gas atoms, an investigation in which it was observed that an increase of Ne atoms hardly produced any effect on the lattice, slightly decreasing the volume of the unit cell. In contrast, the increasing cage occupancy in Ar, Kr and Xe hydrates yielded a considerable expansion of the unit cell volume, specially in the last two noble gases. It is not surprising that the least interacting noble gas atoms, He and Ne, share similar behaviour. What is striking is the augment of the lattice parameter when we move up to the maximum occupancy under study, He(2/4)@sII, and it could be explained due to the fact that the inclusion of 2 He atoms in every single small D cage actually produces a destabilization (repulsive effect) of the system. Hence, these findings suggest that PW86PBE-XDM represents the most suitable approach for capturing the experimentally observed trend, wherein the lattice parameter contracts upon filling the crystal with He atoms up to a (1/4) configuration. Subsequent cage filling is predicted to result in lattice expansion.
, at zero pressure), are listed in Table S1 of the ESI.† As expected, the non-local functionals provide larger a0 values, being specifically 2–3% larger than the PW86PBE ones (with and without dispersion schemes). When it comes to the lattice behaviour with increasing He filling, two distinct patterns emerge. For instance, in the case of PW86PBE and PW86PBE-D4, an increase in the equilibrium lattice parameter is observed as the He-filling rises. Conversely, this functional with the XDM dispersion correction, as well as the vdW-DF and vdW-DF2 approaches, predicts that as we move from the empty sII system to He(1/1)@sII and then to He(1/4)@sII, the lattice parameter gradually decreases. Surprisingly though, the He(2/4)@sII crystal exhibits an increase in a0, reaching values even higher than those of the empty structure. This observation is consistent with the experiment in which they report that a0 decreases from 17.0832 Å to 17.0763 Å as He-filling increases from a hydration number of 5.92 (∼23 He) to 4.56 (∼30 He) at 100 MPa and 80–120 K.12 This finding can be attributed to the enhancement of attractive vdW interactions between the host and guest molecules, which has been previously observed in another clathrate hydrate structure.82 It is the case of the sH system encapsulating different numbers of noble gas atoms, an investigation in which it was observed that an increase of Ne atoms hardly produced any effect on the lattice, slightly decreasing the volume of the unit cell. In contrast, the increasing cage occupancy in Ar, Kr and Xe hydrates yielded a considerable expansion of the unit cell volume, specially in the last two noble gases. It is not surprising that the least interacting noble gas atoms, He and Ne, share similar behaviour. What is striking is the augment of the lattice parameter when we move up to the maximum occupancy under study, He(2/4)@sII, and it could be explained due to the fact that the inclusion of 2 He atoms in every single small D cage actually produces a destabilization (repulsive effect) of the system. Hence, these findings suggest that PW86PBE-XDM represents the most suitable approach for capturing the experimentally observed trend, wherein the lattice parameter contracts upon filling the crystal with He atoms up to a (1/4) configuration. Subsequent cage filling is predicted to result in lattice expansion.
In Fig. 3 we display the relative errors with respect to the experimental data available, namely, a0 =17.125133 ± 0.000167 Å for the empty sII system at zero temperature and pressure13 and a0 = 17.1163 ± 0.0006 Å for the He-filled sII at T = 80 K and ambient pressure.12 The trend is consistent across all three methods employed, with non-local vdW-DF and vdW-DF2 functionals exhibiting an overestimation of the lattice parameter and the highest relative errors, whereas PW86PBE, PW86PBE-D4, and PW86PBE-XDM underestimate it. Focusing our attention on the He(1/4)@sII structure, the relative errors obtained are approximately 0.3% for PW86PBE to 1% for PW86PBE-D4, PW86PBE-XDM and vdW-DF2 and 2% for vdW-DF, corresponding to differences of 0.1, 0.2 and 0.3 Å, respectively. However, one should take into account that the reported experimental values refer to deuterated samples and partially filled systems. These factors, together with the T–P effects, may cause changes in the lattice. Nevertheless, the results available from the experiment are not sufficient for evaluating the impact of these effects on the lattice parameter.
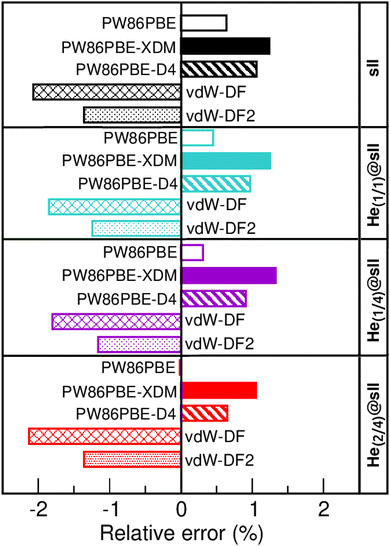 | ||
| Fig. 3 Relative error (in %) with respect to the experimental a0 values of 17.1251 and 17.1163 Å for the empty sII13 and He-filled sII,12 respectively. | ||
In turn, the interatomic He–He distances for both isolated and He-filled sII configurations in the entire crystal are depicted in Fig. 4 as obtained from the PW86PBE-XDM optimization calculations. As expected, both He2 and He4 entities exhibit smaller bond lengths when confined in the sII clathrate cages, as a consequence of the reduction of space. Interestingly, the presence of two He atoms within the D cages has almost no effect on the He4 ensemble in the H cage. This could be attributed to the expansion of the unit cell, which increases the cage diameter and facilitates the formation of a less repulsive configuration than expected. Both predicted He–He distances for the entrapped He2 and He4 entities inside D and H sII cages, respectively, are smaller than those reported by Belosludov et al. in their statistical thermodynamic modeling45 (2.49 Å for He2 inside D and 2.75 Å for He4 inside H).
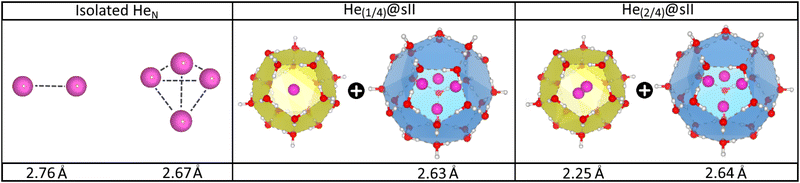 | ||
| Fig. 4 Average He–He bond length in Å of the isolated and encapsulated HeN species as computed by PW86PBE-XDM calculations. | ||
Another structural parameter that we have studied is the pressure effect on the lattice. In Fig. 5 we plot volume as a function of the pressure by following the MEOS equation81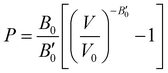 . As one can expect, pressure exerts a compressive effect on the lattice, so the higher the pressure, the lower the volume and consequently, the lower the lattice parameter. Nevertheless, the extent to which the empty and He-filled structures are affected by the pressure is different when using non-local and semi-local functionals. Thus, the PW86PBE curves (with and without dispersion corrections) present a steeper slope than those of vdW-DF and vdW-DF2, meaning that the lattice is more altered by changes in the pressure. Moreover, the B0 and
. As one can expect, pressure exerts a compressive effect on the lattice, so the higher the pressure, the lower the volume and consequently, the lower the lattice parameter. Nevertheless, the extent to which the empty and He-filled structures are affected by the pressure is different when using non-local and semi-local functionals. Thus, the PW86PBE curves (with and without dispersion corrections) present a steeper slope than those of vdW-DF and vdW-DF2, meaning that the lattice is more altered by changes in the pressure. Moreover, the B0 and 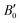 parameters shown in Table S1 of the ESI† give us an idea of how resistant a substance is to compression. They are estimated from the corresponding MEOS fits, assuming linear dependence of the bulk modulus with pressure,
parameters shown in Table S1 of the ESI† give us an idea of how resistant a substance is to compression. They are estimated from the corresponding MEOS fits, assuming linear dependence of the bulk modulus with pressure, 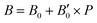 , with B0 being constant and valid for the range
, with B0 being constant and valid for the range 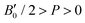 . In this manner, both vdW-DF and vdW-DF2 approaches predict a progressive rise in the resistance to compressibility as the structure is filled with a higher number of helium atoms, thus resulting in He(2/4)@sII and sII being the least and most compressible configurations, respectively. A similar behaviour is observed for PW86PBE-XDM, with the difference that a reduction of B0 occurs in He(2/4)@sII, taking a value even lower than that of the empty system, in such a manner that He(1/4)@sII and He(2/4)@sII are the most and least rigid configurations, respectively. In contrast, the PW86PBE-D4 exhibits a gradual decrease in B0 as the He cage filling increases, meaning that the empty system is predicted to be more resistant to compression than any filled structure. Similar behaviour is observed for PW86PBE, with the exception of He(1/4)@sII being less compressible than the other He-filled sII systems. In general, it is found that there is no agreement among the approaches considered here. Nonetheless, the absence of additional theoretical or experimental findings on the response of the sII lattice to pressure, whether with or without the presence of He atoms, hinders the discernment of the correct trend.
. In this manner, both vdW-DF and vdW-DF2 approaches predict a progressive rise in the resistance to compressibility as the structure is filled with a higher number of helium atoms, thus resulting in He(2/4)@sII and sII being the least and most compressible configurations, respectively. A similar behaviour is observed for PW86PBE-XDM, with the difference that a reduction of B0 occurs in He(2/4)@sII, taking a value even lower than that of the empty system, in such a manner that He(1/4)@sII and He(2/4)@sII are the most and least rigid configurations, respectively. In contrast, the PW86PBE-D4 exhibits a gradual decrease in B0 as the He cage filling increases, meaning that the empty system is predicted to be more resistant to compression than any filled structure. Similar behaviour is observed for PW86PBE, with the exception of He(1/4)@sII being less compressible than the other He-filled sII systems. In general, it is found that there is no agreement among the approaches considered here. Nonetheless, the absence of additional theoretical or experimental findings on the response of the sII lattice to pressure, whether with or without the presence of He atoms, hinders the discernment of the correct trend.
2.2 He-filling influence on energetic properties
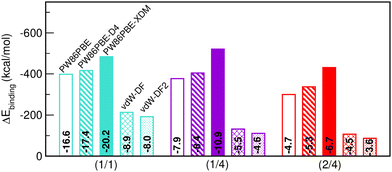
Having discussed the impact of He-filling on structural/mechanical parameters, the focus now shifts to the evaluation of the stability in terms of energy. Firstly, we present in Fig. 6 the energy gain after binding the total number of He atoms to the sII lattice (see eqn (3)). The corresponding energy values per He atom in the sII unit cell are likewise indicated within the bars. All three structures examined are energetically favourable, albeit certain configurations are comparatively more favourable than others. Once again, the PW86PBE and PW86PBE-D4 results exhibit a similar trend, where the single occupation of the cages involves the most favourable filling, with a difference of only 22 kcal mol−1 from the He(1/4)@sII system. The inclusion of additional He atoms does entail a considerable energy loss, with the He(2/4)@sII system being 80–100 kcal mol−1 less energetically favorable. Similarly, the non-local vdW-DF and vdW-DF2 functionals perform in the same line, with the difference between He(1/1)@sII and He(1/4)/He(2/4)@sII systems accounting for 82/106 kcal mol−1, respectively. Finally, PW86PBE-XDM is the functional approach that predicts higher binding energies, with the He(1/4)@sII structure being the most favourable one, resulting in an energy improvement of 12 and 70 kcal mol−1 compared to the He(1/1)@sII and He(2/4)@sII complexes, respectively. From these results, we can infer that the PW86PBE/-XDM/-D4 approaches suggest that the optimal filling may lie between the He(1/1)@sII and He(1/4)@sII structures, while the vdW-DF/vdW-DF2 predict that only the He(1/1)@sII complex is significantly favourable. However, it seems that the non-local functionals are unable to correctly quantify the vdW interactions in helium hydrates and the computed binding energies are noticeably smaller for the non-local functionals than for the PW86PBE one (with and without dispersion corrections). Finally, it should be emphasized that these outcomes serve just as indicators, since there is no reference data to compare with.With respect to the binding energies per He atom, in the semi-local PW86PBE/-XDM/-D4 outcomes it is reduced by half in the He(1/4)@sII and one-third in the He(2/4)@sII configurations with respect to the He(1/1)@sII one. For the non-local functionals, the binding energy per He atom for the He(1/4)@sII and He(2/4)@sII structures is approximately 1.7 and 2.0 times smaller, respectively, than that of the He(1/1)@sII structure.
Saturation energies were also computed in order to estimate the total energy gain upon saturation of all the cages in the sII structure (see Fig. 7). None of the structures is energetically favoured when the pure PW86PBE functional is considered. Nonetheless, the incorporation of dispersion correction schemes decreases the energy, leading to stable structures. When using PW86PBE-D4, the He(1/1)@sII and He(1/4)@sII configurations are energetically favoured, with He(1/4)@sII being the most stable one, whereas the He(2/4)@sII crystal is unstable and has an energy of 8.6 kcal mol−1. The PW86PBE-XDM results show the same pattern, with more distinct saturation energy values. Thus, the difference in energy between the He(1/1)@sII and He(1/4)@sII structures is 8.5 kcal mol−1, compared to 3.6 kcal mol−1 in PW86PBE-D4. Furthermore, He(2/4)@sII is also predicted to be stable, albeit less favorable, which aligns with the observed tendency of this dispersion correction to yield lower energies compared to other schemes. As regards the non-local functionals, an energy reduction of 26 and 45 kcal mol−1 occurs when moving from He(1/1)@sII to He(1/4)@sII with the vdW-DF and vdW-DF2 functionals, respectively. Similarly, a decrease in energy of 10 and 13 kcal mol−1 is found when going from He(1/4)@sII to He(2/4)@sII with the vdW-DF and vdW-DF2 functionals, respectively. Thus, according to both non-local functionals, the most energetically favourable structure is He(2/4)@sII, which is in complete opposition to the findings of the PW86PBE/PW86PBE-D4/PW86PBE-XDM approaches and the experimental report.12
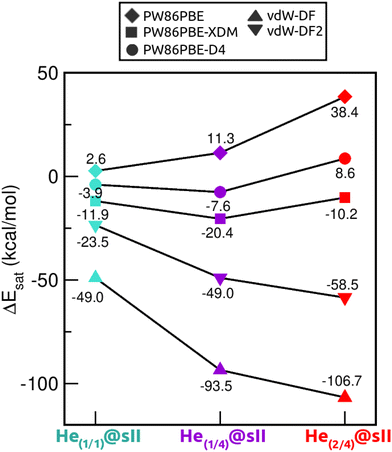 | ||
| Fig. 7 Saturation energies (in kcal mol−1) assuming single- and multiple-cage occupancy in the sII system calculated at PW86PBE, PW86PBE-XDM, PW86PBE-D4, vdW-DF and vdW-DF2. | ||
3 Summary and conclusions
In this study, we have examined the stability of the sII clathrate hydrate considering both single and multiple cage occupancy of the cages based on their structural, mechanical and energetic properties. Whenever feasible, we have conducted a comparative analysis with the experimental data available to corroborate the validity of our findings. The three configurations under consideration present different He-filling of the small D and large H cages found within the sII lattice, resulting in He(1/1)@sII, He(1/4)@sII and He(2/4)@sII structures. These specific configurations were selected based on previous experimental and theoretical studies.12,45–47 Moreover, the empty sII structure was also taken into account in order to evaluate the impact caused by the He atoms on the lattice.Hence, with the objective of exploring the He encapsulation effects, as well as analyzing the significance and impact of dispersion forces in such noble gas clathrate hydrates, both semi-local and non-local, such as PW86PBE, PW86PBE-D4, PW86PBE-XDM, vdW-DF and vdW-DF2, DFT/DFT-D computations have been performed. Total energies through structural geometry relaxation calculations were first computed and cohesive energies were then obtained. The equilibrium lattice parameters and pressure effects were determined using MEOS, and in turn, compared against experimental values. Finally, the energetic stability was investigated on the basis of binding and saturation energies.
The obtained equilibrium lattice parameters exhibit a reasonable agreement, with a mean relative error of 1–2%, compared to the experimental values. The PW86PBE/-D4/-XDM calculations predict lower a0 values, while the vdW-DF and vdW-DF2 calculations yield higher ones. Interestingly, only the PW86PBE-XDM, vdW-DF, and vdW-DF2 approaches successfully capture the experimental tendency, demonstrating that an increase in encapsulated He atoms results in a reduction of the lattice parameter. Regarding binding energies, the PW86PBE/-XDM/-D4 approaches predict that the most favorable He-filled structure lies between the He(1/1)@sII and He(1/4)@sII configurations, while the vdW-DF/vdW-DF2 methods indicate significant favorability only for the He(1/1)@sII structure. With respect to saturation energies, the PW86PBE-D4 and PW86PBE-XDM results infer that the He(1/4)@sII system is the energetically preferred one, whereas for non-local functionals, the He(2/4)@sII structure emerges as the most energetically favored.
Based on these findings, we can conclude that the PW86PBE-XDM approach demonstrates superior performance when compared to experimental data and other theoretical results. It consistently provides reliable outcomes that align with experimental observations. Consequently, the configuration characterized by singly occupied D cages and tetrahedrally occupied H cages is predicted to be the most stable. Nevertheless, it should be noted that the He(2/4)@sII configuration is also expected to be stable, even though the incorporation of 2 He atoms inside the small D cage leads to destabilization of the system. Despite this configuration resulting in an energetically favorable structure, it is not favored over the He(1/1)@sII and He(1/4)@sII crystal structures. It is important to highlight the relevance of the dispersion effects on helium clathrate hydrates. Despite being weak interactions, they play a crucial role in stabilizing the system and should not be disregarded. In this regard, the non-local vdW-DF and vdW-DF2 functionals are not able to correctly quantify the vdW interactions present in these systems.
Finally, it is worth mentioning the relevance of investigating helium inclusion compounds, primarily due to the potential benefits they offer in synthesizing new structures. The unique properties of helium, characterized by its small size and reactivity, make it easily removable from the compounds in which it is encapsulated. Therefore, expanding our knowledge about these relatively unexplored systems can unlock new avenues for discovering novel structures. This investigation offered an initial estimation of the sII crystalline structure's capacity regarding filling with He atoms. To further advance this research, temperature and pressure effects, as well as quantum effects, could be considered, allowing for a more direct alignment with the experimental observations. Besides, conducting a comprehensive thermodynamic analysis could provide valuable insights into the formation and stability of these systems, offering a deeper understanding of their nature. Future research in this field could also encompass the investigation of other clathrate-like or ice-like structures, such as He@C0, He@C1, He@Ih, or the recently discovered superionic He–water compounds. The study of these structures can offer exciting opportunities to unravel new phenomena and expand our knowledge of how helium behaves within different host lattices.
Data availability
The data that support the findings of this study are available within the article and the ESI,† as well as from the authors upon reasonable request.Author contributions
The authors confirm contribution to the paper as follows: RYR (data curation, formal analysis, investigation, methodology, validation, and writing – original draft preparation), RP (funding acquisition, project administration, conceptualization, formal analysis, investigation, methodology, validation, and writing – review and editing).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the “Centro de Cálculo del IFF-CSIC and SGAI-CSIC” and CESGA-Supercomputing centre for allocation of computer time. This work has been supported by the Comunidad de Madrid grant Ref: IND2018/TIC-9467, the MCIN grant no. PID2020-114654GB-I00, and COST Actions CA18212(MD-GAS) and CA21101(COSY).Notes and references
- E. D. Sloan, Nature, 2003, 426, 353–363 CrossRef CAS PubMed.
- C. A. Koh and E. D. Sloan, AIChE J., 2007, 53, 1636–1643 CrossRef CAS.
- J. S. Loveday and R. J. Nelmes, Phys. Chem. Chem. Phys., 2008, 10, 937–950 RSC.
- J. Lee and J. W. Kenney III, in Solidification, ed. A. E. Ares, IntechOpen, Rijeka, 2018, ch. 7 Search PubMed.
- E. Weber, Inclusion Compounds, John Wiley & Sons, Ltd, 2000 Search PubMed.
- E. D. Sloan, C. A. Koh and C. Koh, Clathrate Hydrates of Natural Gases, CRC Press, 2007 Search PubMed.
- J. A. Ripmeester and S. Alavi, Clathrate Hydrates: Molecular Science and Characterization, JWS, 2022 Search PubMed.
- F. Martelli, Properties of Water from Numerical and Experimental Perspectives, Amsterdam University Press, Amsterdam, 2022 Search PubMed.
- D. Londono, W. Kuhs and J. Finney, Nature, 1988, 332, 141–142 CrossRef CAS.
- D. Londono, J. Chem. Phys., 1992, 97, 547 CrossRef CAS.
- C. Lobban, J. L. Finney and W. F. Kuhs, J. Chem. Phys., 2002, 117, 3928–3934 CrossRef CAS.
- W. F. Kuhs, T. C. Hansen and A. Falenty, J. Phys. Chem. Lett., 2018, 9, 3194–3198 CrossRef CAS PubMed.
- A. Falenty, T. Hansen and W. Kuhs, Nature, 2014, 516, 231–233 CrossRef CAS PubMed.
- L. del Rosso, M. Celli and L. Ulivi, Nat. Commun., 2016, 7, 13394 CrossRef CAS PubMed.
- R. V. Belosludov, Y. Kawazoe, E. V. Grachev, Y. A. Dyadin and V. R. Belosludov, Solid State Commun., 1998, 109, 157–162 CrossRef.
- J. Durao. and L. Gales., Materials, 2012, 5, 1593–1601 CrossRef CAS.
- A. V. Ildyakov, A. Y. Manakov, E. Y. Aladko, V. I. Kosyakov and V. A. Shestakov, J. Phys. Chem. B, 2013, 117, 7756–7762 CrossRef CAS PubMed.
- R. V. Belosludov, Y. Y. Bozhko, O. S. Subbotin, V. R. Belosludov, H. Mizuseki, Y. Kawazoe and V. M. Fomin, J. Phys. Chem. C, 2014, 118, 2587–2593 CrossRef CAS.
- L. del Rosso, M. Celli and L. Ulivi, Challenges, 2017, 8, 3 CrossRef.
- D. M. Amos, M. E. Donnelly, P. Teeratchanan, C. L. Bull, A. Falenty, W. F. Kuhs, A. Hermann and J. S. Loveday, J. Phys. Chem. Lett., 2017, 8, 4295–4299 CrossRef CAS PubMed.
- T. A. Strobel, M. Somayazulu, S. V. Sinogeikin, P. Dera and R. J. Hemley, J. Am. Chem. Soc., 2016, 138, 13786–13789 CrossRef CAS PubMed.
- M. Bethkenhagen, E. R. Meyer, S. Hamel, N. Nettelmann, M. French, L. Scheibe, C. Ticknor, L. A. Collins, J. D. Kress, J. J. Fortney and R. Redmer, Astrophys. J., 2017, 848, 67 CrossRef.
- C. Liu, H. Gao, Y. Wang, R. J. Needs, C. J. Pickard, J. S. Adn, H.-T. Wang and D. Xing, Nat. Phys., 2019, 15, 1065–1070 Search PubMed.
- C. Liu, H. Gao, A. Hermann, Y. Wang, M. Miao, C. J. Pickard, R. J. Needs, H.-T. Wang, D. Xing and J. Sun, Phys. Rev. X, 2020, 10, 021007 Search PubMed.
- H. Gao, C. Liu, A. Hermann, R. J. Needs, C. J. Pickard, H.-T. Wang, D. Xing and J. Sun, Natl. Sci. Rev., 2020, 7, 1540–1547 Search PubMed.
- M. Kim, K. Oka, S. Ahmed, M. S. Somayazulu, Y. Meng and C. S. Yoo, J. Condens. Matter Phys., 2022, 34, 394001 Search PubMed.
- V. Kapil, C. Schran, A. Zen, J. Chen, C. J. Pickard and A. Michaelides, Nature, 2022, 609, 512–516 CrossRef CAS.
- E. Uggerud, Eur. J. Mass Spectrom., 2007, 13, 97–100 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319 CrossRef CAS PubMed.
- Computation sparks chemical discovery, Nat. Commun., 2020, 11, 4811 Search PubMed.
- L. C. Jacobson, W. Hujo and V. Molinero, J. Phys. Chem. B, 2009, 113, 10298–10307 CrossRef CAS PubMed.
- N. Plattner and M. Meuwly, J. Chem. Phys., 2014, 140, 024311 CrossRef PubMed.
- K. Murayama, S. Takeya, S. Alavi and R. Ohmura, J. Phys. Chem. C, 2014, 118, 21323–21330 CrossRef CAS.
- F. Izquierdo-Ruiz, A. O. De-la Roza, J. Contreras-García, J. Menéndez, O. Prieto-Ballesteros and J. Recio, High Pressure Res., 2015, 35, 49–56 CrossRef CAS.
- S. P. Kaur and C. N. Ramachandran, Mol. Phys., 2018, 116, 54–63 CrossRef CAS.
- Z. Liu, J. Botana, A. Hermann, S. Valdez, E. Zurek, D. Yan, H. Lin and M. Miao, Nat. Commun., 2018, 9, 951 CrossRef PubMed.
- S. Ferrero, L. Zamirri, C. Ceccarelli, A. Witzel, A. Rimola and P. Ugliengo, Astrophys. J., 2020, 904 Search PubMed.
- P. E. Brumby, D. Yuhara, T. Hasegawa, D. T. Wu, A. K. Sum and K. Yasuoka, J. Chem. Phys., 2019, 150, 134503 CrossRef PubMed.
- A. Cabrera-Ramírez, R. Yanes-Rodríguez and R. Prosmiti, J. Chem. Phys., 2021, 154, 044301 CrossRef PubMed.
- R. Cárdenas, J. Martínez-Seoane and C. Amero, Molecules, 2020, 25, 4783 CrossRef.
- K. K. Irikura and D. J. Frurip, Computational Thermochemistry, ACS Conference Series, 1988, ch. 1, 2–18 Search PubMed.
- M. Zelkowitz and D. Wallace, Computer, 1998, 31, 23–31 CrossRef.
- N. R. Council, Beyond the Molecular Frontier: Challenges for Chemistry and Chemical Engineering, The National Academies Press, Washington, DC, 2003 Search PubMed.
- A. Rimola, S. Ferrero, A. Germain, M. Corno and P. Ugliengo, Minerals, 2021, 11, 26 CrossRef CAS.
- V. Belosludov, O. Subbotin, Y. Bozhko, R. Belosludov, H. Mizuseki, Y. Kawazoe and V. Fomin, Proceedings of the 7th International Conference on Gas Hydrates (ICGH 2011), Edinburgh, Scotland, United Kingdom, 2011, pp. 1–9.
- S. Mondal and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2014, 16, 17943–17954 RSC.
- R. Yanes-Rodríguez and R. Prosmiti, Phys. Chem. Chem. Phys., 2023, 25, 16844–16855 RSC.
- K. Ramya and A. Venkatnathan, Comput. Theor. Chem., 2013, 1023, 1–4 CrossRef CAS.
- D.-Y. Koh, H. Kang, J. Jeon, Y.-H. Ahn, Y. Park, H. Kim and H. Lee, J. Phys. Chem. C, 2014, 118, 3324–3330 CrossRef CAS.
- N. I. Papadimitriou, I. N. Tsimpanogiannis, I. G. Economou and A. K. Stubos, Mol. Phys., 2016, 114, 2664–2671 CrossRef CAS.
- N. Noguchi, T. Yonezawa, Y. Yokoi, T. Tokunaga, T. Moriwaki, Y. Ikemoto and H. Okamura, J. Phys. Chem. C, 2021, 125, 189–200 CrossRef CAS.
- Y. Krishnan, M. R. Ghaani, A. Desmedt and N. J. English, Appl. Sci., 2021, 11, 282 CrossRef CAS.
- R. Yanes-Rodríguez, D. J. Arismendi-Arrieta and R. Prosmiti, J. Chem. Inf. Model., 2020, 60, 3043–3056 CrossRef PubMed.
- R. Yanes-Rodríguez and R. Prosmiti, Phys. Chem. Chem. Phys., 2022, 24, 1475–1485 RSC.
- R. Yanes-Rodríguez, A. Cabrera-Ramírez and R. Prosmiti, Phys. Chem. Chem. Phys., 2022, 24, 13119–13129 RSC.
- F. Takeuchi, M. Hiratsuka, R. Ohmura, S. Alavi, A. K. Sum and K. Yasuoka, J. Chem. Phys., 2013, 138, 124504 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfá, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- A. Cabrera-Ramírez, D. J. Arismendi-Arrieta, A. Valdés and R. Prosmiti, Chem. Phys. Chem., 2020, 21, 2618–2628 CrossRef PubMed.
- A. Cabrera-Ramírez, D. J. Arismendi-Arrieta, A. Valdés and R. Prosmiti, ChemPhysChem, 2021, 22, 359–369 CrossRef.
- M. A. L. Marques, M. J. T. Oliveira and T. Burnus, Comput. Phys. Commun., 2012, 183, 2272–2281 CrossRef CAS.
- A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2012, 136, 174109 CrossRef CAS PubMed.
- Universität-Bonn, D4 - A Generally Applicable Atomic-Charge Dependent London Dispersion Correction, https://protect-eu.mimecast.com/s/H81mC91EgFzwxMQuEFuQM?domain=chemie.uni-bonn.de.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- R. M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, 2nd edn, 2020 Search PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS PubMed.
- N. I. Papadimitriou, I. N. Tsimpanogiannis, I. G. Economou and A. K. Stubos, Mol. Phys., 2017, 115, 1274–1285 CrossRef CAS.
- R. Ma, H. Zhong, J. Liu, J. Zhong, Y. Yan, J. Zhang and J. Xu, Processes, 2019, 7, 699 CrossRef CAS.
- Y. Krishnan, M. R. Ghaani, A. Desmedt and N. J. English, Appl. Sci., 2021, 11, 282 CrossRef CAS.
- Y. Krishnan, M. R. Ghaani and N. J. English, J. Phys. Chem. C, 2021, 125, 8430–8439 CrossRef CAS.
- S. J. Cox, M. D. Towler, D. Alfé and A. Michaelides, J. Chem. Phys., 2014, 140, 174703 CrossRef PubMed.
- C. Pétuya, L. Martin-Gondre, P. Aurel, F. Damay and A. Desmedt, J. Chem. Phys., 2019, 150, 184705 CrossRef PubMed.
- C. Métais, C. Pétuya, S. Espert, J. Ollivier, L. Martin-Gondre and A. Desmedt, J. Phys. Chem. C, 2021, 125, 6433–6441 CrossRef.
- F. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS PubMed.
- S. Alavi, J. A. Ripmeester and D. D. Klug, J. Chem. Phys., 2006, 125, 104501 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05410a |
| ‡ Doctoral Programme in Theoretical Chemistry and Computational Modelling, Doctoral School, Universidad Autónoma de Madrid |
| This journal is © the Owner Societies 2024 |