Simulating high-pressure surface reactions with molecular beams

Abstract

Using a reactive molecular beam with high kinetic energy (E_kin), it is possible to speed gas–surface reactions involving high activation barriers (E_act), which would require elevated pressures (P₀) if a random gas with a Maxwell–Boltzmann distribution is used. By simply computing the number of molecules that overcome the activation barrier in a random gas at P₀ and in a molecular beam at E_kin = E_act, we establish an E_kin–P₀ equivalence curve, through which we postulate that molecular beams are ideal tools to investigate gas–surface reactions that involve high activation energies. In particular, we foresee the use of molecular beams to simulate gas surface reactions within the industrial-range (>10 bar) using surface-sensitive ultra-high vacuum (UHV) techniques, such as X-ray photoemission spectroscopy (XPS). To test this idea, we revisit the oxidation of the Cu(111) surface combining O₂ molecular beams and XPS experiments. By tuning the kinetic energy of the O₂ beam in the range of 0.24–1 eV, we achieve the same sequence of surface oxides obtained in ambient pressure photoemission (AP-XPS) experiments, in which the Cu(111) surface was exposed to a random O₂ gas up to 1 mbar. We observe the same surface oxidation kinetics as in the random gas, but with a much lower dose, close to the expected value derived from the equivalence curve.

---

Introduction

Heterogeneous catalysis is of enormous practical relevance, since it is used to make chemicals and fuels, as well as to reduce car pollution and waste in industry. About 80% of the chemical manufacturing processes make use of heterogeneous catalysts, in one form or another. Successful heterogeneous catalytic reactions are generally governed by three elementary steps that take place at the catalyst surface: chemisorption, surface reactions, and desorption. The first step is often the bottleneck for the reaction to occur, due to the presence of a high barrier for the chemisorption of a relevant molecular species. This limits reaction rates if low or moderate temperatures are required (<600 K), forcing industrial processes to be carried out at very high gas pressures in the 100 bar regime.^1,2

The high gas-pressure needed in industrially viable high-activation energy processes is also the main challenge to carry out fundamental research under realistic operando conditions, because it lies orders of magnitude above the values at which surface sensitive analytical techniques perform best. This limitation, which is known as the “pressure gap”, was already discussed by Ceyer et al.,³ who tested methane dissociation combining molecular beams and electron energy loss spectroscopy, demonstrating, in a qualitative way, that the high pressure requirement could be bypassed by raising the energy of the methane molecule. Such an idea has been poorly exploited so far in surface chemistry and catalysis, and in particular, in combination with X-ray photoelectron spectroscopy (XPS), which stands out as the most accurate to determine the chemical composition of the surface and the bonding state of each atom. Standard XPS requires ultra high vacuum (UHV, <10⁻⁶ mbar), because photoelectrons are intensively attenuated in dense gases, although it can also be performed at near ambient pressure (NAP-XPS, or simply, AP-XPS) by selectively pumping the path travelled by the electron from the surface and inside the spectrometer.⁴ Pressures up to ∼10 mbar are standard in AP-XPS setups,⁵ and a 1 bar pressure has been reached under extraordinary conditions of high-flux, high-energy and grazing incidence X-rays.⁶ Larger pressures appear unattainable nowadays; hence, for XPS, a 100 bar pressure-gap still remains. A radically new approach is thus needed to bridge the pressure gap for XPS research. Here, we quantitatively evaluate the option of performing XPS in an UHV in the presence of a reactive monochromatic molecular beam.

Random gases versus molecular beams in XPS experiments

The gas–surface interaction potential for an activated process with E_act barrier height and E_kin molecular kinetic energy is sketched in Fig. 1a. The potential can be more complex,⁸ but Fig. 1a captures the essence of the molecule–surface interaction for chemisorption processes, including those that lead to an immediate dissociation. For instance, O₂ adsorbs dissociatively on many metal surfaces at 300 K, typically with low to moderate E_act, e.g., 0.1–0.2 eV for different Cu facets,⁹ in contrast to the more inert greenhouse gases, which exhibit larger barriers (>0.6 eV), as CH₄ on Ni and CO₂ on Cu surfaces.^7,10,11 For a random gas hitting a surface at 300 K, the molecular kinetic energy is described by the Maxwell–Boltzmann distribution function shown in Fig. 1b. Note that the majority of the molecules have relatively low energy. In Fig. 1b, we assume a hypothetical E_act = 0.1 eV activation energy, shading in blue the area of the curve with higher E_act values. The total probability above E_act is given by:

Fig. 1 (a) Molecule–surface interaction potential for an activated chemisorption process with E_act barrier height and E_kin molecular energy.⁷ (b) Normalized (area under the curve = 1) probability distribution of molecular energies for a random, Maxwell–Boltzmann gas at 300 K, versus a monochromatic, supersonic molecular beam. Assuming that E_act = 0.1 eV and tuning the beam to E_kin = E_act, the blue and green shadowed areas mark the total probability for a molecule to dissociate in the Maxwell–Boltzmann gas and in the molecular beam, respectively.

Even for the reduced E_act = 0.1 eV energy, τ_gas = 0.05, i.e., only 5% of the molecules will have enough energy to overcome the barrier, chemisorb, dissociate and react.¹² Moreover, due to the exponential decay of the Maxwell–Boltzmann function, for higher E_act, the probability would reduce by orders of magnitude.

A molecular beam (MB) is a collimated stream of gas formed by a supersonic expansion from a high source-pressure.⁸ This process leads to a beam of molecules with well-defined translational energy E_kin and narrow energy spread (10%), as represented by the green Gaussian line in Fig. 1b. MB fluxes of 10¹⁵ cm⁻² s⁻¹ are routinely achieved, which corresponds to a P_beam = 10⁻⁶ mbar effective pressure on the surface,¹³ and energies beyond 1 eV can be obtained, with ample tunability margins. In Fig. 1b, both the MB and the random-gas distributions are normalized, i.e., they represent gases of the same molecular density that exert the same pressure on the surface. Assuming a process with E_act = 0.1 eV and tuning the MB energy to E_kin = E_act, half of the molecules (green area) are active, i.e., τ_beam = 0.5, and the number of active molecules in the MB is 10 times more than that in the random gas (blue area). On the other hand, molecules with a kinetic energy much larger than E_act may not react either, since the excess molecular energy affects its residence time, and may cause its early desorption.

From Fig. 1b, it is also important to deduce that, for high E_act reactions, differences in reactivity between a random gas at 300 K and a regular MB set to E_kin = E_act would be dramatically large. Such a difference is rationalized in the “equivalence” curve shown in Fig. 2. Following eqn (1), here we define P_gas = P_beam/2τ(E_act), i.e., the pressure of a random gas needed to obtain the same number of active molecules as in the standard MB with E_kin = E_act. This leads to an effective “equivalence” between the pressure of a random gas and the kinetic energy of a MB, as represented with the thick blue line in Fig. 2. Analogously, as expressed in the right side scale of Fig. 2, the equivalence can also be defined in terms of dose, i.e., the dose of a 300 K random gas needed to provide the same number of active molecules in a standard molecular beam operating during one second, which is equivalent to 1 Langmuir (L, 10⁻⁶ mbar s⁻¹). In the same figure, we also depict the pressure ranges at which different random-gas XPS approaches work. The pressure gap extends from the 1–2 bar limit achieved in ref. 6 to the 100 bar range needed, e.g., for the efficient CH₄ and CO₂ conversion into fuels.¹ As marked in Fig. 2 with the dotted line, using a regular MB tuned to E_kin = 0.6 eV, within a standard UHV XPS setup, we could simulate operando reactions with random CH₄ and CO₂ gases at 20 bar, i.e., within the pressure gap, and close to industry values.

Fig. 2 Molecular beam energy versus random gas pressure equivalence for gas–surface reactions when tuning the beam to the activation energy E_kin = E_act, as deduced from eqn (1). Such tuning ability allows the use of standard beams (flux of 10¹⁵ mol cm⁻² seg⁻²) to achieve high rates in E_act > 0.6 eV reactions (e.g., CH₄/Ni) that require random gas pressures above the XPS regime. The right side scale expresses the random gas dose that is equivalent to the standard molecular beam operating during 1 second (1 L). It is used here to estimate E_act from the O₂ random gas dose needed to form the surface Cu₂O (see ref. 14 and the text).

The number of high energy, active molecules in a random gas is not the single parameter that governs the reaction probability at a gas–surface interface. The reaction process is dynamic, since the surface does not remain pristine, and hence the activation barrier and the number and nature of active sites change over the time. Moreover, the chemical nature of the surface may also change because low kinetic energy, inactive molecules may become trapped in physisorbed or chemisorbed states (see Fig. 1a). During the CO oxidation on Cu,¹⁵ at high gas pressures, metastable CO condensates form, which disrupt the metal substrate creating active CO/metal–atom clusters that lower the activation barrier. Using the standard P_beam -pressure MB, such high-pressure molecule/metal condensates are not likely to appear. Active surface aggregates are predicted for a variety of molecules and surfaces at high pressures,¹⁶ but their presence under industrial reaction conditions remains to be proved. In any case, high pressures will always limit the use of standard surface science techniques, such as XPS, to study in detail surface reactions with high activation energies, which can only be performed using MBs.

Historically, research on surface reactions exhibiting high activation barriers have greatly benefited from the use of MB sources, which render high reaction rates at E_kin ∼ E_act.^7,8,17–20 In general, MB experiments have been aimed at elucidating reaction kinetics and dynamics, by tuning kinetic energy, vibrational state and incidence angle in the incoming beam of reactants, and probing the same properties in the outcoming gas-phase products.^13,21 To examine the chemical composition of the surface under the simultaneous action of the beam, only infrared spectroscopy has been used,^22–24 although this technique only probes the chemisorbed species, and not the catalyst surface. XPS could probe both adsorbed molecules and surface atoms, but it has only been used in post-mortem analysis of the surface, e.g., to monitor the oxygen uptake kinetics of Cu surfaces after exposure to O₂ beams of variable energy.^25–27 Here, we revisit the Cu(111) surface oxidation process with O₂ beams of variable E_kin with the aim of testing the random-gas-pressure/molecular-beam-energy equivalence curve shown in Fig. 2. Going beyond the total oxygen uptake analysis of Moritani et al.,^25,26,28 we investigate the separate evolution of different oxide species, and compare the spectra with recent AP-XPS experiments of random O₂ exposure at 300 K and up to 1 mbar. We indeed find the same sequence of oxides, and come to the conclusion that the equivalence works well for the surface oxide species.

Experimental details

The experiments were performed using a high resolution MB time-of-flight (TOF) apparatus described in detail elsewhere.²⁹ O₂ beams have been produced by seeding oxygen using He as a carrier gas. A monochromatic seeded MB was formed by expanding the gas from a 20 mm diameter nozzle operated at 10 bar. The kinetic energy was varied by using different oxygen concentrations (1% and 20%) in addition to varying the nozzle temperature between 200 K and 600 K. The mean translational energy of the incoming O₂ molecules was determined by measuring the TOF of He atoms in the beam after adjusting for the corresponding mass difference.³⁰ In this way, we were able to produce O₂ beams with kinetic energies from 240 meV up to 1 eV. At a nozzle temperature of 300 K, the corresponding energy spread is ca. 30% for the 20% O₂ beam and 10% for the seeded beam with 1% O₂ (see Fig. S1 and S2 in the ESI† ³¹).

An electron analyzer (VG CLAM-4) and an X-ray source were inserted into the UHV scattering chamber. Both lie on the scattering plane, defined by the surface normal and the incident MB direction, whereby the sample is placed at the focal point of the analyzer. This arrangement allows measuring XPS spectra immediately after exposing the surface to the MB, simply by rotating the sample 45° in the scattering plane. Clean Cu(111) surfaces were prepared under UHV conditions by repeated cycles of ion sputtering and flash sample annealing. The surface quality and cleanliness were monitored by measuring a high specular reflectivity to He atoms³² and by XPS prior to each exposure to the O₂ beam.

Cu(111) oxidation with low-energy molecular beams

The oxidation of Cu crystal surfaces has been a matter of research since long,³³ although still a number of uncertainties remain.³⁴ In the presence of a random O₂ gas at 300 K, it is generally admitted that the cuprous oxide (Cu₂O) stoichiometry arises first,³⁴ but it is not clear under which conditions the surface oxidation continues into bulk Cu₂O growth, or even further to the formation of a CuO overlayer. Structurally, the growth of the oxide has been shown to proceed, in most cases, through the formation of oxide nano-islands which grow and eventually coalesce to form a surface coating layer,³⁴ with the morphology and orientation of the surface Cu₂O layer notably dependent on the Cu crystal facet.^35–37 In Cu(100) and Cu(110), the early exposure to the random O₂ gas leads to a characteristic low energy electron diffraction (LEED) pattern, with a sizeable change in the surface work function, demonstrating the presence of a well-arranged chemisorbed oxygen layer.³⁶ In contrast, O₂ adsorption on Cu(111) leads to a rapid disappearance of LEED ordering, together with a minor change in the work function, suggesting a considerable disruption of the Cu surface and the early incorporation of the oxygen atoms in the subsurface.³⁵ Higher doses stabilize a bulk-like Cu₂O film with similar spectral properties for all crystal facets.¹⁴

Liu et al. have recently examined the kinetics of the Cu(111) surface oxidation in AP-XPS experiments within a wide pressure/dose range (UHV-mbar).¹⁴ The O1s spectrum shows first the build-up of the surface Cu₂O oxide with a ∼2 × 10⁵ L dose, followed by a rapid transition to a bulk-like Cu₂O spectrum at higher doses (2 × 10⁷ L). Using the experiment by Liu et al. as our random-gas oxidation reference, as shown in Fig. 3 and 4, we test the spectral composition of the oxide formed on the Cu(111) surface under the action of a O₂ MB with standard flux (P_beam). In Fig. 3a, we show the O 1s spectra for increasing molecular beam energies and 10²–10³ L doses. Despite the limited resolution (see the ESI† for XPS fitting details and Fig. S3³¹), a close inspection reveals energy-dependent changes in peak intensity, position and width, which agree with the data of Liu et al. and early O₂ beam experiments.^25,26,28 Such changes are related to the variable contribution of different oxide species, shaded with different colors in Fig. 3a, and sketched in Fig. 3b. More importantly, as indicated in Fig. 3b, we observe as a function of the kinetic beam energy the same oxidation sequence obtained when exponentially increasing the dose in the random-gas experiment. Note that in Fig. 3b we have assumed that the surface oxide is composed of two oxygen species, i.e., the subsurface and the surface, which are expected to possess different Cu coordination, and hence different O 1s emission lines, i.e., at 530 eV and 529.5 eV, respectively. Although Liu et al. showed changes in shape and energy in the surface oxide peak similar to those observed in Fig. 3a, they did not consider such two-peak contribution. This is otherwise obvious in previous experiments with molecular beams,^26,28 as well as in experiments with random gases when the resolution is improved (see Fig. S4 in the ESI† ³¹). It is clear that the subsurface emission is the first one to emerge with the random gas in Fig. 3a, as well as with the smallest dose at any beam energy (see Fig. 4).^26,28 Yet, due to a similar Cu environment, the subsurface oxygen line should lie close to that of bulk Cu₂O, i.e., we may expect similar core-level energies. In fact, this is observed in the fit for the subsurface O peak in Fig. 3a, which exhibits a ∼0.3 eV peak broadening and a small ∼ 0.2 eV higher binding energy shift from E_kin = 0.24 eV to E_kin = 1.0 eV, in line with the literature value for bulk Cu₂O, 530.3 eV.¹⁴

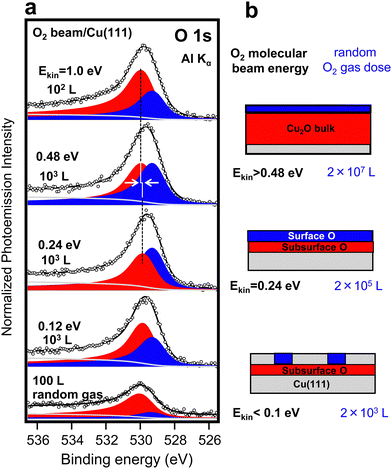Fig. 3 (a) O 1s spectra upon exposure of a clean Cu(111) surface to O₂ MB of increasing kinetic energies E_kin and low 10²–10³ L doses. The changing shape and energy of the feature allows a two-peak fit, which renders the surface O (blue) and the subsurface O (red) contributions. The latter grows, shifts (arrows) and widens at E_kin = 0.48–1 eV, indicating the formation of a bulk-like Cu₂O phase. The bottom spectrum corresponds to 100 L random O₂ gas exposure. (b) Schematic description of the oxidized Cu(111) surfaces, either after exposing to saturation doses with a molecular beam of variable energy (left scale) or for increasing doses (right scale) of a random O₂ gas at 300 K.¹⁴

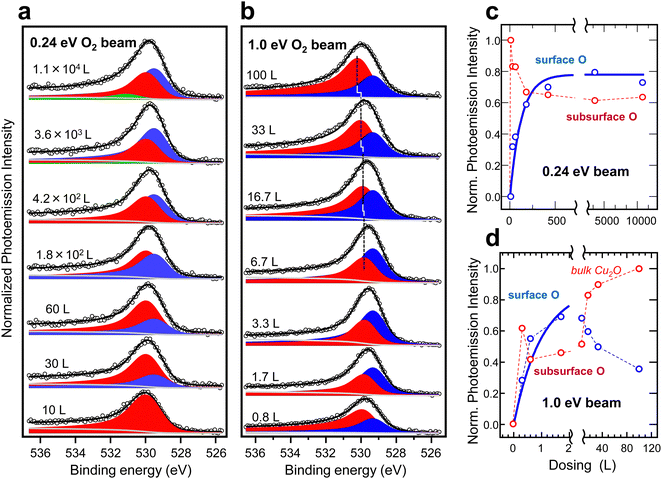Fig. 4 Evolution of the O 1s spectrum for increasing doses of a O₂ MB acting on the Cu(111) surface and tuned to (a) E_kin = 0.24 eV and (b) E_kin = 1.0 eV. Line fitting is performed using two Doniach Sunjic peaks, i.e. the surface (blue) and the subsurface (red) O, in the same way as shown in Fig. 3a. A third peak (green) is considered in (a) to account for the small water build-up (hydroxide) at the longest exposures. In (b), the subsurface O peak exhibits the high-binding-energy shift that characterizes the emergence of a bulk-like Cu₂O layer. The intensity (area under the peak) in each case is represented in panels (c) and (d). The blue thick lines are fits to surface O data points assuming a simplified model of dissociation probability and two-dimensional growth (see the text).

Spectra in Fig. 3a correspond to the doses near saturation at each beam energy, i.e., further exposure to the O₂ beam does not result in remarkable spectral changes. We qualitatively conclude, as expressed in Fig. 3b sketch, that the surface oxide layer (surface + subsurface O) can be synthesized at E_kin = 0.24 eV using a low beam dose, whereas the bulk-like Cu₂O needs beam energies E_kin > 0.48 eV for an efficient growth. Fig. 4 offers a more quantitative assessment of the Cu(111) oxidation kinetics with beams set to E_kin = 0.24 eV (Fig. 4a) and E_kin = 1 eV (Fig. 4b). In agreement with the rather small O₂ dissociation barrier on clean Cu surfaces,⁹ we observe the sharp appearance of subsurface O at both energies, prior to the growth of the surface O layer. As the latter saturates, we also notice a slight 30% drop of the subsurface O peak in both panels, probably due to damping of the photoelectron intensity. The bulk-like Cu₂O signal is only observed with E_kin = 1 eV.

Following the same fitting protocol used in Fig. 3a, we obtain the contribution of each species for a given MB dose. The respective “kinetics” at E_kin = 0.24 eV and E_kin = 1 eV are shown in Fig. 4c and d, respectively. As in the random gas,¹⁴ a three-step process is clearly visible. First, the immediate saturation with subsurface O at the lowest dose, followed by the exponential growth of surface O, and, finally, by the steep rise of the bulk-like Cu₂O signal, although the latter only appears, within the limited dosing of the present experiment, with E_kin = 1 eV. The thick lines in Fig. 4c fit the surface O data points assuming a simple two-dimensional (2D) growth, i.e., a high dissociation probability upon impact on the portion of the surface that remains “uncovered” with the growing (surface O) species:

where K stands for the dissociation probability on the “free” surface (saturated with subsurface O) and Θ represents the oxygen coverage, here represented by the surface O peak intensity normalized to its maximum value Θ^max. In the 2D scenario, n = 2, since the O₂ molecule dissociation requires two contiguous, free adsorption sites, one per each O atom. Then, the integration of eqn (2) leads to:

The fit to Fig. 4c data using eqn (3) renders a small K = 0.023 value, suggesting an effective barrier E_act slightly above E_kin = 0.24 eV. In fact, using Liu et al.'s surface oxide saturation value of 2 × 10⁵(Fig. 3b), we can estimate E_act = 0.3 eV, as indicated in Fig. 2. This value for E_act agrees well with the one reported in recent sticking measurements of O₂ on Cu(111) using molecular beams.^38,39 Assuming the probability hypothesis of Fig. 1b, in which only those molecules with E_kin > E_act are active, K would equal the probability (τ_beam) of about 0.3 eV for a Gaussian distribution with center at E_kin = 0.24 eV and a full-width-half-maximum of 0.3 × E_kin. The algebra is straightforward and leads to τ_beam = 0.025, i.e., essentially the same value K = 0.023 obtained in the fit of Fig. 4c. Therefore, despite the crudity of the approaches made, this result supports the central idea here that the number of active molecules above E_act governs the reaction kinetics, even in the structurally complex oxidation of the Cu(111) surface.

For E_kin = 1 eV (Fig. 4c), the surface O intensity curve (blue data) saturates very fast, clearly following a n < 2 kinetics. This likely reflects the fact that the bulk-like Cu₂O signal is also growing in parallel, hence the strict 2D scenario does not hold. Assuming that K = 1 at this energy, the data fit reasonably with n = 1, meaning that two surface empty sites are no longer needed, since some of the dissociated O atoms incorporate to the bulk directly. Above ∼20 L, the surface O signal decreases and the Cu₂O increases abruptly, in the same way as in the random gas with a 2 × 10⁷ L dose.¹⁴ Such quenching of the surface O signal suggests the structural transformation of the Cu₂O layer, with a residual amount of O at lower coordination sites of the surface. In any case, using E_kin = 1 eV, the MB enables the formation of bulk Cu₂O at doses six orders of magnitude lower than in a random gas experiment.¹⁴

Conclusions

In summary, we have discussed the combined use of molecular beams and XPS to simulate industrially relevant gas–surface reactions of high activation energy. Based on the Maxwell–Boltzmann distribution function of free gases at 300 K, we have determined the equivalent dose required in the random gas to achieve the same number of active molecules of a standard molecular beam set to a kinetic energy equal to the activation energy of the surface reaction. This equivalence curve reveals the fundamental limitations of AP-XPS to investigate many relevant gas–surface reactions with high activation energy, such as those that involve the activation of stable greenhouse gases. As a way of example, we revisited the Cu(111) surface oxidation with O₂ beams of variable energy and focused on the separate kinetics for different oxygen species. We observe the same sequence of oxygen species as in the random gas oxidation, but with a dose which is orders of magnitude lower. In particular, when the kinetic energy of the molecular beam is set close to the activation energy for the surface oxide layer completion, we prove in a quantitative way the accelerated kinetics predicted with the equivalence curve.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We want to express our deep gratitude to Prof. Clemens Laubschat (TU Dresden), who willingly donated all XPS instruments used in our experiments. This work has been partially supported by the Spanish Ministerio de Ciencia e Innovación under projects TED2021-130446B-I00 and PID2020-116093RB-C44. Work funded by MCIN/AEI/10.13039/501100011033/, by “ESF investing in your future”, and by the Basque Government (grants No. IT-1591-22). The COST Action CA21101 is also acknowledged. D. F. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness, through the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M). SVA acknowledges funding from the European Unions Horizon Europe Programme under the Marie Skłodowska-Curie grant agreement no. 101066965 CURVEO.

References

1. E. C. Ra, K. Y. Kim, E. H. Kim, H. Lee, K. An and J. S. Lee, Recycling Carbon Dioxide through Catalytic Hydrogenation: Recent Key Developments and Perspectives, ACS Catal., 2020, 10, 11318–11345.
2. Concepts of Modern Catalysis and Kinetics, ed. I. Chorkendorff and J. W. Niemantsverdriet, John Wiley & Sons Ltd, 2003, ch. 1, pp 1–21.
3. M. B. Lee, Q. Y. Yang and S. T. Ceyer, Dynamics of the activated dissociative chemisorption of CH₄ and implication for the pressure gap in catalysis: A molecular beam-high resolution electron energy loss study, J. Chem. Phys., 1987, 87, 2724–2741.
4. D. F. Ogletree, H. Bluhm, G. Lebedev, C. S. Fadley, Z. Hussain and M. Salmeron, A differentially pumped electrostatic lens system for photoemission studies in the millibar range, Rev. Sci. Instrum., 2002, 73, 3872–3877.
5. J. Schnadt, J. Knudsen and N. Johansson, Present and new frontiers in materials research by ambient pressure x-ray photoelectron spectroscopy, J. Phys.: Condens. Matter, 2020, 32, 413003.
6. P. Amann, D. Degerman, M.-T. Lee, J. D. Alexander, M. Shipilin, H.-Y. Wang, F. Cavalca, M. Weston, J. Gladh and M. Blom, et al., A high-pressure x-ray photoelectron spectroscopy instrument for studies of industrially relevant catalytic reactions at pressures of several bars, Rev. Sci. Instrum., 2019, 90, 103102.
7. L. Juurlink, D. Killelea and A. Utz, State-resolved probes of methane dissociation dynamics, Prog. Surf. Sci., 2009, 84, 69–134.
8. F. Zaera, Use of molecular beams for kinetic measurements of chemical reactions on solid surfaces, Surf. Sci. Rep., 2017, 72, 59–104.
9. M. M. Montemore, M. A. van Spronsen, R. J. Madix and C. M. Friend, O₂ Activation by Metal Surfaces: Implications for Bonding and Reactivity on Heterogeneous Catalysts, Chem. Rev., 2018, 118, 2816–2862 , PMID: 29116787.
10. P. G. Lustemberg, P. J. Ramírez, Z. Liu, R. A. Gutiérrez, D. G. Grinter, J. Carrasco, S. D. Senanayake, J. A. Rodriguez and M. V. Ganduglia-Pirovano, Room-Temperature Activation of Methane and Dry Re-forming with CO₂ on Ni-CeO₂(111) Surfaces: Effect of Ce³⁺ Sites and Metal-Support Interactions on C-H Bond Cleavage, ACS Catal., 2016, 6, 8184–8191.
11. T. Yang, T. Gu, Y. Han, W. Wang, Y. Yu, Y. Zang, H. Zhang, B. Mao, Y. Li and B. Yang, et al., Surface Orientation and Pressure Dependence of CO₂ Activation on Cu Surfaces, J. Phys. Chem. C, 2020, 124, 27511–27518.
12. Here we disregard the small contribution from barrier tunneling at E < E_act.
13. A. W. Kleyn, Molecular beams and chemical dynamics at surfaces, Chem. Soc. Rev., 2003, 32, 87–95.
14. B. H. Liu, M. Huber, M. A. van Spronsen, M. Salmeron and H. Bluhm, Ambient pressure X-ray photoelectron spectroscopy study of room-temperature oxygen adsorption on Cu(1 0 0) and Cu(1 1 1), Appl. Surf. Sci., 2022, 583, 152438.
15. B. Eren, D. Zherebetskyy, L. L. Patera, C. H. Wu, H. Bluhm, C. Africh, L.-W. Wang, G. A. Somorjai and M. Salmeron, Activation of Cu(111) surface by decomposition into nanoclusters driven by CO adsorption, Science, 2016, 351, 475–478.
16. L. Xu, K. G. Papanikolaou, B. A. J. Lechner, L. Je, G. A. Somorjai, M. Salmeron and M. Mavrikakis, Formation of active sites on transition metals through reaction-driven migration of surface atoms, Science, 2023, 380, 70–76.
17. C. T. Rettner, L. A. DeLouise and D. J. Auerbach, Effect of incidence kinetic energy and surface coverage on the dissociative chemisorption of oxygen on W(110), J. Chem. Phys., 1986, 85, 1131–1149.
18. L. Vattuone, C. Boragno, M. Pupo, P. Restelli, M. Rocca and U. Valbusa, Azimuthal dependence of sticking probability of O₂ on Ag(110), Phys. Rev. Lett., 1994, 72, 510–513.
19. R. M. Palomino, E. Stavitski, I. Waluyo, Y. C. K. Chen-Wiegart, M. Abeykoon, J. T. Sadowski, J. A. Rodriguez, A. I. Frenkel and S. D. Senanayake, New In-Situ and Operando Facilities for Catalysis Science at NSLS-II: The Deployment of Real-Time, Chemical, and Structure-Sensitive X-ray Probes, Synchrotron Radiat. News, 2017, 30, 30–37.
20. G. B. Park, B. C. Krüger, D. Borodin, T. N. Kitsopoulos and A. M. Wodtke, Fundamental mechanisms for molecular energy conversion and chemical reactions at surfaces, Rep. Prog. Phys., 2019, 82, 096401.
21. D. J. Auerbach, J. C. Tully and A. M. Wodtke, Chemical dynamics from the gas-phase to surfaces, Nat. Sci., 2021, 1, e10005.
22. J. Libuda and H.-J. Freund, Reaction Kinetics on Complex Model Catalysts under Single Scattering Conditions, J. Phys. Chem. B, 2002, 106, 4901–4915.
23. J. Libuda and H.-J. Freund, Molecular beam experiments on model catalysts, Surf. Sci. Rep., 2005, 57, 157–298.
24. A. Gutiérrez-González and R. D. Beck, Quantum state and surface-site-resolved studies of methane chemisorption by vibrational spectroscopies, Phys. Chem. Chem. Phys., 2020, 22, 17448–17459.
25. K. Moritani, M. Okada, S. Sato, S. Goto, T. Kasai, A. Yoshigoe and Y. Teraoka, Photoemission study of the translational energy induced oxidation processes on Cu(111), J. Vac. Sci. Technol., A, 2004, 22, 1625–1630.
26. K. Moritani, M. Okada, Y. Teraoka, A. Yoshigoe and T. Kasai, Reconstruction of Cu(111) Induced by a Hyperthermal Oxygen Molecular Beam, J. Phys. Chem. C, 2008, 112, 8662–8667.
27. K. Hayashida, Y. Tsuda, T. Yamada, A. Yoshigoe and M. Okada, Revisit of XPS Studies of Supersonic O₂ Molecular Adsorption on Cu(111): Copper Oxides, ACS Omega, 2021, 6, 26814–26820.
28. K. Moritani, M. Tsuda, Y. Teraoka, M. Okada, A. Yoshigoe, T. Fukuyama, T. Kasai and H. Kasai, Effects of Vibrational and Rotational Excitations on the Dissociative Adsorption of O₂ on Cu Surfaces, J. Phys. Chem. C, 2007, 111, 9961–9967.
29. D. Barredo, G. Laurent, P. Nieto, D. Faras and R. Miranda, High-resolution elastic and rotationally inelastic diffraction of D₂ from NiAl(110), J. Chem. Phys., 2010, 133, 124702.
30. G. Scoles, Atomic and Molecular Beam Methods, Oxford University Press, Oxford, UK, 1992, vol. 1.
31. Electronic supplementary information (ESI) available, See  10.1039/d3cp05071h.
32. D. Faras and R. Miranda, in Dynamics of Gas-Surface Interactions: Atomic-level Understanding of Scattering Processes at Surfaces, ed. R. Díez Muiño and H. F. Busnengo, Springer, Berlin, Heidelberg, 2013, pp 51–73.
33. T. Delchar, Oxygen chemisorption on copper single crystals, Surf. Sci., 1971, 27, 11–20.
34. C. Gattinoni and A. Michaelides, Atomistic details of oxide surfaces and surface oxidation: the example of copper and its oxides, Surf. Sci. Rep., 2015, 70, 424–447.
35. A. Spitzer and H. Lüth, The adsorption of oxygen on copper surfaces: II. Cu(111), Surf. Sci., 1982, 118, 136–144.
36. A. Spitzer and H. Lüth, The adsorption of oxygen on copper surfaces: I. Cu(100) and Cu(110), Surf. Sci., 1982, 118, 121–135.
37. L. Luo, Y. Kang, J. C. Yang and G. Zhou, Effect of oxygen gas pressure on orientations of Cu₂O nuclei during the initial oxidation of Cu(100), (110) and (111), Surf. Sci., 2012, 606, 1790–1797.
38. M. Minniti, D. Farías, P. Perna and R. Miranda, Enhanced selectivity towards O₂ and H₂ dissociation on ultrathin Cu films on Ru(0001), J. Chem. Phys., 2012, 137, 074706.
39. D. Zhang, C. Jansen, A. W. Kleyn and L. B. F. Juurlink, Adsorption dynamics of O₂ on Cu(111): a supersonic molecular beam study, Phys. Chem. Chem. Phys., 2023, 25, 14862–14868.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05071h

---