Open Access Article
Open Access ArticleThe influence of the molecular chain length of PVA on the toughening mechanism of calcium silicate hydrates†
Luqing
Cheng
ab,
Yang
Zhou
 *ab,
Hao
Zhang
*b,
Shuai
Xiao
ab,
Weihuan
Li
ab and
Wentao
Chen
ab
*ab,
Hao
Zhang
*b,
Shuai
Xiao
ab,
Weihuan
Li
ab and
Wentao
Chen
ab
aSchool of Materials Science and Engineering, Southeast University, Nanjing, Jiangsu 211189, China. E-mail: tomaszy@seu.edu.cn
bState Key Laboratory of High Performance Civil Engineering Materials, Jiangsu Research Institute of Building Science Co., Nanjing 211103, China. E-mail: zhanghao@cnjsjk.cn
First published on 26th February 2024
Abstract
In recent years, polymers have been demonstrated to effectively toughen cementitious materials. However, the mechanism of interaction between the polymers and C–S–H at the nanoscale remains unclear, and the quantitative impact of the polymer chain length on toughening effectiveness is lacking in research. This study employs molecular dynamics techniques to examine the impact of the polyvinyl alcohol (PVA) chain length on the tensile performance and toughening mechanism of C–S–H. The toughening effect in both the X and Z directions exhibits an initial enhancement followed by a decline with increasing chain length. The optimal degrees of polymerization are determined to be 8 and 12 in the X and Z directions, respectively, resulting in an improvement of fracture energy by 146.7% and 29.5%, respectively. During the stretching process along the X and Z axes, the chain length of PVA molecules significantly influences the variation in the number of Ca⋯O bonds in the system, leading to different stress responses. Additionally, PVA molecules form C–O–Si bonds with the silicate layers of C–S–H, bridging the adjacent layers in a left–right or up–down manner. The toughening effect of PVA on C–S–H depends on the behavior of PVA molecules with different chain lengths, and there exists an optimal range of chain length for PVA, enabling it to enhance structural uniformity and adjust its own conformation to absorb strain energy. When the length of PVA molecular chains is too short, it can easily cause stress concentration in the system and its connection with silicates is not significant. Conversely, when the length of PVA molecular chains is too long, the large molecular structure restricts its extension in the defects of C–S–H, and as the stretching progresses, PVA molecules break and form numerous small segments, thereby losing the advantage of the chain length. This study provides a theoretical basis for the ability of polymers to toughen cementitious materials.
1. Introduction
Inorganic materials are widely used and have significant application and development prospects in various fields due to their diverse types. Traditional inorganic materials have high compressive strength and hardness, but they suffer from low fracture toughness and lack of ductility, making them brittle materials.1,2 Numerous studies have shown that the incorporation of organic materials provides a pathway to enhance the toughness of inorganic materials.3Cementitious materials, as typical inorganic materials, exhibit significant issues such as brittleness and susceptibility to cracking, which affect their application in engineering.4–10 Calcium silicate hydrates (C–S–H) is the main product of cement hydration, which determines the durability, strength, and ductility of cement.11–16 The C–S–H gel contributes significantly to the strength and cohesion of cement paste.17 Currently, enhancing the toughness of cement-based materials by reinforcing C–S–H is a vital direction of research, and one of the main approaches to improve their toughness is through polymer modification. Studies have explored incorporating organic polymers such as polyvinyl alcohol (PVA)18–22 and epoxy resin23–25 into cement-based materials to enhance their toughness. Some research indicates that the addition of an appropriate amount of PVA into the C–S–H gel significantly improves its toughness. PVA is a water-soluble synthetic polymer, belonging to the class of ethylene-based water-soluble non-ionic polymers.26,27 It is considered environmentally friendly and safe, often used as a toughness-enhancing component in cement-based materials. It is suggested that the presence of hydroxyl groups in PVA may alter surface bonding between aggregates, matrix, and fiber reinforcement materials.28 The physical properties of PVA are highly dependent on its polymerization degree (such as the chain length).20 Chain length has a significant influence on key performance metrics such as tensile strength, viscosity, and flexibility.29 Bahraq et al.30 demonstrated that polyethylene (PE) and PVA improve the tensile strength and crack bridging capability of cement-based composite materials (ECC) through strain hardening behavior. F. Pelisser et al.,31 through XRD analysis, discovered that the addition of PVA increases the interlayer spacing of the C–S–H matrix, indicating the potential of low molecular weight PVA to embed within the C–S–H matrix. Moreover, the presence of PVA significantly affects the elastic modulus. Zhou et al.32 conducted a study on the interaction between PVA and C–S–H in PVA/C–S–H composite materials using XRD techniques. They observed that the PVA polymer interferes with the relatively ordered stacking of calcium silicate sheets in C–S–H, and the interaction between PVA and C–S–H on different length scales leads to varied stiffness changes. The incorporation of the PVA polymer modifies the nanoscale and microstructural arrangement of C–S–H, thereby significantly affecting its tensile properties. Currently, the understanding of the toughening mechanism in the C–S–H/PVA system remains incomplete, particularly regarding the impact of the PVA chain length on toughening effectiveness. Further exploration using novel research methodologies is needed in this regard.
On the other hand, considering the properties of C–S–H gel materials and the necessary nanoscale investigations, it is imperative to utilize molecular dynamics (MD) simulation as a research approach. The C–S–H gel is an amorphous colloidal material with a highly porous structure and a large surface area. Investigating the toughening mechanisms of C–S–H/PVA composite materials requires not only macroscopic-level mechanical performance testing and material analysis techniques but also in-depth research into the interactions between molecules at the nanoscale. Currently, molecular dynamics simulation is an important approach for studying material microstructural arrangements and intermolecular interactions. Zhou et al.32 employed molecular dynamics models to verify the feasibility of PVA molecule intercalation within the layers of the C–S–H matrix, and the C–S–H/PVA model exhibited interlayer spacing consistent with samples measured by HP-XRD under ambient pressure. In the study of the interaction between PVA and C–S–H,33 it was found that the polarity of functional groups and the diffusion tendency of polymers affect the bonding at the polymer–cement interface. In the investigation of the reinforcement mechanism of polymer incorporation into C–S–H,34 reactive molecular dynamics simulations based on the ReaxFF force field revealed that during the uniaxial stretching process in the X and Z directions, the PVA polymer bridged adjacent silicate sheets, activating more hydrolysis reactions at the interfaces to avoid strain localization. This mechanism increased tensile strength, delayed fracture, and improved the toughness of the C–S–H matrix. In the study reported by Hou et al.35 on polymer/C–S–H nanocomposites, molecular simulation methods were employed, and the CSH-FF force field was used to investigate the interface structure, dynamics, energetics, and mechanical properties of polymer/C–S–H nanocomposites. In this study, PVA was introduced into the nanochannels of C–S–H, and the results demonstrated that PVA formed hydrogen bonds in the interface region and repaired defects in the silicate chains, thus preventing crack propagation during loading and providing a theoretical reference for the toughening mechanism of PVA.
Although molecular dynamics simulations can characterize the toughening effect of polymers on C–S–H at the nanoscale, the quantitative characterization of the toughening effect with respect to the molecular chain length (an important feature of polymers) is currently infrequent, which is of great significance for the efficient design of polymers.
Based on molecular dynamics simulations, this study selects PVA as the polymer to be introduced into the C–S–H interlayer and investigates the effect of the PVA molecular chain length on the mechanical properties and the toughening mechanism of the PVA/C–S–H system in various directions by changing the polymerization degree of PVA.
2. Simulation method
2.1. Force field
In this study, computational simulation experiments were conducted using the ReaxFF reactive force field for uniaxial tensile loading. The ReaxFF force field combines quantum mechanics and traditional molecular simulation methods and was developed by Duin et al.36 for studying catalysis, gas-phase reactions, and material failure. Currently, it is used for chemical simulations of various materials, including metals, ceramics, silicon, and polymers.37,38 The ReaxFF force field has good compatibility at organic/inorganic interfaces39 and has been successfully applied in both organic40,41 and inorganic36 systems. In this study, the Ca/Si/H/O and C/O/H parameter sets from ref. 39 and 42 were respectively combined. The ReaxFF force field performs well in simulating the interface interactions between C–S–H and organic materials, as well as in studying the mechanical response of CSH/polymer systems under uniaxial tensile loading, and can effectively reflect the stretching process of the material.362.2. Molecular models
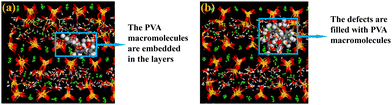
In numerous studies, there is ample evidence to demonstrate that PVA can intercalate into the interlayers of C–S–H,43–45 and the deep interaction between the two phases alters the structure and properties of the nanocomposite materials.31,46–48 Zhou et al.32 constructed PVA molecular chains composed of 8 monomers to verify the possibility of PVA molecules embedding in the interlayer of C–S–H and proposed that larger-sized PVA molecules may reduce the porosity of the C–S–H structure and result in the aggregation of dense particles. Hou et al.35 introduced PVA molecular chains composed of 8 monomers into the nano-channels of C–S–H layers to establish a polymer/C–S–H composite material model. Therefore, to reflect the influence of polymers with different chain lengths on the properties of the composite material when inserted into the interlayers of C–S–H, several sets of PVA molecular models with degrees of polymerization of approximately 8 were constructed in this study. These included PVA molecules with degrees of polymerization of 2 (PVA2), 4 (PVA4), 8 (PVA8), 12 (PVA12), and 16 (PVA16), which were subsequently inserted into the defects of C–S–H.The first and last atoms of the PVA monomer were positioned in a trans configuration. In the PVA molecule, hydroxyl groups were uniformly distributed along the carbon chain, and the carbon atoms can be classified into three types based on the number of hydrogen atoms connected to them: C1, C2, and C3, where C1 was the carbon atom connected to one hydrogen atom, and so on. Different degrees of polymerization were achieved by utilizing the polymerization module in Material Studio to extend monomers into long chains of specific polymerization degrees, as illustrated in Fig. 1(b). The molecular structure of PVA4 is depicted in Fig. 1(b).
The C–S–H gel is a complex multi-scale structure composed of elements and pores of different sizes. XRD experiments on C–S–H have revealed that the structure of the C–S–H nano-gel exhibits a layered crystalline structure.15 In this study, the C–S–H model is based on the 11 Å tobermorite structure,17,49 with a few silicate tetrahedra removed and a calcium-to-silicon ratio (C/S) adjusted to 1.3. This ratio is commonly used for simulating C–S–H/polymer systems. The C–S–H model with C/S = 1.3 has fewer and more concentrated structural defects, and does not produce multiple cracking, making it the optimal structural model for studying polymer intercalation. For example, Matsuyama and Young43–45 found that the maximum intercalation of polymers occurs when C–S–H has a C/S ratio of 1.3. In this study, the hydroxyl groups, water molecules, and calcium ions within the interlayers of C–S–H were initially removed. Subsequently, polymer chains were introduced using the sorption option, followed by the addition of an equivalent amount of calcium ions and hydroxyl groups. Finally, the Grand Canonical Monte Carlo (GCMC) method was employed to add a saturating amount of water molecules. Five C–S–H/PVA composite material systems were constructed by introducing different numbers of PVA molecules with different chain lengths into the pure C–S–H structure, and different methods were used to introduce polymers with different chain lengths. PVA molecules with degrees of polymerization of 2, 4, and 8 were adsorbed into the defects of C–S–H using the Grand Canonical Monte Carlo (GCMC) method. However, due to the complex spatial structure of long-chain PVA molecules with degrees of polymerization of 12 and 16, they could not be introduced using the GCMC method and were manually added with an additional long relaxation process to achieve a stable system state. In practical scenarios, PVA is filled into the defects of C–S–H to ensure the compactness of the system's architecture. To simulate real conditions, the number of PVA molecules introduced into each system equals the maximum adsorbable quantity. Each system is named based on the “number of adsorbed PVA chains – PVA – polymerization degree of PVA chains”, namely 16PVA2, 8PVA4, 4PVA8, 4PVA12, and 4PVA16.
In the C–S–H unit cell, the absence of some silicon–oxygen chains results in defects in the C–S–H structure, which can be used to introduce PVA molecules, as shown in Fig. 1(c). The size of the experimental cell is approximately 40 × 40 × 40 Å3, containing 7400–7800 atoms. The PVA polymer chains are incorporated into the inherent defects of C–S–H by adsorption. Upon the embedding of PVA molecules, it is observed that the main chain of PVA extends parallel to the Y-axis. Due to the insertion of PVA molecules, the number of water molecules in the C–S–H/PVA composite structure cannot be maintained the same as that in pure C–S–H. Therefore, to construct a relatively reasonable C–S–H/PVA system, the number of water molecules is absorbed to a saturated state. Taking the 4PVA12 system as an example, the structure of the system with four PVA molecules with a degree of polymerization of 12 inserted into the C–S–H supercell is shown in Fig. 1(d) and (e).
2.3. Uniaxial tensile simulations
Pure C–S–H and C–S–H/PVA intercalation models were subjected to uniaxial stretching simulations along the x, y, and z axes, with a fixed strain rate of 0.08 ps−1. Prior to the stretching loading, the system was relaxed at 300 K for 50 ps in the canonical (NVT) ensemble to reach an equilibrium state. The total energy of each system during the relaxation process evolves over time as depicted in Appendix A (ESI†), indicating a convergence towards a stable state as the total energy stabilizes with time. This suggests that the system has reached an equilibrium state. Subsequently, a uniaxial tension process was initiated under the isothermal–isobaric (NPT) ensemble (a temperature of 300 K, with zero pressure applied in the remaining two directions to consider the Poisson effect). Uniaxial loading is performed in one direction to simulate the calculation of pressure and strain along each direction. The trajectory of atomic motion during the stretching process and the x, y, and z-axis pressures and system structure lengths were outputted to draw the stress–strain curve of uniaxial stretching, reconstruct the PVA molecule morphology at the interface, and analyze the bonding situation of each atom to explore the micro-toughening mechanism of C–S–H by PVA molecules with different chain lengths.3. Effect of chain length of PVA molecules on the tensile properties of C–S–H/PVA composites
3.1. Mechanical properties of stretching along the X-axis
The stress–strain curves of each system stretched along the X-axis are shown in Fig. 2(a). As the strain increases, the external tensile stress carried by the X-axis direction continues to change, showing a trend of first increasing and then decreasing. During the elastic deformation stage, stress grows proportionally with strain until it gradually reaches its maximum value. The elastic modulus of pure C–S–H is approximately 90 GPa, which is in approximate agreement with the estimation of the elastic modulus of C–S–H units by Murray et al.17 Compared with the stretching process of pure C–S–H, the insertion of PVA molecules has almost no effect on the tensile strength and elastic modulus in the elastic deformation stage. In the plastic deformation stage, the insertion of PVA molecules has increased the ductility of C–S–H to varying degrees, effectively delaying the occurrence of fracture. Among 16PVA2, 8PVA4, and 4PVA8, as the length of the PVA molecule chain increases, the fracture strain of C–S–H gradually increases, indicating that increasing the length of the PVA molecule chain can significantly enhance the toughening effect on C–S–H. For the 4PVA8 system, when the strain reaches 0.15, the stress reaches its peak value, which is nearly identical to the peak value of pure C–S–H, approximately 9 GPa. This closely aligns with the results obtained by Zhou et al.34 from their study on pure C–S–H and PVA8-incorporated systems subjected to tensile loading along the X-axis. When the strain of the 4PVA8 system increases to 0.3, the stress fluctuates around 5 GPa. When the strain is within the range of 0.3 to 0.8, the material remains intact before the strain reaches 0.8. As the length of the PVA molecule chain increases in 4PVA8, 4PVA12, and 4PVA16, the ductility of C–S–H gradually decreases, and the fracture strain gradually decreases. This indicates that increasing the length of the PVA molecule chain significantly weakens the toughening effect on C–S–H when the length of the PVA molecule chain is greater than that of eight monomers. | ||
| Fig. 2 Stress–strain curve of the triaxial tensile process ((a) X-axis; (b) Y-axis; and (c) Z-axis). | ||
During the stretching process along the X-axis, the structural deformation diagrams of pure C–S–H, 4PVA8, and 4PVA16 at different strains are shown in Fig. 3. Pure C–S–H gradually developed cracks and eventually fractured at a strain of approximately 0.4 as the strain increased during the stretching process. In contrast, the 4PVA8 system remained relatively stable with no significant crack formation observed. The effect of PVA16 molecules in delaying crack formation was relatively limited. In the study conducted by Hou et al.,35 PVA8 molecular chains were introduced into the interlayer region of C–S–H. The results indicate that the incorporation of the polymer disrupts the ordered arrangement of calcium silicate layers, leading to atomic repositioning within the layers. This phenomenon can be attributed to the interaction between the PVA molecules and the calcium silicate layers. Therefore, the influence of PVA molecular chains on the toughening effect may be related to the morphology of the PVA molecular chains. PVA molecular chains can adjust their own conformation to maintain stable bonding with the surrounding silicate layers, thereby preventing the propagation of microcracks.
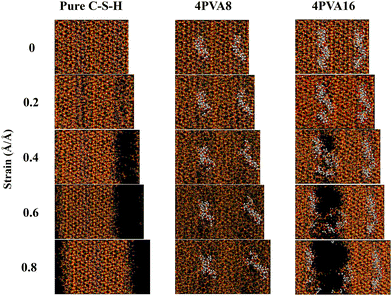 | ||
| Fig. 3 Structural deformation diagrams of pure C–S–H, 4PVA8 system, and the 4PVA16 system stretched along the X-axis. | ||
The stress–strain curves under stretching along the Y-axis are shown in Fig. 2(b). The pure C–S–H system exhibits the highest elastic modulus and tensile strength, with a stress peak of approximately 11.5 GPa, and similar results were obtained by Zhou et al.34 The stress–strain curves of the systems with PVA molecules show a very similar shape to that of pure C–S–H. Up to a strain of 0 to 0.15 Å Å−1, the stress–strain curves of the systems with PVA molecules almost overlap with that of pure C–S–H. Beyond the onset of plastic deformation, the stress of the systems with PVA molecules is slightly lower than that of the pure C–S–H system. The difference in stress values among the systems with PVA molecules of different chain lengths is negligible. Therefore, within the strain range of 0 to 0.8 Å Å−1, the incorporation of PVA molecules with different chain lengths does not significantly affect the mechanical properties of C–S–H in the Y-axis direction. Hence, the subsequent analysis will not focus on the mechanism of the chain length of PVA molecules on the tensile behavior along the Y-axis.
3.2. Mechanical properties of stretching along the Z-axis
The stress–strain curves of pure C–S–H and C–S–H/PVA composite materials under stretching along the Z-axis are shown in Fig. 2(c). Compared to the x and y axes, the Z-axis exhibits the lowest tensile strength and elastic modulus. This observation is consistent with the findings reported by Zhou et al.,34 which may be attributed to the alternating distribution of calcium silicate layers and interlayer regions along the Z-axis in the C–S–H structure. Due to the inherent fragility of the interlayer regions, the occurrence of cracks is more likely under tensile deformation along the Z-axis. The maximum tensile stress of the pure C–S–H system is approximately 5.8 GPa, which is similar to the value reported in ref. 34. Additionally, the stress curves of the pure C–S–H system and the 4PVA8 system exhibit a similar trend to the curves observed in Hou et al.'s study.35 During the elastic deformation stage, the insertion of PVA molecules had minimal effect on the stress values and elastic modulus. Compared to pure C–S–H, the 4PVA12 system achieved the same stress peak value and improved the ductility of C–S–H. Among all the composite systems, the 4PVA12 system had the highest external stress-bearing capacity and the best ductility. The fracture processes of different systems are shown in Fig. 4. There were significant differences in the fracture phenomena between systems with short-chain and long-chain PVA molecules. The 16PVA2 and 8PVA4 systems exhibited large cracks in the interlayer region, and the PVA molecules did not prevent the tendency of crack propagation, resulting in a lower fracture strain. Although cracks were observed in the interlayer region of the 4PVA8, 4PVA12, and 4PVA16 systems, the PVA molecules adjusted their own conformation to prevent the propagation of cracks. In summary, short-chain PVA molecules were unable to prevent the expansion of cracks during the stretching process of the C–S–H structure, and their toughening effect was minimal. In contrast, longer-chain PVA molecules could prevent crack propagation, improve the ductility of the C–S–H structure, and achieve a toughening effect. | ||
| Fig. 4 Deformation diagrams of the Z-axis stretching structures for the 16PVA2 system, 8PVA4 system, 4PVA8 system, 4PVA12 system, and 4PVA16 system. | ||
The ability of PVA molecules with different chain lengths to delay or prevent the expansion of cracks during the stretching process of the C–S–H structure is highly correlated with the conformation of the PVA molecules. Short-chain PVA molecules are embedded in the silicate layers of the C–S–H structure, which prevents their carbon chains from extending to connect the upper and lower silicate layers, making it difficult to prevent the expansion of cracks during the stretching process of the C–S–H structure. As shown in Fig. 5, after relaxation, short-chain PVA molecules are embedded in the silicate layers of the C–S–H structure and are unable to connect the upper and lower silicate layers. For longer-chain PVA molecules, their larger molecular weight and more complex molecular structure can effectively fill the defects in the C–S–H structure, thereby preventing the expansion of cracks and achieving the toughening effect.
4. Discussion
4.1. Comparison of bond breakage in intercalated systems of PVA molecules with different chain lengths
At the microscopic level, the breaking of chemical bonds is a way for the system to consume energy. Previous studies have revealed the hydrolysis reactions that occur during the stretching process in pure C–S–H structures. Hou50 and Zhu51 described two types of hydrolysis reactions that occur in pure C–S–H models due to a decrease in activation energy during the stretching process. These two hydrolysis reactions can be represented by chemical formulas (1) and (2), respectively. In formula (1), the ionic bond between Ca ions and Si–O groups is stretched until it breaks, forming the same amount of Ca–OH and Si–OH in the presence of water molecules. In formula (2), stable covalent Si–O–Si bonds are stretched until they break during the stretching process, and free Si–O groups and Si atoms immediately react with water to form 2Si–OH. In the X-axis stretching process of this paper, there is no bond breakage in the Si–O–Si bond, so the reaction in formula (2) is almost absent when stretching in the X-axis direction, which is consistent with the results of Zhou.34 Zhou's34 study showed that only the hydrolysis reaction in formula (1) occurs during the X-axis stretching process of C–S–H. The bond energy of the Si–O covalent bond is 452 KJ mol−1, while Ca⋯O is an ionic bond, and its bond energy is much lower than that of Si–O. Therefore, during the stretching process, the Ca⋯O ionic bond between Ca ions and O ions exhibits higher fragility when it breaks.| Si–O⋯Ca + H2O → Si–OH + Ca–OH | (1) |
| Si–O–Si + H2O → 2Si–OH | (2) |
During X-axis stretching, although each system has a different number of broken C–O and C–C bonds, the total number of carbon atoms in each system is much smaller than the number of Ca ions. Therefore, in terms of quantity, the number of broken Ca⋯O bonds is much greater than the total number of broken C–O and C–C bonds, and the system mainly relies on the energy consumption of broken Ca⋯O bonds. During relaxation, intercalation of PVA molecules affects the relative positions of atoms in C–S–H, breaking some of the bonds between calcium and oxygen atoms, resulting in fewer initial Ca⋯O bonds in each system compared to pure C–S–H. The comparison of the number of broken Ca⋯O bonds and stress in intercalated systems with different chain lengths of PVA is shown in Fig. 6(a). According to the trend of the number of broken calcium–oxygen bonds, Fig. 6(a) can be divided into three stages: Stage I (strain 0–0.4), Stage II (strain 0.4–0.6), and Stage III (strain 0.6–0.8). The number of broken bonds in pure C–S–H, 16PVA2, and 4PVA16 uniformly increases in Stage I and stops increasing in Stages II and III, when the stress approaches 0 and the system gradually fails. The number of broken Ca⋯O bonds in 8PVA4 uniformly increases in Stages I and II and stops increasing in Stage III, when the stress approaches 0 and the system gradually fails. The number of broken Ca⋯O bonds in 4PVA8 and 4PVA12 uniformly increases in Stages I, II, and III, while the stress remains greater than 0, indicating that the system can withstand a certain load. It can be seen that the ability of the PVA/C–S–H composite system to withstand stress is strongly correlated with the trend of the number of broken Ca⋯O bonds in the system.
In the 4PVA8 and 4PVA12 systems, PVA molecules can fill the defects in the C–S–H interlayer, improve the uniformity of the structure, and make the stress between the silicate layers more uniform. The stress distribution in the systems is shown in Figure (b) and (c) in the Appendix A (ESI†). The observation focuses on the initial stage of crack formation in the system (strain ≈ 0.35). In the 4PVA8 system, the atoms experience uniform force distribution, as indicated by the range of colors from yellow to green, without exhibiting extreme red or blue colors. Conversely, the 4PVA16 group exhibits significant color extremes, indicating the presence of substantial stress concentration within its internal structure. As a result, the number of broken Ca⋯O bonds in the 4PVA8 group shows a consistent and uniform increase with increasing strain. As shown in Fig. 3, the distribution of atoms in the 4PVA8 system is relatively uniform, and PVA molecules can prevent the extension of cracks during the stretching process, resulting in no significant cracks. The number of broken Ca⋯O bonds in 4PVA8 is greater than that in 4PVA12, and its fracture energy of 4.367 GJ m−3 is greater than that of 4PVA12 of 3.875 GJ m−3, indicating that the tensile strength and ductility of the 4PVA8 system are better than those of the 4PVA12 system.
Similar to the previous section, Fig. 7(a) is divided into three stages based on the trend in the number of broken Ca⋯O bonds. The number of broken Ca⋯O bonds in pure C–S–H and 8PVA4 increases in stage I, then begins to decrease before entering stage II, and remains relatively constant in stages II and III as the stress approaches zero, indicating that the system is gradually failing. The number of broken Ca⋯O bonds in the 16PVA2, 4PVA8, and 4PVA16 systems increases in stage I, then increases and decreases in stage II, while the stress approaches zero and the system gradually fails. The number of broken Ca⋯O bonds in the 4PVA12 system increases in stages I and II, then decreases slightly in stage III, while the stress approaches zero. As shown in Fig. 4, the 4PVA12 system exhibits initial cracking within the defect layer of the C–S–H phase during the early stages of stretching. These cracks gradually propagate. However, unlike other systems, the cracks in the 4PVA12 system do not continue to extend unstably, but rather stop expanding and generate new cracks within the non-defect layer of the C–S–H phase. This multi-cracking behavior disperses the input energy, leading to more fracture of the Ca⋯O bonds in various regions of the system, resulting in an overall higher prevalence of Ca⋯O bond rupture. The stress distribution is also demonstrated in Figure (d) and (e) in the Appendix A (ESI†), where the 4PVA12 system does not exhibit significant stress concentration, atoms uniformly bear the stress. In contrast, the 8PVA4 system experiences a lack of stress-carrying capability within the carbon chains, leading to a large number of red-colored atoms, indicating stress concentration, particularly at defect sites. This strongly indicates a high correlation between the fracture and crack propagation behavior of the system and the stress conditions. The trend in the number of broken Ca⋯O bonds in the system determines when the stress approaches zero, i.e., the magnitude of the fracture strain. In other words, when the number of broken Ca⋯O bonds in the system stops increasing, the system begins to gradually fail. In summary, the chain length of PVA molecules has a significant influence on the trend in the number of Ca⋯O bonds in the system, resulting in differences in tensile stress and fracture strain among the various systems.
4.2. Influence of different chain lengths of PVA molecules on the toughening effect
During the stretching process, the insertion of PVA molecules can effectively enhance the toughness of C–S–H. PVA molecules can form bonding interactions with the silicate layers, thereby hindering the propagation of small cracks and improving the ductility of the material. C–O–Si bonds are formed between PVA molecules and silicate tetrahedra, as shown in Fig. 8(a), and a small portion of C–O–Si bonds are formed by the hydroxyl groups of PVA molecules connecting to the silicon of the silicate tetrahedra after hydrogen dissociation, while the formation of the majority of C–O–Si bonds depends on the rupture of Si-O⋯Ca bonds in C–S–H described in Section 4.1. After the rupture of Si-O⋯Ca bonds, the free Si-O groups connect to the carbon atoms of PVA molecules. The radial distribution function can be used to verify the bonding mechanism between the carbon atoms in PVA molecules and the calcium silicate layers in C–S–H, which can be calculated using eqn (3).52 | (3) |
In the equation, gAB(r) represents the probability of atom B appearing in a sphere with radius r centered on atom A; NAB(r) is the number of atoms B within the distance range from r to r + dr from atom A; ρ is the density of atom B; and dV(r) is the volume of the shell structure from atom A at distance r to r + dr.
The radial distribution function (RDF) between the oxygen atoms in the silicate and the carbon atoms in PVA molecules is shown in Fig. 8(b). Within 3 Å between the atoms, there are significant peaks in the RDFs of the three types of carbon atoms in PVA molecules and the oxygen atoms in the silicate tetrahedra, indicating the existence of significant bonding interactions between the oxygen atoms in the silicate and these three types of carbon atoms. It is worth noting that a significant peak is observed within a range of 2 Å between the oxygen atom and the C1 atom, indicating that the formation of a bond between the oxygen atom and the C1 atom is more favorable.
To further investigate the influence of the behavior of PVA molecules with different chain lengths on the toughening effect of the C–S–H structure, the mean square displacement (MSD) of the carbon atoms in PVA molecules was introduced for quantitative analysis to evaluate the degree of expansion of PVA molecules with different chain lengths. In statistical mechanics, the MSD of an atom can be calculated using the following formula:
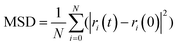 | (4) |
Here, N represents the total number of atoms participating in the statistics, i represents the atom number, ri(t) represents the position of the atom at time t, and ri(0) represents the position of the atom at the initial time, and the MSD of the carbon atoms is calculated every 0.1 ps.
 | ||
| Fig. 9 Morphological changes of PVA molecules with different chain lengths during X-axis tensile deformation. | ||
If the length of the PVA molecule chain is too short or too long, stress concentration may occur, and the system failure cannot be effectively delayed. Due to the small spatial scale of short-chain PVA molecules, PVA molecules are easily embedded in the silicate layer of C–S–H, causing stress concentration, and are not easy to bond with the left and right silicate layers simultaneously. PVA4 molecules can connect the left and right silicate layers at small strains, to some extent, improving the toughness of C–S–H, but cannot achieve the best toughening effect. Due to the large structural size, excessively long PVA molecules do not have enough space to rotate in the defects of the C–S–H interlayer. As seen from the morphology of the PVA16 molecule at the crack in Fig. 9, part of the broken PVA16 molecule adheres to one side of the crack due to the limited motion space, while the other part connects the left and right layers through structural twisting. The adhesion of PVA16 molecules to one side of the crack causes stress concentration in the structure, resulting in fewer broken Ca⋯O bonds. Similarly, although the polymerization degree of 12 for PVA molecules cannot completely match the defects of the C–S–H structure in terms of the spatial scale, it neither embeds the entire molecule in the silicate layer nor exhibits significant adhesion at the crack, so PVA12 can not only increase the structural uniformity of C–S–H but also form certain bonding with the left and right silicate layers, causing more Ca⋯O bonds to break and delaying failure.
During X-axis tensile deformation, the mean square displacement (MSD) of carbon atoms in each system in the X-axis direction is shown in Fig. 10(a). After the system exhibits obvious cracks, the movement of PVA molecule chains can no longer delay the extension of cracks but simply follows the movement of the system. Therefore, the statistical range of MSD is truncated to the point when the system exhibits obvious cracks. The MSD of carbon atoms in PVA molecules in the stretching direction can indicate the degree of self-structural adjustment of PVA molecules. In the X-direction, the MSD values of molecular chains show a trend of first increasing and then decreasing with the increase of the polymerization degree of molecular chains, and the speed of the upward trend on the MSD curve also varies, showing the phenomenon of PVA2 < PVA12 < PVA4 ≈ PVA8 ≈ PVA16. The main reason for this phenomenon is that the rate of chain unfolding is influenced by the length of the molecular chain. Shorter molecular chains are limited by their own scale and cannot combine with the siloxane chains on both sides, resulting in slower unfolding rates and inability to fill the pores in time. Longer molecular chains require larger strains to achieve sufficient displacement, resulting in slower unfolding rates. The anomalous fast stretching rate of PVA molecules with a polymerization degree of 16 is related to the observation of molecular chain breakage into several small segments in Fig. 9. PVA molecules with a chain length of 8 have a faster unfolding rate and a suitable chain length, enabling them to reach a stress-bearing state when the strain reaches 0.8, which is the point when cracks appear.
 | ||
| Fig. 10 (a) MSD curve of carbon atoms during X-axis tensile deformation. (b) MSD curve of carbon atoms during Z-axis tensile deformation. | ||
The carbon chains of PVA molecules are not arranged in a completely straight line but exhibit a certain degree of twisting and bending. With the increase of the carbon chain length, the twisting and bending sites also increase correspondingly, leading to structural complexity. PVA molecules with chain lengths that are too short or too long may cause stress concentration, and the improvement of the tensile properties of the C–S–H structure cannot achieve the best effect. PVA molecules with intermediate chain lengths, such as PVA molecules with a polymerization degree of 8, have a size and structure that match the defects in C–S–H shown in Fig. 1. Combined with the previous content, their spatial scale and appropriate unfolding rate jointly endow PVA8 molecules with the best improvement effect on the tensile properties of C–S–H.
 | ||
| Fig. 11 Morphological changes of PVA molecules with different chain lengths during Z-axis stretching. | ||
Compared with the tensile deformation of pure C–S–H, introducing PVA molecules with a degree of polymerization of 4 weakens the toughness of the system, leading to earlier failure and a significant reduction in strain energy. PVA4 cannot achieve uniform dispersion to fill the dense defects, but instead embeds into the silicate layer of the C–S–H structure, introducing obvious stress concentration. Meanwhile, its chain length is insufficient to connect the upper and lower layers, resulting in the premature generation of cracks that are not effectively prevented, leading to system failure. During the tensile deformation, a large number of small molecular segments are formed by the fracture of PVA16 molecules, which have lost their function as large molecular chains connecting the two sides. Therefore, the toughening effect is poor, but due to the larger molecular weight, the filling effect is better than that of PVA2, resulting in a certain toughening effect.
During the deformation process, PVA molecules with a chain length of 8 can absorb strain energy by adjusting their shape and spatial angles, as shown in Fig. 11. The middle part of the PVA8 molecular chain is fixed, while one free end rotates in the stretching direction, with an angle of 38° with the Y-axis when the strain is 0.2. When the strain reaches 0.4, the angle between the free end and the Y-axis further increases to 50°, resulting in a more obvious angular displacement. However, the other side, which is not connected to the silicate chain, does not show significant movement. When the strain reaches 0.6, due to the limited energy absorption capacity of the molecular chain itself, the molecular chain breaks, and the system fails at this point.
Compared with PVA molecules with a chain length of 12, they exhibit the same phenomenon as PVA8, with a connection between the midpoint of the PVA molecular chain and the Si–O chain, resulting in anchoring at the midpoint of the PVA molecular chain. Both free ends rotate to adjust their spatial positions in the stretching direction, resulting in significant angular displacement. When the strain is 0.2, 0.4, and 0.6, the rotation angles of the two ends reach 28°, 28°, and 63°, and 34°, 42°, and 46°, respectively. In the initial stage of stretching, a large amount of energy is absorbed through the rotation of the lower half. When the strain continues to increase, the lower half reaches its limited energy absorption capacity and breaks. At this point, the upper half of the molecule, due to its longer length, can connect the two side layers, take over the rotation, and continue to absorb some strain energy, thereby maintaining the stability of the system. Compared with PVA8, both PVA8 and PVA12 undergo the same process, but PVA12 has a longer chain length, and both free ends can effectively connect the layers, alternating between rotation and breakage, while PVA8 can only connect one free end due to its limited length, resulting in a weaker toughening ability than PVA12.
Combined with the MSD results, we can further analyze the motion of the molecular chains. From the trend of the MSD curves, it is evident that PVA2, PVA12, and PVA16 exhibit faster motion speeds. Due to its small scale, PVA2 is not fixed on the molecular chain and experiences rapid displacement within the system. PVA16 also fractures into numerous small molecular segments during stretching, exhibiting the same motion pattern as PVA2. PVA4 exhibits minimal displacement during stretching, indicating that it does not absorb strain energy by adjusting its spatial conformation. The displacement produced by PVA8 during stretching is not significant, as half of its molecules are not effectively connected due to their shorter chain length and are thus pulled along, resulting in lower MSD values. This phenomenon is consistent with the MSD curve of PVA12 and the phenomenon shown in Fig. 11, where both free ends of the PVA12 molecule rotate, resulting in rapid motion reflected in the MSD curve. The upward trend of the MSD curve terminates when the strain reaches 0.6, indicating that a significant amount of energy is absorbed by the system through substantial spatial position adjustments, effectively enhancing the system's toughness. Moreover, the motion of the molecular chains is significantly reduced compared to that during X-axis stretching, which matches its weaker toughening ability compared to the X-axis. This effectively demonstrates that the motion of the molecular chains is indeed one of the important influencing factors for toughening ability.
In summary, during Z-axis stretching, the optimal chain length of the molecular chains connected by the Si–O chains on opposite sides of the upper and lower ends is increased from PVA8 in the X-direction to PVA12. Due to the limited chain length of PVA8, only one side of its two free ends rotates and extends, while both free ends of PVA12 can move due to its longer chain length, resulting in rapid and significant displacement reflected in the MSD curve. Such molecular chain rotation absorbs a large amount of energy from the strain, resulting in toughening effects. Molecular chains that are too short cannot achieve this effect, while those that are too long will fracture into numerous small molecular chains, losing their chain length advantage. The MSD results demonstrate that the motion and speed of the molecular chains do indeed affect the toughening effect of the system, which will become one of the important factors to consider when analyzing the effect of molecular polymerization on toughening ability.
5. Conclusion
In the uniaxial stretching simulation, PVA molecules with different chain lengths exhibited different toughening effects. Along the X-axis, the order of the influence of the chain length on the toughening effect was PVA8 > PVA12 > PVA4 > PVA2 > PVA16 > pure CSH. Along the Z-axis, the order of the influence of the chain length on toughening effect changed to PVA12 > PVA8 ≈ PVA16 > PVA2 > pure CSH > PVA4. The different toughening effects along the X-axis and the Z-axis were caused by the inherent structure of C–S–H. PVA molecular chains connect adjacent left and right Si–O chains in the X-axis direction and opposite upper and lower Si–O chains in the Z-axis direction. During the stretching process, the main pathway of energy dissipation is the breaking of Ca⋯O bonds, and the chain length of PVA molecules has a significant influence on the trend of the number of Ca⋯O bonds. The introduction of PVA fills the defects, connects the Si–O chains at the defect sites, prevents the initiation and propagation of cracks, and makes the system more uniformly stressed, allowing more Ca⋯O bonds to break during stretching and absorb energy, thereby enhancing the toughness of the system.The ability of PVA molecules of different chain lengths to prevent crack initiation and propagation depends on their behavior during stretching. In stretching along the X and Z axes, PVA molecules with the optimal chain length range can adjust their own shape to connect the left and right or upper and lower layers of the silicate, prevent crack propagation, and increase the toughness of the material. In addition, the anchoring effect of the C–O–Si bond on PVA molecules also affects the movement of the molecular chain. However, PVA molecules with appropriate lengths can still produce effective displacement while forming anchoring.
In summary, different chain lengths of PVA have different toughening effects, and comprehensive considerations are needed based on factors such as the defect size, stretching direction, and molecular spatial structure. This study analyzed the toughening mechanism of the PVA/C–S–H system through molecular dynamics simulations, but there are still challenges in macroscopic applications, such as a large range of molecular weight and complex toughening mechanisms. By combining machine learning, macroscopic performance, and other experimental methods, further exploration of the toughening mechanism of this system is expected.
Author contributions
Luqing Cheng: investigation, data curation, formal analysis, writing – original draft, and writing – review and editing. Yang Zhou: conceptualization, funding acquisition, project administration, and supervision. Hao Zhang: methodology, resources, and validation. Shuai Xiao: visualization and writing – review and editing. Weihuan Li: software and resources. Wentao Chen: software and resources.Conflicts of interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We acknowledge support from the National Natural Science Foundation of China (Grant No. 52250010, 6512009004A, and 52379120), the National Key Research and Development Program of China (Grant No: 2021YFF0500800), and the Natural Science Foundation of Jiangsu Province (Grant No: BK20230086). We are also grateful to the Big Data Computing Center of Southeast University and the High-Performance Center of Nanjing University for providing the computing support.References
- D. Shopova-Gospodinova, Z. Burghard, T. Dufaux, M. Burghard and J. Bill, Compos. Sci. Technol., 2011, 71, 931–937 CrossRef CAS.
- S. P. Kumar, A. S. Shata, K. V. P. Kumar, R. Sharma, H. Munnur, M. L. Rinawa and S. S. Kumar, Mater. Today: Proc., 2022, 59, 1463–1471 CAS.
- Y. Zhou, S. Xiao, L. Cheng, Y. Chen, J. Tang and W. She, Phys. Chem. Chem. Phys., 2023, 25, 24097–24109 RSC.
- M. O. Mohsen, M. M. Al-Diseet, M. O. Aburumman, M. Abdel-Jaber, R. Taha, M. S. Al Ansari and A. A. Taqa, J. Build. Eng., 2023, 73, 106679 CrossRef.
- B. Xu, C. C. D. Coumes, D. Lambertin and B. Lothenbach, Cem. Concr. Compos., 2023, 143, 105255 CrossRef CAS.
- W. Long, J. Liu and C. He, Constr. Build. Mater., 2023, 404, 133268 CrossRef CAS.
- N. S. Piro, A. S. Mohammed and S. M. Hamad, J. Build. Eng., 2023, 70, 106393 CrossRef.
- H. Nguyen, T. Chang, J. Shih and C. Chen, Cem. Concr. Compos., 2019, 99, 40–48 CrossRef CAS.
- F. Wu, X. You, M. Wang, T. Liu, B. Lu, G. Hou, R. Jiang and C. Shi, Cem. Concr. Compos., 2023, 141, 105128 CrossRef CAS.
- X. Gu, H. Tan, X. He, J. Zhang, X. Deng, Z. Zheng, M. Li and J. Yang, Constr. Build. Mater., 2022, 329, 127208 CrossRef CAS.
- Y. Wang, L. Lei, J. Liu, Y. Ma, Y. Liu, Z. Xiao and C. Shi, Cem. Concr. Compos., 2022, 134, 104762 CrossRef CAS.
- L. B. Skinner, S. R. Chae, C. J. Benmore, H. R. Wenk and P. J. M. Monteiro, Phys. Rev. Lett., 2010, 104, 195502 CrossRef CAS PubMed.
- Y. Zhou, D. Hou, J. Jiang and P. Wang, Constr. Build. Mater., 2016, 126, 991–1001 CrossRef CAS.
- Y. Zhou, D. Hou, J. Jiang, L. Liu, W. She and J. Yu, Microporous Mesoporous Mater., 2018, 255, 23–35 CrossRef CAS.
- R. J. M. Pellenq, N. Lequeux and H. van Damme, Cem. Concr. Res., 2008, 38, 159–174 CrossRef CAS.
- J. Minet, S. Abramson, B. Bresson, A. Franceschini, H. Van Damme and N. Lequeux, J. Mater. Chem., 2006, 16, 1379–1383 RSC.
- S. J. Murray, V. J. Subramani, R. P. Selvam and K. D. Hall, Transp. Res. Rec., 2010, 2142, 75–82 CrossRef CAS.
- E. Knapen and D. Van Gemert, 2006.
- J. H. Kim, R. E. Robertson and A. E. Naaman, Cem. Concr. Res., 1999, 29, 407–415 CrossRef CAS.
- C. C. Thong, D. C. L. Teo and C. K. Ng, Constr. Build. Mater., 2016, 107, 172–180 CrossRef CAS.
- J. Kim and R. E. Robertson, Adv. Cem. Based Mater., 1998, 8, 66–76 CrossRef CAS.
- Y. Chen, Y. Zheng, Y. Zhou, W. Zhang, W. Li, W. She, J. Liu and C. Miao, Nat. Commun., 2023, 14 Search PubMed.
- A. Saccani and V. Magnaghi, Cem. Concr. Res., 1999, 29, 95–98 CrossRef CAS.
- B. Pang, Y. Jia, S. D. Pang, Y. Zhang, H. Du, G. Geng, H. Ni, J. Qian, H. Qiao and G. Liu, Cem. Concr. Res., 2021, 139, 106236 CrossRef CAS.
- G. Al-Bayati, R. Al-Mahaidi and R. Kalfat, Compos. Struct., 2017, 168, 569–581 CrossRef.
- M. Moukwa, D. Youn and M. Hassanali, Cem. Concr. Res., 1993, 23, 122–130 CrossRef CAS.
- M. Sivakumar, Int. J. Civ. Struct. Eng., 2011, 1, 732–740 CAS.
- B. Xu, H. A. Toutanji, T. Lavin and J. A. Gilbert, Key Eng. Mater., 2011, 466, 73–83 CAS.
- F. L. Marten, Editon edn., 2002.
- A. A. Bahraq, M. Maslehuddin and S. U. Al-Dulaijan, Arab J. Sci. Eng., 2020, 45, 7869–7895 CrossRef CAS.
- F. Pelisser, P. J. P. Gleize and A. Mikowski, Cem. Concr. Compos., 2014, 48, 1–8 CrossRef CAS.
- Y. Zhou, L. Tang, J. Liu and C. Miao, Cem. Concr. Res., 2019, 125, 105891 CrossRef CAS.
- Y. Zhou, D. Hou, H. Manzano, C. A. Orozco, G. Geng, P. J. M. Monteiro and J. Liu, ACS Appl. Mater. Interfaces, 2017, 9, 41014–41025 CrossRef CAS PubMed.
- Y. Zhou, D. Hou, G. Geng, P. Feng, J. Yu and J. Jiang, Phys. Chem. Chem. Phys., 2018, 20, 8247–8266 RSC.
- D. Hou, J. Yu and P. Wang, Composites, Part B, 2019, 162, 433–444 CrossRef CAS.
- A. C. T. van Duin, A. Strachan, S. Stewman, Q. Zhang, X. Xu and W. A. Goddard, J. Phys. Chem. A, 2003, 107, 3803–3811 CrossRef CAS.
- T. Y. Pan and Y. Lu, Int. J. Electrochem. Sci., 2011, 6, 4967–4983 CrossRef CAS.
- Y. Yu, B. Wang, M. Wang, G. Sant and M. Bauchy, J. Non-Cryst. Solids, 2016, 443, 148–154 CrossRef CAS.
- D. S. Hou, Z. Y. Lu, X. Y. Li, H. Y. Ma and Z. J. Li, Carbon, 2017, 115, 188–208 CrossRef CAS.
- A. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- K. Chenoweth, A. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- N. Zhang, P. Carrez and R. Shahsavari, ACS Appl. Mater. Interfaces, 2017, 9, 1496–1506 CrossRef CAS PubMed.
- H. Matsuyama and J. F. Young, J. Mater. Res., 1999, 14, 3389–3396 CrossRef CAS.
- H. Matsuyama and J. F. Young, Chem. Mater., 1999, 11, 16 CrossRef CAS.
- H. Matsuyuma and J. F. Young, J. Mater. Res., 1999, 14, 3379–3388 CrossRef.
- J. J. Beaudoin, L. Raki and R. Alizadeh, Cem. Concr. Compos., 2009, 31, 585–590 CrossRef CAS.
- J. J. Beaudoin, H. Drame, L. Raki and R. Alizadeh, Mater. Struct., 2009, 42, 1003–1014 CrossRef CAS.
- S. C. Mojumdar and L. Raki, J. Therm. Anal. Calorim., 2006, 85, 99–105 CrossRef CAS.
- D. Hou, H. Ma, Y. Zhu and Z. Li, Acta Mater., 2014, 67, 81 CrossRef CAS.
- D. S. Hou, T. J. Zhao, H. Y. Ma and Z. J. Li, J. Phys. Chem. C, 2015, 119, 1346–1358 CrossRef CAS.
- T. Zhu, J. Li, X. Lin and S. Yip, J. Mech. Phys. Solids, 2005, 53, 1597–1623 CrossRef CAS.
- S. Abbas, M. L. Nehdi and M. A. Saleem, Int. J. Concr. Struct. Mater., 2016, 10, 271–295 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05000a |
| This journal is © the Owner Societies 2024 |