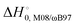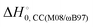Open Access Article
Open Access ArticleEffect of temperature on the gas-phase reaction of CH3CN with OH radicals: experimental (T = 11.7–177.5 K) and computational (T = 10–400 K) kinetic study†
Daniel
González
 ab,
André
Canosa
ab,
André
Canosa
 c,
Emilio
Martínez-Núñez
c,
Emilio
Martínez-Núñez
 d,
Antonio
Fernández-Ramos
d,
Antonio
Fernández-Ramos
 *de,
Bernabé
Ballesteros
*de,
Bernabé
Ballesteros
 ab,
Marcelino
Agúndez
ab,
Marcelino
Agúndez
 f,
José
Cernicharo
f,
José
Cernicharo
 f and
Elena
Jiménez
f and
Elena
Jiménez
 *ab
*ab
aDepartamento de Química Física, Facultad de Ciencias y Tecnologías Químicas, Universidad de Castilla-La Mancha (UCLM), Avda. Camilo José Cela 1B, 13071 Ciudad Real, Spain. E-mail: Elena.Jimenez@uclm.es
bInstituto de Investigación en Combustión y Contaminación Atmosférica, UCLM, Camino de Moledores s/n, 13071 Ciudad Real, Spain
cInstitut de Physique de Rennes-CNRS – UMR 6251, Université de Rennes, F-35000 Rennes, France
dDepartamento de Química Física, Facultade de Química, Campus Vida, Universidade de Santiago de Compostela, Avda. das Ciencias s/n, 15782, Santiago de Compostela, Spain. E-mail: qf.ramos@usc.es
eCentro Singular de Investigación en Química Biológica y Materiales Moleculares (CIQUS), Campus Vida, Universidade de Santiago de Compostela, C/Jenaro de la Fuente s/n, 15782, Santiago de Compostela, Spain
fMolecular Astrophysics Group, Instituto de Física Fundamental (IFF-CSIC), Consejo Superior de Investigaciones Científicas, C/Serrano 123, 28006, Madrid, Spain
First published on 13th January 2024
Abstract
Acetonitrile (CH3CN) is present in the interstellar medium (ISM) in a variety of environments. However, at the ultracold temperatures of the ISM, radical-molecule reactions are not widely investigated because of the experimental handicap of getting organic molecules in the gas phase by conventional techniques. The CRESU (French acronym for Reaction Kinetics in a Uniform Supersonic Flow) technique solves this problem. For this reason, we present in this work the kinetic study of the gas-phase reaction of CH3CN with one of the most ubiquitous radicals, the hydroxyl (OH) radical, as a function of temperature (11.7–177.5 K). The kinetic technique employed to investigate the CH3CN + OH reaction was the pulsed laser photolysis-laser induced fluorescence. The rate coefficient for this reaction k(T) has been observed to drastically increase from 177.5 K to 107.0 K (about 2 orders of magnitude), while the increase in k(T) from 107.0 K to 11.7 K was milder (around 4 times). The temperature dependent expressions for k(T) are provided in the two distinct T-ranges, excluding the upper limit obtained for k(177.5 K): 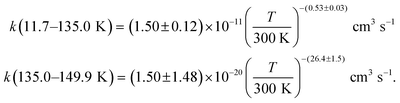 In addition, the rate coefficients estimated by the canonical competitive unified statistical (CCUS) theory show a similar behaviour to the experimental results, when evaluated within the high-pressure limit. This is consistent with the experimentally observed independence of k(T) with total gas density at selected temperatures. Astrochemical networks, such as the KIDA database or UMIST, do not include the CH3CN + OH reaction as a potential depletion process for acetonitrile in the ISM because the current studies predict very low rate coefficients at IS temperatures. According to the model (T = 10 K), the impact of the titled reaction on the abundances of CH3CN appears to be negligible in dark molecular clouds of the ISM (∼1% of the total depletion reactions included in UMIST network). With respect to the potential formation of the CH2CN radical in those environments, even in the most favourable scenario, where this radical could be formed in a 100% yield from the CH3CN + OH reaction, this route would only contribute around 2% to the current assumed formation routes by the UMIST network.
In addition, the rate coefficients estimated by the canonical competitive unified statistical (CCUS) theory show a similar behaviour to the experimental results, when evaluated within the high-pressure limit. This is consistent with the experimentally observed independence of k(T) with total gas density at selected temperatures. Astrochemical networks, such as the KIDA database or UMIST, do not include the CH3CN + OH reaction as a potential depletion process for acetonitrile in the ISM because the current studies predict very low rate coefficients at IS temperatures. According to the model (T = 10 K), the impact of the titled reaction on the abundances of CH3CN appears to be negligible in dark molecular clouds of the ISM (∼1% of the total depletion reactions included in UMIST network). With respect to the potential formation of the CH2CN radical in those environments, even in the most favourable scenario, where this radical could be formed in a 100% yield from the CH3CN + OH reaction, this route would only contribute around 2% to the current assumed formation routes by the UMIST network.
1. Introduction
Acetonitrile, also known as methyl cyanide (CH3CN), is the simplest organic nitrile molecule. This N-bearing species is present in natural environments such as the Earth's atmosphere, solar system objects, interstellar matter, and even nearby galaxies. This prolate symmetric-top molecule is well-suited for millimetre-wave observations due to its large permanent dipole moment (∼4 Debye).1 Regarding the terrestrial atmosphere, CH3CN is a trace gas, essentially issued from biomass burning.2 Its lifetime in the troposphere is about 6 months with deposition in the ocean being the dominant removal process. Therefore, it can be transported to the stratosphere where it can stay for several decades.3 The reaction with the hydroxyl (OH) radical becomes the main sink.In the context of the search for the origin of life, a main concern in modern astrochemistry and astrobiology, CH3CN is of special interest for prebiotic evolution because of the main role played by C–N bonds in the formation of peptide structures, such as amino acids. Then, CH3CN has been searched and detected routinely in a large variety of extraterrestrial environments, becoming one of the most abundant complex organic molecules (COMs) ever seen in space. In the solar system, CH3CN has been frequently observed in comets,4 for instance in Kohoutek,5 Hale-Bopp,6,7 P/Halley8 or 67P/Churyumov–Gerasimenko.9 It has also been identified in one of Saturn's moons, Titan, either by ground-based observations10 or in situ measurements.11 In the interstellar medium (ISM), CH3CN is one of the few prebiotic molecules seen in all main phases of the lifetime cycle of stars from the early stages to the last remnants. Since its first detection towards SgrA and SgrB molecular clouds in 1971,12 it has been observed in diffuse and translucent clouds,13–15 dark clouds,16 photodissociation regions,17,18 circumstellar envelopes,19,20 hot cores,21,22 protostellar objects,23,24 protoplanetary disks25,26 or molecular outflows27,28 as well as in extragalactic sources.29,30 In addition, CH3CN is a good thermometer for interstellar gas31,32 and a useful tracer of shocks33,34 and kinematic structures.28 Its gas-phase formation routes have been very recently discussed by Giani et al.35 As it can be seen, CH3CN is a quite important molecule in the different surroundings of the ISM, including those where the ultra-low temperatures (10–100 K) prevail. For that reason, it is essential to simulate this cold environment in the laboratory to study the gas-phase reactivity of CH3CN towards the most abundant radicals in the ISM, like the OH radical which plays a significant role in many chemical processes.36–39 Nevertheless, although the CH3CN + OH reaction (reaction (1)) has been quite extensively studied both experimentally at T > 250 K40–48 and theoretically at T > 200 K,49–52 it has never been investigated at the ultralow temperatures of the ISM.
| CH3CN + OH → Products k(T) | (1) |
In summary, the experimental kinetic studies of reaction (1) were performed in a wide range of pressures (P = 1.2–760 Torr) and temperatures (T = 250–424 K) using various techniques (see Table 1). Both absolute40–45 and relative47,48 kinetic techniques were employed to determine the rate coefficient k(T) of reaction (1) at a temperature T. At room temperature, k(298 K) has been reported in single temperature experiments42,43,46,48 or as part of the temperature dependence study of reaction (1).40,41,44,45,47 Most of the studies are in agreement, except the ones by Harris et al.40 and Andersen et al.,48 the most recent experimental study, whose k(298 K) both differ by a factor of about 2 with previous measurements. As shown in Table 1, there are several studies on the pressure dependence of k(298 K).43–45 Kurylo and Knable44 observed a 10% increase of the rate coefficient in the range 20–50 Torr of either argon or SF6, while Zetzsch43 found, according to Hynes and Wine,45 an increase of k(298 K) by a factor of 2.5 in the pressure range 5–100 Torr of argon. However, k(298 K) reported by Poulet et al.41 at 1.2 Torr of He is in agreement with high-pressure results. This was confirmed later by Hynes and Wine,45 who essentially found no pressure dependence of k(298 K) between 30 and 700 Torr, neither in N2 nor in He.
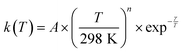
| P/Torr | Buffer gas | T/K | Methoda | k(298 K)/10−14 cm3 s−1 | A/10−13 cm3 s−1 | n | γ/K | Products | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Flash photolysis resonance fluorescence (FP-RF); discharge flow coupled to electron paramagnetic resonance (DF-EPR); pulsed laser photolysis-laser-induced fluorescence (PLP-LIF); Fourier transform infrared (FTIR). b From Hynes and Wine45 at about 100 Torr. c Average rate coefficients using different reference compounds. d Indirectly deduced from HC(O)CN quantification. | |||||||||
| 50 | Ar | 297–424 | FP-RF | 4.94 ± 0.6 | 5.86 | 0 | 756 ± 126 | H-Abst deduced | Harris et al.40 |
| 7 | Ar | 295 | FP-RF | 2.4 ± 0.3 | H-Abst assumed | Fritz et al.42 | |||
| 5–100 | Ar | 298 | FP-RF | 1.9 ± 0.2b | — | Zetzsch43 | |||
| 1.2 | He | 295 | DF-EPR | 2.1 ± 0.3 | H-Abst deduced | Poulet et al.41 | |||
| 393 | |||||||||
| 20; 50 | Ar | 250–363 | FP-RF | 1.94 ± 0.37 | 6.28 | 0 | 1030 | H-Abst deduced | Kurylo and Knable44 |
| SF6 | |||||||||
| 50–700 N2 | N2 | 256–388 | PLP-LIF | 2.48 ± 0.38 | 11 | 0 | 1130 ± 90 | ∼50% H-Abst | Hynes and Wine45 |
| 30–600 He | N2/O2 | ∼50% OH Ad. | |||||||
| (298 K) | He | ||||||||
| 700 | Air | 296 | Smog chamber FTIR | ∼50% H-Abst.d | Tyndall et al.46 | ||||
| ∼50% OH Ad. | |||||||||
| 760 | Ar | 306–393 | FP-FTIR | 1.82 | 18.5 | 0 | 1377 ± 62 | H-Abst deduced | DeMore47 |
| 700 | Air | 296 | Smog chamber FTIR | 4.07 ± 1.21c | H-Abst assumed | Andersen et al.48 | |||
Concerning the temperature dependence of k(T), a positive activation energy has been reported between 250 and 424 K, i.e., k(T) decreases when temperature decreases. The Arrhenius parameters reported by Harris et al.,40 derived from kinetic data obtained at temperatures above room temperature, were slightly lower than those obtained by Kurylo and Knable,44 Hynes and Wine45 and DeMore et al.,47 whose temperature dependences were essentially identical. Harris et al.40 and Kurylo and Knable44 interpreted the observed normal Arrhenius behaviour as a prevalence of the H-abstraction from the methyl group of acetonitrile (channel (1a)):
| CH3CN + OH → CH2CN + H2O | (1a) |
| CH3CN + OH → CH3C(OH)N | (1b) |
| → CH3CN(OH) | (1c) |
From a theoretical point of view, the potential energy surfaces (PES) of various routes from reactant to products49–52 were investigated by diverse methods (see Table 2), and from the obtained PES the temperature dependence of k(T)51–53 was calculated using different variants of the general transition state theory (TST). Li and Wang53 calculated the rate coefficient for the reaction pathway (1a), k1a(T), in the temperature range 250–2500 K using the canonical variational TST (CVT) with a small curvature tunnelling (SCT) correction. The calculated k(298 K) was found to agree with several experiments.41,44,45 As mentioned earlier, the contribution of the OH-addition channels to k(T) was not negligible. Thus, the OH-addition channels were theoretically investigated by Galano,50 concluding that reaction (1c) was endothermic while reaction paths (1a) and (1b) have similar efficiency, based on close Gibbs free energy barriers. No rate coefficients were calculated, however. Additional reaction pathways were explored by Tian et al.51 concluding that reaction channel (1a) was the dominant one whereas the two OH-addition channels were not considered as terminal in the reaction pathways. The rate coefficient k1a(T) was calculated using TST with the Wigner correction to take tunnelling into account. At room temperature their calculation agreed well with the measurements from Harris et al.40 and Andersen et al.48 More recently, Alihosseini et al.52 found 12 viable routes along the PES of the OH + CH3CN reaction. Only the rate coefficient k1a(T) was calculated using TST, at atmospheric pressure over the temperature range of 200–2500 K. In this temperature range, a non-Arrhenius behaviour of k1a(T) was predicted, however the authors fitted the data to a conventional Arrhenius equation which gives a very poor representation of individual k1a(T) (see Fig. 5 in Alihosseini et al.52). Furthermore, k1a(298 K) is about two orders of magnitude higher (2.17 × 10−12 cm3 s−1) than previous investigations either experimental or theoretical.
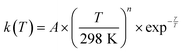
| Method | T (K) | k(298 K)/10−14 cm3 s−1 | A /10−13 cm3 s−1 | n | γ (K) | Products | Ref. |
|---|---|---|---|---|---|---|---|
| a Calculated at 298 K (not from fit). b Obtained in the present work from the data presented in Table 5 from Li and Wang.53 | |||||||
| PMP4/6-311_G(2df,2pd)//MP2/6-311G(d,p) | 250–2500 | 2.38a | 1.4b | 2.89b | 620b | H-Abst only considered | Li and Wang53 |
| QCISD(T)/6-311_G(2df,2pd)//MP2/6-311G(d,p) + CVTST/SCT | 250–2500 | 2.02a | 1.3b | 2.91b | 648b | H-Abst only considered | Li and Wang53 |
| BHandHLYP/6-311++G(2d,2p) + CCSD(T)/6-311++G(2d,2p) | — | — | — | — | — | ∼50% H-Abst | Galano50 |
| ∼50% OH Ad. | |||||||
| B3LYP/CBSB7 | 250–3000 | 5.14 | 7.05 | 3.045 | −780 | 7 routes obtained | Tian et al.51 |
| TST + Wigner correction | H-Abst mainly | ||||||
| CBS-QB3 | 250–430 | 4.79 | 15.6 | 2.36 | −1038 | 7 routes obtained | Tian et al.51 |
| TST + Wigner correction | H-Abst mainly | ||||||
| B3LYP + G3B3 or CCSD(T)/6-311++G(3df,3pd) + TST | 200–2500 | 217 | 489 | 0 | −1277 | 12 routes obtained but H-Abst only considered | Alihosseini et al.52 |
Therefore, there are still matters of controversy concerning the rate coefficient k(T), the branching ratios, and the influence of pressure in the obtained measures. In addition, the extension of experimental and theoretical studies to temperatures lower than 200 K is certainly desirable, especially for the modelling of the chemistry of interstellar objects in which CH3CN and OH have been observed. Astrochemical networks, such as the KIDA database or UMIST, do not include reaction (1) as a potential depletion process for acetonitrile in the ISM. The present investigation aims at studying the gas-phase kinetics of the CH3CN + OH reaction between 11.7 K and 177.5 K from an experimental point of view using a pulsed CRESU (French acronym for Reaction Kinetics in a Uniform Supersonic Flow) reactor and from a theoretical point of view using high level quantum chemistry tools such as the density functional theory (DFT) and the competitive canonical unified theory (CCUS) in the temperature range of 10–400 K. The results reported here were used to model the IS abundance of CH3CN using a pure gas-phase astrochemical model and the implications of our results in the chemistry of IS molecular clouds are discussed.
2. Experimental part
The kinetic study of reaction (1) has been performed at ultralow temperatures (11.7–177.5 K) achieved by a pulsed CRESU apparatus, where the gas is not continuously passing through the Laval nozzle. A detailed description of the technique and the set-up can be found elsewhere.54–61 Hence, a schematic diagram with the experimental novelties of the present work is provided in Scheme 1 and only a brief description is given below.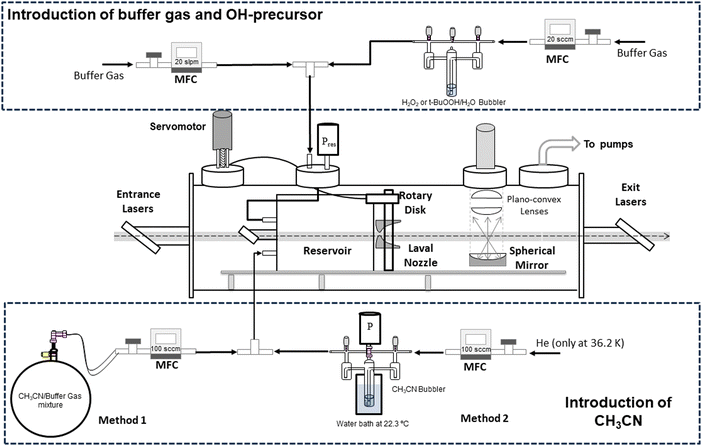 | ||
| Scheme 1 Experimental set-up scheme including both methods to introduce CH3CN into the reservoir. MFC: mass flow controller. | ||
Seven different Laval nozzles and a total of 15 operational conditions were used in this work to fill up the temperature range. The isentropic expansion from a relative high-pressure reservoir (Pres = 9.97–366.48 mbar) to a low-pressure chamber (0.12–6.00 mbar) through the nozzle results in a uniform supersonic cold jet ranging from 11.7 and 177.5 K. A rotary disk with one or two symmetrical apertures was employed to pulse the gas at 5 Hz for T = 11.7 K or 10 Hz for the rest of operational conditions, respectively.
The kinetic technique pulsed laser photolysis-laser-induced fluorescence (PLP-LIF) was also described previously.54,55,59,62–68 The production of OH radicals along the supersonic jet was achieved by PLP of gaseous H2O2 or tert-butyl hydroperoxide (t-BuOOH) at 248 nm, radiation generated by a KrF excimer laser (Coherent, model ExciStar XS 200). Both precursors were introduced in the reservoir by flowing a small portion of the buffer gas (He, N2, or Ar) through the bubbler containing the concentrated solution of the OH precursor (see Scheme 1). Gaseous CH3CN was introduced in the reservoir by flowing diluted mixtures in the buffer gas through a calibrated mass flow controller (method 1) or by bubbling liquid samples of CH3CN with a small portion of the buffer gas (method 2). More details of both methods are given in the ESI.† Once the OH radicals were generated in the electronic ground state, they were excited at ca. 282 nm, radiation achieved with a frequency-doubled dye laser (Lambda Physik, model Scanmate) pumped by the second harmonic of a Nd:YAG laser (Continuum, model Surelite III). Finally, the temporal evolution of OH radicals in the presence and absence of acetonitrile was monitored by LIF (ILIF) at ca. 310 nm, using a photomultiplier tube (Electron Tube, model 9813B) with a bandpass filter centred at 310 nm with a full width at half maximum of 10 nm (Andover Co., model 310FS10-25).
2.1. Kinetic analysis
The kinetic experiments were performed under pseudo-first order conditions, i.e., in large excess of acetonitrile with respect to the initial concentration of OH radicals ([CH3CN] ≫ [OH]0). In such a situation, after an increase due to rotational relaxation (see ESI† and already explained),54,57 the temporal profile of ILIF results in an exponential decay primarily caused by the reaction of OH with CH3CN, but also by the reaction with the OH-precursor (H2O2 or t-BuOOH) or diffusion out of the detection zone. Some examples of the temporal profile of ILIF recorded in the absence and presence of CH3CN at three selected temperatures are shown in Fig. S1 of ESI.† From the analysis of the ILIF decays, the pseudo-first order rate coefficient, k′ (or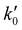 in the absence of CH3CN) was obtained. In these experimental conditions, k′ is proportional to [CH3CN] at a single temperature, according to the relationship given by eqn (E1):
in the absence of CH3CN) was obtained. In these experimental conditions, k′ is proportional to [CH3CN] at a single temperature, according to the relationship given by eqn (E1):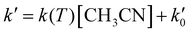 | (E1) |
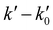 vs. [CH3CN] plots. Reliable knowledge of [CH3CN] in the jet is essential to obtain accurate k(T) at each temperature. These concentrations were determined from flow rate or vapor pressure measurements (see ESI†), according to the way CH3CN is introduced in the reservoir. As shown in Fig. S2 (ESI†), [CH3CN] determined by both methods yield k(T) at 36.2 K in excellent agreement.
vs. [CH3CN] plots. Reliable knowledge of [CH3CN] in the jet is essential to obtain accurate k(T) at each temperature. These concentrations were determined from flow rate or vapor pressure measurements (see ESI†), according to the way CH3CN is introduced in the reservoir. As shown in Fig. S2 (ESI†), [CH3CN] determined by both methods yield k(T) at 36.2 K in excellent agreement.
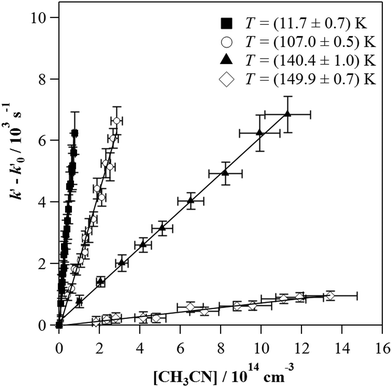
This linear relationship is not accomplished at high [CH3CN] and the bimolecular plots display a curvature. The observed downward curvature is associated with the dimerization process of CH3CN, as previously reported for other OH-reactions with COMs (Fig. S2, ESI†).54–60,62,63,68–70 As can be seen in Fig. S3 (ESI†), the (CH3CN)2 dimer formation is especially enhanced at low temperatures. Then, the onset of such a dimerization, i.e., [CH3CN] from which the bimolecular plots are not linear, increases with temperature for a total gas density of the same order of magnitude 1017 cm−3 (e.g. [CH3CN] = 1.30 × 1014 cm−3 at 21.7 K, 1.96 × 1014 cm−3 at 76.0 K and 5.30 × 1014 cm−3 at 135.0 K). At T > 140 K, 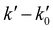 vs. [CH3CN] plots are linear in the entire explored [CH3CN] range, even reaching 1% of the total gas density. Acetonitrile concentration was not increased beyond 1% of the total gas density since it may affect the uniformity of the flow and the jet temperature. In Table 3, [CH3CN] range within which eqn (E1) is valid are listed for every temperature and gas density. Four examples of the
vs. [CH3CN] plots are linear in the entire explored [CH3CN] range, even reaching 1% of the total gas density. Acetonitrile concentration was not increased beyond 1% of the total gas density since it may affect the uniformity of the flow and the jet temperature. In Table 3, [CH3CN] range within which eqn (E1) is valid are listed for every temperature and gas density. Four examples of the 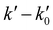 vs. [CH3CN] plots are shown in Fig. 1 at selected temperatures. As shown, the slope of these plots increases when the temperature decreases, implying that the OH-reactivity of CH3CN is enhanced at lower temperatures.
vs. [CH3CN] plots are shown in Fig. 1 at selected temperatures. As shown, the slope of these plots increases when the temperature decreases, implying that the OH-reactivity of CH3CN is enhanced at lower temperatures.
| ≈T/K | T/K | n/1016 cm−3 | [CH3CN]/1013 cm−3 | k(T)/10−11 cm3 s−1 |
|---|---|---|---|---|
| a Uncertainties in k(T) account for statistical (±2σ) and 10% systematic errors. In n the indicated errors result from the aerodynamic fluctuations in the flow (±1σ). b H2O2 as OH-precursor. c t-BuOOH as OH-precursor. d Upper limit calculated as Douglas et al.85 | ||||
| 12 | 11.7 ± 0.7 | 6.88 ± 0.62 | 0.76–7.81 | 8.18 ± 0.85b |
| 1.35–6.15 | 8.45 ± 0.92c | |||
| 8.25 ± 0.89 | ||||
| 22 | 21.1 ± 0.6 | 3.37 ± 0.15 | 0.87–8.93 | 7.03 ± 0.86b |
| 0.87–8.89 | 5.89 ± 0.62c | |||
| 6.05 ± 1.28 | ||||
| 21.7 ± 1.4 | 16.65 ± 1.61 | 1.63–12.7 | 6.17 ± 0.71 | |
| 36 | 36.2 ± 1.2 | 17.73 ± 0.86 | 2.00–14.5 | 5.27 ± 0.57b |
| 1.37–15.0 | 4.91 ± 0.57c | |||
| 5.14 ± 0.71 | ||||
| 50 | 50.5 ± 1.6 | 1.50 ± 0.12 | 1.94–12.5 | 4.04 ± 0.50b |
| 1.19–8.82 | 4.29 ± 0.46c | |||
| 4.23 ± 0.52 | ||||
| 49.9 ± 1.8 | 3.67 ± 0.32 | 1.12–9.99 | 4.33 ± 0.52b | |
| 1.12–10.1 | 3.91 ± 0.57c | |||
| 4.18 ± 0.71 | ||||
| 52.1 ± 0.5 | 19.52 ± 0.28 | 0.83–11.7 | 4.07 ± 0.42b | |
| 0.92–8.08 | 4.00 ± 0.61c | |||
| 4.07 ± 0.41 | ||||
| 76 | 76.0 ± 0.8 | 14.96 ± 0.34 | 2.19–15.8 | 2.70 ± 0.37 |
| 106 | 106.0 ± 0.6 | 14.02 ± 0.11 | 1.26–8.58 | 2.52 ± 0.38b |
| 0.79–6.52 | 2.70 ± 0.35c | |||
| 2.63 ± 0.36 | ||||
| 107.0 ± 0.5 | 4.90 ± 0.06 | 4.11–30.1 | 2.20 ± 0.23b | |
| 4.55–14.8 | 2.28 ± 0.33c | |||
| 2.21 ± 0.23 | ||||
| 135 | 135.0 ± 0.8 | 29.45 ± 0.45 | 6.19–45.4 | 1.82 ± 0.20 |
| 136.1 ± 0.8 | 24.92 ± 0.35 | 8.47–63.9 | 1.40 ± 0.17 | |
| 140 | 140.4 ± 1.0 | 21.68 ± 0.40 | 10.1–113 | 0.60 ± 0.06 |
| 143.3 ± 0.6 | 17.02 ± 0.17 | 13.4–166 | 0.32 ± 0.04 | |
| 150 | 149.9 ± 0.7 | 10.69 ± 0.12 | 18.1–134 | 0.07 ± 0.01 |
| 177 | 177.5 ± 1.2 | 6.71 ± 0.11 | 22.8–67.1 | <0.02 |
2.2. Chemicals
Buffer gases (He, N2, and Ar), all of them with 99.999% purity (Nippon Gases Europe), were used as supplied. Liquid acetonitrile (≥99.9%, Sigma-Aldrich) was degassed by repeated free-pump-thaw cycles prior to use for the experiments in which the storage bulb was used. The aqueous solution of hydrogen peroxide (50% w/w, Sharlab) was preconcentrated as previously reported,66 whereas the t-BuOOH solution (70%, Sigma-Aldrich) was used directly without pre-concentration, because its vapour pressure is higher than that of H2O. When no use, both precursor bubblers were stored in a refrigerator at 2 °C to prevent from thermal decomposition.3. Computational methodology
All geometry optimizations were performed by the M08-HX Density Functional Theory (DFT) method71 with the MG3S basis set,72 as for the recently studied OH + CH3NH2 reaction.68 All zero-point energies (ZPEs) were scaled by the recommended factor of 0.973.73 The two computed reactions are the hydrogen abstraction from the methyl group by the OH radical (reaction (1a)) and the OH-addition to the C of cyano group (reaction (1b)). It is worth noting that reaction (1a) is part of a much larger reaction network recently studied by some of us.74 The OH-addition to the nitrogen atom, as well as other 4 additional channels previously investigated by Tian et al.51 have very high barriers and are not competitive with reactions (1a) and (1b).Additional geometry optimizations were also carried out at ωB97X-D75 with the def2-TZVP basis set.76 All ZPEs were scaled by the recommended factor of 0.975.73 The geometries obtained by both electronic structure levels, that is, M08-HX/MG3S and ωB97X-D/def-2TZVP, were employed as input for the CCSD(T)-F12/cc-pVTZ-F12 single-point calculations77,78 to compare the result of both functionals on an accurate and common ground.
The thermal rate coefficients were evaluated employing the competitive canonical unified theory (CCUS). In this formalism, the rate coefficient for each reaction channel, kCCUSi (where i = 1a or 1b), is given by eqn (E2),79
| kCCUSi = kCCUSαi | (E2) |
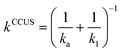 | (E3) |
The rate coefficient for the association reaction is given by the following expression:80
| ka = Cμ−1/2(dOHdCH3CN)2/3T−1/6 | (E4) |
The rate coefficients ki were calculated employing canonical variational transition state theory with small-curvature tunnelling corrections (CVT/SCT),81 according to the following equation:
| kCVT/SCTi = ΓCVTiκCVT/SCTikTSTi | (E5) |
The CCUS prescription allows calculating the thermal rate coefficients in the low-pressure (LPL) and high-pressure (HPL) limits. The only difference between the two regimes is that in the LPL the lowest energy for tunnelling is the energy of reactants plus its ZPE, whereas in the HPL the lowest energy that allows tunnelling is the energy of the pre-reactive complex plus its ZPE. For the latter, it is assumed that the collisions with other molecules will stabilize the complex, a situation that cannot occur at very low pressures. Therefore, the only factor affected by pressure in eqn (E5) is the tunnelling transmission coefficient (see Section 4.2).
4. Results and discussion
4.1. Experimental kinetic study
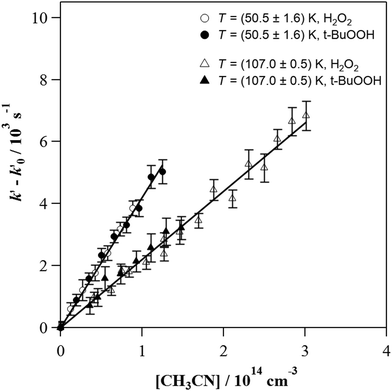
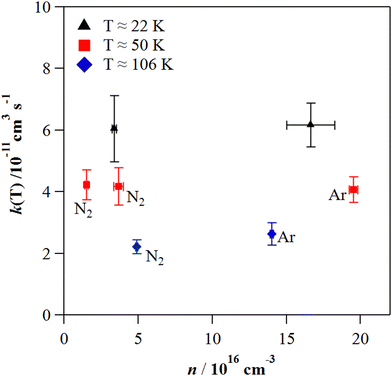
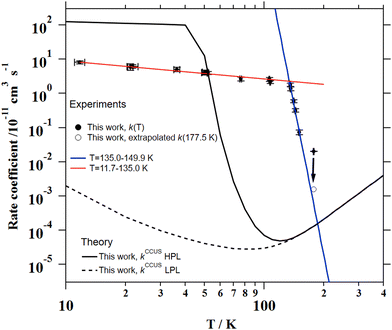
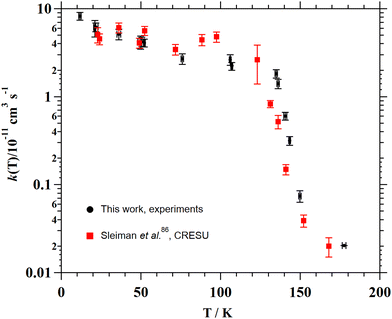
The individual rate coefficients k(T) determined in this work are listed in Table 3 as a function of the OH-precursor (H2O2 or t-BuOOH), gas density (n), and temperature. As it can be seen in the examples depicted in Fig. 2, no influence of the OH-precursor on k(T) was observed. Thus, in Table 3 the weighted average of k(T) obtained using both precursors is given in bold.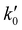 was observed in the timescale of the experiment and within the [CH3CN] range used. This upper limit of k was estimated as explained by Douglas et al.,85i.e., as twice the uncertainty in k′ at the maximum CH3CN concentration, [CH3CN]max, used in the experiment, divided by that [CH3CN]max. In Fig. 4, the log–log plot of average k(T) from Table 3versus T is presented between 11.7 K and 177.5 K. Clearly, two distinct regions in the plot were observed. Between 135.0 K and 177.5 K, an abrupt decrease of k(T) of a factor of around 90 was observed. In this steep region, the expression of k(T) provided by eqn (E6), where the estimated k(177.5 K) is excluded, is presented as the blue line in Fig. 4.
was observed in the timescale of the experiment and within the [CH3CN] range used. This upper limit of k was estimated as explained by Douglas et al.,85i.e., as twice the uncertainty in k′ at the maximum CH3CN concentration, [CH3CN]max, used in the experiment, divided by that [CH3CN]max. In Fig. 4, the log–log plot of average k(T) from Table 3versus T is presented between 11.7 K and 177.5 K. Clearly, two distinct regions in the plot were observed. Between 135.0 K and 177.5 K, an abrupt decrease of k(T) of a factor of around 90 was observed. In this steep region, the expression of k(T) provided by eqn (E6), where the estimated k(177.5 K) is excluded, is presented as the blue line in Fig. 4.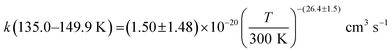 | (E6) |
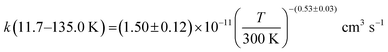 | (E7) |
4.2. Computational study
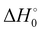 ) with respect to reactants of the complex (C), transition states (TS), and products (P) for reactions (1a) and (1b). Optimizations at the M08-HX and ωB97X-D levels and single-point calculations at the CCSD(T)-F12 level. Energies in kcal mol−1
) with respect to reactants of the complex (C), transition states (TS), and products (P) for reactions (1a) and (1b). Optimizations at the M08-HX and ωB97X-D levels and single-point calculations at the CCSD(T)-F12 level. Energies in kcal mol−1
| ΔEM08/ωB97 | ΔECC(M08/ωB97) | |||
|---|---|---|---|---|
| Reactants | 0.00/0.00 | 0.00/0.00 | 0.00/0.00 | 0.00/0.00 |
| C1 | −5.20/−4.04 | −3.88/−4.03 | −4.24/−3.30 | −2.90/−3.09 |
| TS1a | 5.67/3.12 | 5.71/5.77 | 4.09/1.42 | 4.13/4.05 |
| P1a | −21.21/20.27 | −21.36/−21.40 | −21.91/−21.10 | −22.06/−22.23 |
| TS1b | 2.18/−0.03 | 1.20/1.12 | 3.89/1.69 | 2.91/2.82 |
| P1b | −28.98/−32.31 | −28.46/−28.42 | −24.90/−27.90 | −24.38/−24.01 |
The difference between the two transition states is reduced to 1.22 and 1.23 kcal mol−1 for CCSD(T)-F12/M08-HX and CCSD(T)-F12/ωB97X-D, respectively. These values are in good agreement with the results obtained by Galano,50 where TS1a is above TS1b by 1.00 kcal mol−1. Of the two DFT methods reported here, M08-HX is the most similar to the coupled-cluster calculations. Additionally, it does not revert the stability of the two transition states, as is the case of the coupled-cluster calculations. Therefore, hereafter all thermal rate coefficient calculations will involve M08-HX calculations of the MEP and additional single-point energy corrections for reaction (1b), to correct the difference between this DFT method and the coupled-cluster calculations. Fig. 5 plots a schematic reaction network of the CCSD(T)-F12/M08-HX ZPE-corrected level regarding reactants, which is the basic scheme for further dynamics calculations.
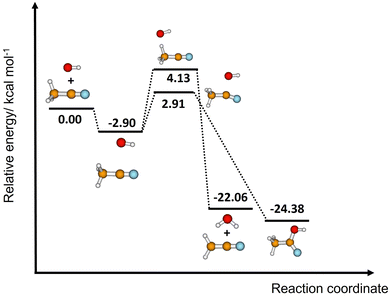 | ||
| Fig. 5 Schematic ZPE-corrected energy diagram at the CCSD(T)-F12/M08-HX level of theory for reactions (1a) and (1b). See the last column of Table 4. | ||
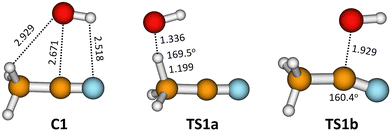
The pre-reactive complex (C1) and the transition states that correspond to reactions (1a) and (1b) obtained at M08-HX/MG3S are depicted in Fig. 6. It can be observed that the C1 complex can easily react through both transition states.
| T (K) | Γ CVT1a | κ CVT/SCT1a,LPL | κ CVT/SCT1a,HPL | k TST1a | Γ CVT1b | κ CVT/SCT1b,LPL | κ CVT/SCT1b,HPL | k TST1b |
|---|---|---|---|---|---|---|---|---|
| 50 | 1.22 × 10−5 | 5.90 × 1012 | 1.60 × 1014 | 1.10 × 10−29 | 0.740 | 4.73 × 108 | 1.67 × 1014 | 1.18 × 10−24 |
| 100 | 3.83 × 10−3 | 1.13 × 104 | 1.48 × 104 | 4.32 × 10−21 | 0.838 | 4.13 × 102 | 9.64 × 102 | 8.70 × 10−19 |
| 150 | 2.63 × 10−2 | 56.5 | 57.8 | 3.31 × 10−18 | 0.854 | 11.4 | 11.4 | 7.33 × 10−17 |
| 200 | 6.93 × 10−2 | 8.87 | 8.89 | 9.91 × 10−17 | 0.852 | 3.58 | 3.58 | 6.93 × 10−16 |
| 300 | 0.181 | 2.56 | 2.56 | 3.50 × 10−15 | 0.838 | 1.71 | 1.71 | 7.25 × 10−15 |
Tunnelling effects are more important for the H-abstraction than for the OH-addition reaction. This is expected as the hydrogen atom is a light particle, whereas the OH-addition involves heavy-atom tunnelling.88 However, variational effects are also more relevant in the H-abstraction reaction, so the result of multiplying the variational coefficient by the tunnelling coefficient favours the addition reaction. Moreover, the potential barrier is higher for the H-abstraction reaction and therefore the OH-addition reaction dominates between 10 and 300 K. In fact, it contributes 100% at 10 K and 87% at 300 K.
The variational effect in the H-abstraction shows the magnitude of recrossing in the reaction. In CVT/SCT, this effect is calculated by finding the maximum of the Gibbs free energy along the reaction coordinate s of the MEP (negative in the reactant site, positive in the products site and zero at the transition state), which for the abstraction reaction is located at s = −0.267 Bohr at 0 K and at s = −0.250 Bohr at 400 K. Variational effects are due to the increasing value of the ZPE as we head toward reactants; it is 31.51 kcal mol−1 at the transition state and 33.17 kcal mol−1 at s = −0.250 Bohr. This ZPE variation displaces the maximum of the free energy towards the reactants site.
For the evaluation of the normal-mode frequencies along the MEP, we have employed redundant internal coordinates, because it is well-known that an accurate evaluation of the ZPE along the reaction path requires the use of internal coordinates. They provide a more physical description of the normal-mode frequencies than the Cartesian coordinates (notice that the calculated normal mode frequencies in non-stationary points depend on the system of coordinates).89 Theoretical methods based on conventional TST that incorporate tunnelling effects (for instance, through the Eckart barrier), completely ignore the recrossing, which in this case has the effect of reversing the contribution of the two channels to the branching ratios.
We have also included torsional anharmonicity in the transition state structures applying the same protocol as for the OH + methylamine system.68 In the case of TS1a, the torsional anharmonicity contains the rotation of the OH about the methyl group (with a harmonic frequency ω = 144.2 cm−1). For TS1b, there are two rotors, the internal rotation of the OH (with ω = 221.2 cm−1) and methyl (with ω = 140.8 cm−1) groups. For the two transition states, the treatment of these motions, as one-dimensional hindered rotors, instead of harmonic oscillators has a modest effect in the rate coefficients. The ratio between the anharmonic and harmonic partition functions is always smaller than 2 between 50 and 400 K (see the ESI†).
The total CCUS rate coefficients are plotted in Fig. 4 and summarized in Table 6 for selected temperatures. At the LPL, ka ≫ k1 and the rate-determining reaction is always k1, so this rate coefficient and kCCUS coincide. Above T = 150 K the thermal rate coefficients evaluated at the two pressure limits coincide, this is because at this temperature and above the molecules populate the same levels with independence of the depth of the lowest energy level. In other words, the pre-reactive complex is irrelevant for the course of the reaction. However, below T = 150 K the HPL rate coefficients start to increase fast and at T ∼ 40 K kHPL becomes larger than the association rate coefficient, being ka the rate-determining reaction. Although the agreement between theory and experiment obtained in this work is not perfect, the HPL results capture the wild variation of the rate coefficients with an astonishing increase of about four orders of magnitude in an interval of less than 100 K.
| T (K) | k CCUS1a | k CCUS1b | k CCUS | k CCUS1a | k CCUS1b | k CCUS |
|---|---|---|---|---|---|---|
| LPL | HPL | |||||
| 10 | 1.083 × 10−37 | 2.003 × 10−14 | 2.003 × 10−14 | 1.123 × 10−16 | 1.275 × 10−9 | 1.275 × 10−9 |
| 50 | 7.89 × 10−22 | 4.102 × 10−16 | 4.102 × 10−16 | 2.241 × 10−20 | 1.266 × 10−10 | 1.266 × 10−10 |
| 100 | 1.867 × 10−19 | 3.013 × 10−16 | 3.015 × 10−16 | 2.440 × 10−19 | 7.032 × 10−16 | 7.034 × 10−16 |
| 150 | 4.192 × 10−18 | 7.155 × 10−16 | 7.204 × 10−16 | 5.024 × 10−18 | 7.161 × 10−16 | 7.211 × 10−16 |
| 200 | 6.063 × 10−17 | 2.068 × 10−15 | 2.129 × 10−15 | 6.079 × 10−17 | 2.068 × 10−15 | 2.129 × 10−15 |
| 300 | 1.600 × 10−15 | 1.030 × 10−14 | 1.190 × 10−14 | 1.601 × 10−15 | 1.030 × 10−14 | 1.190 × 10−14 |
| 400 | 1.152 × 10−14 | 2.871 × 10−14 | 4.022 × 10−14 | 1.152 × 10−14 | 2.871 × 10−14 | 4.022 × 10−14 |
4.3. Comparison with previous studies
For the C2H + CH3CN reaction (T = 165–360 K),94,95 the combination of the kinetic data from Nizamov and Leone94 and Hoobler and Leone95 yields the following Arrhenius expression (1.80 ± 0.35) × 10−11 exp(−(766 ± 38)/T) cm3 s−1. An increase of almost one order of magnitude between 165 K and 296 K was reported by Nizamov and Leone.94 However, the complete picture of the temperature dependence of the rate coefficient for the C2H + CH3CN reaction cannot be seen at very low temperatures since no kinetic measurements were performed below 165 K.
For the C(3P) + CH3CN reaction (T = 50–296 K), even though it is very fast, Hickson et al.96 reported no temperature dependence of k(T) in that temperature range. The same group also investigated the O(1D) + CH3CN reaction at 75, 127 and 296 K,97 obtaining rate coefficients close to the collision limit ((2.4–3.7) × 10−10 cm3 s−1) with a tendency to increase below 127 K. Nonetheless, the authors recommend using a temperature independent value of (2.85 ± 0.70) × 10−10 cm3 s−1 in the explored temperature range.
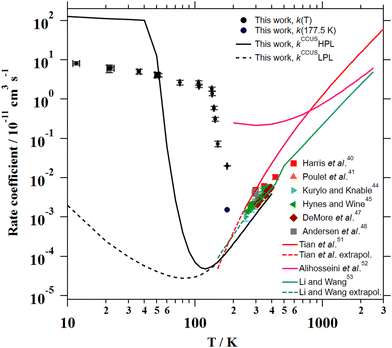 | ||
| Fig. 8 Experimental and theoretical temperature dependencies of the rate coefficient for the CH3CN + OH reaction. | ||
As mentioned in the Introduction, several studies reported branching ratios for channels (1a) and (1b) at room temperature. More particularly, some evidence of the existence of the OH-addition route was pointed out as briefly discussed in the Introduction section and summarized in Tables 2 and 3.
Experimentally, Hynes and Wyne45 claimed that the OH-addition channel (1b) accounted for about 50% of the total reaction process. This is, however, an indirect conclusion based on the observation that, in their reactor, the OH temporal decay was smaller in the presence of molecular oxygen than in its absence. The authors analysed this finding by considering that OH regeneration was occurring in their experiment. This was also observed for the OH + CD3CN reaction in the presence of O2 and they deduced that the OH-addition channel was necessarily open because the other potential product (CD2CN radical) could obviously not release OH by reaction with O2. By simulating their various OH temporal decays they estimated that the two possible channels for reaction (1) have essentially similar rate coefficients. Later, Tyndall et al.46 investigated the title reaction in a smog chamber filled with synthetic air. Infrared observation of the terminal product HC(O)CN with a yield of (40 ± 20)% led them to conclude that their measurement was consistent with the conclusions brought by Hynes and Wine45 concerning the possible routes of reaction (1).
From a theoretical point of view, the OH-addition channel was only investigated by Galano50 who also studied the reaction mechanisms in the presence of O2. She found that, in atmospheric conditions, reaction (1) will eventually lead to the formation of HC(O)CN in agreement with the smog chamber experiment from Tyndall et al.46 Further, she demonstrated that molecular oxygen could attack the N of CH3C(OH)N – product from reaction (1b) – generating a hexagonal structure which will eventually release an OH radical agreeing thus with the suggestions of Hynes and Wine.45 Although Galano50 did not estimate the branching ratios for reactions (1a) and (1b), based on energetic considerations, she stated that reaction (1) should lead to the formation of both species CH2CN and CH3C(OH)N in similar proportions. In the present work, we computed that the OH-addition reaction contributes 87% at 300 K (see ESI†), a temperature for which no pressure dependence is predicted. At lower temperatures, i.e. below 150 K, the OH-addition channel becomes the only viable route.
4.4. Astrochemical modelling
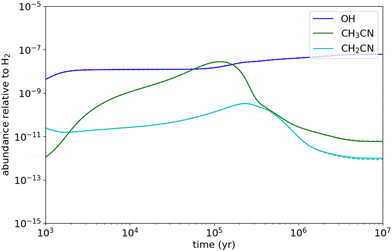
Since densities are very small in interstellar molecular clouds (typically 104–106 cm−3), chemical reactions which are pressure dependent can be of potential interest in their LPL regime only. In a recent study concerning the OH + CH3OH reaction,55,98 it has been shown that, at temperatures of typically 10–20 K, the total rate coefficients in the HPL and the LPL regimes were essentially similar. This is not the case for the present reaction according to our theoretical calculations which suggest that experimental measurements below 20 K are closer to the HPL than to the LPL. Hence, to evaluate the impact of the reaction presently studied on the chemical composition of cold dense clouds, where the gas kinetic temperature is as low as 10 K, we carried out chemical modelling calculations assuming the theoretical kCCUS at the LPL (2 × 10−14 cm3 s−1 at 10 K) and that the main channel is the formation of CH3C(OH)N. We adopted typical parameters of cold dense clouds, i.e. a H2 volume density of 2 × 104 cm−3, a visual extinction of 30 mag, and a cosmic-ray ionization rate of 1.3 × 10−17 s−1. We adopted the elemental abundances commonly known as “low-metal” values, in which the abundances of metals, silicon, and sulphur are reduced with respect to the values observed in diffuse clouds.99 We used the chemical network rate.2012 from the UMIST database.100 The results of the model show that reaction (1b) does not have any effect on the abundance of CH3CN. According to the UMIST network, the main reactions of destruction of CH3CN are those with cations, such as H3O+, HCO+, and C+. The reaction with OH has a marginal (1%) contribution to the destruction of CH3CN. Indeed, the reactions with H3O+ and HCO+ are not fully effective in destroying CH3CN because they produce the protonated form of CH3CN, which partially gives back CH3CN when recombining dissociatively with electrons. The reaction with C+ however is an efficient process of removal of CH3CN. The rate coefficient of this reaction has been measured to be 5.6 × 10−9 cm3 s−1 at 300 K,101 and it is likely even higher at 10 K, following the usual behaviour of ion-polar reactions.102Even though if we assume the total rate coefficient measured at 11.7 K as a higher limit of the reactivity of CH3CN, the impact of reaction (1) on the abundance of CH3CN is very little (see Fig. 9). Furthermore, assuming as well that the CH2CN radical would be the sole product, the CH3CN + OH reaction would contribute to its gas-phase formation with around 2%. According to the UMIST network, the main reaction forming CH2CN is the N + C2H3 reaction. Nevertheless, the N + C2H3 reaction has been measured to be relatively fast, 7.7 × 10−11 cm3 s−1, at 298 K, and the main product channel has been inferred to be CH2CN + H.103 It is however unknown whether this rate coefficient and product distribution holds also at the very low temperatures of cold dense clouds.
It is desirable to have experimental evidence of the formation of CH2CN or CH3C(OH)CN radicals from the CH3CN + OH reaction at very low temperatures.
5. Conclusions
The present experimental results show that acetonitrile (CH3CN) reacts very fast with OH radicals in the gas phase at very low temperatures (∼10–100 K). Since the temperature behaviour of the rate coefficient varies in the explored experimental range, we provide two analytical expressions using a modified Arrhenius expression, (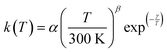 , with α = 1.50 × 10−11 cm3 s−1; β = −0.53 and γ = 0 K) between 11.7 K and 135 K and α = 1.5 × 10−20 cm3 s−1; β = −26.4 and γ = 0 K between 135 K and 149.9 K, a temperature within which the dependence of the rate coefficient k(T) is extremely fast, changing more than one order of magnitude in only 15 K.
, with α = 1.50 × 10−11 cm3 s−1; β = −0.53 and γ = 0 K) between 11.7 K and 135 K and α = 1.5 × 10−20 cm3 s−1; β = −26.4 and γ = 0 K between 135 K and 149.9 K, a temperature within which the dependence of the rate coefficient k(T) is extremely fast, changing more than one order of magnitude in only 15 K.
The computational results indicate that below 150 K, the reaction product is CH3C(OH)N and not CH2CN. Moreover, the experimental rate coefficients have been found to be pressure independent at 22 K, 50 K and 106 K and appear to be much closer to the calculated high-pressure limit than to the low-pressure regime. Above 150 K, the contribution of the H-abstraction channel begins to increase, reaching 13% at 300 K and 29% at 400 K. It is worthwhile to point out that very efficient heavy-atom tunnelling has been highlighted by the present quantum calculations which is quite unusual.
According to the model (T = 10 K), the impact of the titled reaction on the abundances of CH3CN appears to be negligible in dark molecular clouds of the ISM (∼1% of the total depletion reactions included in UMIST network). Respect to the potential formation of the CH2CN radical in those environments, even in the most favourable scenario, where this radical could be formed in a 100% yield from the CH3CN + OH reaction, this route would only contribute around 2% to the current assumed formation routes by UMIST network.
Author contributions
DG and AC performed the experiments and data analysis and wrote the original draft of the paper; EMN and AFR carried out the theoretical calculations; MA and JC run the astrochemical model; BB, AC, and EJ designed and supervised the experiments; EJ got funds for carrying out the present experimental research; all authors contributed to the critical discussion and review of the draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Spanish Ministry of Science and Innovation (MICINN) through CHEMLIFE project (grant PID2020-113936GB-I00), by the regional government of Castilla-La Mancha and the European Regional Development Fund (ERDF) through CINEMOL project (grant SBPLY/19/180501/000052), and by the University of Castilla-La Mancha – UCLM (2022-GRIN-34143) also co-funded by ERDF. This work was partially supported by the Consellería de Cultura, Educación e Ordenación Universitaria (Centro singular de investigación de Galicia acreditación 2019-2022, ED431G 2019/03 and Grupo de referencia competitiva ED431C 2021/40) and ERDF, and the Spanish MICINN through the Grant #PID2019-107307RB-I00. AFR and EMN thank the Centro de Supercomputación de Galicia (CESGA) for the use of their computational facilities. D. González also acknowledges UCLM (Plan Propio de Investigación) for funding his contract during the performance of this investigation. AC is grateful to the University of Rennes for supporting his stay at UCLM under its International Action programme.References
- J. Gadhi, A. Lahrouni, J. Legrand and J. Demaison, J. Chim. Phys., 1995, 92, 1984–1992 CrossRef CAS.
- Q. Li, D. J. Jacob, R. M. Yantosca, C. L. Heald, H. B. Singh, M. Koike, Y. Zhao, G. W. Sachse and D. G. Streets, J. Geophys. Res. Atmos., 2003, 108(D21), 8827 CrossRef.
- J. J. Harrison and P. F. Bernath, Atmos. Chem. Phys., 2013, 13, 7405–7413 CrossRef.
- D. Bockelée-Morvan and N. Biver, Philos. Trans. R. Soc., A, 2017, 375, 20160252 CrossRef PubMed.
- B. L. Ulich and E. K. Conklin, Nature, 1974, 248, 121–122 CrossRef.
- N. Biver, D. Bockelée-Morvan, P. Colom, J. Crovisier, B. Germain, E. Lellouch, J. K. Davies, W. R. F. Dent, R. Moreno, G. Paubert, J. Wink, D. Despois, D. C. Lis, D. Mehringer, D. Benford, M. Gardner, T. G. Phillips, M. Gunnarsson, H. Rickman, A. Winnberg, P. Bergman, L. E. B. Johansson and H. Rauer, Earth, Moon, Planets, 1997, 78, 5–11 CrossRef CAS.
- A. J. Remijan, S. N. Milam, M. Womack, A. J. Apponi, L. M. Ziurys, S. Wyckoff, M. F. A’Hearn, I. de Pater, J. R. Forster, D. N. Friedel, P. Palmer, L. E. Snyder, J. M. Veal, L. M. Woodney and M. C. H. Wright, Astrophys. J., 2008, 689, 613–621 CrossRef CAS.
- J. Geiss, K. Altwegg, H. Balsiger and S. Graf, Space Sci. Rev., 1999, 90, 253–268 CrossRef CAS.
- M. Rubin, K. Altwegg, H. Balsiger, J. J. Berthelier, M. R. Combi, J. de Keyser, M. Drozdovskaya, B. Fiethe, S. A. Fuselier, S. Gasc, T. I. Gombosi, N. Hänni, K. C. Hansen, U. Mall, H. Rème, I. R. H. G. Schroeder, M. Schuhmann, T. Sémon, J. H. Waite, S. F. Wampfler and P. Wurz, Mon. Not. R. Astron. Soc., 2019, 489, 594–607 CrossRef CAS.
- A. Marten, T. Hidayat, Y. Biraud and R. Moreno, Icarus, 2002, 158, 532–544 CrossRef CAS.
- V. Vuitton, R. V. Yelle and M. J. McEwan, Icarus, 2007, 191, 722–742 CrossRef.
- P. M. Solomon, K. B. Jefferts, A. A. Penzias and R. W. Wilson, Astrophys. J., 1971, 168, L107 CrossRef CAS.
- V. Thiel, A. Belloche, K. M. Menten, R. T. Garrod and H. S. P. Müller, Astron. Astrophys., 2017, 605, L6 CrossRef.
- H. Liszt, M. Gerin, A. Beasley and J. Pety, Astrophys. J., 2018, 856, 151 CrossRef.
- M. Araki, S. Takano, N. Kuze, Y. Minami, T. Oyama, K. Kamegai, Y. Sumiyoshi and K. Tsukiyama, Mon. Not. R. Astron. Soc., 2020, 497, 1521–1535 CrossRef CAS.
- H. E. Matthews and T. J. Sears, Astrophys. J., 1983, 267, L53 CrossRef CAS.
- P. Gratier, J. Pety, V. Guzmán, M. Gerin, J. R. Goicoechea, E. Roueff and A. Faure, Astron. Astrophys., 2013, 557, 1–19 CrossRef.
- S. Cuadrado, J. R. Goicoechea, J. Cernicharo, A. Fuente, J. Pety and B. Tercero, Astron. Astrophys., 2017, 603, A124 CrossRef PubMed.
- M. Guélin and J. Cernicharo, Astron. Astrophys., 1991, 244, L21–L24 Search PubMed.
- M. Agúndez, J. Cernicharo, G. Quintana-Lacaci, L. V. Prieto, A. Castro-Carrizo, N. Marcelino and M. Guélin, Astrophys. J., 2015, 814, 143 CrossRef PubMed.
- L. Olmi, R. Cesaroni, R. Neri and C. M. Walmsley, Astron. Astrophys., 1996, 315, 565–577 CAS.
- A. Remijan, E. C. Sutton, L. E. Snyder, D. N. Friedel, S.-Y. Liu and C.-C. Pei, Astrophys. J., 2004, 606, 917–928 CrossRef CAS.
- V. Pankonin, E. Churchwell, C. Watson and J. H. Bieging, Astrophys. J., 2001, 558, 194–203 CrossRef CAS.
- S. Mercimek, C. Codella, L. Podio, E. Bianchi, L. Chahine, M. Bouvier, A. López-Sepulcre, R. Neri and C. Ceccarelli, Astron. Astrophys., 2022, 659, 1–43 CrossRef.
- K. I. Öberg, V. V. Guzmán, K. Furuya, C. Qi, Y. Aikawa, S. M. Andrews, R. Loomis and D. J. Wilner, Nature, 2015, 520, 198–201 CrossRef PubMed.
- J. B. Bergner, V. G. Guzmán, K. I. Öberg, R. A. Loomis and J. Pegues, Astrophys. J., 2018, 857, 69 CrossRef.
- H. G. Arce, J. Santiago-García, J. K. Jørgensen, M. Tafalla and R. Bachiller, Astrophys. J., 2008, 681, L21–L24 CrossRef CAS.
- T. Hung, S.-Y. Liu, Y.-N. Su, J. H. He, H.-T. Lee, S. Takahashi and H.-R. Chen, Astrophys. J., 2019, 872, 61 CrossRef CAS.
- R. Mauersberger, C. Henkel, C. M. Walmsley, L. J. Sage and T. Wiklind, Astron. Astrophys., 1991, 247, 307–314 CAS.
- T. Nakajima, S. Takano, K. Kohno, N. Harada and E. Herbst, Publ. Astron. Soc. Jpn., 2018, 70, 1–36 CrossRef.
- D. J. Wilner, M. C. H. Wright and R. L. Plambeck, Astrophys. J., 1994, 422, 642 CrossRef CAS.
- E. Araya, P. Hofner, S. Kurtz, L. Bronfman and S. DeDeo, Astrophys. J., Suppl. Ser., 2005, 157, 279–301 CrossRef CAS.
- C. Codella, M. Benedettini, M. T. Beltrán, F. Gueth, S. Viti, R. Bachiller, M. Tafalla, S. Cabrit, A. Fuente and B. Lefloch, Astron. Astrophys., 2009, 507, 2005–2008 CrossRef.
- A. Palau, C. Walsh, Á. Sánchez-Monge, J. M. Girart, R. Cesaroni, I. Jiménez-Serra, A. Fuente, L. A. Zapata and R. Neri, Mon. Not. R. Astron. Soc., 2017, 467, 2723–2752 CAS.
- L. Giani, C. Ceccarelli, L. Mancini, E. Bianchi, F. Pirani, M. Rosi and N. Balucani, Mon. Not. R. Astron. Soc., 2023, 526, 4535–4556 CrossRef.
- K. Acharyya, E. Herbst, R. L. Caravan, R. J. Shannon, M. A. Blitz and D. E. Heard, Astron. Astrophys., 2015, 113, 2243–2254 CAS.
- S. Cazaux, V. Cobut, M. Marseille, M. Spaans and P. Caselli, Astron. Astrophys., 2010, 522, A74 CrossRef.
- J. R. Goicoechea, C. Joblin, A. Contursi, O. Berné, J. Cernicharo, M. Gerin, J. Le Bourlot, E. A. Bergin, T. A. Bell and M. Röllig, Astron. Astrophys., 2011, 530, L16 CrossRef.
- H. Linnartz, S. Ioppolo and G. Fedoseev, Int. Rev. Phys. Chem., 2015, 34, 205–237 Search PubMed.
- G. W. Harris, T. E. Kleindienst and J. N. Pitts, Chem. Phys. Lett., 1981, 80, 479–483 CrossRef CAS.
- G. Poulet, G. Laverdet, J. L. Jourdain and G. Le Bras, J. Phys. Chem., 1984, 88, 6259–6263 CrossRef CAS.
- B. Fritz, K. Lorenz, W. Steinert and R. Zellner, Proc. 2nd Eur. Symp. Physico-Chemical Behav. Atmos. Pollut., 1982, p. 192.
- C. Zetzsch, Bunsekolloquium, Battelle Institut, Frankfurt, 1983 Search PubMed.
- M. J. Kurylo and G. L. Knable, J. Phys. Chem., 1984, 88, 3305–3308 CrossRef CAS.
- A. J. Hynes and P. H. Wine, J. Phys. Chem., 1991, 95, 1232–1240 CrossRef CAS.
- G. S. Tyndall, J. J. Orlando, T. J. Wallington and M. D. Hurley, J. Phys. Chem. A, 2001, 105, 5380–5384 CrossRef CAS.
- W. B. DeMore, J. Photochem. Photobiol., A, 2005, 176, 129–135 CrossRef CAS.
- S. T. Andersen, M. Kyte, L. L. Andersen, O. J. Nielsen and M. P. Sulbaek Andersen, Int. J. Chem. Kinet., 2018, 50, 813–826 CrossRef CAS.
- Q. S. Li, X. D. Xu and S. Zhang, Chem. Phys. Lett., 2004, 384, 20–24 CrossRef CAS.
- A. Galano, J. Phys. Chem. A, 2007, 111, 5086–5091 CrossRef CAS PubMed.
- Y. Tian, T. J. He, D. M. Chen and F. C. Liu, Acta Phys.-Chim. Sin., 2008, 24, 587–594 CAS.
- M. Alihosseini, M. Vahedpour and M. Yousefian, Comput. Theor. Chem., 2017, 1113, 72–81 CrossRef CAS.
- Q.-S. Li and C. Y. Wang, J. Comput. Chem., 2004, 25, 251–257 CrossRef CAS PubMed.
- A. J. Ocaña, S. Blázquez, B. Ballesteros, A. Canosa, M. Antiñolo, J. Albaladejo and E. Jiménez, Phys. Chem. Chem. Phys., 2018, 20, 5865–5873 RSC.
- A. J. Ocaña, S. Blázquez, A. Potapov, B. Ballesteros, A. Canosa, M. Antiñolo, L. Vereecken, J. Albaladejo and E. Jiménez, Phys. Chem. Chem. Phys., 2019, 21, 6942–6957 RSC.
- S. Blázquez, D. González, E. M. Neeman, B. Ballesteros, M. Agúndez, A. Canosa, J. Albaladejo, J. Cernicharo and E. Jiménez, Phys. Chem. Chem. Phys., 2020, 22, 20562–20572 RSC.
- E. Jiménez, B. Ballesteros, A. Canosa, T. M. Townsend, F. J. Maigler, V. Napal, B. R. Rowe and J. Albaladejo, Rev. Sci. Instrum., 2015, 86, 45108 CrossRef PubMed.
- A. Canosa, A. J. Ocaña, M. Antiñolo, B. Ballesteros, E. Jiménez and J. Albaladejo, Exp. Fluids, 2016, 57, 1–14 CrossRef CAS.
- A. J. Ocaña, E. Jiménez, B. Ballesteros, A. Canosa, M. Antiñolo, J. Albaladejo, M. Agúndez, J. Cernicharo, A. Zanchet, P. del Mazo, O. Roncero and A. Aguado, Astrophys. J., 2017, 850, 28 CrossRef PubMed.
- S. Blázquez, D. González, A. García-Sáez, M. Antiñolo, A. Bergeat, F. Caralp, R. Mereau, A. Canosa, B. Ballesteros, J. Albaladejo and E. Jiménez, ACS Earth Space Chem., 2019, 3, 1873–1883 CrossRef PubMed.
- B. R. Rowe, A. Canosa and D. E. Heard, Uniform Supersonic Flows in Chemical Physics, World Scientific, Europe, 2022 Search PubMed.
- M. Antiñolo, M. Agúndez, E. Jiménez, B. Ballesteros, A. Canosa, G. El Dib, J. Albaladejo and J. Cernicharo, Astrophys. J., 2016, 823, 25 CrossRef PubMed.
- E. Jiménez, M. Antiñolo, B. Ballesteros, A. Canosa and J. Albaladejo, Phys. Chem. Chem. Phys., 2016, 18, 2183–2191 RSC.
- E. Jiménez, B. Lanza, A. Garzón, B. Ballesteros and J. Albaladejo, J. Phys. Chem. A, 2005, 109, 10903–10909 CrossRef PubMed.
- E. Jiménez, B. Ballesteros, E. Martínez and J. Albaladejo, Environ. Sci. Technol., 2005, 39, 814–820 CrossRef PubMed.
- J. Albaladejo, B. Ballesteros, E. Jiménez, Y. Díaz de Mera and E. Martínez, Atmos. Environ., 2003, 37, 2919–2926 CrossRef CAS.
- M. Antiñolo, E. Jiménez, A. Notario, E. Martínez and J. Albaladejo, Atmos. Chem. Phys., 2010, 10, 1911–1922 CrossRef.
- D. González, A. Lema-Saavedra, S. Espinosa, E. Martínez-Núñez, A. Fernández-Ramos, A. Canosa, B. Ballesteros and E. Jiménez, Phys. Chem. Chem. Phys., 2022, 24, 23593–23601 RSC.
- E. M. Neeman, D. González, S. Blázquez, B. Ballesteros, A. Canosa, M. Antiñolo, L. Vereecken, J. Albaladejo and E. Jiménez, J. Chem. Phys., 2021, 155, 034306 CrossRef CAS PubMed.
- D. González, B. Ballesteros, A. Canosa, J. Albaladejo and E. Jiménez, Front. Astron. Space Sci., 2022, 8, 1–11 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- L. Guerrero-Méndez, A. Lema-Saavedra, E. Jiménez, A. Fernández-Ramos and E. Martínez-Núñez, Phys. Chem. Chem. Phys., 2023, 25, 20988–20996 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 84102 CrossRef PubMed.
- L. G. Gao, J. Zheng, A. Fernández-Ramos, D. G. Truhlar and X. Xu, J. Am. Chem. Soc., 2018, 140, 2906–2918 CrossRef CAS PubMed.
- Y. Georgievskii and S. J. Klippenstein, J. Chem. Phys., 2005, 122, 194103 CrossRef PubMed.
- A. Fernández-Ramos, A. Ellingson, B. C. Garrett and D. G. Truhlar, Rev. Comput. Chem., 2007, 23, 125 Search PubMed.
- M. Page and J. W. McIver Jr., J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- Y.-Y. Chuang, J. C. Corchado and D. G. Truhlar, J. Phys. Chem. A, 1999, 103, 1140–1149 CrossRef CAS.
- D. Ferro-Costas, D. G. Truhlar and A. Fernández-Ramos, Comput. Phys. Commun., 2020, 256, 107457 CrossRef CAS.
- K. M. Douglas, D. I. Lucas, C. Walsh, N. A. West, M. A. Blitz and D. E. Heard, Astrophys. J., Lett., 2022, 937, L16 CrossRef.
- C. Sleiman, S. González, S. J. Klippenstein, D. Talbi, G. El Dib and A. Canosa, Phys. Chem. Chem. Phys., 2016, 18, 15118–15132 RSC.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi, J. Troe and IUPAC Subcommittee, Atmos. Chem. Phys., 2006, 6, 3625–4055 CrossRef CAS.
- C. Castro and W. L. Karney, Angew. Chem., Int. Ed., 2020, 59, 8355–8366 CrossRef CAS PubMed.
- Y.-Y. Chuang and D. G. Truhlar, J. Phys. Chem. A, 1998, 102, 242–247 CrossRef CAS.
- J. C. Gómez Martín, R. L. Caravan, M. A. Blitz, D. E. Heard and J. M. C. Plane, J. Phys. Chem. A, 2014, 118, 2693–2701 CrossRef PubMed.
- R. J. Shannon, M. A. Blitz, A. Goddard and D. E. Heard, Nat. Chem., 2013, 5, 745–749 CrossRef CAS PubMed.
- R. L. Caravan, R. J. Shannon, T. Lewis, M. A. Blitz and D. E. Heard, J. Phys. Chem. A, 2015, 119, 7130–7137 CrossRef CAS PubMed.
- R. J. Shannon, R. L. Caravan, M. A. Blitz and D. E. Heard, Phys. Chem. Chem. Phys., 2014, 16, 3466–3478 RSC.
- B. Nizamov and S. R. Leone, J. Phys. Chem. A, 2004, 108, 1746–1752 CrossRef CAS.
- R. J. Hoobler and S. R. Leone, J. Geophys. Res.: Planets, 1997, 102, 28717–28723 CrossRef CAS.
- K. M. Hickson, J.-C. Loison and V. Wakelam, ACS Earth Space Chem., 2021, 5, 824–833 CrossRef CAS.
- K. M. Hickson and J.-C. Loison, J. Phys. Chem. A, 2022, 126, 3903–3913 CrossRef CAS PubMed.
- T. L. Nguyen, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2019, 150, 084105 CrossRef PubMed.
- M. Agúndez and V. Wakelam, Chem. Rev., 2013, 113, 8710–8737 CrossRef PubMed.
- D. McElroy, C. Walsh, A. J. Markwick, M. A. Cordiner, K. Smith and T. J. Millar, Astron. Astrophys., 2013, 550, A36 CrossRef.
- D. C. Clary, C. E. Dateo and D. Smith, Chem. Phys. Lett., 1990, 167, 1–6 CrossRef CAS.
- T. Su and W. J. Chesnavich, J. Chem. Phys., 1982, 76, 5183–5185 CrossRef CAS.
- W. A. Payne, P. S. Monks, F. L. Nesbitt and L. J. Stief, J. Chem. Phys., 1996, 104, 9808–9815 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04944b |
| This journal is © the Owner Societies 2024 |