Quorum sensing-induced transition from colloidal waves to Turing-like patterns in chemorepulsive active colloids

Abstract

The study of active systems, especially in the presence of a chemical background field, is garnering significant attention. Traditionally, the self-propelled velocity of active colloids was assumed to be constant, independent of the local density of colloids. In this work, we introduce a chemotactic active system that features quorum sensing (QS), wherein particles act as chemorepellents. Interestingly, these particles lose their activity in regions of high local particle density. Our findings reveal that QS leads to a transition from an oscillatory colloidal wave to a Turing-like pattern, with the observation of an intermediate state. With the variation of the sensing threshold, both the mean oscillation frequency of the system and the number of clusters exhibit non-monotonic dependence. Furthermore, the QS-induced pattern differs markedly from systems without QS, primarily due to the competitive interplay between diffusion and chemotaxis. The dynamics of this phenomenon are explained using a coarse-grained mean field model.

---

1 Introduction

Active matter systems are distinguished by their consistent conversion of internal energy into work or movement, thereby maintaining a state of non-equilibrium. The collective behaviors of these systems have garnered significant research attention^1–5 due to their unique properties and the myriad intriguing behaviors they exhibit, spanning from individual to collective scales. At the individual scale, active particles can demonstrate anomalous diffusion in polymer solutions.⁶ On a collective scale, they can form various dynamic structures such as collective vortexes,^7,8 swarms,^9,10 and polar movements.^11,12 In addition to their own dynamic properties, active particles can even act as a bath to influence the dynamics of other systems. For instance, passive particles can exhibit anomalous diffusion and aggregation behavior in the active bath.^13,14

Very recently, one of the frontiers has been the study of active particles in a background field. Typically, in actual active systems, chemical substances present in the background are needed to be considered, which are coupled with the motion of active particles, inducing the movement upward (the “chemoattractive” case) or downstream (the “chemorepulsion” case) the chemical concentration gradient, known as chemotaxis. Employing this chemotaxis mechanism, real microorganisms navigate chemical gradients to optimize their living conditions. Similarly, artificial microswimmers mimic this behavior through diffusiophoresis, a process often facilitated using Janus colloids.^15,16 These colloids are designed with a catalytic coating on one side that produces chemicals, thereby generating a chemical gradient that induces directional movement.

Recent studies have reported many interesting collective behaviors of active Janus particles. For example, the motion of active Janus particles will be suppressed in the cluster, thereby stabilizing the structure and shape of the dynamic clusters.^17–19 Another example is that for the binary mixed system of active Janus particles and passive particles, the mutual effect of active and passive subsystems on each other leads to the expulsion of passive particles in the vicinity of an active swimmer (that can initially be either moving or immobilized) and at the same time to the localization of active swimmers.^20–22 Furthermore, various self-organization behaviors of active Janus particles under the effect of chemotaxis have also been reported in previous works. For example, Saha et al.²³ reported that the fluid flows set up around the chemotactic active Janus particle can turn its axis of orientation to align parallel or antiparallel to the local gradient, leading to clumping and patterning at a low reactant concentration. Besides, Liebchen and co-workers²⁴ established an active Keller–Segel model and studied the collective behavior of active Janus particles under the conditions of chemical attraction and chemical repulsion. The study found that with chemical attraction, a single large droplet structure was finally formed. With chemical repulsion, the system will eventually form a dynamically changing cluster structure with self-limiting size. This is in sharp contrast to the relatively static clusters that are separated by motion at higher densities.^25,26 Following this report, Liebchen et al.²⁷ introduced chirality, and found that in the case of chemical attraction, the system changes from small to large with angular velocity, undergoing a transition from a large droplet to a parallel fringe traveling wave structure with a fixed wavelength. Later, they²⁸ established a more generalized phoretic Brown particle model and found that chemical repulsion can cause the system to form a striped colloidal wave pattern that is chased by a chemical field.

In all these studies, it was assumed that the self-propelled speed of particles is constant. However, recent theoretical^29,30 and experimental³¹ explorations have discovered a mechanism termed quorum sensing (QS), whereby the self-propelled speed of a particle will depend on the local density of particles in the region in which it is located, rather than being simply a constant. This QS feature has significantly influenced the behavior of active particle systems. For instance, Farrell et al.³² theoretically investigated the collective behavior of active particles with both aligned interactions and a decrease in motility with increasing local density of particles. Under such conditions, they observed not only motion-induced phase separation behavior but also the formation of moving clumps, lanes, and arrests, none of which are seen in active systems with only aligned interactions. Experimentally, Tobias Bäuerle et al.³³ used artificial Janus particles instead of live bacteria to artificially set QS rules by laser irradiation and computer decision-making. Their results demonstrate that cluster formation requires not only the coexistence of active and inactive particles but also the ability of the particles to change their motility depending on the local density of particles. Additionally, particles can only aggregate into clusters within a specific threshold value; if this value is too high or too low, the particles will drift in different directions, thus failing to form stable clusters. Nevertheless, to the best of our knowledge, how QS would influence the behavior of a chemotaxis system has not yet been studied.

Motivated by this, in this work, we study the collective behaviors of chemotactic active Janus colloidal particles endowed with a QS-feature. In particular, we investigate scenarios in which particles navigate downstream of the background chemical field gradient (in a chemorepulsive manner), especially in cases where these particles become inactive once the local particle density ρ surpasses a threshold ρ_c. Our primary emphasis is on understanding how ρ_c influences the system's behavior and structure. Our findings reveal that incorporating QS markedly alters the size and count of self-limiting clusters and attenuates the system's oscillatory behavior once ρ_c reaches a particular value. This suggests that the introduction of QS curtails particle aggregation, fostering a more diffusive particle flow. This diffusive flow counterbalances the external chemotactic particle stream, reinforcing the cluster's stability.

The article is organized as follows: Section 2 introduces the dynamical model. Numerical results are given in Section 3, together with discussions in Section 4. Finally, we summarize this article in Section 5.

2 Model

Here, we consider a two-dimensional system which is composed of chemotactic active Janus particles and the chemical background field (as shown in Fig. 1). In particular, the active Janus particle exhibits a QS feature, i.e., its self-propelled velocity actually depends on the local density of current position of particles, described by v_ρ = v₀·Θ(ρ_c − ρ), where v₀ is a constant value and Θ is the Heaviside step function, as shown in panel (A). When local density is lower than ρ_c, the particle possesses self-propel velocity v₀, whose direction is downstream the chemical gradient, corresponding to the chemorepulsion, as shown in panel (B). However, in (C), when particles undergo clustering and go beyond ρ_c, the self-propel velocity v_ρ → 0, and particles transform into diffusion motion.

Fig. 1 Schematic picture (A) shows the variation of the self-driven velocity v_ρ as a function of local density ρ. (B) shows the Janus particles in a directional movement by chemorepulsion with self-propulsion velocity v₀ against the chemical gradient ∇c. (C) Particles undergo clustering, and once the local density of particles’ aggregation exceeds the sensing threshold ρ_c, triggering QS, they will lose their activity and exhibit diffusion motility (Grey dots: chemotaxis signaling molecules produced by the yellow half side of the Janus particles).

It is worth stating that choosing a step function in our work is just a modeling, such that the QS-function can be described by a single threshold parameter ρ_c. In real systems, the QS-rule could be quite complicated, and a smooth function would be more reasonable. Actually, step function has also been used in many recent works related to QS.^33–36 Physically, the step function can be used to describe the intermittent motion of many living organisms, and the motion of light-controlled micromotors in some experiments.^33,34 In a recent QS-related theoretical work,³⁵ the authors also stated that “It requires the derivative of v(ρ), which thus needs to be a continuous function. While in principle a continuous response might be achieved through quorum sensing, in realistic applications as mentioned above, the response is discontinuous”. Therefore, the use of a step-function for the QS mechanism is not that “unphysical”.

To describe the dynamics, we use a coarse-grained-level mean field model.²⁴ Its density and polarization fields, ρ(x,t) and P(x,t), are established, where ρ(x,t) represents the active particles’ local density, and P(x,t) is the local average of polarization describing the direction of self-propulsion. In addition, QS-active particles are immersed in a background chemical field c(x,t), and the polarization direction rotates in response to the gradient of the chemical field c(x,t), leading to

[small rho, Greek, dot above] = −∇·(ρv_ρP) +D_ρ∇²ρ (1)

Ṗ = −γP + D_P∇²P + β∇c − γ₂|p²|P (2)

ċ = D_c∇²c + k₀ρ − k_dc + k_a∇·(ρP) (3)

Here, the evolution of the density field (eqn (1)) contains the self-propelled term and diffusion term with the isotropic diffusivity D_ρ. In eqn (2), the first term contains a relaxation rate γ describing the local decay of polarization, which originates from the fact that the colloid takes a certain amount of time to rotate in response to the fluctuation in chemical concentration. The second term expresses the direction of diffusion with the translational diffusivity D_P. The chemotaxis is introduced by the third term, where β is the chemotactic coupling strength; here, we focus on chemorepulsion, and thus the β is set to be negative. The term in γ₂ describes saturation in P upon strong alignment where the cubic term is used to improve the numerical stability of the equation. The evolution of the chemical field also produces a diffusion, with coefficient D_c, assuming that the chemical substances are created at rate k₀ρ and decay at rate k_d. Finally, the term k_a∇·(ρP) describes an anisotropic correction to the isotropic chemical production term (k₀ρ), which is inevitably brought in by Janus particles covered with a non-uniform coating.

Actually, QS in living systems requires communication between individuals, which is achieved by the release of signaling molecules with a production and degradation rate.³⁷ Because such molecules have a finite lifetime, each organism senses the molecular concentration. Here, such details of the signaling molecules are not explicitly expressed in our modeling. And, for simplicity, the response of the particles to such signal molecules is considered to be instantaneous.

Subsequently, we have non-dimensionalized the equations by using the characteristic length scale time scale t̃ = k_dt, and setting the density of particles [small rho, Greek, tilde] = ρk₀|β|v₀/(k_d²D_ρ), polarization concentration of chemicals c̃ = cv₀|β|/(k_dD_ρ). The independent dimensionless parameters in our model include Γ = γ/k_d, , , κ = k_ak_d/(k₀v₀), Γ₂ = γ₂D_ρ/v₀² and [capital Theta, Greek, tilde] = Θ(ρ_c − ρ), also s = sgn(β) = −1 set for the chemorepulsion. These dimensionless parameters help to reduce the complexity of the model and make it more tractable for both analytical and numerical investigations. Then, we rewrite the equations as follows (for the sake of brevity in the equations, now we omit the tildes):

[small rho, Greek, dot above] = −∇·(ρPΘ_(ρc−ρ)) + ∇²ρ (4)

We solved equations numerically on a square box of side L = 80 using finite difference methods under periodic boundary conditions and a small perturbation of the uniform state (ρ,P,c) = (ρ₀,0,c₀) as initial conditions.

3 Results

First, we analyze the pattern characteristics of the system under various sensing threshold parameters, ρ_c. Subsequently, we examine the general trends of the system oscillation mode, cluster count, and average cluster radius as ρ_c decreases consistently. Detailed parameter settings are provided in the annotations of Fig. 2.

Fig. 2 The curve chart on the right shows the evolution of density ρ (black curve) and chemical concentration c (red curve) over time t at point P in the left-hand corresponding snapshot, under different sensing thresholds (a) ρ_c = +∞ (without QS), (b) ρ_c = 40, (c) ρ_c = 18, and (d) ρ_c = 11. As for (d), a stationary Turing-like pattern is created, thus the corresponding curves are horizontal lines. On the left side of the graph, four sets of snapshots of density field ρ and chemical field c for the corresponding sensing threshold ρ_c as a function of x and y are shown at t = 1525, with the color bar going from dark to light corresponding to the values from low to high. (Parameter space: (specifically, β = − 1, v₀ = D_ρ = D_P = D_c = k₀ = k_d = k_a = γ = 1, γ₂ = 2), time and space units as t_u = 1 and x_u = 0.2).

In the absence of QS (which corresponds to ρ_c = +∞), initial fluctuations for chemorepulsive Janus particles intensify, leading to the formation of dense colloidal clusters from a uniform state. These clusters do not coarsen beyond a specific size for a sufficiently long time. The features of this microflock structure are in agreement with the results as reported in ref. 24. The clusters exhibit an approximation of a hexagonal lattice arrangement, with particles dynamically transitioning between clusters, resulting in a “blinking” pattern. This continuous activity means that the clusters remain in perpetual motion. Both the local particle density and chemical field over time predominantly display sinusoidal waveforms (refer to Fig. 2a). Such oscillatory behavior indicates a consistent periodicity, characterized as a colloidal wave mode, arising from the ongoing particle exchange between clusters. The oscillation induces a drift in the clusters, causing minor deviations from a perfect sine wave at fixed lattice points. Overall, this manifests as a wave moving through the microflocks from the upper right to the lower left. Notably, a time lag is evident between the peak chemical concentration and the minimum particle density, suggesting a relative delay in particle movement concerning the chemical field's evolution.

As delineated in ref. 24, the “blinking” pattern emerges from the interplay of two instability mechanisms: Janus instability and delay-induced instability. Janus instability, induced by the term k_a∇·(ρP), arises due to the anisotropic chemical production of Janus particles. Initial fluctuations cause active particles to reorient towards the chemical density minimum, leading to an inward-facing aster. The cluster's localized anisotropy in chemical production generates a chemical repellent shell, which consolidates its particles and repels external ones, limiting its growth. The delay-induced instability, attributed to −γP, pertains to the relaxation effect of polarization. Colloids initially accumulate at reduced chemical concentrations. As the cluster's size grows, so does the chemical repellent produced at its core, elevating the chemical concentration therein. If particles reorient slowly relative to the timeframe needed to counteract the initial fluctuations, the production of the repellent can exceed the required amount, converting the initial concentration minimum into a maximum. Consequently, particles may drift away, leading to cluster disintegration. The synergistic action of both instability mechanisms induces the periodic fluctuation of the traveling wave pattern, resulting in the observed “blinking” mode.

For a considerably high sensing threshold (ρ_c = 40, as shown in Fig. 2b), the system mirrors the behavior observed when QS is absent. However, upon reducing the sensing threshold to ρ_c = 18, distinct variations emerge. The system's “blinking” becomes notably subdued in both frequency and intensity, accompanied by alterations in cluster size and count (refer to Fig. 2c). The oscillatory waveform deviates from a pure sinusoidal shape, exhibiting sawtooth-like spikes, suggesting a multifrequency oscillation mode. Additionally, the delay between the chemical field's oscillations and the particle density nearly vanishes, aligning the chemical field's minima with the particle density's maxima. One can infer that the introduction of QS potentially dampens the delay-induced instability, consequently attenuating the density oscillation's frequencies and amplitudes. Remarkably, when ρ_c reaches a specific threshold, the system's state exhibits a pronounced transformation, as illustrated in Fig. 2d. Contrasting starkly with the non-QS scenario, the dense colloidal clusters coalesce into significantly larger formations, fewer in count, and adopt a structured arrangement. Notably, the system's oscillatory dynamics cease, giving rise to a stationary Turing-like pattern.

This oscillation's cessation is pivotal, primarily as it emerges as a unique feature resulting from QS. It is plausible that the QS's introduction instills a fresh instability mechanism within the system, curbing its oscillations and predisposing it to stabilize into a Turing-like pattern. Delving into the Turing-like pattern's genesis, Fig. 3 delineates the variations in ρ and c as individual clusters evolve from their initial states. Following an initial random perturbation, active particles gravitate towards areas of diminished chemical concentration due to chemorepulsion against the chemical gradient direction, forming nascent clusters. Subsequently, the particle density at these cluster centers surpasses the sensing threshold, rendering the particles passive. These passive entities, devoid of their chemical field linkages, predominantly diffuse to adjacent regions with lower particle densities. This action not only caps the particle count at the cluster's core but also, facilitated by a lag in orientational response, consolidates the cluster's structure. Concurrently, chemical concentration wanes, attributed to intrinsic degradation, diffusion, and the Janus instability. With the ongoing influx and clustering of active particles, the passive particle domain expands. As the evolution advances, the differential concentration of c—high externally and low internally—creates a protective shell, confining internal particles while repelling external ones. Over time, a balance between outward diffusive flow and central active flow is achieved, enhancing the cluster's symmetry. Ultimately, a sizable stable cluster is formed, which is bordered by active particles and densely packed with passive ones internally.

Fig. 3 The snapshots of the evolution of an individual cluster during the formation of the Turing-like pattern. (a)–(d) Corresponds to the distribution of the density field, and (e)–(h) corresponds to the distribution of the chemical field at the moments t = 4, t = 8, t = 40 and t = 400, respectively, where the white part represents the distribution of passive particles. The upper color bar corresponds to the density value and the lower color bar corresponds to the chemical concentration, where the left side corresponds to the t = 4, t = 8 moment and the right side corresponds to the t = 40, t = 400 moment.

This observation prompts an inquiry into the influence of QS on the particles’ chemotactic behavior. As delineated in Fig. 2, the QS appears most potent at ρ_c = 18. However, the particles seemingly struggle to circumvent regions of elevated chemical concentration when ρ_c = 11 (refer to Fig. 2d). When expansive regions indicate high concentrations of c(x), a substantial fraction of particles must inhabit these areas, rather than being exclusively contained within a circumscribed zone, as discernible in Fig. 3d and h. This raises the question: does an optimal ρ_c exist that maximizes chemical repulsion efficiency? To corroborate this, we compute the integral of ρ(x,t)·c(x,t) over the entire system for an extended time t. Subsequently, we plot this value against t to observe its evolution over time (as shown in Fig. 4A) and average the ρ(x,t)·c(x,t) to assess its temporal evolution (see Fig. 4A) and average the result over an ample timeframe, plotting it against ρ_c (as shown in Fig. 4B) to ascertain any potential minima (refer to Fig. 4B).

Fig. 4 (A) Temporal evolution of the product of particle density, ρ(x,t), and chemical concentration, c(x,t), integrated over all spatial coordinates x for various quorum sensing thresholds, ρ_c. The different curves represent distinct ρ_c values, illustrating how the collective behavior of the particles, in terms of chemorepulsion, changes over time for different levels of quorum sensing. The inline plot is a separate zoomed-in display of the results for ρ_c = 18, in order to show its vibration waveform more clearly. (B) Average value of the integrated product of particle density, ρ(x,t), and chemical concentration, c(x,t), over a sufficiently long time span, plotted against different quorum sensing thresholds, ρ_c. The plot reveals an optimal ρ_c value where chemorepulsion is most effectively realized, indicated by the minimum value in the curve.

As illustrated in Fig. 4A, for ρ_c = +∞ (i.e., in the absence of QS), the integral value exhibits time-dependent oscillations resembling a sinusoidal wave, mirroring the local particle density's evolution. With ρ_c = 40, the oscillation amplitude diminishes, yet its equilibrium position rises slightly, a trend more discernible in Fig. 4B. As ρ_c decreases further (e.g., ρ_c = 18), the integral value stabilizes, exhibiting minor amplitude with an irregular waveform. At even lower thresholds like ρ_c = 11, the integral remains constant, signaling the system's transition to a steady state. Notably, at this juncture, the integral value is so high that the particles do not seem to be able to completely avoid the high chemical concentration region, a deviation from patterns observed at elevated ρ_c levels.

Fig. 4B provides an in-depth analysis of the average product of ρ(x,t) and c(x,t) across varying ρ_c thresholds. As ρ_c decreases, a consistent increase in the average integral value is observed, peaking near ρ_c = 25. This increase suggests that lower chemical concentration areas within clusters produce more passive particles, displacing active particles and preventing them from completely avoiding high-concentration areas. As ρ_c is further reduced, the density of passive particles inside the clusters decreases, subsequently lowering the integral values. Notably, the minimal value at ρ_c ≈ 19 suggests that it may be the optimal threshold for maximizing the chemical repulsion efficiency. With further decreases in ρ_c, the radius of the clusters grows, diminishing the effectiveness of chemotaxis and increasing the overlap with high concentration areas, resulting in higher average integral values.

Based on these observations, we infer the existence of an optimal ρ_c for maximum chemorepulsion, specifically around 19 in this study. This threshold likely represents a harmonious balance between the collective behavior of colloidal particles and chemorepulsion, leading to ideal pattern formation. While the precise value of ρ_c for optimal chemorepulsion may vary with system parameters, our findings offer valuable insights into modulating the colloidal particle behavior by adjusting ρ_c.

To further characterize the change of the system state with decreasing sensing threshold, the dependences of the oscillation frequency, cluster number, and average radius of the system on the sensing threshold ρ_c are presented in Fig. 5. It can be observed that the oscillation frequency and cluster count exhibit analogous trends: both predominantly decrease with a diminishing sensing threshold, showcasing non-monotonicity around ρ_c = 30 and peaking near 25. However, while the oscillation frequency approaches zero around ρ_c = 18, the cluster count hits its nadir at 11. In contrast, the average radius of the clusters continues to increase as the sensing threshold decreases and reaches a maximum at 11. The average radius also shows a slight anomaly around 30 and achieves a minimum around 25, but the manifestation is not particularly pronounced. Since the overall particle density of the system is fixed, a decrease in the number of clusters inevitably leads to an increase in the average radius. Hence, a negative correlation between the two is reasonable.

Fig. 5 (a) The variation of average oscillation frequency f, (b) the variation of cluster number N (black dot) and cluster average radius R̄ (red circle), while the blue curve indicates the predictions made by linear stability analysis, (c) the variation of the average ratio of the number of passive particles (N_P) to the number of active particles (N_A) in each cluster as a function of sensing thresholds ρ_c. According to the different modes of oscillation, Fig. a is divided into 3 phases: (1) steady state structure (Turing-like pattern), (2) multi-frequency oscillation mode, and (3) colloidal wave with a single frequency (where the frequency in the phase (2) is calculated by equation ).

The conducted studies conclusively reveal that a decrease in the sensing threshold ρ_c transitions the system from an ideal sinusoidal spatio-temporal oscillation to a static configuration, namely, a Turing-like pattern, with an intermediate transitional state evident (refer to Fig. 5a).

The system's oscillation modes categorize it into three distinct phases over the sensing threshold range: the phase in the colloidal wave mode oscillating at single frequencies when ρ_c > 30; from ρ_c = 18 to 30, it is the transition region where the system oscillates at multiple frequencies, and finally, from a related small value like ρ_c = 11 to 18, it is the phase formed in a Turing-like pattern with a static structure.

In the initial phase where ρ_c > 30, passive particles are absent from the system (as evidenced in Fig. 5c). The system comprises solely chemically reactive colloidal particles that migrate against the chemical field concentration gradient towards areas of lower chemical concentration, resulting in pronounced local particle density. The chemical production rate of these particles directly correlates with their local density, inducing a rapid surge in the chemical concentration at their locations. As the original chemical gradient diminishes, the delay in particle dispersion, due to the inherent lag in their steering and mobility, fosters continuous chemical accumulation in that vicinity. This leads to a transient concentration overshoot, subsequently inverting the gradient and repelling the colloidal particles. The cyclical nature of this process eventually synchronizes the particles’ collective movement, culminating in the macroscopic “blinking” pattern.

During the phase of multi-frequency oscillations, passive particles start to appear in the system. Initially, active particles cluster towards the areas of low chemical concentration. However, under the influence of QS, particles that aggregate too densely at the cluster's core exceed the threshold value ρ_c and transition to a passive state. These passive particles exhibit only diffusive behavior, resulting in a cluster configuration where active particles envelop a core of passive ones. The cluster's outer layer is primarily influenced by chemorepulsion, while its center is governed by diffusion. Within the ρ_c range of 25 to 30, we observe a marginal increase in the average oscillation frequency, as depicted in Fig. 5a. 2. Concurrently, the ratio of passive to active particles, N_P/N_A, varies from 0 to 0.1, as shown in Fig. 5c. We note that the variation in oscillation frequency mirrors the changes in the integral values as shown in Fig. 4B, suggesting a tight correlation between particle density and chemical concentration overlap and the system's oscillatory behavior. This overlap likely intensifies the chemorepulsive effects on active particles. Additionally, an increased number of clusters in a confined system reduces the distance between them, facilitating faster particle exchange among clusters. Previous studies have reported that passive particles exhibit weak activity and super-diffusion behavior at higher concentrations of active particles.^38,39 Furthermore, the translational diffusion of passive colloids, apart from chemical repellency, plays a crucial role in cluster disbanding.⁴⁰ These observations indicate that similar mechanisms could influence our system. The introduction of weak activity in passive particles may lead to the emergence of additional oscillation frequencies. Simultaneously, enhanced diffusion rates of passive particles could expedite cluster dissociation. These factors collectively may contribute to a slight “blue shift” in the system's average frequency, an intriguing phenomenon that further enriches our understanding of the system's dynamic behavior.

As ρ_c decreases, the proportion of passive particles further increases and the diffusion rate of passive particles will gradually fall back to the normal level. Within the cluster, the loss of chemotaxis and the dominance of pure diffusion prevent colloidal particles from aggregating closely, resulting in an expansion of the average cluster size. As the chemical concentration recoil diminishes, inter-cluster particle exchanges become infrequent, leading to a sharp decline in oscillation frequency.

Once the N_P/N_A ratio approaches 1, passive particles begin to predominate, and the system's oscillatory behavior ceases, culminating in a static Turing-like pattern.

In summary, the QS mechanism affects the proportion of passive particles in the system, thereby determining its state. These passive particles, typically enveloped by active ones, reside in areas of lowest chemical concentration. This insight suggests potential applications for manipulating system behaviors.

4 Discussion

4.1 Linear stability analysis

In order to gain a deeper understanding of the mechanisms underlying the static patterns and oscillatory modes observed in Fig. 2 and 4, we conducted a linear stability analysis on our model. The primary objective of this analysis is to ascertain how minor perturbations near the system's uniform or stable solution evolve over time. Notably, the average colloidal density, denoted as ρ₀, remains conserved throughout the system. We introduced small perturbations to the system, represented by the wave vector q. The growth rate or dispersion relation of these perturbations is given by λ(q). For the step function Θ_(ρc−ρ), we adopt the following approximation:

For ρ ≤ ρ_c, Θ_(ρc−ρ) = 1;

For ρ > ρ_c, Θ_(ρc−ρ) = 0.

In the former case, the step function can be treated as a constant with a value of 1. In the latter case, this term can be disregarded. We will now discuss each scenario separately.

Initially, considering ρ ≤ ρ_c, within a spatial dimension, we introduce perturbations δρ, δP and δc to the system of equations centered around the uniform solution (ρ,P,c) = (ρ₀,0,ρ₀). Neglecting the higher-order terms induced by the perturbation, we obtain the linear equation system describing the temporal evolution of the perturbations as:

For all three fields, we assume that perturbations take the form of plane waves. Consequently, we derive the characteristic polynomial P(λ) concerning λ(z), where z := iq:
This polynomial of degree three in λ(z) provides a characteristic equation by setting P(λ) = 0, which describes the system's stability. By identifying the values of λ(z) that satisfy this equation, we can distinguish between stable and unstable modes. However, the general form of the result for λ(z) is intricate, and its physical interpretation is not immediately apparent. To streamline the equation, we substitute the system's parameter values, yielding:
Subsequently, we numerically compute the dispersion relations λ(q)_1,2,3 and represent the results in Fig. 6 for a more direct physical interpretation.

Fig. 6 Dispersion relations for different values of ρ₀. The top panel illustrates the variation of the real part of the growth rate λ with wave vector q (where the gray horizontal dashed line represents λ(q) = 0). The bottom panel depicts the variation of the imaginary part of λ with q.

Based on the numerical relationship between the growth rate λ and the wave vector q presented in Fig. 6, we identified three distinct regimes: (i) stability of the uniform state, where the growth rate is real and negative; (ii) stationary patterns arising from growing stationary modes with a positive real growth rate; and (iii) moving patterns resulting from oscillatory instabilities, which possess a non-zero imaginary part of the growth rate and manifest primarily at smaller wave vectors, characterizing it as a long-wavelength instability. This insight aligns with the observation of “blinking” patterns in the system at high ρ_c values.

Two primary reasons account for the emergence of finite-sized clusters rather than complete phase separation: firstly, each cluster forms a chemorepellent shell that wards off approaching colloids. Secondly, as the cluster size enlarges, the amount of chemorepellent produced isotropically at its core also escalates, causing the cluster to disintegrate if it becomes overly large.

For ρ > ρ_c, we can derive the following system of equations:

From this, the characteristic polynomial P(λ) for λ(z) is given by:
Substituting the specified parameter values, we further obtain:
Solving this equation yields three solutions: and . For all values of q, λ_1,2,3(q) are real. We will discuss the system states corresponding to these solutions in the subsequent sections.

Within the range of q > 0, both λ₁(q) and λ₂(q) consistently fall below zero, indicating stability in the uniform state at these eigenvalues. However, for λ₃(q), it only exceeds zero at certain q values. Solving for λ₃(q) = 0, we identify as the boundaries for linear instability modes. Modes within these two wavenumber values are unstable, as they possess growth rates above zero, leading to phase separation and the eventual formation of static patterns in the system. The wavenumber corresponding to the maximum growth rate can be determined from the conditions ∂_qλ = 0 and ∂_q²λ < 0, which yields 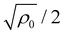. Additionally, a double root appears in the equation when ρ₀ = 4. Hence, linear instability modes exist only when ρ₀ > 4.

Furthermore, given the system's conserved overall average particle density ρ₀, the formation of static clusters entraps numerous particles, leading to a decreased average particle density outside these clusters where ρ ≤ ρ_c. This is equivalent to a reduced initial particle density ρ₀ under conditions ρ ≤ ρ_c. Numerical outcomes from Fig. 6 show that a decline in ρ₀ corresponds to a reduced system's maximum growth rate λ_max(q). This elucidates why, with a decreasing ρ_c value, the system's colloidal wave oscillation intensity also diminishes. Concurrently, at the edge of the clusters, due to the competitive interplay between the diffusion of passive particles and the chemotaxis of active particles, coupled with the intricate continuous transitions between particle deactivation and activation, multiple growth modes might coexist in the system. This could lead to the emergence of multi-frequency oscillatory instability modes in the system.

Lastly, as ρ₀ continues to decrease, as shown in Fig. 6, around ρ₀ < 6, Re[λ_1,2,3(q)] remains below zero. Under these conditions, regions in the system where ρ ≤ ρ_c eventually stabilize into a uniform state. The oscillations in the system dissipate, giving rise to stationary stable patterns.

These findings highlight that QS instability affects the mobility of Janus particles in particle-conserving systems, as emphasized by Bäuerle et al.,³³ shifting the distribution ratio between passive and active particles and subsequently impacting the system's evolutionary patterns and pattern formation. This represents a novel and unique aspect, distinct from the original Janus instability and delay-induced instability.

Cluster sizes in our system are determined by the wavenumber q_max corresponding to the maximum growth rate λ_max. The cluster size is approximately half of the most unstable wavelength, thus l ≈ π/q_max. We have calculated q_max for different values of ρ_c to ascertain this relationship. Initially, with high ρ_c values and only active particles (Θ_(ρc−ρ) = 1), we found λ_max = 0.673 and q_max = 1.758, resulting in a cluster size of l ≈ 1.787. As ρ_c decreases and passive particles become prevalent, a shift occurs around ρ_c ≈ 30, with q_max becoming (where ρ₀ represents the average density of passive particles), suggesting .

For numerical simulations, we considered ρ = 10 as the cluster boundary, necessitating a correction to the predicted results. The corrected results are illustrated in Fig. 4b, which compares the average radius of clusters (R̄) as a function of ρ_c. The figure shows that while there are numerical discrepancies, the trends predicted by linear stability analysis (LSA) align with the trends observed in the simulations. These discrepancies could stem from the limitations of LSA's linear approximation, especially in areas of strong nonlinearity, and the influence of spatial/temporal resolution, initial conditions, and boundary conditions on numerical simulations.

Despite the numerical differences, our model qualitatively captures the key behavior of the system, demonstrating its utility in understanding the physical properties of the system.

In summary, the results from the LSA are generally consistent with our numerical simulations.

4.2 Formation of Turing-like patterns

In fact, in the original system without QS, the Turing-like pattern can also be created, when the diffusion coefficient D_ρ is adjusted to a larger value. Therefore, it is interesting to examine how such a non-QS system develops a Turing-like pattern and whether the underlying mechanisms in the QS and non-QS systems are identical.

To address this, we juxtapose the particle density and chemical concentration distributions of both systems and conduct a radial distribution function (RDF) analysis on the particle density distribution within individual clusters. Our findings indicate that the Turing-like pattern in the non-QS system notably differs from that in the QS system, particularly concerning particle density distribution and cluster size (refer to Fig. 7).

Fig. 7 (a) and (c) Heat map of the particles’ local density and local chemical concentration distribution of the Turing-like pattern induced by QS. (b) and (d) Heat map of the particles’ local density and local chemical concentration distribution of the static Turing-like pattern formed without QS (D_ρ = 1.5, k_a = 0.9, other parameters as in Fig. 2). (e) and (f) Radial distribution functions (RDF) g(r) = ρ(r)/ρ₀ (calculating the mean value by taking the center of each cluster circle as the starting point), corresponding to Fig. a and b, respectively. The orange dashed line g(r) = ρ_c/ρ₀ in (e) represents the division between the passive particle region and the active particle region, above the dashed line: passive particles; below: active particles.

In the scenario involving QS, it is evident that due to diffusion, the distribution of colloidal particles within a cluster is more dispersed, resulting in a larger cluster size compared to the non-QS case. Given the system's finite size, accommodating these larger clusters necessitates a reduction in cluster quantity. This reduction is evident as initial clusters merge and continuously adjust their positions to achieve equilibrium (this behavior is observed during the evolution). The corresponding radial distribution function reveals a nearly uniform distribution of particles within clusters, with a peak at the cluster edges. This peak arises from the concurrent inward flow of active particles and outward diffusion at the cluster boundaries, culminating in a local density extremum.

Conversely, in the absence of QS, while the chemical field distribution remains largely unchanged, the particle density within clusters is centrally concentrated and diminishes outward. The RDF decreases monotonically with the increasing radius. Since the chemotactic strength of the particles is just balanced with the diffusion strength, the aggregation of the particles will not be particularly tight. Benefiting from this, the production, diffusion, and degradation of the chemical substances can be balanced. The overshoot of chemical substance concentration, which causes the reversal of the chemical gradient, will not occur at the location of the original low chemical substance concentration. And when there is the introduction of QS, it leads to a more dispersed high-density particle region and a larger cluster size.

It is the presence of QS that prevents particle aggregation to the extent that would reverse low chemical concentrations in certain areas, thereby preserving the stability of cluster structures and eliminating spatio-temporal oscillatory behaviors. This understanding leads us to conclude that QS, characterized by local density-dependent activity, cannot be merely viewed as a shift in the parameter space of the original non-QS system. Instead, it introduces a novel instability mechanism, altering particle mobility and enhancing diffusion's role in the system. By counteracting chemotaxis, QS mitigates the impact of delay-induced instability, altering both cluster size and oscillatory behavior.

In summary, the pivotal discovery of this study is the QS-induced transition from oscillations and waves to Turing-like patterns, governed by the variation of a single parameter: the QS-threshold ρ_c. While static Turing-like patterns have been identified in non-QS systems, as mentioned in ref. 24, our analysis highlights distinct differences in their outward appearances and underlying mechanisms. The primary distinction is the particle density distribution within clusters. In the presence of QS, clusters exhibit a pronounced core–shell structure with a peak particle density at the boundary. In contrast, without QS, particle density tapers off from the center to the edges, as depicted in Fig. 6. This stark contrast underscores that the Turing-like patterns, both with and without QS, stem from disparate instability mechanisms. Referring to ref. 24, the emergence of Turing-like patterns is attributed to the equilibrium between chemotaxis and diffusion strength of the active particle. In our study, the formation of a Turing-like pattern, influenced by QS, primarily arises from the competition between chemorepulsion of active Janus particles and diffusion from their passive counterparts. When the particle density at the cluster's center surpasses ρ_c, active particles deactivate, transitioning to passive particles. These passive particles, solely driven by diffusion, contest with active particles gravitating towards the center, achieving a competitive equilibrium at the boundary.

Moreover, it is interesting to note that mutual effects of active and passive particles on each other have been reported in the literature studies,^20–22 including some immobilization and localization phenomena, but without considering QS as we have in our study. Similarly, in both kinds of system, the passive particles are driven by active Janus particles, causing them to be compressed and thus to undergo aggregation and immobilization, resulting in a stable pattern. However, the underlying mechanisms are different. In these previous works, the driving mechanism is purely internal, with the photochemical activity of defects residing in the colloidal matrix producing a solidification effect similar to that induced by a blast. In our case, the movement of active Janus particles is also influenced by chemotaxis arising from chemical gradients in the surrounding environment, and the formation of individual clusters is the result of a competing balance between chemorepulsion and passive particle diffusion.

Besides, in Bäuerle et al.'s study,³³ silica particles of diameter σ = 4.4 μm with a 30 nm-thick carbon film were suspended in a critical mixture of water-lutidine at T = 25 °C. Each particle was illuminated individually using a scanned laser beam (beam waist w = 5 μm) aimed at the particle's center, causing self-propulsion opposite to the capped hemisphere. This setup is particularly relevant to our study as it demonstrates the formation of clusters and patterns under varying concentration thresholds (c_th). As c_th decreases, the clusters’ particle density reduces and their size increases, paralleling the trends we observed in our simulations. Moreover, the interplay of motility switching and particle interactions, as controlled by the laser illumination intensity, is crucial for the formation of static clusters and patterns. Such experimental observations strongly align with our numerical findings, highlighting the significance of motility changes and particle interactions in cluster formation. Our study, complemented by the insights from Bäuerle et al.'s experiments, underscores the importance of these factors in understanding and predicting the behavior of such complex systems.

5 Conclusions

In conclusion, QS profoundly impacts pattern formation in chemically repulsive active colloids. Upon introducing QS into the system, stable Turing-like patterns emerge due to QS-induced instabilities, stemming from the competition between diffusion and chemotactic forces. Our findings emphasize the delicate balance the system maintains between collective particle behavior and chemotactic forces. Data suggest an optimal value for ρ_c, below which the efficiency of chemical repulsion diminishes. At ρ_c = 11, particles seem incapable of fully avoiding high-concentration regions. Additionally, the results from the linear stability analysis align well with our numerical simulations.

While the system can form Turing-like patterns in certain parameter spaces without QS, the nature of the patterns under QS induction is distinctly different. QS plays a pivotal role in the behavior of chemotactic systems. Many such systems, including bacteria, exhibit this characteristic, profoundly influencing pattern formation. Our discoveries not only offer insights into real-world bacterial systems but also hint at potential applications in designing colloids with tunable self-assembling patterns. Furthermore, these observations resonate with the idea that “quorum sensing plays a significant role in influencing particle chemotactic behavior.” While the specific optimal value for ρ_c at which chemical repulsion is most effective might vary with other system parameters, our analysis provides foundational understanding of this phenomenon.

In our current research, we have focused solely on the combination of chemical repulsion and activity loss at high local densities. In reality, more research avenues exist for this system. Explorations in other parameter spaces remain intricate, making it challenging to discern patterns. Broadly speaking, like several other scenarios, preliminary studies indicate that the system's behavior, when coupling chemotaxis with low-density inactivity, fundamentally remains similar to the scenarios without QS. Conversely, under conditions of coupling chemotactic force with high-density inactivity, as the sensing threshold changes, the system exhibits structures like large droplets, bands, and large bubbles, consistent with previous research findings.⁴¹ All in all, more detailed investigations warrant our continued efforts in future endeavors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by MOST(2022YFA1303100), NSFC (32090044, 21833007), Anhui Initiative in Quantum Information Technologies (AHY090200).

Notes and references

1. S. C. Takatori and J. F. Brady, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032117.
2. S. Ramaswamy, J. Stat. Mech.: Theory Exp., 2017, 5, 054002.
3. M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199.
4. S. Ramaswamy, Ann. Rev. Condens. Matter Phys., 2010, 1, 323–345.
5. M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189.
6. C. L. Yuan, A. P. Chen, B. J. Zhang and N. R. Zhao, Phys. Chem. Chem. Phys., 2019, 21, 24112–24125.
7. J. X. Pan, H. Wei, M. J. Qi, H. F. Wang, J. J. Zhang, W. D. Tian and K. Chen, Soft Matter, 2020, 16, 5545–5551.
8. Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chate and K. Oiwa, Nature, 2012, 483, 448–452.
9. J. A. Cohen and R. Golestanian, Phys. Rev. Lett., 2014, 112, 068302.
10. T. Vicsek, Nature, 2012, 483, 411–412.
11. L. Giomi, M. C. Marchetti and T. B. Liverpool, Phys. Rev. Lett., 2008, 101, 198101.
12. J. Deseigne, O. Dauchot and H. Chate, Phys. Rev. Lett., 2010, 105, 098001.
13. X. Liu, H. Jiang and Z. Hou, J. Chem. Phys., 2019, 151, 174904.
14. R. K. Xu, H. J. Jiang and Z. H. Hou, Chin. J. Chem. Phys., 2021, 34, 157–164.
15. B. Liebchen and H. Lowen, Acc. Chem. Res., 2018, 51, 2982–2990.
16. H. Stark, Acc. Chem. Res., 2018, 51, 2681–2688.
17. A. P. Solon, M. E. Cates and J. Tailleur, Eur. Phys. J.: Spec. Top., 2015, 224, 1231–1262.
18. W. Yang, V. R. Misko, J. Tempere, M. Kong and F. M. Peeters, Phys. Rev. E, 2017, 95, 062602.
19. W. Yang, V. R. Misko, F. Marchesoni and F. Nori, J. Phys.: Condens. Matter, 2018, 30, 264004.
20. X. Wang, L. Baraban, V. R. Misko, F. Nori, T. Huang, G. Cuniberti, J. Fassbender and D. Makarov, Small, 2018, 14, 1802537.
21. T. Huang, V. R. Misko, S. Gobeil, X. Wang, F. Nori, J. Schütt, J. Fassbender, G. Cuniberti, D. Makarov and L. Baraban, Adv. Funct. Mater., 2020, 30, 2003851.
22. T. Huang, S. Gobeil, X. Wang, V. Misko, F. Nori, W. De Malsche, J. Fassbender, D. Makarov, G. Cuniberti and L. Baraban, Langmuir, 2020, 36, 7091–7099.
23. S. Saha, R. Golestanian and S. Ramaswamy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062316.
24. B. Liebchen, D. Marenduzzo, I. Pagonabarraga and M. E. Cates, Phys. Rev. Lett., 2015, 115, 258301.
25. M. E. Cates and J. Tailleur, Ann. Rev. Condens. Matter Phys., 2015, 6, 219–244.
26. J. Bialke, T. Speck and H. Lowen, J. Non-Cryst. Solids, 2015, 407, 367–375.
27. B. Liebchen, M. E. Cates and D. Marenduzzo, Soft Matter, 2016, 12, 7259–7264.
28. B. Liebchen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2017, 118, 268001.
29. M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715–11720.
30. J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103.
31. C. Liu, X. Fu, L. Liu, X. Ren, C. K. Chau, S. Li, L. Xiang, H. Zeng, G. Chen, L. H. Tang, P. Lenz, X. Cui, W. Huang, T. Hwa and J. D. Huang, Science, 2011, 334, 238–241.
32. F. D. Farrell, M. C. Marchetti, D. Marenduzzo and J. Tailleur, Phys. Rev. Lett., 2012, 108, 248101.
33. T. Bauerle, A. Fischer, T. Speck and C. Bechinger, Nat. Commun., 2018, 9, 3232.
34. F. A. Lavergne, H. Wendehenne, T. Bäuerle and C. Bechinger, Science, 2019, 364, 70–74.
35. A. Fischer, F. Schmid and T. Speck, Phys. Rev. E, 2020, 101, 012601.
36. J. Smith-Roberge, D. Iron and T. Kolokolnikov, Eur. J. Appl. Math., 2019, 30, 196–218.
37. T. I. Yusufaly and J. Q. Boedicker, Phys. Rev. E, 2016, 94, 062410.
38. D. Rogel Rodriguez, F. Alarcon, R. Martinez, J. Ramirez and C. Valeriani, Soft Matter, 2020, 16, 1162–1169.
39. P. Dolai, A. Simha and S. Mishra, Soft Matter, 2018, 14, 6137–6145.
40. J. Sturmer, M. Seyrich and H. Stark, J. Chem. Phys., 2019, 150, 214901.
41. M. Meyer, L. Schimansky-Geier and P. Romanczuk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022711.

---