Rigidifying of the internal dynamics of amyloid-beta fibrils generated in the presence of synaptic plasma vesicles

Abstract

We investigated the changes in internal flexibility of amyloid-β_1–40 (Aβ) fibrils grown in the presence of rat synaptic plasma vesicles. The fibrils are produced using a modified seeded growth protocol, in which the Aβ concentration is progressively increased at the expense of the decreased lipid to protein ratio. The morphologies of each generation are carefully assessed at several fibrils’ growth time points using transmission electron microscopy. The side-chain dynamics in the fibrils is investigated using deuterium solid-state NMR measurements, with techniques spanning line shapes analysis and several NMR relaxation rates measurements. The dynamics is probed in the site-specific fashion in the hydrophobic C-terminal domain and the disordered N-terminal domain. An overall strong rigidifying effect is observed in comparison with the wild-type fibrils generated in the absence of the membranes. In particular, the overall large-scale fluctuations of the N-terminal domain are significantly reduced, and the activation energies of rotameric inter-conversion in methyl-bearing side-chains of the core (L17, L34, M35, V36), as well as the ring-flipping motions of F19 are increased, indicating a restricted core environment. Membrane-induced flexibility changes in Aβ aggregates can be important for the re-alignment of protein aggregates within the membrane, which in turn would act as a disruption pathway of the bilayers’ integrity.

---

Introduction

Amyloid-β (Aβ) species are implicated in the membrane disruption of neuronal cells, thereby causing cytotoxicity and contributing to the pathology of Alzheimer's disease.^1–9 Aβ peptides likely interfere with glutamatergic neurotransmission at pre- and post-synaptic levels.^10,11 Many works have investigated possible pathways of membrane disruptions and structural features of amyloid fibrils and oligomers interacting with the membrane.^{1,2,4–7,11–18} Legleiter et al. found that while lipid composition clearly affected the resulting morphologies of the fibril aggregates, all of the studied aggregates disrupted total brain lipid extract bilayers altering the bilayer's morphological and mechanical properties in a similar fashion.¹⁹ Site-specific studies of structural and dynamics changes of Aβ at the membrane remain to be challenging due to the complexity of kinetics of Aβ-membrane interactions.²⁰ Niu et al.^13,20 have demonstrated that the structure of Aβ_1–40 fibrils in the presence of lipid vesicles differs significantly in comparison to the structure in the absence of the lipids. The differences were attributed at least in part to the templating effect of anionic phospholipids in the nucleation process of the Aβ fibrils. Additional studies²¹ demonstrated that several key hydrophobic core contacts and features of the β-sheet conformation form early in the nucleation stage. In general, the effects appear to be highly complex and dependent on lipid composition of the membranes.²⁰

Aβ aggregates must induce changes in the structure and dynamics of the cell membrane to exert their cytotoxic effect by correlated rearrangements of the membrane structure and Aβ conformation.²² The internal flexibility of the Aβ species could be crucial for effective interaction with the membrane, yet its effects have been relatively understudied. In isolation from the membrane environment, Aβ is known to have a structured,²³ but still considerably mobile,²⁴ hydrophobic core and the disordered N-terminal domain^25–27 (Fig. 1). Our goal is to assess what changes biological membranes may impose on the internal dynamics of the Aβ_1–40 oligomers and fibrils. As the first step in this direction, our approach consists of producing fibrils using the seeded growth protocols, in which the parent generation is grown in the presence of the synaptic membrane vesicles, while the subsequent generations do not have any additional vesicles added.

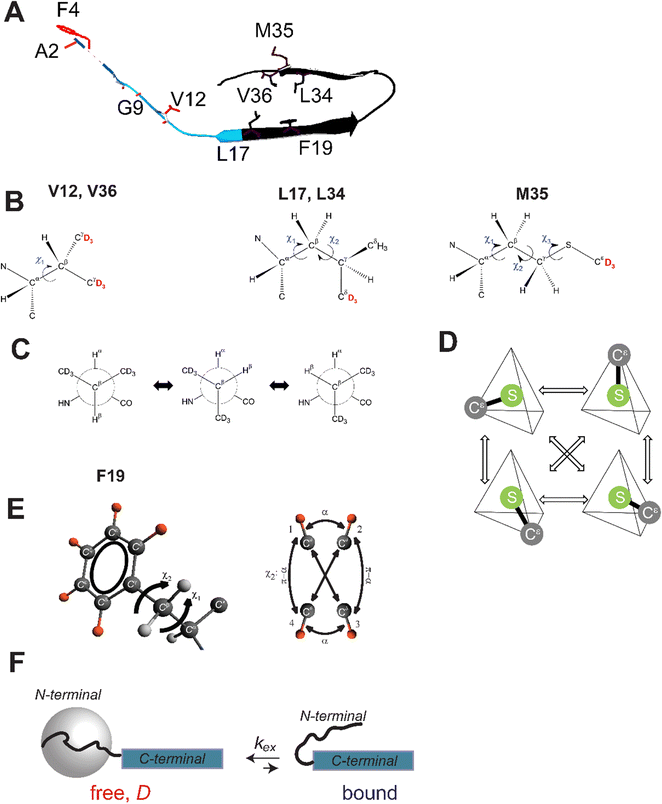Fig. 1 (A) A schematic representation of the monomeric unit of the fibrils based on the 2-fold symmetric structure (PDB ID 2LMN). The disordered N-terminal subdomain spans residues 1–16 (blue ribbon), with the residues 1–8 shown schematically by a dotted line due to their absence in the structural coordinates. The structured C-terminal domain (residues 17–40) is shown in black ribbon. The side-chains probed in this work are labeled in red for the N-terminal domain residues and in black for the C-terminal domain residues. (B) The structures of the methyl-bearing side chains, showing explicitly the deuteration patterns of the methyl groups in red, as well as the side-chain dihedral angles. The bottom panel displays the corresponding motional models of rotameric interconversions: (C) rotameric inter-conversion model in valine side chains, indicating the three possible positions of the χ₁ dihedral angle. (D) The motional model involving rotameric jumps between four magnetically inequivalent positions of the S–C^ε axis, under the assumption of the ideal tetrahedral geometry in all 27 methionine rotamers. Note that the identical motional model is used for the rotameric inter-conversions in leucine, in this case corresponding to the jumps between four magnetically inequivalent conformers of the C^γ–C^δ axis out of total nine conformers.^24,36 (E) The phenylalanine side-chain with the deuteron labeling pattern marked in orange and the motional model for the fluctuations around the χ₂ dihedral angle. The diagram displays sites’ connectivities according to the four-site exchange model, illustrated for one of the C^δ–D bonds. The large-angle flips occur between sites 1–3 and 1–4 with an equal probability; this also holds for the 2–3 and 2–4 pairs.³⁷ The small-angle jumps with the amplitude α occur between sites 1–2 and 3–4. (F) A schematic representation of the model of concerted fluctuations of the N-terminal domain for residues A2, F4, G9 and V12: the disordered N-terminal domain (curved line) transiently interacts with the structured C-terminal domain (blue rectangle). In the free state, the N-terminal domain is assumed to undergo large-scale reorientations, as represented by the gray sphere, while in the bound state, the interactions with the hydrophobic core quench this mode.²⁵ The parameters of the models are shown with the corresponding symbols.

To this end we utilize liposomes extracted from synaptic plasma vesicles of adult rats.²⁸ Neuronal plasma membrane is highly relevant for studies of pathological aggregation pathways of Aβ. The characterization of these membranes, including chemical composition, their effects on fibrils growth kinetics, and several structural features of the resulting fibrils was carried out previously.^15,21,28 In addition, the fibrils’ lower stability (against GdnHCl) and higher cytotoxicity in neuroblastoma N2a cells, as compared to fibrils grown in aqueous buffers, was observed.¹⁵ Prior dynamics nuclear polarization solid-state NMR studies by Deo et al.²¹ enabled ¹³C chemical shift characterization for the Aβ_1–40 species generated in the presence of the same synaptic vesicles used in this study. These works demonstrated the retainment of the β-sheet features and some of the hydrophobic contacts in the early nucleation stages, such as the critical F19/L34 contact found in many Aβ_1–40 structures.¹⁵ Kenyaga et al.¹⁵ observed additional contacts between pairs of residues for fibrils grown in the presence of these synaptic vesicles in comparison to the fibrils grown in isolation from the membranes. They also found restriction of lipid diffusive motions, demonstrating complex structural effects imposed by the interaction with the lipids.

While it is not clear a priori whether the fibrils produced using the seeded growth protocol can retain any features of the original membrane–fibril interactions, we show using deuterium solid-state NMR techniques, that the resulting fibrils have very different internal dynamics at the side-chain sites in comparison with the dynamics observed in the absence of the membranes. In particular, they impose a rigidifying effect on both the structured hydrophobic core of the fibrils and, especially, the flexible disordered N-terminal domain (Fig. 1).

Deuterium solid-state NMR is known for its sensitivity to motions: deuterium is a spin-1 nucleus with the quadrupolar interaction dominating NMR relaxation.^29–35 The quadrupolar coupling constant is on the order of 160–200 kHz, which is one to two orders of magnitude larger than dipolar and chemical shift anisotropy interaction constants defining the NMR properties of spin 1/2 nuclei in biomolecules.^31,35 We consider a variety of motional modes, such as rotameric inter-conversions of methyl-bearing side chains of V12, L17, L34, M35, and V36 (Fig. 1(B)–(D)), ring-flipping motions of F19 located in the hydrophobic core (Fig. 1(E)), and the overall large-scale motions of the N-terminal domain as probed at A2, F4, G9, and V12 sties (Fig. 1(F)). We employ selective deuteration of Aβ peptides to achieve site-specific resolution for these studies. We complement flexibility studies with detailed transmission electron microscopy (TEM) imaging characterizations of the fibrils at the various stages of the seeded growth protocol to assess the resulting morphologies.

Results and discussion

Characterization of fibrils from the seeded growth protocol with TEM and other biophysical approaches

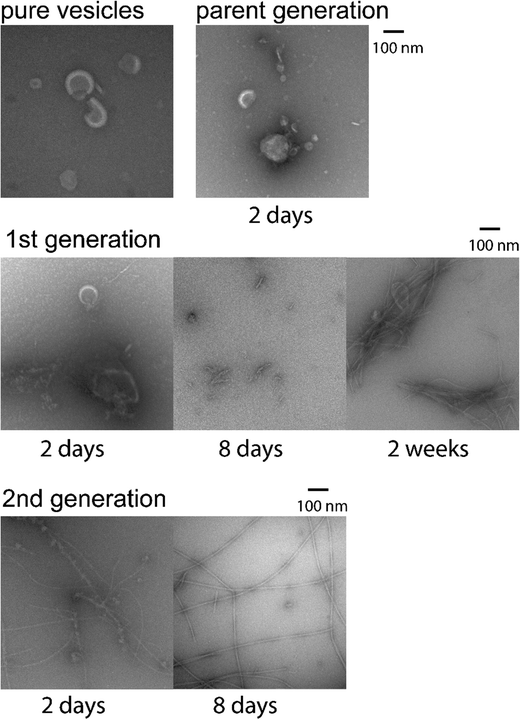
Ideally, to approximate native protein–lipid interactions, it would be desirable to sustain lipids to protein molar ratio on the order of at least 20 to 100.³⁸ However, from the practical perspective of preparing NMR samples, these ratio would yield very low protein content which would preclude the detailed studies of dynamics. Thus, we need to devise a sample preparation strategy which retains major features of original protein–lipid interactions while scaling down the lipid content and increasing the protein content.

To this end, several successful seeded growth protocols have been developed that have been shown to retain fibrillar structures and morphologies.^39,40 In our case we start the seeding protocols with the lipid to protein ratio of 20 (referred to as the “parent generation”) and produce two subsequent generations in which the ratio is decreased progressively by a factor of 10, resulting in the final generation with the 0.2 : 1 lipids to protein ratio with Aβ_1–40 concentration of 50 μM. Before proceeding to NMR analysis, we need to identify optimal fibril growth conditions with these incorporations of the membranes and demonstrate the resulting morphology of the fibrils. This was achieved with the use of negatively stained TEM imaging (Fig. 2), in which for each generation we captured images at different time points of growth by flash-freezing aliquots in liquid nitrogen.

Fig. 2 TEM images of the pure liposomes, the parent generation of Aβ_1–40 with the 20 : 1 lipids to protein molar ratio after 2 days of incubation, and the 1st and 2nd generation of Aβ_1–40 with the seeded growth protocol outlined in the text, with the different incubation times shown directly on the panels.

First, the suspension of synaptic vesicles liposomes in the absence of the Aβ peptide was imaged. The suspension was prepared by previously developed methods, described in Cheng et al.²⁸ and elaborated in SI1. The vesicles originated from hippocampus brain tissue of male adult rats. The majority of the imaged vehicles range in diameter between 50 to 300 nm. The dynamics light scattering measurements (Fig. S1, ESI†) indicate an average size of about 300 nm, with the bulk of intensity between about 180 to 490 nm diameters.

After two days of incubation of the parent generation, one can observe significant changes in the vesicles’ appearance, suggestive of interactions of the vesicles with the Aβ peptide and possible formation of oligomers. Longer incubation times up to 7 days did not lead to any consistent detection of fibrillar species, possibly due to the low concentration of Aβ of 10 μM, for which the bulk of the vesicles dominates the images. The first generation was produced with the total concentration of Aβ of 25 uM and the seeds of the parent generation applied in the 1 : 10 (seeds to fresh peptide) molar ratio. It displays a distinct progression from heterogeneous interactions with vesicles at 2 days, to formation of protofibrils at 8 days, to formation of the fibrils at two weeks. The 2nd generation had the Aβ concentration of 50 μM and the 1 : 10 molar ratio of seeds to fresh peptide, in which the seeds corresponded the fibrils grown in 1st generation. The TEM images of this generation indicate protofibrils and longer fibrils at two days, and a structured network of fibrils at 8 days. The dimensions and morphologies of the resulting fibrils are very similar to the “twisted” morphology found for the wild-type Aβ_1–40 fibrils.^39,41 The analysis of these images guided the design of our preparation protocols for fibrils employed in the NMR analysis.

Additionally, we have performed a qualitative assessment of aggregation kinetics using the thioflavin T fluorescence (ThT) assays (Fig. S2, ESI†).⁴² In particular, we focused on the comparison of the lag phase times, i.e., the plateau region before one observes a significant change in the ThT intensity. The lag phase was shown previously to be considerably expanded by the presence of the synaptic vesicles membranes,^15,28 and we examined whether this feature is retained in the 1st and 2nd generation of the seeded fibrils. Indeed, the comparison demonstrates the approximate lag phases of 15 hours in the control non-seeded Aβ_1–40 solution without the presence of the liposomes, 33–35 hours for the parent generation, 29–33 hours for the first generation, and 25–29 hours for the 2nd generation. Note that for the consistency of data interpretation the concentration of Aβ was kept the same in all generations here and corresponded to 25 μM. This qualitative comparison thus indicates that some features of the vesicles-induced growth kinetics persists into the 2nd generation of the fibrils. While the ThT assays are sensitive to the transition from monomer to a mixture of oligomers of different sizes,⁴³ the TEM results suggest that the elongation process leading to the mature fibrils is also much delayed compared to the seeded growth of the wild-type Aβ_1–40. The elongation times in the absence of lipids are reported as short as 24 hours for the quiescent growth protocol.^39,44 We performed a control using self-seeded Aβ_1–40 in the absence of lipids using the seeds corresponding to the twisted 3-fold polymorph fibrils, and at otherwise identical conditions (50 μM and at room temperature) to those used in the preparation of lipids-containing seeds. TEM imaging of resulting aggregates indicated that the twisted morphology forms within 40–48 hours of incubation. This growth time can be qualitatively compared to the 8 days for the 2nd generation in the lipid-containing preparations, suggesting a significant delay in the formation of the mature fibrils caused by the presence of the lipids in the seeds themselves. No additional lipids were added to the 1st or 2nd generations.

Deuterium solid-state NMR analysis signifies reduced internal flexibility in the fibrils grown in the presence of synaptic vesicles

The 2nd generation of fibrils, grown as outlined above, undergone detailed ²H solid-state NMR analysis, for which the peptides were selectively labeled at one of the residues shown in Fig. 1(A). The labeling patterns are shown in Table 1, along with the experiments used to probe each residue and their most important dynamics mode. The sites were chosen with two objectives in mind: their strategic location along the sequence (several residues dispersed throughout the disordered domain, hydrophobic core residues including methyl and aromatic side-chains pointing toward the core, and the key M35 side-chain defining the interface between the subunits) and the ease of incorporation of specific labels with the solid-state peptide synthesis.⁴⁵ The combination of specific site-labeling and static deuterium solid-state NMR permits for detailed studies of dynamics. In principle, it is possible to conduct similar side-chain dynamics measurements on a fully labeled protein using polarization transfer schemes and magic-angle-spinning (MAS) methods.^31,35,46 However, it would be difficult to achieve the needed resolution for these non-crystalline fibrils, while maintaining the MAS rate low enough to capture the details of the line shapes and avoiding the reduction of the effective quadrupolar coupling constant (C_q) below the sensitivity of ²H R_1ρ measurements.⁴⁷ This consideration would be especially critical for the sites which already display lower effective C_q values due to motional averaging.

Table 1 ²H labeling patterns. NMR experiments employed, and main motional modes present in residues used in this work

Residue	Labeling pattern	^2H static ssNMR experiments	Most important dynamics modes
N terminal domain
A2	-C^βD3	Lineshapes, T1ρ on- and off-resonance	Overall diffusive motion of the N-terminal domain and exchange with core, methyl three-site jumps
F4	-^βCH2-ring-D5	Lineshapes	Overall diffusive motion of the N-terminal domain and exchange with core
G9	-^αCD2	Lineshapes, T1 with QCPMG	Overall diffusive motion of the N-terminal domain and exchange with core
V12	-^βCD2-(^γCD3)2	Lineshapes	Overall diffusive motion of the N-terminal domain and rotameric interconversions
C-terminal domain
F19	-^βCH2-ring-D5	T 1 with QCPMG	Ring-flipping motions
L17, L34	-C^γD3 (50% labeling for each methyl group)	Lineshapes	Rotameric interconversions
M35	-C^εD3
V36	-^βCD2-(^γCD3)2

---

The discussion focuses on the comparison of these various motional modes in the two subdomains in the 2nd generation of Aβ fibrils grown in the presence of vesicles, denoted by “mem” and the fibrils produced previously in the absence of the membranes, denoted by “wt”.

I. Global motions in the disordered N-terminal domain

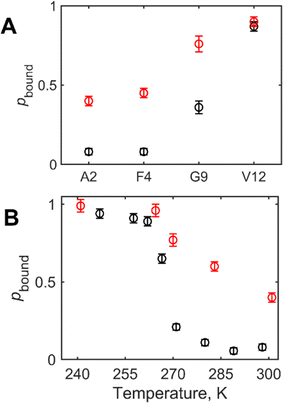
In the wt fibrils the disordered N-terminal domain was found to undergo extensive large-scale rearrangements,²⁵ which could be modeled by diffusive motions. As the simplest approximation we use the isotropic diffusion model, suggesting isotropic reorientations. The extent of the large-scale diffusive rearrangement decreases along the sequence, from the N-terminal to the C-terminal end, such as the large-scale motions are almost entirely quenched at residue V12. In addition, the domain undergoes conformation exchange between the free state, in which the large-scale motions are active, and the bound state, in which these motions are quenched, presumably due to interactions with the structured fibrils’ core.^25,48 The parameters of this model (Fig. 1(F)) are the fraction of the bound state p_bound, the diffusion coefficient D, and the conformational exchange rate constant k_ex. The same model was applied to the mem fibrils. In particular, the values of p_bound can be obtained from the line shape experiments, in which the bound state corresponds to the wide component, and the free state corresponds the narrow spectral component (Fig. 3). The large-scale rearrangements cause significant line narrowing of the free state component. While the value of D can be obtained from the line shapes of the free state fraction,²⁵ we have found that ²H NMR rotating frame relaxation measurements are more accurate in the presence of the conformational exchange.⁴⁸

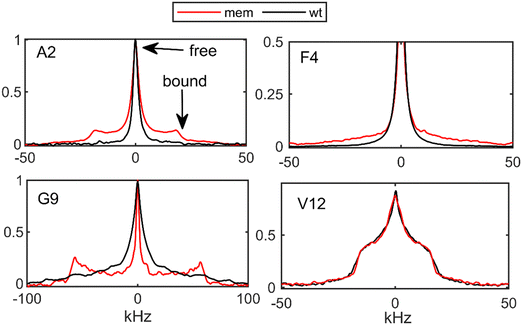Fig. 3 ²H static solid-state NMR line shapes for the N-terminal domain residues of the mem Aβ_1–40 fibrils (red) and wt fibrils (black) at 308–310 K. The arrows indicate the narrow fraction corresponding to the free state and the wide fraction corresponding to the bound state of the fibrils, according to the model of Fig. 1(F).

By comparing the line shapes at 35–37 °C for the N-terminal sites (Fig. 3), it is immediately apparent that the wide spectral component is significantly more pronounced in the mem fibrils than in the wt fibrils for the A2, F4, and G9 sites. Indeed, the line shape decomposition (Fig. S3, ESI†), performed according to previously developed procedures (SI2),^25,49 shows the increase of p_bound for the three residues (Fig. 4(A)), indicating that the large scale rearrangement are quenched by a larger extent is the mem fibrils. For the A2-C^βD₃ site we also performed the dependence of the line shapes on the values of the echo delay in the quadrupolar echo sequence to examine how it affects the resulting value of p_bound (Fig. S4, ESI†). The variations are under 5%, which is within the reported error bars.

Fig. 4 Fractions of the bound state in the mem (red circles) and wt (black circles) fibrils obtained from the line shape decomposition, shown for (A) the N-terminal residues, collected at 308–310 K and (B) for the A2 residues as a function of temperature.

For the most flexible A2 residue we also compared the freezing of the p_bound with temperature: at 270 K the free state is almost entirely frozen in the mem fibrils. This is not the case the wt fibrils, for which at 270 K the value of p_bound is at 0.21 (Fig. 4(B)).

We have recently developed on and off-resonance ²H T_1ρ measurements^25,48,50,51 which can be useful in the determination of the conformational exchange rate constant between the free and the bound states, k_ex. The entire relaxation dispersion curve is fitted to obtain the joint fit of k_ex and D. We applied the method to the mem fibrils labeled at the most flexible A2 residue. In these measurements, we have used the spin-lock field with the RF strength of 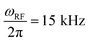. The relaxation decay curves (Fig. 5(A)) were obtained for the values of resonance offsets ranging from 0 to 65 kHz. The resulting relaxation dispersion curves are shown in Fig. 5(B), which demonstrate plots of the relaxation times (²H T_1ρ) as a function of the effective field in the tilted frame,⁵² the latter given by 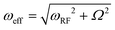, where Ω is the off-resonance term. The best-fit of these experimental data to the motional model of Fig. 1(F) is obtained for the following values of the parameters: p_bound = 0.3, D = 5.9 × 10⁵ rad² s⁻¹, k_ex = 1 × 10⁴–2 × 10⁴ s⁻¹, as compared to the value of p_bound = 0.08, D = 3.5 × 10⁶ rad² s⁻¹, k_ex = 3 × 10⁴ s⁻¹ for the wt fibrils, signifying a more rigid behavior with less pronounced large-scale rearrangements and slower conformational exchange rate constant. To confirm the consistency with the line shape simulations, we checked that inclusion of the conformational exchange explicitly into these simulations does not change the line shapes compared to the ones obtained with the non-exchanging combination of the free and bound fractions (Fig. S5, ESI†).

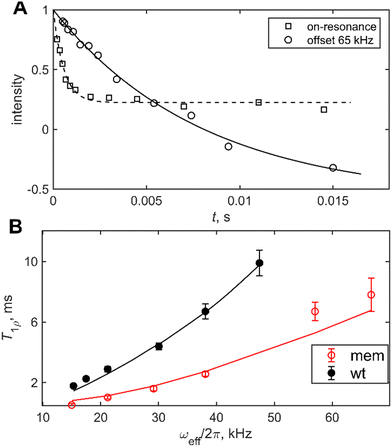Fig. 5 ²H solid-state NMR rotating frame relaxation measurements for the A2-CD₃ site of the mem fibrils, measured at 9.4 T and 310 K under static conditions and the spin-locking RF field strength of 15 kHz. (A) The normalized magnetization decay curves, M(t) versus t, for the on-resonance condition (squares) and the off-resonance example, corresponding to the value of the offset Ω = 65 kHz (circles). The lines represent the fit to the data to the monoexponential function with the baseline. The negative baseline for the off-resonance case is due to the inversion pulse prior to the spin-lock period as described in ref. 50 (B) The values of off-resonance ²H NMR relaxation times T_1ρversus the effective field ω_eff/2π for the wt fibrils (black) and mem fibrils (red). The lines represent the best fit to the model of Fig. 1(F) with the parameters specified in the text.

For the F4 and G9 sites this analysis was not feasible due to a very significant fraction of the bound state, which would render complications in data interpretations of the T_1ρ measurements focused on the narrow spectral component. However, for the G9 site a different approach can be undertaken to probe the conformational exchange rate constant. In particular, we analyzed the longitudinal relaxation behavior under the McConnel model.⁵³ The T₁ relaxation times values can be determined separately for the wide (bound state) and narrow (mobile state) spectral components (Fig. 3 and Fig. S3, ESI†). Under the assumption that 1/T^bound₁ = (1 − p_bound)k_ex, i.e., the McConnel model, and using p_bound = 0.76, as determined from the line shape decomposition, one can calculated the value of k_ex.

To enhance the signal to noise in the difficult-to-detect wide spectral component of the G9 site, we have employed the multiple-echo acquisition scheme (QCPMG),^54,55 in which the powder pattern is broken into a series of spikelets (Fig. 6(A)). The scheme is combined with the T₁ relaxation time measurements to yield T₁ values for the individual spikelets (Fig. 6(B)), thus retaining relaxation anisotropy.⁵⁶ The T₁ value for the bound state is taken as the average for the two spikelet positions at ±48 kHz, and corresponds to 0.18 ± 0.02 s⁻¹. The resulting value of k_ex is 23 s⁻¹, which is three orders of magnitude smaller than the value of 2 × 10⁴ s⁻¹ found for the wt fibrils,⁴⁸ for which the value of p_bound is 0.35.

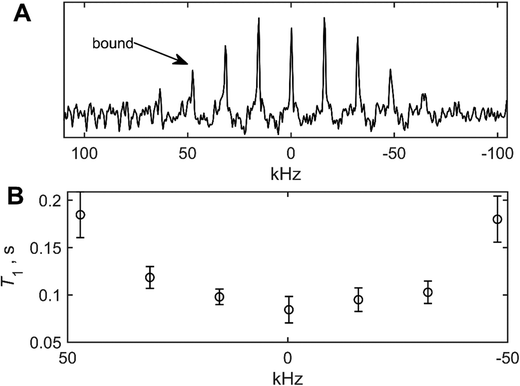Fig. 6 (A) ²H static solid-state NMR spectrum of the G9-C_αD₂ site of the mem fibrils, collected with the QCPMG scheme⁵⁵ at 308 K and 9.4 T. The spikelets are separated by 16 kHz intervals, and the ±48 kHz positions were taken as representative of the bound state, shown with the arrow. (B) Corresponding ²H NMR longitudinal relaxation T₁ times for each of the spikelet positions.

II. Internal motions in the selected structured regions of the fibrils.

For the residues in the structured hydrophobic core, as well as the V12 residues located at the end of the N-terminal domain, we focus on local internal modes, such as rotameric jumps of methyl bearing side chains and aromatic ring flips. The temperature dependence of these motions is governed by the underlying activation energies as well as by the different energies of rotamer states involved in the dynamics. These quantities report on the fibrils packing.

For methyl-bearing side chains the number of all available rotamers depends on the number of dihedral angles: one dihedral angle in valine gives rise to three possible rotamers, two dihedral angles in leucine to 9 rotamers, and three dihedral angles in methionine to 27. While the three rotamers of valine can be modeled explicitly, for leucine and methionine side chains in the restricted protein environment it is sufficient to use approximations to account for only several sufficiently populated rotamers. Under the assumption of the ideal tetrahedral sp³ bond geometry in leucine and methionine side chains, the combined effect of rotations about side-chain dihedral angles leads to only four magnetically inequivalent conformers which differ in their position of the C^γ–C^δ axis (leucine) or S–C^ε axis (methionine), demonstrated in Fig. 1(D) for the case of methionine.^{24,32,36,57,58} Thus, we utilize the model in which C^γ–C^δ axis in leucine and S–C^ε axis in methionine jumps between four different positions pointing toward the corners of the tetrahedron (Fig. 1(D)). The C^β–C^γ axis in the side-chain of valine jumps between three possible positions, which differ by the 120° angle.

In the asymmetric protein environment not all of the rotamers are equally populated.⁵⁹ The simplest assumption is to invoke a single major conformer with the weigh w, such that the relative weights of conformers are given by the ratio w : 1 : 1 in valine and w : 1 : 1 : 1 in leucine or methionine. The rate of rotameric interconversions (k_rot) is assumed to be the same between all rotamers for a given side-chain at a given temperature, again as the simplest assumption. The parameters of the model are listed in Table 2 in the systematic fashion. The temperature dependence of k_rot is taken as Arrhenius k_rot(T) = k₀ exp(−E_a/RT), and it yields the activation energy E_a of the rotameric motions. The temperature dependence of w follows a Boltzmann-type equation, w = e^b/R−ΔE/RT, with the possibility of a non-zero intercept, yielding the energy difference between the energy state ΔE.

Table 2 Definitions of the modeled parameters. Adapted from⁶⁸

Parameter	Definition
w	Occupation number of the dominant rotameric state relative to the minor states
k rot	Exchange rate between any two rotameric states defined as a sum of the forward and backward rates
E a	Activation energy of rotameric exchange, krot = k0e^−Ea/RT
ΔE	Energy difference between the major and minor rotameric states used in the Boltzmann relation, w = e^b/R−ΔE/RT
E ^flipa	Average activation energy for π-flips of a phenylalanine ring
p bound	Fraction of the bound state of N-terminal domain residues
D	Effective diffusion coefficient for the fluctuations of free state of the N-terminal domain

---

Deuterium line shape measurements are sensitive to these rotameric interconversions, if they fall on the time scale of the order of the quadrupolar coupling constants. For methyl groups C_q values are in the 53–58 kHz range, after averaging over fast methyl rotations.^31,46,60,61 Examples of line shapes are shown in Fig. 7(A) and Fig. S4 (ESI†). The line shapes were fitted to the above models (Fig. 7(B)) to yield the modeled parameters using fitting routines established in prior works.^24,36 The dependence of line shapes on quadrupolar echo delay can serve as an additional tool in the confirmation of the model and its parameters.^60,62 We performed these measurements for the V36 and M35 methyl sites at the highest temperatures (Fig. S7, ESI†). The results are in line with the model of rotameric inter-conversions.

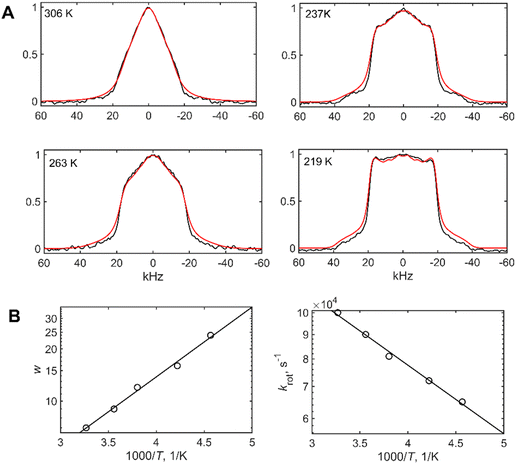Fig. 7 (A) Examples of ²H static solid-state NMR line shape data for the L34-C^γD₃ site, collected at 9.4 T and at different temperatures, shown directly on the panels (black lines) and fits according to the rotameric exchange model of Fig. 1(D) (red). (B) The fitted values of populations, w versus 1000/T, and rotameric exchange rates, k_rotversus 1000/T, on the semi log scales. The lines represent corresponding linear fits to the data using the Boltzmann and Arrhenius-type equations.

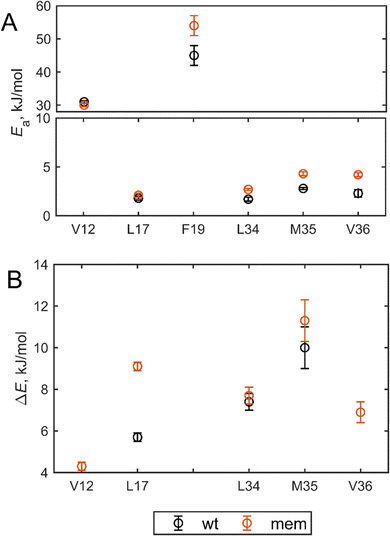
The values E_a and ΔE were fitted from the temperature dependence of k_rot and w, respectively. Note that for V12 residue this analysis was conducted after the fraction of the free state, which is around 10%, with large-scale rearrangements present, was obtained in the line shape decomposition (Fig. 3) and subtracted from the overall shape. This subtraction represents the resulting line shape of the bound state. The E_a values for rotameric inter-conversions are increased in all residues of mem fibrils (Fig. 8(A)), with the exception of V12. The result points to tighter side-chain packing in the structured region and less flexibility in the side-chain motions of the mem fibrils compared to the wt fibrils. The values of ΔE, reflecting the statistical factor of rotameric weights, are only different within the errors for the L17 side-chain with the higher value in the mem fibrils, but similar within errors for all other sites (Fig. 8(B)). Thus, the driving force behind the differences in rotameric interconversions between mem and wt fibrils is kinetic in nature stemming from the differences in the activation energies.

Fig. 8 (A) Activation energies E_a of the rotameric inter-conversions in methyl-bearing side-chains in the hydrophobic core and the V12 side-chain, as well as the average activation energy of ring-flipping motion for the F19 ring. The low range expansion is shown in the bottom panel. (B) The energy differences ΔE between the major and minor rotameric states in the methyl bearing side-chains.

The ring-flipping motions at the F19 site were probed by the line shape measurements and T₁ experiments (Fig. 9 and Fig. S8, S9, ESI†). The line shapes at 305 K are shown in Fig. 9(B). The motionally unaveraged tensor for phenylalanine ring deuterons has the quadrupolar coupling constant C_q = 180 kHz and the asymmetry parameter of zero.^37,63 Thus, in the absence of motions the typical powder pattern with the “horns” at around ±60 kHz is expected. The ring flipping motions on the intermediate time scale, for which the rate constant is on the order of C_q, modify the powder pattern to yield significant intensity in the −15 to 15 kHz region. The overlay of the experimental line shapes for the mem and wt fibrils (Fig. 9(B)) near the physiological temperature has been normalized to the ±60 kHz singularities, such that the higher intensity in the middle region of the spectrum indicates larger ring-flipping rates. The mem fibrils display a pattern of significantly slowed down ring-flipping motions in comparison to the wt fibrils.

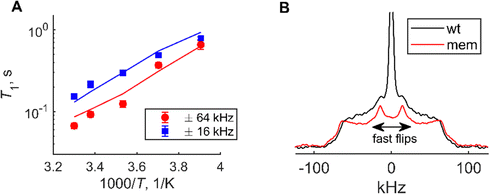Fig. 9 (A) ²H static solid state NMR longitudinal relaxation times data for mem fibrils at the F19-ring-D₅ site at 9.4 T, collected with the multiple echo acquisition scheme.⁵⁵ Longitudinal relaxation times T₁versus 1000/T at two spectral spikelet positions, ±16 kHz (red) and ±64 kHz (blue), obtained from the fit to the stretched exponential function, as elaborated in SI3. The lines represent the fits to the global model across the full temperature range, which allows for the determination of the ring-flipping activation energies. (B) ²H NMR line shapes of the wt (black) and mem (red) fibrils at the F19-ring-D₅ site, normalized to the intensities at the ±60 kHz spectral positions, collected at 305 K.

With lowering of the temperature and the corresponding decrease in the ring-flipping rate constants, the line shape measurements are expected to be less sensitive to the rate of the ring-flipping motions, as the line shapes themselves are expected to approach the rigid limit, in which the rate constant is much slower than the value of the quadrupolar coupling constant. The onset of the rigid limit was observed at around 270 K for the wt fibrils.⁶⁴ However, to assess the temperature dependence of the dynamics across the entire 310 to 250 K range we can utilize the T₁ relaxation measurements. The longitudinal relaxation rates have contributions from two motional modes: the primary mode in this range is due to the ring-flipping motions with minor contributions from small angle fluctuations of the phenyl axis. The latter were determined for the wt fibrils⁶⁴ as well as for a globular protein³⁷ and can be assumed to be the same for the mem fibrils, as they depend overwhelmingly on the local structures of the side chains and are independent of the details of the secondary and tertiary structures. The activation energy range for the ring-flipping motion, E^flip_a, can be inferred from global analysis of the relaxation rates across the entire temperature range.³⁷ We present this technical analysis, performed using a previously developed workflow, in SI2, and the details of the raw data acquisition and processing in Fig. S5 and S6 (ESI†). In similarity to the wt fibrils, there is a distribution of activation energies, which could be approximated to follow the Gaussian shape. The model leads to the apparent non-linear fit of ln T₁versus 1/T.

The fitted mean value for the mem fibrils is E^flip_a is 54 ± 3 kJ mol⁻¹, which is larger compared with the value for the wt fibrils of 45 ± 3 kJ mol⁻¹. The widths of the Gaussian distribution are similar within the precision of the measurements: 6.1 ± 0.4 kJ mol⁻¹ for the mem fibrils and 6.8 ± 0.4 kJ mol⁻¹ for the wt fibrils. The significance of the larger value of E^flip_a goes beyond the rigidity of the F19 side-chain itself, as the ring-flipping motions inside the core require concerted rearrangement of the entire core to occur. Thus, the results at the F19 site report on the overall rigidification of the core from the more global angle.

Discussion and conclusion

The modified seeded growth protocol coupled with TEM and ThT characterizations enabled a controlled preparation of Aβ_1–40 fibrils that retained several of the features of the parent generation, which was prepared at the relatively high lipid to protein content (20 : 1) with the lipid source originating from rat synaptic plasma vesicles. The resulting fibrils demonstrated a distinct rigidification of the dynamics throughout the two domains of mem Aβ_1–40 fibrils in comparison to the wt fibrils. In particular. In the N-terminal domain for residues A2, F4, and G9 we observed larger fractions of the bound state which is characterized by quenched large-amplitude motions. Additionally, the rate constant for the exchange process between the free and the bound states was markedly decreased, by orders of magnitude in the case of G9. In the C-terminal, we observed increased activation energies of rotameric inter-conversions of the methyl bearing side chains (residues L17, L34, M35, V36) as well the elevated value of the average activation energy for the ring-flipping motions of the F19 site, which points inside the hydrophobic core in the wt fibrils.

How the overall rigidification arises in the context of the specific protein–lipid interactions and the potential changes in the fibrils’ structure is not entirely clear. However, our studies provide an initial point of refence for the overall conformational ensemble spanned by the Aβ fibrils generated in the presence of synaptic plasma vesicles, and the effects that the membranes can have on the Aβ aggregates’ flexibility. The charged N-terminal domain, which is disordered in the wt fibrils, likely interacts with the ionic or acidic phospholipids, while the effects on the fibrils’ hydrophobic core could also be partially mediated by the presence of cholesterol. The overall packing environment of the resulting fibrils must change significantly to enable the general restriction of the side-chain dynamics. Alkyl chain of lipids can also provide an additional source of restricted environment,⁶⁵ causing the decrease in the extent of side-chains motions.

Most interestingly, the changes in the flexibility, likely induced in the parent generation in the presence of the relatively high lipid to protein ratio, appear to propagate through at least two generations used in the preparation of the NMR samples. Thus, our work sets the stage for follow-up investigations of inter-related changes in Aβ conformations and membrane rearrangements. It would be interesting to include different types of vehicles in the follow-up studies, which could span model lipid membranes with selected structural components as well as a broader range of synaptic vesicles.

Membrane-induced conformational/mobility changes in amphipathic Aβ aggregates can be important for the re-alignment of protein aggregates within the membrane, which in turn would act as a disruption pathway of the membrane integrity.^2,66 Zanden et al.⁶⁷ identified two different modes of membrane-mediated Aβ toxicity using liquid surface X-ray scattering and Langmuir trough insertion assays: fibril-induced reorganization of lipid packing and membrane destabilization caused by non-fibrillar aggregates. The increased rigidity of the originally disordered N-terminal domain can be particularly relevant in the re-alignment of fibrillar Aβ aggregates and subsequent changes in lipid packing. Further advances in high resolution spectroscopic techniques are needed to capture the changes not only in the structure but also in the dynamics at high lipid to protein ratio.

Materials and methods

Preparation of the fibrils

I. Peptide synthesis. The peptides were prepared using solid-state peptide synthesis (Life Technologies Corporation, Carlsbad CA). The amino acids were purchased from Cambridge Isotopes laboratories (Andover, MA) and CDN isotopes (Pointe-Claire, Canada). The peptides were purified by reversed-phase HPLC to the minimal purity level of 95% and their identity and purity were confirmed by mass spectrometry and reversed-phase HPLC.

II. Liposomes preparation. The preparation of the liposomes from the isolated synaptic plasma membranes was described in Cheng et al.²⁸ In this work the hippocampus region of the 12-month old rats was used, with the chemical composition of the membranes previously determined.²⁸ The total concentration of lipids was determined from ³¹P solution NMR to be 644 μM. The protocols for the extraction of lipids and the determination of concentration closely followed description of Cheng et al.²⁸ The suspension of the liposomes for seeded growth protocols was initiated by diluting the stock solution (described in SI1) by a factor of 1.8 with the 10 mM monosodium phosphate buffer at pH 7.4 and 0.05% w/w NaN₃. The solution was incubated at 4 °C for 14 hours before employing it for the imaging studies and the Aβ generation seeding protocols.

III. The seeded growth protocol. The parent generation of fibrils was prepared using 20 : 1 lipid : protein molar ratio at 10 μM Aβ_1–40 concentration in the 10 mM monosodium phosphate buffer at pH 7.4, by first dissolving the lyophilized monomeric Aβ peptide in 5 mM dimethyl sulfoxide (DMSO). The first generation was prepared using the parent generation as seeds in 1 : 10 molar ratio with the final Aβ concentration of 25 μM. The second generation was prepared using the first generation as seeds in 1 : 10 molar ratio with the final Aβ concentration of 50 μM. The relative content of lipids in the second (final) generation is given by the 0.2 : 1 lipid : protein molar ratio. We did not employ sonication of the seeds to avoid potential damage to the membranes. Each generation was incubated on an orbital shaker with a gentle 40 rpm agitation at 25 °C. The incubation times of the parent and 1st generation were 4–6 days, while the incubation time of the 2nd generation was 7–8 days.

IV. NMR sample preparation. The bulk fibrils for the NMR analysis were collected by centrifugal dialysis using Amicon filters with the 3 kDa molecular weight cut-off. Collected fibrils were re-suspended in deionized water, rapidly frozen with liquid nitrogen, and lyophilized. The samples were packed in 5 mm NMR tubes (cut to 21 mm length) using Teflon tape to center the sample volume in the coil of the NMR probe. A hydrated state with a water content of 200% by weight was achieved by pipetting deuterium-depleted H₂O directly in the NMR tubes, followed by mixing, flash freezing the hydrated fibrils in the tubes in liquid nitrogen, defrosting, and equilibrating for at least 48 hours to ensure homogeneous hydration.

Transmission electron microscopy

Samples were negatively stained by using the drop method⁶⁹ in the following manner.⁷⁰ Four microliter aliquots of the sample, millipore-filtered water, and 2% uranyl acetate aqueous stain were applied sequentially to a freshly glow-discharged Formvar carbon-coated 300 mesh copper grid for the following incubation times: 2 min, 10 s, and 1.5 min, respectively. For the parent and first generations two rounds of sample application were used. For the final generation, a dilution factor of 2 with Millipore-water was required. Each 4 μl droplet was removed by wicking with filter paper for 5 s. The filter paper was blotted prior to the addition of the next droplet. After staining, the grid was air-dried under a vacuum for 20 min. Images were collected under low dose conditions of 120 000× using the FEI Tecnai G2 Spirit Biotwin microscope operating at 80 kV.

NMR procedures

The experiments were performed using a 9.4 T NMR spectrometer equipped with the static Phoenix probe with a 5 mm diameter coil. Temperature calibration was carried out by recording the static lead nitrate line shapes.⁷¹

The ²H static solid-state NMR line shape measurements utilized the quadrupole echo pulse sequence based on an eight-step phase cycle,⁶⁰ with the echo delay of 36 μs between 90° pulses and the 90° pulse width of 2 μs. The echo delay of 36 μs is the shortest delay on our system that consistently yields minimally distorted baseline from the acoustical ringing. For several sites of the mem fibrils (Fig. S4 and S7, ESI†) we also analyzed the dependence of line shapes on different values of the echo delays.

The number of scans ranged between 12 000 to 30 000. Relaxation delays were set to three times the longitudinal relaxation times, which were determined by either inversion recovery or saturation recovery experiments. Time domain free induction decays data in the line shape measurements were left-shifted to the echo maximum and a 500 to 1000 Hz exponential line broadening function was employed.

Longitudinal relaxation time measurements for the G9 and F19 sites involved the quadrupolar multiple-echo acquisition scheme (QCPMG) for signal enhancement.^55,72 This scheme retains relaxation anisotropy.⁵⁶ Ten to twelve QCPMG echoes were collected using 90° pulses with the 2 μs pulse length and with the 63 μs pulse spacing delay. 20 480 were collected for the F4 labeled sample, and from 512 to 4096 for the F19 labeled sample at different temperatures. 8 to 16 dummy scans were used.

Deuterium off-resonance rotating frame NMR relaxation measurements (T_1ρ) under static conditions for the A2 site were performed as described previously.⁵⁰ The spin-lock field ω_RF was set to 15 kHz, with the range of offsets between 3 and 45 kHz. To align the magnetization in the rotating frame, we employed the adiabatic ramp with the “tanh/tan” shape.⁷³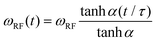, where τ is the duration of the ramp and α is the steepness parameter. The modulation of the offset during the ramp time is given by Ω + ΔΩ(t), where Ω is the final frequency offset after the ramp and ΔΩ(t) is the additional offset during the ramp time. The functional form is 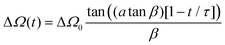, where ΔΩ₀ is the sweep and β is the steepness parameter for the offset. We have used τ = 0.4 ms, α = 1.5, β = 5, ΔΩ = 40 kHz. The magnetization decay curve was sampled between 0.5 and 15 ms. The interscan delay of 1.8 s and 1024 scans were used, with 32 dummy scans The spectral intensities were integrated over the −2.5 to 2.5 kHz spectral region. The fit of the magnetization decay curves utilized the monoexponential function with a baseline of .

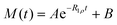Modeling

The line shapes and laboratory frame T₁ relaxation rate were modeled with the EXPRESS program.⁷⁴ After accounting for averaging over the fast methyl jumps, the quadrupolar coupling constant was set to C_q = 53.3 kHz for V12, L17, L34, and V36 methyl groups and 58 kHz for the M35 methyl group, with the asymmetry parameter η = 0.⁷⁵ The fitting parameters of the models, population of the major conformer w, and rotameric exchange rate constant k_rot were obtained using the iterative procedure outlined in prior work.²⁴

For the on and off resonance R_1ρ simulations,^50,51 the direct numerical integration of the full Liouville-von Neumann equation was performed.³³ The evolution during the spin-lock periods is governed by the quadrupolar coupling interactions for spin-1 deuterons. For the off-resonance case, the inclusion of longitudinal relaxation in the model is taken as a phenomenological factor.^50,76 The longitudinal relaxation time was measured as 35 ± 1 ms, with the inversion recovery method. The relaxation delays used in the simulations of the R_1ρ and R^off_1ρ rates matched the experimental ones. The procedure to model isotropic diffusion using a discrete form of the Smoluchovski equation in conjunction with the conformational exchange constant is described in reference²⁵ and involves the use of DistMesh program.⁷⁷ The quadrupolar tensor parameters for the A2 methyl site were taken as C_q = 53.3 kHz, η = 0.

The global motional model (Fig. 1(E)) for modeling the longitudinal relaxation times at the F19-ring-D₅ site over the entire temperature range is described in SI2 and was performed according to previously developed protocols.^37,64

The error limits presented in Fig. 5, 6, and 8 were calculated using the covariance matrix method, while the errors in the value of p_bound were estimated from the visual comparison of the fitted and simulated spectra overlap.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the National Institutes of Health grants 1R15-GM111681 to L. V.

References

1. D. C. Bode, M. Freeley, J. Nield, M. Palma and J. H. Viles, J. Biol. Chem., 2019, 294, 7566–7572.
2. T. L. Williams and L. C. Serpell, FEBS J., 2011, 278, 3905–3917.
3. C. Reitz, Int. J. Alzheimer's Dis, 2012, 2012, 369808.
4. F. J. Sepulveda, J. Parodi, R. W. Peoples, C. Opazo and L. G. Aguayo, PLoS One, 2010, 5, e11820.
5. J. Lee, Y. H. Kim, F. T. Acre, A. L. Gillman, H. Jang, B. L. Kagan, R. Nussinov, J. Yang and R. Lal, ACS Chem. Neurosci., 2017, 8, 1348–1357.
6. M. Zhang, R. Hu, B. Ren, H. Chen, B. Jiang, J. Ma and J. Zheng, ACS Chem. Neurosci., 2017, 8, 524–537.
7. V. Rangachari, D. N. Dean, P. Rana, A. Vaidya and P. Ghosh, Biochim. Biophys. Acta, Biomembr., 2018, S0005–2736(0018), 30084.
8. G. P. Gorbenko and P. K. Kinnunen, Chem. Phys. Lipids, 2006, 141, 72–82.
9. Y. L. Lyubchenko, Alzheimers Res. Ther. Open Access, 2020, 3, 114.
10. P. N. Lacor, M. C. Buniel, L. Chang, S. J. Fernandez, Y. Gong, K. L. Viola, M. P. Lambert, P. T. Velasco, E. H. Bigio, C. E. Finch, G. A. Krafft and W. L. Klein, J. Neurosci., 2004, 24, 10191–10200.
11. J. Marsh and P. Alifragis, Neural Regener. Res., 2018, 13, 616–623.
12. T. L. Mai, H. T. Nguyen, P. Derreumaux and P. H. Nguyen, Proteins, 2023 DOI:10.1002/prot.26508.
13. Z. Niu, W. Zhao, Z. Zhang, F. Xiao, X. Tang and J. Yang, Angew. Chem., Int. Ed., 2014, 53, 9294–9297.
14. X. Yu, Q. Wang, Q. Pan, F. Zhou and J. Zheng, Phys. Chem. Chem. Phys., 2013, 15, 8878–8889.
15. J. M. Kenyaga, Q. Cheng and W. Qiang, J. Biol. Chem., 2022, 298, 102491.
16. H. Jang, J. Zheng and R. Nussinov, Biophys. J., 2007, 93, 1938–1949.
17. M. F. Sciacca, S. A. Kotler, J. R. Brender, J. Chen, D. K. Lee and A. Ramamoorthy, Biophys. J., 2012, 103, 702–710.
18. K. Yanagisawa, Biochim. Biophys. Acta, 2007, 1768, 1943–1951.
19. E. A. Yates and J. Legleiter, Biochemistry, 2014, 53, 7038–7050.
20. Z. Niu, Z. Zhang, W. Zhao and J. Yang, Biochim. Biophys. Acta, 2018, 1860, 1663–1669.
21. T. Deo, Q. Cheng, S. Paul, W. Qiang and A. Potapov, Chem. Phys. Lipids, 2021, 236, 105071.
22. G. Gorbenko, V. Trusova, M. Girych, E. Adachi, C. Mizuguchi and H. Saito, Adv. Exp. Med. Biol., 2015, 855, 135–155.
23. O. N. Antzutkin, R. D. Leapman, J. J. Balbach and R. Tycko, Biochemistry, 2002, 41, 15436–15450.
24. L. Vugmeyster, M. A. Clark, B. I. Falconer, D. Ostrovsky, D. Gantz, W. Qiang and G. L. Hoatson, J. Biol. Chem., 2016, 291, 18484–18495.
25. D. F. Au, D. Ostrovsky, R. Fu and L. Vugmeyster, J. Biol. Chem., 2019, 294, 5840–5853.
26. A. T. Petkova, W. M. Yau and R. Tycko, Biochemistry, 2006, 45, 498–512.
27. H. A. Scheidt, I. Morgado, S. Rothemund and D. Huster, J. Biol. Chem., 2012, 287, 2017–2021.
28. Q. Cheng, Z. W. Hu, Y. Tobin-Miyaji, A. E. Perkins, T. Deak and W. Qiang, Biomolecules, 2020, 10, 881.
29. R. R. Vold, in Nuclear Magnetic Resonance Probes of Molecular Dynamics, ed. R. Tycko, Kluwer academic Publishers, Dordrecht, 1994, pp.27–112.
30. M. F. Brown, M. P. Heyn, C. Job, S. Kim, S. Moltke, K. Nakanishi, A. A. Nevzorov, A. V. Struts, G. F. J. Salgado and I. Wallat, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 2979–3000.
31. X. Shi and C. M. Rienstra, J. Am. Chem. Soc., 2016, 138, 4105–4119.
32. L. Vugmeyster and D. Ostrovsky, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 101, 1–17.
33. L. Vugmeyster, Solid State Nucl. Magn. Reson., 2021, 111, 101710.
34. L. Vugmeyster and D. Ostrovsky, Methods, 2018, 148, 136–145.
35. Ü. Akbey, Solid State Nucl. Magn. Reson., 2023, 125, 101861.
36. L. Vugmeyster, D. Ostrovsky, A. Khadjinova, J. Ellden, G. L. Hoatson and R. L. Vold, Biochemistry, 2011, 50, 10637–10646.
37. L. Vugmeyster, D. Osrovsky, T. R. Villafranca, J. Sharp, W. Xu, A. S. Lipton, G. L. Hoatson and R. L. Vold, J. Phys. Chem. B, 2015, 119, 14892–14904.
38. N. J. Yang and M. J. Hinner, Methods Mol. Biol., 2015, 1266, 29–53.
39. A. T. Petkova, R. D. Leapman, Z. H. Guo, W. M. Yau, M. P. Mattson and R. Tycko, Science, 2005, 307, 262–265.
40. Z. W. Hu, L. Cruceta, S. Zhang, Y. Sun and W. Qiang, ACS Chem. Neurosci., 2021, 12, 3625–3637.
41. A. K. Paravastu, R. D. Leapman, W. M. Yau and R. Tycko, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18349–18354.
42. L. P. Jameson, N. W. Smith and S. V. Dzyuba, ACS Chem. Neurosci., 2012, 3, 807–819.
43. J. Foley, S. E. Hill, T. Miti, M. Mulaj, M. Ciesla, R. Robeel, C. Persichilli, R. Raynes, S. Westerheide and M. Muschol, J. Chem. Phys., 2013, 139, 121901.
44. W. Qiang, K. Kelley and R. Tycko, J. Am. Chem. Soc., 2013, 135, 6860–6871.
45. G. B. Fields, Curr. Protoc. Protein Sci., 2002, 18.11.11 Chapter 18.
46. Ü. Akbey, J. Magn. Reson., 2021, 327, 106974.
47. L. Vugmeyster, D. Ostrovsky, A. Greenwood and R. Fu, J. Magn. Reson., 2022, 337, 107171.
48. L. Vugmeyster, D. F. Au, D. Ostrovsky and R. Fu, ChemPhysChem, 2019, 20, 1680.
49. L. Vugmeyster, D. F. Au, D. Ostrovsky, B. Kierl, R. Fu, Z. W. Hu and W. Qiang, Biophys. J., 2019, 117, 1524–1535.
50. L. Vugmeyster, A. Rodgers, D. Ostrovsky, C. James McKnight and R. Fu, J. Magn. Reson., 2023, 352, 107493.
51. L. Vugmeyster and D. Ostrovsky, ChemPhysChem, 2019, 20, 333–342.
52. A. G. Palmer, J. Biomol. NMR, 2009, 45, 1–4.
53. H. M. McConnell, J. Chem. Phys., 1958, 28, 430–431.
54. F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, Chem. Phys. Lett., 1998, 292, 467–473.
55. F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, J. Phys. Chem. A, 1997, 101, 8597–8606.
56. R. L. Vold, G. L. Hoatson, L. Vugmeyster, D. Ostrovsky and P. J. De Castro, Phys. Chem. Chem. Phys., 2009, 11, 7008–7012.
57. L. S. Batchelder, C. E. Sullivan, L. W. Jelinski and D. A. Torchia, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 386–389.
58. T. H. Huang, R. P. Skarjune, R. J. Wittebort, R. G. Griffin and E. Oldfield, J. Am. Chem. Soc., 1980, 102, 7377–7379.
59. R. L. Dunbrack, Jr. and F. E. Cohen, Prot. Sci., 1997, 6, 1661–1681.
60. R. L. Vold and R. R. Vold, in Advances in Magnetic and Optical Resonance, ed. W. Warren, Acadenic Press, San Diego, 1991, vol. 16, pp.85–171.
61. L. Vugmeyster and D. Ostrovsky, J. Chem. Phys., 2014, 140, 075101.
62. A. J. Vega and Z. Luz, J. Chem. Phys., 1987, 86, 1803–1813.
63. Y. Hiyama, J. V. Silverton, D. A. Torchia, J. T. Gerig and S. J. Hammond, J. Am. Chem. Soc., 1986, 108, 2715–2723.
64. L. Vugmeyster, D. Ostrovsky, G. L. Hoatson, W. Qiang and B. I. Falconer, J. Phys. Chem. B, 2017, 121, 7267–7275.
65. A. Sahoo and S. Matysiak, Phys. Chem. Chem. Phys., 2019, 21, 22679–22694.
66. A. Rice, S. Haldar, E. Wang, P. S. Blank, S. A. Akimov, T. R. Galimzyanov, R. W. Pastor and J. Zimmerberg, Nat. Commun., 2022, 13, 7336.
67. C. M. Vander Zanden, L. Wampler, I. Bowers, E. B. Watkins, J. Majewski and E. Y. Chi, Langmuir, 2019, 35, 16024–16036.
68. A. Rodgers, M. Sawaged, D. Ostrovsky and L. Vugmeyster, J. Phys. Chem. B, 2023, 127, 2887–2899.
69. J. R. Harris and J. W. Horne, in Electron Microscopy in Biology, ed. J. R. Harris, IRL Press, Oxford, 1991, pp.203–228.
70. J. Dubochet, M. Groom and S. Mueller-Neuteboom, in Adv. Opt. Electron Microsc., ed. R. Barrer and V. E. Cosslett, 1082, vol. 8, pp.107–135.
71. P. A. Beckmann and C. Dybowski, J. Magn. Reson., 2000, 146, 379–380.
72. F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, Mol. Phys., 1998, 95, 1185–1195.
73. F. A. A. Mulder, R. A. de Graaf, R. Kaptein and R. Boelens, J. Magn. Reson., 1998, 131, 351–357.
74. R. L. Vold and G. L. Hoatson, J. Magn. Reson., 2009, 198, 57–72.
75. L. Vugmeyster, D. Ostrovsky, J. J. Ford, S. D. Burton, A. S. Lipton, G. L. Hoatson and R. L. Vold, J. Am. Chem. Soc., 2009, 131, 13651–13658.
76. L. Vugmeyster, D. Ostrovsky and R. Fu, ChemPhysChem, 2020, 21, 220–231.
77. P.-O. Persson and G. Strang, SIAM Rev., 2004, 46, 329–345.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04824a

---