The formation energy, phase transition, and negative thermal expansion of Fe2−xScxW3O12†
Gaojie
Zeng‡
 a,
Chunyan
Wang‡
abc,
Huanli
Yuan
ac,
Xi
Zhen
a,
Qilong
Gao
a,
Chunyan
Wang‡
abc,
Huanli
Yuan
ac,
Xi
Zhen
a,
Qilong
Gao
 a,
Juan
Guo
a,
Mingju
Chao
a,
Xiansheng
Liu
*b and
Erjun
Liang
a,
Juan
Guo
a,
Mingju
Chao
a,
Xiansheng
Liu
*b and
Erjun
Liang
 *a
*a
aSchool of Physics & Microelectronics, and Key Laboratory of Materials Physics of Ministry of Education of China, Zhengzhou University, Zhengzhou 450052, China. E-mail: ejliang@zzu.edu.cn; Fax: +86 371 67766629; Tel: +86 371 67767838
bHenan Key Laboratory of Photovoltaic Materials and School of Future Technology (Quantum Information), Henan University, Kaifeng 475004, China. E-mail: xsliu@henu.edu.cn
cSchool of Physics and Telecommunication Engineering, Zhoukou Normal University, Zhoukou 466001, China
First published on 24th November 2023
Abstract
Tungstates with a molecular formula A2W3O12 exhibits a wider negative thermal expansion (NTE) temperature range than molybdates but are challenging to synthesize, especially when A = Fe or Cr with metastable structures. To enhance the structural stability of Fe2W3O12, Sc with lower electronegativity is adopted to substitute Fe according to Fe2−xScxW3O12, considering the thermodynamic stability of Sc2W3O12. It is shown that the solid solutions can be easily synthesized and the phase transition temperature (PTT) can be tuned to well below room temperature (RT). Theoretical calculations and experimental results show that the formation energy decreases and the W–O bond in Fe–O–W gradually strengthens as the substitution of Sc in Fe2−xScxW3O12 increases, indicating an increase in structural stability. NTE is enhanced after phase transition with an increase in the Sc content. The reduction in PTT and the enhancement in NTE properties of Fe2W3O12 could result in a decrease in the effective electronegativity of the Fe-site elements, resulting in a low formation energy and strengthened W–O bond in Fe–O–W, which corresponds to a more stable structure.
1 Introduction
Materials with negative thermal expansion (NTE) properties have potential advantages in modulating the coefficients of thermal expansion (CTEs) and improving the thermal shock resistance of devices and instruments. In recent years, significant progress has been made in NTE materials, such as framework oxides,1–9 fluorides,10–12 and cyanides.13–17However, NTE materials still have some disadvantages in practical applications, such as hygroscopicity,18 toxicity,19 a narrow NTE temperature range,20 sensitivity toward high temperatures,21 negative environment impacts,22 and difficult synthesis.23
Oxide-based NTE materials with a stable structure and wide NTE temperature range offer an excellent platform for designing novel NTE materials with the desired properties for potential applications. One of the oxide-based NTE materials, A2M3O12, where A is a trivalent transition metal or rare earth element and M is Mo6+ or W6+, generally has an NTE in a wide temperature range and is chemically flexible for the design of NTE materials with desired properties.24–30 However, their NTE is observed only after the phase transition from a low-temperature monoclinic to a high-temperature orthorhombic structure. Moreover, they are hygroscopic and, except for Sc2M3O12, their NTE generally appears after the complete depletion of water molecules. Furthermore, tungstates are more challenging to synthesize than molybdates. These limiting factors seriously restrict their industrial applications. Much effort has been devoted to regulating the phase transition and reducing the hygroscopicity toward designing NTE materials with desired properties.1,31
Fe2W3O12 is compositionally cheap, but it is challenging to obtain a high purity regardless of the solid-state reaction or sol–gel method owing to its metastable structure.32,33 Its monoclinic to orthorhombic phase transition is reported at about 687 K and is accompanied by abrupt volume thermal expansion.34 Mary et al. reported that Sc3+ substitution could promote Ga2W3O12 to form a pure phase material.35 Varga et al. reported that Sc2W3O12 is thermodynamically stable, while other tungstates in the A2W3O12 series were only entropically stabilized at high temperatures.30 Therefore, it is reasonable that the metastable structure of Fe2W3O12 could be stabilized by introducing Sc. In this paper, we report a method for synthesizing Fe2W3O12 and reducing its phase transition temperature (PTT) below room temperature (RT) by introducing Sc. Theoretical calculations show that the formation energy decreases and the W–O bond in Fe–O–W gradually strengthens as the substitution amount of Sc in Fe2−xScxW3O12 increases.
2 Materials and methods
Analytical grade reagents of Fe2O3, Sc2O3, and WO3 were used as raw materials, which were weighted and ground according to the molar ratios of the target materials of Fe2−xScxW3O12. The mixed raw materials were pressed into cylinders with a diameter of 10 mm and a thickness of 5 mm using a 769YP-15A tablet machine with a pressure of about 200 MPa on the cylinder's green body. Twice sintering processes at about 1323 K for 4 h with intermediate grinding are needed for the desired products.To identify the crystalline phase and analyze cell volume changes, temperature-dependent XRD patterns were carried out with a Rigaku (Japan, SmartLab 3 kW) diffractometer with Cu Kα radiation (λ = 1.5406 Å), equipped with a high-temperature attachment of the model multi-temperature, with a scan speed of 4° min−1 and a step of 0.01° and 40 kV/40 mA power. The samples were held at each temperature for 20 min to maintain thermal equilibrium before the XRD measurement. Crystal structure refinement was performed using Rietveld refinement with Fullprof software. Raman spectra were recorded with HORIBA Lab RAM HR Evolution (HORIBA Scientific, France), equipped with a Linkam THMS600 Heating and Freezing Stage (Japan Hightech) (an accuracy of ±0.1 K). A laser excitation wavelength of 532 nm was used. The sample was held for about 5 min at each temperature to attain thermal equilibrium before the Raman measurements. The linear CTEs were measured by applying a dilatometer (Linseis DILL76) with a heating rate of 5 K min−1. Differential scanning calorimetry (DSC) measurements were carried out using a thermal analyzer (Netzsch STA 449F3) with a 10 K min−1 heating rate. Scanning electron microscopy coupled with energy dispersive spectroscopy (SEM-EDS) was tested using a field-emission scanning electron microscope (JSM-7001F).
3 Results and discussion
The XRD patterns at RT of Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, 2.0) are shown in Fig. 1a. The primary diffraction peaks for the sample with x = 0.5 correspond to PDF no. 38-0200 of monoclinic Fe2W3O12. Fe2W3O12 is a metastable material that is difficult to synthesize through solid-state reactions. Substitution of Sc3+, even in a small quantity, for Fe3+ in Fe2W3O12 benefits pure phase synthesis, which could be related to the reduction in the formation energy of Fe2W3O12. A comparison of the XRD patterns of x = 1.5 and 2.0 with those of x = 0.5 and 1.0 shows that the featured peak for the monoclinic phase at 26.2° disappears, and a peak at around 22° splits up. The results indicate that Fe2−xScxW3O12 adopts a monoclinic phase for x = 0.5 and 1.0, and an orthorhombic phase for x = 1.5 and 2.0 at RT. The theoretical calculation optimization of the adopted structure is used to find the suitable element substitution position, and the stable structure is depicted in Fig. 2. Fig. 3 shows the refinement results of (a) Fe1.5Sc0.5W3O12, (b) Fe1.0Sc1.0W3O12, (c) Fe0.5Sc1.5W3O12, (d) Fe0.25Sc1.75W3O12, and (e) Sc2W3O12. Structure refinements by applying the Rietveld method demonstrate that Fe2−xScxW3O12 adopt a monoclinic phase with space group P21/c for x = 0.5 and 1.0 and an orthorhombic structure with space group Pnca for x = 1.5, 1.75, 2.0 at RT. Fig. S3 (ESI†) shows the lattice parameters and volume with a substitution ratio of Sc from the refinement results (To facilitate comparison, the cell volumes of the monoclinic phase of x = 0.5, 1.0 are divided by 2, as calculated in ref. 36). With the substitution of Sc3+ for Fe3+ in Fe2W3O12, lattice volume increases gradually. Cell parameters are depicted in Table S1 (ESI†), and structural parameters are presented in Tables S2–S6 in ESI.† It can be observed from Fig. 1a that with the increase in Sc3+ substitution, the peak position shifts slightly toward a smaller angle, indicating an increase in the lattice constants due to the larger cation radius of Sc3+ (74.5 pm) than that of Fe3+ (64 pm). To detect the microstructure and elemental composition, SEM-EDS was performed. In Fig. S1 (ESI†), the SEM images show that with the substitution of Sc in Fe2W3O12, the average particle sizes increase, and the interspaces gradually disappear. As depicted in Fig. S2 (ESI†), the information from the EDS spectra is almost consistent with the molar ratio of Fe/Sc. | ||
| Fig. 1 (a) XRD patterns, (b) Raman spectra, and (c) Raman peak positions shifting with a substituting ratio of Sc3+ by fitting Raman peaks (b) at 800–1025 cm−1, (d) the formation energy change with substituting ratio both in monoclinic phase Fe2−xScxW3O12 (x = 0.5, 1.0) and orthorhombic phase Sc2−xFexW3O12 (x = 0.25, 0.5). (The calculation process is presented in ESI,† and the raw data are depicted in Table S7, ESI†). | ||
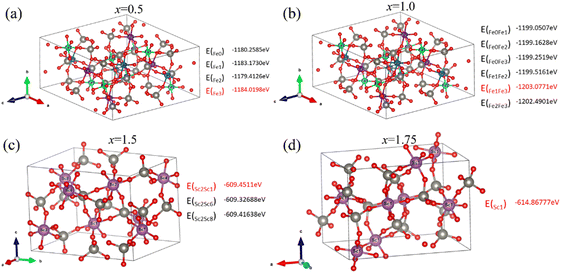 | ||
| Fig. 2 The stable structure and formation energy of Sc substitution in Fe2W3O12 and Fe substitution in Sc2W3O12 (a)–(d) corresponding to Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, and 1.75). | ||
 | ||
| Fig. 3 The Rietveld analysis of XRD patterns at RT (detailed cell parameters are given in Table S1, ESI†): (a) x = 0.5 (Rp = 3.29, Rwp = 4.50, and Rexp = 2.15) and (b) x = 1.0 (Rp = 3.70, Rwp = 4.85, and Rexp = 2.07) for the monoclinic, space group P21/c; (c) x = 1.5 (Rp = 5.29, Rwp = 7.05, and Rexp = 1.95), (d) x = 1.75 (Rp = 5.61, Rwp = 7.47, and Rexp = 2.05) and (e) x = 2.0 (Rp = 5.40, Rwp = 7.18, and Rexp = 2.32) for the orthorhombic, space group Pnca. | ||
The phase transition from monoclinic to orthorhombic with an increase in Sc3+ substitution can also be characterized by Raman spectra. Fig. 1b shows the Raman spectra of Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, 2.0). The bands at about 1000 and 800 cm−1 are attributed to the stretching vibrations of WO4 tetrahedra, and 340 and 100 cm−1 are attributed to the symmetric and asymmetric bending motions of Fe/ScO6 octahedra and WO4 tetrahedra, respectively.18 When x = 1.0 and 0.5, the shoulder peak at about 1000 cm−1 is observed only for the monoclinic phase, which is assigned to the stretching vibrations of the W–O bond. This agrees well with the XRD results. The shoulder peak is only present in the monoclinic phase and disappears with an increase in the substitution of Sc3+ (x = 1.5 and 2.0) for Fe3+ in Fe2W3O12.
The results suggest that the x = 1.5 and 2.0 samples transformed to the orthorhombic phase. Fig. 1c shows the Raman peak positions shifting with the substitution ratio of Sc3+ by fitting Raman peaks in Fig. 1b at 800–1025 cm−1 to explore the change in the stretching vibrations of W–O in Fe–O–W and Sc–O–W with the substitution of Sc for Fe. The peak, corresponding to the asymmetric stretching vibration of W–O, shifts to higher wavenumbers in Fe–O–W but to lower wavenumbers in Sc–O–W. The introduction of Sc strengthens the W–O bond in Fe–O–W, improving the stable performance of Fe2W3O12.
We investigated the stability of the substituted system Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, 1.75) using the first-principles calculations. The thermodynamic stability can be expressed by the formation energy (Eform) both in monoclinic phase (1) and orthorhombic phase (2) as follows:37,38
| Eform = Etot(subst) − Etot(Fe2W3O12) − nμSc + nμFe, | (1) |
| Eform = Etot(subst) − Etot(Sc2W3O12) − nμFe + nμSc, | (2) |
Fig. 4a shows the thermal expansion property with increasing temperatures of Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, 1.75, 2.0). The sample with x = 0.5 shows a normal thermal expansion from RT to 490 K in the monoclinic phase and a low NTE following an abrupt expansion corresponding to the monoclinic–orthorhombic phase transition. By increasing the substitution amount of Sc3+ for Fe3+ in Fe2W3O12, the PTT decreases gradually from 490 to 320 (x = 1.0) and 210 K (x = 1.5). After the phase transition, Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, 1.75, 2.0) show an NTE property with linear thermal expansion coefficients of −0.566 × 10−6 K−1 (523–673 K), −0.606 × 10−6 K−1 (385–673 K), −3.54 × 10−6 K−1 (210–673 K), −2.48 × 10−6 K−1 (160–673 K), and −2.92 × 10−6 K−1 (160–673 K), respectively.
 | ||
| Fig. 4 (a) Relative length change measured using a dilatometer. (b) DSC curves (endothermic peak represents phase transition process), (c) temperature-dependent XRD patterns of Fe1.5Sc0.5W3O12, (d) an increase in cell volume with an increase in temperature of Fe1.5Sc0.5W3O12. (To facilitate comparison, the cell volumes of the monoclinic phase, as calculated in ref. 30, were divided by 2. The corresponding cell parameters change with temperature as shown in Fig. S4, ESI†). | ||
The DSC curves for the samples are shown in Fig. 4b. The endothermic peaks appear for the x = 0.5 and 1.0 curves, corresponding to the phase transition observed in the thermal expansion and temperature-dependent Raman results (Fig. 3).
Fig. 4c displays the temperature-dependent XRD patterns of Fe1.5Sc0.5W3O12. The phase transition process can be recognized with the disappearing and splitting of specific peaks. Fig. 4d shows the cell volume change with temperature. This agrees well with the thermal expansion curves acquired by the dilatometer shown in Fig. 2a.
The temperature-dependent XRD of Fe0.5Sc1.5W3O12 is also investigated (Fig. 5a). Fig. 5b shows a schematic diagram of the crystal structure of Fe0.5Sc1.5W3O12. Fig. 5c depicts the changes in lattice constants for the a-, b- and c-axes with temperatures ranging from RT to 1073 K from the refinement of temperature-dependent XRD patterns, showing anisotropy in thermal expansion. Fig. 5d shows the thermal expansion curve of the sample from RT to 1073 K measured by a dilatometer and the volume change acquired from temperature-dependent XRD. The lattice constants of the a- and b-axes decrease, whereas those of the c-axis increase with heating, yielding a linear thermal expansion coefficient of a cell volume contraction of −1.3 × 10−6 K−1 from 300–1000 K, which is slightly smaller than that measured by the dilatometer. Yuan et al. proposed a linear scaling law in which effective electronegativity can scale the interaction between oxygen atoms and further predicate the phase transition of A2M3O12-based compounds.31 Owing to the lower electronegativity of Sc (1.20, Allred-Rochow39,40) than that of Fe (1.64, Allred-Rochow39,40), with the substitution of Sc3+ for Fe3+ in Fe2W3O12, more effective charges on oxygen produce more significant oxygen–oxygen repulsion, preferring the less compact crystal structure that contributes to the phase transition from the monoclinic to the orthorhombic of Fe2−xScxW3O12 (x = 0.5, 1.0, 1.5, 1.75, 2.0). The PTT (Tt) could also be estimated by averaged effective electronegativity χeff, and the scaling law is given by eqn (3) and (4):
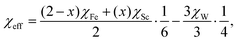 | (3) |
| Tt = c·χeff + d, | (4) |
| Tt = 7176.92 χeff + 1124.27. | (5) |
 | ||
| Fig. 6 The linear fitting of and the scaling law predication curve of Fe2−xScxW3O12 (x = 0.0, 0.5, 1.0, and 1.5) (a), tungstates (b).29,42–46 | ||
Fig. 7a shows the temperature-dependent Raman spectra of Fe2−xScxW3O12 with x = 0.5 ranging from 100 to 700 K. The featured Raman peak for the monoclinic phase at about 1003 cm−1 appears from 100 to 510 K and then disappears above 510 K. For the sample with x = 1.5 in Fig. 7b, the featured Raman peak at about 1032 cm−1 for the monoclinic phase appears at about 210 K, suggesting the monoclinic to orthorhombic phase transition of the sample. However, no monoclinic featured peak appears from 90 to 670 K for the sample with x = 1.75 in Fig. 7c, suggesting that the phase transition occurs at a lower temperature than 90 K for x = 1.75. The temperature-dependent Raman results are consistent with the phase transition observed by the thermal expansion curves, as depicted in Fig. 4a. According to previous reports on temperature-dependent Raman and high-pressure Raman spectra of A2M3O12 framework materials, the phase transition from the orthorhombic to the monoclinic is always accompanied by the appearance of a featured Raman peak aside from the main stretching Raman mode. It is located on the left side of the main peak if M = W and on the right-hand side of M = Mo.28,29,47,48
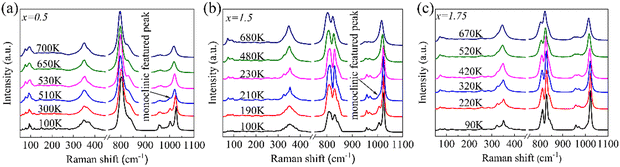 | ||
| Fig. 7 The temperature-dependent Raman spectra of (a) Fe1.5Sc0.5W3O12, (b) Fe0.5Sc1.5W3O12, and (c) Fe0.25Sc1.75W3O12. | ||
4 Conclusions
The solid solutions of Fe2−xScxW3O12 are developed by the substitution of Sc3+ for Fe3+ in Fe2W3O12, and the PTT can be tuned to well below RT. The much easier synthesis of the solid solutions than Fe2W3O12 is attributed to the reduced formation energy by incorporating Sc, as demonstrated by the theoretical calculations. Fe2−xScxW3O12 crystallizes in a monoclinic structure for x = 0.5 and 1.0 and an orthorhombic phase for x ≥ 1.5 at RT. The PTT from the monoclinic to orthorhombic decreases from 490 K to 320 K, 210 K, and temperatures lower than 160 K for x = 0.5, 1.0, 1.5, and 1.75, respectively. The linear scaling law can explain the regulation of the PTT. NTE is observed for the samples above their PTTs. The wider range of NTE for x ≥ 1.5 suggests potential applications in many fields.Author contributions
Erjun Liang, Xiansheng Liu and Gaojie Zeng conceived the idea. Gaojie Zeng designed the experiments, prepared the samples, performed the measurements and analysis and prepared the manuscript. Chunyan Wang conceived the DFT calculations idea and did calculation with Xi Zhen. Qilong Gao, Juan Guo, and Mingju Chao give some suggestions for the prepare process.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11874328, 11574276).Notes and references
- E. Liang, Q. Sun, H. Yuan, J. Wang, G. Zeng and Q. Gao, Front. Phys., 2021, 16, 53302 CrossRef.
- J. Chen, Q. Gao, A. Sanson, X. Jiang, Q. Huang, A. Carnera, C. G. Rodriguez, L. Olivi, L. Wang, L. Hu, K. Lin, Y. Ren, Z. Lin, C. Wang, L. Gu, J. Deng, J. P. Attfield and X. Xing, Nat. Commun., 2017, 8, 14441 CrossRef PubMed.
- N. Khosrovani, A. W. Sleight and T. Vogt, J. Solid State Chem., 1997, 132, 355–360 CrossRef.
- T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92 CrossRef.
- S. Sumithra and A. M. Umarji, Solid State Sci., 2006, 8, 1453–1458 CrossRef.
- J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1997, 133, 580–583 CrossRef CAS.
- Y. Zhou, S. Adams, R. P. Rao, D. D. Edwards and A. Neiman, Chem. Mater., 2008, 20, 6335–6345 CrossRef CAS.
- J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1995, 120, 101–104 CrossRef CAS.
- X. Ge, Y. Mao, X. Liu, Y. Cheng, B. Yuan, M. Chao and E. Liang, Sci. Rep., 2016, 6, 24832 CrossRef CAS PubMed.
- B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498 CrossRef CAS PubMed.
- J. C. Hancock, K. W. Chapman, G. J. Halder, C. R. Morelock, B. S. Kaplan, L. C. Gallington, A. Bongiorno, C. Han, S. Zhou and A. P. Wilkinson, Chem. Mater., 2015, 27, 3912–3918 CrossRef CAS.
- J. Xu, L. Hu, Y. Song, F. Han, Y. Qiao, J. Deng, J. Chen and X. Xing, J. Am. Ceram. Soc., 2017, 100, 5385–5388 CrossRef CAS.
- A. L. Goodwin and C. J. Kepert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 140301 CrossRef.
- A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980–17981 CrossRef CAS PubMed.
- S. d'Ambrumenil, M. Zbiri, A. M. Chippindale, S. J. Hibble, E. Marelli and A. C. Hannon, Phys. Rev. B, 2019, 99, 024309 CrossRef.
- Q. Gao, J. Wang, A. Sanson, Q. Sun, E. Liang, X. Xing and J. Chen, J. Am. Chem. Soc., 2020, 142, 6935–6939 CrossRef CAS PubMed.
- S. J. Hibble, A. M. Chippindale, A. H. Pohl and A. C. Hannon, Angew. Chem., Int. Ed., 2007, 46, 7116–7118 CrossRef CAS PubMed.
- X. Liu, Y. Cheng, E. Liang and M. Chao, Phys. Chem. Chem. Phys., 2014, 16, 12848–12857 RSC.
- S. J. Hibble, A. M. Chippindale, E. Marelli, S. Kroeker, V. K. Michaelis, B. J. Greer, P. M. Aguiar, E. J. Bilbé, E. R. Barney and A. C. Hannon, J. Am. Chem. Soc., 2013, 135, 16478–16489 CrossRef CAS PubMed.
- Y. Du, Q. Gao, A. Sanson, H. Xie, Y. Hu, G. Zeng, J. Guo, X. Ren and E. Liang, Results Phys., 2022, 35, 105415 CrossRef.
- H. Wang, M. Yang, M. Chao, J. Guo, Q. Gao, Y. Jiao, X. Tang and E. Liang, Solid State Ion., 2019, 343, 115086 CrossRef CAS.
- B. R. Hester, J. C. Hancock, S. H. Lapidus and A. P. Wilkinson, Chem. Mat., 2017, 29, 823–831 CrossRef CAS.
- G. Zeng, H. Yuan, J. Guo, Q. Sun, Q. Gao, M. Chao, X. Ren and E. Liang, Phys. Chem. Chem. Phys., 2020, 22, 12605–12612 RSC.
- C. P. Romao, F. A. Perras, U. Werner-Zwanziger, J. A. Lussier, K. J. Miller, C. M. Calahoo, J. W. Zwanziger, M. Bieringer, B. A. Marinkovic, D. L. Bryce and M. A. White, Chem. Mater., 2015, 27, 2633–2646 CrossRef CAS.
- T. Suzuki and A. Omote, J. Am. Ceram. Soc., 2004, 87, 1365–1367 CrossRef CAS.
- B. A. Marinkovic, P. M. Jardim, M. Ari, R. R. DeAvillez, F. Rizzo and F. F. Ferreira, Phys. Status Solidi B, 2008, 245, 2514–2519 CrossRef CAS.
- A. Madrid, P. I. Pontón, F. Garcia, M. B. Johnson, M. A. White and B. A. Marinkovic, Ceram. Int., 2020, 46, 3979–3983 CrossRef CAS.
- X. Ge, Y. Mao, L. Li, L. Li, N. Yuan, Y. Cheng, J. Guo, M. Chao and E. Liang, Chin. Phys. Lett., 2016, 33, 046503 CrossRef.
- F. Li, X. Liu, W. Song, B. Yuan, Y. Cheng, H. Yuan, F. Cheng, M. Chao and E. Liang, J. Solid State Chem., 2014, 218, 15–22 CrossRef CAS.
- T. Varga, J. L. Moats, S. V. Ushakov and A. Navrotsky, J. Mater. Res., 2007, 22, 2512–2521 CrossRef CAS.
- H. Yuan, C. Wang, Q. Gao, G. Zeng, J. Guo, M. Chao, S. Kawaguchi, Y. Jia and E. Liang, Mater. Horiz., 2021, 8, 2562–2568 RSC.
- H. Zhang, Q. Zhang, H. Du and Q. Jia, Chem. Eng. Commun., 2007, 195, 243–255 CrossRef.
- A. K. Sriraman and A. K. Tyagi, Thermochim. Acta, 2003, 406, 29–33 CrossRef CAS.
- G. Yang, X. Liu, X. Sun, E. Liang and W. Zhang, Ceram. Int., 2018, 44, 22032–22035 CrossRef CAS.
- T. Mary and A. Sleight, J. Mater. Res., 1999, 14, 912–915 CrossRef CAS.
- J. S. O. Evans and T. A. Mary, Int. J. Inorg. Mater., 2000, 2, 143–151 CrossRef CAS.
- K. Matsunaga, T. Kubota, K. Toyoura and A. Nakamura, Acta Biomater., 2015, 23, 329–337 CrossRef CAS PubMed.
- C. Tang, L. Zhang, D. Wijethunge, K. K. Ostrikov and A. Du, J. Phys. Chem. C, 2021, 125, 24648–24654 CrossRef.
- A. L. Allred and E. G. Rochow, J. lnorg. Nucl. Chem., 1958, 5, 264–268 CrossRef.
- E. J. Little and M. M. Jones, J. Chem. Educ., 1960, 37, 231–233 CrossRef.
- A. W. Sleight and L. H. Brixner, J. Solid State Chem., 1973, 7, 172–174 CrossRef.
- G. Zeng, H. Yuan, J. Guo, X. Liu, M. Chao and E. Liang, J. Solid State Chem., 2022, 314, 123339 CrossRef.
- H. Liu, Z. Zhang, J. Ma, Z. Jun and X. Zeng, Ceram. Int., 2015, 41, 9873–9877 CrossRef.
- T. Sugimoto, Y. Aoki, E. Niwa, T. Hashimoto and Y. Morito, J. Ceram. Soc. Jpn., 2007, 115, 176–181 CrossRef.
- F. Zhang, Y. Lei, Z. Zhang, H. Liu, X. Zhang, X. Chen and X. Zeng, Ceram. Int., 2020, 46, 7259–7267 CrossRef.
- I. Koseva, A. Yordanova, P. Tzvetkov, V. Nikolov and D. Nihtianova, Mater. Chem. Phys., 2012, 132, 808–814 CrossRef.
- W. Song, J. Wang, Z. Li, X. Liu, B. Yuan and E. Liang, Chin. Phys. B, 2014, 23, 066501 CrossRef.
- M. Maczka, W. Paraguassu, A. G. Souza Filho, P. T. C. Freire, J. Mendes Filho, F. E. A. Melo and J. Hanuza, J. Solid State Chem., 2004, 177, 2002–2006 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04816k |
| ‡ Gaojie Zeng and Chunyan Wang contributed equally to this work. |
| This journal is © the Owner Societies 2024 |

