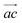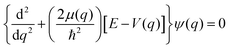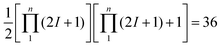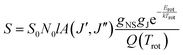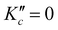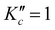High-resolution infrared spectroscopy of jet cooled cyclobutyl in the α-CH stretch region: large-amplitude puckering dynamics in a 4-membered ring radical

Abstract

Gas-phase cyclobutyl radical (c-C₄H₇) is generated at a rotational temperature of T_rot = 26(1) K in a slit-jet discharge mixture of 70% Ne/30% He and 0.5–0.6% cyclobromobutane (c-C₄H₇Br). A fully rovibrationally resolved absorption spectrum of the α-CH stretch fundamental band between 3062.9 cm⁻¹ to 3075.7 cm⁻¹ is obtained and analyzed, yielding first precision structural and dynamical information for this novel radical species. The α-CH stretch band origin is determined to be 3068.7887(4) cm⁻¹, which implies only a modest (≈0.8 cm⁻¹) blue shift from rotationally unresolved infrared spectroscopic studies of cyclobutyl radicals in liquid He droplets [A. R. Brown, P. R. Franke and G. E. Douberly, J. Phys. Chem. A, 2017, 121, 7576–7587]. Of particular dynamical interest, a one-dimensional potential energy surface with respect to the ring puckering coordinate is computed at CCSD(T)/ANO2 level of theory and reveals a double minimum C_s puckered geometry, separated by an exceedingly shallow planar C_2v transition state barrier (E_barr ≈ 1 cm⁻¹). Numerical solutions on this double minimum potential yield a zero-point energy for the ground state (E_zero-point ≈ 27 cm⁻¹) greatly in excess of the interconversion barrier. This is indicative of highly delocalized, large amplitude motion of the four-membered ring structure, for which proper vibrationally averaging of the moment of inertia tensor reproduces the experimentally determined inertial defect remarkably well. Finally, intensity alternation in the experimental spectrum due to nuclear spin statistics upon exchange of three indistinguishable H atom pairs (I_H = ½) matches K_a + K_c = even : odd = 36 : 28 predictions, implying that the unpaired electron in the radical center lies in an out-of-plane p_π orbital. Thus, high-resolution infrared spectroscopy provides first experimental confirmation of a shallow double minimum ring puckering potential with a highly delocalized ground state wave function peaked at a planar C_2v transition state geometry consistent with a cyclobutyl π radical.

---

I. Introduction

Cycloalkanes, also known as naphthenes, are saturated cyclic hydrocarbon compounds prevalent in conventional fuels (as much as 3% in gasolines and even up to 40% in diesels) as well as biomass and liquefied-coal-derived fuels.^1–4 The ability to predictively understand and model the complex combustion and pyrolysis chemistry of these cyclic hydrocarbons is clearly important to the development of alternative fuels. The reactions of cycloalkanes in an oxidative environment begin with H atom abstraction by hydroxyl radicals and/or unimolecular dissociation of the CH bond, resulting in the generation of cycloalkyl radicals.⁵ While many theoretical studies have been performed to investigate the oxidation kinetics of cycloalkanes and thereby characterize the role of cycloalkyl radicals,^6–9 spectroscopic data on these highly reactive combustion intermediates have proven elusive. This absence is unfortunate, as such spectroscopic studies provide important structural and dynamical data with which to benchmark high level ab initio theoretical efforts, and in addition also create opportunities for real-time in situ probing of such cyclic radicals in a complex combustion environment. There have been notable previous spectroscopic successes in these directions, such as rovibrationally-resolved infrared (IR) spectroscopy of the simplest three-carbon cyclic hydrocarbon radical, cyclopropyl (c-C₃H₅), studied in detail by direct laser absorption methods.¹⁰ Furthermore, and only quite recently, the high-resolution IR spectrum of the much larger five-carbon cyclopentyl radical (c-C₅H₉) was successfully obtained and analyzed under jet cooled conditions.¹¹ What proved particularly surprising in these latter studies is that cyclopentyl radical spectra revealed well resolved, completely assignable high-resolution rotational structure in the CH stretch manifold, despite a high predicted density of vibrational states (50–100 states per cm⁻¹) in the 3000 cm⁻¹ region thought to be sufficient to initiate intramolecular vibrational relaxation (IVR) dynamics.¹² Such high-resolution spectra for the three- and five-carbon cycloalkyl radicals leaves the 4-carbon (c-C₄H₇) radical species as yet undetected and unexplored. This is quite relevant, as 4-carbon rings are remarkably ubiquitous in nature (e.g., thiamine dimers) though notably scarcer in synthetic products ostensibly due to ring strain.^13,14 As the main focus of this work, we turn toward the spectroscopic study of this four-membered ring cyclobutyl radical, both bridging the gap between three- and five-membered cycloalkyl radical species, as well as to help elucidate how the ring topology impacts out-of-plane puckering dynamics and cycloalkyl ring strain.

Cyclobutyl radical presents additional challenges because even its ground state gas phase structure has yet to be experimentally determined. Geometric optimization of cyclobutyl radical has been carried out at the couple-cluster with singles, doubles, and perturbative triples CCSD(T) level of theory¹⁵ with a series of ANOn (n = 0, 1, 2) basis sets.¹⁶ As shown in Fig. 1, the equilibrium structure for cyclobutyl radical is predicted to be a puckered (C_s) geometry, with a C_2v planar transition state connecting the two double minima via an out of plane ring puckering (“butterfly”) vibrational motion. Whether the vibrational ground state is dynamically “localized” in each of the 2 equivalent C_s symmetry wells depends on the (i) height of the C_2v interconversion barrier and (ii) the zero-point energy in the ring puckering mode. While high level ab initio methods provide information on energy difference between the electronic minimum and the transition state as well as the ring puckering frequency, experimental identification of the radical via high-resolution infrared spectroscopy with assignable rovibrationally resolved features represents the gold standard with which to evaluate, confirm, or reject such theoretical predictions.

Fig. 1 Top and side views of the CCSD(T)/ANO2 geometric structure for cyclobutyl radical at (A) planar transition state (C_2v point group, {E, C₂, σ_ac, σ_bc}) and (B) puckered electronic minimum (C_s point group, {E, σ_bc}). The puckering coordinate is defined as the dihedral angle between the reflection mirror plane σ_bc (coming out of the page, with in the plane and normal to the plane) and the plane formed by the right/left three carbon atoms, which are 86.828° and 90.000° at puckered and planar geometries, respectively. Note that the equilibrium puckering angle is relatively small (≈5 degrees) and exaggerated in (B) for better visual comparison. The a, b, c principal axes for the planar geometry are plotted, and the α-carbon on the radical is labeled.

Photoelectron spectroscopy of the cyclobutyl radical to generate its corresponding carbonium ion was first investigated by Schultz et al.,¹⁷ providing information about the ionic potential surface in the region where the geometry most closely resembles that of the radical due to the strong Franck–Condon factors. The vertical and adiabatic ionization potential (IP) were found to be 7.66 ± 0.02 eV and 7.54 ± 0.02 eV, respectively, with sufficient resolution to observe vibrational fine structure with vibrational progressions spaced by 990 ± 100 cm⁻¹. Theoretical studies predicted an ionization energy of 7.605 eV at the B3LYP/6-311G(2df,p) level of theory,¹⁸ in very good agreement with the experimental observation. Photodissociation dynamics of cyclobromobutane was then studied by Liu et al. using 2D velocity map imaging (VMI) methods,¹⁹ whereby cyclobutyl radicals were generated from C–Br bond fission at 234 nm and detected using non-resonant 157 nm photoionization. Even though a significant fraction of the cyclobutyl radicals were predicted to be formed with rovibrational energies above the barrier to 1-methylallyl formation (E_barr = 28.3 kcal mol⁻¹ at the G3B3 level), evidence for ring opening/isomerization dynamics was not observed, which was ascribed to large impact parameter partitioning of the excess photolysis recoil energy into overall rotation rather than internal vibration of the radical fragment.

To date, the only direct IR absorption detection of cyclobutyl radical has been from helium nanodroplet isolation studies by Douberly and co-workers.²⁰ In their work, nascent cyclobutyl radicals were formed from low temperature pyrolysis (500–700 °C) of cyclobutylmethyl nitrite, followed by solvation in He nanodroplets and rapid cooling to ∼0.4 K. These studies targeted the CH stretch fundamental region of cyclobutyl radical between 2800 and 3120 cm⁻¹, as detected by vibrationally fragmenting the nanodroplets with IR light from a continuous-wave optical parametric oscillator. As one important theoretical result of these studies, high-level CCSD(T)/ANO1 anharmonic frequencies predicted for the C_2v transition state structure proved to be in much better agreement with the experimentally observed CH stretch frequencies, suggesting that the ground state structure for cyclobutyl radical in the cold nanodroplet environment is better represented by a vibrationally averaged planar CCCC ring geometry. However, high order intramolecular coupling between these CH stretches with near resonant combination states can also introduce shifts in the vibrational states, resulting in potential ambiguity for the inferred ground state structure. Interestingly, higher temperatures in the pyrolysis cell resulted in significant ring opening and decomposition of cyclobutyl radical into 1-methylallyl and 1,3-butadiene, which were both observed and assigned in the cold He nanodroplet spectra. Indeed, a detailed theoretical potential energy surface for the C₄H₇ isomers by Ribeiro et al.²¹ nicely illustrated that after cyclobutyl radical crosses the barrier to ring opening, the nascent allylcarbinyl radical could rearrange to either produce 1-methylallyl or proceed to form the resonance stabilized 1,3-butadiene products via H atom ejection. Under such low temperature, condensed phase conditions, however, all rotational spectral structure is quenched by the He nanodroplet, which eliminates access into further insights for cyclobutyl radical offered by high-resolution gas phase rovibrational spectroscopic methods. To address such issues, this paper reports first high-resolution infrared absorption spectra for gas-phase cyclobutyl radical, with the radicals produced via dissociative electron attachment of cyclobromobutane in a pulsed slit-jet discharge expansion. The jet-cooled cyclobutyl radicals at low rotational temperatures of T_rot = 26(1) K are probed in the sp² hybridized CH stretch region by direct absorption using a difference-frequency IR spectrometer. Detailed high-resolution spectra of the α-CH stretch fundamental band around 3070 cm⁻¹ have been observed and unambiguously assigned, providing first precision gas-phase rovibrational constants for the ground and first α-CH stretch excited state of this radical.

The remainder of this paper is organized as follows. A brief summary of the slit-jet discharge IR spectrometer and the generation of cyclobutyl radicals is provided in Section II. Experimental high-resolution absorption spectra along with detailed rovibrational analysis of the observed α-CH stretch fundamental band are reported in Section III, which yield superb agreement (i.e., <1 cm⁻¹ in the gas phase vibrational band origin) with results from helium droplet IR studies.²⁰ Discussions on the ab initio 1D potential energy surface (PES) along the lowest-frequency ring puckering coordinate computed at CCSD(T)/ANOn (n = 0, 1, 2) levels of theory and its solutions using Numerov–Cooley methods are presented in Section IV A. In Section IV B, the expectation values of the moment of inertia tensor along the ring puckering coordinate are computed, which yield a theoretical inertial defect that agrees well with the experiment. The discussion continues in Section IV C, with a detailed analysis of the experimentally observed intensity alternation (K_a + K_c = even : odd = 36 : 28). This alternation originates from nuclear spin statistics for 3 pairs of identical Fermionic (spin ½) hydrogen nuclei, which confirms that cyclobutyl is a π radical with the unpaired electron on the radical C center to reside in an out-of-plane p_π orbital. Finally, in Section IV D, Boltzmann analysis of the rotational populations are used to characterize both the rotational temperature and absolute radical densities in the slit-jet discharge expansion source, with conclusions and future directions summarized in Section V.

II. Experiment

The high-resolution difference-frequency IR spectrometer and the pulsed slit supersonic discharge beam source have been described in detail elsewhere.²² In brief, the high sensitivity is achieved through: (i) the use of slit supersonic discharge expansions to generate and to cool hot radicals, increasing population per quantum state while reducing spectral congestion, (ii) perpendicular intersection of the IR light through the slit molecular beam source to yield reduced Doppler linewidths (60 MHz) and enhanced peak absorption cross sections, (iii) increased absorption path length in a multi-pass Herriott cell design, (iv) high frequency modulation of radical concentrations (50 kHz) to avoid 1/f noise, and (v) fast electronic subtraction circuits to eliminate common mode laser noise.

Narrow-band continuous-wave IR light (<1 MHz linewidth, 5–10 μW, and tunable from 2600–3500 cm⁻¹) is generated via difference frequency generation between a single mode tunable ring dye laser (Spectra-Physics 380A, Rhodamine 590 dye) and a single mode Ar⁺ laser (Spectra-Physics model 2020, 514.5 nm), with a 40 mm long magnesium-doped periodically poled lithium niobate (MgO:PPLN) crystal used for non-linear difference frequency conversion into the near/mid IR. As described previously by Riedle et al.,²³ a temperature and PZT controlled Fabry–Pérot etalon is locked onto the output of a polarization-stabilized HeNe laser and acts as an optical transfer cavity for frequency stabilization of the Ar⁺ laser (ν_Ar⁺). During a spectral scan, the dye laser frequency (ν_dye) is monitored by transmission fringes through this stabilized Fabry–Pérot etalon, from which the IR frequency (ν_IR = ν_Ar⁺ − ν_dye) is obtained directly. The resulting difference-frequency IR light is then split into two beams, with one beam directly sent to a liquid-nitrogen cooled InSb detector (reference), and the other one through an 18-pass Herriott cell (total path length 72 cm) parallel to the slit discharge expansion in the vacuum chamber before being focused onto the signal InSb detector (signal). The outputs of the two InSb detectors are then finely balanced with homebuilt circuits (1 MHz bandwidth) to subtract common mode laser technical noise with −30 dB dynamic range suppression. For frequency calibration, a travelling Michelson interferometer is compared daily against well-resolved rovibrational features in the ν₃ R(4) manifold of CH₄ transiently doped into the slit expansion,²⁴ resulting in a frequency accuracy on the order of 10 MHz (0.0003 cm⁻¹).

Cyclobromobutane (c-C₄H₇Br) is purchased from TCI America (purity > 96%) and used without further purification as a precursor molecule to generate cyclobutyl radicals (c-C₄H₇) in the slit discharge source. Neon and helium gases are bubbled through the liquid precursor and further diluted to produce a 70% Ne, 30% He, and ∼0.5–0.6% cyclobromobutane mixture before flowing into the pulsed valve at a total stagnation pressure of ∼400 mbar. Gas delivery to the slit expansion orifice (40 mm × 0.3 mm) occurs with a pulsed valve operating at 19 Hz repetition rate and 1000 μs pulse duration (<50 μs rise and fall times). The cyclobutyl radicals are generated in a tightly contained discharge behind the slit orifice with a −840 V 50 kHz square wave applied across the 1 mm insulating polymer between the slit jaws and the grounded valve body, resulting in peak discharge currents of 460 mA. Cyclobutyl radicals are generated via thermal electron dissociative attachment in the discharge region prior to the free jet expansion,^19,25

c-C₄H₇Br + e⁻ → c-C₄H₇ + Br⁻

whereby modulated radical species undergo rapid cooling down to 20–30 K rotational temperatures and collisional collimation along the slit axis for 10–20 fold reduced-Doppler broadening. The 50 kHz modulated absorption signals are then extracted using (i) lock-in detection in the frequency domain followed by (ii) gated integration over the 1000 μs gas pulse in the time domain.

III. High-resolution cyclobutyl radical α-CH stretch fundamental spectra and analysis

Reduced-Doppler IR absorption spectra of jet-cooled cyclobutyl radical in the α-CH stretch fundamental band region have been measured from 3062 cm⁻¹ to 3076 cm⁻¹ in 12.5 MHz (0.000417 cm⁻¹) frequency steps, with each spectral data point averaged over 10 gas pulses. To achieve further noise suppression and unambiguously confirm reproducibility for each of the transitions reported, the final spectrum is obtained by summing over ≈ 4 independent spectral scans in the P and R branch region, and ≈ 6–10 scans in the weaker Q branch region (as demonstrated over a small sample region in Fig. 2), yielding strong P, Q, and R branch features with signal-to-rms noise ratio (S/N) of ∼13, 9, and 19, respectively. The resulting experimental linewidths are 75 MHz (0.0025 cm⁻¹), slightly broader than the reduced-Doppler slit jet linewidth of 60 MHz (0.0020 cm⁻¹) due to the summation of the high-resolution spectra. Crucially, however, such data averaging offers an additional increase in S/N essential to spectral analysis of cyclobutyl radical, and which would be experimentally inaccessible without the long-term absolute laser frequency stability offered by the Fabry–Pérot optical transfer cavity methods described in Section II.

Fig. 2 Four experimental spectra in the 3065.75 cm⁻¹ region taken on different days are shown in black (spectral baselines translated upwards for visual ease of comparison). The spectrum in blue represents the average of the four raw spectra, revealing a √4 = 2-fold reduction in the noise necessary to clearly identify some of the weaker cyclobutyl radical transitions. Note that such high-resolution signal averaging would be impossible without day-to-day stability, sub-MHz precision, and accuracy of the He–Ne stabilized optical transfer cavity (free spectral range = 0.008298620(9) cm⁻¹).

An overview spectrum of the cyclobutyl radical α-CH stretch fundamental region is displayed in Fig. 3, revealing distinctive b-type (ΔK_a = odd, ΔK_c = odd) sub-bands since the displacement along the α-CH stretch vibrational coordinate (thus the transition dipole moment direction) lies mostly along the b principal axis (Fig. 1). Even though the spin multiplicity is a doublet (2S + 1 = 2) due to presence of an unpaired electron (S = ½) on the radical carbon center, the ab initio predicted spin-rotation constants are quite small (<20 MHz) and thus spin-rotation structure remains unresolved for the N states populated even under slit jet reduced-Doppler resolution conditions. Consequently, we can even neglect coupling between overall rotational end-over-end tumbling angular momentum (N) and the intrinsic spin angular momentum of the unpaired electron. In the interest of simplicity, therefore, standard asymmetric top spectroscopic notation N_KaKc is used throughout, where K_a (K_c) represents approximate quantum numbers for angular momentum projection along the a (c) body-fixed principal rotation axes, respectively.

Fig. 3 An overview of the rovibrationally resolved infrared spectrum for gas phase cyclobutyl radical in the α-CH stretch fundamental band region. The strongest P and R branch progressions are labeled with the ground state rotational quantum number along the top. Spin-rotation structure in cyclobutyl radical is certainly present but too small to be resolved even with slit jet reduced-Doppler resolution. The simulated PGOPHER spectrum (blue, inverted) is based on the experimental constants reported in Table 1 and assumes a least-squares fitted Boltzmann rotational temperature of 25.6 K and a Gaussian linewidth in the slit jet of 75 MHz.

Since this work represents the first rovibrationally resolved gas-phase spectrum of cyclobutyl radical, neither the ground nor the excited state spectroscopic constants are available in the literature, preventing spectral assignment via conventional two-line ground state combination differences. Instead, preliminary analysis of the α-CH stretch rovibrational band is guided by comparison with a PGOPHER simulation,²⁶ based on CCSD(T)/ANO1 anharmonically computed rotational and vibration-rotation interaction constants (summarized in Table 1) and the vibrational band origin from the He nanodroplet studies of Douberly and coworkers²⁰ (summarized in Table 2). For a b-type band and a near-oblate top cyclobutyl radical framework, where A ∼ B > C (i.e. moments of inertia I_a ∼ I_b < I_c), one predicts progressions of ^pP_Ka,Kc(N) and ^rR_Ka,Kc(N) branch transitions with a 2C ≈ 0.42 cm⁻¹ spacing, supplemented by a weaker but more spectrally congested Q branch features near the band origin. In agreement with these predictions, the prominent features in Fig. 3 can be readily assigned to these P and R branch progressions ( and ΔN = ΔK_c) with spacings between 0.37 and 0.44 cm⁻¹. The assignment of ground state rotational quantum number for the progressions is further confirmed by matched shifts and splittings in the P and R branch transitions accessing N_1,N and N_0,N (N = 4, 9, and 10) upper levels. The reason for this is that one or more of these upper rovibrational states are strongly coupled with a nearly resonant dark state manifold, resulting in readily detected shifts that cause the spectrally overlapped P and R branch transitions accessing these states to be shifted and/or split. These series of ^pP_Ka,Kc(N) and ^rR_Ka,Kc(N) progressions are therefore included in an initial fit to extract preliminary ground and excited state spectroscopic constants, with visual confirmation of the correct N labeling and vibrational band origin by accurate prediction of Q branch transitions near 3068.8 cm⁻¹. With improved constants and new predictions/comparisons between experimental and simulated spectra, a total of 200 rovibrational transitions can be readily assigned (N′′ = 0–13 and 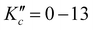), with frequencies and rovibrational assignments made available in the ESI.† Furthermore, this higher quality assignment of P, Q, and R branch lines permits assignment of 11 four-line combination differences that agree to within experimental uncertainty (Table S2, ESI†), thus confirming these sets of transitions to originate from the same lower state. As a result of (i) precision 4-line combination differences, (ii) agreement with ab initio rotational constant predictions and vibrational band origin from previous He nanodroplet study, as well as (iii) the predictability of cyclobromobutane chemistry in such a discharge, we are confident that the data unambiguously reflect first high-resolution infrared spectra of jet-cooled gas-phase cyclobutyl radical.

Table 1 Ground and first α-CH stretch excited state rotational constants in cm⁻¹

	Ground		Excited
	CCSD(T)/ANO1	Exp	CCSD(T)/ANO1	Exp
A	0.3948	0.396454(6)	0.3943	0.39592(9)
B	0.3576	0.363438(7)	0.3573	0.36297(9)
C	0.2081	0.212820(3)	0.2080	0.21279(2)
σ	—	0.0004	—	0.0101

---

Table 2 Theoretical and experimental band origin of the α-CH fundamental in cm⁻¹

	Origin
a Anharmonic frequency computed at the coupled cluster under second-order vibrational perturbation theory (VPT2). b Ref. 20.
Theoretical^a	3083.6
Helium nanodroplet^b	3069.6
Gas phase (this work)	3068.7887(4)

---

Cyclobutyl radical is a near oblate asymmetric top molecule with c as the unique principal rotation axis; therefore, a Watson rigid asymmetric top Hamiltonian in the III^r representation is chosen.²⁷ The centrifugal distortion (CD) terms are neglected because only low N levels are populated in the supersonic jet expansion, which are insufficient to determine CD values in a least squares fit. As there is visual evidence of irregular progressions (Fig. 3) due to perturbations in the upper rovibrational manifold, we first fit a total of 122 lower state combination differences (105 unique combination differences) to best determine the ground vibrational state. This yields the ground state A, B, C rotational constants reported in Table 1, with a standard deviation of the fit (σ ≈ 0.0004 cm⁻¹) comparable to experimental uncertainty. We next turn our focus onto the ν_{α-CH stretch} = 1 excited state, for which the ground state constants can be fixed and all 200 rovibrational transitions included in the least squares fit. The experiment vs simulation for a typical 1 cm⁻¹ spectral region in the R-branch is displayed in Fig. 4. Though the agreement is qualitatively quite good, isolated small spectral shifts (e.g., near 3071.80 cm⁻¹) make the ν_{α-CH stretch} = 1 excited state fit (σ ≈ 0.0101 cm⁻¹) now considerably worse (25×) than the frequency measurement uncertainty, which are attributed to local rotational crossings with near resonant “dark” states in the upper vibrational manifold. Due to the highly localized nature of the level shifts observed only in a few upper N′ states, it is reasonable to conclude that these perturbations arise from accidental a- or c-type Coriolis interactions with nearby overtone and/or combination band states.

Fig. 4 Spectral blowup of a small section (1 cm⁻¹) of the R-branch region of cyclobutyl radical near 3072 cm⁻¹, highlighting the agreement between high-resolution experimental data and the PGOPHER simulation from least-squares fit. Careful inspection, however, reveals small residual frequency shifts (∼0.01 cm⁻¹) and unassigned transitions due to intramolecular vibrational coupling with nearby “dark” states in resonance with the α-CH stretch manifold.

As summarized in Table 1, the difference between ground state A′′ and B′′ rotational constants is appreciable [(A′′ − B′′)/B′′ = 10%], consistent with a near-oblate top with significant asymmetry. This immediately confirms that the high-resolution spectra do not arise from trace cyclobutane in the discharge, which due to fast tunneling between puckered D_2d equilibrium geometries should exhibit pure oblate top (D_4h) behavior with A′′ = B′′. In addition, the least squares fit for the α-CH stretch cyclobutyl band origin at 3068.7887(4) cm⁻¹ differs appreciably from any sp³ CH stretch fundamentals in closed shell alkanes (2800–3000 cm⁻¹). Even more relevantly, the current band origin results are in remarkably quantitative agreement with infrared cyclobutyl radical spectroscopic studies in He nanodroplets by Douberly and coworkers,²⁰ which would imply only a small but finite blue shift (+0.8 cm⁻¹) possibly due to the additional He–H repulsion with respect to the CH bond coordinate.²⁸ Nevertheless, it should also be noted that red shifts of the H–X vibration due to the He nanodroplet environment have been found previously.²⁹ Our experimentally determined band origin is also in reasonable agreement with high-level CCSD(T)/ANO1 ab initio calculations for cyclobutyl radical, from which second-order vibrational perturbation theory (VPT2) predicts an anharmonic frequency of 3083.6 cm⁻¹.

IV. Discussion

A. Ab Initio 1D potential energy surface along the ring puckering coordinate

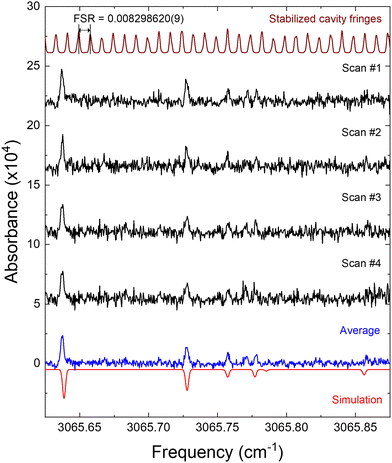
The equilibrium geometry for cyclobutyl radical likely reflects a C_2v to C_s symmetry breaking due to out-of-plane puckering of the four-carbon framework. The one-dimensional PES along the out-of-plane (oop) puckering coordinate therefore represents a symmetric yet highly anharmonic double well potential. In order to better characterize the barrier height/shape for such a double minimum potential, calculations at the CCSD(T)/ANOn (n = 0, 1, 2) level have been pursued to determine optimized (in 3N-7 orthogonal coordinates) geometries and energies as a function of oop puckering angle. This ring puckering coordinate is defined via Z matrix construction that maintains C_s symmetry throughout but achieves C_2v symmetry at the planar ring transition state geometry. The dihedral puckering angle between the right/left three C atoms and the reflection plane σ_bc (Fig. 1) is scanned from 90° to 110° (in 1° steps) and from 110° to 130° (in 5° steps) with all other coordinates fully optimized. A series of 1D potential curves along this ring puckering coordinate are plotted in Fig. 5 (top) at various levels of ab initio theory (CCSD(T)/ANOn, n = 0, 1, 2), revealing remarkably flat double minimum potentials with increasingly shallow barriers. Worth noting is that as the level of basis set increases, the potential becomes extremely shallow (with only a 1.0 cm⁻¹ barrier at the highest ANO2 level of theory) with the wall becoming correspondingly steeper. Indeed, the magnitude of this puckering barrier decreases so dramatically with increasing basis set quality that one cannot preclude the likely possibility of it vanishing entirely in the complete basis set (CBS) limit.

Fig. 5 (Top) Relaxed 1D potential energy surface along the ring-puckering coordinate computed at CCSD(T)/ANOn (n = 0, 1, 2) level of theory. A dihedral angle of 90° corresponds to the planar (C_2v) geometry. The puckering barriers are 9.586, 6.097, and 1.014 cm⁻¹ at CCSD(T)/ANO0, ANO1, and ANO2 level of theory, respectively. The empty data points are from theoretical calculations, and the solid curves represent spline interpolations of the ab initio data points. Also note the dramatic changes in potential barrier height and shape with increasing basis set level, which suggests the complete loss of symmetric double minimum character at even higher levels of ab initio theory and basis set size. (Bottom) The effective moment of inertia (in cm⁻¹ units) of the cyclobutyl radical along the ring puckering coordinate.

It is worth calculating the vibrational eigenvalues for this large amplitude 1D puckering motion, which requires solving the 1D time independent Schrodinger equation using Numerov–Cooley methods.^30,31 For such large amplitude displacements, the moment of inertia changes significantly in a path-dependent manner. To take this into account, we use the MULTIWELL program^32–34 to calculate the reduced moment of inertia along the ring puckering coordinate, with results summarized in Fig. 5 (bottom). The 1D Schrodinger equation is then solved numerically as a second-order differential equations of the form,³⁵

where q is the ring puckering coordinate, μ(q) is the coordinate-dependent reduced moment of inertia, and V(q) is the CCSD(T)/ANO2 double minimum potential function, with spline interpolation used to generate a smooth representation for μ(q) and V(q). The first three lowest energy puckering eigenfunctions are plotted in Fig. 6 with respect to their eigenenergies on the 1D double minimum potential. It should be noted that the ground state zero-point energy (26.98 cm⁻¹) is already greatly in excess of the double minimum barrier, resulting in peaking of the 1D wave function at the planar C_2v transition state geometry, instead of localization into the two symmetric wells.

Fig. 6 Lowest three cyclobutyl eigenfunctions for a 1D CCSD(T)/ANO2 ring puckering potential, solved numerically using Numerov–Cooley methods. Note that the vibrational ground state (E_zero-point = 26.976 cm⁻¹) is energetically in considerable excess of the 1.0 cm⁻¹ interconversion barrier. As a result, the corresponding ground state wave function is strongly peaked at the vibrationally averaged planar (C_2v) transition state geometry, with energies of the first and second excited states at 98.433, and 198.107 cm⁻¹, respectively.

B. Expectation values of the rotational constants

The high-resolution jet-cooled rovibrational spectra reported herein permit ground state rotational constants for gas phase cyclobutyl radicals to be experimentally measured for the first time. Based on CCSD(T)/ANO2 calculations, ab initio predictions of rotational constants at the C_s minimum puckered geometry are already reasonably close (<2%) to experiment (Table 3). However, such levels of discrepancy are certainly not unexpected, as any equilibrium geometry treatment necessarily ignores large amplitude 1D motion in the anharmonic ring puckering coordinate, for which vibrational averaging is crucial to reliable theoretical prediction and comparison with experimental values. To implement such corrections for large amplitude dynamics, we exploit the eigenfunctions obtained from the above Numerov Cooley analysis to average over the inverse moment of inertia tensor³⁶ as a function of the 1D puckering coordinate, for which an embedded Eckart reference geometry is used to minimize Coriolis interactions.^37,38 The results are summarized in Table 3, where the rotational constants, (i) first evaluated at the planar transition state (C_2v) and (ii) puckered minimum (C_s) and then as (iii) expectation values over large amplitude zero-point vibrational motion along the ring puckering coordinate, are compared with (iv) experimental ground state values. Although vibrational averaging along the oop puckering coordinate does result in some improvements, this process still yields substantial discrepancies between prediction and experiment, suggesting that residual errors in the optimized geometry may exist even at the highest CCSD(T)/ANO2 level of theory.

Table 3 Comparison between experimental ground state, theoretical, and large amplitude motion (LAM) corrected rotational constants in cm⁻¹, along with the inertial defects Δ in amu Ų. Note the quantitative agreement of predicted and observed inertial defects based on quantum vibrational averaging of the rotational constants over the LAM in the out-of-plane puckering mode

	A	B	C	Δ	Δ exclude H atoms
a The inertial defect of the planar geometry arises solely from the out-of-plane hydrogen atoms. Therefore, to only include the four-member carbon ring framework contribution, Δ at the planar transition state is subtracted from Δ to exclude the out-of-plane H atoms contribution. b The experimental rotational constants are the same as the ones shown in Table 1. However, they are listed here for ease of comparison.
Transition state (C2v)	0.3985	0.3641	0.2129	−9.421	0
Electronic minimum (Cs)	0.3983	0.3644	0.2133	−9.553	−0.132
LAM expectation	0.3982	0.3646	0.2137	−9.686	−0.265
Experimental^b	0.3965	0.3634	0.2128	−9.694(2)	−0.273

---

We can attempt a more targeted probe of large amplitude quantum effects by considering the inertial defect, Δ = I_C − I_A − I_B, a quantity which vanishes for any planar distribution of point masses. Of course, the inertial defect in cyclobutyl radical has non-vanishing contributions even at the planar transition state from the 6 methylenic H atoms and finite out-of-plane widths of the molecular orbital electron densities. However, focusing only on these residual non-zero deviations in Δ allows us to more selectively sample contributions from the CCCC ring framework.³⁹ In good qualitative agreement with expectations, the inertial defect (see Table 3) is negative and systematically decreases (becomes more negative) between the C_2v planar transition state and C_s puckered global minimum. Furthermore, the Δ value based on expectation values from vibrational averaging becomes additionally more negative. Such behavior is consistent with significant sampling at large puckering angles even though the ground state wave function is clearly peaked at the planar geometry. Finally, the inertial defect (Δ = −9.686 amu Ų) obtained from expectation values is now seen to be in extremely close agreement with experiment (Δ = −9.694(2) amu Ų), indicating near-quantitative success for capturing the effects due to vibrational averaged non-planarity of the four-member carbon ring.

C. Nuclear-spin intensity alternation

As described in Section IV A, the interconversion barrier for the 1D puckering potential is substantially smaller than any zero-point energy contributions. Thus, high-level ab initio methods predict a diffuse vibrationally averaged planar “structure”, with 3 pairs of H atoms interchanged and indistinguishable by a C₂ rotation around the b axis.⁴⁰ This of course places rigorous constraints on the symmetry of the total molecular wave function (Ψ_tot). Specifically, Ψ_tot must be antisymmetric with respect to the exchange of 3 pairs of identical H atoms, which leads to either exchange symmetric (+, ortho) or exchange antisymmetric (−, para) nuclear spin eigenstates. In the context of the Born Oppenheimer approximation (Ψ_tot ≈ Ψ_eleΨ_rovib) and for sufficiently small vibrational displacements (Ψ_rovib ≈ Ψ_vibΨ_rot), the rovibronic Hamiltonian is approximately separable, and the total wave function can be written as a product of electronic (Ψ_ele), vibrational (Ψ_vib), rotational (Ψ_rot), and the nuclear spin (Ψ_ns) components:

Ψ_total ≈ Ψ_eleΨ_vibΨ_rotΨ_ns

Breaking these symmetry effects down further, the electronic wavefunction Ψ_ele can in principle be either antisymmetric or symmetric due to a half filled out-of-plane (π) or in-plane (σ) orbital on the radical carbon atom, while the ground state vibrational wavefunction Ψ_vib is always symmetric. For C₂ rotation of a near oblate asymmetric top, the rotational wavefunction 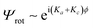is symmetric for K_a + K_c = even and antisymmetric for K_a + K_c = odd. For a molecule with n = 3 pairs of exchangeable spin ½ H nuclei, there are

symmetric and
antisymmetric spin functions,⁴¹ resulting in a K_a + K_c = even : odd = 36 : 28 or 28 : 36 (∼1.3 : 1 or ∼1 : 1.3) ratio of nuclear spin weights for symmetric and antisymmetric rotational levels, depending on the electronic symmetry of the half-filled radical orbital.

Intensity alternation, resulting from the 36 : 28 nuclear spin statistics, is clearly observed in the high-resolution experimental spectrum. Specifically, Fig. 7 displays a detailed section near 3068.8 cm⁻¹, where the relative intensities of the Q branch progressions ^pQ_N,0(N) (shaded to the red) and ^rQ_N−1,1(N) (shaded to the blue) nicely match the 36 : 28 but not the 28 : 36 nuclear spin weight ratios. This requires the electronic wave function to be antisymmetric, and therefore cyclobutyl to be a π radical with the unpaired electron in an out-of-plane p_π orbital on the radical C atom. In addition, ab initio calculations on the singly occupied molecular orbital (SOMO) for the planar transition state have been carried out. The resulting SOMO is shown in Fig. 7 and supports the out-of-plane π character of the radical as predicted by experimentally observed nuclear spin statistics. Alternatively stated, the 36 : 28 intensity alternation required by wave function symmetry arises from the zero-point energy lying far above the interconversion barrier, which results in a symmetric ground state wavefunction peaked at the planar C_2v transition state. At the complete opposite extreme, the bottom panel (K_a + K_c = even : odd = 1 : 1 nuclear spin weight predictions) reflects the other limit (definitely not the case for cyclobutyl) where the interconversion barrier is so high that the 36 : 28 and 28 : 36 weighted tunneling doublets would overlap within experimental resolution.

Fig. 7 High-resolution tests of nuclear spin statistics and electronic wavefunction symmetry for cyclobutyl radical. The experimental observed intensity alternation (top, black) originating from the nuclear spin statistics matches the K_a + K_c = even : odd = 36 : 28 prediction (blue), confirming that the unpaired electron on the radical carbon atom must be in a vibrationally averaged out-of-plane p_π orbital (inset figure). Simulated spectra for different values of nuclear spin statistical weights are calculated using PGOPHER based on a rotational temperature of 25.6 K. Theoretical out-of-plane SOMO distribution shown in the top panel is in agreement with the experimental intensity alternation. Finally, the three additional lines marked with asterisk are likely the hot ^rQ_N−1,1(N) transitions from the first excited puckering state with opposite nuclear spin weights (intensity alternation matches the right three lines in e : o = 28 : 36 simulation).

Finally, it should be noted that there is evidence for hot band transitions from the first excited puckering state in our experimental spectrum. As shown in Fig. 7, three additional lines around 3068.7 cm⁻¹ (marked with asterisks) are likely to arise from the hot ^rQ_N−1,1(N) transitions. The inverted 28 : 36 ratio (cf., the 36 : 28 ratio observed for the fundamental band) would indicate that the lower vibrational state wavefunction is antisymmetric with respect to the unpuckered (i.e., planar) CCCC geometry, which would indeed be consistent with transitions out of the first excited puckering state (Fig. 6). However, due to smaller thermal populations and weaker signal intensities, only 16 transitions (8 lower state combination differences) have been identified and thus conclusive assignments are not reported at this time. Nevertheless, we hope to remeasure this spectral region with a home built continuous wave mid-IR optical parametric oscillator system designed and assembled at JILA. With the enhanced signal-to-noise due to a 10⁵-fold increase (Watt vs. 10's of microwatts) in cw IR laser power, the hot band transitions should be readily observable and enable further insights into the quantitative shape of the double minimum puckering potential for cyclobutyl radical.

D. Boltzmann analysis

Boltzmann analysis of the cyclobutyl rotational populations provides a powerful method for characterizing temperatures in the slit-jet expansion. After including nuclear spin statistics due to the three pairs of identical hydrogen atoms, the integrated absorbance (in cm⁻¹) of individual rovibrational transitions S can be expressed as:
where S₀ is the integrated absorption cross section (cm² cm⁻¹ per molecule) of the rovibrational band, N₀ is the number density of cyclobutyl radicals in the lower vibrational state, l is the total multi-pass absorption length, g_NS is the nuclear spin weight, g_J is the m_J degeneracy, A(J′,J′′) is the PGOPHER computed asymmetric top Hönl–London factor, E_rot is the energy of the ground rovibrational state, kT_rot is the thermal energy associated with rotation, and Q(T_rot) is the rotational partition function. The above expression predicts a simple linear relationship between 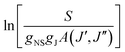and E_rot, with the slope and intercept proportional to inverse temperature T_rot and local density of cyclobutyl radicals in the laser probe region, respectively.

Fig. 8 displays a standard semi-logarithmic Boltzmann plot of the degeneracy scaled experimental populations vs. rotational energy in the ground vibrational state. A linear regression least squares analysis yields a slope of −0.056 ± 0.003, corresponding to a rotational temperature of 25.6 ± 1.4 K, which is characteristic of efficient supersonic expansion cooling from the much higher electronic temperatures (T_elec > 1500 K) behind the slit orifice. Of equal interest is the intercept of such a Boltzmann plot, which informs on radical populations in the expansion region. Based on a known path length and calculated integrated absorption strength of S₀ of 25 km mol⁻¹ from CCSD(T)/PVTZ anharmonic VPT2 calculations, simple Beer's Law analysis allows us to estimate ∼3.5 × 10¹¹ radicals per cm³ total ground state cyclobutyl radical densities at ∼1 mm downstream from the slit. This can be referenced to total density in the slit orifice using the standard supersonic expansion expression,⁴²

for a Ne/He heat capacity ratio γ = 5/3 and predicted Mach number M = 3.9 for a 1D expansion geometry, which translates into 5.3 × 10¹² cyclobutyl radicals per cm³ exiting the slit orifice. With respect to the cyclobromobutane precursor in the stagnation region (4.9 × 10¹⁶ radicals per cm³), this corresponds to only quite modest radical generation efficiencies of ∼0.01%, indeed >2 orders of magnitude smaller than the ∼1% CH₂I radical generation from CH₂I₂ observed previously.⁴³ This lack of efficiency certainly reflects the shortness of time (1 μs) spent in the 1 mm slit discharge, but also may signal the presence of efficient alternative pathways accessible from electron bombardment of cyclobromobutane, (e.g., cyclobutyl ring opening to form 1-methylallyl radical). Finally, it is worth emphasizing that one can make up for such 100-fold loss in radical densities by combination of quantum shot noise limited slit discharge absorption methods and averaging over multiple scans.

Fig. 8 Boltzmann plot of the high-resolution spectral data for the α-CH stretch fundamental band. Data from b-type transitions out of and are shown in black and blue, respectively. Dashed line (red) reflects a least-square fit of the data to a common rotational temperature of 25.6 ± 1.4 K.

V. Conclusion

High-resolution IR spectra of gas-phase cyclobutyl radicals formed in a slit-jet discharge expansion have been recorded and analyzed for the first time in the α-CH stretch fundamental band around 3069 cm⁻¹. A total of 200 asymmetric top b-type rovibrational transitions are successfully observed and measured for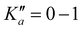 , 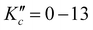and N′′ = 0–13 lower rotational states, with unambiguous assignment of the spectral structure confirmed by four-line ground state combination differences. Precision ground state and α-CH stretch excited state spectroscopic constants are determined from least-squares fits to a Watson asymmetric top rigid rotor Hamiltonian. The experimentally determined α-CH stretch band origin at 3068.7887(4) is in excellent agreement with previous non-rotationally resolved IR spectroscopic studies in helium droplets²⁰ as well as ab initio prediction at CCSD(T)/ANO1 VPT2 levels of theory. The long-standing question of whether the ground state of cyclobutyl radical is described by a “puckered” C_s geometry or a “vibrationally averaged planar” C_2v geometry is resolved by both high-resolution spectroscopy and high-level ab initio calculations. Specifically, based on eigenvalues/eigenfunctions for a 1D double minimum potential energy surface, the ground state of the ring puckering vibrational mode (E_zero-point ≈ 26.98 cm⁻¹) is found to energetically lie far above the interconversion barrier (E_barr ≈ 1.0 cm⁻¹) computed at the highest CCSD(T)/ANO2 levels. Interestingly, the height and shape of this puckering barrier proves to be remarkably sensitive to increasing quality of basis set, making it entirely possible that any such barrier vanishes in the complete basis set (CBS) limit. Furthermore, expectation values based on 1D Numerov–Cooley solutions for the eigenfunctions quantitatively reproduce experimental inertial defects, which highlights a first principles theoretical success in capturing the non-planar dynamics of the cyclobutyl radical originating from large amplitude ring puckering motion. Finally, intensity alternation is observed in the high-resolution IR spectrum, arising from nuclear spin statics for 3 pairs of identical spin ½ H atoms. Spectral intensities match the K_a + K_c = even : odd = 36 : 28 ratio predicted for the unpaired electron in an out-of-plane p_π orbital. Therefore, this work provides direct evidence for cyclobutyl as a π radical with vibrationally averaged C_2v symmetry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by grants from the Department of Energy (DE-FG02-09ER16021), with funds for construction of the slit-jet laser spectrometer initially provided by the National Science Foundation (CHE 2053117, PHY 1734006/2317149). The authors would also like to thank Prof. Gary Douberly for encouraging us to obtain complementary high-resolution gas phase infrared spectra for cyclobutyl radical, as well as Prof. John Stanton for his patient help with implementing high level CCSD(T)/ANOn (n = 0, 1, 2) calculations on the CFOUR platform.

References

1. Y. Briker, Z. Ring, A. Iacchelli, N. McLean, C. Fairbridge, R. Malhotra, M. Coggiola and S. Young, Energy Fuels, 2001, 15, 996–1002.
2. B. Sirjean, P.-A. Glaude, M. Ruiz-Lopez and R. Fournet, J. Phys. Chem. A, 2008, 112, 11598–11610.
3. T. Edwards, J. Propul. Power, 2003, 19, 1089–1107.
4. X. Lei, X. Cao, J. Wang and X. Li, Combust. Flame, 2022, 237, 111881.
5. B. Sirjean, P.-A. Glaude, M. Ruiz-Lopez and R. Fournet, J. Phys. Chem. A, 2006, 110, 12693–12704.
6. K. Wang, S. M. Villano and A. M. Dean, Phys. Chem. Chem. Phys., 2016, 18, 8437–8452.
7. Y. Sun, C.-W. Zhou, K. P. Somers and H. J. Curran, J. Phys. Chem. A, 2019, 123, 9019–9052.
8. K. Wang, S. M. Villano and A. M. Dean, J. Phys. Chem. A, 2015, 119, 7205–7221.
9. D. M. Matheu, W. H. Green Jr. and J. M. Grenda, Int. J. Chem. Kinet., 2003, 35, 95–119.
10. F. Dong, S. Davis and D. J. Nesbitt, J. Phys. Chem. A, 2006, 110, 3059–3070.
11. A. Kortyna, M. A. Reber and D. J. Nesbitt, J. Chem. Phys., 2022, 157, 034302.
12. A. McIlroy and D. J. Nesbitt, J. Chem. Phys., 1990, 92, 2229–2243.
13. T. Dudev and C. Lim, J. Am. Chem. Soc., 1998, 120, 4450–4458.
14. H. C. Brown, R. S. Fletcher and R. B. Johannesen, J. Am. Chem. Soc., 1951, 73, 212–221.
15. D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108.
16. J. Almlöf and P. R. Taylor, J. Chem. Phys., 1987, 86, 4070–4077.
17. J. C. Schultz, F. Houle and J. Beauchamp, J. Am. Chem. Soc., 1984, 106, 7336–7347.
18. K.-C. Lau, W. Zheng, N.-B. Wong and W.-K. Li, J. Chem. Phys., 2007, 127, 154302.
19. Y. Liu, K.-C. Lau and L. J. Butler, J. Phys. Chem. A, 2006, 110, 5379–5385.
20. A. R. Brown, P. R. Franke and G. E. Douberly, J. Phys. Chem. A, 2017, 121, 7576–7587.
21. J. M. Ribeiro and A. M. Mebel, J. Phys. Chem. A, 2016, 120, 1800–1812.
22. S. Davis, M. Fárník, D. Uy and D. J. Nesbitt, Chem. Phys. Lett., 2001, 344, 23.
23. E. Riedle, S. H. Ashworth, J. T. Farrell and D. J. Nesbitt, Rev. Sci. Instrum., 1994, 65, 42.
24. A. S. Pine, J. Opt. Soc. Am., 1976, 66, 97.
25. C. Blondel, P. Cacciani, C. Delsart and R. Trainham, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 3698.
26. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221.
27. J. K. Watson, Vibrational spectra and structure, Elsevier, Amsterdam, 1977.
28. C. M. Lovejoy and D. J. Nesbitt, J. Chem. Phys., 1990, 93, 5387–5407.
29. K. Nauta and R. Miller, J. Chem. Phys., 2000, 113, 9466–9469.
30. B. R. Johnson, J. Chem. Phys., 1977, 67, 4086–4093.
31. J. Cooley, Math. Comput., 1961, 15, 363–374.
32. J. R. Barker, Int. J. Chem. Kinet., 2001, 33, 232–245.
33. J. R. Barker, Int. J. Chem. Kinet., 2009, 41, 748–763.
34. J. R. Barker, T. L. Nguyen, J. F. Stanton, C. Aieta, M. Ceotto, F. Gabas, T. J. D. Kumar, C. G. L. Li, L. L. Lohr, A. Maranzana, N. F. Ortiz, J. M. Preses, J. M. Simmie, J. A. Sonk and P. J. Stimac, MultiWell-2022Software, University of Michigan, Ann Arbor, 2022.
35. D. J. Rush and K. B. Wiberg, J. Phys. Chem. A, 1997, 101, 3143–3151.
36. A. B. McCoy, Int. Rev. Phys. Chem., 2006, 25, 77–107.
37. C. Eckart, Phys. Rev., 1935, 47, 552.
38. B. M. Wong, R. L. Thom and R. W. Field, J. Phys. Chem. A, 2006, 110, 7406–7413.
39. T. Oka, J. Mol. Struct., 1995, 352, 225–233.
40. P. R. Bunker and P. Jensen, Molecular symmetry and spectroscopy, NRC research press, 2006.
41. C. H. Townes and A. L. Schawlow, Microwave spectroscopy, Courier Corporation, 2013.
42. G. Scoles, Atomic and molecular beam methods, Oxford University Press, New York, 1988.
43. A. Kortyna, D. M. B. Lesko and D. J. Nesbitt, J. Chem. Phys., 2018, 148, 174308.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04812h

---