Non-resonant inelastic X-ray scattering for discrimination of pigments

Abstract

Inelastic X-ray scattering (IXS) spectroscopy has been used in many fields of solid-state physics and theoretical chemistry as an accurate and quantitative probe of elementary excitations. We show that non-resonant IXS spectra in the energy loss range below 100 eV exhibit a strong contrast across a wide range of commercially available pigments, opening new routes for their discrimination. These signatures combine plasmonic transitions, collective excitations and low energy absorption edges. We have performed IXS to discriminate different artists' pigments within complex mixtures and to quantitatively determine rutile and anatase polymorphs of TiO₂. The integration of experimental data on pigment powders with suitable ab initio simulations shows a precise fit of the spectroscopic data both in the position of the resonances and in their relative intensity.

---

1 Introduction

Studying the chemistry of pigments is challenging, as they are powders whose composition often results from mixtures of mineral compounds. A typical example is artists' pigments, which may have been produced through various synthetic routes and are susceptible to chemical alteration in works of art. However, pigment identification in paint materials, as raw materials, in artists' workshop, and/or within artworks, is critical for understanding the artistic practices, and the chemical and physical alterations of artworks over time.^1–3 Traditional pigments used over centuries by master painters have been extensively studied by analytical methods to identify their composition and production methods (e.g., de Meyer et al.⁴ or Gonzalez et al.⁵) and to characterise the chemical mechanisms leading to the formation of degradation products.^6–8 Since the late 19th century, innovations in industrial synthesis methods have broadened the range of materials and the complexity of pigment minerals, thus increasing the difficulty of disambiguating pigments and prompting the need for new methods.⁹

X-ray absorption spectroscopy (XAS) methods, often combined with other X-ray techniques, have become key in gaining electronic and geometric structure information (oxidation state, coordination number, and site symmetry) for inorganic paint materials in both crystalline and amorphous forms.^10,11 For example, X-ray absorption near-edge structure (XANES) spectroscopy combined with X-ray fluorescence (XRF) has been used to identify oxidised arsenic species resulting from the migration of arsenic sulphide-based yellows (As₂S₃), reds and oranges (As₄S₄) in photodegraded 19th century artworks.¹² The combination of μ-XANES and μ-XRF with micro-X-ray diffraction (XRD) has been used to evaluate the darkening of chromium-based yellows (PbCrO₄, PbCr_1−xS_xO₄) through photoreduction in one of the paintings in Van Gogh's Sunflowers series (1888–1889) by determining the oxidation state and spatial distribution of the paint compounds on the microscale.⁷ These methods were also coupled to understand the reactivity of crystal defects in cadmium-based (CdS) nanoparticles in yellows from Pablo Picasso's Femme (1907) by correlating elemental and structural distributions with optical emissions to identify degradation mechanisms.¹³ In these studies, analysis was performed on prepared samples from the painting, usually in the form of cross-sections. Alternatively, some studies only explored the sample surface due to the limited depth of information constrained by the appropriate edge energy.

XAS has several limitations for the study of artistic materials: (i) The depth probed is imposed by the energy of the studied edge, which requires the study of cross-sections or sample surfaces that may not be representative of the bulk material or whose preparation may alter heterogeneous or reactive samples.¹⁰ (ii) XAS on artistic materials is mainly performed in the hard or tender X-ray regime, which is not suitable for studying elements with a low atomic number (Z).^10,14 This is particularly problematic for recent paint formulations, which may include a range of synthetic organic dyes or extenders made of light elements.¹⁵ (iii) XAS yields only a partial view of the electronic structure as it primarily reflects the projected density of empty states of the excited atom, accessible mainly through the dipole selection rule. It therefore lacks information about the symmetry-forbidden density of empty states, the density of occupied states, and, importantly, about elementary excitations that are beyond the X-ray range but might be valuable for material characterisation.

Here, we apply non-resonant inelastic X-ray scattering (IXS) as a powerful method for the identification and analysis of mineral pigments. IXS is a technique capable of revealing electronic excitations over a wide range of energies and momenta. It not only addresses different degrees of freedom compared to infrared or Raman spectroscopy (successfully applied to titanium dioxide^16,17), but it is also complementary to optical techniques, like absorption, optical reflectivity, or photoluminescence.¹⁸ Specifically, IXS, as a scattering technique, allows analysis of a new dimension, namely, the momentum transfer (q). This capability unveils excitations that would remain undetected in the dipole limit intrinsic to optical absorption experiments. Another noteworthy emerging technique is the resonant counterpart of IXS, known as RIXS. Similar to IXS, RIXS is a scattering technique that examines both energy and momentum, and it has been proven highly effective in the description of titanium compounds.^19–21 RIXS offers a different excitation pathway²² and complements IXS. It is more focused on specific aspects of the excitation, due to its resonant condition of the incoming photon, like electron–phonon coupling,²³ d–d excitations, and pre-peak features of X-ray absorption edges. The resonant condition, even though it increases the signal/noise ratio of the experiment, also limits the momentum range that can be investigated. Probably the closest technique to IXS is electron energy loss spectroscopy (EELS), which enables the study of excitations over a wide range of energies with unrivalled spatial resolution. EELS has also been proven effective in highlighting differences in bulk polymorphs of titanium,²⁴ but the spectral differences between rutile, anatase, and brookite are too small to be useful in powder compounds.

For these reasons, we conducted a combined experimental–theoretical study focusing on non-resonant IXS, an approach that allows us to address a broader momentum range and explore various aspects of electronic excitations. In particular, we demonstrate the ability of low energy loss IXS to discriminate between common commercial pigments, by exploiting resonances resulting from the electron structure of the materials, including electron–hole or charge transfer excitations, collective excitations related to the plasmonic response, gap transitions, in addition to absorption edges. We show that significant contrasts within spectroscopic signatures hold promise for material differentiation. The dependence of these features on the momentum transfer provides additional signatures not observed by any other analysis. Finally, we show that titanium dioxide, TiO₂, which constitutes the most commonly used white pigment since the 20th century, can be readily identified by IXS with a number of characteristic spectral features. In particular, the two main crystalline phases encountered (rutile and anatase) show spectroscopic differences in very good agreement with theoretical calculations of the electronic dynamic structure factor (DSF) as a function of the momentum transfer. We therefore present a state-of-the-art integration of experimental and theoretical methodologies for studying mineral pigments. At the same time, we wish to provide a practical illustration that highlights the applicability of IXS to a wider spectrum of complex materials than those that have been previously studied using this approach.

2 Methods

IXS experiments were carried out at the GALAXIES beamline at the SOLEIL synchrotron. All measurements were carried out at an incident energy E_i of 6470 eV. Low-resolution (∼1.2 eV) spectra were obtained using the main Si(111) double crystal monochromator (DCM), while high-resolution (∼300 meV) spectra were obtained by insertion of the beamline's four-bounce Si(220) high-resolution monochromator (HRM) in the symmetric mode. The beam flux was 3 × 10¹³ and 5 × 10¹² photons per s in low-resolution and with the HRM, respectively. The beam size was 100 μm × 30 μm (H × V). The scattered photons were measured using the MATRIXS spectrometer, which comprises 40 spherically-bent Si(110) crystals with a diameter of 100 mm and a bending radius of 1 m, and has a total angular spread of 44°. The spectrometer was arranged in Rowland geometry with a Bragg angle of 87°, positioned at a distance of 1 m from the sample. The photons were detected using a hybrid pixelated position sensitive 2D X-ray detector with a pixel size of 55 μm. The signal from all 40 analysers was collected in a single image on the 2D detector, with each analyser resulting in a specific spot on the detector.

The pigment powder samples were mounted by pressing them into the 200 μm diameter holes of a 2.5 cm × 2 cm steel sample holder. The setup for spectroscopy was configured in the forward scattering mode with the spectrometer aligned at a scattering angle 2θ = 55° with respect to the centre of the spectrometer, corresponding to q ranging from 1.9 to 4.0 Å⁻¹ from end to end. Spectra for all samples were recorded in the low-resolution mode (Fig. S2.1a, ESI†) for an energy loss range of ΔE = 0–100 eV with an energy step size of 200 meV for ΔE = 0–30 eV and an energy step size of 500 meV for ΔE = 30–98 eV. The acquisition time was 4 s per energy point (∼20 min per spectrum). High-resolution spectra (Fig. S2.1b, ESI†) were obtained for titanium white pigment samples at the plasmonic resonance ΔE = −2 to 18 eV, with a step size of 200 meV and an acquisition time of 20 s per energy point (∼67 min per spectrum). For spectral imaging, the configuration was changed to the backscattering mode with the spectrometer aligned at a scattering angle of 2θ = 130° for higher spatial resolution, and spectra were acquired in the low-resolution mode (1.2 eV) (Fig. S2.1c, ESI†). Spectra were acquired by scanning horizontally across the sample (y) at a fixed energy for 100 ms per spatial point, for all energies from ΔE = −5 to 25 eV with a step size of 1 eV. The vertical position (z) was modified and the scans were repeated.

3 Results

Low-energy excitation spectra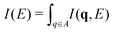 (A is finite) were collected in the 0–100 eV energy loss range with q values ranging from 1.90 to 4.05 Å⁻¹ using a series of commercial artist pigments (Fig. 1). Pigment composition and predominant phases were identified (Table 1), along with minor phases and trace elements using the information provided by manufacturers and complementary analyses (Table S1.1, ESI†). These spectra result from the accumulation of scattered photons detected over an extended range of q values. The spectra were classified into three main categories: (Fig. 1, 1–3) peaks in the 10–20 eV region, a shoulder around 25 eV and a bundle of peaks from 30–45 eV, (4–7) a broad peak centred around 40 eV, with a sharp peak at 57 eV, and (8–11) a major broad peak centred around 30–40 eV. The M-shell and L-shell edges for pigment elements were identified, along with plasmonic resonances (denoted p) and interband transitions (i). In general, the shell edges and plasmon peaks were identified by their sharp peak shapes, whereas interband transitions were observed as broad peaks or shoulders. For spectra 1–3, a plasmon peak is observed as a sharp peak for TiO₂1 and CoAl₂O₄2 between 10–20 eV. For ZnO 3, the broad peak at ∼10–20 eV can be attributed to the combined M_4,5-shell of Zn and the plasmon peak. Broad peaks classified as interband transitions were observed in the range of ∼25–40 eV for 1–3. The absorption edge for the O L₁-shell (O) is observed at around 45 eV, while the Ti M_2,3-shell is observed around 35 eV, and the Ti M₁-shell and Co M_2,3-shells (M) are observed around 60 and 62 eV, respectively. Spectra 4–7 correspond to Fe-containing pigments (Fe₂O₃ and/or Fe₃O₄4–6, Fe₄[Fe(CN)₆]₃7). The M_2,3-edge for Fe was characterized by a sharp peak at 57 eV, and the interband transitions were observed as a shoulder at ∼25 eV. The broad peak centred around 40 eV was attributed to Compton scattering. The peaks from the O L₁-shell were not observed in 4–6. An additional peak around 40 eV was present for 7 along with plasmon peaks at 10 and 14 eV. In samples 4–7, a high energy feature is observed around 90 eV. This was not clearly identified as electronic excitations, and presumably arises from powder-like diffraction. In spectra for 8–11, the dominant feature is a broad peak at 35–40 eV attributed to Compton scattering along with a shoulder at 20 eV. The M₁-shell peak for Ca at 25 eV and L₁-shell peak for O at 45 eV were observed for Ca(PO₄)₃(OH) 8 and Ultramarine Blue 9 (also containing CaCO₃ and CaMg(CO₃)₂). For 8 and 9, plasmon peaks were observed around 15 eV. In comparison, spectra from NiC₈H₆N₆O₆10 and C₂₂H₁₆N₂O₂11, predominately organic, do not show spectral features attributable to plasmon resonances or absorption edges.

Fig. 1 Normalised inelastic X-ray scattering intensity as a function of energy loss, for 11 commercial artists' pigments: titanium white (1, TiO₂-based), light turquoise (2, CoAl₂O₄-based), zinc white (3, ZnO-based), vine black (4, Fe₂O₃,Fe₃O₄-based), mars black (5, Fe₂O₃,Fe₃O₄-based), burnt umber (6, FeO₂,Fe₂O₃-based), Prussian blue (7, Fe₇C₁₈N₁₈-based), ivory black, (8, Ca(PO₄)₃(OH) based), ultramarine blue, (9, sodalite-based), imitation Indian yellow (10, NiC₈H₆N₆O₆-based), and quinacridone red (11, C₂₂H₁₆N₂O₂-based). All pigments are from Laverdure, except 2 and 11 from Sennelier. The spectra were acquired from the sum of intensities over q values from 1.90 to 4.05 Å⁻¹ (experimental conditions: energy loss 0–100 eV, energy step 0.4 eV, and acquisition time 1 s). Under the conditions used, the energy resolution is 0.8 eV. Spectra are shown in the colour of their pigment, except for white pigments, which are shown in black. The spectra are offset for better visualisation.

Table 1 Pigments analysed in this work. ^bSR-μ-XRPD identified both anatase and rutile phases. Elemental and/or structural characterisation studies indicate that the pigment contains SiO₂^s, CaCO₃^c, or other minor phases^o

No.	Pigment designation	Diagnostic phases
1	Titanium white	TiO2 (rutile)
2	Turquoise Clair	CoAl2O4^o
3	Blanc de Zinc	ZnO
4	Noir de Vigne	Fe3O4, Fe2O3^s,o
5	Noir de Mars	Fe3O4^s,o
6	Terre Ombre Brûlée	Fe2O3, Fe3O4^s,o
7	Bleu de Prusse	Fe4[Fe(CN)6]3
8	Noir d'Ivoire	Ca(PO4)3(OH)
9	Bleu Outremer	Sodalite-type phases^c,o
10	Jaune Indien Imitation	NiC8H6N6O6
11	Rouge de Quinacridone	C22H16N2O2
12	Titanium white	TiO2 (anatase^b)
13	Titanium white	TiO2 (anatase^b)
14	Titanium white	TiO2 (rutile)
15	Titanium white	TiO2 (rutile^b)
16	“Rutile”	TiO2 (rutile^b)

---

We further experimentally examined the plasmon resonance dependence on the momentum transfer q for the two crystal structures of TiO₂ found in titanium white pigments, anatase and rutile, focusing on pigment 12 and 1, respectively. For this purpose, we used the specific geometry of the MATRIXS spectrometer at the GALAXIES beamline at the SOLEIL synchrotron facility. The 40 Si(110) analyser crystals are arranged in a compact 8 × 5 array (H × V), divided into 4 panels of 2 × 5 analysers (H × V). Each V column corresponds to a specific q value, whose contribution to the IXS spectrum can be isolated by selecting the corresponding signal on the PSD. Four spectra were plotted, each corresponding to one q value (Fig. 2). The most notable effect, observed for both samples, is the decreasing intensity of the plasmon peak as q increases. Two notable differences between the crystal polymorphs were observed: (1) at lower q (1.9–2.2 Å⁻¹), two broad peaks, centred around 25 eV and 35 eV are present for 1, and observed as one broad peak centred around 30 eV for 12, and (2) a broad peak around 8 eV is highlighted for q at 2.6–2.9 Å⁻¹ for 12 and q at 3.2–3.5 Å⁻¹ for 1.

Fig. 2 Experimental spectra (black, energy resolution 800 meV) of anatase-based (12) and rutile-based (1) titanium white pigments and corresponding theoretical DSF calculations for anatase (blue) rutile (red) for increasing q values from 1.9 to 4.0 Å⁻¹. Experimental spectra are normalised and offset for visualisation.

We then calculated the DSF of rutile and anatase crystals at different q values, both in the XY plane and in the Z direction (both structures are tetragonal). For each q, we then qualitatively compared the experimental results on the powder with the arithmetic mean of the amplitude of the simulated spectra as a function of energy (0–50 eV) in the three directions X, Y and Z. This theory–experiment comparison can only be qualitative since the exact distribution in orientation of TiO₂ crystallites in the powder samples is unknown. However, the anisotropy in both structures, although present, is not huge (see Fig. S4.1, ESI†), and the averaging operation permits one to carefully analyse the spectra and recognise the characteristic features. We observed a very good agreement between theoretical and experimental spectra, inspite of the important difference between the experimental sample and the theoretically ideal infinite bulk anatase and rutile. In addition, there is a quantitative juxtaposition between theory and experiments in different spectral features, like the sharp plasmon peak at 14 eV or the broad structure around 50 eV. At all investigated q values, we noticed a correctly matching relative intensity of the different peaks. This permitted us to carry out a full analysis of the different spectral features (see Discussion). According to the results of this comparison, we can suggest a criterion to use low-loss DSF to disentangle the contribution of rutile from anatase, thus permitting to distinguish between the two.

High energy resolution spectra (E_res ∼ 300 meV) were collected for energy losses below 16 eV for rutile and anatase-based pigments (1, 12–16). The differences observed experimentally were most notable at q ∼ 2.6–2.9 Å⁻¹, where a broad peak at ∼8 eV was observed for the two anatase-based pigments, 12 and 13, only (see Fig. S3.3 and S3.4, ESI†). The DSF calculations show good agreement with the experimental spectra for both pigments in terms of the relative intensities of the plasmon peak at ∼14 eV and interband transitions O-2p → Ti-3d at ∼8 eV (Fig. 3). Both theory and experiments agree in highlighting that the peak at 8 eV is the most discriminant between anatase and rutile phases.

Fig. 3 Normalised spectra at q 2.6–2.9 Å⁻¹ for anatase (12) and rutile based (15) titanium white pigments and their corresponding calculations of the DSF at q: 2.8 Å⁻¹ for anatase; 2.74 Å⁻¹ for rutile (left). For (12), DSF calculations along the XY plane and along the Z plane show the effect along the Z plane axis (right). Experimental spectra have been normalised by the integrated area (sum) of the signal over the energy range from 4–16 eV, and DSF calculations have been adjusted for better visualisation.

4 Discussion

IXS signatures were effective in discriminating between different pigments by identifying low energy-loss resonances and the M- and L-shell edges for alkali or transition metal-containing pigments. In addition, noticeable plasmon resonances were detected for the metal oxide pigments, 1 titanium white (TiO₂), 2 light turquoise (CoAl₂O₄) and 3 zinc white (ZnO), as well as other pigments including Prussian blue (Fe₇C₁₈N₁₈) and ultramarine blue (sodalite-type phases). Interband transitions discriminated pigments 1–3 and also Fe-oxide pigments 4–6. They were observed as broad peaks for all samples, except 1, which showed two separate broad peaks. The broadness of this peak is dependent upon the number of transitions available in the d states of the t metal.²⁵ This could potentially explain why this peak is slightly broader for 2 compared to 1, due to the increased number of transitions available with higher occupancy of d states in Co d² compared to Ti d¹.²⁵

Furthermore, this peak is broader, observed as a shoulder in pigments 4–6 Fe d³. Compton scattering dominates in pigments containing light elements, and no spectral features are observed in synthetic organic samples, as expected. Although outside the scope of this contribution, IXS spectroscopy would enable the study of their speciation by extending the energy loss range to the C and O edges.²⁶ Additional spectral features were observed that could not be identified at this stage. Indeed, for many samples, references in low energy-loss ranges were not available in the EELS databases, such as the one from Hitchcock and Mancini,²⁷ nor mentioned in the literature; the identification of these resonances would require the acquisition of new reference data and/or future simulations.

We observed a decrease in the intensity of the plasmonic peak of 1 (titanium white, rutile-based TiO₂) with increasing q from ∼2 Å⁻¹, until it was no longer observed at ∼4 Å⁻¹. This phenomenon results from q exceeding the critical value q_c for TiO₂, where the plasmon merges with the particle–hole continuum that dominates the DSF for a wide range of frequencies. The same behaviour was reported for many materials, including silicon²⁸ or SrVO₃.²⁹ IXS relies on the energy and momentum transfers measured from a high-energy incident photon in the X-ray range that is defined by its wave vector, energy, and polarisation (k₁, ħω₁, ε₁) by the electron system and the scattered photon (k₂, ħω₂, ε₂) defined by the same parameters.^30,31 The measured energy transfer ħω is given by the law of conservation of energy,

ħω = ħω₁ − ħω₂

and momentum transfer q is a function of the scattering angle. The number of photons being measured in a certain energy range is defined by the double differential scattering cross-section (DDSCS),
where according to Fermi's Golden rule and under first-order perturbation theory, the probability of the transition from a ground state to a final state can be described; on one hand, it is related to Thomson scattering, associated with the strength of photon–electron coupling and, on the other hand, it is related to the strength of the DSF S(q,ω), which is directly related to the allowed excitations of the scattering system.³²

The IXS spectrum is accurately represented by the S(q,ω) of a material, i.e., encompassing all the observed excitations in the system, for a wide range of energies and momenta. The DSF contains multiple pieces of information, ranging from core excitations and edges to collective plasmons, from excitons to the Compton regime. It does not suffer from the limitations of other X-ray spectroscopy techniques, like the low signal for low-Z elements, or the necessity to have a perfect crystal. In addition, being a scattering technique, IXS can (i) go beyond the dipole regime, giving access, e.g., to d–d or orbital excitations and (ii) be extremely bulk-sensitive, with the use of hard X-rays.³² Some known limitations include the difficulties at low energy loss (typically in the phonon excitation regime). Here, we particularly want to emphasise the dispersion analysis, made possible by acquiring spectra with varying q, which opens the way to an entirely additional dimension for the discrimination of different structures.

Theoretical ab initio calculations of IXS have been used for the study of materials found in pigments, such as titanium dioxide (TiO₂); these materials are chosen due to the simplicity of their structure and their wide range of applications in industrial methods.³³ Past results for titanium dioxide using ab initio quantum chemistry approaches showed the quality and accuracy of the methods for rutile at vanishing momentum transfer, in comparison with EELS experiments.³⁴ Here we extend this analysis to more polymorphs and to high momentum, in order to compare with IXS.

The dynamical structure factor can be related to the inverse dielectric function

which can be related to the full polarizability χ (described in Text S3, ESI†).

Theoretical and computational details are shown in Text S6 (ESI†). Here, we can discuss the results and analyse the experiment–theory comparison in more detail. First, by focusing on a specific momentum transfer, e.g., for rutile at q = 2.03 Å⁻¹, we can identify the contributions to the spectrum, via the imaginary part of the dielectric function, Im(ε), that is directly related to the interband transitions, and so to band-structure calculations³⁵ (Fig. 4). We can distinguish four zones: (i) the 0–13 eV range originates from transitions close to the Fermi energy, involving O 2p states, slightly hybridised with Ti 3d's; (ii) excitation of oxygen 2s states is responsible for the region 18–30 eV and (iii) Ti 3p excitations are involved above 35 eV; (iv) the sharp peak at 14 eV serves as a reminder of the plasmon peak at zero-momentum transfer (see Fig. S8.2, ESI†) for the full dispersion DSF, from 0 to high momentum transfer. This analysis permits us to identify all the features in the experimental spectra. Furthermore, our calculations are not affected by the elastic peak, which means that we can unambiguously identify even barely visible shoulders in the experimental peak, like at 5–10 eV in Fig. 1. Here we do not report band structure calculations, band gaps, and bandwidths, that are in line with the already published results.^35–39 The DSF is also a pertinent tool to distinguish the anatase from rutile phase, but only if we know, in advance, the q and energy loss range to consider. Unlike optical properties, in fact, which clearly distinguish rutile and anatase (an absorption spectrum strongly depends on the optical bandgap,³⁵ for instance), the DSF spectra of the different pigments might appear, at first glance, very similar. Theory can help us to explain the reason. The two allotropic structures are overall very similar, with the same number of atoms in the unit cell, and the same coordination for the titanium centres. If the experiment is conducted on powders, in addition, the anisotropy of the sample cannot be revealed. A comprehensive study of the dispersion of the DSF with the momentum transfer over a wide range of energy can suggest where the contrast between rutile and anatase signals is higher (see also Fig. S5.1, S6.1 and S6.2, ESI†). The small differences between theory and experiments, notably the missing double-plasmon peak in anatase are due to the particular sample used (powder) here and are explained by highlighting the role of the local field effects (Text S9, ESI†).

Fig. 4 Dynamical structure factor of rutile TiO₂ for the specific momentum transfer q = 2.03 Å, together with the respective real and imaginary part of the dielectric function. The comparison between the Im(ε) and the DSF permits one to associate the different contributions of the interband transitions to the peaks and structure of the DSF. The analysis of the Re(ε) also permits to identify the prominent structure at 14 eV as a reminder of the zero-momentum transfer plasmon peak. Here ω has the meaning of absorption frequency or energy loss for the DSF. The real and imaginary parts of ε are expressed in absolute units (they are adimensional) while the DSF is expressed in arbitrary units (curves offset vertically from one another for greater clarity).

Despite a low cross-section, recent instrumental advancements now enable the collection of 2D or 3D volumes, providing valuable insights into speciation and chemical identification in real-life systems.^40,41 Noteworthy progress has been achieved in X-ray Raman spectroscopy for the analysis of cultural heritage materials.^26,42 Specifically, spectral variations observed in transitions at the carbon K-edge (280–320 eV) could be used to segment voxels containing diverse organics within the bulk of palaeontological samples.⁴³

In the case of 3d t-metals with five or fewer unoccupied states, a broad peak representing the collective excitations – a combination of band structure effects – is observed between 20–30 eV.²⁵ Theoretical calculations of the dynamical structure factor show the broadening of his peak with an increase in the number of electrons in the 3d band, due to the increase the number of electrons available for transitions from 3d states to the unoccupied 3p states of the t-metal structure.²⁵ This seems to be in agreement with the spectral results where the band around 25 eV of TiO₂-rutile 1 is seen more clearly as a broad peak and for CoAl₂O₄2 and the Fe-based pigments 4–7, this is observed more as a shoulder covered by a broad band from 30–40 eV. For ZnO 3, the absence of this band is observed, given its nature as a d¹⁰ metal where no electrons are available for transition from the occupied t-metal 3d bands to the unoccupied 3p bands.

High-dose X-ray irradiation in the hard and soft X-ray domains can induce damage to paint samples.^44,45 In our experiments, we did not observe any photodegradation of the unsupported pigments, either through optical effects or signal modification during data collection. This is particularly remarkable for the (sensitive) organic samples, which did not evolve towards a graphitic signature. Although most significant changes were identified for pigments associated with binding media,^46,47 alteration was also reported for unsupported powder pigments, particularly when using micro-focused low-energy X-ray beams.^48,49 The absence of alteration observed in our experiments is attributed to the use of a large beam, with correspondingly low fluences (Table S2.1, ESI†) and high energy X-rays, which interact significantly less with mater than low energy photons because of the reduced photoelectric cross-section. However, a colour change was observed post-analysis on the raster-scanned paint. Future studies investigating paints should take into account the increased risks due to the use of smaller beams and the presence of a binder that can play a critical role in redox exchanges. For example, studies on the photoreactivity of pigments, such as TiO₂, showed the effect of organic media.^50–54 As a highly sensitive probe of chemical speciation, IXS spectroscopy could also be a useful approach for studying the mechanisms induced by irradiation in situ and quantitatively.

5 Conclusion

Low-energy-loss IXS opens the way to a novel spectroscopic approach for discriminating modern pigments, with applications across a very wide range of compounds in terms of composition and structure. The additional degree of freedom offered by momentum transfer appears to be an important factor in highlighting specific spectral features at low-energy transitions, including interband transitions and plasmon resonances, demonstrated by the example of TiO₂ pigments. This was confirmed by comparison with DSF calculations of the crystalline polymorphs found in titanium white pigments. At the same time, we showcase the effectiveness of the IXS method, the only approach capable of ensuring measurements in the wide range of momenta essential for distinguishing the polymorphs, highlighting its complementarity with related spectroscopy techniques (RIXS or EELS). In addition, the high-resolution mode of our setup has demonstrated the ability to differentiate these crystalline polymorphs experimentally, particularly through plasmon resonances. We have initiated the exploration of the potential of this plasmonic spectroscopy for imaging. Using 2D scanning, we have collected the low-resolution plasmon resonance spectral image of a mock paint sample, comprising four different pigments on a white preparation layer of TiO₂. The image was segmented using unsupervised K-means clustering, which has shown promise for imaging the distribution of artists' pigments on a canvas and providing structural information complementary to X-ray fluorescence and diffraction (Fig. 5). Non-resonant IXS spectroscopy could therefore provide interesting insights into the future for in-depth and in situ analysis of paint-binder systems.

Fig. 5 2D spectral image of a canvas painted with 1, 7, 9, 10, and 11 and image segmented by unsupervised K-means clustering based on their IXS spectra (energy losses: 2–25 eV, q: 5.3–5.5 Å⁻¹).

Inelastic X-ray scattering is a powerful technique that can be applied to a wide range of sample types. It is applicable not only to powders (like the pigments in our study), but also to monocrystals (as we report in the Text S7, ESI†) and even liquids. The method can provide insights under various temperature and pressure conditions. Its broad applicability makes it a valuable tool for a wide spectrum of scientific investigations. In this work, we supplemented the experimental measurements with theoretical calculations using an ab initio approach based on TDDFT. This predictive tool does not rely on experimental results or on models, and permits a full description of the optical and dielectric properties of a vast range of materials with high accuracy. In conclusion, we showcase a powerful and cutting-edge integration of experimental and theoretical methodologies to study pigments. Simultaneously, we provide a practical illustration that underscores its applicability to a broader spectrum of complex materials.

Author contributions

L. B. and J.-P. R. conceived the original idea and coordinated the research. L. D., L. B. and J.-P. R. performed the synchrotron experiments. L. H. and F. S. performed the modelling. All authors contributed toward the interpretation of the analytical data. L. B. and L. D. coordinated the writing of the manuscript, with contributions from all authors. All authors read and approved the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L. D.'s doctoral project was funded by ENS Paris-Saclay. The MATRIXS detector at GALAXIES was financially supported by the MATRIXS4H project of the DIM Matériaux anciens et patrimoniaux (Région Île-de-France). L. C. and L. B. acknowledge funding provided through the GoGreen project of the European Commission (GA no. 101060768). Computational time was granted by GENCI (project no. 544). The authors would like to thank Uwe Bergmann for his valuable suggestions to improve the readability of this article.

Notes and references

1. B. H. Berrie, Annu. Rev. Anal. Chem., 2012, 5, 441–459.
2. B. Borg, M. Dunn, A. Ang and C. Villis, J. Cult. Herit., 2020, 44, 239–259.
3. T. Kleynhans, C. M. Schmidt Patterson, K. A. Dooley, D. W. Messinger and J. K. Delaney, Heritage Sci., 2020, 8, 84.
4. S. De Meyer, F. Vanmeert, R. Vertongen, A. Van Loon, V. Gonzalez, J. Delaney, K. Dooley, J. Dik, G. Van der Snickt, A. Vandivere and K. Janssens, Sci. Adv., 2019, 5, eaax1975.
5. V. Gonzalez, G. Wallez, T. Calligaro, M. Cotte, W. De Nolf, M. Eveno, E. Ravaud and M. Menu, Anal. Chem., 2017, 89, 13203–13211.
6. V. Gonzalez, I. Fazlic, M. Cotte, F. Vanmeert, A. Gestels, S. De Meyer, F. Broers, J. Hermans, A. Van Loon, K. Janssens, P. Noble and K. Keune, Angew. Chem., Int. Ed., 2023, 62, e202216478.
7. L. Monico, K. Janssens, E. Hendriks, F. Vanmeert, G. Van der Snickt, M. Cotte, G. Falkenberg, B. G. Brunetti and C. Miliani, Angew. Chem., 2015, 127, 14129–14133.
8. J. L. Mass, R. Opila, B. Buckley, M. Cotte, J. Church and A. Mehta, Appl. Phys. A: Mater. Sci. Process., 2013, 111, 59–68.
9. O. Chiantore and A. Rava, Conserving contemporary art: issues, methods, materials, and research, Getty Conservation Institute, Los Angeles, 2012.
10. M. Cotte, A. Genty-Vincent, K. Janssens and J. Susini, C. R. Phys., 2018, 19, 575–588.
11. L. Bertrand, M. Cotte, M. Stampanoni, M. Thoury, F. Marone and S. Schöder, Phys. Rep., 2012, 519, 51–96.
12. K. Keune, J. Mass, F. Meirer, C. Pottasch, A. van Loon, A. Hull, J. Church, E. Pouyet, M. Cotte and A. Mehta, J. Anal. At. Spectrom., 2015, 30, 813–827.
13. M. Ghirardello, V. Gonzalez, L. Monico, A. Nevin, D. MacLennan, C. S. Patterson, M. Burghammer, M. Réfrégiers, D. Comelli and M. Cotte, Microsc. Microanal., 2022, 28, 1504–1513.
14. K. Janssens, M. Alfeld, G. Van der Snickt, W. De Nolf, F. Vanmeert, M. Radepont, L. Monico, J. Dik, M. Cotte, G. Falkenberg, C. Miliani and B. G. Brunetti, Annu. Rev. Anal. Chem., 2013, 6, 399–425.
15. T. Learner, Analysis of modern paints, Getty Conservation Institute, Los Angeles, 2004.
16. A. Artesani, S. Mosca, M. V. Dozzi, G. Valentini and D. Comelli, Microchem. J., 2020, 155, 104739.
17. A. P. Middleton, H. G. M. Edwards, P. S. Middleton and J. Ambers, J. Raman Spectrosc., 2005, 36, 984–987.
18. O. Carp, Prog. Solid State Chem., 2004, 32, 33–177.
19. S. Moser, S. Fatale, P. Krüger, H. Berger, P. Bugnon, A. Magrez, H. Niwa, J. Miyawaki, Y. Harada and M. Grioni, Phys. Rev. Lett., 2015, 115, 096404.
20. C.-H. Chuang, C.-M. Chen, Y.-C. Shao, P.-H. Yeh, C.-M. Chang, W.-F. Pong, M. Kapilashrami, P.-A. Glans, S. Gul, G. Wang, Y. Li, J. Zhang, J. Miyawaki, H. Niwa, Y. Harada, J.-M. Chen and J. Guo, J. Vac. Sci. Technol., A, 2021, 39, 063204.
21. J. Guo, P.-A. Glans, Y. S. Liu and C. Chang, in On Solar Hydrogen & Nanotechnology, ed. L. Vayssieres, John Wiley & Sons, Ltd, Chichester, UK, 2010, pp. 123–142.
22. C. Vorwerk, F. Sottile and C. Draxl, Phys. Rev. Res., 2020, 2, 042003.
23. K. Gilmore, Phys. Chem. Chem. Phys., 2023, 25, 217–231.
24. A. Gordeeva, T. Thersleff, Y.-J. Hsu, C. Liebske, P. Ulmer, O. Andersson and U. Häussermann, J. Solid State Chem., 2023, 322, 123952.
25. I. G. Gurtubay, J. M. Pitarke, W. Ku, A. G. Eguiluz, B. C. Larson, J. Tischler, P. Zschack and K. D. Finkelstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125117.
26. R. Georgiou, R. S. Popelka-Filcoff, D. Sokaras, V. Beltran, I. Bonaduce, J. Spangler, S. X. Cohen, R. Lehmann, S. Bernard, J.-P. Rueff, U. Bergmann and L. Bertrand, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116021119.
27. A. Hitchcock and D. Mancini, J. Electron Spectrosc. Relat. Phenom., 1994, 67, 1–12.
28. H.-C. Weissker, J. Serrano, S. Huotari, E. Luppi, M. Cazzaniga, F. Bruneval, F. Sottile, G. Monaco, V. Olevano and L. Reining, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085104.
29. K. Ruotsalainen, A. Nicolaou, C. J. Sahle, A. Efimenko, J. M. Ablett, J.-P. Rueff, D. Prabhakaran and M. Gatti, Phys. Rev. B, 2021, 103, 235136.
30. J.-P. Rueff, in Magnetism and Synchrotron Radiation, ed. E. Beaurepaire, H. Bulou, F. Scheurer and K. Jean-Paul, Springer, Berlin, Heidelberg, 2010, vol. 133, pp. 263–277.
31. R. Georgiou, C. J. Sahle, D. Sokaras, S. Bernard, U. Bergmann, J.-P. Rueff and L. Bertrand, Chem. Rev., 2022, 122, 12977–13005.
32. W. Schülke, Electron dynamics by inelastic X-ray scattering, Oxford Univ. Press, Oxford, 2007.
33. I. G. Gurtubay, W. Ku, J. M. Pitarke, A. G. Eguiluz, B. C. Larson, J. Tischler and P. Zschack, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 201201.
34. N. Vast, L. Reining, V. Olevano, P. Schattschneider and B. Jouffrey, Phys. Rev. Lett., 2002, 88, 037601.
35. L. Chiodo, J. M. García-Lastra, A. Iacomino, S. Ossicini, J. Zhao, H. Petek and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045207.
36. R. Asahi, Y. Taga, W. Mannstadt and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7459–7465.
37. F. Labat, P. Baranek, C. Domain, C. Minot and C. Adamo, J. Chem. Phys., 2007, 126, 154703.
38. P. J. Hardman, G. N. Raikar, C. A. Muryn, G. Van Der Laan, P. L. Wincott, G. Thornton, D. W. Bullett and P. A. Dale, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7170–7177.
39. K. M. Glassford and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1284–1298.
40. S. Huotari, C. J. Sahle, C. Henriquet, A. Al-Zein, K. Martel, L. Simonelli, R. Verbeni, H. Gonzalez, M.-C. Lagier, C. Ponchut, M. Moretti Sala, M. Krisch and G. Monaco, J. Synchrotron Radiat., 2017, 24, 521–530.
41. C. J. Sahle, A. D. Rosa, M. Rossi, V. Cerantola, G. Spiekermann, S. Petitgirard, J. Jacobs, S. Huotari, M. Moretti Sala and A. Mirone, J. Synchrotron Radiat., 2017, 24, 269–275.
42. P. Gueriau, J.-P. Rueff, S. Bernard, J. A. Kaddissy, S. Goler, C. J. Sahle, D. Sokaras, R. A. Wogelius, P. L. Manning, U. Bergmann and L. Bertrand, Anal. Chem., 2017, 89, 10819–10826.
43. R. Georgiou, P. Gueriau, C. J. Sahle, S. Bernard, A. Mirone, R. Garrouste, U. Bergmann, J.-P. Rueff and L. Bertrand, Sci. Adv., 2019, 5, eaaw5019.
44. L. Bertrand, S. Schöeder, D. Anglos, M. B. Breese, K. Janssens, M. Moini and A. Simon, TrAC, Trends Anal. Chem., 2015, 66, 128–145.
45. L. Bertrand, S. Schöder, I. Joosten, S. M. Webb, M. Thoury, T. Calligaro, T. Anheim and A. Simon, TrAC, Trends Anal. Chem., 2023, 117078.
46. C. Gervais, M.-A. Languille, S. Reguer, M. Gillet, E. P. Vicenzi, S. Chagnot, F. Baudelet and L. Bertrand, Appl. Phys. A: Mater. Sci. Process., 2013, 111, 15–22.
47. C. Gervais, M. Thoury, S. Réguer, P. Gueriau and J. Mass, Appl. Phys. A: Mater. Sci. Process., 2015, 121, 949–955.
48. M. Godet, L. Binet, S. Schöder, L. Brunel-Duverger, M. Thoury and L. Bertrand, J. Anal. At. Spectrom., 2022, 37, 1265–1272.
49. L. Monico, M. Cotte, F. Vanmeert, L. Amidani, K. Janssens, G. Nuyts, J. Garrevoet, G. Falkenberg, P. Glatzel, A. Romani and C. Miliani, Anal. Chem., 2020, 92, 14164–14173.
50. T. Schmitt, F. Rosi, E. Mosconi, K. Shull, S. Fantacci, C. Miliani and K. Gray, Heritage Sci., 2022, 10, 99.
51. B. A. Van Driel, K. J. Van Den Berg, M. Smout, N. Dekker, P. J. Kooyman and J. Dik, Heritage Sci., 2018, 6, 21.
52. S. Morsch, B. A. Van Driel, K. J. Van Den Berg and J. Dik, ACS Appl. Mater. Interfaces, 2017, 9, 10169–10179.
53. P. A. Christensen, A. Dilks, T. A. Egerton and J. Temperley, J. Mater. Sci., 1999, 34, 5689–5700.
54. P. A. Christensen, A. Dilks, T. A. Egerton and J. Temperley, J. Mater. Sci., 2000, 35, 5353–5358.

---

Footnote

† Electronic supplementary information (ESI) available: manufacturer and chemical information of commercial pigments, experimental configurations, additional experimental and simulated DSF spectra for anatase and rutile-based pigments, anisotropy of rutile and anatase, theoretical approach, computational details of the numerical calculations of TiO₂, experimental and calculated IXS spectra of TiO₂ crystals, dispersion of bulk rutile and anatase along the Z direction, comparison of the experiment with theory, and the role of local field effects. See DOI: https://doi.org/10.1039/d3cp04753a

---