Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How microstructures, oxide layers, and charge transfer reactions influence double layer capacitances. Part 1: impedance spectroscopy and cyclic voltammetry to estimate electrochemically active surface areas (ECSAs)†
Maximilian
Schalenbach
 *a,
Victor
Selmert
*a,
Victor
Selmert
 ab,
Ansgar
Kretzschmar
ab,
Ansgar
Kretzschmar
 a,
Luc
Raijmakers
a,
Yasin Emre
Durmus
a,
Luc
Raijmakers
a,
Yasin Emre
Durmus
 a,
Hermann
Tempel
a,
Hermann
Tempel
 a and
Rüdiger-A.
Eichel
ab
a and
Rüdiger-A.
Eichel
ab
aFundamental Electrochemistry (IEK-9), Institute of Energy and Climate Research, Forschungszentrum Jülich, Wilhelm-Johnen-Straße, 52425 Jülich, Germany. E-mail: m.schalenbach@fz-juelich.de
bInstitute of Physical Chemistry, RWTH Aachen University, 52062 Aachen, Germany
First published on 4th December 2023
Abstract
Varying the electrode potential rearranges the charges in the double layer (DL) of an electrochemical interface by a resistive-capacitive current response. The capacitances of such charge relocations are frequently used in the research community to estimate electrochemical active surface areas (ECSAs), yet the reliability of this methodology is insufficiently examined. Here, the relation of capacitances and ECSAs is critically assessed with electrochemical impedance spectroscopy (EIS) and cyclic voltammetry (CV) data on polished (Au, Ti, Ru, Pt, Ni, glassy carbon, graphite plate) and porous (carbon fleeces) electrodes. By investigating this variety of electrodes, the frequency-dependencies observed in the measured capacitances are shown to arise from the inherent resistive-capacitive DL response, charge transfer reactions, and resistively damped capacitive currents in microstructures (such as pores, pinholes, or cracks). These frequency-dependencies are typically overlooked when capacitances are related to ECSAs. The capacitance at the specimen-characteristic relaxation frequency of the resistive-capacitive DL response is proposed as a standardized capacitance-metric to estimate ECSAs. In 1 M perchloric acid, the polished gold electrode and the high-surface area carbon fleeces show ratios of capacitance-metric over surface-area of around 3.7 μF cm−2. Resistively damped currents in microstructures and low-conducting oxide layers are shown to complicate trustworthy capacitance-based estimations of ECSAs. In the second part of this study, advanced equivalent circuits models to describe the measured EIS and CV responses are presented.
Introduction
The electrochemical double layer (DL) describes the local charge distribution at the interface of an electrode and an electrolyte.1,2 In electrostatic equilibrium, the DL shields the electrode potential and leads to a potential drop at the electrolyte–electrode interface.3 A change of the electrode potential leads to a dynamic field penetration into the electrolyte that rearranges ions and that changes the captured charge in the DL.4 The resulting ion movement and charge capture lead to a resistive-capacitive current response.5 This current response is commonly ascribed to the DL capacitance, whereas the naming is a misleading simplification that neglects the resistive contributions of the ion migration in the DL. The DL plays decisive roles for charge transfer reactions6,7 and the ion transport at the reaction interface.8–10 Application of the DL-phenomena can be found for instance in sensors11,12 and supercapacitors.13,14Electrochemical impedance spectroscopy (EIS)15,16 and cyclic voltammetry (CV)17 are standard methods that probe the current responses of electrodes under sinusoidal and triangular electrode potential variations, respectively. The current response of an electrode with dominating contributions of DLs (often referred to as blocking electrode) is in the following denoted as ‘DL response’. DLs of polished electrodes are typically parameterized by constant phase elements (CPEs),18–20 which describe a constant phase angle in impedance spectra.21 This constant phase characteristic can be represented by resistive-capacitive transmission line models,22 which describe semi-infinite ladder networks of resistances and capacitances. The transmission line model was interpreted as a direct physical representation of the ion transport in the DL, describing resistive-capacitive ion displacements under an alternating electrode potential.5,23,24 DL responses of the time-domain operating CV were recently modelled based on the frequency-domain based CPEs in combination with Fourier or LaPlace transformations.25–27 A more direct approach to model the DL responses of CV measurements can be obtained by applying the differential calculus in the time domain on transmission line models.23,24 For a polished gold electrode, the CPE-parameterization of the DL was reported to be valid for amplitudes up to 0.1 V, whereas higher amplitudes were shown to increase intrinsic potential-dependencies of the DL response.26
In the field of aqueous electrochemistry, studies presenting protocols to characterize electrocatalysts can be found among the most cited publications.28,29 A central part of these protocols is the estimation of the electrochemically active surface area (ECSA) by EIS or CV, which was afterwards further addressed by several research groups.28–31 The ECSA can also be estimated by methods such as specific adsorption or underpotential deposition,32–35 which are, however, only applicable to specific material-dependent adsorption sites. For instance, the electrochemical stripping of carbon monoxide from platinum group metal catalysts is an established standard to determine ECSAs.34,36,37 In contrast, capacitance measurements were considered as promising for ECSA estimations as they can be done for all types of uniform electrodes,28,29 whereas distinguishing capacitive contributions of substrate and active materials (e.g. Pt/C catalysts) is not possible.
In the case of porous carbon structures, several studies38–41 reported linear relations between surface areas determined with gas adsorption measurements via the Brunauer–Emmett–Teller (BET) method and electrochemical capacitances. In contrast, Jung et al.42 showed that BET surface areas of metal oxide powders do not correlate to electrochemical capacitances, partially showing orders of magnitudes different ratios of capacitances over surface areas. Even for a model system, such as a polished gold electrode, reported literature values for capacitances span between 6–100 μF cm−2.43–50 A recent study5 showed a similar span of capacitances measured for one polished gold electrode in 1 M perchloric acid, as the DLC intrinsically depends on the frequency due to its CPE-character. In CV, different scan rates were also reported to impact the estimation of the capacitance,30,31 further underlining the intrinsic frequency dependence of the capacitance.
Based on the above discussed literature, it remains questionable, in which framework capacitance measurements are trustworthy measures for ECSA estimations. Therefore, this study aims to present a systematic analysis of the physicochemical mechanisms that affect the capacitances of various plane (Au, Ti, Ru, Pt, Ni, glassy carbon, graphite plate) and porous electrodes (carbon fleeces). These various electrodes reveal the effects of probing frequencies, electrode morphologies, oxide layers, and charge transfer reactions on measured DL responses, showing the reliability and pitfalls of the relation between capacitance and ECSA. In the second part of this study, equivalent circuit models (ECMs) are presented to describe the measured DL responses in detail.51
Theory
Simple equivalent circuit models (ECMs)
In ECMs, the DL of a polished electrode is typically represented by a constant phase elements (CPE), which portrays a frequency independent phase angle in the impedance spectrum.5,19,20,44–47 In combination with a series resistance (Rs), a simple ECM can be used to parametrize DL responses. The series resistance contains the ionic electrolyte resistance, the electric resistance of the examined electrode, and contact resistances. This ECM is shown in Fig. 1A and has been used to simulate all impedance data presented in this study, following the fitting procedure described in a previous published article.24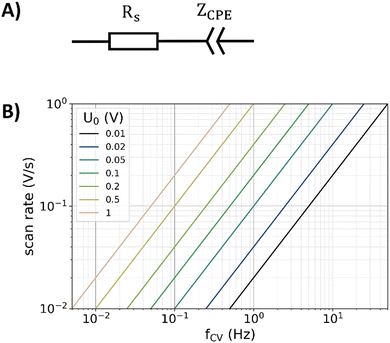 | ||
| Fig. 1 (A) Simple equivalent circuit model used for simulating the impedance response of the double layer, consisting of a series resistance Rs and a constant phase element with the impedance ZCPE. (B) Relation of scan rate, frequency, and amplitude (U0) for the triangular potential variation during CV calculated with eqn (7). | ||
Impedance
The impedance of a CPE is defined20,30,52 as | (1) |
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(−0.5πn), so that the capacitance dispersion of a CPE (defined as CCPE(f)) can be calculated with:5
sin(−0.5πn), so that the capacitance dispersion of a CPE (defined as CCPE(f)) can be calculated with:5 | (3) |
 | (4) |
Another useful definition to characterize the DL response is the relaxation, which in physics generally describes the transition of a perturbated system into equilibrium. The resistive-capacitive relaxation describes the transition from a capacitive-dominated regime at high frequencies to a resistive-dominated regime at lower frequencies. In the high-frequency part the perturbation occurs much faster than the time required to equilibrate the system, whereas in the low-frequency part the time scale of the perturbation is much slower than the response-time of the charge displacement. The resistive and capacitive parts equally contribute to the impedance at a phase angle of −45°. The frequency at this phase angle is here defined as f−45°. At this frequency, the capacitance of the polished gold electrode was reported as almost independent of the electrolyte concentration.5 Based on this work, f−45° will be used below to estimate the capacitance-metric C−45°, which corresponds to the value of CEIS(f) at f−45°.
In proximity of f−45°, a serial connection of a resistor and capacitor is reported to provide a good estimation of the impedance and capacitance dispersion of the DL response, showing just slight deviations from the ECM displayed in Fig. 1A.5 In the RC-series circuit, the resistive-capacitive time constant τRC describes the exponential decay of the current to potential changes. The time constant equals the product of resistance and capacitance. By approximating the CPE with C−45°, the time constant can be calculated by5
| τRC = RsC−45°. | (5) |
For this approximation, the relaxation frequency fr is consequently estimated to5
 | (6) |
In a RC-series circuit fr equals f−45°. The difference of both frequencies can serve as a measure5 for the RC-series approximation for the relaxation properties of the circuit in Fig. 1A.5 In 1 M perchloric acid, C−45° of a polished gold electrode is nearly potential-independent.5 Generally, at such high molarities, the intrinsic potential dependence of the differential capacitance predicted by the classical Gouy–Chapman type models is typically not observable, which appears just for lower molarities and frequencies.50
Cyclic voltammetry (CV)
In CV, a potential scan in the form of a triangular wave is applied to the working electrode while the current is simultaneously measured. The triangular wave is typically characterized by the amplitude U0 and scan rate ν, while its frequency fCV can be calculated by26 | (7) |
This equation is visualized in Fig. 1B. The capacitance can then either be determined by integrating the current30 during the up-going or down-going scan of the CV measurement, or by taking the difference of the currents Iup and Idown of both branches at the middle position divided by the scan rate.28,29 With reference to the latter case, the capacitance of the electrode can be extracted from the CV data by:
 | (8) |
Electrochemical active surface area
The capacitance from eqn (2) is used to estimate the EIS based ECSA (denoted as AECSAEIS), while the capacitance from eqn (8) is used to estimate the CV based ECSA (denoted as AECSACV) by | (9) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec denotes the specific capacitance of the DL that defines a reference value for the capacitance per electrode area.
spec denotes the specific capacitance of the DL that defines a reference value for the capacitance per electrode area.
Experimental
Electrochemical setup
Schematic sketches of the electrochemical cell used for the EIS and CV measurements are supplied in the ESI.† In brief, two different variations of the cell were used to measure plane and porous electrodes. In both variations, a three-electrode setup with separated electrode compartments was used. A platinum mesh served as the counter electrode, while an Ag/AgCl reference electrode (Metrohm) with 3 M KCl electrolyte was used. Plane specimens were placed at the bottom of the cell. A geometric area of 0.78 cm2 (1 cm diameter) of the specimen was exposed to the electrolyte, sealed with a 1 mm thick flat ethylene propylene diene monomer rubber. To measure porous electrodes, punched discs of 12 mm diameter were prepared from sheet material. These discs were pressed onto a gold foil (0.2 mm) with a hole of 10 mm diameter that served as an electrical contact. The cell was filled by pushing the electrolyte through a channel below the porous specimens, so that the upcoming electrolyte penetrated the porous structure. The electrolyte flow carried air trapped in the pores upstream and ensured the complete flooding of the porous structure. Detailed information on the cleaning of the cell and measurement preparations are given in the ESI.†The following plane electrodes were used for the measurements: (i) a polished polycrystalline cold rolled 2.5 mm thick gold plate (Junker Edelmetalle GmbH). (ii) The same gold specimen prepared with a 4000 grid sandpapered surface, denoted as rough gold electrode. (iii) A type 1 glassy carbon plate (Alfa Aesar). (iv) A type 2 glassy carbon plate (Alfa Aesar). (v) A graphite plate (Alfa Aesar). (vi) A titanium plate (HMW Hauner GmbH). (vii) A ruthenium plate (HMW Hauner). (viii) A platinum plate (Mateck GmbH). (ix) A nickel plate (HMW Hauner GmbH). Except for the graphite plate, all plane samples were thoroughly grinded down with 4000 grid SiC sandpaper (Struers). Afterwards, all specimens, except for the graphite plate and the rough gold electrode, were first polished with a suspension of 1 μm diamond particles (Struers), followed by a final polishing step performed with a 0.25 μm diamond particles suspension (Struers). For uniform and reproducible surface preparation, an automated machine (Struers, Tegramin) was used for grinding and polishing. In between all surface preparation steps the specimen surfaces were thoroughly rinsed with ultrapure water.
The porous electrodes are all made of carbon fleece. Besides commercial available carbon fleece (Freudenberg E20 and E35), a porous carbon fleece was manufactured from polyacrylonitrile (PAN) fibres, pyrolyzed at 1000 °C as reported in the literature.53 The carbon fleece specimens were all weighted with a precision balance and then immersed in 1 M perchloric acid solution prior to the measurements to remove impurities. The plane and porous specimens did not receive any additional surface cleaning procedures, whereas in the literature often potential cycling or flame annealing approaches are used to clean the surface.54 These procedures have been avoided intentionally as they cause roughening due to surface reconstruction.24 For instance, oxidizing and reducing the surface of platinum electrodes by potential cycling leads to stable CVs.54 However, the recrystallization, dissolution, and redeposition during the potential cycling are discussed to increase the surface area.24 In this study, potential cycling is shown to increase the capacitance for the case of the platinum electrode (Fig. 7C). To preserve the surface of the gold and carbon electrodes examined in this study from such surface-area increasing effects, a maximum potential of 0.6 V vs. RHE was applied to these electrodes. In contrast, this effect was explicitly examined for titanium, ruthenium, platinum, and nickel electrodes by applying potentials up to 1.5 V vs. RHE.
A Zahner Zennium XC potentiostat was used for all electrochemical measurements. Aqueous solutions of perchloric acid (Alfa Aesar) or sodium hydroxide (Merck, Suprapure) were made with ultrapure water and served as electrolytes. All measurements were performed in a temperature-controlled lab at 20 °C. Before performing the EIS and CV measurements, the amount of dissolved oxygen was reduced by purging the electrolytes for 15 min with nitrogen at a flow rate of 100 ml min−1 through a glass frit with fine pores. During the EIS and CV measurements, nitrogen was purged through the cell below the electrolyte level with a flow of 20 ml min−1 (see ESI†) to reduce the diffusion of air into the electrolyte. The gas inlet was 25 mm above the sample, so that the nitrogen bubbles could not get in direct contact with the examined electrodes. Even with nitrogen purging small traces of oxygen remain in the electrolyte, which can be measured with the very sensitive electrochemical measurements. In one of the presented measurements, the purging procedure was conducted with oxygen instead of nitrogen, to intentionally saturate the electrolyte with oxygen and to see its effect of the measured DL response.
The measurement protocol to characterize the gold and carbon electrodes consisted of the following steps: (i) a CV between 0.05 and 0.6 V vs. RHE was recorded with a scan rate of 0.2 V s−1. (ii) A constant electrode potential of 500 mV vs. RHE was applied for 2 minutes with simultaneous current monitoring. The averaged current of the last 20 seconds of this potentiostatic method is in the following defined as the potentiostatic bypass current Ibypass,PS. This potentiostatic bypass current serves as a measure for side reactions such as the oxygen reduction reaction. (iii) An impedance spectrum with an amplitude of 10 mV in a frequency range between 0.01 Hz and 1 MHz with 6 logarithmically distributed steps per decade was recorded. The ECM in Fig. 1 has been used for fitting the data of the EIS measurements according to the procedure describe in the literature.24 (iv) CV measurements with an amplitude of 0.01 V and a scan rate of 0.01 V s−1 were conducted. Prior to the CV measurements, the start potential (500 mV vs. RHE minus half of the employed CV amplitude) was applied for 30 s to reduce capacitive charge and discharge currents. (v) Repeating the fourth step for scan rates of 0.02, 0.05, 0.1, 0.2, 0.5 and 1 V s−1. (vi) Repeating the fourth and fifth step with an amplitude of 50 mV.
The impact of the oxidation on the DL response was examined with the titanium, ruthenium, platinum, and nickel electrodes. The corresponding measurement protocol consists of the following steps: (i) applying a constant electrode potential of 0.1 V vs. RHE for two minutes. (ii) Recording an impedance spectrum. (iii) Repeating the first two steps by a stepwise potential increase of 0.1 V until a potential of 1.5 V vs. RHE (for titanium, platinum, and nickel) or 1.3 V vs. RHE (for ruthenium) was reached. The vertex potential of ruthenium is lower to avoid excessive oxygen evolution, bubble coverage, and dissolution. (iv) Repeating the first three steps for two times to examine the irreversibility of the oxide layer formation.
Gas adsorption measurements
BET surface areas were obtained from argon isotherms measured at 87 K with a 3P micro device (3P Instruments) using argon as the adsorptive. The temperature was adjusted using a Cryotune (3P Instruments). The examined carbon specimens were cut into pieces and inserted into the gas adsorption probe (glass tube). To accurately determine the weight of the specimen, the glass tube was weighed in the empty state and the filled state after inserting the sample and degassing at 150 °C for 6 hours. The surface areas of the specimens were determined applying the BET method in a relative pressure range from 0.1 to 0.3. A detailed evaluation of the BET data is provided in the ESI† to this article.Results and discussion
The following results and discussion are focused on EIS data, as the impedance calculus summarizes the response by the easy-interpretable impedance magnitude and phase angle as a function of frequency. In contrast, the CV data is typically more difficult to parameterize due to the versatile shape of the current response in the time-domain.26 After evaluating the physicochemical mechanisms of the double layer (DL) responses with the EIS measurements, the CV data is exemplarily compared to EIS data. A more detailed analysis of the CV response follows in the second part of this study,51 while a full collection of the total CV data of all examined electrodes is given in the ESI,† including full range CVs of the examined electrodes between 0 and 0.6 V. The EIS data are displayed in Bode plots. Nyquist plots on the EIS data of all examined electrodes are supplied in the ESI† for more interested readers.Polished gold electrode
Polished gold electrodes are ideal model systems to study the DL response due to their nobleness55,56 and the negligible impact of their morphology on the current distribution at the surface. Before considering more complex electrodes, first the polished gold electrode is examined in detail to understand the basic physicochemical effects of the DL response. Fig. 2A–C display the measured impedance magnitude, phase angle, and capacitance dispersion (eqn (2)) of a polished gold electrode, respectively. The electrode was exposed to three different electrolytes: (i) nitrogen purged 1 M perchloric acid electrolyte. (ii) Oxygen purged 1 M perchloric acid electrolyte. (iii) Nitrogen purged 1 M sodium hydroxide electrolyte. | ||
| Fig. 2 Measured (dots) and simulated (lines) impedance data of a polished gold electrode in nitrogen purged 1 M perchloric acid, oxygen purged 1 M perchloric acid, and nitrogen purged 1 M sodium hydroxide. Magnitude, phase, and capacitance dispersion (eqn (2)) of the impedance are shown in (A), (B), and (C), respectively. The solid lines represent fits of the equivalent circuit from Fig. 1A to the measurements. | ||
The impedance spectrum of the polished gold electrode with the used geometric surface area of 0.78 cm2 in nitrogen purged 1 M perchloric acid is discussed in the literature5 in detail. In brief, the phase angle approaches 0° close to the highest displayed frequencies. In the high-frequency range above 50 kHz, |Z| is almost constant due to the dominance of the Ohmic resistance. As the phase angle approaches 0°, the impact of measurement errors on capacitance dispersion in the high-frequency regime becomes more pronounced.5 Due these measurement errors, the high-frequency impedance data above −2° is not graphed in this study for all specimens. The resistive-capacitive relaxation takes place between 1 and 100 kHz, which characterizes the transition between capacitive dominance at the low frequencies and Ohmic dominance at the high frequencies. Between 1 Hz and 1 kHz, the constant phase characteristic of the DL dominates. At lower frequencies side reactions (such as the reduction of oxygen impurities of the electrolyte) lead to significant Ohmic contributions to the impedance that increase the phase angle. The CPE parameterization of the DL is an empirical-based description of the measurement data. Deviations from this ECM may indicate more complex physicochemical interactions than that described by the physics of the transmission line model (see Introduction).
Table 1 summarizes the following properties of the impedance spectra: (i) the frequency f−45° at which the phase angle equals −45° during the resistive-capacitive relaxation of the DL contributions to the impedance. (ii) The capacitance value C−45° of CEIS(f−45°). (iii) The capacitance value CEIS@1Hz of the CEIS(1 Hz). (iv) The fit parameters Rs,fit, nfit, and ξfit, that describe the values of the equivalent circuit of Fig. 1A. (iv) The relaxation frequency fr, as calculated based on eqn (5) and (6) with the values of Rs,fit and C−45°. As discussed in the “Theory section”, fr equals f−45° in a serial RC circuit, which is a good approximation for the resistive-capacitive relaxation of the DL response.5 The quality of this approximation can be assessed by the deviations between fr and f−45° as discussed in the literature.5 (v) The specific capacitance ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec, which is determined by the ratio of C−45° over the surface area A (see eqn (9)). The lowest possible surface area of the polished gold electrode is to identify with the geometric surface of the electrode exposed to the electrolyte, which equals 0.78 cm2 (see “Experimental section”). The polishing quality is a decisive factor for the surface roughness, as even thorough polishing does not lead to plane surface on an atomic level. The surface roughness is estimated to increase the geometric surface area of the gold electrode to 1 ± 0.2 cm2.
spec, which is determined by the ratio of C−45° over the surface area A (see eqn (9)). The lowest possible surface area of the polished gold electrode is to identify with the geometric surface of the electrode exposed to the electrolyte, which equals 0.78 cm2 (see “Experimental section”). The polishing quality is a decisive factor for the surface roughness, as even thorough polishing does not lead to plane surface on an atomic level. The surface roughness is estimated to increase the geometric surface area of the gold electrode to 1 ± 0.2 cm2.
| f −45° (Hz) | f r (Hz) | C −45° (μF) | C EIS@1Hz (μF) | C CV@1Hz (μF) | A (cm2) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec (μF cm−2)
spec (μF cm−2) |
I bypass,CV (nA) | I bypass,PS (nA) | R s,fit (Ω) | n fit (°) | ξfit (Ω Hzn) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Au 1 M HClO4 N2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624 624 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 003 003 |
4 | 9.7 | 8.1 | 1 | 4 | 53 | 2 | 1.6 | 0.92 | 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 448 |
| Au 1 M HClO4 O2 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417 417 |
3.9 | 13.6 | 11.7 | 1 | 3.9 | −1517 | −530 | 1.6 | 0.92 | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 955 |
| Au 1 M NaOH N2 | 7381 | 7857 | 6.3 | 12 | 10.1 | 1 | 6.3 | −3328 | −3244 | 3.2 | 0.94 | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 993 993 |
| Au rough 1 M HClO4 | 9094 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 686 686 |
8.5 | 51.4 | 40.2 | — | — | 154 | −134 | 1.6 | 0.8 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 265 |
| Type 2 GC 1 M HClO4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 820 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 105 |
6.6 | 16.2 | 13.3 | — | — | 346 | 142 | 1.6 | 0.9 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 867 |
| Type 1 GC 1 M HClO4 | 9198 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 780 |
7.2 | 40.3 | 37 | — | — | −87 | −80 | 1.6 | 0.84 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 305 |
| Graphite plate 1 M HClO4 | 71.8 | 87 | 775 | 2172.7 | 2189.7 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300# 300# |
0.2 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 477 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301 301 |
2.3 | 0.8 | 471 |
| 4xE35 10 mM HClO4 | 1 | 1.1 | 1476 | 1478.4 | 1210.1 | 461# | 3.2 | −256 | −515 | 95 | 0.94 | 626 |
| 4xE35 100 mM HClO4 | 5.9 | 6.5 | 1638 | 1776.2 | 1759.5 | 461# | 3.5 | 2907 | −309 | 15 | 0.96 | 541 |
| 4xE35 1 M HClO4 | 34.3 | 40.4 | 1791 | 2053.1 | 2004.6 | 461# | 3.9 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
194 | 2.2 | 0.96 | 456 |
| PAN 1 M HClO4 | 6.1 | 7 | 7545 | 7982.6 | 7963.7 | 2017# | 3.7 | 9959 | −5745 | 3 | 0.96 | 124 |
In the case of the oxygen purged 1 M perchloric acid electrolyte, the contributions of the oxygen reduction reaction become more prominent and significantly increase the capacitance below 1 Hz (Fig. 2C). The response in the frequency regime of the resistive-capacitive relaxation between 1 and 100 kHz is almost identical for the nitrogen and oxygen purged perchloric acid electrolyte. At frequencies below 10 Hz, the charge transfer resistance of the oxygen reduction reaction increases the phase angle (Fig. 2B). The reduction of oxygen is, besides the kinetic barriers, also diffusion limited. Such diffusion limitations of charge transfer reactions are typically described by CPEs,57–59 as further evaluated in the second part of this study.51
After the measurements of the gold electrode were completed in perchloric acid, the same electrode is subsequently examined with EIS and CV in nitrogen purged 1 M sodium hydroxide electrolyte without any polishing in between. With reference to Table 1, the value of the serial resistance Rs,fit is approximately 2-times larger while that of C−45° is 1.6-times larger in the alkaline electrolyte than that in the acidic electrolyte. The sodium hydroxide solution is less ionically conducting than the perchloric acid solution, leading to a higher value of Rs,fit. Hydroxide ions are dipoles, and their polarizability is expected to significantly contribute to the dielectric contributions of the DL response. In contrast, the perchlorate anion (ClO4−) is spherical without dipole moments. Hence, the hydroxide ions are expected to enlarge the capacitive contributions of the DL to the response in comparison to those in the perchloric acid electrolyte. A study that examined the effect of the electrolyte polarizability on the DL response in detail could not be found in the literature. Besides the different polarizability, hydroxide ions are reported to adsorb pseudo-capacitively on the gold electrode,60 which may display another cause for the increased capacitance caused by the change of the electrolyte.
With the nitrogen purged alkaline electrolyte, the gold electrode shows similar contributions of the oxygen reduction to the impedance as that with the oxygen purged acidic electrolyte. The kinetic barriers for the oxygen reduction on gold are lower in the alkaline electrolyte than that of the acidic electrolyte due to different reaction pathways and intermediates.61–63 The dynamics of the gas solubility in acidic and alkaline regimes are also different, as nitrogen purging seem to replace dissolved oxygen in acidic solutions faster than in alkaline solutions. A detailed study on this physicochemical effect could not be found in the literature and is planned by the authors of this article.
Table 1 also summarizes the bypass currents Ibypass,PS that were determined with a potentiostatic protocol at a constant potential of 500 mV vs. RHE (see Experimental section). The bypass currents of the gold electrode in oxygen purged perchloric acid and in nitrogen purged sodium hydroxide both show reductive bypass currents more negative than −500 nA, which are responsible for the observed decrease of the phase angle towards low frequencies in Fig. 2. In contrast, the bypass current of the polished gold electrode in the nitrogen purged perchloric acid solution was 2 nA. Hence, the bypass current serves as a measure for contributions of the oxygen reduction reaction to the measured DL response. The experiments presented in the following are conducted with acidic electrolytes to minimize the effect of the oxygen reduction reaction, owed to: (i) a more effective exchange of dissolved oxygen by nitrogen purging in acidic electrolytes than in alkaline electrolytes. (ii) Most electrodes are better oxygen reduction catalysts in alkaline than in acidic regime. Thus, the same amounts of dissolved oxygen impurities are expected to lead to larger bypass currents with alkaline than with acidic electrolytes.
Plane electrodes: roughness, cracks, and holes
The aim of the following evaluation is to show how surface roughness, cracks, and holes affect the DL response of plane specimens. Fig. 3 shows the impedance spectra of four of the electrodes introduced in the Experimental section: (i) the rough gold electrode. (ii) The type 2 glassy carbon electrode displays an inert surface in the potential range considered. With the same polishing procedure, the hardness of the glassy carbon electrode leads to rougher surfaces than that of gold. The polished surface of the glassy carbon plate has cracks, pits, and craters, as shown with scanning electron microscopy images in the ESI.† (iii) The type 1 glassy carbon electrode shows more cracks, pits, and craters than the glassy carbon type 2 electrode. (iv) The graphite plate consists of a pressed structure of graphite particles. The cracks and holes in this structure lead to significant electrolyte uptake that increases the specimen's weight by approximately 5% (derived from the dry and wetted weight). | ||
| Fig. 3 Measured impedance spectra and capacitance dispersions (scatters) of a rough gold electrode, a type 1 glassy carbon plate, a type 2 glassy carbon electrode, and a graphite plate. All measurements were performed in nitrogen purged 1 M perchloric acid electrolyte. The golden line with the label “Au reference” shows the fit to the polished gold in 1 M perchloric acid electrode from Fig. 2. Fits of the equivalent circuit from Fig. 1A are displayed as solid lines. (A) Impedance magnitude. (B) Impedance phase angle. (C) Capacitance dispersion. | ||
The value of C−45° of the rough gold surface is approximately 2.1-times larger than that of the polished gold electrode (Table 1), which can be attributed to its larger surface area. In Table 1, the polished gold electrode shows an CPE-exponent nfit of 0.92, while it is 0.8 for the rough gold electrode. The higher the value of the exponent, the more capacitive is the DL response and the flatter (eqn (3) and (4)) is the slope in the capacitance dispersion CEIS(f). The detailed physical origin of the significant different values of the exponents of the rough and polished gold electrode is beyond the scope of this article but may be attributable to stray fields at the rough interface that increase the Ohmic proportion of the DL response.
The glassy carbon type 1 electrode shows larger capacitance values than that of the glassy carbon type 2 electrode in Fig. 3C, which is attributed to more holes and cracks at the surface. These morphology features are in the following denoted as microstructures. Towards low frequencies, the phase angles of the glassy carbon electrodes increase in a larger extent than the expectation from the fit (described by eqn (3) and (4)). Unlike the gold electrode, this low-frequency increase of the phase angle cannot be related to the oxygen reduction reaction as their impedance spectra are equal in nitrogen and oxygen purged perchloric acid electrolyte (graphed in the ESI†). Accordingly, in acidic media the oxygen reduction reaction is not significantly catalysed on glassy carbon at 0.5 V vs. RHE.
The capacitive currents are resistively damped in the microstructures. In the second part of this study,51 this phenomena is explained with equivalent circuit models. Qualitatively, the frequency dependence of the resistively damped currents can be explained as follows: towards lower frequencies the impedance magnitude increases for which the magnitude of the current decreases (Ohm's law). This current decrease causes smaller Ohmic voltage drops, so that the resistive damping of capacitive currents in microstructures is reduced towards lower frequencies. As a result, cracks and pores increasingly contributed to the capacitance dispersion towards lower frequencies. For instance, the capacitance of the type 1 glassy carbon electrode is at the relaxation frequency 1.1-times times larger than that of the type 2 glassy carbon electrode. At 1 Hz, this ratio increases to a factor of 1.7, as more of the microstructures contribute to the measured capacitance.
The more the capacitive currents are resistively damped in microstructures, the lower becomes the value of nfit. The response of glassy carbon type 1 electrode is with nfit = 0.84 significantly more resistive than that of the glassy carbon type 2 electrode with nfit = 0.9. Weakly conducting structures such as the electrolyte in pores and cracks are often described by CPEs that account for the transmission line character of electrolyte channels.47,52,64 Towards increasing hole-depth and longer transmission lines the response becomes more resistive, as examined in detail in the second part of this article.51
The graphite plate shows an approximately 190 times larger value for C−45° than that of the polished gold electrode, showing that the electrolyte uptake of the graphite plate significantly increases the ECSA. Like the type 1 glassy carbon specimen, the graphite plate shows a prominent increase of the capacitance below 1 Hz, which is attributed to capacitances of resistively damped microstructures. The surface area of the graphite plate (length & width 2.5 cm, thickness 1.25 cm) is determined by with reference to the gas adsorption measurements to 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm2, whereas the polished gold electrode has an estimated surface area of 1 cm2. Hence, the 190 times larger value for C−45° does not correlate linearly with the difference in the surface areas. Most of the capacitive contributions of the microstructure in the graphite plate are resistively damped and thus do not significantly contribute to the capacitance dispersion. The CPE exponent of nfit = 0.8 in combination with the increasing capacitance towards low frequencies underline the resistive contribution of the microstructure to the DL response. The bypass current of Ibypass,PS = 12.5 μA of the graphite plate indicates a significant amount of side reactions insides it structures with an unknown physicochemical origin. However, in relation to its surface area of 42
300 cm2, whereas the polished gold electrode has an estimated surface area of 1 cm2. Hence, the 190 times larger value for C−45° does not correlate linearly with the difference in the surface areas. Most of the capacitive contributions of the microstructure in the graphite plate are resistively damped and thus do not significantly contribute to the capacitance dispersion. The CPE exponent of nfit = 0.8 in combination with the increasing capacitance towards low frequencies underline the resistive contribution of the microstructure to the DL response. The bypass current of Ibypass,PS = 12.5 μA of the graphite plate indicates a significant amount of side reactions insides it structures with an unknown physicochemical origin. However, in relation to its surface area of 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm2, the bypass currents are even smaller than that of the gold electrode in nitrogen purged 1 M perchloric acid.
300 cm2, the bypass currents are even smaller than that of the gold electrode in nitrogen purged 1 M perchloric acid.
The similar CPE-parameterization of conductivity limiting microstructures and diffusion limited charge transfer reactions both shift the DL response to a more resistive regime towards lower frequencies. Hence, the effect of both contributions to impedance spectra are difficult to distinguish. As a result, the drastic capacitance increase of the graphite plate towards low frequencies cannot be unambiguously assigned to conductivity limiting structures or side reactions.
Porous carbon fleece electrodes
Like the graphite plate with electrolyte-flooded cracks and pores, flooded porous electrodes have a three-dimensional structure of electrolyte channels and the electron conducting carbon phase. However, unlike the narrow channels with weak ion conduction in the cracks and pinholes of the above discussed electrodes, the porous carbon fleece structures examined in the following have wide electrolyte channels that supply low resistivity for the ion conduction. PTFE coatings are applied in many commercially available porous carbon structures for gas diffusion electrodes, which hinder the wetting of the electrode. Moreover, polymer coatings affect the electrodes capacitance in a similar fashion as oxide layers by an additional serial capacitance.51 To avoid the contribution of such surface layers in between the electron conduction phase and the electrolyte, the uncoated and commercially available Freudenberg E35 carbon felt is examined as a model system for porous carbon electrodes.Fig. 4 shows the impedance data and capacitance dispersion of four stacked Freudenberg E35 carbon felts (denoted as “4xE35”) in 10 mM, 100 mM, and 1 M perchloric acid. Table 1 shows that the values of C−45° are comparable despite the different electrolyte concentration, while the value of f−45° changes approximately linearly with the electrolyte concentration. A detailed analysis of a variation of the electrolyte concentration at the polished gold electrode is reported in literature5 and showed similar trends. Unlike the glassy carbon and graphite plate electrodes, the capacitance dispersions of the stacked Freudenberg E35 carbon felts do not show distinct deviations from the fits of the equivalent circuit in Fig. 1A below the individual values of f−45°, respectively. Hence, in this low-frequency regime, these electrodes neither show effects of charge transfer reactions nor resistive damping of capacitive currents.
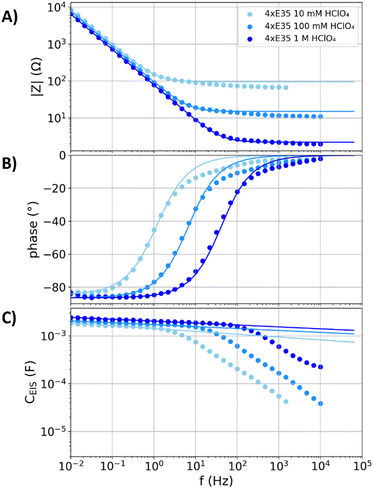 | ||
| Fig. 4 Measured impedance spectra and capacitance dispersions (scatters) of four stacked Freudenberg E35 carbon fleeces (denoted as “4xE35”) in nitrogen purged perchloric acid with concentrations of 10 mM, 100 mM, and 1 M. The solid lines represent fits of the equivalent circuit from Fig. 1A to the measurements. (A) Impedance magnitude. (B) Impedance phase angle. (C) Capacitance dispersion. | ||
At higher frequencies than the individual f−45°, the distributions of the resistances in the porous structures undergo a relaxation process, which results to significant deviations from the plotted fits (see second part for details). The resistances Rs,fit obtained from the fits (95, 15, and 2.2 Ω) do not exactly match the values for the high-frequency resistance of the impedance spectra (66, 10, and 1.9 Ω) in the 10 mM, 100 mM, and 1 M perchloric acid. The resistance of the fit partly accounts for the relaxation in the porous structure, representing a mean electrolyte resistance between the porous electrode and the reference electrode (see second part for a detailed model and discussion).51 In contrast, the high-frequency resistance is associated to the closest distance between the porous layer and the reference electrode, to which the pores do not significantly contribute.
Comparing capacitance values: specific capacitances
The aim of the following evaluation is to relate capacitance values to surface areas. The surface areas of the carbon fleeces and the graphite plate were measured by gas adsorption, whereas the surface area of the gold electrode was estimated based on the expected surface roughness of the polishing procedure (see above) with an accordingly high error. Fig. 5A shows the ratios of capacitances over surface areas, with capacitance values determined at f−45°, 0.01 Hz, 1 Hz, and 100 Hz for five different specimens: (i) the polished gold specimen in 1 M perchloric acid. (ii) The Freudenberg carbon fleece in 10 mM perchloric acid. (iii) The Freudenberg carbon fleece in 1 M perchloric acid. (iv) The pyrolyzed PAN carbon fleece in 1 M perchloric acid. (v) The graphite plate in 1 M perchloric acid. The frequencies f−45° (at a phase angle of −45°) serve as a measure for the relaxation frequencies fr, with respect to the in Table 1 presented similarities of both values and the discussion in the “Theory section”. | ||
| Fig. 5 (A) Ratio of capacitances over surface areas for the polished gold electrode, the four stacked Freudenberg E35 carbon fleeces, the PAN fleece, and the graphite plate in nitrogen purged perchloric acid electrolyte. The capacitances for the ratios were determined at f−45°, 0.01 Hz, 1 Hz, and 100 Hz. The errors describe the measurement error of the surface area. The horizontal dotted line represents a guide to the eye with a reference value of 3.7 μF cm−2. The value of the C/A for the gold electrode at 0.01 Hz is with 18.8 μF cm−2 outside of the y-axis limit of this plot. (B) Capacitance C−45° from impedance data as a function of the surface area for the polished gold plate, different amount of Freudenberg E20 and E35 fleeces in 1 M perchloric acid, the data from Fig. 4 with the electrolyte variation, and the PAN fleece. | ||
In the following, the discussion focusses on the data of gold electrode and the carbon fleeces, the measurements of the graphite plate are discussed afterwards. Fig. 3C and 5A show that the values of the capacitance dispersion CEIS for the stacked carbon fleeces lead between 0.01 and 1 Hz to similar values of the capacitance. Hence, in a certain set of parameters, the frequency dispersion of the capacitance can lead to an almost negligible effect on the ratios of capacitances over surface areas. Similar observations are also reported in the literature,38–41 which showed linear relations for the capacitance of porous carbon electrodes as a function their BET surface areas by using the same probing frequency. However, also a capacitance limit for porous electrodes was reported,39 which contradict the previous references and our findings. Maybe this reported observation is attributable to a resistively saturated capacitive current at a probing frequency that is higher than the relaxation frequency. Fig. 5A also shows, that none of the graphed static frequencies (0.01, 1, and 100 Hz) leads to an simultaneous agreement of the ratios of capacitance over surface area for the gold electrode and the carbon fleeces. However, for these specimens the ratios agree within the error bars when f−45° is used as a variable probing frequency. The surface area estimation by gas adsorption is most reliable for the PAN specimen (see ESI†), as this has the highest surface area per weight. For this specimen, the ratio of C−45° over the surface area equals 3.7 μF cm−2, which is in the following used as a reference for the specific capacitance ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec.
spec.
All examined electrodes show the same trend: higher frequencies than f−45° lead to smaller capacitance values than C−45°, while lower frequencies than f−45° lead to higher capacitance values than C−45°. These relations are attributable to the intrinsic capacitance dispersion (eqn (3)). In addition, the resistive damping of capacitive currents in the pores (see model in the second part of this study) amplifies this effect.51 Per definition, the contributions of resistive and capacitive to the DL response are equal at f−45°. As a result, the capacitances at the individual f−45° are affected by similar conditions for the ion displacement in the DL. As a result, the ratios of capacitance over surface area become comparable even for electrodes with orders of magnitude different surface areas (∼1 cm2 for the polished gold electrode and ∼2000 cm2 for the PAN carbon fleece electrode). In Fig. 2C, the capacitance dispersion of the gold electrode in oxygen purged 1 M perchloric acid electrolyte reached values in the milli-Farad regime towards low frequencies, whereas the value of C−45° (see Table 1 for comparison) is equal to that in the nitrogen purged 1 M perchloric acid electrolyte. Hence, as parasitic reactions mainly influence the low-frequency regime, they do not necessarily need to falsify the ECSA estimation by C−45° in the high-frequency regime. Hence, f−45° seems a reasonable choice as the probing frequency to determine a capacitance-metric to estimate ECSAs. With this capacitance-metric, the specific capacitance is determined to ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec = 3.7 μF cm−2 for the gold electrode and all carbon fleeces.
spec = 3.7 μF cm−2 for the gold electrode and all carbon fleeces.
In Fig. 5A, the ratios of capacitances over surface area of the graphite plate are significantly lower than 3.7 μF cm−2. Unlike the other specimen in Fig. 5, the response of the graphite plate is affected by resistively damped capacitive currents caused by its microstructure. Table 1 shows that the ratio of the capacitance over surface area (determined with the value of C−45°) of the graphite plate is 0.2 μF cm−2. At the lowest measured frequency of 0.01 Hz, the ratio of capacitance to surface area of the graphite plate is 1.6 μF cm−2, which comes closer to the above introduced reference value of 3.7 μF cm−2. Towards higher frequencies the resistive damping of the capacitive currents increases (see discussion above), for which f−45° in the high-frequency regime does not represent a reasonable choice to determine a capacitance value. Hence, the proposed capacitance-metric in terms of C−45° is not a reasonable choice for an ECSA-estimation of an electrode with resistively damped capacitive currents. However, at lower frequencies, the capacitance dispersion may be affected by the high amount of bypass currents. Hence, the ECSA of the graphite plate cannot be reliably determined from capacitance measurements.
Fig. 5B shows measured values for C−45° as a function of surface areas, including the data of the gold plate from Fig. 5A, the carbon fleeces from Fig. 5A, and a variation of the amount of stacked Freudenberg E35 and E20 carbon fleeces in 1 M perchloric acid. In this depiction, the specific capacitance ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec equals the slope. The mean slopes of these specimens are approximately equal to the previously stated reference value of
spec equals the slope. The mean slopes of these specimens are approximately equal to the previously stated reference value of ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec = 3.7 μF cm−2, confirming a linear relation of C−45° and surface area. In the literature, the electronic structure of the electrode is reported to affect the DL capacitance.65–67 Such dependencies are expected mainly at low electrolyte molarities and with the used 1 M perchloric acid electrolyte a significant impact of the different electronic structures of the gold and carbon electrode on the current response could not be observed.
spec = 3.7 μF cm−2, confirming a linear relation of C−45° and surface area. In the literature, the electronic structure of the electrode is reported to affect the DL capacitance.65–67 Such dependencies are expected mainly at low electrolyte molarities and with the used 1 M perchloric acid electrolyte a significant impact of the different electronic structures of the gold and carbon electrode on the current response could not be observed.
To summarize, a linear relation of the capacitance-metric C−45° and surface areas was established for the polished gold electrode and the porous carbon fleeces. From this relation, a specific capacitance of ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec = 3.7 μF cm−2 was derived. It was not possible to establish a linear relation of capacitance and surface for the electrodes that show resistively damped capacitive currents in microstructures, i.e. the glassy carbon and graphite plate electrodes.
spec = 3.7 μF cm−2 was derived. It was not possible to establish a linear relation of capacitance and surface for the electrodes that show resistively damped capacitive currents in microstructures, i.e. the glassy carbon and graphite plate electrodes.
CV and impedance
Thus far, the physicochemical mechanisms of the DL on plane and porous electrodes have been discussed with EIS data. EIS and CV both are probing the current response to a potential variation. The aim of the following discussion is to show similarities and differences of the capacitances extracted from both measurement methods. With CV, the current responses are measured in the time domain, whereas EIS measures the response in the frequency domain. The CPE-based ECM for the DL can be transformed from the frequency domain into the time domain or vice versa,25–27,68–71 as discussed in the second part of this study in more detail.51 The maximum frequency that is obtainable during CV is limited by the smallest possible amplitude and the highest possible scan rate of the used potentiostat, as visualized in Fig. 1B. For the used potentiostat, CVs with amplitudes lower than 10 mV and scan rates higher as 1 V s−1 were of poor quality, for which these values determine the highest possible CV-frequency of 50 Hz.In Fig. 6A, the capacitance values extracted from the EIS and CV data for the polished gold electrode in contact with the oxygen enriched electrolyte are compared as a function of frequency. In this system, the oxygen reduction contributes to the current response and the determined capacitances. Moreover, the capacitances of the stack of Freudenberg carbon fleeces in 100 mM perchloric acid electrolyte are shown. The maximum frequency accessible via CV (50 Hz) is about 500-times lower than the relaxation frequency (f−45°) of the polished gold specimen of approximately 22 kHz. For the gold electrode, EIS and CV show similar capacitances in their overlapping frequency range. The frequencies below 50 Hz showed in Fig. 5A an overestimation of the capacitances of polished gold electrode with EIS, which consequently also applies to the CV data.
In the impedance data, the contribution of charge transfer by oxygen reduction leads to a decrease of the phase angle in Fig. 2. Differences between the CPE-type contributions of conductivity limited capacitance and diffusion limited oxygen reduction were above discussed to lead to similar contributions to the impedance spectra. An analysis of potentiostatic bypass current Ibypass,PS (see above) helps to estimate the contributions of the oxygen reduction to the capacitance dispersion. During CV, the bypass current Ibypass,CV can be directly measured by the mean current during a scan. Besides the bypass current, the oxygen reduction also affects the amplitude of the current response during CV and eventually the extracted capacitance in the same manner as during EIS, leading to the comparable capacitances in Fig. 6. The oxygen reduction reaction is potential dependent, for which the voltage perturbation also changes the charge transfer, which is in CV often misinterpreted as capacitive current.
In Fig. 6A, the capacitances determined from CV and EIS data of the four stacked carbon fleeces in 100 mM perchloric acid reasonably agree below the relaxation frequency of approximately 6 Hz. However, above the relaxation frequency, the capacitances derived from the CV data decay drastically faster than that of the EIS data towards higher frequencies. To understand this difference, the related CV data is graphed in Fig. 6B. The current of the CV data is normalized to the scan rate, resulting in the dimension of a capacitance, which allows to compare the multiple orders of magnitude different currents that result from a scan rate variation.26 Moreover, this depiction of the CV data allows to read out the capacitance values directly from the graph. The relaxation frequency in the EIS data for this specimen is 6 Hz, which corresponds to a scan rate of 0.62 V s−1 at an amplitude of 50 mV. The graphed CV data with scan rates of 0.2 V s−1 shows already resistive damping, whereas at 0.5 V s−1 the resistive contributions reduce the capacitance extracted from the CV by 22.5% compared to 0.1 V s−1. Resistive contributions and the intrinsic frequency dispersion of the DL are difficult to distinguish in the CV data. In contrast, the phase angle in EIS allows to separately analyze resistive and capacitive contributions. Moreover, another advantage of EIS is that the relaxation frequency can be easily estimated by f−45°, which is not straightforward for the measured CV data.
To summarize, EIS shows in comparison to CV the following advantages: (i) EIS comes with a broader frequency range. Especially polished electrodes with low surface areas require the high-frequency range of EIS to characterize the relaxation behaviour at several kHz. (ii) EIS provides the phase angle as an indicator for the resistive contributions to the response, which allows to estimate the relaxation frequency. (iii) The impedance calculus provided an easy fitting procedure to the data, whereas CV modelling and data fitting is more advanced.26 However, CV is a method of choice to examine whether potential dependencies affect the DL response.23,26 Moreover, in CV the current offset allows to directly estimate bypass currents such as that of the oxygen reduction in relation to the capacitive currents. Hence, both methods are complementary. Depending on the examined specimen, both measurement methods should be considered to ensure the precision of the estimated capacitance.
Oxides and pseudocapacitances
Thus far, the capacitance of carbon and gold electrodes have been examined, providing oxide free and chemically inert surfaces in the considered potential range up to 0.6 V vs. RHE. However, most metallic electrodes in aqueous electrolytes form distinct oxide layers or even porous oxide structures. Metal oxides are typically semiconducting or insulating, IrO2 and RuO2 both display extraordinary exceptions with metallic conductivities.72 Non-conducting surface oxides can be described by a capacitance which is connected in series to that of the DL.73 Such serial connection of an oxide layer with a capacitance Coxide and capacitance CDL for the DL lead to a total capacitance Ctotal of: | (10) |
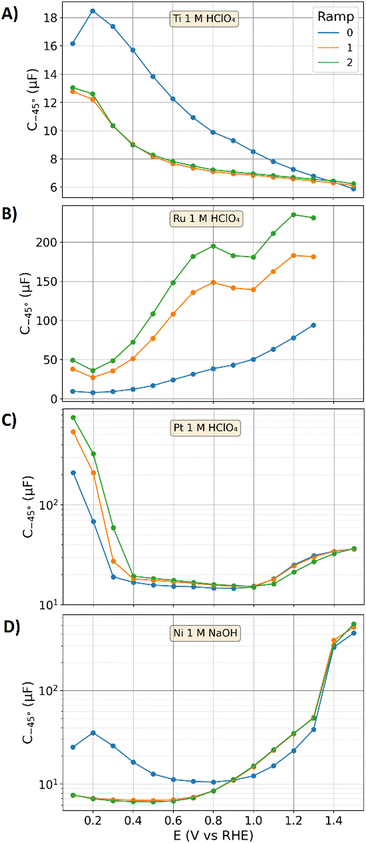
In the following, the capacitance will be discussed under the potential-driven formation of surface oxides. Polished titanium, ruthenium, and platinum electrodes were examined in nitrogen purged 1 M perchloric acid. In addition, a polished nickel electrode was examined in nitrogen purged 1 M sodium hydroxide electrolyte. All these metals are harder than gold, for which the same polishing procedure is expected to result in higher surface roughness. Fig. 7 shows the capacitance values of C−45° obtained via EIS as a function of the electrode potential with the procedure discussed in the “Experimental section”. In brief, the freshly polished species were mounted into the electrochemical cell, exposed to the electrolyte, and a potential of 0.1 V was applied. A potential variation with three cycles in sequence has been performed, starting at 0.1 V vs. RHE with an incremental potential increase of 0.1 V until a potential of 1.3 V for ruthenium or 1.5 V for titanium, platinum, and the nickel electrode was reached. The maximum voltage at the ruthenium specimen is smaller to avoid excessive oxygen evolution. The procedure of the stepwise potential increase in combination with EIS measurements is in the following defined as “potential-increase-ramp”. The impedance spectra of these measurement are presented and discussed in the ESI† and further evaluated in the second part of this study.51 Moreover, potentiostatic bypass currents for the presented data are also discussed in the ESI.† For the polished gold electrode in 1 M perchloric acid, a similar potential increase ramp is reported,5 which showed negligible influence of the potential on the value of C−45°.
Fig. 7A shows the capacitances of the polished titanium specimen for three repetitions of the potential-increase-ramp. The capacitance increases during first potential step from 16.2 μF cm−2 at 0.1 V to 18.5 μF cm−2 at 0.2 V. Towards higher potential it decreases, ending at a capacitance of 5.9 μF cm−2 at an applied potential of 1.5 V. Despite the porous oxide layers on titanium are expected to significantly increase the ECSA with the ongoing oxidation towards higher electrode potentials, the determined capacitance drops. This contradictionary relation can be attributed to the effect of surface oxides on the capacitance in terms of eqn (10). In the beginning of the second potential-increase-ramp, the capacitance increases back to 12.8 μF at 0.1 V, which is however 21% lower than that of the previous potential-increase-ramp. Once oxidized, titanium dioxide is formed on the surface,74,75 which cannot be electrochemically reduced by the applied potentials, for which the oxide layers on titanium can only grow and not decline. Hence, the capacitances of the second potential-increase-ramp remain smaller than those during the first potential increase ramp. The third potential-increase-ramp leads to similar capacitances as those of the second potential-increase-ramp.
The titanium dioxide oxide layer is semiconducting.75,76 It interacts with the electronic structure of the metal substrate and the electrolyte. These interactions between the semiconductor and electrolyte77,78 may also influence the charge distribution in the solid and electrolytic phase. Thus, the capacitance-ECSA relation of the well conducting metal and carbon surfaces cannot be directly transferred to electrodes covered with weakly conducting oxides.
Fig. 7B shows the capacitances of the ruthenium specimen examined with the potential-increase-ramps. During the first potential-increase-ramp the capacitances steadily increase from approximately 9.7 μF at 0.1 V to 94 μF at 1.3 V. Ruthenium is expected to grow an electrochemically formed porous oxide layer with increasing electrode potential.79,80 As ruthenium oxide is characterized by a metallic conductivity,72 the above gained understanding of the physicochemical mechanisms of the DL dynamics from gold and carbon electrodes are applicable. The entire surface area of this conductive hydrous and porous oxide layer is expected to contribute to the measured capacitance, whereas conductivity limiting contributions to the DL (such as that of the graphite plate) due to the nano-porosity in the formed electrochemical oxide cannot be observed in the impedance spectra (see ESI†).
In the beginning of the second potential-increase-ramp on the ruthenium electrode, the capacitance drops back to approximately 38 μF. The surface oxide of the noble metal may be partly reduced, by which some of the material is expected to dissolve, other may rearrange in a more packed form than that in the porous oxide layer.81 As a result, the ECSA and capacitance decrease by going from 1.3 V back to 0.1 V. During the second ramp, the capacitance increases from 0.2 to 0.8 V, where it forms a plateau until 1 V is reached. Towards higher potentials the capacitance further increases. The detailed physicochemical mechanisms of this potential dependence of the capacitance are beyond the scope of this study and may be an interesting topic for future works. The third potential-increase-ramp leads to similar results as that of the second potential-increase-ramp but with higher capacitances, which is attributed to the further growth of the porous oxide layer.
Fig. 7C shows the results on the platinum electrode, for which the measured capacitances are graphed in a semi-logarithmic plot (to make the distinct potential dependent changes better visible). The hydrogen adsorption on platinum displays a pseudo-capacitance, which is in the literature attributed to the interaction of the DL and an instantons charge transfer.24 Hydrogen adsorption is discussed to occur up to a potential of 0.4 V.54 Above 0.6 V, oxygen adsorption on Pt is reported,54 however, the more sluggish kinetics than that of the hydrogen adsorption on platinum are discussed in the literature24 to just partially contribute to the pseudo-capacitance. As a result, the hydrogen adsorption manifests more distinct in the measured capacitances in Fig. 3C than that at of the oxygen adsorption.
During the first potential-increase-ramp at the platinum electrode, the capacitance drops from to 210 μF at 0.1 V to 15.3 μF at 0.5 V. The second potential-increase-ramp starts with a capacitance of approx. 540 μF at 0.1 V, which is 2.6-times higher than that of the previous potential-increase-ramp. The oxide formation on platinum and the subsequent reduction at 0.1 V increased its surface area in agreement to literature data.24,54 This increase of the capacitance of the second potential-increase-ramp remains up 0.9 V. Above 1 V, the capacitances of the first and second potential-increase-ramp are equal. In the beginning of the third potential-increase-ramp the measured capacitance shows 750 μF at 0.1 V vs. RHE, which is attribute to a further ECSA increase. Above 1 V, the capacitances of the third potential-increase-ramp are smaller than that of the second and first potential-increase-ramp, although a higher surface area is expected. Like the titanium specimen, the formation of weakly conducting platinum oxide may affect the DL response and reduce the measured capacitance.
Fig. 7D shows the capacitances of a freshly polished nickel electrode in 1 M sodium hydroxide. Like the titanium electrode, a porous oxide might be formed prior to the measurement. Of the four oxide systems discussed, nickel displays the most complex system, as the capacitances are affected by the differently conducting oxides (hydroxide and oxyhydroxide) and their transition.82,83 In the first potential-increase-ramp of the nickel electrode, the capacitance drops from 25 μF at 0.1 V to 10.5 μF at 0.8 V, which might be attributable to a growth of a hydroxide layer. This semiconducting82,83 hydroxide coverage is expected to increase the ECSA. However, like the titanium electrode, this oxide-coverage reduces the capacitance. This drop of the capacitance was also previously reported in the literature73 and correlated with an XRD characterization of the surface film. Towards higher potentials the capacitance increases. At 1.4 V a significant increase of the capacitance due to the formation of oxyhydroxides is observable,84 which show higher conductivity as that of the hydroxides.82,83 In addition, the oxide transition itself is expected to contribute with its potential dependence to the capacitance, boosting it values up to 412 μF for the plane specimen. During the second and third potential-increase-ramp, the capacitances are almost equal and show significant lower values at potentials between 0.1 V and 0.8 V in comparison to the first potential-increase-ramp. A thicker hydroxide coverage may decrease the electrode's capactiance. Above 0.9 V, the second and third potential-increase-ramp led to higher capacitances than that of the first potential-increase-ramp, which may be attributable to larger ECSAs resulting from the oxide transitions and the higher conductivity of oxyhydroxide than that of hydroxide.
The oxide layers grown on the four different metals discussed above complicate the ESCA estimation via capacitance measurements. Ruthenium displays an exception due to the metallic conductivity of its oxide that may make the reference value (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec = 3.7 μF cm−2) applicable to estimate the ECSA viaeqn (9). However, whether the observed increase of the capacitance fully resolves the ECSA increase by the formed porous oxide remains a question for further research. In the case of the other metal electrodes examined, the oxidation led to a decrease of the capacitance, which is contrary to the expected increase of the ECSA by the formation of porous oxide layers. This decrease of the capacitance can be qualitatively explained by a serial connection of capacitors that represent the oxide layer and the double layer (see eqn (10)), respectively. Jung et al.42 reported that RuO2 and IrO2 nanoparticles show an approximately linear relation of BET surface areas and measured capacitances, which may underline the theory that their conductance allows a reliable capacitance-based ECSA determination. In contrast, the data of Jung et al.42 reported a severe underestimation of the capacitance-estimated ECSAs of other metal oxide nanoparticles, which is here attributed to the above discussed effect of weakly-conducting oxides on the measured capacitance. In addition, pseudocapacitances at platinum and nickel electrode further contribute to the measured capacitance that further complicate the ECSA estimation.
spec = 3.7 μF cm−2) applicable to estimate the ECSA viaeqn (9). However, whether the observed increase of the capacitance fully resolves the ECSA increase by the formed porous oxide remains a question for further research. In the case of the other metal electrodes examined, the oxidation led to a decrease of the capacitance, which is contrary to the expected increase of the ECSA by the formation of porous oxide layers. This decrease of the capacitance can be qualitatively explained by a serial connection of capacitors that represent the oxide layer and the double layer (see eqn (10)), respectively. Jung et al.42 reported that RuO2 and IrO2 nanoparticles show an approximately linear relation of BET surface areas and measured capacitances, which may underline the theory that their conductance allows a reliable capacitance-based ECSA determination. In contrast, the data of Jung et al.42 reported a severe underestimation of the capacitance-estimated ECSAs of other metal oxide nanoparticles, which is here attributed to the above discussed effect of weakly-conducting oxides on the measured capacitance. In addition, pseudocapacitances at platinum and nickel electrode further contribute to the measured capacitance that further complicate the ECSA estimation.
Many readers will expect a guideline for the ECSA estimations via capacitance measurements at the end of this article. The presented measurements above showed that for some electrodes C−45° is a reliable choice to estimate ECSAs based on measured capacitances. However, in each individual case it must be thoroughly validated whether the DL response is affected by resistively damped capacitive currents in microstructures, parasitic reactions, and/or the contributions of oxides layers. In these cases, the ECSA estimations based on capacitance measurements can be by orders of magnitudes misleading. Supplying a simple guideline is prone to misuse and will be a further component that exacerbate the current reproducibility crisis in science.85 To use ECSA determination a detailed understanding of the above discussed pitfalls and methods is necessary, which we aimed to provide by this detailed scientific study.
Conclusions
In this study, capacitances extracted from electrochemical impedance spectroscopy (EIS) and cyclic voltammetry (CV) measurements on a variety of plane and porous electrodes were related to their surface areas, respectively. Capacitance dispersions (capacitive contributions to the impedance as a function of frequency) were calculated directly from EIS data. At the relaxation frequency of the EIS data, specific capacitances of approximately 3.7 μF cm−2 were measured for the polished gold electrode and porous carbon fleeces in perchloric acid, respectively. In direct comparison to CV, EIS showed the advantages of a broader frequency range, an easier fitting procedure of equivalent circuits, and the phase angle as a measure to determine the relaxation frequency. In pores, resistive damping of capacitive currents was discussed to introduce additional frequency dependencies to the capacitance dispersion. Moreover, charge transfer reactions and semi-conducting or insulating oxides were discussed to complicate the ECSA determination. With respect to these pitfalls and limitations, reliable capacitance-based ECSA estimations were only possible for few of the examined electrodes. In the second part of this study, the contributions of microstructures and oxide layers to DL responses are modelled, aiming to understand the presented EIS and CV data in more detail.51List of abbreviations and symbols
| BET | Brunauer–Emmett–Teller method |
| CPE | Constant phase element |
| CV | Cyclic voltammetry |
| DL | Double layer |
| ECM | Equivalent circuit model |
| ECSA | Electrochemically active surface area |
| EIS | Electrochemical impedance spectroscopy |
| A (cm2) | Surface area |
| A ECSACV (cm2) | ECSA estimated with CV |
| A ECSAEIS (cm2) | ECSA estimated with EIS |
| C (F) | Capacitance |
| C −45° (F) | Capacitance value of CEIS at a phase angle of −45° during the resistive-capacitive relaxation |
| C CPE(f) (F) | Capacitance dispersion of a CPE in impedance spectroscopy |
| C CV (F) | Capacitance determined by CV measurements |
| C CV@1Hz (F) | Capacitance determined by CV measurements at fCV = 1 Hz |
| C EIS(f) (F) | Capacitance dispersion in impedance spectroscopy |
| C EIS@1Hz (F) | Value of CEIS(f) at f = 1 Hz |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) spec (F cm−2)
spec (F cm−2) | Specific capacitance (capacitance normalized to surface area) |
| f (Hz) | Frequency |
| f −45° (Hz) | Frequency value at a phase angle of −45° during the resistive-capacitive relaxation |
| f CV (Hz) | Frequency of CV as determined by eqn (8) |
| f r (Hz) | Relaxation frequency calculated by eqn (6) |
| i | Complex number |
| I down (A) | Current at the mean potential of the down scans of CV data |
| I up (A) | Current at the mean potential of the up scans of CV data |
| I bypass,CV (A) | Bypass current determined from CV data |
| I bypass,PS (A) | Bypass current determined from potentiostatic measurements |
| n | Exponent of the CPE |
| n fit | Exponent of the CPE determined by a fit to an impedance spectrum |
| Phase (°) | Phase angle of the impedance |
| R s (Ω) | Serial resistance of the equivalent circuit from Fig. 1A |
| R s,fit (Ω) | Serial resistance determined by a fit to an impedance spectrum |
| U 0 (V) | Peak-to-peak amplitude of EIS or CV measurements |
| |Z| (Ω) | Impedance magnitude |
| Z′′ (Ω) | Imaginary part of the impedance |
| Z CPE (Ω) | Impedance of a CPE |
| ν (V s−1) | Scan rate in CV |
| π | Pi |
| ξ (Ω Hzn) | Prefactor CPE |
| ξ fit (Ω Hzn) | Prefactor CPE determined by a fit to an impedance spectrum |
| τ RC (s) | Time constant describing the charge decay in an RC-circuit that is proportional to exp(−t/τRC) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the German Federal Ministry of Education and Research (BMBF) within the Project Phaskat (033RC028E).References
- W. Schmickler and D. Henderson, New models for the structure of the electrochemical interface, Prog. Surf. Sci., 1986, 22, 323–419 CrossRef CAS.
- J. Huang and Y. Chen, Combining theory and experiment in advancing fundamental electrocatalysis, Curr. Opin. Electrochem., 2019, 14, A4–A9 CrossRef.
- B. B. Damaskin and O. A. Petrii, Historical development of theories of the electrochemical double layer, J. Solid State Electrochem., 2011, 15, 1317–1334 CrossRef CAS.
- C. S. Mangelsdorf and L. R. White, The dynamic double layer: Part 1. Theory of a mobile Stern layer, J. Chem. Soc., Faraday Trans., 1998, 94, 2441–2452 RSC.
- M. Schalenbach, Y. E. Durmus, S. Robinson, H. Tempel, H. Kungl and R. Eichel, The Physicochemical Mechanisms of the Double Layer Capacitance Dispersion and Dynamics: An Impedance Analysis, J. Phys. Chem. C, 2021, 125, 5870–5879 CrossRef CAS.
- S. Vavra, E. Ahlberg and A. Martinelli, Charge transfer and electrical double layer of an amphiphilic protic ionic liquid in bulk and when confined in nanochannels, Phys. Chem. Chem. Phys., 2022, 24, 24469–24479 RSC.
- C. Lin, E. Laborda, C. Batchelor-Mcauley and R. G. Compton, Electrical double layer effects on ion transfer reactions, Phys. Chem. Chem. Phys., 2016, 18, 9829–9837 RSC.
- R. Alicki, D. Gelbwaser-Klimovsky, A. Jenkins and E. Von Hauff, Dynamical theory for the battery's electromotive force, Phys. Chem. Chem. Phys., 2021, 23, 9428–9439 RSC.
- S. I. Hernández, B. Altava, J. A. Portillo-Rodríguez, I. Santamaría-Holek, C. García-Alcántara, S. V. Luis and V. Compañ, The Debye length and anionic transport properties of composite membranes based on supported ionic liquid-like phases (SILLPS), Phys. Chem. Chem. Phys., 2022, 24, 29731–29746 RSC.
- M. Schalenbach, Y. E. Durmus, H. Tempel, H. Kungl and R.-A. Eichel, Ion transport and limited currents in supporting electrolytes and ionic liquids, Sci. Rep., 2022, 12, 1–10 CrossRef PubMed.
- S. Chun, Y. Kim, H. S. Oh, G. Bae and W. Park, A highly sensitive pressure sensor using a double-layered graphene structure for tactile sensing, Nanoscale, 2015, 7, 11652–11659 RSC.
- G. Li, S. Wang and Y. Y. Duan, Towards conductive-gel-free electrodes: Understanding the wet electrode, semi-dry electrode and dry electrode-skin interface impedance using electrochemical impedance spectroscopy fitting, Sens. Actuators, B, 2018, 277, 250–260 CrossRef CAS.
- E. Frackowiak, Carbon materials for supercapacitor application, Phys. Chem. Chem. Phys., 2007, 9, 1774–1785 RSC.
- G. Li, M. Ren and H. Zhou, Observably boosted electrochemical performances of roughened graphite sheet/polyaniline electrodes for use in flexible supercapacitors, Surf. Interfaces, 2022, 30, 101874 CrossRef CAS.
- B.-Y. Chang and S.-M. Park, Electrochemical impedance spectroscopy, Annu. Rev. Anal. Chem., 2010, 3, 207–229 CrossRef CAS PubMed.
- D. D. MacDonald, Reflections on the history of electrochemical impedance spectroscopy, Electrochim. Acta, 2006, 51, 1376–1388 CrossRef CAS.
- J. Heinze, Cyclic Voltammetry-“Electrochemical Spectroscopy”, Angew. Chem., Int. Ed. Engl., 1985, 23, 813–918 Search PubMed.
- P. Córdoba-Torres, T. J. Mesquita, O. Devos, B. Tribollet, V. Roche and R. P. Nogueira, On the intrinsic coupling between constant-phase element parameters α and Q in electrochemical impedance spectroscopy, Electrochim. Acta, 2012, 72, 172–178 CrossRef.
- W. R. Fawcett, Z. Kováčová, A. J. Motheo and C. A. Foss, Application of the ac admittance technique to double-layer studies on polycrystalline gold electrodes, J. Electroanal. Chem., 1992, 326, 91–103 CrossRef CAS.
- P. Zoltowski, On the electrical capacitance of interfaces exhibiting constant phase element behaviour, Electroanal. Chem., 1998, 443, 149–154 CrossRef CAS.
- G. J. Brug, A. L. G. van den Eeden, M. Sluyters-Rehbach and J. H. Sluyters, The analysis of electrode impedances complicated by the presence of a constant phase element, J. Electroanal. Chem., 1984, 176, 275–295 CrossRef CAS.
- J. C. Wang, Realizations of Generalized Warburg Impedance with RC Ladder Networks and Transmission Lines, J. Electrochem. Soc., 1987, 134, 1915–1920 CrossRef CAS.
- M. Schalenbach, Y. E. Durmus, H. Tempel, H. Kungl and R. A. Eichel, A Dynamic Transmission Line Model to Describe the Potential Dependence of Double-Layer Capacitances in Cyclic Voltammetry, J. Phys. Chem. C, 2021, 125, 27465–27471 CrossRef CAS.
- M. Schalenbach, Y. E. Durmus, H. Tempel, H. Kungl and R. A. Eichel, The role of the double layer for the pseudocapacitance of the hydrogen adsorption on platinum, Sci. Rep., 2022, 12, 1–10 CrossRef PubMed.
- C. Yun and S. Hwang, Analysis of the Charging Current in Cyclic Voltammetry and Supercapacitor's Galvanostatic Charging Profile Based on a Constant-Phase Element, ACS Omega, 2021, 6, 367–373 CrossRef CAS PubMed.
- M. Schalenbach, Y. E. Durmus, H. Tempel, H. Kungl and R.-A. Eichel, Double Layer Capacitances Analysed with Impedance Spectroscopy and Cyclic Voltammetry: Validity and Limits of the Constant Phase Element Parameterization, Phys. Chem. Chem. Phys., 2021, 23, 21097–21105 RSC.
- P. Charoen-amornkitt, T. Suzuki and S. Tsushima, Effects of Voltage-Dependence of the Constant Phase Element and Ohmic Parameters in the Modeling and Simulation of Cyclic Voltammograms, J. Electrochem. Soc., 2020, 167, 166506 CrossRef CAS.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, Benchmarking Heterogeneous Electrocatalysts for the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, Benchmarking HER and OER Electrocatalysts for Solar Water Splitting Devices, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed.
- O. Gharbi, M. T. T. Tran, B. Tribollet, M. Turmine and V. Vivier, Revisiting cyclic voltammetry and electrochemical impedance spectroscopy analysis for capacitance measurements, Electrochim. Acta, 2020, 343, 136109 CrossRef CAS.
- D. M. Morales and M. Risch, Seven steps to reliable cyclic voltammetry measurements for the determination of double layer capacitance, JPhys Energy, 2021, 3, 034013 CrossRef CAS.
- S. Trasatti and O. A. Petrii, Real Surface Area Measurements in Electrochemistry, J. Electroanal. Chem., 1992, 327, 353–376 CrossRef CAS.
- L. L. Fang, Q. Tao, M. F. Li, L. W. Liao, D. Chen and Y. X. Chen, Determination of the real surface area of palladium electrode, Chin. J. Chem. Phys., 2010, 23, 543–548 CrossRef CAS.
- D. Chen, Q. Tao, L. W. Liao, S. X. Liu, Y. X. Chen and S. Ye, Determining the Active Surface Area for Various Platinum Electrodes, Electrocatalysis, 2011, 2, 207–219 CrossRef CAS.
- H. Steininger, S. Lehwald and H. Ibachi, On the adsorption of CO on Pt(111), Surf. Sci. Lett., 1982, 123, A453 CrossRef.
- J. Sobkowski and A. Czerwinski, Voltammetric study of CO and CO2 adsorption on smooth and platinized platinum electrodes, J. Phys. Chem., 1985, 89, 365–369 CrossRef CAS.
- H. A. Gasteiger, N. Markovic, P. N. Ross and E. J. Cairns, CO electrooxidation on well-characterized Pt-Ru alloys, J. Phys. Chem., 1994, 98, 617–625 CrossRef CAS.
- H. Shi, Activated carbons and double layer capacitance, Electrochim. Acta, 1996, 41, 1633–1639 CrossRef CAS.
- O. Barbieri, M. Hahn, A. Herzog and R. Kötz, Capacitance limits of high surface area activated carbons for double layer capacitors, Carbon, 2005, 43, 1303–1310 CrossRef CAS.
- T. J. Rabbow and A. H. Whitehead, Deconvolution of electrochemical double layer capacitance between fractions of active and total surface area of graphite felts, Carbon, 2017, 111, 782–788 CrossRef CAS.
- V. Komanicky, K. C. Chang, A. Menzel, N. M. Markovic, H. You, X. Wang and D. Myers, Stability and Dissolution of Platinum Surfaces in Perchloric Acid, J. Electrochem. Soc., 2006, 153, B446 CrossRef CAS.
- S. Jung, C. C. L. McCrory, I. M. Ferrer, J. C. Peters and T. F. Jaramillo, Benchmarking nanoparticulate metal oxide electrocatalysts for the alkaline water oxidation reaction, J. Mater. Chem. A, 2016, 4, 3068–3076 RSC.
- B. Piela and P. Wrona, Capacitance of the gold electrode in 0.5 M H2SO4 solution: a.c. impedance studies, J. Electroanal. Chem., 1995, 388, 69–79 CrossRef.
- A. J. Motheo, A. Sadkowski and R. S. Neves, Electrochemical immittance spectroscopy applied to the study of the single crystal gold/aqueous perchloric acid interface, J. Electroanal. Chem., 1997, 430, 253–262 CrossRef CAS.
- A. J. Motheo, J. R. Santos, A. Sadkowski and A. Hamelin, The gold (210)/perchloric acid interface: impedance spectroscopy, J. Electroanal. Chem., 1995, 397, 331–334 CrossRef.
- T. Pajkossy, Capacitance dispersion on solid electrodes: anion adsorption studies on gold single crystal electrodes, Solid State Ionics, 1997, 94, 123–129 CrossRef CAS.
- T. Pajkossy, Impedance spectroscopy at interfaces of metals and aqueous solutions - Surface roughness, CPE and related issues, Solid State Ionics, 2005, 176, 1997–2003 CrossRef CAS.
- G. M. Schmid and N. Hackerman, Double Layer Capacities of Single Crystals of Gold in Perchloric Acid Solutions, J. Electrochem. Soc., 1962, 109, 243–247 CrossRef CAS.
- B. B. Berkes, A. Maljusch, W. Schuhmann and A. S. Bondarenko, Simultaneous acquisition of impedance and gravimetric data in a cyclic potential scan for the characterization of nonstationary electrode/electrolyte interfaces, J. Phys. Chem. C, 2011, 115, 9122–9130 CrossRef CAS.
- A. Hamelin, The surface state and the potential of zero charge of gold (100): a further assessment, J. Electroanal. Chem., 1995, 386, 1–10 CrossRef.
- M. Schalenbach, L. Raijmakers, V. Selmert, A. Kretzschmar, Y. E. Durmus, H. Tempel and R.-A. Eichel, How Microstructures, Oxide Layers, and Charge Transfer Reactions influence Double Layer Capacitances. Part 2: Equivalent Circuit Models, work in preparation.
- J.-B. Jorcin, M. E. Orazem, N. Pébère and B. Tribollet, CPE analysis by local electrochemical impedance spectroscopy, Electrochim. Acta, 2006, 51, 1473–1479 CrossRef CAS.
- A. Kretzschmar, V. Selmert, H. Weinrich, H. Kungl, H. Tempel and R. A. Eichel, Tailored Gas Adsorption Properties of Electrospun Carbon Nanofibers for Gas Separation and Storage, ChemSusChem, 2020, 13, 3180–3191 CrossRef CAS PubMed.
- V. Climent and J. M. Feliu, Thirty years of platinum single crystal electrochemistry, J. Solid State Electrochem., 2011, 15, 1297–1315 CrossRef CAS.
- B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240 CrossRef CAS.
- K. P. Kepp, Chemical Causes of Metal Nobleness, ChemPhysChem, 2020, 21, 360–369 CrossRef CAS PubMed.
- A. Tymosiak-Zielińska and Z. Borkowska, Double layer capacitance of Pt(111) single crystal electrodes, Electrochim. Acta, 2001, 46, 3063–3071 CrossRef.
- D. Leikis, K. Rybalka, E. Sevatyanov and A. Frumkin, Determination of the potetnials of zero charge of solid metals by means of differential capacity measurements, J. Electroanal. Chem. Interfacial Electrochem., 1973, 46, 161–169 CrossRef CAS.
- W. G. Pell, A. Zolfaghari and B. E. Conway, Capacitance of the double-layer at polycrystalline Pt electrodes bearing a surface-oxide film, J. Electroanal. Chem., 2002, 532, 13–23 CrossRef CAS.
- A. Chen and J. Lipkowski, Electrochemical and spectroscopic studies of hydroxide adsorption at the Au(111) electrode, J. Phys. Chem. B, 1999, 103, 682–691 CrossRef CAS.
- P. Quaino, N. B. Luque, R. Nazmutdinov, E. Santos and W. Schmickler, Why is gold such a good catalyst for oxygen reduction in alkaline media?, Angew. Chem., Int. Ed., 2012, 51, 12997–13000 CrossRef CAS PubMed.
- A. Ignaczak, R. Nazmutdinov, A. Goduljan, L. M. de Campos Pinto, F. Juarez, P. Quaino, G. Belletti, E. Santos and W. Schmickler, Oxygen Reduction in Alkaline Media—a Discussion, Electrocatalysis, 2017, 8, 554–564 CrossRef CAS.
- B. B. Blizanac, P. N. Ross and N. M. Markovic, Oxygen electroreduction on Ag (1 1 1): The pH effect, Electrochim. Acta, 2007, 52, 2264–2271 CrossRef CAS.
- B. Hirschorn, M. E. Orazem, B. Tribollet, V. Vivier, I. Frateur and M. Musiani, Constant-Phase-Element Behavior Caused by Resistivity Distributions in Films: I. Theory, J. Electrochem. Soc., 2010, 157, C452–C457 CrossRef CAS.
- W. Schmickler, A Jellium-Dipole Model for the Double Layer, J. Electroanal. Chem., 1983, 150, 19–24 CrossRef CAS.
- W. Schmickler, Electronic effects in the electric double layer, Chem. Rev., 1996, 96, 3177–3200 CrossRef CAS PubMed.
- A. Groß and S. Sakong, Modelling the electric double layer at electrode/electrolyte interfaces, Curr. Opin. Electrochem., 2019, 14, 1–6 CrossRef.
- A. Allagui, T. J. Freeborn, A. S. Elwakil and B. J. Maundy, Reevaluation of Performance of Electric Double-layer Capacitors from Constant-current Charge/Discharge and Cyclic Voltammetry, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed.
- M. E. Fouda, A. S. Elwakil, A. Allagui, H. Rezk and A. M. Nassef, Convolution-Based Estimation of Supercapacitor Parameters under Periodic Voltage Excitations, J. Electrochem. Soc., 2019, 166, A2267–A2269 CrossRef CAS.
- A. Allagui and M. E. Fouda, Inverse problem of reconstructing the capacitance of electric double-layer capacitors, Electrochim. Acta, 2021, 390, 138848 CrossRef CAS.
- A. Allagui, A. S. Elwakil and M. E. Fouda, Revisiting the Time-Domain and Frequency-Domain Definitions of Capacitance, IEEE Trans. Electron Devices, 2021, 68, 2912–2916 Search PubMed.
- W. Ryden and A. Lawson, Temperature Dependence of the Resistivity of RuO2 and IrO2, Phys. Lett., 1968, 26A, 209–210 CrossRef.
- S. L. Medway, C. A. Lucas, A. Kowal, R. J. Nichols and D. Johnson, In situ studies of the oxidation of nickel electrodes in alkaline solution, J. Electroanal. Chem., 2006, 587, 172–181 CrossRef CAS.
- W. Simka, A. Sadkowski, M. Warczak, A. Iwaniak, G. Dercz, J. Michalska and A. MacIej, Characterization of passive films formed on titanium during anodic oxidation, Electrochim. Acta, 2011, 56, 8962–8968 CrossRef CAS.
- J. Pouilleau, D. Devilliers, F. Garrido, S. Durand-Vidal and E. Mahé, Structure and composition of passive titanium oxide films, Mater. Sci. Eng. B, 1997, 47, 235–243 CrossRef.
- D. Mardare, C. Baban, R. Gavrila, M. Modreanu and G. I. Rusu, On the structure, morphology and electrical conductivities of titanium oxide thin films, Surf. Sci., 2002, 507–510, 468–472 CrossRef CAS.
- J. Bisquert, P. Cendula, L. Bertoluzzi and S. Gimenez, Energy diagram of semiconductor/electrolyte junctions, J. Phys. Chem. Lett., 2014, 5, 205–207 CrossRef CAS PubMed.
- T. Mayer, M. Lebedev, R. Hunger and W. Jaegermann, Elementary processes at semiconductor/electrolyte interfaces: Perspectives and limits of electron spectroscopy, Appl. Surf. Sci., 2005, 252, 31–42 CrossRef CAS.
- J. P. Zheng, P. J. Cygan and T. R. Jow, Hydrous Ruthenium Oxide as an Electrode Material, J. Electrochem. Soc., 1995, 142, 2699–2703 CrossRef CAS.
- S. Ardizzone, G. Fregonara and S. Trasatti, ‘Inner’ and ‘Outer’ Active Surface Electrodes of RuO2 Electrodes, Electrochim. Acta, 1989, 35, 263–267 CrossRef.
- S. Cherevko, S. Geiger, O. Kasian, N. Kulyk, J. P. Grote, A. Savan, B. R. Shrestha, S. Merzlikin, B. Breitbach, A. Ludwig and K. J. J. Mayrhofer, Oxygen and hydrogen evolution reactions on Ru, RuO2, Ir, and IrO2 thin film electrodes in acidic and alkaline electrolytes: A comparative study on activity and stability, Catal. Today, 2016, 262, 170–180 CrossRef CAS.
- J. W. Weidner and P. Timmerman, Effect of Proton Diffusion, Electron Conductivity, and Charge-Transfer Resistance on Nickel Hydroxide Discharge Curves, J. Electrochem. Soc., 1994, 141, 346–351 CrossRef CAS.
- Y. Chen, K. Rui, J. Zhu, S. X. Dou and W. Sun, Recent Progress on Nickel-Based Oxide/(Oxy)Hydroxide Electrocatalysts for the Oxygen Evolution Reaction, Chem. – Eur. J., 2019, 25, 703–713 CrossRef CAS PubMed.
- D. S. Hall, D. J. Lockwood, C. Bock and B. R. MacDougall, Nickel hydroxides and related materials: a review of their structures, synthesis and properties, Proc. R. Soc. A, 2014, 471, 20140792 CrossRef PubMed.
- M. Baker, 1500 scientists lift the lid on reproducibility, Nature, 2016, 533, 452–454 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Schematic sketches of the electrochemical cells used for the measurements. Scanning electron microscopy pictures of the pinholes and craters on the glassy carbon electrode. Hg porosity measurements on the Freudenberg E35 carbon fleece. BET measurements and evaluation. EIS data of the glassy carbon type 2 electrode in nitrogen and oxygen purged 1 M perchloric acid. EIS data for different amounts of stacked Freudenberg E35 carbon fleeces. EIS data of a porous carbon specimen with reduced electron conductivity. EIS data of the pyrolyzed PAN specimen. All CV data of the examined electrodes. All EIS data of the examined electrodes as Nyquist plots. EIS data and bypass currents of the examined Ti, Ru, Pt, and Ni specimens. See DOI: https://doi.org/10.1039/d3cp04743a |
| This journal is © the Owner Societies 2024 |