The energetics of N₂ reduction by vanadium containing nitrogenase

Abstract

The main class of nitrogenases has a molybdenum in its cofactor. A mechanism for Mo-nitrogenase has recently been described. In the present study, another class of nitrogenases has been studied, the one with a vanadium instead of a molybdenum in its cofactor. It is generally believed that these classes use the same general mechanism to activate nitrogen. The same methodology has been used here as the one used for Mo-nitrogenase. N₂ activation is known to occur after four reductions in the catalytic cycle, in the E₄ state. The main features of the mechanism for Mo-nitrogenase found in the previous study are an activation process in four steps prior to catalysis, the release of a sulfide during the activation steps and the formation of H₂ from two hydrides in E₄, just before N₂ is activated. The same features have been found here for V-nitrogenase. A difference is that five steps are needed in the activation process, which explains why the ground state of V-nitrogenase is a triplet (even number) and the one for Mo-nitrogenase is a quartet (odd number). The reason an additional step is needed for V-nitrogenase is that V³⁺ can be reduced to V²⁺, in contrast to the case for Mo³⁺ in Mo-nitrogenase. The fact that V³⁺ is Jahn–Teller active has important consequences. N₂H₂ is formed in E₄ with reasonably small barriers.

---

I. Introduction

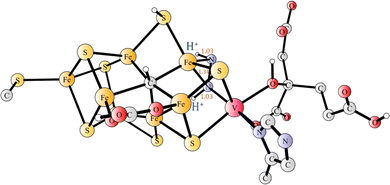
In nature, the reduction of N₂ is performed by enzymes termed nitrogenases. The by far dominating nitrogenase is molybdenum-containing nitrogenase, which has a cofactor (FeMoco) including one molybdenum and seven irons bound together by sulfides. A cysteine and a histidine are ligands of the cofactor, as well as a homocitrate, which is unusual in biology.¹ Almost twenty years after the first X-ray structure, it was discovered that there is also a central carbide in the structure, only seen at a very high resolution of 1.0 Å.² A less common nitrogenase employs vanadium instead of molybdenum. An X-ray structure with a resolution of 1.35 Å has been determined.³ The active site is shown in Fig. 1. The structure of the cofactor (FeVco) is very similar to FeMoco. A notable difference is that, instead of one of the sulfides (S3A) in FeMoco, there is a carbonate bridging two irons (Fe4 and Fe5).

Fig. 1 The X-ray structure of the active site of vanadium containing nitrogenase (PDB 5N6Y).³

The mechanism for Mo-nitrogenase has been extensively studied for decades, but the understanding has still major unresolved issues. It has long been known that the state of Mo-nitrogenase that activates N₂ is reached after four reductions in the catalytic cycle.^4,5 The states involved are termed E₀–E₄ and, therefore, the state that activates N₂ is E₄. The understanding of the mechanism for Mo-nitrogenase has seen significant progress during the past decade. In a set of EPR studies, it has been shown that, just before N₂ activation, two hydrides leave the cofactor as H₂.^6–8 The release of H₂ was considered obligatory for N₂ activation, and explained a long-standing mystery that the activation of N₂ in Mo-nitrogenase is always accompanied by a loss of one H₂. Suggestions that there should be a pre-activation before catalysis starts have been made in a series of theoretical modeling papers.^9–12 However, the presence of a pre-activation has been questioned in other studies.^6–8 The best experimental evidence for the presence of a pre-activation is that two different assignments of the E₁ state have been made in two experiments, where the preparations of the states have been different.^13,14 The reason for that difference has been analyzed recently by a modeling study and it was concluded that a likely explanation for the results is that there is an activation prior to catalysis.¹⁵ Several experimental studies have furthermore led to the conclusion that catalysis is preceded by an activation.^16–19

In the present study, the mechanism of V-nitrogenase has been investigated using a theoretical modeling. It has been shown experimentally that Mo- and V-nitrogenase in the EPR active E₄ state use the same general mechanism for the activation of N₂.²⁰ While Mo-nitrogenase has been intensively studied during the past decades by theoretical methods, there are only a few such studies of V-nitrogenase. A significant problem has been that the electronic ground state of the cofactor has not been safely determined until very recently.²¹ It was found that the oxidation state for the ground state should be (V³⁺ 4Fe³⁺ 3Fe ²⁺), which is an S = 0 (or integer spin non-Kramers) state. For many years it was assumed that the ground state instead was (V³⁺ 3Fe³⁺ 4Fe ²⁺) in contrast to FeMoco, which has been determined to be (Mo³⁺ 4Fe³⁺ 3Fe ²⁺). In a recent theoretical study, performed before the new assignment of the ground state of FeVco was determined, it was for that reason assumed that the ground state for FeVco was more similar to the E₁ state of FeMoco, obtained after one reduction.²² That difference was also suggested to be an explanation for the experimentally observed differences in reactivities, such as the ones towards CO and CO₂. The present study is the first one built on the new assignment of the ground state.²¹ The nature of the four-atom bridging ligand in FeVco, not found in FeMoco, was also investigated in those studies. Analysis of the X-ray structure for FeVco has led to the conclusion that the bridging four atom ligand should be an unprotonated CO₃²⁻.²² The same conclusion concerning that ligand was drawn in another theoretical study, which also suggested that the sulfide ligands in FeVco are unprotonated in the X-ray structure.²³

V-nitrogenase is a much less common enzyme than Mo-nitrogenase. The importance of studying V-nitrogenase is the generally accepted similarity of the mechanisms of these enzymes. It is of high interest to investigate if calculations give a mechanism for V-nitrogenase following the same general principles as the one suggested for Mo-nitrogenase.¹⁰ If not, it casts a doubt on the mechanism reached for Mo-nitrogenase.

II. Methods

The methods used here to study V-nitrogenase are the same as those used in other recent studies of nitrogenase.^9–12,24 The starting point is DFT with the standard hybrid functional B3LYP.²⁵ The geometries were optimized with a medium size basis (LACVP*). Single point energies in the optimized geometries using B3LYP with 15% were calculated using a large basis with cc-pvtz(-f) for the first-row atoms, and with LACV3P* for the metals. For the large basis set, the energies had to be computed without the pseudo-spectral approach. In the optimized points, dielectric effects were added, obtained using a Poisson–Boltzmann solver,²⁶ with a dielectric constant of 4.0. D2 dispersion²⁷ and zero-point effects were finally added. An empirical value of 14 kcal mol⁻¹ was used for the cost of taking a water molecule from bulk water and placing it on the cofactor. That value can be approximately derived from the experimental free energy for the binding of one water molecule to bulk water of −6.3 kcal mol⁻¹.³⁵ A large entropy effect is obtained in that case since the water is moved from the gas phase. In the present case, essentially no such entropy effect should be present. The programs used were Jaguar²⁶ and Gaussian.²⁸

The methods used here have been carefully tested.^29,30 In the most recent of these studies, redox mechanisms have been tested for Photosystem II, cytochrome c Oxidase, NiFe and FeFe hydrogenases, NiFe–CO dehydrogenase, multi-copper oxidases and acetyl–CoA synthase. The results are in all cases in very good agreement with experimental findings.³⁰ There are no counter-examples found for redox enzymes, which are all stable at room temperature, which is an important reason for the high accuracy. It is also important to note that the cases mentioned are relevant for the present study since they deal with energies not higher than 20 kcal mol⁻¹ from their ground states, Failures of the methods for excited states and structures 30 kcal mol⁻¹ or higher in energy are not relevant for the present study. In the literature, there are many such cases of failures. At higher energies, multireference effects start to appear which cannot be handled by the present single determinant approach. Unsaturated systems, not present in the enzymes mentioned, may also be cases of failures.

A cluster model was used for the active site.³¹ Besides the ligands of the cofactor, homocitrate, Cys257 and His423, the amino acids Lys83, Gln176, His180, Thr335, Arg339, Lys361 and Phe362 were included in the model, see Fig. 1. Some coordinates, marked with red circles in Fig. S1 (ESI†), were frozen from the X-ray structure, in order to avoid artificial movements. The model is of the same size as the most recent models used for Mo-nitrogenase.^11,12 Since a positive region outside the homocitrate was left out of the model the homocitrate was additionally protonated, which is a common procedure in the cluster modeling. The necessity for including Phe362 was realized at a late stage of the present investigation. The results for the mechanism for the two models, with and without Phe362, were found to be quite similar and, therefore, some qualitative conclusions from the tests of the mechanisms were taken from the earlier investigations of the model without Phe362. The energetic results reported below are all for the model with Phe362. The total charge of the model of the active site is −1, which is different from the charge of −2 for Mo-nitrogenase.

Concerning the size of the model, it is of high importance to emphasize that the calculated reduction energies are all (H⁺,e⁻) additions, which do not have long-range effects, since the additions are neutral. For that purpose, models with about 200 atoms are quite sufficient. pK_a values and redox potentials require larger models than the one used here, but no such values are reported.

There are many possible spin-couplings for each of the structures investigated. One of them is a coupling (+ −−+ + + −) with a numbering of the iron atoms from the X-ray structure. That coupling is here written as (−2,−3,−7) to conform with a convention used earlier, indicating which irons have negative spins. The list of different spin-states that were investigated were taken from a thorough spin-investigation for the ground state for Mo-nitrogenase.³² However, it should be noted that at the time of that study, it was believed that the spin on molybdenum was zero. It was later discovered that there are three unpaired spins on molybdenum and two on vanadium. Those spins interact strongly with the iron spins and make new investigations necessary. Clusters for an odd number of reductions were here found to be doublets (except for the ground state) and for an even number triplets.

In order to obtain the energetics for the different reductions, an energy value for the addition of a (H⁺, e⁻) is needed. The same value as in our previous studies for Mo-nitrogenase of 348.6 kcal mol⁻¹ was used.^9–11 This value is based on a redox potential for the reductant of −1.6 V and a solvation energy for a proton in water of 279.8 kcal mol⁻¹ at pH = 7.³³ It also includes a driving force of 3 kcal mol⁻¹ for the electron transfer process.

III. Results

An interesting difference between V- and Mo-nitrogenase is that they do not have the same spin for their ground states. Assuming the activation of N₂ in E₄ to be the same,²⁰ the E₄ state should probably be a doublet in both cases. In our previous studies on Mo-nitrogenase, an activation prior to catalysis consisting of four reduction steps was suggested,.^9–12 Therefore, for V-nitrogenase, there should be an odd number of steps in the activation process to reach a doublet E₄ state. As will be discussed below, the calculations indicate an activation consisting of five steps.

Another difference between the nitrogenases is the limiting overall reaction. For V-nitrogenase it is usually written:²¹

N₂ + 12H⁺ +24MgATP +12e⁻ → 2NH₃ +3H₂ +24MgADP +24P_i (1)

For Mo-nitrogenase, only one H₂ is produced.

In a study of the present type, where there are many reduction steps, a decision on the nature of the reductions may significantly simplify the calculations. In the case of Mo-nitrogenase, all reductions were assumed to be proton coupled. With an addition of a (H⁺·e⁻) couple, the charge of the model does not change, which leads to a technical simplification. It means that inhomogeneous long range electrostatic effects from regions outside the model can be neglected, which is not the case when the charge is changed as in cases of reductions that are not proton coupled. The homogeneous long-range effects are well covered by the dielectric cavity model. The assumption of proton coupled reductions is in general a very good approximation for models of the present size, as shown in previous studies.^29,30 In the present case of V-nitrogenase, it is quite clear that all reductions are proton coupled, since for each electronic reduction, the calculated pK_a values are much higher than 7.

An important difference between Mo- and V-nitrogenase is that the charges of the models for the active sites differ by one unit. The reason is that for V-nitrogenase there are three positive residues outside the cofactor, two lysines and one arginine, while for Mo-nitrogenase there are only two, both arginines. That leads to a model of the active site with a charge of −1 for V-nitrogenase and −2 for Mo-nitrogenase.

There are many possible spin-couplings for each structure in the mechanism. Many of them were tried here, but far from all of them. The choice of spin-coupling makes most difference for the first redox states, where there are still Fe³⁺ atoms (with five unpaired spins) present. As the Fe³⁺ atoms are reduced to Fe²⁺ (with four unpaired spins), the couplings between the irons decrease in strength, and the coupling to the spins on vanadium becomes the most important factor. A surprising finding, from the many investigations of spin states performed here, was that one spin-coupling was favorable for all E-states in the catalytic cycle except E₀. That spin-coupling is (−2,−3,−7). Interestingly, a similar result was found in our study on Mo-nitrogenase. In that case, another spin-coupling dominates for the more reduced states, the one with (−2,−3,−4). That difference between V- and Mo-nitrogenase is due to the higher spin for Mo³⁺.

The activation steps A₀–A₅

The recent experimental assignment for the oxidation state of the ground state (A₀) of FeVco with (V³⁺, 3Fe²⁺, 4Fe³⁺) is used in the present study.²¹ This is the same redox level as the one for FeMoco. Ten different spin-couplings were investigated for A₀ and the best one found was (2-,3-,5-), which is the same as the one found for A₀ in a previous study of V-nitrogenase.²² It should be noted that even though the protonation state is the same for A₀ in the two studies, there is a different assignment of A₀ with (V³⁺, 4Fe²⁺, 3Fe³⁺) in the previous study. The energy for spin-coupling (1-,5-,6-) is +2.8 kcal mol⁻¹ higher and for (2-,3-,4) +3.9 kcal mol⁻¹ higher (lacvp*). The calculations show that the ground state is a triplet, with the singlet +18.5 kcal mol⁻¹ higher, using the same spin-coupling. The optimized (triplet) structure, shown in Fig. S1 (ESI†), is very close to the X-ray structure shown in Fig. 1.

For the first proton-coupled reduction step from A₀ to A₁, the belt sulfide S2B becomes protonated. That is the same sulfide which was most easily protonated for Mo-nitrogenase. The oxidation state of the cofactor is now (V³⁺, 4Fe²⁺, 3Fe³⁺). The best spin-coupling found for A₁ is (2-,3-,5-). This is the same as the one found for A₀ in the previous study,²² which is logical since the oxidation state for A₀ used in that study is the same as the one for A₁ here. The transition from A₀ to A₁ was here found to be exergonic by −13.9 kcal mol⁻¹. The energy for a protonated carbonate is only +1.2 kcal mol⁻¹ higher.

In the transition from A₁ to A₂, the proton ends up on the carbonate (Fig. S2, ESI†). The exergonicity is again quite large with −13.2 kcal mol⁻¹. The best spin-coupling found was (2-,4-,5-) and the oxidation state is (V³⁺, 5Fe²⁺,2Fe³⁺). In the A₂ to A₃ transition, the second (and final) belt sulfide S5A is protonated. The optimized structure of A₃ is shown in Fig. S3 (ESI†). Six different spin-couplings were tried with the best one (2-,3-,7-) with an exergonicity of −9.7 kcal mol⁻¹. The oxidation state for A₃ is (V³⁺, 6Fe²⁺, 1Fe³⁺). An interesting finding is that the spin-population on vanadium increases from 2.1 to 2.4 in the direction towards V²⁺, which has an ideal spin of 3.0.

In the next transition from A₃ to A₄, an interesting and important effect appears. When the proton on S5A was moved to S3B, the V-S3B distance increased very much from 2.54 Å in A3 to nearly 4 Å in A₄, leading to a 5-coordination for vanadium. That is due to a Jahn–Teller effect, since V³⁺ has an octahedral geometry and a high-spin d² configuration. The effect only becomes strong when S3B is protonated and, therefore, the effect was not seen in A₃, where S3B was un-protonated. Since there is now an open site on vanadium, a hydride can be placed on vanadium. In the optimization of that structure (Fig. S4, ESI†), the hydride formed a short bond both to vanadium and Fe6. Placing a hydride between Fe2 and Fe6 and moving S2B over to a terminal position on Fe6 has a much higher energy. The transition from A₃ to this A₄ structure is exergonic by only −1.0 kcal mol⁻¹. The protonated sulfides are now S2B and S3B, and the carbonate remains protonated. The best spin-coupling is (2-,3-,5-) and the oxidation state is (V³⁺, 5Fe²⁺, 2Fe³⁺).

There is a second important structure of A₄, here termed (Fig. S5, ESI†). In that structure a sulfide has been released. The sulfide that is most easily released is S3B. The release involves a proton being transferred from S2B to S3B, and after that a H₂S can be released. At the TS, the H-S2B distance is 1.68 Å and the H-S3B distance 1.64 Å. The Fe6 to S3B distance is increased to 3.10 Å from 2.40 Å and shows that S3B is about to be released. The barrier is +17.2 kcal mol⁻¹, which is feasible. It is exergonic by −5.9 kcal mol⁻¹, using an energy for a bound H₂S in the enzyme of 14 kcal mol⁻¹ as for a water. The argument for that is that H₂S should be in equilibrium with H₂S in the surrounding water. H₂S in water should have approximately the same type of hydrogen bonds as a water molecule. The exact value is not important in the present case. The TS is shown in Fig. 2. The total exergonicity from A₃ to is −6.9 kcal mol⁻¹, which fulfills the requirement for a driving force of at least 3 kcal mol⁻¹ to secure catalytic progress. Without the sulfide release, that requirement would not be fulfilled. Finally, it can be noted that a sulfide release was also found in A₄ for Mo-nitrogenase.¹⁵

Fig. 2 The optimized transition state for the release of H₂S in A₄.

The preferred protonation site in A₅ (Fig. 3) is S2B, which is exergonic by −16.3 kcal mol⁻¹.

Fig. 3 The E₀ (A₅) structure formed after the five activation steps. The carbonate and S2B are protonated and there is one hydride.

However, the most favorable one is the carbide but to reach the carbide, the proton has to pass a TS, which turned out to be too high. The fifth reduction step completes the activation process to reach E₀. This process is done only once before the catalytic cycling starts. It is important to note that the release of the sulfide occurs before catalysis and, therefore, it does not need to be replaced during catalysis. The oxidation state is (V³⁺, 6Fe²⁺, 1Fe³⁺) and the best spin-coupling is (2-,3-,5-). The reason the activation process contains five steps for V-nitrogenase, and only four for Mo- nitrogenase will become evident below. What has been achieved for V-nitrogenase in the activation process is that the cluster has been reduced and only one Fe³⁺ remains. A sulfide has been released and a hydride has been placed between Fe6 and vanadium, and will remain that way to E₄ where N₂ will be activated. In Mo-nitrogenase, the first hydride is instead placed in the region between Fe1, Fe2, Fe4, which has consequences for where the activation of N₂ occurs, see further below. The oxidation state after the pre-activation can be compared to the corresponding one after the four-step pre-activation process for Mo-nitrogenase, which leads to (Mo³⁺,5Fe²⁺, 2Fe³⁺) with two Fe³⁺.

Otherwise, the nitrogenases are very similar at E₀. Most notably, a sulfide has been released and only one sulfide (S2B) is protonated in both cases. The suggested mechanism for the activation steps from A₀ to A₅ is shown in Scheme 1 and the energies are summarized in a diagram in Fig. 4.

Scheme 1 Suggested mechanism for the activation steps from A₀ to A₅.

Fig. 4 Energy diagram for the activation steps from A₀ to A₅.

E₀–E₄ in the catalytic cycle

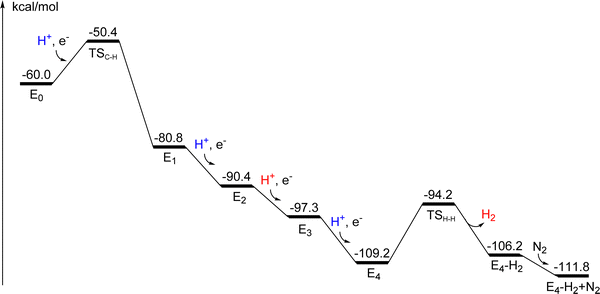
At E₀ the catalytic cycling starts. According to experiments, N₂ should be activated after four additional reductions. In the reduction from E₀ to E₁, there is a protonation of the carbide. The incoming proton is first bound as a hydride between Fe4 and Fe5 and then moves to the carbide. The optimized TS is shown in Fig. 5. The proton has a short bond of 1.63 Å to Fe5 and to the carbide the distance is 2.07 Å. The local barrier is +5.3 kcal mol⁻¹, but since the resting state has a proton on S5A, which is bound by −4.3 kcal mol⁻¹, the actual barrier becomes (4.3 + 5.3) = +9.6 kcal mol⁻¹. Since the barrier is so low, the protonation of the carbide can probably not be avoided. That is unlike the situation for Mo-nitrogenase,¹² where the corresponding barrier (in A₄) is +17.9 kcal mol⁻¹, which is higher than for the release of a sulfide. For Mo-nitrogenase, the avoidance of the carbide protonation is important for the mechanism. For V-nitrogenase, there is no corresponding advantage of avoiding carbide protonation, see further below. The protonation of the carbide might actually occur already in A₄, with a barrier of +16.3 kcal mol⁻¹. The calculations give a small endergonicity of +0.1 kcal mol⁻¹, but an exergonicity is possible considering the uncertainty of the methods. That scenario would lead to the avoidance of carbide protonation and deprotonation in the catalytic cycling. At the present stage, it is not clear if that avoidance is an advantage. The exergonicity of the reduction from E₀ to E₁ (Fig. S6, ESI†) is −20.8 kcal mol⁻¹ for V-nitrogenase. The irons are now all reduced to Fe²⁺ and the oxidation state is (V³⁺, 7Fe²⁺). The spin-coupling is (2-,3-,7-), which will actually remain the best one all the way until N₂ is activated.

Fig. 5 The optimized transition state for formation of a protonated carbide in E₁.

The presence of two hydrides is necessary for the mechanism of N₂ activation in E₄, as suggested experimentally.^6–8 In E₂, the second hydride becomes bound, bridging between Fe6 and Fe7 (Fig. S7, ESI†), with a bond-distance of 1.82 Å to both of them. The reason the second hydride can bind in that region is that the carbide is protonated and moves away somewhat from its central position, which leaves enough space for the second hydride to bind rather close to the first one. In A₄, where there is an un-protonated carbide, there is not enough space and the hydride that entered in that state was instead bound between Fe6 and vanadium, see above. Since the second hydride takes an electron from the irons, the oxidation state in E₂ becomes (V³⁺, 6Fe²⁺, 1Fe³⁺), the same as in E₀. The exergonicity of the reduction from E₁ to E₂ is −9.6 kcal mol⁻¹. The spin-coupling is the same as in E₁. In E₃, S5A becomes protonated (Fig. S8, ESI†) and the oxidation state is back to (V³⁺, 7Fe²⁺). The best spin-coupling is again the same as in E₁. The exergonicity of the E₂ to E₃ transition is −6.9 kcal mol⁻¹.

E₄ is according to experiments, the state which activates N₂.^4–8 Since this is the most important state in the nitrogenase mechanism, a thorough investigation of spin-couplings, for 10 different cases, was made again. The lowest energy was again found for (2-,3-,7-) but with (2-,3-,4-) only +1.8 kcal mol⁻¹ higher with all effects included. It might have been expected that it should be difficult to reduce the cofactor further from (V³⁺, 7Fe²⁺) in E₃, since all irons are now Fe²⁺. However, it turns out that also vanadium can be reduced, from V³⁺ to V²⁺. After the reduction, the spin on vanadium is −2.93, close to the ideal spin of −3.0 for V²⁺. In E₃ the spin on vanadium is −2.52, in between the ideal spin of −3.0 for V²⁺ and −2.0 for V³⁺. The sulfide most easily protonated in E₄ was found to be S1A. The exergonicity of the E₃ to E₄ transition is −11.9 kcal mol⁻¹. This means that for V-nitrogenase with the ground state (V³⁺, 3Fe²⁺, 4Fe³⁺) there are five easily reduced metal atoms, while for Mo-nitrogenase with the ground state (Mo³⁺, 3Fe²⁺, 4Fe³⁺) there are only four. That explains the necessity of one more activation step in V-nitrogenase. Apart from the five reductions of the metals, four reductions are needed to produce two hydrides, and still keep a low oxidation state of the cofactor. That means altogether 9 reduction steps from A₀, 5 prior activation steps and 4 steps in the catalytic cycle. In E₄ there are now two hydrides, a protonated carbide and three protonated sulfides, S2B, S5A and S1A, see Fig. 6. In Mo-nitrogenase there are four protonated sulfides, since the carbide is not protonated in that case.¹²

Fig. 6 The E₄ structure where the activation of N₂ occurs. There are two hydrides, a protonated carbonate, a protonated carbide and three protonated sulfides, S2B, S5A and S1A.

At this stage, H₂ can be formed from the two hydrides, as required for the activation of N₂. The purpose of the formation of H₂ from the two hydrides is to reduce the (formal) oxidation state of the cofactor by two units to become very low with (V²⁺, 5Fe²⁺, 2Fe¹⁺), which is needed for electron transfer to N₂. A straightforward reduction from Fe²⁺ to Fe¹⁺ without the release of the hydrides is not energetically possible with the redox potential of −1.6 V. The barrier for H₂ formation is +15.0 kcal mol⁻¹. The transition state is shown in Fig. 7. In the TS there are two short bonds of the hydrides to Fe6 with 1.65 Å and 1.71 Å, and the distance between the hydrides is 1.26 Å. The distance from one of the hydrides to vanadium is 2.05 Å, and the distance from the other hydride to Fe7 is 2.03 Å. The distance to Fe2 is much longer with 2.74 Å. The release of H₂ is endergonic by +3.0 kcal mol⁻¹, which is quite different from the situation in Mo-nitrogenase, where this release was found to be endergonic by +8.7 kcal mol⁻¹.¹² There is a large gain of entropy of −8.4 kcal mol⁻¹ as H₂ is released. After H₂ release, the irons with the lowest spins are Fe2, Fe5 and Fe6 with 3.3 and the one with highest is Fe1 with 3.66.

Fig. 7 The transition state for H₂ formation.

After H₂ is released, N₂ can bind. Several positions for N₂ were tried and one of them has a much lower energy than the other ones. The structure is shown in Fig. 8. N₂ is bound end-on to Fe6, with a short distance of 1.91 Å. The N–N distance is 1.14 Å, elongated from 1.11 Å for free N₂. These distances indicate that N₂ is clearly activated. The charge transfer from the cofactor to N₂ is −0.26 and the spin on N₂ is −0.33. The iron with the lowest spin is Fe6 with 3.20 and the one with highest Fe1 with 3.68. The enthalpic binding energy for N₂ compared to the structure after H₂ release is as large as −15.5 kcal mol⁻¹, which with the entropy penalty of +9.9 kcal mol⁻¹ is reduced to −5.6 kcal mol⁻¹. Since the release of H₂ is endergonic by +3.0 kcal mol⁻¹, see above, the release of H₂ and binding of N₂ is altogether exergonic by −2.6 kcal mol⁻¹. For Mo-nitrogenase, the corresponding energy is +5.9 kcal mol⁻¹, where the difference comes from the much less favorable release of H₂ in that case.

Fig. 8 The optimized structure after N₂ binding.

It is interesting, and very important, to note that the position for N₂ binding on Fe6 is different from the one of Mo-nitrogenase, where N₂ is bound on Fe₄.¹² The preference compared to other positions is very large in both cases. The origin of that difference is clearly connected to the preferred positions of the hydrides. For V-nitrogenase, the preferred positions for the hydrides are close to V and Fe6, because of the Jahn–Teller distortion of V³⁺, see above, while for Mo-nitrogenase the preferred positions are close to Fe4. The conclusion drawn here is that when the hydrides are released as H₂, the two electrons which stay on the cofactor and are donated to N₂, remain in the region where the hydrides were bound. That is a very surprising result, since with a look at the spin-populations, the electrons on the cofactor appear to be very delocalized. In contrast to the present conclusion, there is no obvious conclusion concerning the position for N₂ binding that can be drawn from the positions of the amino acids surrounding the cofactor.

The mechanism from E₀ to E₄ is shown in Scheme 2 and the energies are summarized in a diagram in Fig. 9. E₀ is the same state as A₅ in Fig. 3. The transition energies are all reasonably large, ranging from −6.9 kcal mol⁻¹ for E₂ to E₃, to −20.8 kcal mol⁻¹ for E₀ to E₁. The requirement that the transition energy should be larger than −3 kcal mol⁻¹ to drive catalysis forward is fulfilled for all of them. The oxidation state starts with (V³⁺, 1Fe³⁺, 6Fe²⁺) for E₀. The reason there is still one Fe³⁺ present is that there is a hydride which has taken an electron from one of the irons in E₀. The second hydride, necessary for the activation of N₂, enters in E₂. There are three protonated sulfides at the start of E₄. All E-states lack one sulfide, which was released in A₄ prior to catalysis. The first step in E₄ is to form H₂ from the two hydrides. In the TS, both hydrides are bound to Fe6. The barrier for H-H formation is +15.0 kcal mol⁻¹, which can easily be overcome. The barrier will not be seen on the kinetics, since the barrier for electron transfer is +18 kcal mol⁻¹. The reaction energy for the release of H₂ is slightly endergonic by +3.0 kcal mol⁻¹. The oxidation state is now (V²⁺, 5Fe²⁺, 2Fe¹⁺), which is exceptionally low. The hydrides leave an empty site on Fe6, where N₂ can bind end-on and electrons can flow over from the cofactor. The binding of N₂ is exergonic by −5.9 kcal mol⁻¹.

Scheme 2 Suggested mechanism for the catalytic cycle from E₀ to E₄–H₂ + N₂.

Fig. 9 Energy diagram for the catalytic cycle from E₀ to E₄–H₂ + N₂.

H₂ release and N₂ binding in E₄ has also been studied for the spin-coupling (2-,3-,4-), which is the second lowest one in energy. The comparison was made for the model without Phe362. In the starting E₄ state, the energy for (2-,3-,7-) is lower by −1.8 kcal mol⁻¹. The barrier for H₂ formation is higher by +2.5 kcal mol⁻¹ for (2-,3-,7-), and the endergonicity is larger by +2.7 kcal mol⁻¹. The most significant difference between the spin-couplings occurs for the binding of N₂, which is more exergonic by −7.3 kcal mol⁻¹ for (2-,3-,7-). This means that the overall process of releasing H₂ and binding N₂ becomes more exergonic for (2-,3-,7-) by −4.6 kcal mol⁻¹. A similar effect of changing spin-coupling in E₄ was found also for Mo-nitrogenase. Besides having slightly lower energies, the results for (2-,3-,7-) are in better agreement with experiments.

Some tests of the accuracy of the results in E₄ were also obtained in the usual way by varying the fraction of exact change with 10%, 15% and 20%. The model without Phe362 was used. The barrier for H₂ formation has an uncertainty with a variation of 0.9 kcal mol⁻¹ for each percent. The endergonicity for H₂ release has a variation of 0.5 kcal mol⁻¹ for each percent and the binding of N₂ a similar uncertainty of also 0.5 kcal mol⁻¹. The variation of the energies with the fraction of exchange showed as usual a nearly linear behavior. Based on previous experience, considering the results with 15% as most reliable, an estimate of the accuracy of the results with +/− 3 kcal mol⁻¹ appears reasonable.

The next step in E₄, is a protonation of N₂. The proton in the best position for the protonation is the one on S2B. However, this is not the sulphide with the lowest pK_a. Following the order in which the sulphides were protonated, the sulfide with the lowest pK_a is the one on S1A, see further below. The TS for the protonation of N₂ is shown in Fig. 10, and the product in Fig. 11. It is very important for lowering the barrier and stability of the product that N₂ is stabilized by a bond to vanadium. After the protonation, all the irons have similar spins between 3.4 and 3.6. The spin on vanadium is hardly changed with 3.9 indicating a redox state with V²⁺. The calculated barrier is 19.3 kcal mol⁻¹ and the proton transfer is endergonic by +9.2 kcal mol⁻¹. The values are similar to the ones for Mo-nitrogenase with 17.6 kcal mol⁻¹ and +4.0 kcal mol⁻¹. For V-nitrogenase the resting state for the proton transfer is the state where N₂ is bound, but that is not the case for Mo-nitrogenase, where the protonation starts at an energy of +5.9 kcal mol⁻¹ above the resting state in E₄. The calculated effective barrier for Mo-nitrogenase is therefore +23.5 kcal mol⁻¹, which is too high to be allowed. It was therefore concluded that the calculated barrier for this complicated case, where two electrons and one proton are transferred, is overestimated by 4–5 kcal mol⁻¹. There is probably an overestimation also for V-nitrogenase. For Mo-nitrogenase this step is rate-limiting, and that could be the case also for V-nitrogenase, see further below.

Fig. 10 The transition state for N₂H formation.

Fig. 11 The optimized structure for N₂H with S1A protonated.

Before the second proton binds to N₂H, the proton on S1A needs to be transferred to S2B, in a step which is exergonic by 2.5 kcal mol⁻¹. That, apparently trivial, step turned out to be more complicated than expected. Moving protons from one sulphide to another one has recently been shown to be trivial in most cases, with low barriers, when one or two water molecules could be used in the transfer.³⁴ However, in the present case there is a complicating factor. In the reactant, there is a long distance of 4.0 Å between S1A and Fe2, but in the product the distance is only 2.4 Å. Without moving the sulphide towards Fe2, the barrier is quite high, but with the sulphide moved much closer to Fe2 in the starting structure for the TS (Fig. 12) search, the optimized barrier is only 6.7 kcal mol⁻¹. Since the N₂H reactant is not the resting state, but +9.2 kcal mol⁻¹ higher, the effective barrier becomes as high 15.9 kcal mol⁻¹. It can be added that the two water molecules are strongly bound in the reactant, so there is no cost for taking them from the bulk water.

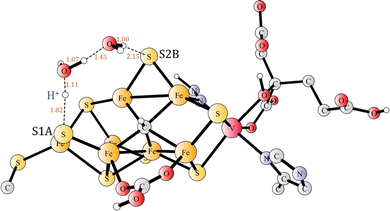Fig. 12 The transition state for the transfer of the proton between S1A and S2B using two water molecules.

The final step in the activation of N₂ in E₄ is to form N₂H₂. This is done by moving the proton on S5A over to N₂H. The TS is shown in Fig. 13. Since the transfer (Fig. 14) is strongly exergonic by −17.4 kcal mol⁻¹, an early TS was found. The S–H distance is 1.41 Å and the N–H distance 1.97 Å. The local barrier is 13.3 kcal mol⁻¹, but since the reactant N₂H is 6.7 kcal mol⁻¹ higher than the resting state, the overall barrier becomes 20.0 kcal mol⁻¹. That means a barrier somewhat higher than the one for the first protonation of N₂. Attempts to reduce the barrier by the use of water molecules were not done but would probably reduce the barrier by a few kcal mol⁻¹.

Fig. 13 The transition state for N₂H₂ formation.

Fig. 14 The optimized structure of the N₂H₂ product (E_N2H2).

The energy diagram from the point where N₂ became bound to the final point with N₂H₂ is shown in Fig. 15. As for the case of Mo-nitrogenase, there are no observable intermediates. However, the starting point might be possible to observe in this case but not for Mo-nitrogenase. The rate-limiting barrier for Mo-nitrogenase is the first protonation of N₂, and is probably also the one for the same step for V-nitrogenase. A key for the activation of N₂ in V-nitrogenase is that one nitrogen of N₂ forms a bond to vanadium in the TS.

Fig. 15 Energy diagram from E₄–H₂ + N₂ to E₄–N₂H₂.

IV. Conclusions

The mechanism for V-nitrogenase has been studied using the same methodology as has recently been used to study Mo-nitrogenase.^11,12 The studies start at the respective ground states and continues to the activation of N₂ in the E₄ state. The goal of the reduction processes is to achieve a state with the lowest possible stable oxidation state. This means both for V- and Mo-nitrogenase a reduction of all irons to Fe²⁺. An important difference in the reduction processes is that V³⁺ can be rather easily reduced, but Mo³⁺ cannot. Since there are four Fe³⁺ in both cases, this difference leads to a necessity for five activation steps for V-nitrogenase, but only four for Mo-nitrogenase. In turn, this leads for V-nitrogenase to different spin-states for the ground states of these enzymes, a result that has recently been demonstrated experimentally.²¹ The activation processes lead to a presence of a hydride in E₁ in both cases, in agreement with recent experiments.¹⁴ For the present case of V-nitrogenase, the hydride states obtained after one or two reductions of the resting state are very high in energy, more than 20 kcal mol⁻¹ higher than the ones with a protonated sulfide or bicarbonate.¹⁵

There are important similarities and differences of the mechanisms in E₄ for V- and Mo-nitrogenase. A similarity is that the release of a sulfide occurs already in the activation process before the catalytic cycling starts. For V-nitrogenase, there is a binding of a hydride to vanadium, which also occurs in the activation process at A₄. The origin of that binding is that V³⁺ is Jahn–Teller active, which leads to a possibility for opening up a coordination site. That open site can later be used for hydride binding. In contrast, Mo³⁺ is not Jahn–Teller active and, therefore, hydride binding to molybdenum is much harder. For Mo-nitrogenase the formation of H₂ has a barrier of +17.3 kcal mol⁻¹ and is endergonic by 8.7 kcal mol⁻¹, while for V-nitrogenase the barrier is +15.0 kcal mol⁻¹ and endergonic by only 3.0 kcal mol⁻¹. It should be mentioned in this context that the rate-limiting step for the nitrogenase mechanism is not N₂ activation but electron transfer from the Fe-protein in both cases.^4,5,7

The binding site for N₂ is different in the two cases. In V-nitrogenase, N₂ binds exergonically by −5.6 kcal mol⁻¹ to Fe6 in the neighborhood of vanadium. In Mo-nitrogenase, N₂ instead binds to Fe4 exergonically by −2.8 kcal mol⁻¹ far away from molybdenum. In both cases, the enthalpic binding is larger than the large loss of entropy of +9.9 kcal mol⁻¹. As has been demonstrated experimentally, N₂ binding has to be preceded by a loss of H₂ from two hydrides.^6–8 The reason for the necessary loss of H₂ is that an oxidation state with the presence of two Fe¹⁺ can be formed, which would otherwise be very endergonic by straight reductions. The oxidation state of the cofactor just before N₂ binding is (V²⁺, 5Fe²⁺, 2Fe¹⁺) while for Mo-nitrogenase it is (Mo³⁺, 5Fe²⁺, 2Fe¹⁺).

For both V- and Mo-nitrogenase, the end-point in E₄ is formation of N₂H₂. The first protonation of N₂ is the most difficult step. In Mo-nitrogenase, that step is rate-limiting which is probably also the case for V-nitrogenase. There are several other steps in V-nitrogenase with similar barriers and the methods are not accurate enough to conclude which step is rate-limiting. The formation of N₂H is quite endergonic in both cases.

The competing reaction to nitrogen activation is formation of H₂ from a proton on a sulfide and a hydride. In Mo-nitrogenase, the only H₂ formed is the one from the two hydrides, which is necessary for the activation of N₂.^6–8 In V-nitrogenase, it has been found experimentally that there are two additional H₂ formations, see eqn (1). There are no indications in the present study that these two additional H₂ formations should be necessary for N₂ activation. Instead, they are here concluded to occur because they cannot be avoided. For Mo- and V-nitrogenase, there are protonated sulfides that could potentially form unproductive H₂ with a hydride. Interestingly, there are four protonated sulfides in Mo-nitrogenase but only three in V-nitrogenase even though more unproductive H₂ is formed in V-nitrogenase. Clearly, there are also other reasons than the number of protonated sulfides that lead to a loss of H₂.

After catalysis, as ATP or N₂ ceases, the cluster should return to the ground state A₀. Starting from the E₄ state. One possible scenario is that the hydrides are lost as two H₂ by combining with protons, either from solution or from the protonated sulfides. After catalysis, the P-cluster should return to its redox potential of −0.4 V and would then be a strong oxidant for FeMoco for its strongly reduced state in E₄. The remaining 5 electrons should therefore leave FeMoco over the P-cluster and out of the enzyme. A₀ is the most stable form of the cofactor.

There are actually not many results definitely known by experiments for V-nitrogenase. One of them is the spin and oxidation state of the ground state. The second one is the process of activating N₂. The activation of N₂ occurs after a preceding loss of two hydrides as H₂. The process is reversible. All the results found here using the present methodology are in very good agreement with these experiments.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at National Supercomputer Centre (NSC) partially funded by the Swedish Research Council through grant agreements no. 2022-22-955 and no. 2018-05973. This work was supported by the Swedish Research Council and the China Scholarship Council.

References

1. J. Kim and D. C. Rees, Structural models for the metal centers in the nitrogenase molybdenum-iron protein, Science, 1992, 257, 1677–1682.
2. T. Spatzal, M. Aksoyoglu, L. M. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Evidence for Interstitial Carbon in Nitrogenase FeMo Cofactor, Science, 2011, 334, 940.
3. D. Sippel and O. Einsle, The Structure of Vanadium Nitrogenase Reveals an Unusual Bridging Ligand, Nat. Chem. Biol., 2017, 13, 956–960.
4. R. N. F. Thorneley and D. J. Lowe, Molybdenum Enzymes, ed. T. Spiro, Wiley, N.Y., 1985, p. 221.
5. B. K. Burgess and D. J. Lowe, Mechanism of Molybdenum Nitrogenase, Chem. Rev., 1996, 96, 2983–3012.
6. B. M. Hoffman, D. Lukoyanov, D. R. Dean and L. C. Seefeldt, A Draft Mechanism, Acc. Chem. Res., 2013, 46, 587–595.
7. B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Mechanism of Nitrogen Fixation by Nitrogenase: The Next Stage, Chem. Rev., 2014, 114, 4041–4062.
8. D. Lukoyanov, Z.-Y. Yang, N. Khadka, D. R. Dean, L. C. Seefeldt and B. J. Hoffman, Identification of a Key Catalytic Intermediate Demonstrates That Nitrogenase Is Activated by the Reversible Exchange of N₂ for H₂, J. Am. Chem. Soc., 2015, 137, 3610–3615.
9. P. E. M. Siegbahn, Model Calculations Suggest that the Central Carbon in the FeMo-cofactor of Nitrogenase Becomes Protonated in the Process of Nitrogen Fixation, J. Am. Chem. Soc., 2016, 138, 10485–10495.
10. P. E. M. Siegbahn, The mechanism for nitrogenase including all steps, Phys. Chem. Chem. Phys., 2019, 21, 15747–15759.
11. W.-J. Wei and P. E. M. Siegbahn, A Mechanism for Nitrogenase Including a Loss of a Sulfide, Chem. – Eur. J., 2022, e202103745.
12. P. E. M. Siegbahn, The mechanism for N₂ activation in the E₄ – state of nitrogenase, Phys. Chem. Chem. Phys., 2023, 25, 23602–23613.
13. C. Van Stappen, A. T. Thorhallsson, L. Decamps, R. Bjornsson and S. DeBeer, Resolving the structure of the E₁ state of Mo nitrogenase through Mo and Fe K-edge EXAFS and QM/MM calculations, Chem. Sci., 2019, 10, 9807–9821.
14. D. A. Lukoyanov, D. F. Harris, Z.-Y. Yang, A. Pérez-González, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, The One-Electron Reduced Active-Site FeFe-Cofactor of Fe-Nitrogenase Contains a Hydride Bound to a Formally Oxidized Metal–Ion Core, Inorg. Chem., 2022, 61, 5459–5464.
15. P. E. M. Siegbahn, Can the E₁ state in nitrogenase tell if there is an activation process prior to catalysis?, Phys. Chem. Chem. Phys., 2023, 25, 3702–3706.
16. T. Spatzal, A. Kathryn, K. A. Perez, O. Einsle, J. B. Howard and D. C. Rees, Ligand binding to the FeMo-cofactor: Structures of CO-bound and reactivated nitrogenase, Science, 2014, 345, 1620–1623.
17. D. Sippel, M. Rohde, J. Netzer, C. Trncic, J. Gies, K. Grunau, I. Djurdjevic, L. Decamps, S. L. A. Andrade and O. Einsle, A bound reaction inter-mediate sheds light on the mechanism of nitrogenase, Science, 2018, 359, 1484–1489.
18. T. M. Buscagan and D. C. Rees, Rethinking the Nitrogenase Mechanism: Activating the Active Site, Joule, 2019, 3, 2662–2678.
19. W. Kang, C. C. Lee, A. J. Jasniewski, M. W. Ribbe and Y. Hu, Structural evidence for a dynamic metallocofactor during N₂ reduction by Mo-nitrogenase, Science, 2020, 368, 1381–1385.
20. D. F. Harris, D. A. Lukoyanov, H. Kallas, C. Trncik, Z.-Y. Yang, P. Compton, N. Kelleher, O. Einsle, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Mo-, V-, and Fe-Nitrogenases Use a Universal Eight-Electron Reductive-Elimination Mechanism to Achieve N₂ Reduction, Biochemistry, 2019, 58, 3293–3301.
21. Z.-Y. Yang, E. Jimenez-Vicente, H. Kallas, D. A. Lukoyanov, H. Yang, J. S. Martin del Campo, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, The electronic structure of FeV-cofactor in vanadium-dependent nitrogenase, Chem. Sci., 2021, 12, 6913–6922.
22. B. Benediktsson and R. Bjornsson, Quantum Mechanics/Molecular Mechanics Study of Resting-State Vanadium Nitrogenase: Molecular and Electronic Structure of the Iron−Vanadium Cofactor, Inorg. Chem., 2020, 59, 11514–11527.
23. J. Bergmann, E. Oksanen and U. Ryde, Quantum-refinement studies of the bidentate ligand of V-nitrogenase and the protonation state of CO-inhibited Mo-nitrogenase, J. Inorg. Biochem., 2021, 219, 111426.
24. P. E. M. Siegbahn and M. R. A. Blomberg, A Systematic DFT Approach for Studying Mechanisms of Redox Active Enzymes, Front. Chem., 2018, 6, 644.
25. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
26. Jaguar, version 8.9, Schrodinger, Inc., New York, 2015; A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142.
27. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009.
29. M. R. A. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Quantum Chemical Studies of Mechanisms for Metalloenzymes, Chem. Rev., 2014, 114, 3601–3658.
30. P. E. M. Siegbahn, A quantum chemical approach for the mechanisms of redox-active metalloenzymes, RSC Adv., 2021, 11, 3495–3508.
31. P. E. M. Siegbahn and F. Himo, The Quantum Chemical Cluster Approach for Modeling Enzyme Reactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336.
32. T. Lovell, J. Li, T. Liu, D. A. Case and L. Noodleman, FeMo Cofactor of Nitrogenase: A Density Functional Study of States M^N, M^OX, M^R and M^I, J. Am. Chem. Soc., 2001, 123, 12392–12410.
33. D. M. Camaioni and C. A. J. Schwerdtfeger, Comment on “Accurate Experimental Values for the Free Energies of Hydration of H⁺, OH⁻, and H₃O⁺”, Phys. Chem. A, 2005, 109, 10795–10797.
34. P. E. M. Siegbahn, How protons move in enzymes – the case of nitrogenase, J. Phys. Chem. B, 2023, 127, 2156–2159.
35. C. P. Kelly, C. J. Cramer and D. G. Truhlar, Aqueous Solvation Free Energies of Ions and Ion-Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton, J. Phys. Chem. B, 2006, 110, 16066–16081.

---

Footnote

† Electronic supplementary information (ESI) available: Coordinates for all structures discussed in the text are given as supporting information. See DOI: https://doi.org/10.1039/d3cp04698b

---