Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The sensitive aspects of modelling polymer–ceramic composite solid-state electrolytes using molecular dynamics simulations†
Melania
Kozdra
 a,
Daniel
Brandell
a,
Daniel
Brandell
 a,
C. Moyses
Araujo
bc and
Amber
Mace
a,
C. Moyses
Araujo
bc and
Amber
Mace
 *a
*a
aDepartment of Chemistry – Ångström Laboratory, Uppsala University, Box 538, 75121 Uppsala, Sweden. E-mail: amber.mace@kemi.uu.se
bDepartment of Engineering and Physics, Karlstad University, Karlstad, Sweden
cDepartment of Physics and Astronomy, Materials Theory Division, Uppsala University, Box 516, 75120 Uppsala, Sweden
First published on 12th January 2024
Abstract
Solid-state composite electrolytes have arisen as one of the most promising materials classes for next-generation Li-ion battery technology. These composites mix ceramic and solid-polymer ion conductors with the aim of combining the advantages of each material. The ion-transport mechanisms within such materials, however, remain elusive. This knowledge gap can to a large part be attributed to difficulties in studying processes at the ceramic–polymer interface, which are expected to play a major role in the overall ion transport through the electrolyte. Computational efforts have the potential of providing significant insight into these processes. One of the main challenges to overcome is then to understand how a sufficiently robust model can be constructed in order to provide reliable results. To this end, a series of molecular dynamics simulations are here carried out with a variation of certain structural (surface termination and polymer length) and pair potential (van der Waals parameters and partial charges) models of the Li7La3Zr2O12 (LLZO) poly(ethylene oxide) (PEO) system, in order to test how sensitive the outcome is to each variation. The study shows that the static and dynamic properties of Li-ion are significantly affected by van der Waals parameters as well as the surface terminations, while the thickness of the interfacial region – where the structure–dynamic properties are different as compared to the bulk-like regime – is the same irrespective of the simulation setup.
1 Introduction
In recent years, solid-state electrolytes have attracted much attention for battery applications due to possible benefits when compared to the currently used liquid electrolytes.1 Both polymer and ceramic solid electrolytes are possible candidates for use in this context. However, both these categories of materials, when used as a single phase, display drawbacks in terms of either electrochemical stability, Li+ conductivity, mechanical properties or interfacial compatibility. Since ceramic and polymer electrolytes have complimentary advantageous characteristics, it is therefore frequently suggested that composites – produced by embedding conductive ceramic particles in a polymer matrix – could constitute a promising strategy to obtain the benefits of both material types.2Although considerable attention has been dedicated to studying the performance and Li+ transport phenomena in such composite solid-state electrolytes, scientific literature display plenty of contradictory findings and hypotheses concerning the Li+ transport mechanisms. On the one hand, some experimental studies show a decrease in Li+ conductivity in the composite material compared to a single polymer phase electrolyte, such as has been observed for garnet Li7La3Zr2O12 (LLZO) combined with poly(ethylene oxide) (PEO).3,4 On the other hand, other studies show an increase of conductivity when these two electrolyte materials are combined.5,6 Such opposing results demonstrate that the true nature of Li+ transport in a composite electrolyte system remains elusive. For many composites, it is unclear which is the main ion-conducting phase: the polymer or the ceramic. Moreover, what is the interplay between the solid polymer electrolyte (SPE) salt and the ceramic particles? And is a space-charge region formed between the two electrolyte phases, and how important is it for the Li+ conduction?
There are several hypotheses in the field that address the questions listed above. Concerning the role of the salt, it has been suggested that the presence of ceramic particles induces adsorption of anions at the surface, which generates an improved ion–ion separation and thereby a higher cationic conductivity.7 Another suggestion is that continuous conduction pathways through the ceramic phase are formed, especially at higher particle loadings. An active ceramic filler is often a better ionic conductor in comparison to a solid polymer electrolyte, and can thereby render high overall conductivity.8 Moreover, Li et al.9 proposed a possible scenario in which a network of connected space-charge regions is formed at the surface of the LLZO ceramic. That creates fast conduction pathways at the ceramic surfaces. In contrast, Zagórski et al.4 argued that LLZO micro-fillers do not contribute positively to the transport of Li+ when embedded in the PEO polymer matrix. The presence of the ceramic active filler was shown to slow down the polymer chain mobility, resulting in a decrease in conductivity which is dominated by the polymer segmental motions. Thus, it remains unclear if lithium ions are transported within the ceramic phase, solely in the polymer phase, or along the ceramic–polymer interfaces, and if the addition of ceramic improves the conductivity or not.
The broad spectrum of proposed mechanisms of Li+ transport in composite electrolytes illustrates the complexity of the problem at hand and is, in the literature, discussed in a wide range of composite electrolyte compositions, spanning from the ceramic-in-polymer to polymer-in-ceramic extremes.10 This variation depends on the content of polymer and ceramic phases where the Li+ transport pathways typically depend on the specific composition. Furthermore, there are many materials properties that may also affect the Li+ mobility; for example, particle size,11,12 ceramic phase morphology13,14 or salt concentration15 which makes it troublesome to compare results between studies and draw general conclusions, even for the most studied composite electrolyte system: LLZO/PEO. This material comprises garnet LLZO ceramic particles immersed in a PEO polymer matrix, and is the composite model system also considered in the present study. In order to obtain better insight into the dynamical and structural properties at the interface of LLZO and PEO materials, classical molecular dynamics (MD) methodology is employed. MD simulations can provide atomistic insights that are not directly accessible by the experiment, while they can resolve structure–dynamic properties which are difficult to assess with other simulation techniques.
The atomistic level MD simulations entail a length scale of the composite interphase that is too limited to differentiate into any specific composite electrolyte composition. However, understanding the behavior of Li+ where the ceramic and polymer meet becomes mainly important for the ceramic-in-polymer electrolyte composition because transport across and along this interphase is expected to be dominant and rate-limiting. In the polymer-in-ceramic composition, the ions are anticipated to primarily transport along the ceramic phase and along/across the ceramic–ceramic interphase instead.
The aim of this work is to gain more understanding about the importance of different MD parameters when constructing a model of PEO/LLZO interfaces by determining how and to what extent different simulation setups affect the results. While this composite system has been examined by means of MD simulations in the past,16,17 the effects of crucial simulation parameters have not yet been explored. The focus of this work thereby differs from previous studies; here we explore how sensitive the simulation outcome is to the choice of these specific simulation model parameters. This will provide us with important information on which parts of the model are the weakest links, which input parameters need to be provided with the highest accuracy and which are less sensitive to change. In this study, the focus is specifically on how the MD simulation outcome is affected by changes of partial charges on atoms, van der Waals (vdW) cross interactions between polymer and ceramic, polymer chain length and surface termination. These offer valuable guidelines on how we can direct our research efforts most efficiently when further developing and improving the model accuracy of structure–dynamic processes that control the ionic transport. The primary focus of this study is thus to establish the foundation for conducting reliable and reproducible MD simulations of composite electrolytes rather than specifically providing a description of ionic transport phenomena at the current stage.
The choice of studied simulation parameters is divided into two categories: force field and structurally related aspects. vdW parameters together with partial charges belong to the first category. We use vdW parameters that have previously not been specifically optimised to describe the interfacial interactions between the ceramic and polymer phases. These sets of parameters have originally been developed to account for the interactions in a bulk material, and it is not yet clear if these interactions are compatible with an interfacial system. To our knowledge, there are no specifically optimised vdW parameters to account for cross-interactions between PEO and LLZO, or any other similar composite electrolyte systems.
Given that Li+ interacts via vdW and Coulomb interactions, it is a natural choice to evaluate the importance of partial charges on the atoms. Atomic partial charge is an artificial concept, and there are many diverse methods to estimate these values. Thereby, we have used two sets of partial charges: (1) DDEC6 (abbreviated DDEC) charges computed based on atomic population analysis18 and (2) REPEAT charges, which are derived from the electrostatic potential.19 In addition, we used one set of charges that were employed in the past to simulate the LLZO material.20
Structurally related aspects are considered by studying the influence of the polymer chain length and surface termination on the simulation outcomes. The polymer chain length affects both polymer flexibility and the number of termination groups present. Surface–polymer interactions affect the polymer flexibility directly, and therefore ionic transport in the polymer. Moreover, the terminal group can significantly influence the coordination chemistry at the surfaces, and comparing simulations with different polymer chain lengths should therefore bring valuable insights about the model systems. Finally, the surface properties are known to significantly modify the interactions between two phases. Hence, we study the effect of surface termination while keeping the orientation constant.
2 Methods
2.1 Simulation box setup
The cubic LLZO structure was obtained from the ICSD crystallographic database.21 In the LLZO crystal, there exists two types of Li sites, 24 d and 96 h, that are partially occupied, with the respective occupation numbers 0.542 and 0.448.22 Taking this into account, we generated an initial LLZO geometry that contained 13 and 43 Li atoms per unit cell in the 24 d and 96 h Li sites, respectively. This was done by randomly distributing these numbers of Li atoms among the specific site types. The initial slab configuration was generated using the Pymatgen “surface” module.23,24 The slab was chosen to have a (100) orientation and a c-shift equal to 0.09 (as defined in the SlabGenerator class in Pymatgen), according to the surface energy analysis by Thompson et al.25 Thereafter, a 3 × 3 × 3 LLZO slab was generated that was used in all simulations. Next, fftool26 was used to assign partial charges to LLZO atoms and create a LAMMPS data file that was then used to generate the polymer–ceramic interface. In order to generate initial polymer coordinates and assign simulation parameters, the Enhanced Monte Carlo code27 was used. This tool allows generating the polymer phase with different polymer chain lengths. The z-axis was chosen to be the axis perpendicular to the LLZO surface. This was then used to create a large enough box that contains both LLZO and PEO phases using the Moltemplate package.28 All necessary details related to the simulation boxes, together with the system acronyms used throughout the text, are listed in Table 1. An example simulation box of the PEO:LiTFSI/LLZO interface is presented in Fig. 1. Finally, these initial geometries described in Table 1 were subjected to a thorough equilibration procedure. Due to the structural asymmetry in the z-direction, the construction of the slab generates two different surfaces: one terminated with oxygen and one terminated with lithium. Those are referred to as the left LLZO surface oxygen-terminated (L-LLZO) and right LLZO surface lithium-terminated (R-LLZO), respectively. The effects of this is dealt with in more detail in Section 3.2.1.| System name | Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EO EO |
No. chains | No. units | x, y [Å] | z [Å] | Density [g cm−3] | vdW force field | Partial charges PEO | Partial charges LLZO |
|---|---|---|---|---|---|---|---|---|---|
| DDEC | — | 1 | 900 | 39.26 | 83.25 | 2.91 | UFF | DDEC | DDEC |
| REPEAT, LONG | — | 1 | 900 | 38.87 | 80.04 | 3.09 | UFF | REPEAT | REPEAT |
| OX | — | 1 | 900 | 38.65 | 80.36 | 3.11 | UFF | REPEAT | OX |
| SHORT | — | 45 | 20 | 38.86 | 83.47 | 3.00 | UFF | REPEAT | REPEAT |
| SHORT:LiTFSI | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
45 | 20 | 38.85 | 90.59 | 3.00 | UFF | REPEAT | REPEAT |
| LONG:LiTFSI, vdW-UFF | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
1 | 900 | 38.86 | 87.25 | 2.90 | UFF | REPEAT | REPEAT |
| vdW-LiZrO | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
1 | 900 | 38.87 | 86.51 | 3.02 | vdW-LiZrO | REPEAT | REPEAT |
2.2 Equilibration and production run details
The LAMMPS package29 was employed to perform all molecular dynamics simulations using periodic boundary conditions. To describe bonded interactions in the PEO polymer, the OPLS-AA30 force field as defined in the enhanced Monte Carlo27 software was used. Parameters for the TFSI− anions were adopted from Lopes et al.31 The bond, angle and improper interactions were set as the harmonic style while dihedral interactions were multi/harmonic. The cutoff for all non-bonded interactions was equal to 12 Å. The non-bonded interactions of PEO and LiTFSI salt were described with Lennard-Jones (LJ) and Coulomb potentials. van der Waals interactions within the LLZO phase were described by a Buckingham potential with parameters determined by Jalem et al.20 Due to the lack of explicitly calculated parameters for cross interactions between the polymer phase and the LLZO ceramic, two sets of LJ parameters were tested for the LLZO atoms: universal force field (UFF) and another set consisting of Li+ parameters from Wu et al.,32 Zr and O from Martins et al.,33 while the rest of the parameters were the same as in the UFF parameter set. This set is referred to as vdW-LiZrO in this paper. Since all atoms have associated LJ parameters, this allowed us to use Lorenz–Bertheloth mixing rules for interactions between non-identicle atom pairs. Electrostatic interactions were modeled by performing a standard Ewald summation as implemented in LAMMPS, and fixed partial charges were assigned to all atoms in the system. The partial charges for LLZO and PEO atoms were obtained using the DDEC618 and REPEAT19 methods; see Section S5 of the ESI† for details.To equilibrate the composite systems, a 21 step procedure was followed according to the approach by Larsen et al.,34 with the exception that the last NPT equilibration was extended to 32 ns. We used the last 2 ns of the final NPT to extract possible structures (every 10 ps) for the production NVT simulation. This was done in order to start the NVT simulation with the volume as close as possible to the equilibrium value extracted from the final NPT simulation. Hydrogen's atomic mass was substituted with the mass of a deuterium atom, while all simulations were run with a time step of 1 fs. Temperature and pressure were maintained using a Nosé–Hoover thermostat and barostat as defined in LAMMPS. After the 21 step equilibration process, NVT simulations were run at 400 K for a duration of 500 ns. 499 ns was used for analysis of the properties in the system.
2.3 Analysis of atom distribution and Li+ mobility
In order to have an initial look at the structural behavior of different atom types at the interface, number density profiles ρ(z) were calculated. First, the LLZO center of geometry was placed in the middle of the box. Next, a trajectory snapshot was obtained every 50 ps, and the positions of selected atoms were placed in bins with a thickness of 0.05 Å. The number density was plotted as a function of the z coordinate (perpendicular to the LLZO surface). Lastly, the average number of atoms per bin was divided by the volume of the 3D bin. Additionally, charge density profiles were calculated using the following equation,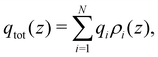 | (1) |
The survival probability R(t) was calculated in order to obtain insight into the mobility of Li+ in the direction perpendicular to the LLZO surface. This was calculated by,
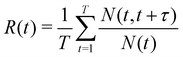 | (2) |
The box was divided in 4.5 Å thick virtual bins with zero being at the center of the simulation box, which is also the center of LLZO. In this way, a symmetric description of the two LLZO surfaces is obtained. The calculations of R(t) were performed every 5 ns to obtain satisfactory statistics. The survival probability, as defined by Liu et al.,35 thereby contains all the history of a particle remaining in the respective artificial layer. It should be noted that fluctuations that may happen within 5 ps are ignored, e.g. if an atom travels out from and back into the layer within 5 ps, this is not detected.
It is worth noting that the survival probabilities can be used to estimate the Li+ diffusion coefficient parallel to the slab, as described by Liu et al.35 This method has been used in a recent study on a similar system.16 The mean square displacement functions used to calculate the parallel diffusion coefficient with this method are themselves calculated from the Li+ that remain in a fictitious layer, as defined for the calculation of the corresponding R(t). However, in our simulations the Li+ ions leave the fictitious layers before diffusive behavior is observed. For that reason, this method could not here be rigorously used to determine the parallel diffusion coefficients, but only for qualitative indications for comparative purposes (the calculated MSDs from our trajectories that did not reach the diffusive regime are not reported here).
3 Results and discussion
3.1 General observations of the structure–dynamic properties
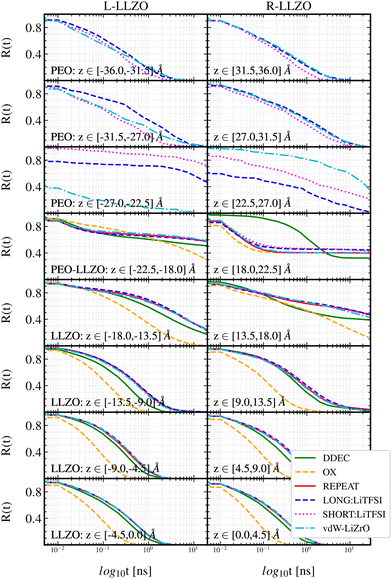 | ||
| Fig. 3 Survival probability functions. The different boxes correspond to different segments in the simulation box, with the respective z-values stated in each box. The bottom boxes thereby represent the bulk of the LLZO phase, while the top represents the bulk of the polymer phase (acronyms in the legend are explained in Table 1). | ||
Moreover, the general trends for all systems, and for both LLZO surfaces, are that the survival probability decays the fastest ∼100 ns in layers that are in the center of the LLZO ceramic [0.0, ±9.0] Å. From Fig. 3 it can be seen that 50% of the Li+ moves out of the [0.0, ±4.5] and [±4.5, ±9.0] layers within 1 ns, and after 1.1 ns all Li+ in a given fictitious layer have been exchanged for new ions. Next, in the interfacial region that spans both ceramic and polymer phases, i.e. [±9.0, ±27.0] Å, R(t) gradually increases to be at its maximum >101 ns within the [±18.0, ±27.0] Å region. This means that Li+ remains the longest time in this region. In other words, the presence of the interface hinders Li+ mobility perpendicular to the ceramic surface both in the polymer and ceramic phase. Lastly, towards the center of the polymer phase above/below ±27.0 Å, the survival probability decays faster, similarly to the ceramic phase, reaching values at the level of ∼101 ns in all except the vdW-LiZrO system. This case will be discussed in more detail in Section 3.3.2.
3.2 Structural effects
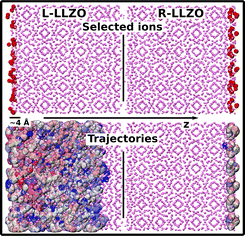
Surface effects on the Li+ density distribution. In the initial input of the MD simulation, the L-LLZO surface is terminated with OLLZO atoms. However, within the simulation time, mobile LiLLZO+ ions populate the surface. Here, the LiLLZO+ atom density at the surface is about 0.01 Å−3, and the distance between this density peak and the first OPEO maximum is about 1.2 Å; see Fig. 2. The polymer and LLZO phases on this side thereby seem to repel each other. Since the atom density of LiLLZO+ is above zero everywhere in this region, there is a possibility of LiLLZO+ changing between different LLZO layers, indicating disorder and flexibility. The R-LLZO surface, in turn, is initially terminated with LiLLZO+ ions. At this surface the LiLLZO+ atom density at the surface is almost three times the density of L-LLZO surface, i.e. almost 0.03 Å−3, while the distance between this peak and the first OPEO maximum is only about 0.7 Å. This indicates a tighter adhesion of the polymer to the R-LLZO surface compared to the L-LLZO side, see Fig. 2. The interfacial LiLLZO+ peaks on the R-LLZO side are also characterised by precise positions. Ion exchange between LLZO layers is therefore less likely, which indicates a higher level of ordering and rigidity compared to the L-LLZO surface. A common characteristic for both surfaces is that the interfacial LiLLZO+ layers, except for the terminal ones, have noticeably higher atom density compared to the center of the LLZO phase. This means that LiLLZO+ tend to accumulate near the surfaces within a region of ca. z = [±15.0, ±18.0] Å, see Fig. 2.
Surface effects on the Li+ mobility. To further highlight the differences in ion exchange between LLZO layers at the two surfaces, the LiLLZO+ trajectories (up to 4 Å from the surface) are displayed in Fig. 4. Indeed, the mobility of LiLLZO+ ions is much higher at the L-LLZO side compared to the R-LLZO side. From the trajectories, it is observed that the L-LLZO surface atoms travel almost the entire interior of the LLZO phase while the R-LLZO surface atoms hardly move from their initial positions, hence the trajectory covers only a thin region around the R-LLZO surface.
Surface effects on the charge distribution. Qualitatively, the analysis of Zr, La, OLLZO and LiLLZO+ density profiles of L-LLZO and R-LLZO surfaces indicate that there is an increased accumulation of positively charged Zr and La close to the R-LLZO surface as compared to the L-LLZO surface. Moreover, these positive charges are shielded by negatively charged OLLZO atoms to a lesser extent at R-LLZO than at L-LLZO. This suggests that the L-LLZO surface is more negatively charged than the R-LLZO surface, which can explain the differences in charge accumulation from the polymer phase.
Chain length effects on the TFSI− density distribution. Interestingly, the interactions of anions with LLZO surfaces are affected by the difference in the polymer chain length. For example, the density profiles of the components of the LiTFSI salt show that the TFSI− ions are found closer by about 1 Å to both surfaces and the peaks have a higher intensity in the SHORT as compared to the LONG system; see Fig. 5. Concerning the system with short polymer chains, the TFSI− ions show a similar atom distribution at both sides of the LLZO slab in the regions z = [±25.0, ±30.0] Å. This corresponds to an observed increase of anion density as compared to other areas in the simulation box. At the same time in the LONG system, there is a discrepancy in the atom distribution of TFSI− ions between the left and right side of the LLZO slab. At the L-LLZO surface, a decrease in TFSI− ions is observed in the region z = [−30.0, −25.0] Å while an increase is visible at the R-LLZO side at the corresponding distance from the surface. These observations are highlighted in the ESI,† Fig. S2, which shows the trajectories of NTFSI− atoms selected within 7 Å from the surface. Indeed, the TFSI− ions seem to populate larger regions perpendicular to the surface in the SHORT system as compared to the LONG system. Moreover, a TFSI−-free volume is found in the LONG simulation at the L-LLZO side, shown in the ESI,† Fig. S2. This means that there is a consistency between the ESI,† Fig. S2 and the NTFSI− density profiles shown in Fig. 5a. As explained above, a decrease of TFSI− atom density is observed in the region z = [−30.0, −25.0] Å. There is a 4 and 5 Å thick anion depletion area, respectively, at the L-LLZO surface in both SHORT and LONG simulations.
These discrepancies between density profiles of the TFSI− ions in the LONG and SHORT systems may have a twofold explanation. First, it is possible that the distribution of the anions in the polymer phase has reached equilibrium in the SHORT system but not in the LONG system. Simulations of a bulk PEO-LiTFSI system with short polymer chains (<100 monomers) show ca. 2.5 times faster diffusion of TFSI− in comparison to higher molecular weight polymer chains.38 This indicates that the TFSI− density profiles of the SHORT system are more likely to be the equilibrium atom distribution, compared to the LONG system. However, the anion diffusive regime in the bulk PEO-LiTFSI simulations was reached within 400 ns, even in the simulations with the long polymer chains (>100 monomers).38 Therefore, it seems that short and long polymer chains interact differently with the L-LLZO surface, which in turn affects the TFSI− ions distribution. The longer PEO chain creates a thicker shell around the L-LLZO surface in the LONG system compared to the SHORT system; see the OPEO atom density plots in the ESI,† Fig. S6. The observed thinner and more permissible shell, that the shorter PEO chains form around the L-LLZO surface, is likely due to a higher chain flexibility. This results in a more accessible PEO interfacial shell for the TFSI− ions in the SHORT system as compared to the LONG system.
Chain length effects on the Li+ interphase penetration. Another discrepancy between the interfacial atom distributions in the SHORT and LONG systems is that there is an uptake of LiPEO+ ions into the LLZO slab only in the system with short polymer chains. Penetration of Li+ occurs only through the L-LLZO surface and the ions do not cross the LLZO phase entirely. One example of a Li+ ion entering the ceramic phase through the L-LLZO surface is shown in Fig. 6, which shows 300 ns of a trajectory of a LiPEO+. The highlighted Li+ spends about 100 ns in each region: the polymer phase, at the interface and in the ceramic phase. Density profiles of LiPEO+ in Fig. S6 in the ESI† show a more quantitative picture of LiPEO+ entering the LLZO phase, while in the SHORT system the peaks in the LLZO phase (at z > −20 Å) indicate the presence of LiPEO+. In the LONG system, no peaks are observed in the LLZO phase.
Despite the uptake of LiPEO+ into the LLZO phase, which is observed in SHORT but not in the LONG simulations, the survival rate R(t) is not affected in the ceramic region [0.0, ±22.5] Å by the presence of additional Li+ ions in the crystal structure; see Fig. 3. It is common for both polymer lengths for LiPEO+ ions to be adsorbed at the LLZO surfaces, but LiLLZO+ do not leave the LLZO phase. Fig. S3 in the ESI† shows how the number of Li+ present in the LLZO phase and its surface (z-span [−22, 22] Å) evolves as a function of simulation time. Fig. S3 in the ESI† indicates that the process of LiPEO+ uptake in the ceramic phase has not reached an equilibrium stage in any of the simulations, which is deduced from the fact that a stable plateau is not reached. By the end of the simulation time, the polymer phase contains 82% and 93% of the initial number of LiPEO+ ions, in the SHORT and LONG systems respectively.
One possible explanation for the discrepancies between the long and short polymer chain simulations is that the ionic transport occurs faster in SHORT due to the increased chain flexibility. This would mean that the same Li+ and TFSI− distribution will be reached in LONG if it was simulated for a longer time. However, the Li+ survival probability in the regions z = [±22.5, ±27.0] Å, is higher in the system with shorter chains, which indicates that the cationic transport perpendicular to the surface occurs on a shorter timescale in the system with the long polymer chain. This is contrary to what would be expected given that in the simulations of a bulk PEO electrolyte, it was found that shorter polymer chains correlate with faster Li+ diffusion.38 Although the LiPEO+ remain longer in the region z = [±22.5, ±27.0] Å in the SHORT system, they pass through it to reach the areas near the surfaces, as indicated in the ESI,† Fig. S6. This corroborates with data in Fig. S3 in the ESI,† which shows that more LiPEO+ ions reach the LLZO surfaces in the SHORT system compared to the LONG system. These reasons indicate that polymer flexibility, and therefore the timescale of ion transport, may be a reason for discrepancy in the simulations.
Polymer chain terminations. Another difference between the systems is the number of polymer chain terminations, comprising 2 and 90 terminations in the LONG and SHORT systems, respectively. Although the chains in these simulations are terminated with relatively inert methyl groups, there is a difference in adhesion of OPEO to the surfaces in the interfacial layers z = [±20, ±27] Å. OPEO density profiles in the ESI,† Fig. S6, demonstrate this difference in the interfacial atoms arrangement that does not overlap for the SHORT and LONG systems respectively. 100 ns of trajectories of CterminalPEO atoms are shown in the ESI,† Fig. S1. It is visible that terminations accumulate at the surface in SHORT while they remain at the center of the polymer phase in the LONG system. This could be a result of the difference in flexibility of the long and short polymer chains which may lead to a modification of the more likely polymer configuration at the surface. At the same time, the polymer chain length does not affect density profiles of OPEO in systems without the salt in the polymer phase; see Fig. S5 in the ESI.† This indicates that the presence of LiTFSI salt in the polymer phase, and possibly its interaction with chain terminations, has a more prominent effect on the interfacial OPEO distribution than a difference in the polymer chain length alone.
3.3 Force field effects
Charge effects on the polymer adhesion to the LLZO surface. The interaction of OPEO is stronger with the LLZO surface in OX and REPEAT compared to DDEC. This difference may be explained by analyzing the interactions of OPEO with the cations of the LLZO phase; this is indicated in Fig. 7, which shows charge density distribution along the z-axis. The distance between the closest OPEO and Zr peaks to the interface is about 3–4 Å. At that distance, the attraction energy between these species reaches about 400 kJ molpair−1 (i.e., the sum of Coulomb and van der Waals pair interactions) in the OX and REPEAT systems, but only about 180 kJ molpair−1 in the DDEC system. Similarly, when the interaction energy of the OPEO-La pair is studied, it can be noticed that the interaction energy reaches about 250 kJ molpair−1 and 700 kJ molpair−1 in DDEC and REPEAT/OX respectively, at the typical interfacial distance of 2.5 Å. This interaction energy analysis can explain the difference in polymer adhesion to the surface; i.e. that the REPEAT and OX have higher attractive interaction energies between the polymer and ceramic atoms compared to the DDEC system. This is consistent with weaker interactions between the phases in this system, which is seen in Fig. 7 by observing the distance and intensity of OPEO and LiLLZO+ interfacial peaks.
Charge effects on the LiLLZO+–OPEO interactions. Moreover, the character of the first OPEO adhering layer is different in these systems. For example, in Fig. 7a at the region [−23, −21] Å, the DDEC system shows only one peak located slightly further from the surface, while in the other systems the first adhering layer is split into two peaks. In the OX and REPEAT systems, a small number of LiLLZO+ are adsorbed to the first layer of the polymer at the L-LLZO side. The OX system is different from REPEAT only by the partial charges in the LLZO phase, while both systems have the same set of charges in the polymer phase. This effect is not observed in any of the systems at the R-LLZO side, neither is it observed on any side of LLZO in the DDEC system. The fact that we do not observe LiLLZO+ migration towards the first PEO layer in the DDEC system may be explained by the interaction energies of Li+ ions with other atoms in the system. Due to the lower magnitude of partial charges, there is much lower attractive Coulomb interaction between the polymer atoms and Li+ in the DDEC system compared to the REPEAT system. For example, the Li+–OPEO interactions at 2 Å is about 110 kJ molpair−1 and 300 kJ molpair−1 in the respective systems. At the same time, the interactions of Li+ with LLZO atoms are comparable for both systems. This means that the DDEC charges induce a weaker interaction of Li+ ions with the PEO atoms, which prevents the migration of LiLLZO+ atoms towards the polymer phase.
Charge effects on the Li+ mobility in the LLZO phase. In Fig. 3, vital differences between the employed partial charges on the survival rates can be observed. The OX system shows about one order of magnitude faster decay of R(t) compared to both DDEC and REPEAT. The survival probability of Li+ in system OX varies between ∼ 5 × 10−1 ns to ∼ 1 × 101 ns in the regions [0.0, ±18.0] Å, while R(t) in systems DDEC and REPEAT is about one order of magnitude higher. A trend can be seen that the survival probability decays the slowest in the REPEAT system, while it is slightly faster in DDEC as compared to REPEAT. This observation is valid for both L-LLZO and R-LLZO sides. Despite the higher magnitude of charges in the OX system (which implies stronger Coulomb interactions between atoms), the LiLLZO+ mobility perpendicular to the surface proceeds on shorter timescales in that system than in DDEC and REPEAT systems. It is not possible to directly pinpoint the exact reason for the discrepancies between these simulations due to the high number of pair interactions. However, the two possibly dominant interactions in LLZO, the Li–O and Li–Li pairs, may provide some insights. At about 2 Å (the typical distance between the nearest Li–O neighbours) the interaction energy in the OX system is 50 kJ molpair−1 and 100 kJ molpair−1 weaker (i.e., lower attractive interaction) compared to DDEC and REPEAT systems respectively. The Li–Li repulsive pair interaction is the weakest in the OX system with a difference of at least 80 kJ molpair−1 compared to other systems. This means that there may be more flexibility for LiLLZO+ in the LLZO structure, which therefore leads to the higher mobility perpendicular to the surface in the OX system compared to other systems. This analysis is consistent with the work of Jalem et al.,39 where it is shown that the unstable residence of LiLLZO+ at the 24d site is one of the main factors for the fast concerted Li+ migration mechanism in cubic LLZO.
Force field effects on the Li+ depletion region. A first observation from the Li+ density distribution is that in the vdW-UFF system at the L-LLZO surface [−25.0, −18.0] Å, there are three peaks corresponding to the most probable positions of LiPEO+, while in vdW-LiZrO only two peaks are observed. In other words, a ∼ 4 Å thick depletion region of LiPEO+ species appear in vdW-LiZrO but not in the vdW-UFF simulation; see the [−26.0, −22.0] Å region in Fig. 8a. This kind of depletion region is also observed in both systems at the R-LLZO surface, and has also been noted in previous atomistic simulation of the same system.16 Additionally, changing cross vdW parameters affects the intensities and positions of several maxima and minima in the interfacial region of the density profiles of LiLLZO+ on both surface sides, which is seen when comparing the LiLLZO+ peak positions in Fig. 8.
Force field effects on the adhesion of OPEO to the LLZO surfaces. The character of the interfacial OPEO peaks is also visibly affected by the change of vdW parameters. There is one minimum less, and some maxima are also shifted or have higher/lower intensity in the vdW-LiZrO system compared to the vdW-UFF system. In Fig. 8a, it can be noted that adhesion of OPEO is stronger in vdW-LiZrO compared to vdW-UFF (see the brown-dashed and violet-solid lines, respectively). The above analysis suggests that modification of the vdW cross parameters affects the arrangement of interfacial OPEO which may induce a LiPEO+ depletion region at the L-LLZO interface. Furthermore, adhesion of OPEO to the R-LLZO surface is stronger compared to L-LLZO in the vdW-UFF system, while in vdW-LiZrO OPEO adhesion on both surface sites is comparable. These results indicate that the choice of vdW parameters affects adhesion of OPEO differently depending on the surface terminating atoms. This can be rationalised by the fact that different LLZO terminations have different electrostatic interactions, i.e. that the atoms possessing the same charge will be exposed to different Coulomb interaction regions when the vdW parameters are modified.
Force field effects on the Li+ survival probabilities. The effect of vdW parameters on the survival probability R(t) is most pronounced in the regions [±22.5, ±27.0] Å (Fig. 3). In particular, the vdW-LiZrO system shows the fastest decay of all systems at the L-LLZO side. Concerning R-LLZO, the opposite situation takes place with the vdW-LiZrO system showing slower R(t) decay when compared to the vdW-UFF system. The vdW-LiZrO system shows a significantly faster decay of the survival probability in the region [−27.0, −22.5] Å compared to ceramic and polymer far from the surface, which again is a strikingly different result than for the other systems. This region coincides with the Li+ depletion region observed in the density profile at the L-LLZO surface (Fig. 8a). If combining the analysis of survival probabilities and density profiles, a distinctive mode of transport at the L-LLZO side can be observed in the vdW-LiZrO system, which is not present in the vdW-UFF simulations. The depletion region seen in Fig. 8a in region [−27.0, −22.0] Å in the vdW-LiZrO system corresponds to an exceptionally quick decay of R(t). This correlation indicates there are almost no stationary Li+ in this region, and the quick decay of R(t) suggests a flux of Li+ that pass through the polymer layer to reach the L-LLZO surface. A different mechanism is observed at the R-LLZO surface in the vdW-LiZrO system. Fig. 8b shows a pronounced peak in the region [22.0, 27.0] Å which is also characterised by a high survival probability (Fig. 3). This means that the LiPEO+ at the R-LLZO side are fairly stationary. The flux of Li+ can still occur, but on a significantly longer time scale.
Comparing non-bonded potentials in the vdW-UFF and vdW-LiZrO systems shows that irrespective of the atom pair, the difference between the potentials becomes negligible above 3 Å and in many cases above 2.5–3 Å. However, in the region below that, the discrepancy between the interaction energies increases significantly. For example, the CPEO–OLLZO pair interaction energy difference between the vdW-UFF and vdW-LiZrO systems at about 2 Å is equal to 70 kJ molpair−1, while for the OPEO–Li+ pair it is equal to 10 kJ molpair−1. The interaction analysis suggests that the Li+ migration properties at the interface are very sensitive to the choice of vdW cross integration parameters. While the actual variation of the interaction energy is only pronounced up to 3 Å from an atom, this still renders a noticeable impact on the density profiles, survival probabilities and on the mode of Li+ transport perpendicular to the surface.
4 Conclusions
In this study, classical molecular dynamics simulations were used in order to investigate the static and dynamic properties of a ceramic–polymer interface comprising PEO-based polymer electrolyte and cubic LLZO ceramic phases. The aim was to assess the influence of several model parameters on the simulation outcome, and was evaluated by how density profiles and survival probabilities are affected by the atomic partial charges, vdW cross interactions, polymer chain length and LLZO surface termination.There are three main conclusions made from this study: (i) structural effects, in particular surface terminations, have a significant impact on the interfacial atomic arrangements in both polymer and ceramic phases. This was clearly seen from the distinct differences in the atomic density profiles between the two LLZO surfaces, and the fact that LiPEO+ enters the ceramic phase only through the left surface terminated with oxygen. (ii) Force field effects, especially van der Waals cross phase interactions modify the mode of Li+ transport at the interface. (iii) Independent of the simulation setup, the interphase regions stretch across the same distance perpendicular to the LLZO surfaces. This is reflected in atomic density profiles and survival probabilities which are modified compared to the bulk-like regions. The distance that is affected by the existence of the interface, for any of the studied structure–dynamic properties, spans about 15 Å and about 11 Å from the LLZO surface in the PEO and LLZO phase respectively. This suggests that even without a perfectly optimised force-field, we may still draw some conclusions about Li+ mobility at the PEO/LLZO interface.
The complexity of these composite systems makes it challenging to systematically check every aspect of importance for the model. For this reason, the analysis here consists of a limited number of setups, targeting the exploration of the sensitivity of certain simulation parameters. This certainly does not exhaust the topic of important aspects that should be verified before a more definite picture of Li+ transport phenomena in the composite material can be provided. For example, the present study has only examined the surface with one orientation, and one surface cleavage. It is thereby still not clear to what extent these findings can be generalised with respect to different surface orientations and terminations.
The picture of Li+ transport in the PEO–LLZO composite material is still far from understood, and the molecular dynamics simulations described here primarily demonstrate that certain aspects of the simulation setup can significantly affect the outcomes of the study. It is crucial to highlight that, while this paper does not aim to determine realistic details regarding Li+ transport phenomena at the interface, we are actively exploring the most suitable setup to address the remaining physical questions related to lithium mobility in this category of electrolytes. In this context, the results of this study constitute a step forward towards more accurate and reproducible simulations of ceramic–polymer interfaces, which is particularly relevant in the field of all solid-state batteries.
Author contributions
Melania Kozdra: conceptualization, investigation, writing – original draft; Daniel Brandell: conceptualization, supervision, resources, writing – original draft, funding acquisition; Carlos Moyses Araujo: conceptualization, supervision, funding acquisition; Amber Mace: conceptualization, methodology, writing – original draft, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Swedish Energy Agency (project 50098-1), Swedish Research Council (Registration No. 2019-05366 and 2020-05223), and STandUP for Energy and Swedish National Strategic e-Science programme (eSSENCE) for the financial support. The calculations were performed on resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at PDC.Notes and references
- J. Janek and W. G. Zeier, Nat. Energy, 2023, 8, 230–240 CrossRef.
- A.-G. Nguyen and C.-J. Park, J. Membr. Sci., 2023, 675, 121552 CrossRef CAS.
- J. Zheng and Y. Y. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 4113–4120 CrossRef CAS PubMed.
- J. Zagórski, J. M. López Del Amo, M. J. Cordill, F. Aguesse, L. Buannic and A. Llordés, ACS Appl. Energy Mater., 2019, 2, 1734–1746 CrossRef.
- W. Zhang, K. S. Kjær, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubiček, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. Van Driel, T. C. Weng, D. Zhu, K. Wärnmark, V. Sundström and K. J. Gaffney, Chem. Sci., 2016, 8, 515–523 RSC.
- W. Li, C. Sun, J. Jin, Y. Li, C. Chen and Z. Wen, J. Mater. Chem. A, 2019, 7, 27304–27312 RSC.
- W. Wieczorek, Z. Florjanczyk and J. R. Stevens, Electrochim. Acta, 1995, 40, 2251–2258 CrossRef CAS.
- J. Zheng, M. Tang and Y.-Y. Hu, Angew. Chem., 2016, 128, 12726–12730 CrossRef.
- Z. Li, H. M. Huang, J. K. Zhu, J. F. Wu, H. Yang, L. Wei and X. Guo, ACS Appl. Mater. Interfaces, 2019, 11, 784–791 CrossRef CAS PubMed.
- J. Fu, Z. Li, X. Zhou and X. Guo, Mater. Adv., 2022, 3809–3819 RSC.
- J. Zheng and Y. Y. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 4113–4120 CrossRef CAS PubMed.
- J. Zhang, N. Zhao, M. Zhang, Y. Li, P. K. Chu, X. Guo, Z. Di, X. Wang and H. Li, Nano Energy, 2016, 28, 447–454 CrossRef CAS.
- X. Peng, K. Huang, S. Song, F. Wu, Y. Xiang and X. Zhang, ChemElectroChem, 2020, 7, 2389–2394 CrossRef CAS.
- Z. Wan, D. Lei, W. Yang, C. Liu, K. Shi, X. Hao, L. Shen, W. Lv, B. Li, Q. H. Yang, F. Kang and Y. B. He, Adv. Funct. Mater., 2019, 29, 1805301 CrossRef.
- D. Brogioli, F. Langer, R. Kun and F. La Mantia, ACS Appl. Mater. Interfaces, 2019, 11, 11999–12007 CrossRef CAS PubMed.
- M. R. Bonilla, F. A. García Daza, P. Ranque, F. Aguesse, J. Carrasco and E. Akhmatskaya, ACS Appl. Mater. Interfaces, 2021, 13, 30653–30667 CrossRef CAS PubMed.
- M. R. Bonilla, F. A. García Daza, H. A. Cortés, J. Carrasco and E. Akhmatskaya, J. Colloid Interface Sci., 2022, 623, 870–882 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
- C. Campañá, B. Mussard and T. K. Woo, J. Chem. Theory Comput., 2009, 5, 2866–2878 CrossRef PubMed.
- R. Jalem, M. J. Rushton, W. Manalastas, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Chem. Mater., 2015, 27, 2821–2831 CrossRef CAS.
- G. Bergerhoff, I. Brown and F. Allen, Int. Union Crystallogr., Crystallogr. Symp., 1987, 360, 77–95 Search PubMed.
- H. Xie, J. A. Alonso, Y. Li, M. T. Fernández-Díaz and J. B. Goodenough, Chem. Mater., 2011, 23, 3587–3589 CrossRef CAS.
- W. Sun and G. Ceder, Surf. Sci., 2013, 617, 53–59 CrossRef CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- T. Thompson, S. Yu, L. Williams, R. D. Schmidt, R. GarciaMendez, J. Wolfenstine, J. L. Allen, E. Kioupakis, D. J. Siegel and J. Sakamoto, ACS Energy Lett., 2017, 2, 462–468 CrossRef CAS.
- A. Padua, K. Goloviznina and Z. Gong, fftool v1.2.1 DOI:10.5281/zenedo.593728.
- P. J. in’t Veld and G. C. Rutledge, Macromolecules, 2003, 36, 7358–7365 CrossRef.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. N. Lopes and A. A. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef CAS.
- H. Wu and C. D. Wick, Macromolecules, 2010, 43, 3502–3510 CrossRef CAS.
- L. R. Martins, M. S. Skaf and B. M. Ladanyi, J. Phys. Chem. B, 2004, 108, 19687–19697 CrossRef CAS.
- G. S. Larsen, P. Lin, K. E. Hart and C. M. Colina, Macromolecules, 2011, 44, 6944–6951 CrossRef CAS.
- P. Liu, E. Harder and B. J. Berne, J. Phys. Chem. B, 2004, 108, 6595–6602 CrossRef CAS.
- M. Ebadi, L. T. Costa, C. M. Araujo and D. Brandell, Electrochim. Acta, 2017, 234, 43–51 CrossRef CAS.
- A. Thum, D. Diddens and A. Heuer, J. Phys. Chem. C, 2021, 125, 25392–25403 CrossRef CAS.
- D. J. Brooks, B. V. Merinov, W. A. Goddard, B. Kozinsky and J. Mailoa, Macromolecules, 2018, 51, 8987–8995 CrossRef CAS.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04617f |
| This journal is © the Owner Societies 2024 |