 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photo-excited charge transfer from adamantane to electronic bound states in water†
Xiangfei
Wang
 ab,
Pascal
Krause
a,
Thorren
Kirschbaum
ab,
Pascal
Krause
a,
Thorren
Kirschbaum
 ac,
Karol
Palczynski
ac,
Karol
Palczynski
 a,
Joachim
Dzubiella
a,
Joachim
Dzubiella
 *d and
Annika
Bande
*d and
Annika
Bande
 *ae
*ae
aHelmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109 Berlin, Germany. E-mail: annika.bande@aci.uni-hannover.de
bInstitute of Chemistry and Biochemistry, Freie Universität Berlin, Arnimallee 22, 14195 Berlin, Germany
cInstitute of Mathematics, Freie Universität Berlin, Arnimallee 14, 14195 Berlin, Germany
dApplied Theoretical Physics – Computational Physics, Albert-Ludwigs-Universität Freiburg, Hermann-Herder Straße 3, 79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
eInstitute of Inorganic Chemistry, Leibniz University Hannover, Callinstr. 9, 30167 Hannover, Germany
First published on 14th February 2024
Abstract
Aqueous nanodiamonds illuminated by UV light produce free solvated electrons, which may drive high-energy reduction reactions in water. However, the influence of water conformations on the excited-state electron-transfer mechanism are still under debate. In this work, we offer a theoretical study of charge-transfer states in adamantane-water structures obtained by linear-response time-dependent density-functional theory. Small water clusters with broken hydrogen bonds are found to efficiently bind the electron from adamantane. A distinction is made with respect to the nature of the water clusters: some bind the electron in a water cavity, others along a strong permanent total dipole. These two types of bound states are more strongly binding, the higher their electron affinity and their positive electrostatic potential, the latter being dominated by the energy of the lowest unoccupied molecular orbital of the isolated water clusters. Structural sampling in a thermal equilibrium at room temperature via molecular dynamics snapshots confirms under which conditions the underlying waters clusters can occur and verifies that broken hydrogen bonds in the water network close to adamantane can create traps for the solvated electron.
I. Introduction
The solvated electron has attracted the interest of researchers for more than 60 years as the most fundamental reducing agent as well as a highly reactive intermediate in a variety of physical, chemical, and biological reactions.1 In particular, the electron solvated in water is an important intermediate in many photo-catalytic reactions,2,3 redox-chemistry,4 and radiation damage processes.5 Despite its long history, the solvated electron is still one of the most mysterious chemical species that deserves investigation using the most advanced theoretical simulations and experiments to clarify its structural and dynamic properties.A recent ab initio molecular dynamics (AIMD) simulation of an electron in water6 using a machine-learned force field based on Møller–Plesset second-order training data shows a cavity formed by four to five water molecules with each having one of their OH bonds pointing to the center of the cavity. In addition, a recent AIMD simulation using density functional theory (DFT) has confirmed that such a so-called cavity-bound state shows the experimentally observed redshift of the infrared absorption spectrum when the temperature increases.7 On the contrary, some non-cavity models suggest that the solvated electron is delocalized in water regions where the water density is enhanced compared to neutral water.8 Furthermore, high-accuracy ab initio simulations show that the non-cavity model can correctly reproduce the infrared absorption spectrum of the solvated electron,9 particularly the redshift of the O–H stretching motion compared to that in bulk water.10
Experimentally, the generation of solvated electrons usually requires techniques with high-energy inputs, such as electrolysis,11 ionizing radiation,5,12 or direct injection of plasma.13 Other techniques rely on novel photo-catalytic materials and excitations within the visible spectral range.3 One particularly interesting type of catalysts are nanodiamonds, which can act as electron donors upon radiation with UV/Vis light.14,15 Nanodiamonds, similar to a planar diamond surface in general, have a negative electron affinity (NEA), i.e., the lowest unoccupied molecular orbital (LUMO) of a nanodiamond has a higher energy than a free electron in the vacuum. Furthermore, the outwards-pointing surface dipoles of the diamond C–H bonds facilitate the movement of the electron from the diamond surface into the adjacent medium.16 Accordingly, nanodiamonds have been used as a source of water-solvated electrons to catalytically drive high-energy reduction reactions, such as the reduction of N2 to NH3,17 and CO2 to CO.18,19
The solvation process of electrons from illuminated nanodiamonds is believed to proceed through the following stages:16 first, the nanodiamond is excited into a state with high electron density on the surface. Then, due to the NEA, the electron diffuses into the water over a negligible barrier. After the emission, the actual solvation of the electron in water undergoes the following steps:20 (i) ultrafast liberation (tens of (fs)),21 (ii) capturing of the excess electron in a preexisting trap (100 fs),22,23 and (iii) the complete solvation assisted by the translational motion of water molecules (<300 fs).24 Despite the significance of the solvation process, theoretical studies on the charge transfer dynamics from nanodiamonds to water molecules are still missing, because of the large size and complexity of the system.
Isolated nanodiamonds are semiconductors with a band gap around 5.4 eV25 and unique electron emission properties26,27 that dependent on their size, shape and symmetry.28,29 The band gap is widely tunable by doping and surface termination.30–33 While the electronic structure of nanodiamonds has been relatively well-studied,34,35 the electronic structures of bulk water, however, are much more complicated due to the incessant movement of the water molecules. Bulk water in equilibrium can be regarded as a semiconductor with a band gap of about 10 eV and a conduction band minimum (CBM) at about −0.8 eV.36 However, it has been suggested that due to thermal fluctuations, the rearrangement of water configurations can give rise to inter-bandgap bound states that lie below the conduction band minimum.37–39 In addition, previous work has shown that these bound states may play a dominant role in the formation mechanism of solvated electrons in neutral water.40 They arise from substructures formed by a limited number of water molecules that deviate from the hydrogen-bond network20,41 and give rise to dangling O–H that are common at the surfaces of small water clusters. The respective hydrogen atoms resulting from broken hydrogen bonds can point either to a common center, allowing the formation of a cavity-bound state for the electron, or they may point away from the center, giving rise to a dipole-bound state in which the electron localizes at one or several dangling O–H following the static dipole moment of the involved O–H bonds.42,43
In this work, we study the properties of low-lying charge-transfer excited states of adamantane (C10H16) in water. Using this reduced-size model for nanodiamonds allows the deployment of high-accuracy electronic structure calculations to account for the diffuse properties of the solvated electron, which may have a distribution expanding across several water molecules.22 In addition, adamantane as the minimal-size nanodiamond shares key properties with a full-size nanodiamond, including NEA,26,27 and can hence act as an accurate model for the electronic properties of the electron donor. For the water environment, water clusters of various sizes – from monomer through pentamer – are used and placed at different positions relative to adamantane to provide a systematic analysis of the electron-transfer characters of arising excited states. To extrapolate findings to realistic scenarios, we use snapshots from molecular dynamics (MD) simulations to analyze a cavity-bound and a dipole bound state in an extended water environment. For these calculations, the use of finite-temperature MD snapshots allows to get realistic snapshots of the room-temperature geometries and hydrogen bond networks of the water droplets in addition to the 0 K geometries from DFT optimizations and geometric arrangement. We reveal that the lowest unoccupied molecular orbital (LUMO) of the water molecules is the system's key property for capturing the photo-excited electron from adamantane. The energies and the shapes of the cluster LUMOs provide a quantitative description of various types of bound states of the electron in the water clusters.
The use of different-sized water clusters as a representation of the bulk water environment comes with certain limitations. Previous research stated that the excess electron after injected into bulk water will first occupy a diffuse state delocalized over only a few water molecules.44,45 On the other hand, in equilibrated finite-size water droplets, the injected electron will instead localize on the surface of the water cluster, where it is stabilized by dangling hydrogen bonds.43,46 While the previous studies on this subject focused on the injection of an excess electron into the water clusters to create anionic clusters, we here investigate the effect of injecting an electron from a nanodiamond into the adjacent water cluster. Within this approach, we investigate the charge transfer states of the excited electrons for which finite-temperature MD snapshots provide meaningful geometric arrangements. However, others have pointed out that the charge transfer state of the electron is closely associated with the breaking of hydrogen bonds.46 Hence, to supplement our study on small water clusters, which always have a surface with broken hydrogen bonds, we take a large shell of water using snapshots from MD to better resemble the properties of the water bulk.
II. Methods and theory
A. Electronic structure calculations of the ground and excited states
In this work, the method to calculate structures and ground state properties is DFT. As a first step, the geometries of adamantane as well as of the isolated water clusters in different geometries (monomer, dimers, trimers, etc.) are optimized to study their individual electronic properties, including molecular orbitals, transition dipole moments, and electrostatic potentials. The geometry of adamantane is optimized using CAM-B3LYP/aug-cc-pVDZ.47–49 The geometries of the water monomer and dimer structures are taken from the literature,42 and in addition, two new dimer configurations, C2h and C2h*, were optimized under the constraints of a fixed symmetry and center of mass (CM) distances. Likewise, the construction of trimers through pentamers adapts the structures of Kim et al.,42 with the dipole-bound structures undergoing a full optimization of the geometry, and the cavity-bound structures that have fixed CM distance and predefined arrangement. The joint structures for adamantane and the different small water clusters are composed according to Fig. 1(a) of Section III. For these structures, orbital properties also have been calculated with the long-range corrected functionals LC-BLYP, ωB97X, and ωB97X-D3. As summarized at the end of Section IIIC, the observed trends are largely unchanged, therefore, in the following the results and discussions are presented for the CAM-B3LYP calculations.The subsequent excited state calculations use linear-response time-dependent density functional theory (LR-TDDFT) in the Tamm-Dankov approximation. The exchange–correlation functional is the same range-separated hybrid functional CAM-B3LYP47 as used for the ground state calculations, which has shown to deliver an accurate description of the charge-transfer excitation in large organic molecules or molecular arrays.50–54 The basis set for the excited states is the same Dunning's augmented basis set, aug-cc-pVDZ,48,49 since the diffuse functions are needed for the description of largely delocalized virtual orbitals of the adamantane-based structures.55–58 This part of the calculations are done using the ORCA software.59
The LUMO energies from DFT are closely related to the electron affinities60 defined as the total energy difference between the anionic and neutral molecular species, namely the vertical detachment energy. To calculate this for the excess electron, we execute a ΔSCF calculation, which is commonly done when examining charge-transfer properties with TDDFT calculations.61 For self-consistency with the previous TDDFT calculations, the exchange–correlation functional is the same CAM-B3LYP used previously. Here, extra diffuse basis functions are necessary to account for the highly diffuse additional electron in the anionic water clusters. Accordingly, we use the aug-cc-pVTZ48,49 basis set with two additional sets of diffuse shells (2s,2p/2s), where the exponents are set equal to 1/8 of the outmost exponents of the original set.62 The computation for the electron affinity is carried out in the Gaussian software63 using the SG-1 grid64 for integration in DFT. These settings can provide accurate electron affinities in small anionic water clusters.62
B. Particle and hole NTO densities
We target charge-transfer excited states, in which the photo-excited electron has moved from adamantane to water, and where particle and hole are spatially separated. We investigate the lowest-energy states with a charge transfer of at least qw = 0.1e, and for (nearly) degenerate excited states, we choose those with the highest charge transfer on the water. For a direct visualization of the excitations of particles and holes at different segments of the molecules, the natural transition orbital (NTO) analysis65 provides a compact representation independent of the underlying multi-transitional character of excited states. The particle and hole NTO densities derive from the one-particle transition density matrix of the excited state n, | (1) |
 | (2) |
 | (3) |
| ρp/hNTO = |Ψp/hn|2. | (4) |
C. Integrated NTO densities
There are three categories of excited states identified in the adamantane and water system. Depending on the location of the hole and particle NTO densities on water molecules or adamantane, there are water-localized excitations, adamantane-localized excitations, and charge-transfer excitations. The localized excited states have both the hole and particle NTO density on either adamantane or water, while for the charge-transfer excited states, the hole NTO density is on adamantane and the particle NTO density is on one or several water molecules. We focus in this study on those charge-transfer excited states that have a significant amount of charge being transferred from adamantane to water.To quantitatively describe the distribution of particles and holes in various molecules, it is common to calculate the total NTO densities on each atom. There are multiple schemes to determine the volume for each atom to perform spatial integrations. One chemically intuitive and consistent method is the Hirshfeld population analysis.66–70 It assumes that atoms with more electrons occupy a larger space than a few-electron atom. Hence, in a molecule, the atomic contribution to the total NTO density should also be proportional to the volumes defined by the electron density of the individual atoms. The weight function γad/w on adamantane (ad) and water (w) molecules is defined from the electron density ρ0i of the isolated atom i as
 | (5) |
It defines the spatial contribution of NTO densities from the water molecules and adamantane separately. The total integrated particle and hole density of water molecules are then
 | (6) |
| qw = qpw − qhw, | (7) |
D. Electrostatic potentials
The electrostatic potential V(r) is by definition the repulsion/attraction (positive/negative value) experienced by a unit of positive charge at a given position r in the vicinity of a molecule. It is obtained from the Coulomb interaction with the positively charged nuclei at positions RA and the negatively charged electrons at positions r′ as71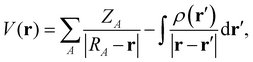 | (8) |
E. Large water cluster conformers from molecular dynamics
To obtain structures of adamantane in a more extended aqueous environment, we perform atomistically resolved molecular dynamics simulations of adamantane in water using the Lammps72 simulation package in combination with the generalized Amber force field (GAFF)73 for organic molecules. The partial charges of adamantane are calculated using the Gaussian09 software63 by employing the B3LYP functional74 with the cc-pVTZ basis set48 using the electrostatic potential fitting method.75 The SPC/E model is used to simulate the water molecules.76 The particle–particle particle-mesh method is used to calculate long-range electrostatic interactions.77 The cut-off lengths of the van-der-Waals and real-space electrostatic interactions are set to 1.2 nm each.We use a cubic simulation box with periodic boundary conditions. The simulation box contains 417 water molecules and a single adamantane molecule in its center. We first equilibrate the system in the NPT ensemble at P = 1 bar and T = 300 K until the total density of the system converges to a value slightly above 1 g cm−3. The temperature and pressure are controlled by a Nose–Hoover thermostat and barostat. The subsequent production simulation is performed in the NVT ensemble for 10 ns with a time step of 1 fs. Meanwhile, the adamantane is retained in the box center by subtracting the center-of-mass velocity of the adamantane from all atoms in the system.
The structures of all water cluster from the DFT calculation are optimized at 0 K. Therefore, they are the minimum structures each with many hydrogen bonds. However, at room temperature, due to the thermal fluctuations, water can have more configurations with broken hydrogen bonds. The eruption of the hydrogen bond networks provides a trap for the electron that can form the cavity-bound state.20 To purposely simulate a cavity-bound state where water molecules can encapsulate an electron, a single negative point charge is added to the water in the first solvation shell. The Lennard-Jones and Coulomb parameters of the point charge are obtained by fitting the radial distribution function between the electron (represented by the negative charge) and the surrounding water molecules to the results with a real electron from ab initio MD simulations from literature.6
A spherical cut-off centered at the negative charge is used to create a series of cavity-bound states with eight, sixteen, or 32 water molecules adjacent to adamantane. For the thermal-equilibrium water surrounding the adamantane, we apply a spherical cut-off from the center of the adamantane to create a shell of water molecules around the adamantane. These two types of truncated water structures and adamantane are then used for the excited state property analysis using a higher accuracy quantum chemistry method as described in Section IIA.
III. Results and discussion
We present a systematic investigation of the electronic structure and characteristics of the lowest electron-transfer excited state of adamantane adjacent to water clusters of increasing size. The first case is a water monomer (Section IIIA) in all possible combinations of the orientation and position relative to the adamantane surface. For more water molecules, dimer and trimer clusters of various geometries are investigated first without and later including adamantane (Sections IIIB–IIID). Two types of water structures are favorable for the solvated electron. One of those are dipole-bound states with at least one dangling O–H bond of water pointing away from the cluster rather than being part of a hydrogen bond. The other is a cavity-bound state with several OH moieties pointing to the common center. As structures of thermo-equilibrated water fluctuate constantly, the orientation of OH can be random. The MD simulation includes a negative charge, which acts as a reference of the center and constrains the water structure into a cavity similar to that of a solvated electron (Section IIIE). For the non-cavity case, we take snapshots of the first solvation shell from the MD simulation to find possible electron-binding states (Section IIIF).A. Adamantane and a single water molecule
For the setup of different structures with a single water molecule adjacent to adamantane, its position and orientation in each of the conformers is defined according to the first solvation-shell structure of adamantane as reported in previous molecular dynamics studies.78Fig. 1(a) summarizes the selected arrangements in a Cartesian coordinate system, with the CM of adamantane in the origin and one of its C3 axis parallel to the x axis. In each chosen configuration (1–6), the CM of the water molecule is placed in one of the six peaks of the MD water density distribution.78 Moreover, for each position the water molecule takes orientations around the rotation angles α and β as defined in Fig. 1(a) at their distinct values 0°, 90°, and 180°.We start our investigations with the electronic properties of a single water molecule obtained from DFT. The HOMO and LUMO energies obtained are −10.700 eV and 0.1170 eV, respectively. The HOMO energy is approximately the ionization energy of the water molecules, which is in the range of 9.9 eV.79 The LUMO energy is a positive value, which indicates a single water molecule has a negative electron affinity. The result from orbital considerations agrees with the calculated dipole moment, which is 1.88 D, too small for stable binding of an excess electron to form the anionic monomer. The minimum magnitude of the dipole moment is 2.6 D.80 Accordingly, we can anticipate that the electron transfer from the adamantane to a single water molecule will be difficult.
Nonetheless, the magnitude of the electron transfer to the single water molecule is computed for the first CT state in all different positions and orientations as indicated in Fig. 1(a). Fig. 1(b) shows the charge transfer towards the respective water molecule qw, calculated as the difference of integrated particle and hole NTO density at the water molecule as defined in eqn (7). The position of the monomer does not have a systematic influence on the electron transfer. Only position 4 is slightly less favorable. On the other hand, the rotation angles show a systematic trend across all positions. Except for position 1, where α = 0° is favorable, α = 180° is most favorable at the other positions. However, the combination of α = 90° and β = 90° always gives the largest electron transfer to the water monomer. That means that here the most favorable configuration has the water dipole moment parallel to the surface of adamantane and one of the O–H moieties is closer to adamantane. On average, the electron transfer to the monomer is qw = 0.18 with a span of 0.13–0.3, which is only a fraction compared to a complete electron transfer (qw = 1). The small charge transfer confirms that a single water molecule is insufficient for the complete binding of an excess electron.
B. Water dimers
For the water dimer, we consider two classes of possible structures. Fig. 2(a) shows the first category of water dimers, which corresponds to geometry-optimized neutral and anionic structures with two water molecules connected by a hydrogen bond, taken from the literature.42 The second category corresponds to structures with broken hydrogen bonds as shown in Fig. 2(b) and (c). In (b) the four high-symmetry structures are termed by their symmetry groups D2d, C2h C2h* are constructed by fixing the CM distance of the two water molecules to the averaged water–water distance in bulk water (2.85 Å).81 Similar structures with the same CM distance and random orientations of the water molecules are shown in Fig. 2(c). | ||
| Fig. 2 Structures of the isolated water dimers and their respective symmetries. (a) Hydrogen-bonded structures from Kim et al.:42 CsT, CsI, and CsC are geometry-optimized anionic dimer structures, “Neutral” represents the most stable dimer without an excess electron for which different structural angles are defined. (b) Water dimers without hydrogen bonds. D2d, C2h, and C2v indicate symmetric structures taken from the literature,42C2h* was created in this work. (c) Random structures with the two non-hydrogen-bonded water molecules in arbitrary configurations. | ||
For the anionic and neutral dimers (a), the intra- and intermolecular O–H bond lengths are approximately the same and there are only minor differences in the H–O–H angles of around 0.3° for each water molecule.42 However, the presence of an excess electron affects the water molecules’ relative orientation, leading to three different conformers among which the CsC has the lowest energy and is therefore the energetically most favorable anionic dimer structure.
The dimers with hydrogen bonds are the smallest and yet most abundant water structures that allow for dipole-bound states82 to trap a solvated electron. Going from left to right in Fig. 2(a), they have increasing net dipole moments pointing from the O–H bond of one water molecule to the oxygen atom of the other molecule along the hydrogen bond. The proton donor has an O–H bond pointing slightly off the inter-oxygen axis, while the proton acceptor has a larger torsional angle (Ψ), which can vary in a large range and thus create different conformers in a Cs symmetry. For example, the neutral conformer has Ψ = 57°, while the trans (CsT) and cis (CsC) anionic dimers have Ψ = 38° and γ = −26°, respectively. The conformer CsI represents a transition state between CsT and CsS, which are two local stable states on the potential energy surface.42
The LUMOs of neutral water clusters appear to be crucial for capturing the excess electron. To provide a visual understanding of the LUMO shapes and their connection with the structure of six different dimers, Fig. 3 collects LUMOs and their orbital energies εL. Total dipole moments are listed, indicating the nature of a cavity in the CT state. Finally, on the right-hand side, the electrostatic potentials as defined in eqn (8) are depicted together with their maximal value Vm. Already from visual inspection, it can be observed that the distribution of the LUMO has a high correlation with the electrostatic potential, i.e., it has a large value, where there is also a high electrostatic potential value. For example, the zero-dipole dimers C2h and D2d show the localization of the LUMO between the water molecules’ hydrogen atoms, which creates a positive electrostatic potential trap in the middle. We can thus identify these structures as hosting cavity-bound states. For the dipole-bound states, namely the CsT, CsI, and CsC dimer with the respective total dipole moments of 3.57, 3.95, and 4.30 D, a positive electrostatic potential arises at each dangling hydrogen atom of the O–H bond. Likewise, the LUMO accumulates at the same position.
C. Water trimers through pentamers
To further verify the relation between the LUMO energies, electron affinities, and electrostatic potential in water clusters, we continue this analysis for increasingly larger clusters starting with three water molecules. Fig. 4 shows the detailed properties of different types of trimers. First, we consider the high symmetry structures with a center of inversion. Then there are the ones with three rotation axes, namely the 3Ic3h and one with three dihedral axes denoted as 3Id3d. The two structures on top represent cavity-bound states with all hydrogen atoms pointing to a common center. For the dipole-bound states with the three water molecules in a line (denoted 3L), the direction of the dipole is either perpendicular to (3Laa, 3Ldd) or along (3Lda) the chain of the hydrogen bonds. In the 3Rda dipole-bond state, the dipole moment points vertically away from the plane of the ring-like water structure as the dangling O–H all point to the same side. For all the bound states, the shapes and positive values of the LUMO (central graph) agree with those of the electrostatic potential (right). As already observed in the previous section, higher maximal electrostatic potential values Vm correspond to lower LUMO energies εL and to stronger electron affinities EA. The 3Rda* structure is the only non-bound state as the O–H bonds point in all directions, below or above the plane or in the plane level. Consequently, the structure has only a small net dipole moment, which manifests in the absence of a positive electrostatic potential center. When considering the ring structures 3Rda* and 3Rda and their relation to all other structures, they have the largest number of hydrogen bonds and have the lowest likeliness of accepting an extra electron (lowest, even negative EA). Therefore, the breaking of the hydrogen bond is the key to forming a bound state. This was likewise observed for larger clusters (tetramers and pentamers) as can be seen from the figures in the appendix.The negative correlation between the LUMO energy and the electron affinity found for water dimers and trimers also holds for dipole- and cavity-bound states in larger water clusters, as we observed in tetramers and pentamers. Detailed information about four- and five-molecular structures including the respective dipole moments, electrostatic potentials, and LUMO energies, are given in the appendix. Fig. 5(a) shows for all these cluster sizes that the LUMO energy has a negative correlation with the electron affinity. It is stronger for dipole-bound states represented by black squares and weaker for cavity-bound states (red triangles). The sign change of the LUMO energy indicates whether it can form a bound state for the electron. Moreover, the positive LUMO energies correspond to the structures that have negative electron affinities.
The increase of the electron affinity is closely related to the enhanced positive electrostatic potential due to two factors: broken hydrogen bonds and the orientation of the dangling O–H parallel to one another or pointing towards a common geometric center. Consequently, the electrostatic potential creates a trap for the photo-excited electron. To verify the above analysis, Fig. 5(b) shows the electron affinity as a function of the maximum of the electrostatic potential, which increases nearly linearly with one another. The increase, however, follows a weaker trend in cavity-bound states, which are no equilibrium structures.
DFT is notably sensitive to the choice of functional. For all small water clusters, we have re-calculated some properties with ORCA using the B3LYP and the range-separated hybrid functionals LC-BLYP, ωB97X, and ωB97X-D3. The latter is a modified version of the ωB97X functional, which includes dispersion correction as part of the functional. Fig. 6 shows the calculations of the differences of the various physical properties obtained from the tested functionals versus the CAM-BLYP functional. The comparison is in the form of averaged values and standard deviations across all small water clusters. The results show orbital energies of (a) HOMO and (b) LUMO, as well as the (c) HOMO–LUMO gap and the amount of charge transfer (d). Our findings can be summarized as follows: the long-range corrected ωBX97, ωBX97-D3, and LC-BLYP functionals tend to give higher LUMO energies (about +0.8 eV), lower HOMO energies (about −0.7 eV), and hence larger HOMO–LUMO gaps (around 1.5 eV). The amount of charge transfer, qw, employing Hirshfeld charges with these three functional is about 0.2e lower in average, while showing a broader distribution along the structures. For the B3YLP functional, which is known to be not suitable for CT processes, we observe the opposite trends: an increase of the HOMO energies (+1.8 eV) and a decrease of LUMO energies (−0.7 eV) as well as HOMO–LUMO gaps (−2.5 eV), while our prediction of the charge transfer increases by +0.3 e on average. The orbital shapes, however, remain largely the same. As an example, Fig. 6(e) shows the similarity of the HOMO and LUMO orbitals for a water dimer adjacent to adamantane for all used the functionals.
 | ||
| Fig. 6 Comparison of water-cluster properties obtained by different functionals. Shown for the functionals B3LYP, LC-BLYP, ωB97X, and ωB97X-D3 are the (a) HOMO, (b) LUMO, and (c) HOMO–LUMO gap energies, and (d) charge transfer, qw, in terms of the averaged values and their standard deviation over all cluster structures of the manuscript and, for comparison, plotted as the differences to the CAM-B3LYP results. The HOMO and LUMO orbitals of all functionals are shown in (e) along with their energies exemplarily for the CsI water cluster adjacent to adamantane. The isovalues for all plots are the same as in Fig. 3. | ||
D. Charge-transfer states of adamantane and small water clusters
To analyze the character of the charge-transfer states, we investigate here water dimers and trimers in the vicinity of an adamantane molecule. We commence by placing the CM of different water dimers at position 1 relative to adamantane (cf.Fig. 1), then compute the excited states via TDDFT, inspect the NTO densities, and select the first excited state with hole NTO density on adamantane, i.e., the lowest-energy state in which an electron is removed from the nanodiamond. Fig. 7 shows the respective NTO densities of holes (bottom panels) and particles (upper panels). For all dipole- and cavity-bound states displayed, the electron NTO density is located at the positive electrostatic region of the water dimer as was shown in Fig. 3 Since the shape of the electrostatic potential and the LUMO are very similar, the shape of the electron NTO density also resembles that of the LUMO of the isolated water dimer. This clearly shows that the charge transfer has a distinct character from the HOMO of adamantane to the joint LUMO of the neighboring water molecules. Contrary, the non-bound water dimer C2h* with its positive electron affinity does not attract an extra electron from adamantane. The main reason is that the electrostatic negative potential of the two oxygen atoms facing one another pushes the particle NTO density to the opposite side of adamantane.So far, we can summarize that each charge-transfer state shows a shift of electron density from the HOMO of adamantane to the water cluster's LUMO, which has a clear connection with the electron affinity and the electrostatic potential of the respective water dimer. For an energy consideration regarding the orbitals involved in the charge-transfer states, Fig. 8 collects the HOMO and LUMO energies of adamantane and of the water dimers in the C2h and CsC configurations, which are both placed near adamantane, but at different positions 1 and 6 alternating in the two subfigures. Due to the overall lowest LUMO energy of the C2h dimer, the lowest-energy CT states of both assemblies reveal that the particle NTO density prioritizes the C2h dimer, which also has the highest electrostatic potential. This electron transfer is independent of the relative positions of the water clusters to adamantane.
Other studies report on small anionic water clusters that reflect the situation after successful transfer of an electron without the notion of the source of a trapped electron. The spin density of the additional electron shown by Taylor et al.,43 as well as the HOMO shape of the anionic water clusters obtained by Kim et al.42 have similar distributions as obtained by us, cf.Fig. 3, 4 and 7. In particular, the solvated electron can be regarded as a pseudo-atom in the cavity of small water clusters.43 This agrees with our observation that the cavity-bound state of the C2h and D2d water clusters have a somewhat higher charge transfer capacity, as shown in Fig. 6. This has its origin in the higher electrostatic potential (0.124 eV for C2h and 0.112 eV for D2d) at their centers, compared to the other water clusters, CsT (0.088 eV), CsI (0.089 eV), CsC (0.091 eV), and C2h* (0.058 eV).
To further verify that the charge-transfer states incorporate transitions from the HOMO of adamantane to the LUMO of water and that they are independent of the relative positions of the water clusters at equal CM distance, Fig. 9 compares exemplarily arrangements of the non-bound 3Rda* trimer, the dipole-bound trimer 3Ldd, and the likewise dipole-bound dimer CsC around the adamantane molecule. The lowest charge-transfer state locates the excitation of the particle on the 3Ldd trimer, which has the lowest LUMO energy of the three water clusters irrespective of the relative water cluster positions.
To quantify the transfer of charge to water clusters with different LUMO energies, Fig. 10(a) displays the magnitude of the charge transfer given by qw, the difference of integrated NTO densities of particle and hole on the water dimers and trimers, which is plotted against the LUMO energy difference between the respective water cluster and adamantane. The difference of energies is always negative or zero. The general trend is that when the LUMO energy of the water cluster is lower than that of adamantane, the magnitude of charge transfer increases. Inversely, if the LUMO energy of water is equal or larger than the LUMO energy of adamantane, then there are no charge-transfer states.
 | ||
| Fig. 10 (a) Difference of the integrated particle and hole NTO density qw (eqn (7)) on the water cluster of indicated size versus the LUMO energy differences between the water cluster and adamantane. (b) Energies of each first charge-transfer excited state that has the hole NTO density only on adamantane versus the energy differences between the LUMO of the different water clusters and the HOMO of adamantane. For both figures, the black squares represent the dipole-bound states and the red triangles represent the cavity-bound states. | ||
Furthermore, Fig. 10(b) shows that the excited-state energy of the lowest-energy charge-transfer state of the investigated structures (ordinate) is proportional to the energy differences between the LUMO of the water cluster and the HOMO of adamantane (abscissa). This demonstrates that the charge transfer is from the adamantane's HOMO to the water's LUMO. As discussed in the previous section, the LUMO energy has a high correlation with the electron affinity, therefore, the charge transfer should also be proportional to the electron affinity and the maximum electrostatic potential of water molecules.
E. Cavity-bound states in larger water clusters
As pointed out in the literature, a cavity-bound state in a realistic water environment only forms in large water clusters with dozens of water molecules for energetic reasons.83 To obtain such a state and analyze its stabilization by increasing cluster sized, we run a classical MD simulation in which we introduce a negative (classical) point charge in the first layers of the solvation shell. The point charge creates a stable cavity that is easily visually identified over all MD time steps. Therefore, only an arbitrary snapshot is selected when the total system is in equilibrium. Spherical cutouts from the MD, representing larger water clusters than the ones studied in the previous section, with eight, sixteen, and 32 water molecules around the negative charge are analyzed to consider the size effect of the cavity-bound state.Fig. 11 shows in the first column the LUMOs of the water's cavity for increasingly large water clusters. The second column shows the lowest excited state properties and the charge transfer from the adamantane to the water cavity, including the NTO density for particles and holes and the corresponding excitation energies. When the size of the sample is increased from eight to 32, the LUMO energies decrease from −1.230 eV, over −2.540 eV to −3.391 eV, which is mainly due to the quantum-size effect.84 Likewise, the excitation energies for the first charge-transfer states decrease from 5.271 eV over 5.208 eV to 4.531 eV. Together with the increasing hole NTO density on adamantane (0.93, 0.97 to 0.99) this suggests that the charge transfer to the water molecules is more efficient for the increased size of the water cluster. The electron NTO densities in all cases are (nearly) unity on the water molecules and its shape resembles the LUMO of the water cavity.
The MD snapshots of water molecules reveal some prominent features of the cavity-bound state in the water environment. The most nearby water molecules are arranged such that the dangling H atoms point to the center of the cavity owing to the presence of the extra charge. When adding water molecules near the center (e.g. the third water molecule from the top in Fig. 11(b) or the inner one at the 8 o’clock position in (c)), they also orient their dangling O–H bond into that center. Therefore, the maximum electrostatic potential rises with the number of water molecules contributing to the cavity. According to the previous conclusions from small water clusters, the enhanced electrostatic potential always leads to lower LUMO energies and stronger electron affinity, which means the trap is also energetically deeper for the solvated electron. Note that most of the additional atoms do not engage in the formation of the cavity, but incorporate into the hydrogen-bond network of the surrounding. This suggests a stabilization of the cavity with more water molecules, even if they are not strictly part of the cavity, i.e. if they do not have dangling H atoms pointing to the cavity center. Instead, the water molecules will give rise to additional hydrogen bonds that bind water molecules together so that the water molecules hosting the cavity are more difficult to repel one another.
However, the cavity-bound state created by the negative charge is an idealized structure representing a situation in which only the electron has already been released from adamantane and transferred to the water environment. For studying a charge transfer situation in the water shell before the final solvation of the electron, we study the weakly-bound trap states in extended, and thus more realistic, water environments and find the corresponding charge-transfer states as discussed in the following.
F. Dipole-bound states in extended water environments
Although the long-range structure of bulk water is dominated by an extended hydrogen network, the formation of dipole-bound states is possible due to thermal fluctuations. With the constant motion of water molecules, the conduction band minimum rises and falls around −0.4 to −0.8 eV.36,79 Therefore, there are times when the water structures form a trap for the electron with an energy below the average CBM. These low energies may be connected with broken hydrogen bonds, which can in principle either be parallel or directed towards a common center of all dipole moments, where the latter are also features of the cavity-bound state discussed in the previous section.Around a nanodiamond like adamantane, a solvation shell of several layers of water molecules is forming that structurally differs significantly from the structure of bulk water.78 The dipole moments of individual water molecules in the first solvation shells have a higher probability of aligning either in parallel or outwards.85 In addition, the infrared spectra of water-solvated nanodiamonds suggest a broken hydrogen-bond network due to the decrease of the OH bending vibration.86 Therefore, it is interesting to check whether representative water structures in the solvation shell can form a bound state that can trap an electron. By MD sampling with a sufficiently large shell of water molecules, it is possible to take snapshots that include one of these bound states from the water shell surrounding adamantane and study the charge-transfer properties.
To analyze one of the snapshots, Fig. 12(a) shows adamantane and the surrounding water molecules within a radius of 8 Å from the centrally placed adamantane. The size of the water shell is big enough to include the first solvation shell,3 which has a radius around 5 Å. It was created by cutting off the rest of the water molecules in the MD simulation box, which introduces a surface. The presence of a surface is inevitable as the complete inclusion of water is too challenging for the current computational power. Though not existing in an idealized solution, such a surface of water molecules may occur at any water interface. Physically, it can offer a competing trap site for the solvated electron, compared to the inner area of the solvation shell. And indeed, the 4th excited state, which is the first state that shows charge transfer from the adamantane to water, incorporates the surface of the solvation shell, as visualized by the hole and particle NTO density in Fig. 12(a). Panel (b) shows the zoom-in view of the particle NTO density superimposed on the geometries, where the black arrows mark a large number of broken hydrogen bonds. This corresponds to the situation we know from the dipole-bound state for electrons discussed in the previous chapters.
As the surface of the water shell comes from the computation setup and a typical chemical reaction solution would be largely surface free, we investigated if charge-transfer states in the immediate higher energy range exist that do not incorporate the solvation shell surface. Fig. 12(c) shows the particle and hole NTO density of the 20th excited state. The particle NTO densities are now inside the first solvation shell, while the hole NTO densities on adamantane represent the excitation of adamantane as seen in all previous cases. To compare the water structures near this inner bound state, Fig. 12(d) shows the same zoom-in view of the water structure near the particle NTO densities. The water structure here has only a single water molecule with a dangling hydrogen bond. Therefore, the inner bound state for the electron is shallow compared to the surface. The broken hydrogen bond in the hydrogen bond network agrees with the previous study on the electron solvation dynamics, where a single broken hydrogen bond in the hydrogen bond network forms the trap state for the electron at the early solvation stage.20
IV. Conclusion and outlook
This study of excited-state properties of adamantane – a representative of larger-sized nanodiamonds – in water, including a systematic exploration of water structures, provides theoretical insights into the process of generating solvated electrons through photo-excitation. The lowest-energy charge-transfer states have similar features across different conformations in small water clusters. Their holes reflected by natural transition orbital densities are almost identical to the HOMOs of the isolated adamantane while the particle NTO densities strongly resemble the LUMOs of the various isolated water clusters that this study combines with adamantane. Furthermore, the relative LUMO energies for different water clusters are unambiguous indicators for the trends in electron affinities and maximum electrostatic potential values that both increase with smaller LUMO energies. When the LUMO energy is smaller than zero, the small water cluster forms a bound state for the electron, facilitating the charge transfer from the adamantane.We also investigated the charge transfer to a complete hydration shell. For this larger number of water molecules, the photo-excited electron prioritizes sites with dipole- or cavity-bound state character as known in smaller clusters. These sites include broken hydrogen bonds, a high maximal electrostatic potential, and low LUMO energies of the water alone. The information unavailable from our study is whether the photo-excited electron, after leaving the nanodiamond, first propagates along the hydrogen-bonded water network and then gets trapped at one of the bound states with broken hydrogen bonds or whether it immediately transfers to such sites. Hence, future work could include the simulation of the actual solvation process by electron dynamics methods. Ideally, this should involve the translations and rotations of water molecules on an expected only slightly longer time scale. Such a study would require a multi-scale approach at a quantum-mechanical/molecular mechanical (QM/MM) level of theory.
Conflicts of interest
There are no conflicts to declare.Appendix
Fig. 14 and 15 | ||
| Fig. 13 Structures and properties of different anionic and neutral water tetramers. 4N is the optimized neutral water cluster. 4Lbif is a line of water molecules with parallel dipole moments. 4Y32, and 4Lda are the optimized conformers corresponding to dipole-bound states of the anionic tetramer. The isolvaues and the subfigures are the same as in Fig. 3 and 4. | ||
 | ||
| Fig. 14 Structures and properties of different anionic water tetramers and pentamers with representation parameters as in Fig. 13. | ||
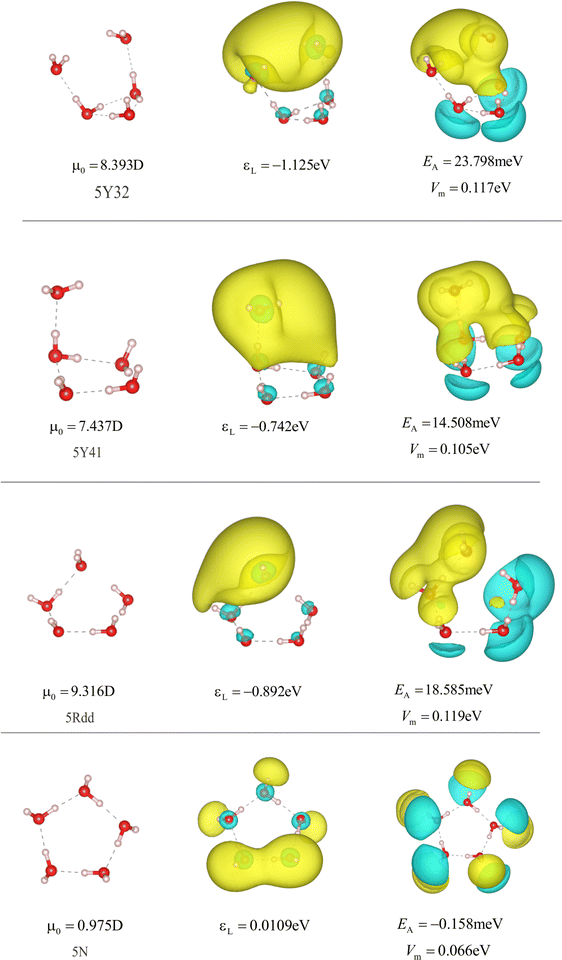 | ||
| Fig. 15 Structures and properties of different anionic and neutral water pentamers. 5Y32, 5Y41, and 5Ydd42 indicate dipole-bound states of anionic pentamers. 5N is the optimized neutral water cluster. Representation parameters are chosen as in Fig. 13. | ||
AIP publishing data sharing policy
The data that support the findings of this study are available from the corresponding author upon reasonable request.Create the reference section using BibTeX:
Acknowledgements
X. W.'s work receives support from the Chinese Scholar Council (CSC). T. K. acknowledges the support from the Helmholtz Einstein International Berlin Research School in Data Science (HEIBRiDS). The computing resources come from the Freie Universität Berlin (HPC cluster Curta87) and the Dirac HPC of the Helmholtz-Zentrum Berlin.References
- E. J. Hart and J. W. Boag, J. Am. Chem. Soc., 1962, 84, 4090–4095 CrossRef CAS.
- D. Luo, K. Nakata, A. Fujishima and S. Liu, J. Photochem. Photobiol., C, 2017, 31, 139–152 CrossRef CAS.
- H. Ou, C. Tang, X. Chen, M. Zhou and X. Wang, ACS Catal., 2019, 9, 2949–2955 CrossRef CAS.
- D. Behar, P. Neta and C. Schultheisz, J. Phys. Chem. A, 2002, 106, 3139–3147 CrossRef CAS.
- A. Kumar, D. Becker, A. Adhikary and M. D. Sevilla, Int. J. Mol. Sci., 2019, 20, 3998 CrossRef CAS PubMed.
- J. Lan, V. Kapil, P. Gasparotto, M. Ceriotti, M. Iannuzzi and V. V. Rybkin, Nat. Commun., 2021, 12, 1–6 CrossRef PubMed.
- S. J. Park and B. J. Schwartz, J. Chem. Theory Comput., 2022, 18, 4973–4982 CrossRef CAS PubMed.
- J. R. Casey, A. Kahros and B. J. Schwartz, J. Phys. Chem. B, 2013, 117, 14173–14182 CrossRef CAS PubMed.
- J. R. Casey, R. E. Larsen and B. J. Schwartz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 2712–2717 CrossRef CAS PubMed.
- A. Kumar, J. A. Walker, D. M. Bartels and M. D. Sevilla, J. Phys. Chem. A, 2015, 119, 9148–9159 CrossRef CAS PubMed.
- H. W. Sternberg, R. E. Markby, I. Wender and D. M. Mohilner, J. Am. Chem. Soc., 1967, 89, 186–187 CrossRef CAS.
- J. Lan, Y.-i Yamamoto, T. Suzuki and V. V. Rybkin, Chem. Sci., 2022, 13, 3837–3844 RSC.
- P. Rumbach, D. M. Bartels, R. M. Sankaran and D. B. Go, J. Phys. D: Appl. Phys., 2015, 48, 424001 CrossRef.
- F. Maier, J. Ristein and L. Ley, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 165411 CrossRef.
- F. Buchner, T. Kirschbaum, A. Venerosy, H. Girard, J.-C. Arnault, B. Kiendl, A. Krueger, K. Larsson, A. Bande, T. Petit and C. Merschjann, Nanoscale, 2022, 14, 17188–17195 RSC.
- B. F. Bachman, D. Zhu, J. Bandy, L. Zhang and R. J. Hamers, ACS Meas. Sci. Au, 2021, 2, 46–56 CrossRef PubMed.
- D. Zhu, L. Zhang, R. E. Ruther and R. J. Hamers, Nat. Mater., 2013, 12, 836–841 CrossRef CAS PubMed.
- L. Zhang, D. Zhu, G. M. Nathanson and R. J. Hamers, Angew. Chem., Int. Ed., 2014, 126, 9904–9908 CrossRef.
- L. Zhang and R. J. Hamers, Diamond Relat. Mater., 2017, 78, 24–30 CrossRef CAS.
- D. Nordlund, H. Ogasawara, H. Bluhm, O. Takahashi, M. Odelius, M. Nagasono, L. G. Pettersson and A. Nilsson, Phys. Rev. Lett., 2007, 99, 217406 CrossRef CAS PubMed.
- M. F. Emde, A. Baltuska, A. Kummrow, M. S. Pshenichnikov and D. A. Wiersma, Phys. Rev. Lett., 1998, 80, 4645 CrossRef CAS.
- J. Savolainen, F. Uhlig, S. Ahmed, P. Hamm and P. Jungwirth, Nat. Chem., 2014, 6, 697–701 CrossRef CAS PubMed.
- R. Laenen, T. Roth and A. Laubereau, Phys. Rev. Lett., 2000, 85, 50 CrossRef CAS PubMed.
- C. Silva, P. K. Walhout, K. Yokoyama and P. F. Barbara, Phys. Rev. Lett., 1998, 80, 1086 CrossRef CAS.
- T. Willey, C. Bostedt, T. Van Buuren, J. Dahl, S. Liu, R. Carlson, R. Meulenberg, E. Nelson and L. Terminello, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 205432 CrossRef.
- N. Drummond, A. Williamson, R. Needs and G. Galli, Phys. Rev. Lett., 2005, 95, 096801 CrossRef CAS PubMed.
- W. L. Yang, J. Fabbri, T. Willey, J. Lee, J. Dahl, R. Carlson, P. Schreiner, A. Fokin, B. Tkachenko and N. Fokina, et al. , Science, 2007, 316, 1460–1462 CrossRef CAS PubMed.
- L. Landt, K. Klünder, J. E. Dahl, R. M. Carlson, T. Möller and C. Bostedt, Phys. Rev. Lett., 2009, 103, 047402 CrossRef PubMed.
- M. Vörös and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 161411 CrossRef.
- T. Kirschbaum, B. von Seggern, J. Dzubiella, A. Bande and F. Noé, J. Chem. Theory Comput., 2022, 19, 4461–4473 CrossRef PubMed.
- N. Brown and O. Hod, J. Phys. Chem. C, 2014, 118, 5530–5537 CrossRef CAS.
- M. Vijayalakshmi and R. Padmanaban, J. Chem. Sci., 2018, 130, 1–14 CrossRef.
- J. L. Teunissen, F. De Proft and F. De Vleeschouwer, J. Chem. Theory Comput., 2017, 13, 1351–1365 CrossRef CAS PubMed.
- T. Berg, E. Marosits, J. Maul, P. Nagel, U. Ott, F. Schertz, S. Schuppler, C. Sudek and G. Schönhense, J. Appl. Phys., 2008, 104, 1247 CrossRef.
- Y. Chang, H. Hsieh, W. Pong, M.-H. Tsai, F. Chien, P. Tseng, L. Chen, T. Wang, K. Chen and D. Bhusari, et al. , Phys. Rev. Lett., 1999, 82, 5377 CrossRef CAS.
- J. Staähler, J.-C. Deinert, D. Wegkamp, S. Hagen and M. Wolf, J. Am. Chem. Soc., 2015, 137, 3520–3524 CrossRef PubMed.
- C. E. Krohn, P. Antoniewicz and J. Thompson, Surf. Sci., 1980, 101, 241–250 CrossRef CAS.
- A. Bernas, C. Ferradini and J.-P. Jay-Gerin, Chem. Phys., 1997, 222, 151–160 CrossRef CAS.
- T. A. Pham, C. Zhang, E. Schwegler and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060202 CrossRef.
- L. Ban, C. W. West, E. Chasovskikh, T. E. Gartmann, B. L. Yoder and R. Signorell, J. Phys. Chem. A, 2020, 124, 7959–7965 CrossRef CAS PubMed.
- D. Madsen, C. Thomsen, J. Thøgersen and S. Keiding, J. Chem. Phys., 2000, 113, 1126–1134 CrossRef CAS.
- J. Kim, S. B. Suh and K. S. Kim, J. Chem. Phys., 1999, 111, 10077–10087 CrossRef CAS.
- A. Taylor, C. F. Matta and R. J. Boyd, J. Chem. Theory Comput., 2007, 3, 1054–1063 CrossRef CAS PubMed.
- J. Wilhelm, J. VandeVondele and V. V. Rybkin, Angew. Chem., Int. Ed., 2019, 58, 3890–3893 CrossRef CAS PubMed.
- M. Pizzochero, F. Ambrosio and A. Pasquarello, Chem. Sci., 2019, 10, 7442–7448 RSC.
- O. Marsalek, F. Uhlig, J. Vandevondele and P. Jungwirth, Acc. Chem. Res., 2012, 45, 23–32 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- S. Klinkusch and J. C. Tremblay, J. Chem. Phys., 2016, 144, 184108 CrossRef PubMed.
- J. Ehrmaier, T. N. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754–4764 CrossRef CAS PubMed.
- S. Kümmel, Adv. Energy Mater., 2017, 7, 1700440 CrossRef.
- F. Weber, J. C. Tremblay and A. Bande, J. Phys. Chem. C, 2020, 124, 26688–26698 CrossRef CAS.
- D. López-Carballeira and T. Polcar, Diamond Relat. Mater., 2020, 108, 107959 CrossRef.
- N. D. Drummond, A. J. Williamson, R. J. Needs and G. Galli, Phys. Rev. Lett., 2005, 95, 096801 CrossRef CAS PubMed.
- C. E. Patrick and F. Giustino, Nat. Commun., 2013, 4, 1–7 Search PubMed.
- P. Han, D. Antonov, J. Wrachtrup and G. Bester, Phys. Rev. B, 2017, 95, 195428 CrossRef.
- T. Kirschbaum, T. Petit, J. Dzubiella and A. Bande, J. Comput. Chem., 2022, 43, 923–929 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- C.-G. Zhan, J. A. Nichols and D. A. Dixon, J. Phys. Chem. A, 2003, 107, 4184–4195 CrossRef CAS.
- E. Vandaele, M. Mališ and S. Luber, J. Chem. Phys., 2022, 156, 130901 CrossRef CAS PubMed.
- J. M. Herbert and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 5217–5229 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- B. Baranyi and L. Turi, J. Chem. Phys., 2019, 151, 204304 CrossRef PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- R. J. MacDonell, S. Patchkovskii and M. S. Schuurman, J. Chem. Theory Comput., 2022, 18, 1061–1071 CrossRef CAS PubMed.
- F. Bauch, C.-D. Dong and S. Schumacher, J. Mater. Chem. C, 2023, 11, 12992–12998 RSC.
- J. Carmona-Espndola and J. L. Gázquez, Theor. Chem. Acc., 2022, 141, 1–10 Search PubMed.
- M. Orozco and F. J. Luque, Theoretical and Computational Chemistry, Elsevier, 1996, vol. 3, pp.181–218 Search PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- R. Hockney and J. Eastwood, Computer simulation using particles (Bristol: Hilger), Section 6–5–2, 205 technical report, 1988.
- M. Ohisa and M. Aida, Chem. Phys. Lett., 2011, 511, 62–67 CrossRef CAS.
- A. P. Gaiduk, T. A. Pham, M. Govoni, F. Paesani and G. Galli, Nat. Commun., 2018, 9, 1–6 CrossRef CAS PubMed.
- E. Fermi and E. Teller, Phys. Rev., 1947, 72, 399 CrossRef CAS.
- C. Schran and D. Marx, Phys. Chem. Chem. Phys., 2019, 21, 24967–24975 RSC.
- M. Armbruster, H. Haberland and H.-G. Schindler, Phys. Rev. Lett., 1981, 47, 323 CrossRef CAS.
- T. Sommerfeld, J. Chem. Phys., 2007, 126, 024307 CrossRef PubMed.
- A. I. Ekimov, A. L. Efros and A. A. Onushchenko, Solid State Commun., 1985, 56, 921 CrossRef CAS.
- K. Palczynski, T. Kirschbaum, A. Bande and J. Dzubiella, J. Phys. Chem. C, 2023, 127, 3217–3227 CrossRef CAS.
- T. Petit, L. Puskar, T. Dolenko, S. Choudhury, E. Ritter, S. Burikov, K. Laptinskiy, Q. Brzustowski, U. Schade and H. Yuzawa, et al. , J. Phys. Chem. C, 2017, 121, 5185–5194 CrossRef CAS.
- L. Bennett, B. Melchers and B. Proppe, Curta: A General-purpose High-Performance Computer at ZEDAT, Freie Universität Berlin, Freie Universität Berlin, Germany, 2020 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04602h |
| This journal is © the Owner Societies 2024 |









