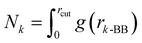Modulation of Aβ 16–22 aggregation by glucose

Abstract

The self-assembly of amyloid-beta (Aβ) peptides into fibrillar structures in the brain is a signature of Alzheimer's disease. Recent studies have reported correlations between Alzheimer's disease and type-2 diabetes. Structurally, hyperglycemia induces covalent protein crosslinkings by advanced glycation end products (AGE), which can affect the stability of Aβ oligomers. In this work, we leverage physics-based coarse-grained molecular simulations to probe alternate thermodynamic pathways that affect peptide aggregation propensities at varying concentrations of glucose molecules. Similar to previous experimental reports, our simulations show a glucose concentration-dependent increase in Aβ aggregation rates, without changes in the overall secondary structure content. We discovered that glucose molecules prefer partitioning onto the aggregate–water interface at a specific orientation, resulting in a loss of molecular rotational entropy. This effectively hastens the aggregation rates, as peptide self-assembly can reduce the available surface area for peptide–glucose interactions. This work introduces a new thermodynamic-driven pathway, beyond chemical cross-linking, that can modulate Aβ aggregation.

---

1 Introduction

Accumulation of peptides and protein-based deposits in neuronal membranes is associated with several neurodegenerative pathologies such as Alzheimer's disease (AD).¹ This condition is characterized by progressive cognitive decline and is currently recognized as a major socio-economic concern around the world. AD is a complex disease, marked by aggregates of Aβ and tau peptides, with consensus among researchers that aggregation of Aβ peptides is an upstream phenomenon among a cascade of steps leading to neuronal death.^2,3 The Aβ peptide is commonly 40–42 residue long fragments cleaved from the amyloid precursor protein (APP) by β-secretase and γ secretase.² While Aβ peptides can aggregate into large deposits and plaques, recent evidence has suggested that the smaller oligomers are the primary toxic species.^1,4 In a physiological environment, several external factors can contribute to variations in Aβ aggregation behavior.^5–7

Several studies have suggested pathological correlations and epidemiological linkages between a very common metabolic disease, type II diabetes (T2D) and Alzheimer's disease.^8–11 T2D involves the development of cellular insulin resistance, leading to improper sugar/glucose metabolism and high blood sugar/glucose concentrations. Recent fMRI studies have suggested a decline in the cognitive performance of patients suffering from T2D.¹¹ Another study suggested that patients with T2D have a 50% higher chance of developing AD.⁸ However, the mechanistic event pathways of this correlation are still not clear. Although numerous experimental and computational studies have investigated changes in Aβ conformations and aggregation in aqueous environments,^12,13 studies investigating the structures of Aβ-peptide aggregates and glucose-induced peptide aggregation at elevated concentrations of glucose in the case of T2D are limited.¹⁴

Previous research efforts have postulated post-translational glycation (advanced glycation end products – AGE) related increased aggregation as a possible pathological pathway correlating AD and T2D.^15–17 These covalent modifications stabilize peptide aggregates against degradation, thereby linking them to neuronal dysfunction. However, in vitro studies have reported that AGE formation can take up to a month (with incubation) at very high concentrations of glucose. AGE formation has not been reported at the early stages of Aβ aggregation.¹⁸ Experiments involving cellular culture have revealed the upstream effects of glucose on the production of Aβ peptides and the prevention of the degradation of amyloid precursor proteins.¹⁹ Glucose also induces structural changes in peptide aggregates and alters their interactions with physiological structures. A recent experiment by Kedia et al. has suggested that the presence of glucose molecules can lead to the faster formation of toxic, unstructured and membrane-active oligomers that are probably taken up by the cells and interfere with mitochondrial activity.¹⁸

Co-solutes modulate protein folding and peptide aggregation pathways, prompting the use of simple saccharides as macromolecular crowding agents.^20–22 They are often used to simulate cell-like crowded conditions in in vitro experiments. Several experimental, computational and theoretical studies have outlined the effects of such crowded conditions, from altering the thermodynamic phase space to modulating the kinetics of processes.^23–26 This poses the question of whether there are thermodynamic pathways that can explain the behavior of Aβ peptides in hyperglycemic conditions, beyond our current understanding of covalent modifications.

Computational studies on Aβ peptides under hyperglycemic conditions are limited. A recent atomistic molecular dynamics study with a beyond-physiological (∼800 mM) glucose concentration and Aβ 1–42 revealed a caging effect of glucose molecules on peptide monomers and dimers, which led to increased hydration of protein structures.²⁷ A complete biophysical picture of peptide aggregation shaped by hyperglycemic conditions is missing because in atomistic simulations, due to timescale constraints, only small-sized oligomers can be characterized²⁸ whose formation kinetics and secondary structures are strongly dependent on the forcefield used.²⁹

In this work, we adopt coarse-grained molecular dynamics simulations to investigate the aggregation behavior of Aβ 16–22 peptides under hyperglycemic conditions. Aβ 16–22 peptide is recognized as one of the smallest fragments capable of forming fibrillar structures, which has prompted research studies using this segment as a template.^30–33 With coarse graining, we reduce the number of interaction centers in our simulation system to access spatio-temporal scales that are not typically accessible by traditional atomistic molecular dynamics simulations. Here, we have used the in-house developed coarse-grained protein model, water-explicit polarizable coarse-grained model (WEPCGM) that can capture protein's secondary structural transitions starting from a primary sequence of amino acids, specifically in the presence of external stimuli.^34–37 The coarse-grained model can reproduce cross-beta-like Aβ 16–22 aggregate structures in an aqueous solution and ordered membrane-adsorbed beta-sheet aggregates in the presence of model membranes.^36,38 In this article, we present the unique structural features of Aβ 16–22 and glucose co-aggregates and discuss the mechanistic perspectives of glucose-accelerated Aβ aggregation.

2 Methods

2.1 Peptide and glucose model

The Aβ fragment K₁₆LVFFAE₂₂ was modeled with the in-house WEPROM forcefield,³⁹ where each residue was modeled with a backbone (BB) bead and sidechain beads. A brief outline of the protein coarse-grained model is presented here. The coarse-grained interaction centers (beads) were defined with chemical specificity corresponding to the atoms that they represented. The bead types in the CG model can be broadly classified into polar, hydrophobic and charged beads, with specific interactions between each bead type (Fig. S1, ESI†). While most of the bead types and interaction levels in WEPROM are identical to those in MARTINI, there are two noticeable differences between them. First, polar beads feature explicit off-center drude-like charges attached to the bead center, which couple environmental effects to the protein's structure through electrostatics. Second, the interactions between hydrophobic beads and solvent beads were scaled down to enable β-sheet folding.³⁴ The peptide backbone was exclusively created with this polar CG bead type. The side chains are specific to each amino acid type, with two hydrophobic beads for phenylalanine and one each for valine and leucine. The side chains for the charged amino acids lysine and glutamate were modeled with one hydrophobic and one charged bead. We refer readers to previous publications for details on the CG model.^34–36

The CG model for glucose molecules used in this work was borrowed from the MARTINI forcefield.^40–42 The glucose molecule has carbons numbered C1–C6 starting from the aldehyde group. Carbons C1 and C2 and their associated oxygen atoms are mapped to the CG interaction site B3, C3 and C4 are mapped to B2 and C5 and C6 are mapped to B1. The sites B1, B2 and B3 are all constrained together to form a planar, triangular shape representing glucose in its cyclic closed form (both α and β anomers). Dummy charges are added to each CG bead of the glucose molecule to incorporate molecular polarizability and directional hydrogen bond capabilities (Fig. 1). The charges on the dummy particles are parameterized to match the dipole moment of the glucose molecule. The MARTINI polarizable water model⁴³ was used to represent CG water in our simulations.

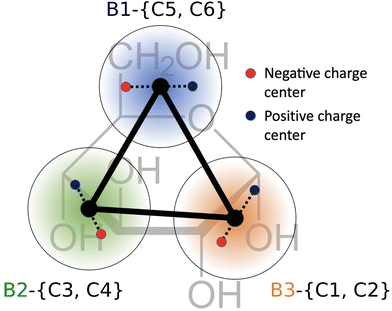Fig. 1 Geometry of the glucose molecule. The atomistic numbering is in black, and the corresponding coarse-grained numbering is shown in color.

Details on the bonded and nonbonded interaction parameters in the peptide can be found in Sahoo et al.³⁶ Most of the cross-interaction parameters were primarily borrowed from the MARTINI model with the polar–polar and polar–charged interactions being scaled down to account for the increased Coulomb interactions because of the added dipoles. We have curated these cross-interaction terms as tables in the ESI† section (Tables S1 and S2). To verify the fidelity of the glucose–glucose and glucose–water interactions in polarizable water, we calculated the second virial coefficient, B₂₂, of the osmotic pressure, which is a measure of deviation from ideal solutions and compared it with experimental measurements. To calculate B₂₂, we followed the simulation protocol outlined by Schmalhorst et al.⁴⁴ wherein a simulation box of (19)³nm³ was created with 420 randomly placed glucose molecules and then solvated with Martini polarizable water. Then, an approximate strategy is followed to derive B₂₂ using the radial-distribution function g(r) and cumulative number distribution function N(r′) developed by Schmalhorst et al.⁴⁴ We obtained an average B₂₂ value of 0.084 (±0.04) L mol⁻¹, close to the reported experimental B₂₂ for glucose (0.117 L mol⁻¹)⁴⁵.

2.2 Simulation setup

The concentration of Aβ was constant at around 33 mM while the concentration of glucose ranged from 0, 0.31, 1.55 to 3.10% (w/v). In a cubic periodic box, 100 molecules of Aβ 16–22 and 0, 60, 300 and 600 molecules of glucose were placed randomly. Each box was solvated with around 42000 CG water beads. The 0% glucose system containing only Aβ peptides and water particles serves as a reference system while the three different glucose compositions (0.31, 1.55, and 3.10% (w/v)) were created for analyzing the effect of increasing glucose concentration on Aβ aggregation. Fig. S2 (ESI†) displays sample snapshots of the peptide aggregation trajectory at various time steps for 1.55% glucose. The glucose concentrations used in this work are higher than the physiological levels to expedite the aggregation process. Using higher than physiological concentrations is common in simulations, and similar approaches have often been leveraged by the MD community to study the aggregation process as it reduces the time between diffusion-controlled protein encounters in computer simulations.^46–49

The initial configurations were energy minimized and equilibrated for 5 ns (time step of 10 fs) with constant volume ensemble. A temperature of 300 K was maintained using a Nose–Hoover thermostat with a time-constant of 1 ps. A subsequent production simulation was run with a constant pressure ensemble using a Parinello–Rahman barostat⁵⁰ (time constant, τ = 1 ps, compressibility, 3 × 10⁻⁵/bar and isotropic pressure coupling at 1 bar). Long range electrostatics were computed using the particle mesh Ewald (PME) method^51,52 with a relative dielectric constant of 2.5 and a cutoff distance of 1.6 nm. The GROMACS shift scheme was used to modify the Lennard-Jones interactions, starting from the original value at 0.9 nm to 0 at 1.2 nm. Two independent replica simulations with a random set of initial velocities were performed for all the glucose concentrations.

2.3 Analysis

An Aβ aggregate is characterized by two or more peptides having at least one backbone (BB-BB) contact. A backbone contact is defined using an interaction cut-off of 7 Å between the backbone beads (the distance cutoff is obtained via the radial distribution function between BB beads, as shown in Fig. S3, ESI†).

We quantified the structure of these peptide aggregates using a β-sheet and a α-helical fraction metric. Peptides are considered as part of the β-sheet if they have at least three continuously aligned backbone dipoles, similar to the metric applied in previous papers to quantify ordered aggregation³⁸ (Fig. S4(a), ESI†). These aligned dipoles can be considered analogous to the interacting dipoles involved in hydrogen bonding.

For the α-helical fraction, we calculated the backbone dihedral angle of the peptides. We classified each backbone dihedral as a α helical turn if the dihedral angle was within a tolerance of 15 degrees from 50.4 degrees, which corresponds to the Cα dihedral turn in α helices as surveyed from PDB³⁷ (Fig. S4(b), ESI†). The proportion of such helical backbone dihedral turns per peptide was then averaged over all the peptides per time-frame to yield the α-helical fraction.

We report the relative enrichment of glucose molecules as a function of the distance from the peptide aggregate calculated as follows:

Here, N_i and N_ow are the total number of species i and water molecules, respectively, while n_i(r) and n_ow(r) are the number of species i and water molecules present at a distance r from the atoms of the protein aggregate. This metric has been used to study the solvation effects of proteins and protein aggregation.^53–56 Here, we compared the relative enrichment of different parts of the glucose molecule (B1, B2 and B3) near the peptide aggregates.

Finally, we also quantified the total molecular entropy change (ΔS) caused by the interaction of the glucose molecules with the peptide aggregate. To that end, we first characterized glucose CG sites as interacting if they were present within the first coordination shell (r_cut ∼ 7 Å) of the aggregate, as measured by the radial distribution function between the peptide backbone (BB) and a specific glucose CG site (a)—g(r_a-BB). We calculated P_a as the probability of the site being identified as interacting.

where

Considering a simple rotating three-bead coarse-grained molecule, this approach allows us to calculate the absolute rotational Gibbs entropy of the interacting glucose molecule.

Now, for a freely rotating glucose molecule, all the CG interaction sites would have an equal probability of interaction with the aggregate 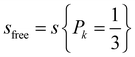, which we leveraged for the calculation of the total loss in rotational entropy.

ΔS = 〈N〉·(s{P_k} − s_free),

where 〈N〉 is the average number of glucose molecules interacting with the peptide.

A similar analysis was performed to calculate the change of the total molecular rotational entropy of glucose molecules in bulk water. Bulk water was defined as the region beyond a distance of 12 Å from the peptide backbone (BB) beads. This distance cutoff was determined from the second minima of the radial distribution function between the peptide backbone beads and the CG interaction sites of the glucose molecule, as shown in Fig. S7(b) (ESI†).

3 Results and discussion

3.1 Impact of glucose on Aβ 16–22 aggregation

To characterize the effect of glucose on peptide aggregation, we analyzed peptide aggregate size in simulations with varying glucose concentrations. Fig. 2(a)–(d) shows the time evolution of the weighted average size of peptide aggregates for different glucose concentrations. Data for the independent simulations are included in the ESI† (Fig. S5). We observed large aggregates with all peptides involved (snapshots – Fig. S2(d), ESI†) for all simulations across all glucose concentrations. In our simulations, due to the high concentration of Aβ peptides (∼33 mM), there was a fast initial growth of aggregate sizes in all simulation systems. We observed a concentration dependence in peptide aggregation kinetics, with fast complete aggregation at increased glucose concentrations and slower evolution for reduced ones. We fitted a curve to Fig. 2(a)–(d) to obtain t_half values for various glucose concentrations to evaluate the correlation between the aggregation kinetics and the concentration of glucose molecules. t_half is defined as the time required to reach an aggregation size equal to half of the total number of peptides in the simulation. Table 1 shows the values of t_half for various concentrations of glucose molecules. We observe that t_half decreases as glucose concentration increases, with the value plateauing around 160 ns for the two higher concentrations, probably due to the correlation reaching a threshold at 1.55% glucose. This correlation between increased hyperglycemia and Aβ fibrillation has been previously noted in experiments by Kedia et al.¹⁸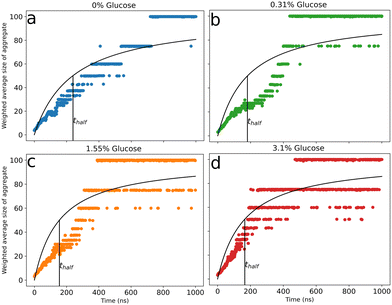

Fig. 2 Evolution of the weighted average size of peptide aggregates for 0% (a), 0.31% (b), 1.55% (c), and 3.10% (d) glucose (w/v). Data are the weighted mean of the three replicates and are fitted with a curve to obtain t_half (time required to reach an aggregate size equal to half of the total number of peptides) for various percentages of glucose. The data for the three independent simulation runs are presented in the ESI.†

Table 1 Values of t_half for various concentrations of glucose molecules

% Glucose (w/v)	t half (ns)
0	239 ± 5.2
0.31	181 ± 6.0
1.55	155 ± 4.8
3.10	165 ± 3.9

---

The glucose molecules are predominantly concentrated at the interface of the aggregate, forming a cage-like structure at a distance of about 5–7 Å, with glucose exchanges between the interface and the bulk solvent (Fig. S2(d), ESI†), similar to the organization suggested by Menon et al. in their atomistic study with Aβ 1–42. Such organization of glucose molecules can influence local environmental alterations.²⁷ However, contrary to experimental reports by Kedia et al.,¹⁸ the authors here reported a decrease in protein dimerization because of the co-solvated glucose. This could be attributed to the significantly higher concentration (800 mM) coupled with the slow kinetics in atomistic simulations. Slower peptide and aggregate diffusion can result in fewer peptide–peptide interactions, which are necessary for an increase in the aggregate size. Such diffusion-limited peptide aggregation behavior has been noted in previous research on macromolecular crowding and aggregation.²⁴

3.2 Secondary structure in protein aggregates

We analyzed the secondary structure content in our protein aggregates and tracked their growth over time. There is a quick gain in ordered structures at the start of the simulation, followed by a β-sheet content close to 0.4–0.5 and a α-helical content close to 0.05–0.10. This trend in the amount of ordered β-sheets (Fig. 3(a)) and α-helices (Fig. 3(b)) is observed over all the glucose concentrations and for all the simulation runs. The secondary structure data for the replica simulations are shown in Fig. S6 (ESI†). Increased glucose levels led to fast aggregation but did not affect the β-sheet and α-helical content in agreement with experimental observations.¹⁸ Previous experimental reports by Kedia et al. also reported this increased aggregation in the presence of glucose without any changes in ultraviolet circular dichroism.¹⁸

Fig. 3 Time evolution of β-sheet (a) and α-helical (b) fractions present in Aβ aggregates for all glucose concentrations in an independent simulation run. Data for the replica simulations are presented in the ESI.†

3.3 Restricted rotation of interfacial glucose molecules

Finally, we quantified the local enhancement of glucose molecules close to the peptide aggregate. Fig. 4(a) shows the relative enrichment (RE) of each CG interaction site of glucose compared to water molecules as a function of the distance from the protein aggregate for the simulation with 1.55% glucose (w/v). As glucose is an asymmetric molecule, we investigated the directional nature of the glucose–peptide interactions.

Fig. 4 (a) Relative enrichment of individual coarse-grained interaction sites of glucose for simulation with 1.55% glucose (w/v). Data were obtained from the last 500 ns of the simulation run. (b) Loss of molecular rotational entropy (in eV) for various % compositions (w/v) of glucose molecules compared with the values in bulk water. The data represent the mean values of the three replicates from the last 500 ns of the simulation, and the error bars are the standard errors of the mean.

We found that B1 beads (representing C5 and C6) were closer to the peptide than B2 (representing C3 and C4) and B3 (representing C1 and C2). Previous ab initio calculations of hydrogen-bonding patterns of glucose in water have reported a similar asymmetric set of interactions.⁵⁷ The authors found that the oxygens at C5 and C6 have lower hydrogen bonding capabilities compared to other oxygens. We observed a similar trend, with C5 and C6 partitioning closer to the peptide aggregate. This preferential orientation results in restricted rotations of the glucose molecules near the aggregate, resulting in a loss of molecular rotational entropy. This loss of molecular rotational entropy of the glucose molecules near the aggregate was determined and compared with the value in bulk water, as shown in Fig. 4(b). This can explain our concentration-dependent increase in aggregation rates. With an increase in the size of the aggregate (concurrent increase in aggregation rates), the aggregate surface area accessible for interaction with glucose decreases, which in turn reduces the entropic penalty. This leads to an increase in the fraction of glucose molecules present in bulk water as the peptide aggregate grows in size at higher glucose concentrations (1.55% and 3.10%), as shown in Fig. S7(a) (ESI†). Therefore, with an increased local concentration of glucose, there is an effective preference for larger aggregates. Similar macromolecular crowding and entropy-associated effects (folding/denaturation) have also been observed for RNA and protein systems.^58,59

While epidemiological studies have correlated AD and T2D, the primary reason for this has been attributed to the covalent modification of arginine and lysine (AGE), resulting in the cross-linking of amyloid aggregates. These covalent cross-links prevent the dissolution of the peptide aggregates. Previous studies have suggested a possible temporal mismatch between peptide aggregation and chemical modifications.¹⁸ Here, we uncover a complementary thermodynamic pathway for the observed increase in peptide aggregation with glucose.

Systematic studies of protein thermodynamics in response to crowded environments have revealed unique structural transitions and phase behaviors.⁶⁰ In the case of protein aggregation, research on macromolecular crowding effects has been generally limited to non-interacting (steric) crowders and very high concentrations to mimic physiological viscosity in biological environments.^24,61 Latsaw et al. reported that such crowders can lead to a decrease in the effective sizes of aggregates, resulting in an increased number of smaller oligomers. In some instances, the addition of an ad hoc hydrophobic effect to the crowder can shape the structural features of the aggregate. Finally, adding soft non-specific crowder interactions has been shown to have unique implications and to reverse the effect of systems with only steric crowders.^62,63 In this work, we reported a specific directional interaction of glucose molecules with peptides, leading to increased aggregate size, which is in contrast with the effects observed for steric crowders, as noted by Latsaw et al.²⁴

In this article, we have focused on the central hydrophobic fragment of the Aβ peptide as a template (similar to^24,64,65) to understand its aggregation under hyperglycemic conditions. While a similar non-specific caging effect has been noted for the full-length Aβ peptide in previous research,²⁷ which can point to accelerated aggregation of full-length Aβ at increased glucose concentrations, it is still difficult to accurately ascertain this response. Several other factors might impact full-length Aβ aggregation, such as disordered N-terminus and local partial structures in the C-terminus. Moreover, there are several other physiological small molecules and peptide assemblies linked to T2D and AD that can also affect this behavior through various physical processes and chemical modifications. This is beyond the scope of the current work and should be further investigated in future research.

4 Conclusion

Self-assembly of Aβ peptides into specific deposits is noted as an essential upstream process in Alzheimer's disease. Several recent studies have suggested interlinks between high blood glucose levels and Alzheimer's disease. This has led to biophysical research to uncover the connection between hyperglycemic conditions and Aβ aggregation. Several research studies have indicated the ability of glucose to chemically modify amino acids and create covalent cross-links that are resistant to dispersion. Currently, to the best of our knowledge, limited studies exist which aim to uncover thermodynamics-based mechanisms, which can explain the initial peptide aggregation in the presence of glucose molecules. In this work, we approach this research question from a computational lens using coarse-grained molecular simulations to understand the aggregation of Aβ 16–22 with varying concentrations of glucose. Using a simplified modeling approach, our simulations could probe physiological responses at much larger spatio-temporal scales than those afforded by the fine-grained models.

Our analyses of coarse-grained simulation trajectories, in agreement with experimental findings, suggest a glucose concentration-dependent increase in the aggregation rate. We did not observe changes in the secondary structure content due to the presence of glucose molecules. The glucose molecules close to the peptide aggregate preferred a particular orientation, with C5 and C6 partitioning closer to the aggregate than the other CG interaction centers associated with other carbon molecules. The restricted rotation of this ring molecule would result in a loss of molecular rotational entropy, which can force a reduction of the accessible area for glucose molecules to interact, thereby hastening the peptide aggregation process. The preferred orientation limits how freely the glucose molecules can rotate, resulting in a loss of molecular rotational entropy. Now, peptide aggregation could reduce this loss by decreasing the available region for peptide–glucose interactions. Therefore, at a high concentration of glucose molecules, the peptides aggregate faster. This could be a possible thermodynamic mechanism for the concentration-dependent increase in the aggregation rate of Aβ fragments in the presence of glucose molecules.

Although the effect of steric crowders on peptide aggregation has been noted in previous computational studies, in this work, we report the results with crowders (glucose molecules) having a distinct restrictive geometry and specific interactions with the peptides. This contributed to an alternative thermodynamic link between glucose and peptide aggregates, beyond chemical modifications, that can explain observations from experiments. Future research in this direction could focus on exploring these thermodynamic links and how cellular environment and full-length peptides, beyond these simplified model systems, can affect it. Moreover, this presents an opportunity to develop rational therapeutics that can target and/or perturb this thermodynamic link.

Data availability

All files required to set up and perform the simulations described in this work can be found at: https://github.com/meenaljainumd/glucose_amyloid_beta_repo.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from the National Science Foundation under grant CBET-1760879 and to computational resources at the University of Maryland. ASs contribution to this research was supported in part by the National Science Foundation award DGE-1632976.

Notes and references

1. D. M. Walsh and D. J. Selkoe, J. Neurochem., 2007, 101, 1172–1184.
2. M. Goedert and M. G. Spillantini, Science, 2006, 314, 777–781.
3. B. A. Yankner, L. R. Dawes, S. Fisher, L. Villa-Komaroff, M. L. Oster-Granite and R. L. Neve, Science, 1989, 245, 417–420.
4. D. M. Walsh and D. J. Selkoe, Neuron, 2004, 44, 181–193.
5. J. A. Lemkul and D. R. Bevan, Biochemistry, 2013, 52, 4971–4980.
6. P. Das, S.-g Kang, S. Temple and G. Belfort, PLoS One, 2014, 9, e113041.
7. J. Legleiter, D. L. Czilli, B. Gitter, R. B. DeMattos, D. M. Holtzman and T. Kowalewski, J. Mol. Biol., 2004, 335, 997–1006.
8. A. Jayaraman and C. J. Pike, Curr. Diabetes Rep., 2014, 14, 476.
9. W. Xia, S. Wang, Z. Sun, F. Bai, Y. Zhou, Y. Yang, P. Wang, Y. Huang and Y. Yuan, Psychoneuroendocrinology, 2013, 38, 2493–2501.
10. C. Moran, T. G. Phan, J. Chen, L. Blizzard, R. Beare, A. Venn, G. Münch, A. G. Wood, J. Forbes, T. M. Greenaway, S. Pearson and V. Srikanth, Diabetes Care, 2013, 36, 4036–4042.
11. S. M. Manschot, A. M. Brands, J. van der Grond, R. P. Kessels, A. Algra, L. J. Kappelle and G. J. Biessels and on behalf of the Utrecht Diabetic Encephalopathy Study Group, Diabetes, 2006, 55, 1106–1113.
12. M. Yagi-Utsumi and K. Kato, Molecules, 2022, 27, 4787.
13. F. Bossis and L. L. Palese, Biochim. Biophys. Acta, Proteins Proteomics, 2013, 1834, 2486–2493.
14. G.-f Chen, T.-h Xu, Y. Yan, Y.-r Zhou, Y. Jiang, K. Melcher and H. E. Xu, Acta Pharmacol. Sin., 2017, 38, 1205–1235.
15. N. Sasaki, R. Fukatsu, K. Tsuzuki, Y. Hayashi, T. Yoshida, N. Fujii, T. Koike, I. Wakayama, R. Yanagihara, R. Garruto, N. Amano and Z. Makita, Am. J. Pathol., 1998, 153, 1149–1155.
16. Y. Kong, F. Wang, J. Wang, C. Liu, Y. Zhou, Z. Xu, C. Zhang, B. Sun and Y. Guan, Front. Aging Neurosci., 2020, 12, 217.
17. S.-Y. Ko, H.-A. Ko, K.-H. Chu, T.-M. Shieh, T.-C. Chi, H.-I. Chen, W.-C. Chang and S.-S. Chang, PLoS One, 2015, 10, e0143345.
18. N. Kedia, M. Almisry and J. Bieschke, Phys. Chem. Chem. Phys., 2017, 19, 18036–18046.
19. Y. Yang, Y. Wu, S. Zhang and W. Song, PLoS One, 2013, 8, e69824.
20. C. N. Patel, S. M. Noble, G. T. Weatherly, A. Tripathy, D. J. Winzor and G. J. Pielak, Protein Sci., 2002, 11, 997–1003.
21. S. Shahid, I. Hasan, F. Ahmad, M. I. Hassan and A. Islam, Biomolecules, 2019, 9, 477.
22. L. Bai, X. Guo, X. Zhang, W. Yu and D. Yang, Langmuir, 2019, 35, 5931–5936.
23. I. Kuznetsova, K. Turoverov and V. Uversky, Int. J. Mol. Sci., 2014, 15, 23090–23140.
24. D. C. Latshaw, M. Cheon and C. K. Hall, J. Phys. Chem. B, 2014, 118, 13513–13526.
25. F. Musiani and A. Giorgetti, International Review of Cell and Molecular Biology, Elsevier, 2017, vol. 329, pp. 49–77.
26. L. A. Munishkina, A. Ahmad, A. L. Fink and V. N. Uversky, Biochemistry, 2008, 47, 8993–9006.
27. S. Menon and N. Sengupta, ACS Omega, 2017, 2, 2134–2147.
28. B. Khurshid, A. U. Rehman, R. Luo, A. Khan, A. Wadood and J. Anwar, ACS Omega, 2022, 7, 15132–15144.
29. M. Carballo-Pacheco, A. E. Ismail and B. Strodel, J. Chem. Theory Comput., 2018, 14, 6063–6075.
30. A. K. Mehta, K. Lu, W. S. Childers, Y. Liang, S. N. Dublin, J. Dong, J. P. Snyder, S. V. Pingali, P. Thiyagarajan and D. G. Lynn, J. Am. Chem. Soc., 2008, 130, 9829–9835.
31. K. Lu, J. Jacob, P. Thiyagarajan, V. P. Conticello and D. G. Lynn, J. Am. Chem. Soc., 2003, 125, 6391–6393.
32. K. Tao, J. Wang, P. Zhou, C. Wang, H. Xu, X. Zhao and J. R. Lu, Langmuir, 2011, 27, 2723–2730.
33. J. J. Balbach, Y. Ishii, O. N. Antzutkin, R. D. Leapman, N. W. Rizzo, F. Dyda, J. Reed and R. Tycko, Biochemistry, 2000, 39, 13748–13759.
34. S. J. Ganesan, H. Xu and S. Matysiak, Phys. Chem. Chem. Phys., 2016, 18, 17836–17850.
35. S. J. Ganesan and S. Matysiak, J. Chem. Theory Comput., 2014, 10, 2569–2576.
36. A. Sahoo, H. Xu and S. Matysiak, Phys. Chem. Chem. Phys., 2019, 21, 8559–8568.
37. A. Sahoo, P.-Y. Lee and S. Matysiak, J. Chem. Theory Comput., 2022, 18, 5046–5055.
38. A. Sahoo and S. Matysiak, Phys. Chem. Chem. Phys., 2021, 23, 20627–20633.
39. S. J. Ganesan and S. Matysiak, Phys. Chem. Chem. Phys., 2016, 18, 2449–2458.
40. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
41. D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697.
42. C. A. López, A. J. Rzepiela, A. H. de Vries, L. Dijkhuizen, H. H. Philippe and S. J. Marrink, J. Chem. Theory Comput., 2009, 5, 3195–3210.
43. S. Yesylevskyy, L. Schäfer, D. Sengupta and M. SJ, PLoS Comput. Biol., 2010, 6, 1–17.
44. P. S. Schmalhorst, F. Deluweit, R. Scherrers, C.-P. Heisenberg and M. Sikora, J. Chem. Theory Comput., 2017, 13, 5039–5053.
45. D. Stigter, J. Phys. Chem., 1960, 64, 118–124.
46. M. Carballo-Pacheco, A. E. Ismail and B. Strodel, J. Phys. Chem. B, 2015, 119, 9696–9705.
47. D. Matthes, V. Gapsys, V. Daebel and B. L. de Groot, PLoS One, 2011, 6, 1–18.
48. B. Barz, D. J. Wales and B. Strodel, J. Phys. Chem. B, 2014, 118, 1003–1011.
49. D. Matthes, V. Gapsys and B. L. de Groot, J. Mol. Biol., 2012, 421, 390–416.
50. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
51. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
52. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
53. A. Lerbret, F. Affouard, P. Bordat, A. Hédoux, Y. Guinet and M. Descamps, Chem. Phys., 2008, 345, 267–274.
54. N. Zhang, F.-F. Liu, X.-Y. Dong and Y. Sun, J. Phys. Chem. B, 2012, 116, 7040–7047.
55. A. Lerbret, P. Bordat, F. Affouard, A. Hédoux, Y. Guinet and M. Descamps, J. Phys. Chem. B, 2007, 111, 9410–9420.
56. F.-F. Liu, L. Ji, X.-Y. Dong and Y. Sun, J. Phys. Chem. B, 2009, 113, 11320–11329.
57. C. Molteni and M. Parrinello, J. Am. Chem. Soc., 1998, 120, 2168–2171.
58. N. F. Dupuis, E. D. Holmstrom and D. J. Nesbitt, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8464–8469.
59. M. Senske, L. Törk, B. Born, M. Havenith, C. Herrmann and S. Ebbinghaus, J. Am. Chem. Soc., 2014, 136, 9036–9041.
60. A. G. Gasic, M. M. Boob, M. B. Prigozhin, D. Homouz, C. M. Daugherty, M. Gruebele and M. S. Cheung, Phys. Rev. X, 2019, 9, 041035.
61. K. A. Sharp, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7990–7995.
62. M. Sarkar, C. Li and G. J. Pielak, Biophys. Rev., 2013, 5, 187–194.
63. W. M. Aumiller, B. W. Davis, E. Hatzakis and C. D. Keating, J. Phys. Chem. B, 2014, 118, 10624–10632.
64. S. Pal and S. Paul, J. Phys. Chem. B, 2020, 124, 210–223.
65. S. Dasari and B. S. Mallik, RSC Adv., 2020, 10, 33248–33260.

---

Footnotes

† Electronic supplementary information (ESI) available: Schematic geometries of coarse-grained amino acids; type of coarse-grained beads present in the Aβ fragment, glucose molecule and MARTINI polarizable solvent; non-bonded interactions for various beads; snapshots from the peptide aggregation trajectory; radial distribution function between the backbone beads; schematic description of the β-sheet and α-helix metric; evolution of the size of peptide aggregates for various glucose concentrations for all replica simulations; time evolution of β-sheet and α-helical fractions for the replica simulations; time evolution of the fraction of glucose molecules present in bulk water for various % compositions of glucose molecules. See DOI: https://doi.org/10.1039/d3cp04494g

‡ M. J. and A. S. contributed equally to this work.

---