Unravelling photoisomerization dynamics in a metastable-state photoacid

Abstract

Direct access to trans–cis photoisomerization in a metastable state photoacid (mPAH) remains challenging owing to the presence of competing excited-state relaxation pathways and multiple transient isomers with overlapping spectra. Here, we reveal the photoisomerization dynamics in an indazole mPAH using time-resolved fluorescence (TRF) spectroscopy by exploiting a unique property of this mPAH having fluorescence only from the trans isomer. The combination of these experimental results with time-dependent density function theory (TDDFT) calculations enables us to gain mechanistic insight into this key dynamical process.

---

Introduction

Photoisomerization represents the first step in the complex photoreaction of an mPAH, a novel class of photoacid capable of producing a large proton concentration with high efficiency, good reversibility, and an extremely long-lived acidic state with a half-life ranging from seconds to hours.^1–3 The mPAHs have enabled the successful demonstration of various chemical, energy, materials, and biomedical applications, such as photochemically-driven CO₂ release^4,5 and dissipative assembly.^2,6 While multiple isomers with various connected pathways during a photoreaction cycle are often considered to promote their unique functionalities, the transient intermediates and associated structural dynamics of mPAHs remain poorly understood. This is reflected in the poor understanding of the very first step of such a photoreaction cycle, the trans–cis isomerization process.^1,3 To this end, the photoinduced isomerization for other molecular systems has been extensively studied using a gamut of time-resolved experimental techniques in combination with a variety of experimental conditions such as through synthesis of different functional derivatives⁷ or using binary solvent/solvent systems with various viscosities, pressure and temperature variations.^8,9 However, to the best of our knowledge, Sension and coworkers reported the only study on the photoisomerization timescales of mPAHs using femtosecond transient absorption spectroscopy.¹⁰ The involvement of various isomers with strongly overlapped absorption spectra, along with inherent complex contributions to these signals, made determination of the timescales for this key process possible only through sophisticated spectral analysis in combination with density functional theory calculations. It remains unclear if the early time dynamics identified for a merocyanine photoacid would occur in an indazole photoacid, a different type of mPAH that has attracted much attention in recent years.^1,5

So far, there have been only a few studies on indazole mPAHs,^5,11–13 and their photoreactions remain poorly understood. First, the origin of photoacidity has not been determined for this class of mPAH. Because the photoacidity of such a photoacid is not as high as those of the most studied merocyanine mPAHs, an intramolecular proton transfer may take place prior to the intermolecular proton transfer to a protic solvent. This consideration is supported by the relative stabilities of the protonated and deprotonated forms of the cis and the spiro isomer. The acidity of the cis isomer is only slightly higher than the acidity of the trans isomer, but the acidity of the spiro form is significantly higher.¹² This suggests that the proton transfer happens when the cis isomer is converted to the spiro form, either synchronically or sequentially. This is in contrast to merocyanine type mPAHs, where both experimental and calculation results have indicated the absence of the protonated metastable state and thus the photoacidity is defined by the equilibrium between the deprotonated metastable state and the protonated cis-intermediate.^2,3,14 Second, it was proposed recently that the cis isomer possesses a cis-quinoidal structure based on NMR and absorption spectral measurements under different conditions, and its stabilization was speculated to result from interactions with water molecules through proton exchange and hydrogen bonding.¹² Third, the kinetic scheme of the proton transfer reaction has not been reported. Although the relative free energies of reactants, intermediates, and reaction products before and after the proton transfer were computed recently,¹² the reaction kinetics involving proton transfer to a solvent have not been explicitly examined. Since such an intermolecular proton transfer process takes place in the electronic ground state after excited-state relaxation, this proton transfer process is not directly relevant to the excited-state processes probed in this work. Obviously, the molecular detail during this intermolecular proton transfer process would be an interesting subject for subsequent studies.

Here, we report a time-resolved fluorescence (TRF) spectroscopic study on an indazole-mPAH (structure shown in Fig. 1), along with the electronic structure and TDDFT calculations. Through identifying a unique property of this mPAH with the only fluorescent species being the nascent trans isomer, we were able to directly probe the photoisomerization process by performing TRF measurements at different aqueous solvent viscosities. The combination of these experimental results with TDDFT calculations enables us to gain not only the timescales of this key dynamical process but also mechanistic insight into its energy barrier and detailed structural changes. We further identified several salient features, including pronounced negative solvatochromism of absorption spectra, excitation wavelength-independent fluorescence emission spectra, and notable mismatch between fluorescence excitation and absorption spectra.

Fig. 1 Chemical structures of trans and cis isomers of indazole-mPAH.

Experimental and computational methods

Materials

Synthesis, purification, and characterization of indazole-mPAH were performed following the procedure described previously.¹² Glycerol (≥99.5% purity) was purchased from Sigma Aldrich and used without further purification. All water/glycerol mixtures were prepared using ultrapure water (18.2 MΩ cm).

Absorption measurements

Three absorption spectrometers were employed for this work. A Cary 4E UV-VIS-NIR absorption spectrometer was used to record the absorption spectra before and after time-resolved fluorescence measurements (Fig. S1, S2, and S4, ESI†). An Agilent 8453 spectrometer was used to acquire the absorption spectrum shown in Fig. S3 (ESI†). A Shimadzu UV-1900i spectrometer was used to measure the absorption spectra shown in Fig. 2 and Fig. S6 (ESI†).

Fig. 2 (a) Absorption spectra acquired for freshly prepared mPAH solutions using different water/glycerol (w/w) mixtures and (b) the corresponding spectral shift in wavenumber as a function of dielectric constants (symbols) along with a linear fit (line).

Steady-state fluorescence measurements

Similarly, two fluorometers were employed for acquiring steady-state fluorescence data reported in this work; in both cases the fluorescence emission was collected at 90° to the incident excitation beam. Specifically, a Fluorolog-QM spectrofluorometer equipped with single grating excitation and emission monochromators was used to record the fluorescence data shown in Fig. S6 and S7 (ESI†). Two aqueous solutions of mPAH with concentrations of 5.5 μM and 0.5 μM, respectively, corresponding to maximum absorbances of 0.112 and 0.01 per cm at 411 nm, were used to measure the fluorescence data shown in Fig. 5. At these low concentrations, both reabsorption and inner filter effect should be negligible. To minimize the occurrence of photoisomerization prior to the experiment, fresh sample solutions were prepared on the same day of the experiment and were kept in the dark until measurements. The corrected fluorescence excitation spectra were recorded by monitoring fluorescence emission at 527 nm, and the emission spectra were collected upon excitation at 370 nm. A slit width of 3 nm was used for both excitation and emission data acquisition, along with a step size of 1.0 or 2.0 nm and an integration time of 1.0 s. The fluorescence data shown in Fig. S7 (ESI†) were acquired using a ∼25 μM aqueous solution of mPAH before and after irradiation upon excitation at 410 nm and 315 nm, respectively. A 425 nm LED lamp was used to irradiate the mPAH solution for ∼2 h to form protonated cis isomer and the photon flux was kept at ∼500 μmol m⁻² s⁻¹.¹² The slit width, integration time and step size are the same as those used for acquiring data shown in Fig. S6 (ESI†).

The corrected fluorescence emission intensity shown in Fig. 3 was measured as a function of both excitation wavelength (from 300 to 500 nm) and emission wavelength (from 300 to 800 nm), with corresponding steps of 0.8 and 2.0 nm, respectively, using a Fluorolog-3 spectrofluorometer. The resulting 63 001 measurements are depicted as a contour plot. These spectral measurements used the same slit width of 3 nm for excitation and emission, as well as an integration time of 0.5 s.

Fig. 3 Contour plot of steady-state fluorescence data measured through excitation (vertical axis) and emission (horizontal axis) scans. The panels on the top and right-hand side show the emission spectrum collected upon excitation at 416 nm and the excitation spectrum recorded by monitoring fluorescence emission at 531 nm, respectively. Y axes of 1-D spectra correspond to emission intensities in arbitrary units. Note that the signal along the oblique direction arises from excitation light scattering.

Time-resolved fluorescence measurements

Picosecond time-resolved fluorescence measurements were performed using time-correlated single-photon-counting (TCSPC) apparatus based on an actively quenched single photon avalanche photodiode (PDM 50CT module, Micro Photon Devices) in combination with a PicoQuant TCSPC system (PicoHarp 300, Picoquant).¹⁵ The excitation light source was generated using a small portion of the output of a 250 kHz Ti:Sapphire femtosecond regenerative amplifier (RegA 9000, Coherent), which was further frequency doubled using a 2 mm thick BBO crystal to obtain excitation pulses centered at 402 nm with a typical <2 nJ pulse energy. Fluorescence emission at 510, 530, and 550 nm was selected by using 10 nm (FWHM, Thorlabs) bandpass filters. The shortest instrument response function (IRF) showed a FWHM of ∼40 ps as recorded at several wavelengths within the spectral range of our fluorescence emission detection using dilute suspensions of coffee creamer in water. A 4.0 ps channel time was chosen and data acquisition at each wavelength took a few minutes to accumulate >30 000 counts in the peak channel. The relative polarization between the fluorescence emission and the linearly polarized laser excitation was set to the magic angle (54.7°) using an emission polarizer. This enables us to eliminate potential contribution from molecular rotation dynamics to the measured time-resolved data.

Quantitative analysis of the time-resolved data was performed individually using a least-squares deconvolution fitting algorithm (FluoFit, PicoQuant) with explicit consideration of the finite IRF in combination with a model function consisting of a sum of exponential components. The quality of each fit was assessed by its reduced chi-square (χ²) and the residual between the raw data and its corresponding fit.

Computational methods

Electronic structure calculations were carried out using the Gaussian 16 Revision A.03 software package¹⁶ with the CAM-B3LYP flavor of density functional¹⁷ and the 6-311+G(d,p) basis set. Time-dependent density functional theory (TDDFT) was employed to model the absorption spectra, analyze the nature of the transitions and the change of the dipole moment upon the excitation in the Franck–Condon geometry, and predict the topology of the potential energy surface (PES) in the first singlet excited-state (S₁) for rotation around the double bond. Zero-point energies and thermal corrections were obtained for all the stationary points on the ground-state (S₀) and S₁ PES using the rigid rotor-harmonic oscillator approximation without scaling, except that vibrational frequencies lower than 60 cm⁻¹ were raised to 60 cm⁻¹.¹⁸ A flexible 3-sulfonatopropyl group in the indazole-mPAH was replaced by the methyl group in all calculations and the resulting structure is referred to as a model indazole-mPAH. It was found that such truncation has little effect on the predicted absorption spectra and relative stability of trans and cis isomers. Two water molecules were added to explicitly solvate two nitrogen atoms in the indazole moiety of the photoacid. On top of that, implicit solvent corrections for water were included using the SMD¹⁹ solvation model in Gaussian 16 for geometry optimization in the S₀ and S₁ states.

Results and discussion

The trans–cis isomerization process in an mPAH is commonly considered to take place along a double bond linking an electron-accepting moiety and a weakly acidic nucleophilic moiety.^1,3 As this large-scale structural change is extremely sensitive to solvent viscosity, time-resolved spectroscopic measurements at different solvent viscosities should provide a straightforward means to validate this consideration. Here, we chose different water/glycerol mixtures to vary solvent viscosity (η) from 0.89 to 45.9,²⁰ corresponding to a glycerol content ranging from 0% to 80% by weight. Note that the variable contents of glycerol in these mixtures also cause a change in the solvent dielectric constant (ε) from 80.37 to 50.64,²¹ resulting in a relatively weak polarity effect compared to the viscosity effect.

Negative solvatochromism of absorption spectra

As shown in Fig. 2a, the change in ε leads to a clear blue shift of the absorption spectra recorded prior to TRF measurements with increasing solvent polarity. A quantitative measure of this spectral shift can be made reliably using the longer wavelength edges of the main absorption band peaking at ∼410 nm, which is dominated by the trans form with negligible contributions from other isomers. Specifically, the wavelength at half of the absorption maximum of each normalized spectrum, corresponding to an absorbance of 0.5 at the long wavelength edge, is plotted in Fig. 2b in wavenumber as a function of ε taken from the literature.²¹ A linear correlation between the spectral shift and the solvent polarity is clearly evident as indicated by the solid line. The observed negative solvatochromism indicates that the permanent dipole moment in the ground state is larger than the dipole moment in the excited state.²² This observation is supported by our TDDFT calculations detailed in the Computational methods section, along with supporting computational results in the ESI,† which show a decrease in the dipole moment from 42.4 D in the ground state (S₀) to 37.9 D in the lowest singlet excited state (S₁) owing to a change in the electron density (Fig. S11, ESI†). Such a difference in the dipole moments is commonly observed for push–pull molecular structures with either positive or negative solvatochromism.^23–28 Since this indazole-mPAH is a conjugated push–pull structure as well (see Fig. 1),¹ our observation of this negative solvatochromism is therefore expected. Moreover, we found that the short wavelength (< 350 nm) portions of these absorption spectra are more complex owing to the contributions from other isomers such as cis, spiro, etc.¹² depending on how long the sample solution was exposed to room light during preparation.

The absorption spectra acquired after the TRF measurements (Fig. S1, dash lines, ESI†) exhibit substantial differences from those shown in Fig. 2a due to additional photoisomerization induced by the excitation laser light during TRF data acquisition. Given that the recovery of the multistep photoreaction back to its initial trans isomer can take 4–6 hours owing to the long-lived metastable state,^5,12 the spectra shown in Fig. S1 (ESI†) report on the coexisting trans, cis and spiro forms, etc., whose contributions to these spectra intrinsically depend on the time duration of laser excitation and room light exposure. These contributions can be assessed through spectral deconvolution analysis of any chosen spectrum employing the characteristic absorption spectra of trans, cis and spiro isomers acquired at the corresponding concentration as inputs, which were recorded using the procedure described in ref. 12. As shown in Fig. S2 (ESI†), the spectrum acquired for the ∼25 μM mPAH in water after TRF measurement (Fig. S1, dashed line in the 0% panel, ESI†) can be reasonably well reproduced with a dominant contribution from the cis isomer. However, we notice clear deviation when this analysis is applied to an absorption spectrum measured for 1 mM mPAH in water at a photostationary state under continuous irradiation (Fig. S2, timepoint 3 in ref. 5, ESI†), corresponding to a constant solution pH. As shown in Fig. S3 (ESI†), under this condition the trans isomer contribution appears negligible. This deviation likely points to the occurrence of additional isomers at such a photostationary state and requires future studies that are focused on identifying and quantifying these various isomer compositions at a given reaction time. It should be emphasized that such a photostationary state could not be established during our spectral experiments due to the finite excitation volumes with respect to the total sample solution in the cuvettes. This is clearly evidenced by the continuous variation of fluorescence excitation spectra during data acquisition owing to the changes in the mPAH absorption spectrum and its resulting excitation light attenuation, which can be seen from the contour plot of Fig. 3. Despite these changes, the absorption spectra acquired after TRF measurements again exhibit negative solvatochromism, which can be clearly seen from the normalized absorption spectra shown in Fig. S4 (ESI†). Observation of the same negative solvatochromism before and after TRF measurements within the experimental uncertainty (see Fig. 2b and Fig. S4b, ESI†) further confirms no sample damage during TRF measurements.

The solvent effect on the absorption spectral shift warrants further discussion as the plot of spectral shift as a function of solvent dielectric constant shown in Fig. 2b and Fig. S4b (ESI†) overlooks specific interactions between the solvent and the solute, especially hydrogen-bonding interactions. To identify if hydrogen-bonding interactions between the mPAH molecule and the binary water/glycerol solvent play a significant role in the observed pronounced negative solvatochromism of absorption spectra shown in Fig. 2 and Fig. S4 (ESI†), we perform a multi solvent parameter analysis using the well-known Kamlet–Taft (K–T) solvent scale. In this K–T approach,^29–31 any solvent-influenced property of the solute may be correlated using a multiparameter fit to the following equation: P_s–s = P⁰_s–s + sπ* + aα + bβ, where P_s–s is the measured solvent-influenced property of the solute, P⁰_s–s is the numerical value of the chosen solute property in a known reference solvent, or ideally, in the gas phase, π* is the normalized solvent polarity scale, α and β are the solvent acidity and basicity scales, respectively, s, a, and b are the empirical numerical coefficients that characterize the solute. Using the reported π*, α, and β values for neat water (α = 1.17, β = 0.47, π* = 1.14) and glycerol (α = 1.2, β = 0.67, π* = 1.04),^32–34 we estimated the corresponding values for different water/glycerol mixtures by calculating the averages of neat glycerol and water values weighted by their relative volumes³⁴ and converting their weight ratios to volume ratios using water and glycerol densities. Based on the results, we plot the spectral shift shown in Fig. 2b as a function of α, β, π*, and their linear combinations, i.e., P_s–s by treating P⁰_s–s, s, a and b as fitting parameters that can produce the best fit to the spectral shift. The resulting plots are shown in Fig. S5 (ESI†). The clear derivation from linear correlation observed in all cases does not appear to favor the presence of pronounced hydrogen-bonding interactions. Instead, dielectric constants do provide a straightforward characterization for the observed spectral shift shown in Fig. 2b and Fig. S4b (ESI†).

Excitation wavelength-independent fluorescence emission

In contrast to the high sensitivity of absorption spectra to light exposure shown in Fig. 2 and Fig. S1 (ESI†), steady-state fluorescence emission spectra appear wavelength independent. Fig. 3 shows the results acquired from an aqueous solution of this mPAH through two-dimensional excitation (from 300 to 500 nm) and emission (from 300 to 800 nm) scans. Upon normalization, the widths and peak positions of these emission spectra are found to be invariant with excitation wavelengths within the experimental uncertainty, albeit these spectra were acquired upon excitation light exposure for different times. Of particular interest is the notable mismatch between the fluorescence excitation and its corresponding absorption spectra as shown in Fig. S6 (ESI†). Acquisition of these spectra was made using two freshly prepared aqueous solutions of mPAH with concentrations of 5.5 μM and 0.5 μM, respectively, corresponding to maximum absorbances of 0.112 and 0.01 per cm at 411 nm. At these low concentrations, an intense water Raman signal is observed in both excitation and emission spectra, which further enhances remarkably in the spectra acquired using the 0.5 μM solution. To ease comparison, the absorption and emission spectra recorded for each aqueous solution were normalized at 411 and 542 nm, respectively. In addition, the intensities of these excitation spectra were adjusted to match the longer wavelength edges of the corresponding absorption spectra in view of the exclusive contribution from trans isomer to these spectra, which is the common and appropriate way to compare. From this comparison, we find that the overlap area accounts for 70% of the total area under the excitation spectra after subtracting the Raman signal. As the absorption spectrum of the trans isomer has an additional side band peaking at ∼325 nm as shown in Fig. S2 (ESI†), the minor difference between the absorption and excitation spectra may indicate that excitation of this side band can produce stronger fluorescence, or alternatively, potential contribution from deprotonated trans isomer which also absorbs at around 325 nm.¹² In view of the low sample concentrations (0.5 and 5 μM) used for collecting the fluorescence spectra shown in Fig. S6 (ESI†) and their identical absorption spectra, we can safely exclude the occurrence of any mPAH aggregation, which might otherwise contribute to the observed minor difference between absorption and excitation spectra. Furthermore, the fluorescence emission spectrum (Fig. S7, ESI†) measured on a mPAH solution with a significant content of protonated cis isomer immediately after 425 nm irradiation exhibits a reduced intensity but nearly identical shape to the one acquired prior to irradiation, which is known to arise from the trans isomer. The ∼4 nm shift between the spectra shown in Fig. S7 (ESI†) is probably caused by photoinduced acidity change in the solution. This observation does not support the occurrence of fluorescence emission from cis isomer unless its spectrum is identical to the emission from trans isomer, which is highly unlikely.

We also note that the difference between the excitation spectra shown in Fig. 3 (right-hand) and Fig. S5 (ESI†) arises from distinct experimental conditions used for data acquisition. Specifically, the excitation spectrum shown in Fig. 3 was acquired through an excitation-emission matrix scan, which involved measurements of 251 emission spectra using different excitation wavelengths from 300 to 500 nm with a step size of 0.8 nm. Each emission spectrum ranging from 300 to 800 nm with a step size of 2 nm has 250 data points. With an integration time of 0.5 s, acquisition of the entire dataset took 250 × 0.5 × 251 = 31 375 seconds without taking into account the wait time between scans. This acquisition time corresponds to 8.7 hours. To achieve a reasonable signal-to-noise ratio without further extending the data acquisition time, a more concentrated sample was employed. This leads not only to the complete elimination of the water Raman signal observed for less concentrated samples as shown in Fig. S6 (ESI†), but also to pronounced attenuation of the excitation light in the short wavelength region where the sample absorbs. As a result, the reduction of fluorescence emission upon excitation in this region is expected. Further reduction arises from the formation of the cis isomer due to excitation light exposure as shown in Fig. S7b (ESI†), which absorbs in this region (see Fig. S7a, ESI†). These reductions can explain at least qualitatively the difference between excitation spectra shown in Fig. 3 and Fig. S6 (ESI†). Although the photoreaction of mPAH due to continuous excitation light exposure during this long data acquisition will lead to different isomer compositions with time,^5,12 which would in turn inevitably alter both the mPAH absorption spectrum and excitation light attenuation, the key finding is that the fluorescence emission spectra upon normalization remain unchanged. This would be possible only when a single species, the trans isomer, emits. Note that the minimum overlap between absorption and emission spectra (see Fig. S6, ESI†) indicates the absence of significant reabsorption. Because of this long data acquisition time, it is simply infeasible to use either longer integration time or more data average. This is why the excitation spectrum shown in the right panel in Fig. 3 has greater noise than the corresponding spectra shown in Fig. S6 (ESI†).

The wavelength independent fluorescence emission spectra (Fig. 3), and the notable mismatch between fluorescence excitation and absorption spectra (Fig. S6, ESI†) indicate that the isomer(s) that contribute to the absorption and fluorescence spectra are different. Specifically, all isomers should contribute to the absorption spectra, but based on all our available results only the trans isomer appears to be fluorescent and therefore can be observed in the fluorescence measurements. As a result, the occurrence of the trans–cis isomerization owing to exposure to room light and laser excitation can result in significantly altered absorption spectra as shown in Fig. S1 (ESI†), but these spectral changes will not affect the photoisomerization dynamics, since only the trans form is fluorescent and detectable in the TRF experiment. Given the coexistence of various isomers at any given time but only trans form is fluorescent, this offers a rare opportunity to unambiguously separate this critical dynamical process from those competing ones using TRF spectroscopy for the first time. It also provides significant technical convenience to probe such an mPAH with a slow recovery time of 4–6 hours using a pulsed light source for optical excitation, as those commonly used approaches (rapid sample flow through excitation volume or use of a fast-spinning sample cell) would not be fast enough to refresh the sample for each successive laser pulse.

Wavelength and viscosity dependence of fluorescence kinetics

Based on the steady-state fluorescence emission data shown in Fig. 3, we chose three detection wavelengths of 510, 530 and 550 nm for our TRF measurements under different solvent viscosities. Fig. 4a shows the experimental data acquired at 530 nm along with the corresponding deconvolution fits, and the results obtained at 510 and 550 nm are included in Fig. S8 (ESI†). From these results, we first notice that all fluorescence data exhibit a complex kinetics behavior regardless of solvent viscosities, and satisfactory description of these kinetics requires a model function consisting of three exponential components, including a rise component in some cases but with a very small absolute relative amplitude (<6%). All the fitting parameters including reduced chi-squared values as a quantitative measure of the fit quality and amplitude weighted average lifetimes are included in Table S1 in the ESI.† Second, all fluorescence kinetics depend strongly on the solvent viscosity, which slows down significantly with increasing viscosity. This observation means that large-scale structural rearrangements are indeed involved in this trans–cis isomerization process. Because such a viscosity change affects the entire fluorescence kinetics, we can safely assign the fluorescence kinetics observed at different viscosities to the trans–cis isomerization of mPAH. Specifically, we found that the photoisomerization of this indazole-mPAH in water occurs primarily in a timescale ranging from 20.5 to 24 ps depending on the wavelength of fluorescence detection (see Table S1, ESI†). Note that this timescale is approximately one order of magnitude slower than the recently reported values for two metastable merocyanine/spiropyran photoacids.¹⁰ More importantly, this observation fully supports our conclusion that only the trans form is fluorescent and therefore dominates the fluorescence measurements. Third, as the occurrence of the trans–cis photoisomerization results in a fully relaxed fluorescence emissive electronic excited-state of the indazole-mPAH to its ground state, all the subsequent steps of its photoreaction will not contribute to the detected TRF data. Finally, by comparing the results shown in Fig. 4 and Fig. S8 (ESI†) along with the fitting parameters summarized in Table S1 (ESI†), one can also find a clear dependence of the fluorescence kinetics on detection wavelength. Taking the results obtained at the highest viscosity as an example, the average lifetime increases from 140.9 ps at 510 nm to 211.1 ps at 530 nm and 263.7 ps at 550 nm. This detection wavelength dependence likely arises from solvation owing to, in part, the reduced dipole moment in the S₁ state in combination with the distinct position of these detection wavelengths on the S₁ potential energy surface (PES).³⁵

Fig. 4 (a) Normalized TRF data measured at 530 nm for different water/glycerol (w/w) mixtures as indicated. (b) Double logarithmic plots of the average fluorescence decay rates at 530 nm as a function of solvent viscosity, along with a linear fit (line).

To further examine the viscosity effect on the fluorescence kinetics, we now focus on how the amplitude weighted average lifetime change with viscosity variations. We chose the average lifetimes instead of the lifetimes of any individual exponential components since (1) the viscosity change affects the entire fluorescence kinetics, and (2) all amplitudes and lifetimes were treated as free variables in the deconvolution fitting without constraints and therefore the resulting parameters may be, to some extent, mutually dependent. Fig. 4b shows the average fluorescence decay rate, k = 1/[small tau, Greek, macron], as a function of viscosity, η, for the TRF data acquired at 530 nm, and the results obtained at 510 and 550 nm are included in Fig. S9 (ESI†). In all cases, a linear correlation is clearly evident in the double logarithmic plots with an R² value of 0.997, 0.999, and 0.999 at 510, 530, and 550 nm, respectively. This linear correlation confirms that the viscosity dependence of the average fluorescence decay rate can be adequately described by the empirical power law k = Bη^−γ exp(−E_a/kT), where the parameter γ describes the interaction between the solvent and solute, E_a is the height of the potential barrier separating the initial and final states on the one-dimensional PES describing the reaction coordinate, and B is an adjustable parameter.^9,36–45 By applying this empirical power law, we assume that E_a is independent of the solvent composition⁴⁶ and properties. The linear correlation shown in Fig. 4b and Fig. S9 (ESI†) does support this assumption. Note that in the linear fitting, we treated the product B·exp(E_a/kT) and γ as two independent fitting parameters for each probe wavelength, which correspond to the intercept and slope of the linear fit, respectively. The resulting γ values are 0.445, 0.534, and 0.567 at 510, 530, and 550 nm, which are very similar to those reported in previous studies on a wide range of systems using such binary water/glycerol mixtures.³⁷

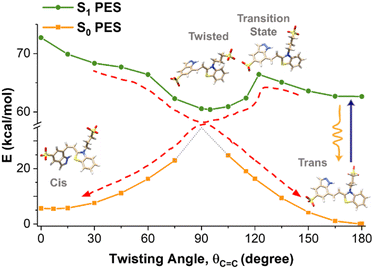
Energy barrier in trans–cis isomerization

The nonexponential fluorescence kinetics and the wavelength dependence of the fluorescence lifetimes further imply that photoisomerization is a weakly activated process.^35,47 To estimate the potential energy barrier E_a, we computed the PES for the rotation around the double bond in the S₁ state using TDDFT calculations. As detailed in the ESI,† this involves geometry optimization for excited states and validation of its accuracy by computing and comparing vertical S₁ → S₀ transition wavelengths of a model indazole-mPAH with the experimental data (Fig. S10, ESI†). While optical excitation of the trans isomer and its subsequent relaxation to S₁ minimum does not break the planarity of the molecule, our calculations predict that the cis isomer is not a stable minimum on the S₁ surface. Instead, the cis isomer undergoes a barrierless rotation around the C=C bond and adopts a twisted geometry with a dihedral angle close to 90° upon geometry optimization. The potential energy scan for the rotation around the double bond in the S₁ state further confirms a very different landscape of the PES for the trans and cis forms (Fig. 5). A transition state search was further performed to identify the structure connecting the trans and the twisted geometry on the S₁ PES and to provide a more accurate estimate of the potential energy barrier. We identified a transition state with the C–C=C–C and H–C=C–H torsional angles of 122° and 113°, respectively, and the energy barrier was estimated to be 2.6 kcal mol⁻¹, corresponding to 910 cm⁻¹ after taking into account the vibrational contributions to the electronic energies. Our calculated energy barrier indeed supports the notation of a weakly activated photoisomerization of this mPAH in water at room temperature. Our calculations further predict zero oscillator strength for the S₁ → S₀ transition at the twisted S₁ global minimum geometry. While the S₁ → S₀ transition of the cis isomer at the C–C=C–C twisting angle of zero degree possesses an oscillator strength of 0.6808 and a fluorescence emission peak at 516 nm according to our calculations, the absence of a corresponding energy minimum on the S₁ PES suggests that the fluorescence decay from the cis photoproduct if happens may be too fast to be detected in our current experiments.

Fig. 5 The potential energy surface for the rotation around the double bond in a model indazole-mPAH in the S₁ and S₀ state. TDDFT calculations predict an energy barrier for the isomerization starting from the trans form, but no such barrier for the isomerization starting from the cis form. The vertical upward arrow depicts the optical excitation of the trans isomer, the orange wavy arrow denotes the radiative emission (fluorescence), and the red dashed arrows describe excitation population relaxation from the S₁ to the S₀ states of either the trans or the cis isomer. In the twisted geometry of the S₀ state, the dotted region signifies the biradical character of the molecule, which imposes limitations on the application of the DFT approach in this region.

Our finding for the photoisomerization process of this indazole-mPAH can be visualized through a schematic description depicted in Fig. 5. Upon optical excitation of the trans isomer, the excitation population on the S₁ state undergoes a weakly activated isomerization process through a transition state with a distinct conformation towards the potential minimum of the twisted geometry via a barrierless rotation around the C=C bond of the cis isomer. Because the S₁ → S₀ transition at the twisted S₁ global minimum geometry is predicted to be not fluorescent, and the fluorescence decay from the cis photoproduct may be too fast to be detected even if it occurs owing to the absence of a corresponding energy minimum on the S₁ PES, both isomers will not contribute to the steady-state (Fig. 3) and TRF signals (Fig. 4 and Fig. S8, ESI†). This photoisomerization process is followed by a very rapid nonradiative relaxation to the S₀ states of either the trans or cis isomers following the pathways indicated by dashed arrows. In view of the extremely slow recovery from the cis geometry to trans isomers, a large potential barrier between the cis and trans isomers in the ground state is also expected, which is fully supported by the calculated S₀ PES as shown in Fig. 5. It should be noted that in the twisted geometry of the S₀ state, the dotted region signifies the biradical character of the molecule, which imposes limitations on the application of the DFT approach in this region. Standard DFT and TDFT are ill-suited for detecting a conical intersection between the S₁ and S₀ because of the incorrect topology of the region surrounding the conical intersection. The identification of such an intersection necessitates the application of multireference calculations, which fall outside the scope of this paper.

The strong solvent effects on the spectral and time-resolved fluorescence kinetics observed in this work suggests that the use of organic solvents, especially non-protonic organic solvents such as acetonitrile and DMSO will result in different results. Besides the variations induced by different dielectric constants and viscosities, the use of such organic solvents may further lead to distinct isomer structures. For instance, a regular Kekulé cis structure was recently identified in DMSO and methanol instead of the quinoidal cis structure formed in water.¹² Moreover, restricted or even eliminated intermolecular proton transfer in non-protonic solvents^31,48,49 may alter the photoreaction pathways and mechanisms found for neat water solution of mPAH.¹² Obviously, those applications that rely on this intermolecular proton transfer would no longer be feasible in these solvents.

In summary, we identified that the initial trans isomer is only fluorescent species in this mPAH through absorption and steady-state fluorescence measurements manifested by pronounced negative solvatochromism, wavelength independent fluorescence emission spectra, and notable mismatch between fluorescence excitation and absorption spectra. By leveraging this unique property, we realized direct access to the photoisomerization process without the influence of any other competing electronic excited-state relaxation processes using TRF spectroscopy. The combination of these experimental results with TDDFT calculations further enabled us to identify this photoisomerization as a weakly activated process with an energy barrier of 2.6 kcal mol⁻¹. Our findings offer not only mechanistic insight into this key dynamical process but also useful information for optimizing its applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Separation Sciences. A. R. M. was supported in part by the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists (WDTS) under the Science Undergraduate Laboratory Internships program. Part of the steady-state fluorescence spectral measurements was conducted as part of a user project at the Center for Nanophase Materials Sciences (CNMS), which is a US Department of Energy, Office of Science User Facility at Oak Ridge National Laboratory. This work was produced by UT-Battelle LLC under Contract No. AC05-00OR22725 with the U. S. Department of Energy. The publisher acknowledges the U.S. Government license to provide public access under the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).

References

1. Y. Liao, Acc. Chem. Res., 2017, 50, 1956–1964.
2. Y. Liao, Phys. Chem. Chem. Phys., 2022, 24, 4116–4124.
3. C. Berton, D. M. Busiello, S. Zamuner, E. Solari, R. Scopelliti, F. Fadaei-Tirani, K. Severin and C. Pezzato, Chem. Sci., 2020, 11, 8457–8468.
4. R. Bennett, S. Clifford, K. Anderson and G. Puxty, Energy Proc., 2017, 114, 1–6.
5. U. I. Premadasa, V. Bocharova, A. R. Miles, D. Stamberga, S. Belony, V. S. Bryantsev, A. Elgattar, Y. Liao, J. T. Damron, M. K. Kidder, B. Doughty, R. Custelcean and Y.-Z. Ma, Angew. Chem., Int. Ed., 2023, 62, e202304957.
6. Z. Wang and Y. Liao, Nanoscale, 2016, 8, 14070–14073.
7. V. Papper, D. Pines, G. Likhtenshtein and E. Pines, J. Photochem. Photobiol., A, 1997, 111, 87–96.
8. S. P. Velsko and G. R. Fleming, J. Chem. Phys., 1982, 76, 3553–3562.
9. S. H. Courtney and G. R. Fleming, J. Chem. Phys., 1985, 83, 215–222.
10. C. R. Aldaz, T. E. Wiley, N. A. Miller, N. Abeyrathna, Y. Liao, P. M. Zimmerman and R. J. Sension, J. Phys. Chem. B, 2021, 125, 4120–4131.
11. N. Abeyrathna and Y. Liao, J. Am. Chem. Soc., 2015, 137, 11282–11284.
12. A. Elgattar, O. Alghazwat, A. B. Brown, V. S. Bryantsev, V. Bocharova and Y. Liao, J. Photochem. Photobiol., A, 2023, 439, 114599.
13. O. Alghazwat, A. Elgattar and Y. Liao, Photochem. Photobiol. Sci., 2023, 22, 2573–2578.
14. C. Berton, D. M. Busiello, S. Zamuner, R. Scopelliti, F. Fadaei-Tirani, K. Severin and C. Pezzato, Angew. Chem., Int. Ed., 2021, 60, 21737–21740.
15. Y.-Z. Ma, H. Lin, M.-H. Du, B. Doughty and B. Ma, J. Phys. Chem. Lett., 2018, 9, 2164–2169.
16. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Wallingford, CT, 2016.
17. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
18. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
19. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
20. Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 1994.
21. G. Akerlof, J. Am. Chem. Soc., 1932, 54, 4125–4139.
22. S. Nigam and S. Rutan, Appl. Spectrosc., 2001, 55, 362A–370A.
23. F. Effenberger and F. Würthner, Angew. Chem., Int. Ed. Engl., 1993, 32, 719–721.
24. B. Carlotti, G. Consiglio, F. Elisei, C. G. Fortuna, U. Mazzucato and A. Spalletti, J. Phys. Chem. A, 2014, 118, 3580–3592.
25. S. Meng, S. Caprasecca, C. A. Guido, S. Jurinovich and B. Mennucci, Theor. Chem. Acc., 2015, 134, 150.
26. M. J. Wildervanck, R. Hecht and A. Nowak-Król, Molecules, 2022, 27, 5510.
27. A. S. Klymchenko, Acc. Chem. Res., 2017, 50, 366–375.
28. F. Bureš, RSC Adv., 2014, 4, 58826–58851.
29. R. W. Taft and M. J. Kamlet, J. Am. Chem. Soc., 1976, 98, 2886–2894.
30. M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377–383.
31. E. Pines, D. Pines, Y.-Z. Ma and G. R. Fleming, ChemPhysChem, 2004, 5, 1315–1327.
32. L. Zhang, H. Yu, S. Liu, Y. Wang, T. Mu and Z. Xue, Ind. Eng. Chem. Res., 2023, 62, 11723–11734.
33. S. Spange, N. Weiß, C. H. Schmidt and K. Schreiter, Chemistry–Methods, 2021, 1, 42–60.
34. C. Nançoz, G. Licari, J. S. Beckwith, M. Soederberg, B. Dereka, A. Rosspeintner, O. Yushchenko, R. Letrun, S. Richert, B. Lang and E. Vauthey, Phys. Chem. Chem. Phys., 2018, 20, 7254–7264.
35. B. Bagchi, G. R. Fleming and D. W. Oxtoby, J. Chem. Phys., 1983, 78, 7375–7385.
36. T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939.
37. V. Sundström and T. Gillbro, Chem. Phys., 1981, 61, 257–269.
38. K. M. Keery and G. R. Fleming, Chem. Phys. Lett., 1982, 93, 322–326.
39. G. Rothenberger, D. K. Negus and R. M. Hochstrasser, J. Chem. Phys., 1983, 79, 5360–5367.
40. S. P. Velsko, D. H. Waldeck and G. R. Fleming, J. Chem. Phys., 1983, 78, 249–258.
41. N. S. Park and D. H. Waldeck, J. Chem. Phys., 1989, 91, 943–952.
42. S. Schneider, B. Brem, W. Jäger, H. Rehaber, D. Lenoir and R. Frank, Chem. Phys. Lett., 1999, 308, 211–217.
43. A. Espagne, D. H. Paik, P. Changenet-Barret, M. M. Martin and A. H. Zewail, ChemPhysChem, 2006, 7, 1717–1726.
44. B. Dietzek, A. N. Tarnovsky and A. Yartsev, Chem. Phys., 2009, 357, 54–62.
45. A. Magni, G. Bondelli, G. M. Paternò, S. Sardar, V. Sesti, C. D’Andrea, C. Bertarelli and G. Lanzani, Phys. Chem. Chem. Phys., 2022, 24, 8716–8723.
46. H. A. Kramers, Physica, 1940, 7, 284–304.
47. B. Bagchi and G. R. Fleming, J. Phys. Chem., 1990, 94, 9–20.
48. N. Sülzner, B. Geissler, A. Grandjean, G. Jung and P. Nuernberger, ChemPhotoChem, 2022, 6, e202200041.
49. E. Pines, D. Pines, O. Gajst and D. Huppert, J. Chem. Phys., 2020, 152, 074205.

---

Footnote

† Electronic supplementary information (ESI) available: Supporting experimental results including Fig. S1; absorption spectra before and after time-resolved experiments; Fig. S4: normalized absorption spectra after time-resolved experiments along with the corresponding spectral shift; Fig. S2 and S3: spectral deconvolution for absorption spectra acquired under different conditions; Fig. S5: absorption spectral shift shown in Fig. 2b as a function of the Kamlet–Taft parameter α (a), β (b), π* (c), and their linear combinations P_s–s by treating P⁰_s–s, s, a and b as fitting parameters (d); Fig. S6: normalized steady-state fluorescence excitation and emission spectra, along with the absorption spectrum (dashed line) plotted as 1 − T (transmission) for two aqueous solutions of indazole-mPAH with 11 times difference in concentration; S7: absorption and fluorescence emission spectra acquired using an ∼25 μM aqueous solution of mPAH before and after irradiation; S8: time-resolved fluorescence data measured at 510 and 550 nm upon excitation with laser pulses centered at 405 nm for indazole-mPAH in different water/glycerol (w/w) mixtures, the corresponding fits and instrument response function, as well as the residuals of these fits; Fig. S9: double logarithmic plots of the average fluorescence decay rates as a function of solution viscosity for time-resolved fluorescence data acquired at 510 and 550 nm; Table S1 deconvolution fitting parameters for time-resolved fluorescence decays measured at 510, 530 and 550 nm for various water/glycerol (w/w) mixtures; and supporting computational results including Fig. S10 and S11. See DOI: https://doi.org/10.1039/d3cp04454h

---