 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unraveling the origin of the high photocatalytic properties of earth-abundant TiO2/FeS2 heterojunctions: insights from first-principles density functional theory†
Oluwayomi F.
Awe
 a,
Henry I.
Eya
a,
Henry I.
Eya
 a,
Ricardo
Amaral
a,
Ricardo
Amaral
 a,
Nikhil
Komalla
a,
Nikhil
Komalla
 a,
Pascal
Nbelayim
b and
Nelson Y.
Dzade
a,
Pascal
Nbelayim
b and
Nelson Y.
Dzade
 *a
*a
aDepartment of Energy and Mineral Engineering, Pennsylvania State University, University Park, PA 16802, USA
bDepartment of Materials Science and Engineering, School of Engineering Sciences, College of Basic and Applied Sciences, University of Ghana, Accra, Ghana. E-mail: nxd5313@psu.edu
First published on 29th March 2024
Abstract
Herein, first-principles density functional theory calculations have been employed to unravel the interfacial geometries (composition and stability), electronic properties (density of states and differential charge densities), and charge carrier transfers (work function and energy band alignment) of a TiO2(001)/FeS2(100) heterojunction. Analyses of the structure and electronic properties reveal the formation of strong interfacial Fe–O and Ti–S ionic bonds, which stabilize the interface with an adhesion energy of −0.26 eV Å−2. The work function of the TiO2(001)/FeS2(100) heterojunction is predicted to be much smaller than those of the isolated FeS2(100) and TiO2(001) layers, indicating that less energy will be needed for electrons to transfer from the ground state to the surface to promote photochemical reactions. The difference in the work function between the FeS2(100) and TiO2(001) heterojunction components caused an electron density rearrangement at the heterojunction interface, which induces an electric field that separates the photo-generated electrons and holes. Consistently, a staggered band alignment is predicted at the interface with the conduction band edge and the valence-band edge of FeS2 lying 0.37 and 2.62 eV above those of anatase. These results point to efficient charge carrier separation in the TiO2(001)/FeS2(100) heterojunction, wherein photoinduced electrons would transfer from the FeS2 to the TiO2 layer. The atomistic insights into the mechanism of enhanced charge separation and transfer across the interface rationalize the observed high photocatalytic activity of the mixed TiO2(001)/FeS2(100) heterojunction over the individual components.
I. Introduction
Rising global energy demand and related environmental pollution issues are among the greatest technological challenges facing humanity in the 21st century. To ensure environmental sustainability and the long-term development of human society, there is a pressing need for the development of environmentally friendly and renewable technologies for green energy production and environmental remediation. Among the various emerging technologies, semiconductor-based photocatalysis has immense potential owing to its ability to directly utilize the abundant and freely available solar energy for both the production of valuable chemical fuels, such as hydrogen and hydrocarbon fuels, and the degradation of harmful pollutants.1–6The development of inexpensive, highly stable, and recyclable photocatalysts with large specific surface areas and high photocatalytic activity is the key to the large-scale implementation of photocatalytic technology. In the past decade, several photocatalytic materials including TiO2,7,8 g-C3N4,9 Ga2O3,10 ZnIn2S4,11 Bi2WO6,12 SrNb2O6,13 and ZnO14 have been developed. Among them, TiO2 has attracted the most attention as an active photocatalyst for several environmental and energy applications owing to its abundance, low cost, chemical stability, non-toxicity, and resistance toward photocorrosion.15,16 However, the restricted light absorption ability (3–5% of the entire sunlight spectrum) owing to the wide band gap (3.2–3.35 eV) and the fast recombination of photogenerated electron–hole pairs remain as two major factors that limit the practical applications of TiO2.17 To overcome these limitations and promote efficient separation of photogenerated charge carries, various strategies including doping,18 metal loading,19 surface modification,20 and introducing heterojunctions21 have been adopted.
Among the various strategies explored to efficiently separate the photogenerated electron–hole pairs in semiconductor photocatalysts, heterojunction formation using different functional materials in a single photocatalyst has been proven to be one of the most effective strategies.22–26 The combined beneficial synergistic effects in heterojunction photocatalysts (particularly, properly engineered type-II band aligned heterojunctions) have the potential for broadening light harvesting properties, improving chemical stability, promoting the efficient separation and transfer of charge carriers to the appropriate active sites for the desired redox reactions, and thus boosting photocatalytic activity.22,27 Therefore, photoelectrochemical devices based on dual absorbers (heterojunctions) can achieve thermodynamic efficiencies of up to 41% for water splitting and 32–42% for CO2 reduction.28–30 For instance, enhanced photocatalytic activity has been reported for Cu2O/TiO2,31 WO3/TiO2,32–34 TiO2/CdS,35,36 and TiO2/CsPbBr337 heterojunctions.
Pyrite (FeS2) is a potential earth-abundant and non-toxic cocatalyst for next-generation photoelectrochemical (PEC) applications owing to its narrow band gap (0.95 eV) and large optical absorption coefficient (>105 cm−1).38 Furthermore, FeS2 displays great stability against photocorrosion in photoelectrochemical (PEC) applications.39,40 Because the coupling of FeS2 with a large band gap semiconductor like TiO2 can promote the efficient separation of photogenerated carriers, the fabrication of TiO2/FeS2 heterojunction photocatalysts has recently been explored for photoelectrocatalytic reduction of CO2 to methanol under visible light,41 the hydrogen evolution reaction (HER),39,42 the oxygen evolution reaction (OER),43 and photocatalytic degradation of organic compounds.44 The TiO2/FeS2 heterojunction photocatalysts show enhanced photocatalytic activity compared with the corresponding single photocatalysts. For instance, the formation of FeS2/anatase-TiO2 core/shell composites has been demonstrated to enhance hydrogen production by methanol/water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) due to a narrower band gap than those of isolated TiO2 and FeS2.45 Furthermore, the coupling of pyrite FeS2 with hierarchical top-porous bottom-tubular TiO2 nanotubes has been applied to realize PEC performance enhancement by more than 3-orders of magnitude from the ultraviolet and visible light regions compared to that of the isolated TiO2 nanotubes.46 However, the origin of the enhanced photocatalytic performance is not well known and there have been no comprehensive theoretical studies dedicated to uncovering the detailed mechanism of carrier dynamics of FeS2-based heterostructures. It is, therefore, highly desirable to investigate the factors influencing the photocatalytic properties of the TiO2/FeS2 composite and the nature of the interfacial interactions between them.
1) due to a narrower band gap than those of isolated TiO2 and FeS2.45 Furthermore, the coupling of pyrite FeS2 with hierarchical top-porous bottom-tubular TiO2 nanotubes has been applied to realize PEC performance enhancement by more than 3-orders of magnitude from the ultraviolet and visible light regions compared to that of the isolated TiO2 nanotubes.46 However, the origin of the enhanced photocatalytic performance is not well known and there have been no comprehensive theoretical studies dedicated to uncovering the detailed mechanism of carrier dynamics of FeS2-based heterostructures. It is, therefore, highly desirable to investigate the factors influencing the photocatalytic properties of the TiO2/FeS2 composite and the nature of the interfacial interactions between them.
In this work, first-principles density functional theory (DFT) calculations have been employed to unravel the interfacial structure and stability, density of states, differential charge densities, work function, and energy band alignment of the TiO2(001)/FeS2(100) heterojunction. The TiO2/FeS2 heterojunction is demonstrated to be stabilized by the formation of interfacial Fe–O and Ti–S ionic bonds. A staggered band alignment with a small conduction band offset of 0.37 eV is predicted for the TiO2(001)/FeS2(100) heterojunction, which is small enough to promote the efficient separation of photogenerated electrons from FeS2 to TiO2 under light irradiation. Consistently, a lower work function is predicted for the FeS2(100) surface (ϕ = 5.03 eV) than the TiO2(001) surface (ϕ = 5.22 eV). Compared to the isolated materials, the TiO2(001)/FeS2(100) heterojunction has a much lower work function (ϕ = 4.09 eV), which should promote the easy transfer of electrons to the photocatalyst surface for photochemical reactions. The efficient separation of electron–hole pairs in the TiO2(001)/FeS2(100) junction is beneficial for improving the photocatalytic activity, explaining well the high-photocatalytic performances reported in previous experimental investigations.
II. Computational details
The first-principles calculations were performed using the plane augmented-wave (PAW)47 as implemented in the Vienna Ab initio Simulation Package (VASP).48,49 Geometry optimizations were performed using the PBE (Perdew–Burke–Ernzerhof) generalized gradient approximation functional50 until the residual forces on all atoms reached 10−3 eV Å−1. The kinetic plane-wave energy cut-off was set to 600 eV, which converged the total energies of the studied materials to within 10−6 eV. Non-local dispersion forces were accounted for using the Grimme DFT-D3 scheme.51 Monkhorst–Pack52k-points meshes of (7 × 7 × 7) and (9 × 9 × 5) were used to sample the Brillouin zone of FeS2 and TiO2, respectively. The pyrite FeS2 was modeled in the cubic Pa3 space group, whereas anatase TiO2 was modeled in the tetragonal I41/amd space group as shown in Fig. 1. To accurately predict the electronic bandgap of FeS2 and TiO2, we have used the Hubbard correction (DFT+U) approach,53 which adds an on-site Coulomb repulsion to the DFT Hamiltonian, providing a better treatment of the strong electron correlation in the localized Fe and Ti d-orbitals. An effective U of 2.0 eV for Fe-3d in FeS2 and that of 7.3 eV for Ti-3d in TiO2 have been tested to provide an accurate description of the structural parameters and the electronic bandgaps. Fig. S1 and S2 (ESI†) show the variation of the bandgap and lattice parameters calculated at different effective U-values. | ||
| Fig. 1 The total and partial density of states of (a) pyrite FeS2 and (b) anatase TiO2. The Fermi level is set to zero. The insets are the optimized crystal structures in polyhedral representation. | ||
The FeS2(100) and TiO2(001) surfaces were coupled together to form the TiO2(001)/FeS2(001) heterojunction because they are often reported as the stable surfaces and they do not contain dangling bonds that could lead to the formation of a non-coherent interface.54,55 A vacuum region of 20 Å was added to the c-direction to avoid spurious interactions between periodic slabs. The work function (Φ), which represents the minimum energy needed to remove an electron from the bulk of a material through a surface to a point outside the material, was calculated as Φ = Evac − EF, where Evac is the vacuum level and EF is the Fermi level. Dipole corrections perpendicular to all surfaces were accounted for using the Makov–Payne scheme,56 which ensured that there is no net dipole perpendicular to the surfaces that may affect the potential in the vacuum level. Charge transfer between the FeS2(100) and TiO2(001) slabs in the TiO2(001)/FeS2(001) heterojunction is quantified using the Bader charge analysis code developed by Henkelman and co-workers.57
III. Results and discussion
A. Structural and electronic properties of bulk FeS2 and TiO2
Pyrite FeS2 crystallizes in the cubic Pa3 space group.58 The cubic pyrite structure can be described as trigonally distorted FeS6 octahedra and tetrahedrally coordinated sulfur atoms (inset in Fig. 1a).58–61 The lattice parameter of FeS2 is predicted at a = 5.409 Å in close agreement with the experimental value (5.416 Å)62,63 and a range of earlier theoretical results of pyrite.64–68 The Fe–S and S–S bond distances in pyrite are calculated as 2.252 and 2.159 Å, respectively.Anatase TiO2 crystallizes in the tetragonal structure with the space group I41/amd symmetry (inset in Fig. 1b).69,70 The structure consists of distorted TiO6 octahedra sharing two adjacent edges so that infinite planar double chains are formed. In the ab-plane, every O ion has neighboring Ti ions either in the a or the b directions. The equilibrium lattice parameters of anatase TiO2 are predicted at a = 3.803 Å and c = 9.517 Å, in good agreement with the experimental lattice parameters (a = 3.785 Å and c = 9.514 Å).70 The electronic density of states projected (PDOS) on the Fe d-states and S p-states of FeS2 is displayed in Fig. 1a. An analysis of the PDOS of FeS2 reveals that the valence and conduction band edges are composed mainly of the Fe 3d states with a small contribution of the S 3p states, indicating that the pyrite Fe 3d → Fe 3d charge transfer semiconductor is in good agreement with earlier theoretical predictions.64,71 The band gap of pyrite is calculated to be 0.96 eV, in good agreement with the value obtained from photoconductivity measurements (0.90–1.00 eV).38,72,73 The electronic PDOS of anatase TiO2 is shown in Fig. 1b, wherein the valence band edge is dominated by O 2p, and the conduction band edge is dominated by Ti 3d states. The electronic band gap of anatase TiO2 is predicted to be 3.21 eV, in good agreement with the experimental value of 3.23 eV.74
The pyrite FeS2(100) and anatase TiO2(001) surfaces (Fig. 2a and b), which have been investigated extensively in previous studies75–78 because of their stability and expression in the morphology of their respective crystals,79,80 were employed as a reference for comparison with the interface models, wherein we analyze the interactions between these two surfaces. The electronic project density of states (PDOS) of the pyrite FeS2(100) and anatase TiO2(001) are shown in Fig. 2c and d, respectively. The semiconductor characters of both FeS2 and TiO2 were observed with the bandgaps computed at 0.96 eV and 2.46 eV, respectively. The reduction in the TiO2(001) surface compared to the bulk value can be rationalized by considering the fact that the change in the coordination of the surface atoms compared to those in the bulk modifies the shape of the bands of the O 2p and Fe 3d hybridization, which consequently reduce the bandgap.
 | ||
| Fig. 2 Surface structures and the corresponding total and partial density of states (PDOS) of (a–b) FeS2(100) and (c–d) TiO2(001) surface models. The Fermi level is set to zero. | ||
B. Structural, electronic and optical properties of the TiO2(001)/FeS2(100) heterojunction
Considering their surface stabilities and reasonable lattice match, the FeS2(100) and TiO2(001) surfaces were employed in building the TiO2(001)/FeS2(100) interface model. The FeS2(100) unit cell was placed on the relaxed TiO2(001) surface and adjusted along the interfacial plane to fit the substrate's lattice parameters. A (2 × 2) supercell of the FeS2(100) surface (10.808 × 10.808) and a (3 × 3) supercell of the TiO2(001) surface (11.588 × 11.588) were employed, which yield a small lattice mismatch of 6.73% in both the x and y directions in the interface of FeS2(100) epi-layer and a TiO2(001) substrate. Fig. 3a shows that the TiO2(001)/FeS2(100) interface is stabilized through the formation of Fe–O and Ti–S bonds. The average Fe–O and Ti–S bond distances are predicted to be 2.176 Å and 2.634 Å, respectively, which are short enough, in particular the Fe–O bonds, to stabilize the interface structure.The interfacial adhesion energy (Ead) was calculated to ascertain the stability of the TiO2(001)/FeS2(100) interface. It is defined as Ead = (ETiO2/FeS2 − (ETiO2 + EFeS2))/S, where ETiO2/FeS2 is the total energy of the TiO2/FeS2 heterojunction with the interface surface area S, while ETiO2 and EFeS2 are the total energies of the TiO2 and FeS2 surfaces, respectively. The interface adhesion energy between the TiO2(001) and FeS2(100) surfaces was predicted to be −0.26 eV Å−2, which indicates that the interface structure is thermodynamically stable. To understand the charge transfer and bonding type in the TiO2(001)/FeS2(100) nanocomposite, the differential charge density iso-surface contours are determined as shown in Fig. 3b. The formation of a stable interface is evident by the accumulation of charges between the Fe–O and Ti–S atoms. Further insight into the bonding nature at the TiO2(001)/FeS2(100) interface was gained by determining the electron localization function plots as shown in Fig. 4. It can be evident from Fig. 4a that the electron clouds are localized around S and O atoms (yellow color) and delocalized from Fe and Ti atoms, suggesting ionic bonds in both FeS2 and TiO2. In the two-dimensional electron localization function (Fig. 4b), the localized electron clouds on the FeS2 interface atoms do not connect with those of the TiO2 interface atoms, which suggests the formation of Fe–O and Ti–S atom ionic bonds at the TiO2(001)/FeS2(100) interface.
Furthermore, Bader charge analysis (Table S1, ESI†) was carried out to quantify any charge transfer between the FeS2(100) and TiO2(001) layers when they are coupled together. A total charge of 0.87 e− is predicted to be transferred from the FeS2(100) layer to the top of the TiO2(001) layer. The work functions (Φ) of FeS2(100) and TiO2(001) surfaces were calculated to help understand the origin of the charge transfer across the interface. The work function of the FeS2(100) surface is 5.03 eV vs. vacuum as shown in Fig. 5a, which is in excellent agreement with the value of 5.0 eV obtained from ultraviolet photoelectron spectroscopy measurements.38,81 As shown in Fig. 5b, the work function of the TiO2(001) surface is 5.22 eV, which is larger than that of the FeS2(100) surface and is consistent with experimental results (5.1 eV).82 Therefore, the spontaneous interfacial charge transfer from the FeS2(100) layer to the TiO2(001) layer when they are coupled together can be rationalized by the higher work function of the TiO2(001) surface.
Generally, when two photocatalytic materials are coupled to fabricate heterojunction photocatalysts, the electrons tend to transport from the material with the lower work function (where they are less tightly bound) and travel to the higher work function material. The work function difference between the components of the heterojunction causes a rearrangement of electron density at the heterojunction interface (Fig. 3b) and results in an induced electric field that separates the oppositely charged photo-generated electrons and holes. The work function of the TiO2(001)/FeS2(100) heterojunction calculated to be 4.09 eV vs. vacuum as shown in Fig. 5c is lower than those of isolated FeS2(100) and TiO2(001) surfaces. As the value of the photocatalyst work function dictates its ability to easily transfer electrons and thus its photoactivity, the predicted lower work function for the TiO2(001)/FeS2(100) heterojunction is the origin of the observed enhanced photocatalytic performances.31–36
To further ascertain the effect of coupling FeS2(100) and TiO2(001) on the photocatalytic performance, the layer-resolved projected density of states of the TiO2(001)/FeS2(100) heterojunction was determined as shown in Fig. 6. The PDOS indicates the presence of strong interfacial interactions between FeS2(100) and TiO2(001). Compared to the isolated surface models (Fig. 2), it is worth noting that the variations in the interface PDOS are particularly strong in the TiO2(001) layer (L4) interacting with the FeS2(100) surface. We observe a reduction in the bandgap of the TiO2(001) layers towards the interface region, calculated to be 3.07, 2.70, 2.45, and 1.11 eV for L1, L2, L3, and L4, respectively. The reduction and the changes in the features of the PDOS of the TiO2(001) interface layer (L4) can be rationalized by considering the fact that the interactions between Fe 3d and O 2p states at the interface (average Fe–O = 2.176 Å) are much stronger than between Ti 3d and S 2p states (average Ti–S = 2.634 Å). The stronger interface Fe–O bond formation resulted in the pulling up of the interacting O atoms towards the interface FeS2 layer (L5) by 0.521–0.696 Å. However, due to the weaker interface Ti–S bonds, the S atoms remained negligibly displaced upward/down, which is consistent with small variations observed in the PDOS features and bandgaps of the different FeS2(100) layers, which remained at 1.1 eV. These results indicate that the electronic structure and bandgap of TiO2 can be modified by the introduction of FeS2 thin films.
 | ||
| Fig. 6 The calculated layer-resolved density of states (PDOS) for the FeS2(100)–TiO2(001) heterojunction. The Fermi level is set to zero. | ||
Considering that the optical absorption properties of photocatalysts are of great importance for their photocatalytic activity, we have determined the absorption spectra of isolated FeS2(100) and TiO2(001) and compared them with that of the TiO2(001)/FeS2(100) heterojunction as shown in Fig. 7. The linear absorption properties were calculated from the frequency-dependent complex dielectric function ε(w) and expressed as ε(w) = ε1(w) + iε2(w), where ε1(w) and ε2(w) are the real and imaginary parts of the dielectric function, respectively, and w is the photon frequency. The absorption coefficient α(w) is calculated from ε1(w) and ε2(w) as follows:
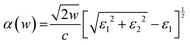 | (1) |
 | ||
| Fig. 7 Calculated optical absorption spectra of FeS2(100), TiO2(001), and FeS2(100)–TiO2(001) heterojunctions as a function of photon energy. | ||
Compared to isolated TiO2(001), the optical absorption edge of the TiO2(001)/FeS2(100) heterojunction is clearly red-shifted to lower photon energy with a higher absorption intensity observed in the visible-light region. Consistent with its lower bandgap, the FeS2(100) surface shows the highest absorption intensity. The enhancement in the optical absorption of TiO2(001) when coupled with FeS2(100) suggests improvement in the photocatalytic activity of the heterojunction.
C. Band alignment at the TiO2(001)/FeS2(100) interface
The band alignment of the heterojunction is of fundamental importance to achieve an efficient charge carrier separation, i.e., to reduce electron–hole recombination and improve photoactivity. Thus, an accurate prediction of the nature of band alignment and offsets of valence and conduction bands in the heterojunction is of key importance. Herein, the band alignment at the TiO2(001)/FeS2(100) interface has been estimated by the potential line-up method.83,84 The first step requires the determination of the electronic structure (density of states or band structure) calculation for the bulk materials.85 From the bulk electronic structure, the position of the valence-band maximum (VBM) can be determined with respect to the average electrostatic potential in the infinite solid. However, the average electrostatic potential is not properly defined for bulk calculations using periodic boundary conditions.86 To obtain an appropriate reference for aligning the valence and conduction bands, a superlattice calculation is performed, which allows aligning the electrostatic potentials in the bulk-like regions of the two materials, as shown in Fig. 8a. The space-dependent electrostatic potential V(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) is calculated by solving the Poisson equation. The planar-averaged potential
) is calculated by solving the Poisson equation. The planar-averaged potential ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) across the interface was obtained by the following equation:
(z) across the interface was obtained by the following equation: | (2) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (Z′) with respect to the z-direction in the two phases can be removed by determining the macroscopic average potential
(Z′) with respect to the z-direction in the two phases can be removed by determining the macroscopic average potential ![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z), which is given by:
(z), which is given by: | (3) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (Z′). Using the macroscopic average
(Z′). Using the macroscopic average ![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z) as in ref. 85 and 87, the valence band offset (ΔEVBO) at the TiO2(001)/FeS2(100) heterojunction was determined as follows:
(z) as in ref. 85 and 87, the valence band offset (ΔEVBO) at the TiO2(001)/FeS2(100) heterojunction was determined as follows: | (4) |
![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z) denotes the difference of
(z) denotes the difference of ![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z) between the two materials in the heterojunction as shown in Fig. 8a. The last two terms denote the difference between the valence band maximum energy (EVBM) and
(z) between the two materials in the heterojunction as shown in Fig. 8a. The last two terms denote the difference between the valence band maximum energy (EVBM) and ![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z) of the corresponding isolated materials in the heterojunction. The conduction-band offset (ΔECBO) at the TiO2(001)/FeS2 (100) can be calculated using the following formula:
(z) of the corresponding isolated materials in the heterojunction. The conduction-band offset (ΔECBO) at the TiO2(001)/FeS2 (100) can be calculated using the following formula: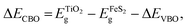 | (5) |
The macroscopic average (![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z)) values of FeS2 and TiO2 far away from the interface of the TiO2(001)/FeS2(100) heterojunction are −17.67 and −13.62 eV, respectively, giving rise to a Δ
(z)) values of FeS2 and TiO2 far away from the interface of the TiO2(001)/FeS2(100) heterojunction are −17.67 and −13.62 eV, respectively, giving rise to a Δ![[V with combining double overline]](https://www.rsc.org/images/entities/i_char_0056_033f.gif) (z) value of 4.05 eV. The energy differences between the macroscopic average potential and the VBM for the bulk TiO2 and FeS2 are calculated to be 1.24 eV and 7.91 eV, respectively. Based on eqn (3), the ΔEVBO value at the FeS2/TiO2 heterojunction is determined to be 2.62 eV, whereas the ΔECBO value is calculated to be 0.37 eV based on eqn (4). As schematically shown in Fig. 8b, the band alignment shows both the VBM and CBM of FeS2 to be above that of TiO2, resulting in the formation of a type-II band alignment.
(z) value of 4.05 eV. The energy differences between the macroscopic average potential and the VBM for the bulk TiO2 and FeS2 are calculated to be 1.24 eV and 7.91 eV, respectively. Based on eqn (3), the ΔEVBO value at the FeS2/TiO2 heterojunction is determined to be 2.62 eV, whereas the ΔECBO value is calculated to be 0.37 eV based on eqn (4). As schematically shown in Fig. 8b, the band alignment shows both the VBM and CBM of FeS2 to be above that of TiO2, resulting in the formation of a type-II band alignment.
The higher valence and conduction band edges of FeS2 than those of TiO2 suggest that upon irradiation of the TiO2(001)/FeS2(100) heterojunction, photogenerated conduction electrons will transfer from FeS2 to TiO2, and vice versa for photogenerated valence holes. The spatial distribution of the photogenerated electron–hole pairs in the two materials will inhibit their recombination, which is of great benefit for enhancing photocatalytic activity. Consistently, enhanced photocatalytic activity has been reported for methanol under visible light,41 a hydrogen evolution reaction (HER),42 an oxygen evolution reaction (OER),43 and photocatalytic degradation of organic compounds over FeS2/TiO2-based semiconductor composites.44 Our results on the electronic properties and band alignment characteristics compare well with previous theoretical and experimental investigations that observed type-II band alignment formation at SrTiO3/TiO2,88 CeO2/TiO2,89 and Cu2O/TiO290 heterojunctions as the primary reason for favoring efficient charge-carrier separation to enhance photocatalytic activity.
IV. Summary and conclusions
In summary, the interface structure and stability, electronic structure, and charge carrier dynamics in the TiO2(001)/FeS2(100) heterojunction were unraveled by the first-principles density functional theory methodology. It is demonstrated that the FeS2(100) surface can form a stable interface with the TiO2(001) surface via strong ionic Fe–O and Ti–S interactions. A strong variation in the interface density of states is observed particularly in the TiO2 region compared to isolated surface models, which can be ascribed to the stronger Fe–O bonds and surface reconstruction induced by the introduction of FeS2. Based on calculated electronic work functions and predicted type-II staggered band alignments at the TiO2(001)/FeS2(100) interface with both the conduction band edge and the valence-band edge of FeS2 lying above that of TiO2, efficient separation and transfer of photogenerated charge carriers from the FeS2 layer to the TiO2 layer would occur. The migration of electrons to the TiO2 layer is also expected to enhance its stability by keeping it in a reduced state. The atomic-level insights provided into the structure and interfacial phenomena in TiO2(001)/FeS2(100) heterojunctions rationalizes the often-observed enhancement of photocatalytic performance and provides promising strategies for designing and engineering more efficient TiO2-based photocatalysts.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support of the College of Earth and Mineral Sciences and the John and Willie Leone Family Department of Energy and Mineral Engineering of Pennsylvania State University. This research was supported in part by a Seed Grant award from the Penn State Institute for Computational and Data Sciences and the Institutes of Energy and the Environment. Pascal Nbelayim acknowledges support from the University of Ghana Building a New Generation of Academics in Africa (BANGA-Africa) Project Seed Research Grant [UG-BA/SRG-008/2022] with funding from the Carnegie Corporation in New York. Computations for this research were performed on the Pennsylvania State University's Institute for Computational and Data Sciences’ Roar supercomputer.References
- G. C. Xie, K. Zhang, B. D. Guo, Q. Liu, L. Fang and J. R. Gong, Graphene-based materials for hydrogen generation from light-driven water splitting, Adv. Mater., 2013, 25, 3820–3839 CrossRef CAS PubMed.
- A. Kudo and Y. Miseki, Heterogeneous photocatalyst materials for water splitting, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- M. Marszewski, S. Cao, J. Yub and M. Jaroniec, Semiconductor-based photocatalytic CO2 conversion, Mater. Horiz., 2015, 2, 261–278 RSC.
- H. Tong, S. Ouyang, Y. Bi, N. Umezawa, M. Oshikiri and J. Ye, Nano-photocatalytic materials: possibilities and challenges, Adv. Mater., 2012, 24, 229–251 CrossRef CAS PubMed.
- U. I. Gaya and A. H. Abdullah, Heterogeneous photocatalytic degradation of organic contaminants over titanium dioxide: A review of fundamentals, progress, and problems, J. Photochem. Photobiol., C, 2008, 9, 1–12 CrossRef CAS.
- A. Fujishima, X. Zhang and D. A. Tryk, TiO2 photocatalysis and related surface phenomena, Surf. Sci. Rep., 2008, 63, 515–582 CrossRef CAS.
- A. Fujishima and K. Honda, Electrochemical photolysis of water at a semiconductor electrode, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Understanding TiO2 Photocatalysis: Mechanisms and Materials, Chem. Rev., 2014, 114(19), 9919–9986 CrossRef CAS PubMed.
- W.-J. Ong, L.-L. Tan, Y. H. Ng, S.-T. Yong and S.-P. Chai, Graphitic Carbon Nitride (g-C3N4)-Based Photocatalysts for Artificial Photosynthesis and Environmental Remediation: Are We a Step Closer to Achieving Sustainability?, Chem. Rev., 2016, 116(12), 7159–7329 CrossRef CAS PubMed.
- M. Akatsuka, Y. Kawaguchi, R. Itoh, A. Ozawa, M. Yamamoto, T. Tanabe and T. Yoshida, Preparation of Ga2O3 photocatalyst highly active for CO2 reduction with water without cocatalyst, Appl. Catal., B, 2020, 262, 118247 CrossRef CAS.
- S. Wang, B. Guan and X. W. D. Lou, Construction of ZnIn2S4–In2O3 Hierarchical Tubular Heterostructures for Efficient CO2 Photoreduction, J. Am. Chem. Soc., 2018, 140, 5037–5040 CrossRef CAS PubMed.
- S. Cao, B. Shen, T. Tong, J. Fu and J. Yu, 2D/2D Heterojunction of Ultrathin MXene/Bi2WO6 Nanosheets for Improved Photocatalytic CO2 Reduction, Adv. Funct. Mater., 2018, 28, 1800136 CrossRef.
- S. Xie, Y. Wang, Q. Zhang, W. Deng and Y. Wang, SrNb2O6 nanoplates as efficient photocatalysts for the preferential reduction of CO2 in the presence of H2O, Chem. Commun., 2015, 51, 3430–3433 RSC.
- S. R. Lingampalli, M. M. Ayyub, G. Magesh and C. N. R. Rao, Photocatalytic reduction of CO2 by employing ZnO/Ag1-xCux/CdS and related heterostructures, Chem. Phys. Lett., 2018, 691, 28–32 CrossRef CAS.
- K. Li, B. Peng and T. Peng, Recent Advances in Heterogeneous Photocatalytic CO2 Conversion to Solar Fuels, ACS Catal., 2016, 6, 7485–7527 CrossRef CAS.
- H. Yang, B. Yang, W. Chen and J. Yang, Preparation and Photocatalytic Activities of TiO2-Based Composite Catalysts, Catalysts, 2022, 12, 1263 CrossRef CAS.
- M. Ge, C. Cao, J. Huang, S. Li, Z. Chen, K. Zhang, S. S. AlDeyabd and Y. Lai, A review of one-dimensional TiO2 nanostructured materials for environmental and energy applications, J. Mater. Chem. A, 2016, 4, 6772–6801 RSC.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Visible-Light Photocatalysis in Nitrogen-Doped Titanium Oxides, Science, 2001, 293, 269 CrossRef CAS PubMed.
- V. Subramanian, E. E. Wolf and P. V. Kamat, Catalysis with TiO2/Gold Nanocomposites. Effect of Metal Particle Size on the Fermi Level Equilibration, J. Am. Chem. Soc., 2004, 126, 4943 CrossRef CAS PubMed.
- X. Zhang, H. Cui, M. Humayun, Y. Qu, N. Fan, X. Sun and L. Jing, Exceptional performance of photoelectrochemical water oxidation of single-crystal rutile TiO2 nanorods dependent on the hole trapping of modified chloride, Sci. Rep., 2016, 6, 21430 CrossRef CAS PubMed.
- L. Wei, C. Yu, Q. Zhang, H. Liud and Y. Wang, TiO2-based heterojunction photocatalysts for photocatalytic reduction of CO2 into solar fuels, J. Mater. Chem. A, 2018, 6, 22411–22436 RSC.
- R. Marschall, Semiconductor Composites: Strategies for Enhancing Charge Carrier Separation to Improve Photocatalytic Activity, Adv. Funct. Mater., 2014, 24, 2421–2440 CrossRef CAS.
- T. Kawahara, Y. Konishi, H. Tada, N. Tohge, J. Nishii and S. Ito, A Patterned TiO2(Anatase)/TiO2(Rutile) Bilayer-Type Photocatalyst: Effect of the Anatase/Rutile Junction on the Photocatalytic Activity, Angew. Chem., 2002, 114, 2935 CrossRef.
- M.-G. Ju, G. Sun, J. Wang, Q. Meng and W. Liang, Origin of High Photocatalytic Properties in the Mixed-Phase TiO2: A First-Principles Theoretical Study, ACS Appl. Mater. Interfaces, 2014, 6, 12885–12892 CrossRef CAS PubMed.
- X. Wang, Q. Xu, M. Li, S. Shen, X. Wang, Y. Wang, Z. Feng, J. Shi, H. Han and C. Li, Photocatalytic overall water splitting promoted by an α-β phase junction on Ga2O3, Angew. Chem., Int. Ed., 2012, 51, 13089 CrossRef CAS PubMed.
- K. Afroz, M. Moniruddin, N. Bakranov, S. Kudaibergenov and N. Nuraje, A heterojunction strategy to improve the visible light-sensitive water-splitting performance of photocatalytic materials, J. Mater. Chem. A, 2018, 6, 21696–21718 RSC.
- J. Low, J. Yu, M. Jaroniec, S. Wageh and A. A. Al-Ghamdi, Heterojunction Photocatalysts, Adv. Mater., 2017, 1601694 CrossRef PubMed.
- R. T. Ross and T.-L. Hsiao, Limits on the yield of photochemical solar energy conversion, J. Appl. Phys., 1977, 48, 4783–4785 CrossRef.
- M. C. Hanna and A. J. Nozik, Solar conversion efficiency of photovoltaic and photoelectrolysis cells with carrier multiplication absorbers, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- M. R. Singh, E. L. Clark and A. T. Bell, Thermodynamic and achievable efficiencies for solar-driven electrochemical reduction of carbon dioxide to transportation fuels, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E6111–E6118 CAS.
- A. Paracchino, V. Laporte, K. Sivula, M. Gratzel and E. Thimsen, Highly active oxide photocathode for hotoelectrochemical water reduction, Nat. Mater., 2011, 10, 456–461 CrossRef CAS PubMed.
- C. Sotelo-Vazquez, R. Quesada-Cabrera, M. Ling, D. O. Scanlon, A. Kafizas, P. K. Thakur, T.-L. Lee, A. Taylor, G. W. Watson, R. G. Palgrave, J. R. Durrant, C. S. Blackman and I. P. Parkin, Evidence and Effect of Photogenerated Charge Transfer for Enhanced Photocatalysis in WO3/TiO2 Heterojunction Films: A Computational and Experimental Study, Adv. Funct. Mater., 2017, 27, 1605413 CrossRef.
- S. Higashimoto, M. Sakiyama and M. Azuma, Photoelectrochemical properties of hybrid WO3/TiO2 electrode. Effect of structures of WO3 on charge separation behavior, Thin Solid Films, 2006, 503, 201–206 CrossRef CAS.
- W. Smith, A. Wolcott, R. C. Fitzmorris, J. Z. Zhang and Y. Zhao, Quasi-core-shell TiO2/WO3 and WO3/TiO2 nanorod arrays fabricated by glancing angle deposition for solar water splitting, J. Mater. Chem., 2011, 21, 10792–10800 RSC.
- Z. Chen and Y.-J. Xu, Ultrathin TiO2 Layer Coated-CdS Spheres Core-Shell Nanocomposite with Enhanced Visible-Light Photoactivity, ACS Appl. Mater. Interfaces, 2013, 5, 13353–13363 CrossRef CAS PubMed.
- H. Ge, F. Xu, B. Cheng, J. Yu and W. Ho, S-Scheme Heterojunction TiO2/CdS Nanocomposite Nanofiber as H2- Production Photocatalyst, ChemCatChem, 2019, 11, 6301–6309 CrossRef CAS.
- F. Xu, K. Meng, B. Cheng, S. Wang, J. Xu and J. Yu, Unique Sscheme heterojunctions in self-assembled TiO2/CsPbBr3 hybrids for CO2 photoreduction, Nat. Commun., 2020, 11, 4613 CrossRef CAS PubMed.
- A. Ennaoui, S. Fiechter, C. Pettenkofer, N. Alonso-Vante, K. Büker, M. Bronold, C. Höpfner and H. Tributsch, Iron Disulfide for Solar Energy Conversion, Sol. Energy Mater. Sol. Cells, 1993, 29, 289–370 CrossRef CAS.
- D.-Y. Wang, C.-H. Li, S.-S. Li, T.-R. Kuo, C.-M. Tsai, T. R. Chen, Y.-C. Wang, C.-W. Chen and C.-C. Chen, Iron Pyrite/Titanium Dioxide Photoanode for Extended Near Infrared Light Harvesting in a Photoelectrochemical Cell, Sci. Rep., 2016, 6, 20397 CrossRef CAS PubMed.
- L. Wu, N. Y. Dzade, L. Gao, D. O. Scanlon, Z. Öztürk, N. Hollingsworth, B. M. Weckhuysen, E. J. M. Hensen, N. H. de Leeuw and J. P. Hofmann, Enhanced Photoresponse of FeS2 Films: The Role of Marcasite–Pyrite Phase Junctions, Adv. Mater., 2016, 28, 9602–9607 CrossRef CAS PubMed.
- E. Han, F. Hu, S. Zhang, B. Luan and P. Li, Hongqi Sun, and Shaobin Wang. Worm-like FeS2/TiO2 Nanotubes for Photoelectrocatalytic Reduction of CO2 to Methanol under Visible Light, Energy Fuels, 2018, 32, 4357–4363 CrossRef CAS.
- T.-R. Kuo, H.-J. Liao, Y.-T. Chen, C.-Y. Wei, C.-C. Chang, Y.-C. Chen, Y.-H. Chang, J.-C. Lin, Y.-C. Lee, C.-Y. Wen, S.-S. Li, K.-H. Lin and D.-Y. Wang, Extended visible to near-infrared harvesting of earth-abundant FeS2–TiO2 heterostructures for highly active photocatalytic hydrogen evolution, Green Chem., 2018, 20, 1640–1647 RSC.
- Z. Chen, R. Zheng, S. Deng, W. Wei, W. Wei, B.-J. Ni and H. Chen, Modular design of an efficient heterostructured FeS2/TiO2 oxygen evolution electrocatalyst via sulfidation of natural ilmenites, J. Mater. Chem. A, 2021, 9, 25032–25041 RSC.
- J. Rashid, S. Saleem, S. U. Awan, A. Iqbal, R. Kumar, M. A. Barakat, M. Arshad, M. Zaheer, M. Rafique and M. Awad, Stabilized fabrication of anatase-TiO2/FeS2 (pyrite) semiconductor composite nanocrystals for enhanced solar light-mediated photocatalytic degradation of methylene blue, RSC Adv., 2018, 8, 11935–11945 RSC.
- G. Lee and M. Kang, Physicochemical properties of core/shell structured pyrite FeS2/anatase TiO2 composites and their photocatalytic hydrogen production performances, Curr. Appl. Phys., 2013, 13, 1482–1489 CrossRef.
- Y. Xin, L. Li, W. Wu, F. Fu and Z. Zhang, Pyrite FeS2 Sensitized TiO2 Nanotube Photoanode for Boosting Near-Infrared Light Photoelectrochemical Water Splitting, ACS Sustainable Chem. Eng., 2016, 4(12), 6659–6667 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H–Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- D. R. Alfonso, Computational investigation of FeS2 surfaces and prediction of effects of sulfur environment on stabilities, J. Phys. Chem. C, 2010, 114, 8971–8980 CrossRef CAS.
- L. Chu, Z. Qin, J. Yang and X. Li, Anatase TiO2 Nanoparticles with Exposed {001} Facets for Efficient Dye-Sensitized Solar Cells, Sci. Rep., 2015, 5, 12143 CrossRef CAS PubMed.
- G. Makov and M. C. Payne, Periodic boundary conditions in ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, Phys. Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. S. Schmøkel, L. Bjerg, S. Cenedese, M. R. V. Jørgensen, Y.-S. Chen, J. Overgaarda and B. B. Iversen, Atomic properties and chemical bonding in the pyrite and marcasite polymorphs of FeS2: a combined experimental and theoretical electron density study, Chem. Sci., 2014, 5, 1408–1421 RSC.
- F. Hulliger and E. Mooser, Semiconductivity in pyrite, marcasite and arsenopyrite phases, J. Phys. Chem. Solids, 1965, 26, 429–433 CrossRef CAS.
- G. Brostigen and A. Kjekshus, On the relationships between the structure types pyrite, marcasite, and arsenopyrite, Acta Chem. Scand., 1970, 24, 2983–2992 CrossRef CAS.
- M. L. Huggins, The crystal structures of marcasite (FeS2), arsenopyrite (FeAsS) and loellingite (FeAs2), Phys. Rev., 1922, 19, 369–373 CrossRef CAS.
- G. Brostigen and A. Kjekshus, Redetermined crystal structure of FeS2 (Pyrite), Acta Chem. Scand., 1969, 23, 2186–2188 CrossRef CAS.
- R. Murphy and D. R. Strongin, Surface reactivity of pyrite and related sulfides, Surf. Sci. Rep., 2009, 64, 1–45 CrossRef CAS.
- R. Sun, M. K. Y. Chan and G. Ceder, First-principles electronic structure and relative stability of pyrite and marcasite: Implications for photovoltaic performance, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235311 CrossRef.
- P. Xiao, X.-L. Fan, L.-M. Liu and W.-M. Lau, Band gap engineering of FeS2 under biaxial strain: a first principles study, Phys. Chem. Chem. Phys., 2014, 16, 24466–24472 RSC.
- J. Hu, Y. Zhang, M. Law and R. Wu, First-principles studies of the electronic properties of native and substitutional anionic defects in bulk iron pyrite, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085203 CrossRef.
- T. Rozgonyi and A. Stirling, DFT Study of Oxidation States on Pyrite Surface Sites, J. Phys. Chem. C, 2015, 119, 7704–7710 CrossRef CAS.
- P. H. L. Sit, M. H. Cohen and A. Selloni, Interaction of Oxygen and Water with the (100) Surface of Pyrite: Mechanism of Sulfur Oxidation, J. Phys. Chem. Lett., 2012, 3, 2409–2414 CrossRef CAS PubMed.
- D. T. Cromer and K. Herrington, The Structures of Anatase and Rutile, J. Am. Chem. Soc., 1955, 77(18), 4708–4709 CrossRef CAS.
- C. J. Howard, T. M. Sabine and F. Dickson, Structural and thermal parameters for rutile and anatase, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 462–468 CrossRef.
- T. Schena, G. Bihlmayer and S. Blügel, First-principles studies of FeS2 using many-body perturbation theory in the G0W0 approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 235203 CrossRef.
- A. Schlegel and P. Wachter, Optical Properties, Phonons and Electronic Structure of Iron Pyrite (FeS2), J. Phys. C: Solid State Phys., 1976, 9, 3363–3369 CrossRef CAS.
- A. Zaka, S. M. Alhassan and A. Nayfeh, Iron pyrite in photovoltaics: a review on recent trends and challenges, ACS Appl. Electron. Mater., 2022, 4, 4173–4211 CrossRef CAS.
- L. Kavan, M. Grätzel, S. E. Gilbert, C. Klemenz and H. J. Scheel, Electrochemical and photoelectrochemical investigation of single-crystal anatase, J. Am. Chem. Soc., 1996, 118, 6716–6723 CrossRef CAS.
- T. Liu, I. Temprano, S. J. Jenkins, D. A. King and S. M. Driver, Nitrogen adsorption and desorption at iron pyrite FeS2(100) surfaces, Phys. Chem. Chem. Phys., 2012, 14, 11491–11499 RSC.
- M. Sacchi, M. C. E. Galbraith and S. J. Jenkins, The interaction of iron pyrite with oxygen, nitrogen and nitrogen oxides: a first-principles study, Phys. Chem. Chem. Phys., 2012, 14, 3627–3633 RSC.
- F. Xiong, L.-L. Yin, F. Li, Z. Wu, Z. Wang, G. Sun, H. Xu, P. Chai, X.-Q. Gong and W. Huang, Anatase TiO2(001)-(1 × 4) Surface Is Intrinsically More Photocatalytically Active than the Rutile TiO2(110)-(1 × 1) Surface, J. Phys. Chem. C, 2019, 123(40), 24558–24565 CrossRef CAS.
- H. Sun, W. Lu and J. Zhao, Structure and Reactivity of Anatase TiO2(001)-(1 × 4) Surface, J. Phys. Chem. C, 2018, 122, 14528–14536 CrossRef CAS.
- H. Xian, J. Zhu, X. Liang and H. He, Morphology controllable syntheses of micro- and nano-iron pyrite mono- and poly-crystals: a review, RSC Adv., 2016, 6, 31988–31999 RSC.
- S. Yang, N. Huang, Y. M. Jin, H. Q. Zhang, Y. H. Su and H. G. Yang, Crystal shape engineering of anatase TiO2 and its biomedical applications, CrystEngComm, 2015, 17, 6617–6631 RSC.
- L. Samad, M. Cabán-Acevedo, M. J. Shearer, K. Park, R. J. Hamers and S. Jin, Direct Chemical Vapor Deposition Synthesis of Phase-Pure Iron Pyrite (FeS2) Thin Films, Chem. Mater., 2015, 27, 3108–3114 CrossRef CAS.
- G. Xiong, R. Shao, T. C. Droubay, A. G. Joly, K. M. Beck, S. A. Chambers and W. P. Hess, Photoemission electron microscopy of TiO2 anatase films embedded with rutile nanocrystals, Adv. Funct. Mater., 2007, 17, 2133–2138 CrossRef CAS.
- E. Cerrato, C. Gionco, M. C. Paganini, E. Giamello, E. Albanese and G. Pacchioni, Origin of Visible Light Photoactivity of the CeO2/ZnO Heterojunction, ACS Appl. Energy Mater., 2018, 1, 4247–4260 CrossRef CAS.
- C. G. Van de Walle and R. M. Martin, Theoretical study of band offsets at semiconductor interfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 8154–8165 CrossRef CAS PubMed.
- L. Weston, H. Tailor, K. Krishnaswamy, L. Bjaalie and C. G. Van de Walle, Accurate and efficient band-offset calculations from density functional theory, Comput. Mater. Sci., 2018, 151, 174–180 CrossRef CAS.
- L. Kleinman, Comment on the average potential of a Wigner solid, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 7412 CrossRef CAS.
- J. Jia, Y. Li, B. Yao, Z. Ding, R. Deng, Y. Jiang and Y. Sui, Band offsets of Ag2ZnSnSe4/CdS heterojunction: An experimental and first-principles study, J. Appl. Phys., 2017, 121, 215305 CrossRef.
- G. Di Liberto, S. Tosoni, F. Illas and G. Pacchioni, Nature of SrTiO3/TiO2 (anatase) heterostructure from hybrid density functional theory calculations, J. Chem. Phys., 2020, 152, 184704 CrossRef CAS PubMed.
- M. A. Sha, P. C. Meenu, V. S. Sumi, T. C. Bhagya, B. R. Sreelekshmy and S. M. A. Shibli, Tuning of electron transfer by Ni–P decoration on CeO2–TiO2 heterojunction for enhancement in photocatalytic hydrogen generation, Mater. Sci. Semicond. Process., 2020, 105, 104742 CrossRef.
- Y. Liao, P. Deng, X. Wang, D. Zhang, F. Li, Q. Yang, H. Zhang and Z. Zhong, A facile method for preparation of Cu2O–TiO2 NTA heterojunction with visible-photocatalytic activity, Nanoscale Res. Lett., 2018, 13, 221 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04453j |
| This journal is © the Owner Societies 2024 |




