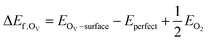Computational screening of single-atom doped In2O3 catalysts for the reverse water gas shift reaction†
Yuchen
Wang
 ab and
Shenggang
Li
ab and
Shenggang
Li
 *abc
*abc
aSchool of Physical Science and Technology, ShanghaiTech University, Shanghai 201210, P. R. China
bCAS Key Laboratory of Low–Carbon Conversion Science and Engineering, Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201203, P. R. China. E-mail: lisg@sari.ac.cn
cUniversity of Chinese Academy of Sciences, Beijing 100049, P. R. China
First published on 29th November 2023
Abstract
The reverse water gas shift (RWGS) reaction is an important method for converting carbon dioxide (CO2) into valuable chemicals and fuels by hydrogenation. In this paper, the catalytic activity of single-atom metal-doped (M = Pt, Ir, Pd, Rh, Cu, Ni) indium oxide (c-In2O3) catalysts in the cubic phase for the RWGS reaction was investigated using density functional theory (DFT) calculations. This was achieved by identifying metal sites, screening oxygen vacancies, followed by further calculating the energy barriers for the direct and indirect dissociation pathways of the RWGS reaction. Our results show that the single-atom dopant in the indium oxide lattice promotes the creation of oxygen vacancies on the In2O3 surface, thereby facilitating the adsorption and activation of CO2 by the oxide surface and initiating the subsequent RWGS reaction. Furthermore, we find that the oxygen vacancy (OV) formation energy on the surface of the single-atom metal doped c-In2O3(111) surface can be used as a descriptor for CO2 adsorption, and the higher the OV formation energy, the more stable the CO2 adsorption structure is. The Cu/In2O3 structure has relatively high energy barriers for both direct (1.92 eV) and indirect dissociation (2.09 eV) in the RWGS reaction, indicating its low RWGS reactivity. In contrast, the Ir/In2O3 and Rh/In2O3 structures are more conducive to the direct dissociation of CO2 into CO, which may serve as more efficient RWGS catalysts. Furthermore, microkinetic simulations show that single atom metal doping to In2O3 enhances CO2 conversion, especially under high reaction temperatures, where the formation of oxygen vacancies is the limiting factor for CO2 reactivity on the M/In2O3 (M = Cu, Ir, Rh) models. Among these three single-atom catalysts, the Ir/In2O3 model was predicted to have the best CO2 reactivity at reaction temperatures above 573 K.
1 Introduction
Carbon dioxide (CO2) is one of the major greenhouse gases responsible for global warming and climate change.1–5 The reverse water gas shift (RWGS) reaction (CO2 + H2 → CO + H2O) is an important method for the conversion of CO2 into the more useful carbon monoxide (CO),6,7 which is a versatile chemical intermediate for making commodity chemicals, such as methane, formic acid, hydrocarbons as liquid fuels, alcohols, and olefins, thus providing a promising alternative to the traditional fossil fuel-based chemical industry.8–12 The RWGS reaction can also be directly coupled with CO hydrogenation to produce higher value C2+ products, such as ethanol (C2H5OH). Huang's group13 recently reported a dual-functional Ir1–In2O3 monatomic catalyst that integrates two catalytically active centers by anchoring the monatomic Ir to the In2O3 support. The Ir1–In2O3 catalyst can efficiently hydrogenate CO2 in liquid with high selectivity for ethanol (>99%). This and similar approaches can not only help reduce CO2 emission but also provide an alternative source of valuable chemicals and fuels. Therefore, the RWGS reaction can serve as a pivotal technology for transforming the abundant CO2 resource into chemicals and hydrocarbon fuels, which is attractive for CO2 utilization and is of significance in building an ecological system for unconventional fuels.14Research into the RWGS reaction has been ongoing for hundreds of years, but it has gained renewed interest in recent years due to the urgent need to address climate change. However, a big challenge to this issue is the rational design of high temperature endurable RWGS catalysts with desirable CO product selectivity. The RWGS catalysts usually consist of well-dispersed metal active sites on high surface area metal oxide supports.15 In terms of metal sites, copper16 and several noble metals (Pt,17 Pd,18 Rh19) have been extensively studied. For the support, CeO216 is one of the most widely explored for the RWGS reaction because of its excellent redox properties.
In2O3 has been predicted and proven to be an excellent catalyst for CO2 conversion, for both hydrogenation to methanol (CH3OH) at relatively low temperature and the RWGS reaction. Ye et al.20 investigated CO2 hydrogenation on the defective In2O3(110) surface with a surface oxygen vacancy using periodic density functional theory (DFT) calculations. They showed that the D1 surface with the Ov1 site is thermodynamically the most stable, whereas the D4 surface with the Ov4 site is the least stable, and the CO2 hydrogenation to methanol reaction is more favorable on the D4 surface. In our previous studies,21 DFT calculations and experiments demonstrated that two distinct CO2 adsorption structures can be formed on the In2O3 surfaces of both the cubic and hexagonal phases, corresponding to CH3OH and CO formations, respectively. The (104) surface of the hexagonal phase of In2O3 exhibits higher activity and methanol selectivity in the CO2 hydrogenation reaction. In addition, the c-In2O3 catalyst mainly exposing the (110) surface was found to have good performance for the RWGS reaction. Therefore, optimizing the concentration of oxygen vacancies and improving the structure of the catalyst will be key to further increasing the activity of indium oxide.
Metal particle size plays an important role in controlling the stability of the CO2 hydrogenation catalysts and the distribution of the active sites, which dictate the catalytic reactivity and product selectivity. Recently, the development of single-atom catalysts (SACs) has gained significant attention due to their high activity and product selectivity towards various catalytic reactions.22,23 For example, a recent study24 shows that incorporating atomic Rh species into In2O3 can lead to high methanol productivity by creating oxygen vacancies for CO2 activation. Li et al.25 doped Pt atoms into In2O3 to form atomically dispersed Ptn+ species, most of which are stable under operating conditions, and their results show that adding atomically dispersed Ptn+ improves methanol selectivity, while Pt nanoparticles on In2O3 mainly promote the RWGS reaction. Zhu et al.26 found that the Ni promotor facilitates CH3OH synthesis from CO2, which was mainly attributed to the low energy barrier of H2 dissociation on the reduced surface Ni species, facilitating hydrogenation of the adsorbed CO2 at the oxygen vacancy (OV) site. Cannizzaro et al.27 elucidated the promotional role of Ni in In2O3-catalyzed CO2 hydrogenation, where three representative models have been investigated, namely (i) a single Ni atom doped In2O3(111) surface, (ii) a single Ni atom adsorbed on In2O3(111), and (iii) a small Ni8 cluster adsorbed on In2O3(111). Their microkinetic simulations reveal that only the supported Ni8 cluster can lead to high methanol selectivity, whereas single Ni atoms either doped or adsorbed on the In2O3 surface mainly catalyse CO formation. Qi et al.28 studied monatomic systems anchored on defective metal oxide surfaces, and used the anchoring energy to screen the stability of 232 monatomic systems under vacuum and CO2 reduction reaction conditions. They predicted that Ru/VO–ZrO2(111) would maintain a single atom form and show excellent catalytic performance in the RWGS reaction.
Although In2O3 has excellent catalytic activity and stability for CO2 hydrogenation, CO2 conversion is limited by the relatively low activity of indium oxide in dissociating molecular H2. A previous study13 indicated that bifunctional monatomic catalysts provide an effective approach for designing complex catalysts by synergistically utilizing the unique catalytic properties of single atomic sites and the supports. In order to explore the effect of doping for In2O3 with monatomic metal (M/In2O3) on the RWGS reaction, we selected copper (Cu), nickel (Ni), palladium (Pd), rhodium (Rh), platinum (Pt) and iridium (Ir) as the dopant on the In2O3 surface, and investigated the RWGS activity on these catalysts using DFT calculations.
2 Computational methods
2.1 Density functional theory calculations
We perform DFT calculations using the Vienna ab initio simulation package (VASP).29,30 The generalized gradient approximation (GGA) with the Bayesian error estimation functional including the van der Waals correlation (BEEF-vdW)31 was employed to account for the electron exchange and correlation in the Kohn–Sham theory. The detailed parameters used in this work are similar to those in our previous works.21,32,33 A plane wave energy cut-off of 400 eV and the Gaussian smearing width of 0.05 eV were employed. Convergence thresholds for the energy and force were set to 10−4 eV and 0.01 eV Å−1, respectively. Both the climbing image nudged elastic band (CI-NEB) method34,35 and the dimer method36 were used to find the transition states (TS), which were further confirmed through frequency analysis.We also investigated the effect of including the Hubbard U correction to the energies of some of our calculations. For the Ni/In2O3 system, DFT+U calculations were further performed with an effective Ueff value of 2.4 eV (Ueff = U − J) for Ni37 for CO2 direct dissociation. The difference in the absorption energy of [bt-CO2*] with and without adding the Hubbard U correction is 0.38 eV, but the difference in the CO2 dissociation energy with and without adding the Hubbard U correction is very small at 0.1 eV (Fig. S5, ESI†), so we conclude that its effect on most of the energetics calculated in this work should be relatively small. Furthermore, as the Hubard U correction was not included in most previous DFT studies,27,38–40 we also chose not to include this correction in the rest of our DFT calculations.
The c-In2O3(111) surface was built from the optimized primitive unit cell similar to our previous work,41 and the surface was modelled with a p(1 × 1) slab consisting of 48 In atoms and 72 O atoms distributed in three O–In–O trilayers. The supercell has a dimension of 14.44 Å × 14.44 Å × 17.99 Å. The vacuum layer thickness is 10 Å between adjacent slabs. All atomic layers are allowed to relax. The Brillouin zone is sampled using a (3 × 3 × 1) Monkhorst–Pack k-point mesh. For the Ni-doped model, spin polarization was enabled. Spin polarization was enabled by setting ISPIN to 2 in the INCAR input file, and several other related parameters were also set to their recommended values (e.g. AMIX = 0.2, BMIX = 0.0001, AMIX_MAG = 0.8, BMIX_MAG = 0.0001).
Substitution of an In atom on the topmost layer of the c-In2O3(111) surface by a metal atom (Pt, Ir, Pd, Rh, Cu, Ni) is considered, and the resulting models are denoted as Pt/In2O3, Ir/In2O3, Pd/In2O3, Rh/In2O3, Cu/In2O3, and Ni/In2O3, respectively. Definitions of the formation energy of an OV site and the adsorption energy of an adsorbate on a slab surface are similar to our previous works.33,42 An OV site on the defective c-In2O3 surface forms upon removing one O atom from the stoichiometrically perfect c-In2O3 surface. The formation energy of an OV site (ΔEf,OSV) is calculated as the reaction energy of the thermal desorption of molecular O2:
| Ead,A = Etotal − (Eslab + EA) |
2.2 Microkinetic simulations
CatMAP44 was used to simulate the reaction kinetics of the RWGS reaction under the typical reaction conditions of 450–700 K and 50 MPa. The elementary reactions considered in this model are listed in Table S8 (ESI†). Two different sites were considered. The s_site denotes the OV site for the adsorption of various intermediates arising from CO2 hydrogenation, and the t_site denotes the In site for hydrogen adsorption in the form of a hydride or a proton. The t_site is a “hydrogen reservoir” site, so it does not compete with other adsorbates for the s_site, which is the free site. The enthalpy and entropy of the gaseous species were calculated using the ideal gas model, while those of the surface adsorbates and the transition states were evaluated using the harmonic approximation. The degrees of rate control (DRC)45,46 as proposed by Campbell and implemented in CatMAP were also calculated to provide further insights into the rate determining steps.3 Results and discussion
3.1 Monatomic metal doping site
The pristine c-In2O3(111) surface consists of 16 In and 12 O atoms on the topmost layer, as can be seen in Fig. 1(a), on which the In and O atoms are labelled as In1–In16 and O1–O12, respectively. Fig. 1(b) shows the side view of the three-layer slab model of c-In2O3(111), indicating that each layer roughly consists of the O–In–O trilayers. In this study, the O on the topmost layer of the surface is considered for vacancy formation. To determine the location of the single M atom (Pt, Ir, Pd, Rh, Cu, Ni) on the doped In2O3(111), all the possible structures for substitution in the topmost In layer were calculated and compared for stability, as shown in Fig. 1(c) and Fig. S1 (ESI†). It can be clearly seen that the doped single metal atom at the topmost layer of c-In2O3(111) has several sites with the same relative energy, which have the same chemical environment and are equivalent sites due to symmetry. This indicates that the 16 In sites could be divided into 6 groups labelled by a–f, as listed in Table S1 (ESI†).In addition, as shown in Table 1, the adhesive energy (ΔEadh) was also calculated, which was defined as the binding energy of an M atom from its bulk state to a surface In vacancy (VIn) on the In2O3(111) slab from the following equation
| ΔEadh = EM/In2O3 − EM − EVIn/In2O3 |
| Site | Pt7 | Ir7 | Pd7 | Rh11 | Cu7 | Ni11 |
|---|---|---|---|---|---|---|
| ΔEadh/eV | −9.78 | −12.84 | −8.75 | −10.79 | −8.01 | −10.11 |
| ΔEcoh/eV | −5.39 | −8.02 | −4.25 | −5.65 | −3.23 | −5.44 |
E M/In2O3 is the energy of the M/In2O3(111) surface, EM is the energy of an M atom in its bulk state, and EVIn/In2O3 is the energy of the In2O3(111) slab with a surface In vacancy. Our calculations show that these six metal dopants prefer to replace the surface In7 and In11 sites. Furthermore, the ΔEadh value is much more negative than the cohesive energy (ΔEcoh) of bulk M (M = Pt, Ir, Pd, Rh, Cu, Ni), indicating strong interaction between the atomic M dopant and the In2O3(111) surface, which may prevent the M dopant from self-aggregation.
In addition, for Ir/In2O3, the possibility for the migration of the Ir dopant from the surface to the subsurface layer was also explored. The migration energy, which was defined as the energy difference between the Ir/In2O3 slab with the Ir dopant located at the surface and subsurface layers, for the 16 sites on the surface was found to range from −0.72 eV to 0.44 eV (Fig. S6, ESI†), indicating that some of the surface Ir dopants might migrate to the subsurface layer, although it might incur a significant energy barrier unless there was already a subsurface In vacancy.
The heat map in Fig. 1(c) shows that the c doping site has the highest relative energy for the elements involved, whereas the f doping site has the lowest relative energy for four metal elements (Pt, Ir, Pd, Rh), and the e doping site has the lowest relative energy for the remaining two metal elements (Cu, Ni). In addition, except for the f doping site, the relative energy of metal doping to the surface of c-In2O3(111) increases as the row in the periodic table increases.
We selected the doping site with the lowest relative energy for each metal in our further calculations. In addition, according to the previous studies of our group,33 the OV6 site (we note the slight changes in the ordering of our labels from our previous works) has the highest OV formation energy with the highest CO2 reactivity, so the M7, M8 and M11 metal doping sites near the OV6 site are also included in our calculations. The metal doping sites and oxygen vacancies can be divided into M9/12–OV4/7, M9/12–OV8/10, M7–OV2, M7–OV5, M7–OV6, M8–OV6, and M11–OV6 as shown in the heat map in Fig. 1(d) for the OV formation energy with further details listed in Table S2 (ESI†). Overall, the OV formation energies of the single-atom metal doped structures near the OV6 site are higher than those of the other sites. Ir (5d76s2) and Rh (4d85s1) doped single metal atoms with the same nine valence electrons have a similar OV formation energy. In addition, the doped metal elements Pt, Ir, Pd, and Rh in the sixth and fifth rows in the periodic table have relatively higher OV formation energies than the doped elements Cu and Ni in the fourth row.
Furthermore, we examined the stability of the oxygen vacancy on the monatomic metal doped surface. For the Ir/In2O3 model, when the surface OV6 is present, the adsorption energy ΔE of another Ir atom adsorbed at the OV6 site was calculated to be 1.13 eV from the following equation
| ΔE = EIr–ads − EIr − EIr7–OV6 |
E Ir–ads is the energy of Ir7–OV6 with another Ir atom adsorbed at the vacancy OV6, EIr is the energy of the Ir atom in its bulk state, and EIr7−OV6 is the energy of the Ir7–OV6 structure. Thus, the presence of oxygen vacancies may not lead to the aggregation of Ir monoatoms.
3.2 Dissociative adsorption of H2
Heterolytic dissociation of H2 on the perfect surface results in two H adatoms adsorbed at the O6 and In sites near the single-metal atom M site (M = Pt, Ir, Pd, Rh, Cu, Ni, In). Fig. 2 shows the potential energy for OV formation via H2 reduction of the M/In2O3 surfaces with further details given in Table S5 (ESI†). The detailed structures of Cu/In2O3 with the M7 doping site and Ni/In2O3 with the M11 doping site are shown in this figure. The resulting In–Ha and O–Hb bond lengths are 1.77 Å and 0.97 Å, respectively. Here, the first transition state [TS–2H]* has an energy barrier between 0.66 eV, and the In–Ha and O–Hb bond lengths are 2.20 Å and 1.33 Å, respectively. This is followed by hydride transfer from In–Ha to the adjacent hydroxyl group (OHb) to form an adsorbed H2O molecule with an energy barrier of 0.64 eV, and the In–Ha, O–Ha and O–Hb bond lengths are 1.84 Å, 1.58 and 0.98 Å, respectively.We find that the energy barrier of H2 dissociation ([TS–2H]*) after single-metal atom doping is lower than that on the pure indium oxide surface (Ea = 1.08 eV), and that for H2 dissociation on the Cu/In2O3 structure is the lowest. However, for the transition state of water formation ([TS–H2O]*), the energy barriers for the M/In2O3 structures are higher than that of c-In2O3(111) (Ea = 0.52 eV). Overall, Cu/In2O3 is the most favourable for OV formation through H2 dissociation considering both the energy barrier and reaction energy.
Furthermore, for OV formation, H2 reduction may occur at either the In–O or M–O site. For the Pt/In2O3 model, the energy barrier for [TS–2H]* for H2 dissociation at the Pt and O sites is lower than that at the In and O sites by 0.50 eV, as shown in Fig. S8 (ESI†). However, since the [MH–OH]* structure is always more stable than the [InH–OH]* structure as shown in Table S9 (ESI†), the subsequent hydrogen transfer to form the oxygen vacancy becomes more difficult, as the Ea of OV formation from the [PtH–OH]* structure is 1.57 eV, which is 0.74 eV higher than that from the [InH–OH]* structure, as shown in Fig. S8 (ESI†).
3.3 CO2 adsorption and activation on single-atom doped In2O3 surfaces
We further performed Bader charge analysis for these sites, and found that the single metal atom site on the doped c-In2O3(111) surface underwent a change in the oxidation state after OV formation. As shown in Table 2, on surfaces where an oxygen vacancy is present, the oxidation states of the doped metals are all reduced, with the number of electrons gained by the doped metal ranging from 0.26 electrons (Rh) to 0.47 electrons (Pt). The number of electrons gained by In on the pure c-In2O3(111) is 0.41 electrons. Compared to the other doped metals, Pt and Ir, which belong to the sixth row in the periodic table, gain more electrons after OV formation. Upon OV formation, the oxidation state of the Pt dopant is reduced by the largest amount, whereas those of the Cu and Ni dopants are reduced by much less. Thus, the ΔQa value can be correlated to the oxygen vacancy formation energy of the M/In2O3 models, consistent with the much lower oxygen vacancy formation energies of Cu and Ni than other metals.| Q/|e| | Pt7 | Ir7 | Pd7 | Rh11 | Cu7 | Ni11 | In2O3 |
|---|---|---|---|---|---|---|---|
| Q1 (M_P) | 1.19 | 1.44 | 1.08 | 1.22 | 1.17 | 1.23 | 1.79 |
| Q2 (M_OV) | 0.72 | 1.00 | 0.74 | 0.96 | 0.86 | 0.89 | 1.38 |
| Q3 (M_CO2) | 0.96 | 1.23 | 0.87 | 1.07 | 0.96 | 1.04 | 1.61 |
| ΔQa (= Q2 − Q1) | −0.47 | −0.44 | −0.34 | −0.26 | −0.31 | −0.34 | −0.41 |
| ΔQb (= Q3 − Q2) | 0.24 | 0.23 | 0.13 | 0.11 | 0.10 | 0.15 | 0.23 |
Adsorption and activation of CO2 at the above representative Ov sites on the M/In2O3 surfaces are further studied, which are important in the CO2 hydrogenation reaction. According to our previous study on the In2O3 surfaces,32 sites with higher OV formation energy tend to favour CO2 adsorption and activation. Therefore, we focused on the adsorption of CO2 at the M7/8/11–OV6 sites as shown in Table S3 and Fig. S2 (ESI†). The most stable adsorption structures of CO2 at the single metal sites were screened. Our calculations show that doping a single metal atom on the In2O3 catalyst can improve CO2 adsorption and activation. The optimized structures of the surfaces with these monatomic metal doping sites and oxygen vacancy (OV6) sites are shown in Fig. 3(a), and our subsequent calculations on the RWGS reaction are performed on these structures.
Previous studies in our group32 have revealed two different CO2 adsorption configurations. Again, taking the Cu7–OV6 structure as an example, the bent CO2 (bt-CO2*) structure adsorbed on the surface is shown in Fig. S2 (ESI†), where the CO2 adsorbate is distorted, resulting in an O–C–O angle of 132.7°, compared to the linear O–C–O configuration in a free CO2 molecule. One O atom of the CO2 adsorbate occupies the OV6 site, whereas the C atom binds the Cu atom. The C–O bonds in the CO2 adsorbate are elongated to 1.20 Å and 1.31 Å from those of 1.18 Å in a free CO2 molecule. These results indicate that the CO2 adsorbate is activated. Compared with the pure indium oxide surface, monatomic metal doping benefits CO2 adsorption in the bt-CO2*, and CO2 adsorption at the Pt7–OV6 site is the most stable.
Bader charge analysis further shows that the doped metal site in the M/In2O3 structure undergoes a significant change in the oxidation state upon CO2 adsorption in the bt-CO2*. As shown in Table 1, the number of electrons lost from the monatomic metal after CO2 adsorption ranges from 0.10 e to 0.24 e. Combined with the above analysis of the CO2 adsorption energies on these structures, electron transfer from the doped metal may contribute to the strong CO2 adsorption, and the greater the number of electrons transferred from the doped metal, the more stable the CO2 adsorption structure is. For example, the CO2 adsorption energy at the Cu site is −0.5 eV with ΔQb = 0.10 |e|, whereas that at the Pt site it is −1.46 eV with ΔQb = 0.24 |e|.
In addition, at these monatomic metal doping sites, the larger the OV formation energy, the more stable the CO2 adsorption is. As shown in Fig. 3(b), except for c-In2O3(111), the OV formation energy can be approximately linearly correlated with the bt-CO2* adsorption energy. For instance, the Cu7–OV6 site has the lowest OV formation energy (2.18 eV) and its corresponding CO2 adsorption energy (−0.5 eV) is also the least negative. From Fig. 3(b), CO2 adsorption on all the M/In2O3 structures are more stable than that on the pure c-In2O3(111).
3.4 RWGS reaction pathway
The main mechanisms reported for the RWGS reaction are direct dissociation and indirect conversion via carboxylic acid (COOH*). The intermediate bt-CO2* is involved in the direct dissociation pathway, which dissociates to form CO* and O*, with CO* desorption to yield CO. The second pathway occurs via CO2* hydrogenation to form the intermediate COOH*; its C–OH bond is then broken to give CO* and OH*, followed by CO* desorption to produce CO.Fig. 4(a) shows the energy profile for the direct dissociation of CO2 on the M/In2O3 surfaces with the detailed energies given in Table S6 (ESI†). Taking the Cu/In2O3 structure with an OV as an example, the bt-CO2* structure is formed, where the C–Cu bond length is 1.95 Å, and the C–O bond length is 1.20 Å and 1.30 Å (near OV6), respectively. Then, the C–O bond in the CO2* adsorbate with the O atom near OV6 breaks with an energy barrier (Ea) of 1.92 eV, whose bond length in the transition state is 1.95 Å. The CO2 is thus reduced to CO, whereas the leaving O atom fills the OV6. In the CO* structure, the C–Cu and C–O bond lengths are 3.73 Å and 1.14 Å, respectively, and CO desorption from the CO* adsorbed at the Cu site to give CO in the gas phase is endothermic by 0.14 eV.
For the Rh/In2O3 structure, the C–O bond breaking in the bt-CO2* structure to form CO* has an exothermicity of −0.77 eV and an energy barrier of 0.01 eV, where for the Ir/In2O3 structure, it has an exothermicity of −1.27 eV and an energy barrier of 0.08 eV. With very low energy barriers, the Rh/In2O3 and Ir/In2O3 structures are conducive to direct dissociation of CO2. In contrast, the energy barriers of CO2 direct dissociation for the other M/In2O3 models are higher than that for the c-In2O3 (111) (Ea = 0.32 eV), so there is a lower probability for the adsorbed bt-CO2* to directly dissociate for these models. Doping of the monatomic metals enhances the absorption of bt-CO2* on the In2O3 surface (Table S6, ESI†). The bt-CO2* adsorption structure on the In2O3 surface is unstable as indicated by its positive adsorption energy of 0.13 eV, so CO2 is either physisorbed as the ln-CO2* structure with a slightly negative adsorption energy of −0.16 eV or adsorbed as the carb-CO2* structure with a more negative adsorption energy of −0.36 eV. In addition, the CO generated from CO2 dissociation may occupy the surface M–OV site, which will become unavailable for CO2 adsorption, thus causing catalyst poisoning. Our DFT calculations show that the CO adsorption energy on the Pt/In2O3 structure is the most negative (Eads = −3.07 eV) as shown in Table S4 (ESI†), while that on the Cu/In2O3 structure is the least negative (Eads = −0.71 eV). Moreover, CO adsorption on all the M/In2O3 structures are stronger than CO2 adsorption, so it may hinder CO2 adsorption on the catalyst surface for the subsequent reaction.
The energies of the CO*_P adsorption state (Eads,CO*_P) for the different M/In2O3 structures vary greatly (Fig. 4(a) and Table S6, ESI†). Similar to the linear relationship between the oxygen vacancy formation energy and the adsorption energy of bt-CO2*, the Eads,CO*_P value also has an approximately linear relationship with the Ea value for CO2 dissociation, and a more positive Eads,CO*_P value corresponds to a higher Ea value for CO2 dissociation, as shown in Fig. 4(b).
The indirect dissociation pathway of the RWGS reaction on the M/In2O3 models is further shown in Fig. 5 and Fig. S3 (ESI†). For the Cu/In2O3 structure, all the transition states along this reaction pathway are found as shown in Fig. 5. The bt-CO2* first reacts with the H* adsorbed at the In site to form COOH*, which is endothermic by 1.38 eV with an energy barrier of 2.09 eV. The C–OH bond in the COOH* breaks to form CO* and OH*, which is also exothermic by −0.39 eV with an energy barrier of 0.01 eV. The C–O bond lengths in the [TS–COOH]*, [COOH]*, and [TS–CO–OH]* structures are 1.41 Å, 1.46 Å and 1.63 Å, respectively. CO desorption from the CO* adsorbed at the Cu site to give CO in the gas phase is endothermic by 0.23 eV. Thus, our calculations show that the rate-determining step along the indirect dissociation pathway of the RWGS reaction on the Cu/In2O3 structure is the first step for [CO2 + H]* to [TS–COOH]*.
 | ||
| Fig. 5 Energy profiles for CO2 hydrogenation to form CO via the direct and indirect dissociation pathways on the Cu/In2O3 model. | ||
For the other M/In2O3 models, the transition states are difficult to locate, so only the relative energies of the reaction intermediates are given in Fig. S3 and Table S7 (ESI†). Furthermore, the [COOH]* structure is also not stable on these surfaces, so hydrogenation of the adsorbed CO2* in the [CO2 + H]* directly leads to the [CO + OH]* by breaking one of the C–O bonds. The C–O bond length of the C from CO* to the O from OH* is 2.82–3.12 Å. For these M/In2O3 models, the relative energies of the [CO2 + H]* structures range from −2.90 eV (Rh/In2O3) to −0.06 eV (Ir/In2O3), whereas those of the [CO + OH]* structures range from −0.81 eV (c-In2O3(111)) to −3.07 eV (Ir/In2O3). In addition, the [CO2 + H]* structure adsorbed on Pd/In2O3, Pt/In2O3 and Rh/In2O3 are very stable, which may be detrimental to the subsequent reaction of the COOH*.
3.5 Microkinetic simulations
For the above-mentioned single-atom metal doped models with a low CO2 direct dissociation energy barrier of the RWGS reaction, first principles-based microkinetic simulations were further performed to study the reaction kinetics over the Ir/In2O3 and Rh/In2O3 models. In addition, since we also obtained a complete indirect dissociation pathway for the Cu/In2O3 model, we also performed microkinetic simulations despite its high energy barrier. Fig. 6(a) shows the calculated turnover frequencies (TOFs) for CO2 consumption under the typical reaction conditions of 473–673 K and 5 MPa (H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 = 3
CO2 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). These results show that single-atom metal doping significantly enhances CO2 reactivity over the pure In2O3 catalyst at above 573 K. In addition, among the above three SACs, the Ir/In2O3 model was predicted to have the highest TOF, which was followed by that of the Cu/In2O3 model, whereas the lowest TOF was predicted for the Rh/In2O3 model, at temperatures above 573 K, indicating that the Ir/In2O3 model has the best CO2 reactivity. Although the RWGS reaction was experimentally performed under medium to high temperature conditions, we also calculated the turnover frequencies (TOFs) from 300 K to 450 K (Fig. S7, ESI†), although for the Ir/In2O3 model, only TOFs in the temperature range of 400–450 K could be calculated due to the convergence issue.
1). These results show that single-atom metal doping significantly enhances CO2 reactivity over the pure In2O3 catalyst at above 573 K. In addition, among the above three SACs, the Ir/In2O3 model was predicted to have the highest TOF, which was followed by that of the Cu/In2O3 model, whereas the lowest TOF was predicted for the Rh/In2O3 model, at temperatures above 573 K, indicating that the Ir/In2O3 model has the best CO2 reactivity. Although the RWGS reaction was experimentally performed under medium to high temperature conditions, we also calculated the turnover frequencies (TOFs) from 300 K to 450 K (Fig. S7, ESI†), although for the Ir/In2O3 model, only TOFs in the temperature range of 400–450 K could be calculated due to the convergence issue.
Fig. 6(b) further shows the calculated degrees of rate control (DRCs) for CO2 consumption on the Cu/In2O3(111) model. The DRC of the transition state for OH* hydrogenation to H2O* ([H + OH]* → H2O*) is the largest, suggesting that this elementary step is rate-limiting, so lowering its energy barrier will lead to higher CO2 reactivity. On the other hand, the DRC of the transition state for bt-CO2* hydrogenation to COOH* ([bt-CO2 + H]* → COOH*) increases noticeably from 598 K to 673 K. Fig. 6(c) and (d) display the calculated DRC values for the CO2 reaction rate on the Ir/In2O3 and Rh/In2O3 models, where the DRCs of the OH* intermediate and the transition state for its hydrogenation to generate the VO site ([H + OH]* → H2O*) are the largest, suggesting the VO formation is the rate limiting step.
Although the potential energy profiles of the Ir/In2O3 and Rh/In2O3 models in the CO2 direct dissociation pathway are very close, the energy barrier of the first transition state [TS–2H]* to generate the oxygen vacancy site through H2 reduction for the Ir/In2O3 model is 0.31 eV lower than that of the Rh/In2O3 model (Fig. 2), consistent with the much higher CO2 reactivity of the Ir/In2O3 model than that of the Rh/In2O3 model, as oxygen vacancy formation is much easier for the Ir/In2O3 model. In addition, the higher reactivity of the Cu/In2O3 model than the In2O3 model may be due to the fact that its CO2 adsorption is much stronger than that on In2O3, although the energy barrier of CO2 direct dissociation on the Cu/In2O3 model is substantial. Furthermore, as shown in Fig. S4 (ESI†), the free site coverage for the Cu/In2O3 model is higher than the In2O3 model, which should also contribute to the higher turnover frequency for the Cu/In2O3 model.
3.6 Discussion
In recent years, a series of metal oxide-supported SACs have been synthesized and investigated for CO2 hydrogenation reactions.47–49 For these catalysts, the OV sites play a key role in stabilizing the SACs.50 The previous study of Qi et al.28 calculated the anchoring energy of transition metal single atoms (TMSA) at the OV site, although single metal atom doped In2O3 was not examined. In the present work, we first investigated the thermal stability of metal doping on c-In2O3(111) for M = Pt, Ir, Pd, Rh, Cu, and Ni, and screened the most stable doping site from the relative energy of the doped surface, whereas the optimal active site was further determined by comparing the OV formation energy. In addition, single metal atom doping was found to significantly enhance CO2 adsorption on the In2O3 surface, and there is an approximate linear relationship between the OV formation energy and the CO2 adsorption energy in the bt-CO2* structure, where a higher OV formation energy corresponds to stronger CO2 adsorption in this structure. This suggests that the OV formation energy for the M/In2O3 models may be used as a catalyst descriptor for CO2 conversion, so the strength of the bt-CO2* adsorption can be determined from the OV formation energy, and CO2 adsorption in the bt-CO2* structure further facilitates the subsequent dissociation and/or hydrogenation steps involved in the RWGS reaction.Recent studies mainly focused on the RWGS activity over three major kinds of heterogeneous catalysts, including supported metal catalysts, mixed oxide catalysts, and transition metal carbides.14 Rui et al.51 used In2O3 powder mixed with Pd/peptide composites and then heat-treated them to remove peptides to obtain a Pd/In2O3 catalyst. The Pd nanoparticles on this catalyst facilitate the dissociative adsorption of hydrogen and promote the generation of oxygen vacancies. The interfacial site also enhances the adsorption and hydrogenation of CO2. In this work, our calculations show that Pd monatomic doped In2O3 also favours the dissociative adsorption of hydrogen and promotes the formation of oxygen vacancies, consistent with the above experimental work. Thus, our work shows that single-atom doped In2O3 SAC catalysts are promising for the RWGS reaction, and further experimental studies are needed to verify our findings.
In our previous work,21 the c-In2O3(111) surface was found to favour methanol formation from CO2 hydrogenation. In this work, we find that the Rh and Ir monatomic doped c-In2O3(111) models favour CO formation via the RWGS reaction, indicating that single atom doping can regulate product selectivity of CO2 hydrogenation. Previously, Ye et al.13 designed a bifunctional Ir1–In2O3 single-atom catalyst that can efficiently hydrogenate CO2 in liquids with a high ethanol selectivity of >99%. Their characterization showed that isolated Ir atoms combined with adjacent oxygen vacancies to form Lewis acid–base pairs, which promoted the adsorption and activation of CO2 to CO*. Our calculations are consistent with the above conclusion, and the energy barrier for CO2 dissociation to generate CO over Ir/In2O3 is 0.24 eV lower than that over In2O3 (Fig. 4).
Our results expand the choice of catalysts for the RWGS reaction and increase the variety of monatomic metal doped In2O3 catalysts. The linear relationship between oxygen vacancy formation energy and CO2 adsorption energy and the energy barrier of the reaction pathway show that the magnitude of oxygen vacancy formation energy is an effective descriptor for screening the SACs for their catalytic performance in the RWGS reaction. Microkinetic simulations show that the CO2 turnover frequencies on the doped M/In2O3(M = Cu, Ir, Rh) models are greater than that of the pure In2O3, especially at reaction temperatures above 573 K, and the Ir/In2O3 model was predicted to have the highest CO2 reactivity. The rate controlling step of the CO2 hydrogenation reaction is the hydrogenation of the OH species to form H2O, indicating that the formation of the oxygen vacancy site is the most important limiting factor for CO2 reactivity. In the best-case scenario, these In2O3 SACs may be applied in both the RWGS reaction and FT synthesis, allowing for the direct conversion of CO2 into fuels.
4 Conclusions
In summary, we have investigated the single-atom doped In2O3 catalysts for the RWGS reaction using DFT calculations. Our results show that over the single-atom metal doped c-In2O3(111) structure for M = Pt, Ir, Pd, Rh, Cu, Ni, the energy barrier for H2 dissociation to form the [TS–2H]* structure can be considerably lower than that of pure In2O3 by up to 0.4 eV. These structures are thus conducive to the dissociative adsorption of H2, promoting the generation of surface oxygen vacancies and thereby increasing CO2 adsorption and activation over the In2O3 surface. Compared to pure In2O3, single-atom metal doping strengthens CO2 adsorption in the bt-CO2* structure, suggesting the SACs facilitate CO2 adsorption and activation over the In2O3 catalyst. Furthermore, the OV formation energy on the M/In2O3 surface may serve as an effective descriptor for CO2 adsorption, where higher OV formation energy results in more stable CO2 adsorption. For the direct dissociation pathway of the RWGS reaction, the Ir/In2O3 and Rh/In2O3 structures are conducive to CO2 direct dissociation to form CO. In contrast, the energy barriers for CO2 direct and indirect dissociations over the Cu doped structure are much higher at 1.92 eV and 2.09 eV, respectively, suggesting that the Cu/In2O3 structure is the least active for CO formation via the RWGS reaction. The adsorption energies of [CO*_P] for the M/In2O3 models can be linearly correlated with the Ea of CO2 direct dissociation, so the higher adsorption energy of [CO*_P] corresponds to the higher activation energy of CO2 direct dissociation. Microkinetic simulations further confirm that single-atom metal doping to In2O3 greatly benefits the CO2 conversion, especially under relatively high reaction temperatures, and the formation of the oxygen vacancy site mainly limits the CO2 reactivity on the M/In2O3 (M = Cu, Ir, Rh) models. Among the three single-atom catalysts, the turnover frequency was predicted to follow the order of Ir/In2O3 > Cu/In2O3 > Rh/In2O3 at reaction temperatures above 573 K, indicating that the Ir/In2O3 structure should have the best CO2 reactivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22172188, 22293023), the Shanghai Sailing Program from the Science and Technology Commission of Shanghai Municipality (23YF1453400), the Joint Fund of the Yulin University and the Dalian National Laboratory for Clean Energy (Grant No. YLU-DNL Fund 2022001), China National Offshore Oil Corporation (KJGG-2022-12-CCUS-030402), Qinchuangyuan “Scientists + Engineers” Team Construction Program of Shaanxi Province (2023KXJ-276), and the research program from Shaanxi Beiyuan Chemical Industry Group Co., Ltd. (2023413611014).References
- H. Kirsch, U. Sommer, P. Pfeifer and R. Dittmeyer, Chem. Eng. Sci., 2020, 227, 124553 CrossRef
.
- M. R. Allen, D. J. Frame, C. Huntingford, C. D. Jones, J. A. Lowe, M. Meinshausen and N. Meinshausen, Nature, 2009, 458, 1163–1166 CrossRef PubMed
.
- P. Friedlingstein, R. M. Andrew, J. Rogelj, G. P. Peters, J. G. Canadell, R. Knutti, G. Luderer, M. R. Raupach, M. Schaeffer, D. P. van Vuuren and C. Le Quere, Nat. Geosci., 2014, 7, 709–715 CrossRef
.
- J. Hansen, M. Sato, R. Ruedy, K. Lo, D. W. Lea and M. Medina-Elizade, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14288–14293 CrossRef PubMed
.
- M. Aresta, A. Dibenedetto and A. Angelini, Chem. Rev., 2014, 114, 1709–1742 CrossRef PubMed
.
- G. Centi, E. A. Quadrelli and S. Perathoner, Energy Environ. Sci., 2013, 6, 1711–1731 RSC
.
- W. Wang, S. Wang, X. Ma and J. Gong, Chem. Soc. Rev., 2011, 40, 3703–3727 RSC
.
- B. Hu, S. Frueh, H. F. Garces, L. Zhang, M. Aindow, C. Brooks, E. Kreidler and S. L. Suib, Appl. Catal., B, 2013, 132–133, 54–61 CrossRef CAS
.
- I. A. Fisher and A. T. Bell, J. Catal., 1996, 162, 54–65 CrossRef CAS
.
- J. H. Kwak, L. Kovarik and J. Szanyi, ACS Catal., 2013, 3, 2094–2100 CrossRef CAS
.
- M. Mikkelsen, M. Jorgensen and F. C. Krebs, Energy Environ. Sci., 2010, 3, 43–81 RSC
.
- P. Kaiser, R. B. Unde, C. Kern and A. Jess, Chem. Ing. Tech., 2013, 85, 489–499 CrossRef CAS
.
- X. Ye, C. Yang, X. Pan, J. Ma, Y. Zhang, Y. Ren, X. Liu, L. Li and Y. Huang, J. Am. Chem. Soc., 2020, 142, 19001–19005 CrossRef CAS PubMed
.
- X. Su, X. Yang, B. Zhao and Y. Huang, J. Energy Chem., 2017, 26, 854–867 CrossRef
.
- M. D. Porosoff, B. Yan and J. G. Chen, Energy Environ. Sci., 2016, 9, 62–73 RSC
.
- G. Zhou, F. Xie, L. Deng, G. Zhang and H. Xie, Int. J. Hydrogen Energy, 2020, 45, 11380–11393 CrossRef
.
- D. Kobayashi, H. Kobayashi, K. Kusada, T. Yamamoto, T. Toriyama, S. Matsumura, S. Kawaguchi, Y. Kubota, M. Haneda, S. M. Aspera, H. Nakanishi, S. Arai and H. Kitagawa, J. Mater. Chem. A, 2021, 9, 15613–15617 RSC
.
- M. Zhu, Q. Ge and X. Zhu, Trans. Tianjin Univ., 2020, 26, 172–187 CrossRef
.
- R. Tang, Z. Zhu, C. Li, M. Xiao, Z. Wu, D. Zhang, C. Zhang, Y. Xiao, M. Chu, A. Genest, G. Rupprechter, L. Zhang, X. Zhang and L. He, ACS Mater. Lett., 2021, 3, 1652–1659 CrossRef CAS
.
- J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306 CrossRef CAS
.
- S. S. Dang, B. Qin, Y. Yang, H. Wang, J. Cai, Y. Han, S. G. Li, P. Gao and Y. H. Sun, Sci. Adv., 2020, 6, 2375–2548 Search PubMed
.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641 CrossRef CAS
.
- X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed
.
- N. H. M. D. Dostagir, C. Thompson, H. Kobayashi, A. M. Karim, A. Fukuoka and A. Shrotri, Catal. Sci. Technol., 2020, 10, 8196–8202 RSC
.
- Z. Han, C. Tang, J. Wang, L. Li and C. Li, J. Catal., 2021, 394, 236–244 CrossRef CAS
.
- J. D. Zhu, F. Cannizzaro, L. Liu, H. Zhang, N. Kosinov, I. A. W. Filot, J. Rabeah, A. Bruckner and E. J. M. Hensen, ACS Catal., 2021, 11, 11371–11384 CrossRef CAS PubMed
.
- F. Cannizzaro, E. J. M. Hensen and I. A. W. Filot, ACS Catal., 2023, 1875–1892 CrossRef CAS
.
- R. Qi, B. E. Zhu, Z. K. Han and Y. Gao, ACS Catal., 2022, 12, 8269–8278 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- J. Wellendorff, K. T. Lundgaard, A. Mogelhoj, V. Petzold, D. D. Landis, J. K. Norskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef
.
- B. Qin, Z. M. Zhou, S. G. Li and P. Gao, J. CO2 Util., 2021, 49, 2212–9820 Search PubMed
.
- B. Qin and S. Li, Phys. Chem. Chem. Phys., 2020, 22, 3390–3399 RSC
.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS
.
- Y. S. Mohammed, Y. Yan, H. Wang, K. Li and X. Du, J. Magn. Magn. Mater., 2010, 322, 653–657 CrossRef
.
- M. S. Frei, C. Mondelli, R. García-Muelas, K. S. Kley, B. Puértolas, N. López, O. V. Safonova, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, Nat. Commun., 2019, 10, 3377 CrossRef
.
- C. Shen, K. Sun, Z. Zhang, N. Rui, X. Jia, D. Mei and C.-J. Liu, ACS Catal., 2021, 11, 4036–4046 CrossRef CAS
.
- M. S. Frei, C. Mondelli, R. García-Muelas, J. Morales-Vidal, M. Philipp, O. V. Safonova, N. López, J. A. Stewart, D. C. Ferré and J. Pérez-Ramírez, Nat. Commun., 2021, 12, 1960 CrossRef CAS
.
- P. Gao, S. G. Li, X. N. Bu, S. S. Dang, Z. Y. Liu, H. Wang, L. S. Zhong, M. H. Qiu, C. G. Yang, J. Cai, W. Wei and Y. H. Sun, Nat. Chem., 2017, 9, 1019–1024 CrossRef CAS
.
- Z. M. Zhou, B. Qin, S. G. Li and Y. H. Sun, Phys. Chem. Chem. Phys., 2021, 23, 1888–1895 RSC
.
- Materials Studio, Biovia Software Inc., 5005 Wateridge Vista Drive, San Diego, CA 92121, USA, 2018.
- A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807 CrossRef CAS
.
- C. T. Campbell, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS
.
- C. Stegelmann, A. Andreasen and C. T. Campbell, J. Am. Chem. Soc., 2009, 131, 13563 CrossRef CAS
.
- K. Samson, M. Śliwa, R. Socha, K. Góra-Marek, D. Mucha, D. Rutkowska-Zbik, J. F. Paul, M. Ruggiero-Mikołajczyk, R. Grabowski and J. Słoczyński, ACS Catal., 2014, 4, 3730–3741 CrossRef
.
- P. Du, R. Qi, Y. Zhang, Q. Gu, X. Xu, Y. Tan, X. Liu, A. Wang, B. Zhu, B. Yang and T. Zhang, Chem, 2022, 8, 3252–3262 Search PubMed
.
- J. Chen, S. K. Iyemperumal, T. Fenton, A. Carl, R. Grimm, G. Li and N. A. Deskins, ACS Catal., 2018, 8, 10464–10478 CrossRef
.
- J. C. Matsubu, S. Zhang, L. DeRita, N. S. Marinkovic, J. G. Chen, G. W. Graham, X. Pan and P. Christopher, Nat. Chem., 2017, 9, 120–127 CrossRef PubMed
.
- N. Rui, Z. Wang, K. Sun, J. Ye, Q. Ge and C.-J. Liu, Appl. Catal., B, 2017, 218, 488–497 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04352e |
| This journal is © the Owner Societies 2024 |