 Open Access Article
Open Access ArticleCost-effective approach for atmospheric accretion reactions: a case of peroxy radical addition to isoprene†
Dominika
Pasik
ab,
Siddharth
Iyer
 c and
Nanna
Myllys
c and
Nanna
Myllys
 *ab
*ab
aDepartment of Chemistry, University of Helsinki, Helsinki 00014, Finland. E-mail: nanna.myllys@helsinki.fi
bInstitute for Atmospheric and Earth System Research, University of Helsinki, Helsinki 00014, Finland
cAerosol Physics Laboratory, Tampere University, Tampere FI-3720, Finland
First published on 3rd January 2024
Abstract
We present an accurate and cost-effective method for investigating the accretion reactions between unsaturated hydrocarbons and oxidized organic radicals. We use accretion between isoprene and primary, secondary and tertiary alkyl peroxy radicals as model reactions. We show that a systematic semiempirical transition state search can lead to better transition state structures than relaxed scanning with density functional theory with a significant gain in computational efficiency. Additionally, we suggest accurate and effective quantum chemical methods to study accretion reactions between large unsaturated hydrocarbons and oxidized organic radicals. Furthermore, we examine the atmospheric relevance of these types of reactions by calculating the bimolecular reaction rate coefficients and formation rates under atmospheric conditions from the quantum chemical reaction energy barriers.
1 Introduction
Volatile organic compounds (VOCs) are primarily emitted into the atmosphere by forests and have immense significance in the lives of plants, animals, and microorganisms, influencing their functioning.1–4 High emissions of anthropogenic volatile organic compounds (AVOCs) are observed mainly in urbanized areas due to human activity.1,5,6 Nonetheless, it is biogenic volatile organic compounds (BVOCs) which play a crucial role in atmospheric chemistry due to their larger global scale emissions and higher reactivity than many AVOCs.5 These compounds have an impact on health and climate and also interact with entire ecosystems. Among BVOCs, isoprene is the dominant non-methane hydrocarbon present in the atmosphere, with estimated emissions of 500 Tg C per year.7–11 Due to its abundance and the presence of carbon–carbon double bonds (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), this compound plays a significant role in atmospheric processes, and its reactions have implications not only for regional air quality but also climate models.8,9
C), this compound plays a significant role in atmospheric processes, and its reactions have implications not only for regional air quality but also climate models.8,9
The primary source of isoprene is the de novo synthesis in plants, where carbon dioxide from the Calvin cycle is processed.3,8 It has been confirmed that isoprene also originates from the ocean, with estimated emissions ranging around 10 Tg C per year. However, this source is much less significant compared to the synthesis from plants.12,13 Due to its short atmospheric lifetime of approximately 1 hour, isoprene does not travel far from its source before undergoing oxidation.8,14,15 There exists a substantial body of literature elucidating the oxidation reactions of isoprene that it readily and rapidly undergoes.7,8,11,16–18 Of particular significance is the reaction with the hydroxyl radical (OH), considered to be the primary sink for isoprene.3,8,19,20 This reaction is deemed to be rapid (k298K = (1.00 ± 0.15) × 10−10 cm3 molecule−1 s−1). At sufficiently high reagent concentrations, the reaction of isoprene with OH accounts for 66–95 percent of isoprene removal.3 Other important reactions occur with ozone as well as with NO and NO3.7,21,22 Isoprene oxidation products may also contribute to the production of Secondary Organic Aerosols (SOAs). As the volatility of oxidized organic species is strongly linked to its ability to drive SOA formation, isoprene oxidation products are likely to participate only in SOA growth as the volatility of C5 compounds is unlikely to be extremely low. However, if isoprene forms accretion products, which have a higher molar mass, and they further oxidize, those products could have significantly lower vapor pressures.1,8,12,16,23–25
The purpose of this study is to develop a cost-effective, computationally efficient, and accurate methodology for investigating accretion reactions between unsaturated hydrocarbon and oxygenated organic radicals. We used reactions between isoprene and four peroxy radicals (methyl, ethyl, 1-propyl, and 2-propyl) as simple model systems. These reactions offer a good balance between computational simplicity and complexity. They are relatively simple to model as isoprene only contains five carbon atoms and its molecular structure is rigid due to conjugated double bonds. Furthermore, the selected alkyl peroxy radicals contain a maximum of five heavy atoms (propyl peroxy radicals has three carbon and two oxygen atoms). The reaction still contains some complexity as the peroxy radical can add four different carbons into the isoprene structure leading to different transition state (TS) and product structures (see Fig. 1), and the TS and product structures contain multiple different conformers as the structure of the isoprene carbon chain becomes flexible. This provides us with perfect test reactions to find a computational approach which (1) leads to an accurate description of the potential energy surface, (2) is cost-effective and fast, (3) can handle an enormous number of TS conformers, and (4) is directly applicable to much larger reactions. Additionally, this allows us to gain chemical information about (A) how the structure of an alkyl peroxy radical affects its reactivity, (B) how the structure of an organic peroxide containing a carbon-centered radical affects its stability, and (C) how the structure of an unsaturated hydrocarbon affects its reactivity with peroxy radicals.
2 Computational details
2.1 Configurational sampling
The products of the accretion reaction between isoprene and peroxy radicals as well as the reactants and transition states have been studied using accurate quantum chemical methods. The lowest energy conformers were identified using the free software CREST at the extended tight-binding level GFN2-xTB.26,27 To determine an effective method for describing these systems, we employed two strategies using a combination of the GFN2-xTB method and density functional theory (DFT) level ωB97X-D/6-31+G*. In the first one (Approach 1), the conformational search begins with the accretion product, and after optimizing the geometrical structure at the DFT level,28,29 the transition state of the accretion reaction is located from the relaxed potential energy surface scan using the DFT level. The highest energy relaxed structure is identified, and subsequent TS optimization and frequency calculation is performed. The correct TS structure is verified through one imaginary frequency. In the second approach (Approach 2), first one TS structure is located at the GFN2-xTB level and that structure is used in the CREST configurational search by freezing the reactive area of the TS structure (i.e., the distance when forming the C–O bond). As a result, varying numbers of TS conformers were obtained (around 30 for small systems, over 300 for large systems). The next step was to optimize structures at the DFT level still keeping the C–O bond distance frozen. This allows the structure to relax on the DFT structure, which simplifies the subsequent full TS state optimization and frequency calculation. Indeed, TS structures were identified to be correct through one imaginary frequency. Scheme of different approaches is presented in Fig. 2. The results comparing these configurational sampling techniques are presented in Section 3.1. | ||
| Fig. 2 A comparison of the TS conformer search process using two approaches. The most time- and resource-consuming part of the process is highlighted using dashed lines. | ||
2.2 Computational methods
To find an efficient quantum chemical method for describing such systems, the lowest energy conformers for each TS structure were optimized and the frequencies were calculated using the ωB97X-D functional with three different basis sets: 6-31+G*, aug-cc-pVTZ, and Def2TZVPP.29–33 The choice of the functional is driven by the fact that it has proven to be effective in studying similar systems.28,34,35 Subsequently, coupled-cluster with single and double excitations as well as perturbative inclusion of triples (CCSD(T)) calculations were performed using the DLPNO-CCSD(T)/aug-cc-pVDZ, DLPNO-CCSD(T)/aug-cc-pVTZ, and CCSD(T)-F12/cc-pVDZ-F12 levels.36–38 Domain-based local pair natural, DLPNO, approximation leads to linear scaling of computational resources when the system size increases, whereas the canonical coupled cluster scales to the seventh power, making it only possible for applications in small molecular systems. We used tight pair natural orbital (TightPNO) criteria in all DLPNO calculations.39 All the DFT calculations were performed using Gaussian 16 RevC.02 software.40 Single-point energies were calculated in ORCA version 5.0.3.41,42 For all conformers, the zero-point corrected energies were calculated. Barrier heights were computed as a difference between TS and reactants energies.The reaction rate coefficients were calculated with the multiconformational transition state theory (MC-TST) approach for the bimolecular reaction following the expression:43–47
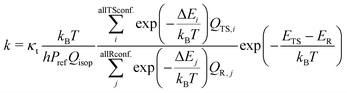 | (1) |
To estimate the significance of considering multiple conformers in reaction kinetics calculations, we also compute the reaction rate coefficient using the lowest-conformer transitions state theory (LC-TST)
 | (2) |
3 Results and discussion
Our goal is to find a cost-effective but accurate computational approach to study the reactions between any unsaturated hydrocarbons and oxygenated hydrocarbon radicals. We are searching for reactions with sufficiently low energy barriers so that, at the current known atmospheric concentrations of the reactants, the reaction rates would be high enough to consider them as feasible. For this reason, we calculate the value of the energy barrier for the studied reactions between isoprene and peroxy radicals, which allows us to estimate whether the reaction will have atmospheric significance.3.1 Cost-effective transition state search
To achieve this, the conformational space for all isoprene + peroxy radical systems was explored in two approaches, aiming to identify the lowest energy conformer for each system. We found that Approach 1 and Approach 2 might lead to different lowest energy TS structures, and consequently, the calculated reaction barriers differ (see Table 1).| Approach 1 | Approach 2 | ΔE | |
|---|---|---|---|
| me-1 | 6.66 | 6.66 | 0.00 |
| me-2 | 14.39 | 14.11 | 0.28 |
| me-3 | 15.54 | 15.00 | 0.55 |
| me-4 | 7.47 | 7.47 | 0.00 |
| et-1 | 6.46 | 6.46 | 0.00 |
| et-2 | 14.54 | 14.36 | 0.18 |
| et-3 | 14.57 | 14.57 | 0.00 |
| et-4 | 7.05 | 7.05 | 0.00 |
| p-1.1 | 6.10 | 6.00 | 0.10 |
| p-1.2 | 13.97 | 13.96 | 0.01 |
| p-1.3 | 16.25 | 14.29 | 1.96 |
| p-1.4 | 6.67 | 6.67 | 0.00 |
| p-2.1 | 6.44 | 6.44 | 0.00 |
| p-2.2 | 14.75 | 14.65 | 0.10 |
| p-2.3 | 15.45 | 14.83 | 0.62 |
| p-2.4 | 7.10 | 7.10 | 0.00 |
The accuracy of this observation is evidenced for the me-3, p-1.3, and p-2.3 TS structures, for which the calculated energy barriers in the two approaches differ, 0.55, 1.96, and 0.62 kcal mol−1, respectively. For the remaining systems, the calculated energy barrier values are comparable or identical in both approaches, indicating that the identified conformers are the same in both cases. Notably, when the found TS structure is different, the better (lower energy) TS structure is always found in Approach 2. This indicates that that Approach 2, in which the TS conformer search has been done using the xTB method and freezing the reactive TS area in CREST sampling, is a superior way to search TS conformers over the traditional relaxed scan DFT approach.
Furthermore, we observed that for systems with more than one carbon, Approach 1 consistently resulted in finding a higher number of initial CREST conformers compared to Approach 2 (see Fig. 3). This is an interesting finding, as Approach 2 results in a better or the same TS structure even though Approach 1 finds a larger number of initial CREST conformers. This can be explained by the fact, that in Approach 1 the CREST conformers are product conformers, for which DFT optimization and further relaxed potential energy surface scanning leads to many duplicate structures. For instance, in the case of system p-1.1, Approach 1 initially found 261 product conformers, but after TS scanning and removing the duplicates, only 41 unique TS conformers remained at the DFT level. In contrast, Approach 2 identified 124 initial TS conformers for the same system, which resulted in 54 unique TS conformers at the DFT level. Furthermore, only the low-energy conformers contribute significantly to the reaction rate.48 To ensure that MC-TST remains computationally feasible, it is important to reduce the number of conformers before computationally demanding high-level calculations. This indicates that Approach 1 leads to a larger consumption of computational resources without improving the quality of the results, which has a great importance while considering large accretion reactions in future research.
 | ||
| Fig. 3 The number of initial conformers found in the CREST conformational search for investigated systems in Approach 1 (blue) and Approach 2 (orange). Approach 1 produces initial product structures and Approach 2 initial TS structures. The exact values can be found in the ESI.† | ||
Aiming to further reduce computational costs, we analyzed the correlation between the relative energies of the identified conformers at the xTB level, and the same structures were re-optimized using DFT.49 We found a remarkable correlation (R2 = 0.87) between the relative conformer energies compared to the lowest energy conformer at DFT and xTB levels, ΔE(DFT) and ΔE(GFN2-xTB), respectively (see Fig. 4 as an example for the correlation plot of the me-1 TS conformers). This implies that in the case of a large number of conformers, there is no need to optimize all of them; optimizing only a subset (e.g., within 2 kcal mol−1) is sufficient. This result is consistent with a recent study where relative xTB and DFT conformer energies were strongly correlating in the case of acid–base cluster conformers.50 For the me-1 system, the lowest energy conformer was among the first 10 structures.
We found that Approach 2 always leads to the same or better TS conformer than Approach 1 (see Table 1). As the TS search on the xTB level of theory is significantly faster than that at the DFT level, our finding makes it possible to perform a systematic TS search for large and flexible systems. In addition, there is no need to do a TS search at the DFT level, and we also found a remarkable correlation between xTB and DFT relative conformer energies, indicating that only a subset of the lowest energy xTB conformers are needed for computations at the DFT level. This allows accurate but cost-effective studies of atmospheric accretion reactions which often contain a plethora of different TS configurations.
3.2 Cost-effective quantum chemistry approach
In the previous section, we optimized the geometries and calculated frequencies using the ωB97X-D/6-31+G* level of theory. Here we will test whether this small basis set is good enough to accurately describe the studied systems. Due to the fact that Approach 2 has proven to yield better results than Approach 1 and considering its simpler and less resource-intensive nature in finding the lowest-energy conformer, we focus exclusively on structures obtained through Approach 2 in the following sections of the article. Information and calculations for structures from Approach 1 can be found in the ESI.†Here we use the previously found lowest energy ωB97X-D/6-31+G* structures, which are reoptimized and the frequencies are calculated using the ωB97X-D functional with larger Def2TZVPP and aug-cc-pVTZ basis sets. Barrier height energies with these three level of theories are presented in Table 2.
| Approach 2 | 6-31+G* | Def2TZVPP | aug-cc-pVTZ |
|---|---|---|---|
| me-1 | 6.66 | 8.54 | 8.37 |
| me-2 | 14.11 | 16.21 | 15.97 |
| me-3 | 15.00 | 16.98 | 16.76 |
| me-4 | 7.47 | 9.38 | 9.20 |
| et-1 | 6.46 | 8.28 | 8.15 |
| et-2 | 14.36 | 16.18 | 15.98 |
| et-3 | 14.57 | 16.36 | 16.18 |
| et-4 | 7.05 | 8.87 | 8.74 |
| p-1.1 | 6.00 | 7.93 | 7.76 |
| p-1.2 | 13.96 | 15.78 | 15.57 |
| p-1.3 | 14.29 | 16.11 | 15.95 |
| p-1.4 | 6.67 | 8.51 | 8.30 |
| p-2.1 | 6.44 | 8.26 | 8.11 |
| p-2.2 | 14.65 | 16.40 | 16.22 |
| p-2.3 | 14.83 | 16.54 | 16.38 |
| p-2.4 | 7.10 | 8.93 | 8.78 |
Assuming that the most reliable results are provided by calculations using the largest aug-cc-pVTZ basis set, we compared the energies calculated using the 6-31+G* and Def2TZVPP basis sets to aug-cc-pVTZ energies. Using the smallest 6-31+G* basis set, the results are consistently 1.5–2.0 kcal mol−1 lower in energy, and at the Def2TZVPP basis the values are quite similar, consistently 0.2–0.3 kcal mol−1 higher in energy compared to the aug-cc-pVTZ results. This has also been presented in Fig. 5. This is consistent with previous results for acid–base clusters, which have shown that when calculating binding energies at the DFT level, at least a triple zeta basis set is required to produce converged results.28,51,52 However, those studies have also shown a highly correlated electronic energy method is needed for electronic energy correction to lead to chemically accurate results. When energy correction is performed on top of the DFT structure, a significantly smaller basis set might be needed.
 | ||
| Fig. 5 Differences in the DFT energies calculated using the 6-31+G* and Def2TZVPP basis sets, relative to energies calculated with the aug-cc-pVTZ basis set. | ||
To obtain a more accurate description of electronic energy compared to what DFT offers, single point Coupled Cluster (CC) calculations were performed on top of the calculated DFT structures. For each structure optimized with a DFT/basis combination, we conducted Coupled Cluster calculations using three approaches: DLPNO-CCSD(T)/aug-cc-pVDZ (DLPNO/aVDZ), DLPNO-CCSD(T)/aug-cc-pVTZ (DLPNO/aVTZ), and CCSD(T)-F12/cc-pVDZ-F12 (F12/VDZ). The Coupled Cluster energy barrier values for the studied systems are presented in Table 3.
| DLPNO/aVDZ | DLPNO/aVTZ | F12/VDZ | |
|---|---|---|---|
| ωB97X-D/6-31+G* | |||
| me-1 | 6.73 | 8.34 | 8.52 |
| me-2 | 11.42 | 13.59 | 13.98 |
| me-3 | 12.96 | 14.86 | 15.24 |
| me-4 | 7.38 | 8.93 | 9.25 |
| et-1 | 5.95 | 7.87 | 8.13 |
| et-2 | 11.23 | 13.54 | 13.92 |
| et-3 | 12.38 | 14.34 | 14.61 |
| et-4 | 6.33 | 8.35 | 8.75 |
| p-1.1 | 5.48 | 7.50 | 7.90 |
| p-1.2 | 10.65 | 13.15 | 13.58 |
| p-1.3 | 11.80 | 13.98 | 14.25 |
| p-1.4 | 5.85 | 8.05 | 8.56 |
| p-2.1 | 5.48 | 7.72 | 8.06 |
| p-2.2 | 11.13 | 13.69 | 14.07 |
| p-2.3 | 12.26 | 14.46 | 14.74 |
| p-2.4 | 5.97 | 8.28 | 8.73 |
| ωB97X-D/Def2TZVPP | |||
| me-1 | 6.62 | 8.21 | 8.43 |
| me-2 | 11.37 | 13.62 | 13.99 |
| me-3 | 12.83 | 14.85 | 15.19 |
| me-4 | 7.25 | 8.87 | 9.17 |
| et-1 | 5.77 | 7.77 | 8.03 |
| et-2 | 11.03 | 13.42 | 13.77 |
| et-3 | 12.25 | 14.29 | 14.52 |
| et-4 | 6.14 | 8.21 | 8.58 |
| p-1.1 | 5.46 | 7.58 | 7.89 |
| p-1.2 | 10.51 | 13.03 | 13.43 |
| p-1.3 | 11.70 | 13.96 | 14.19 |
| p-1.4 | 5.74 | 8.00 | 8.47 |
| p-2.1 | 5.30 | 7.68 | 7.96 |
| p-2.2 | 10.87 | 13.56 | 13.90 |
| p-2.3 | 12.08 | 14.36 | 14.60 |
| p-2.4 | 5.80 | 8.23 | 8.61 |
| ωB97X-D/aug-cc-pVTZ | |||
| me-1 | 6.62 | 8.20 | 8.41 |
| me-2 | 11.36 | 13.61 | 13.98 |
| me-3 | 12.83 | 14.86 | 15.18 |
| me-4 | 7.22 | 8.84 | 9.14 |
| et-1 | 5.80 | 7.81 | 8.06 |
| et-2 | 11.04 | 13.43 | 13.78 |
| et-3 | 12.24 | 14.28 | 14.51 |
| et-4 | 6.18 | 8.25 | 8.62 |
| p-1.1 | 5.45 | 7.58 | 7.87 |
| p-1.2 | 10.50 | 13.04 | 13.44 |
| p-1.3 | 11.66 | 13.93 | 14.15 |
| p-1.4 | 5.70 | 7.97 | 8.43 |
| p-2.1 | 5.31 | 7.69 | 7.96 |
| p-2.2 | 10.88 | 13.55 | 13.89 |
| p-2.3 | 12.08 | 14.36 | 14.59 |
| p-2.4 | 5.81 | 8.24 | 8.61 |
Similarly to the DFT results, the lowest activation barriers are observed for the largest systems (1-propyl and 2-propyl substituents), while the highest barriers are found for the smallest system (methyl substituent) indicating that with an increase in system size smaller activation energy values are observed (methyl > ethyl > propyl), which can be attributed to the greater structural stabilization resulting from the enlargement of the system. Additionally, the lowest energy barriers occur for reaction pathways 1 and 4. This is because these pathways yield secondary and tertiary radicals, which stabilize the structure compared to the primary radical structures. Furthermore, it should be noted that the conformers corresponding to pathways 1 and 4 exhibit lower energy than the conformers associated with pathways 2 and 3 and also lead to products with significantly lower energy compared to the energy of the substrates making them more favorable due to the system's tendency to achieve lower energy states (see the ESI†).
Although the results are consistent for all methods and functional bases, it is clear that the activation energy calculated at the DLPNO-CCSD(T)/aug-cc-pVDZ level is notably lower than that obtained using the other two methods. The canonical CCSD(T)-F12/cc-VDZ-F12 energies calculated on top of the ωB97X-D/aug-cc-pVTZ structures are assumed to offer the most accurate energies, and therefore, we have calculated the values of root square mean error (RMSE) relative to the level of theory (see Fig. 6, and the calculated mean absolute error (MAE) values can be found in the ESI†).
 | ||
| Fig. 6 Calculated RSME [kcal mol−1] for all methods and basis sets (reference CCSD(T)-F12/cc-pVDZ-F12//ωB97X-D/aug-cc-pVTZ). | ||
Interestingly, the results are quite consistent regardless of the DFT/basis used for structure optimization. These results confirm that for the studied accretion reactions, DFT optimization and frequency calculations can be carried out using a small basis set such as 6-31+G* when the electronic energy correction at a higher level of theory is performed. In relation to the selection of the CC method, as previously noted, computations employing DLPNO-CCSD(T)/aug-cc-pVDZ produce imprecise outcomes. Conversely, results from the remaining two methods are quite similar. Hence, we propose the application of DLPNO-CCSD(T)/aug-cc-pVTZ due to its computational speed and reduced resource demands.
3.3 MC-TST bimolecular reaction rate coefficient
For the investigated systems, the atmospheric significance can be defined by calculating the reaction rate. Due to the fact that the lowest energy barrier values among all investigated systems were obtained for reaction pathway 1, we focus exclusively on this structure in the following sections of the article. As mentioned before, calculating the value of the bimolecular reaction rate allows us to estimate whether a given reaction is feasible under atmospheric conditions.Table 4 presents the calculated rate coefficients for the reaction of isoprene and four peroxy radicals following pathway 1 and the estimated rates of formation. The adopted reagent concentrations are the upper limits that we managed to find in the literature. Unfortunately, specific concentrations for peroxy radicals like ethyl, 1-propyl, and 2-propyl were not available. Hence, the values of formation rates are calculated based on concentrations derived from measurements of total RO2 systems. We used the following upper limit value concentrations: [methyl peroxy radical] = 6 × 108,53,54 [other peroxy radicals] = 109,55–57 [isoprene] = 1011 cm−3.58,59
| LC-TST rate coefficient [cm3 molecules−1 s−1] | MC-TST rate coefficient [cm3 molecules−1 s−1] | Rate of formation [molecules cm−3 s−1] | LC-TST/MC-TST ratio [molecules cm−3 s−1] | |
|---|---|---|---|---|
| me-1 | 1.22 × 10−21 | 2.30 × 10−21 | 1.38 × 10−1 | 0.53 |
| et-1 | 1.85 × 10−21 | 1.10 × 10−21 | 1.10 × 10−1 | 1.68 |
| p-1.1 | 2.01 × 10−21 | 3.37 × 10−21 | 3.37 × 10−1 | 0.60 |
| p-2.1 | 1.66 × 10−21 | 2.18 × 10−22 | 2.18 × 10−1 | 0.76 |
Rate coefficients calculated for the reactions between isoprene and peroxy radicals using LC-TST and MC-TST yield values of a similar order of magnitude. However, analysis of the LC-TST/MC-TST ratios reveals that, in reactions with methyl and 1-propyl radicals, the calculated rate coefficient at MC-TST is nearly two times greater than that of LC-TST. This disparity has significant implications for reaction kinetics. Therefore, we recommend the utilization of the MC-TST approach, as it provides more accurate results.
MC-TST rate coefficients for investigated reactions are in the order of 10−21 cm3 molecules−1 s−1. Under atmospheric isoprene and peroxy radical concentrations, the reaction rates are in the order of 10−1 molecules cm−3 s−1. Even when the estimated upper limit concentrations of the reactants are taken into consideration, these reactions are still much slower than the dominant oxidation with the OH radical making its contribution negligible in the atmosphere.3
Recently, it has been proposed that unsaturated alkenes and peroxy radicals can form accretion products ROOR′, involving an addition to the double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond under atmospheric conditions.60 Although our study focuses on isoprene, we are a bit skeptical that the accretion reaction between atmospheric unsaturated hydrocarbons and aliphatic peroxy radicals could have meaningful atmospheric importance. We investigated primary, secondary and tertiary alkyl peroxy radical additions to isoprene leading to primary, secondary and tertiary carbon-centered radicals: None of these reactions yielded reaction rates which could have non-negligible contributors to atmospheric chemistry. Despite the high reaction barriers in peroxy radical reactions with unsaturated hydrocarbons, it is possible that more reactive radical structures such as acyl peroxy radicals, could potentially form accretion products with unsaturated hydrocarbons such as isoprene and monoterpenes under atmospheric conditions. Additionally, unimolecular ring-forming reactions between double bond and peroxy radical groups could occur under atmospheric conditions as they are kinetically feasible also at higher activation energy barriers. This could lead to new mechanistic insights, e.g., in α-pinene oxidation pathways.
C bond under atmospheric conditions.60 Although our study focuses on isoprene, we are a bit skeptical that the accretion reaction between atmospheric unsaturated hydrocarbons and aliphatic peroxy radicals could have meaningful atmospheric importance. We investigated primary, secondary and tertiary alkyl peroxy radical additions to isoprene leading to primary, secondary and tertiary carbon-centered radicals: None of these reactions yielded reaction rates which could have non-negligible contributors to atmospheric chemistry. Despite the high reaction barriers in peroxy radical reactions with unsaturated hydrocarbons, it is possible that more reactive radical structures such as acyl peroxy radicals, could potentially form accretion products with unsaturated hydrocarbons such as isoprene and monoterpenes under atmospheric conditions. Additionally, unimolecular ring-forming reactions between double bond and peroxy radical groups could occur under atmospheric conditions as they are kinetically feasible also at higher activation energy barriers. This could lead to new mechanistic insights, e.g., in α-pinene oxidation pathways.
4 Conclusions
We have investigated the mechanism of the accretion reaction between isoprene and aliphatic peroxy radicals using a set of different computational approaches. Based on the conducted calculations for various methods and basis sets, we propose an efficient approach for investigating these chemical systems. For conformational space exploration to find the lowest energy transition state structures, we employed two approaches. We found that the reactive area frozen CREST sampling at the xTB level with subsequent DFT calculations yields quicker and superior results compared to the traditional relaxed scan at the DFT level. This is a significant discovery as it allows an accurate TS search also for accretion reactions between large reactants which would be unfeasible with DFT scanning.For the studied accretion reactions, geometry optimization at the DFT level is insensitive to the applied basis set when electronic energy correction is performed on top of the DFT structure. Therefore, we recommend utilizing the Pople's basis set (6-31+G*) for geometry optimization and frequency calculation, as it is faster and computationally feasible also for large system sizes. The outcomes indicate that coupled cluster calculations using DLPNO-CCSD(T)/aug-cc-pVTZ offer computational accuracy of the canonical CCSD(T)-F12/cc-VDZ-F12 method with a significantly reduced computational cost. Due to that and the linear scaling behavior of the DLPNO method, we suggest electronic energy computations at the DLPNO-CCSD(T)/aug-cc-pVTZ level of theory.
The calculated activation barrier values for the studied reactions indicate that the reaction between isoprene and peroxyl radical most likely follows pathway 1, as this pathway exhibits the lowest barrier for the reaction. This can be explained by the formation of tertiary radical TS and product structures, which exhibit greater stability compared to the secondary radical (R4) and the primary radicals (R2, R3) in alternative pathways. Comparing the four examined radicals, it can be observed that the calculated activation barriers increase in the order: 1-propyl < 2-propyl < ethyl < methyl. This can be explained by the fact that larger radicals lead to higher internal structural stabilization, resulting in lower barriers.
The atmospheric significance of these reactions was also determined by defining the rate coefficient and calculating the formation rates. The calculated rate coefficients were in the order of 10−21 cm3 molecule−1 s−1 indicating that under atmospherically relevant conditions, reactions between unsaturated hydrocarbons and peroxy radicals are unlikely to have an atmospheric impact.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Research Council of Finland for funding (grant no. 347775 and 355966) and the CSC-IT Center for Science in Espoo, Finland, for computational resources. We thank Dr Nino Runeberg for the insightful discussions.Notes and references
- A. Mozaffar and Y.-L. Zhang, Curr. Pollut. Rep., 2020, 6, 250–263 CrossRef CAS.
- E. David and V.-C. Niculescu, Int. J. Environ. Res. Public Health, 2021, 18, 13147 CrossRef CAS PubMed.
- C. Gu, S. Wang, J. Zhu, S. Wu, Y. Duan, S. Gao and B. Zhou, Atmos. Environ., 2022, 270, 118870 CrossRef CAS.
- S. E. Paulson, R. C. Flagan and J. H. Seinfeld, Int. J. Chem. Kinet., 1992, 24, 79–101 CrossRef CAS.
- S. Gu, A. Guenther and C. Faiola, Environ. Sci. Technol., 2021, 55, 12191–12201 CrossRef CAS PubMed.
- B. Li, S. S. H. Ho, X. Li, L. Guo, A. Chen, L. Hu, Y. Yang, D. Chen, A. Lin and X. Fang, Environ. Int., 2021, 156, 106710 CrossRef CAS PubMed.
- T. J. McGenity, A. T. Crombie and J. C. Murrell, ISME J., 2018, 12, 931–941 CrossRef CAS PubMed.
- P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes and M. D. Smarte, et al. , Chem. Rev., 2018, 118, 3337–3390 CrossRef CAS PubMed.
- L. Conte, S. Szopa, O. Aumont, V. Gros and L. Bopp, J. Geophys. Res.: Oceans, 2020, 125, e2019JC015946 CrossRef CAS.
- A. P. Teng, J. D. Crounse and P. O. Wennberg, J. Am. Chem. Soc., 2017, 139, 5367–5377 CrossRef CAS PubMed.
- J. Peeters, T. L. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939 RSC.
- L. Conte, S. Szopa, O. Aumont, V. Gros and L. Bopp, J. Geophys. Res.: Oceans, 2020, 125, e2019JC015946 CrossRef CAS.
- W. Zhang and D. Gu, npj Clim. Atmos. Sci., 2022, 5, 83 CrossRef CAS.
- B. Bonsang, C. Polle and G. Lambert, Geophys. Res. Lett., 1992, 19, 1129–1132 CrossRef CAS.
- J. M. Hurst, D. J. Barket Jr, O. Herrera-Gomez, T. L. Couch, P. B. Shepson, I. Faloona, D. Tan, W. Brune, H. Westberg and B. Lamb, et al. , J. Geophys. Res.: Atmos., 2001, 106, 24335–24346 CrossRef CAS.
- K. H. Bates and D. J. Jacob, Atmos. Chem. Phys., 2019, 19, 9613–9640 CrossRef CAS.
- W. P. Carter and R. Atkinson, Int. J. Chem. Kinet., 1996, 28, 497–530 CrossRef CAS.
- K. H. Møller, K. H. Bates and H. G. Kjaergaard, J. Phys. Chem. A, 2019, 123, 920–932 CrossRef PubMed.
- T. Pugh, A. MacKenzie, B. Langford, E. Nemitz, P. Misztal and C. Hewitt, Atmos. Chem. Phys., 2011, 11, 4121–4134 CrossRef CAS.
- H. Fuchs, A. Hofzumahaus, F. Rohrer, B. Bohn, T. Brauers, H. Dorn, R. Häseler, F. Holland, M. Kaminski and X. Li, et al. , Nat. Geosci., 2013, 6, 1023–1026 CrossRef CAS.
- S. E. Paulson and J. H. Seinfeld, J. Geophys. Res.: Atmos., 1992, 97, 20703–20715 CrossRef.
- R. H. Schwantes, A. P. Teng, T. B. Nguyen, M. M. Coggon, J. D. Crounse, J. M. Clair, X. Zhang, K. A. Schilling, J. H. Seinfeld and P. O. Wennberg, J. Phys. Chem. A, 2015, 119, 10158–10171 CrossRef CAS PubMed.
- B. H. Lee, S. Iyer, T. Kurtén, J. G. Varelas, J. Luo, R. J. Thomson and J. A. Thornton, Environ. Sci.: Atmos., 2023, 3, 399–407 CAS.
- J. H. Kroll and J. H. Seinfeld, Atmos. Environ., 2008, 42, 3593–3624 CrossRef CAS.
- G. McFiggans, T. F. Mentel, J. Wildt, I. Pullinen, S. Kang, E. Kleist, S. Schmitt, M. Springer, R. Tillmann and C. Wu, et al. , Nature, 2019, 565, 587–593 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- N. Myllys, J. Elm and T. Kurten, Comput. Theor. Chem., 2016, 1098, 1–12 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- R. V. Otkjær, H. H. Jakobsen, C. M. Tram and H. G. Kjaergaard, J. Phys. Chem. A, 2018, 122, 8665–8673 CrossRef PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- A. Köhn, G. W. Richings and D. P. Tew, J. Chem. Phys., 2008, 129, 201103 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- N. Myllys, T. Ponkkonen, S. Chee and J. Smith, Atmosphere, 2019, 11, 35 CrossRef.
- L. P. Viegas, Chem. Phys. Lett., 2022, 803, 139829 CrossRef CAS.
- L. P. Viegas, J. Phys. Chem. A, 2021, 125, 4499–4512 CrossRef CAS PubMed.
- L. Viegas, ChemPhysChem, 2023, e202300259 CrossRef CAS PubMed.
- L. P. Viegas, J. Phys. Org. Chem., 2023, 36, e4470 CrossRef CAS.
- L. P. Viegas, Atmosphere, 2022, 13, 1256 CrossRef CAS.
- K. H. Møller, R. V. Otkjær, N. Hyttinen, T. Kurtén and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 10072–10087 CrossRef PubMed.
- S. Lin, M. Elanany and M. Khawaji, SoftwareX, 2022, 20, 101242 CrossRef.
- J. Kubecka, V. Besel, T. Kurtén, N. Myllys and H. Vehkamaki, J. Phys. Chem. A, 2019, 123, 6022–6033 CrossRef CAS PubMed.
- N. Myllys, J. Elm, R. Halonen, T. Kurten and H. Vehkamaki, J. Phys. Chem. A, 2016, 120, 621–630 CrossRef CAS PubMed.
- J. Elm, N. Myllys and T. Kurtén, Mol. Phys., 2017, 115, 2168–2179 CrossRef CAS.
- L. Onel, A. Brennan, P. W. Seakins, L. Whalley and D. E. Heard, Atmos. Meas. Tech., 2017, 10, 3985–4000 CrossRef CAS.
- A. D. Brennan, PhD thesis, University of Leeds, 2019.
- C. A. Cantrell, D. H. Stedman and G. J. Wendel, Anal. Chem., 1984, 56, 1496–1502 CrossRef CAS.
- M. Duncianu, A. Lahib, A. Tomas, P. S. Stevens and S. Dusanter, Atmos. Environ., 2020, 222, 117106 CrossRef CAS.
- Y. Liu, R. Morales-Cueto, J. Hargrove, D. Medina and J. Zhang, Environ. Sci. Technol., 2009, 43, 7791–7796 CrossRef CAS PubMed.
- C. E. Batista, J. Ye, I. O. Ribeiro, P. C. Guimarães, A. S. Medeiros, R. G. Barbosa, R. L. Oliveira, S. Duvoisin Jr, K. J. Jardine and D. Gu, et al. , Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19318–19323 CrossRef CAS PubMed.
- S. Kundu, B. L. Deming, M. M. Lew, B. P. Bottorff, P. Rickly, P. S. Stevens, S. Dusanter, S. Sklaveniti, T. Leonardis and N. Locoge, et al. , Atmos. Chem. Phys., 2019, 19, 9563–9579 CrossRef CAS.
- X. Shi, R. Tang, Z. Dong, H. Liu, F. Xu, Q. Zhang, W. Zong and J. Cheng, Sci. Total Environ., 2022, 848, 157494 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04308h |
| This journal is © the Owner Societies 2024 |


