X-ray induced ultrafast charge transfer in thiophene-based conjugated polymers controlled by core-hole clock spectroscopy

Abstract

We explore ultrafast charge transfer (CT) resonantly induced by hard X-ray radiation in organic thiophene-based polymers at the sulfur K-edge. A combination of core-hole clock spectroscopy with real-time propagation time-dependent density functional theory simulations gives an insight into the electron dynamics underlying the CT process. Our method provides control over CT by a selective excitation of a specific resonance in the sulfur atom with monochromatic X-ray radiation. Our combined experimental and theoretical investigation establishes that the dominant mechanism of CT in polymer powders and films consists of electron delocalisation along the polymer chain occurring on the low-femtosecond time scale.

---

1 Introduction

The process of charge transfer (CT) involving electron and nuclear dynamics is a long-standing research topic, which nevertheless remains bustling, essentially due to its significance for multiple applications in chemistry, biology and materials sciences.¹ Continuous progress in experimental and theoretical methods provides for an increasingly deeper understanding of the CT process. Rapid development of time-resolved spectroscopy allows nowadays probing the dynamics of CT in various systems on femtosecond and even attosecond time scale.² In complex systems, the control over nuclear and electron dynamics in time and space requires for a localised excitation of the CT process. This can be achieved by X-ray sources allowing for element-specific core–shell excitation. A combination of attosecond resolution with the X-ray photon energy range is at the heart of the current developments at free-electron laser and high-harmonic sources.^3–5

Meanwhile, high-resolution X-ray spectroscopy in the energy domain can also provide a useful insight into ultrafast dynamical processes in molecular systems. Using monochromatic synchrotron X-ray radiation, resonant excitation of a specific atomic core–shell in a molecule becomes possible. The lifetime of a core-excited state varies from a few femtoseconds for relatively shallow core holes with excitation energy up to 1 keV, down to the attosecond time scale for deep core holes with higher excitation energy. Relaxation of a resonantly core-excited molecule via emission of an X-ray photon or an Auger electron, occurring within the lifetime of a core-excited state, can serve as a probe of any dynamical process taking place in the molecule on the same time scale. This is the basic concept of “core-hole clock” spectroscopy (CHCS).⁶ Didactic reviews on applications of CHCS in relation to various CT processes can be found in ref. 7 and 8.

X-ray induced site-specific electron dynamics, monitored by CHCS, offers an exciting opportunity to explore the conduction properties of macromolecules. A remarkable example of attosecond intramolecular electron delocalisation in a genomic DNA molecule was demonstrated using resonant Auger spectroscopy of the powdered samples pressed onto a solid substrate.⁹ The mechanism of electron delocalisation was attributed to the presence of extended unoccupied electronic states along the phosphate groups in the DNA backbone. This finding may constitute an additional pathway of CT in DNA, along with the widely accepted mechanism of long-range charge transport through the π-stacked arrays of bases of the DNA double helical structure.¹⁰ Importantly, the intramolecular conductivity of DNA is directly related to its structural integrity and therefore, can serve for the diagnostics and repair of the radiation induced damage.¹¹

The phenomenon of electron dynamics in organic molecules is also of great relevance in optoelectronics, where charge transport in organic polymers is the key issue for the efficiency of organic photovoltaic devices. In conjugated polymers characterised by a sequence of alternating single and double bonds, electric conduction is mainly due to the π-electrons delocalised over several carbon atoms along the polymer backbone. Apart from delocalisation of π-electrons, key factors for charge transport are inter-chain π–π stacking interactions through the aromatic rings and side groups.^12,13

The conduction properties of conjugated polythiophene polymers were explored in ref. 14 using CHCS upon the resonant excitation of sulfur atoms near the S K-edge. Interestingly, no signature of electron delocalisation has been observed in the resonant Auger spectra of the powdered samples. However, a subsequent study of the same polymer deposited on a substrate as a thin film clearly revealed electron delocalisation in the low-femtosecond regime.¹⁵ This effect was attributed to the interaction between the polymer chains in the highly ordered films, since in powder form, the electrons may only be delocalised along the polymer chain (intra-chain mechanism), while in polymer films the delocalisation path can be two-fold: intra-chain and/or between the polymer chains (inter-chain mechanism). However, experimental restrictions in the previous studies,^14,15 in terms of a limited number of the recorded Auger spectra and their insufficient statistical quality, may have affected the reliability of the spectral assignment, which results in ambiguity concerning the role of polymer chain ordering in oriented films for the electron transport.

In the light of above discussions on the electron delocalisation in conjugated polythiophene, the motivation for our work is to find answers to the following open questions: What is the dominant mechanism of electron delocalisation in thiophene-based polymer powders and films upon resonant excitation at the S K-shell – along the polymer backbone (intra-chain) or through the π–π stacks (inter-chain)? Can we control the electron localisation/delocalisation by selective excitation of a specific resonance in the sulfur atom? Can we quantify the probability of electron delocalisation from the specific core-excited state?

In this paper we address the issue related to the mechanism of CT in sulfur-containing polymers – polythiophene (PT) powder and poly(3-hexylthiophene-2,5-diyl), commonly known as P3HT, film. The CT is locally induced by resonant excitation of sulfur atoms at the S K-shell and monitored by resonant Auger electron spectroscopy. Our experimental results reveal the signature of CT in both P3HT film and in PT powder occurring on the low-femtosecond time scale. The fact that CT is observed both in powder and in film points towards the dominance of an intra-chain electron delocalisation mechanism. Theoretical analysis of the dynamic processes, using real-time time-dependent density functional theory (RT-TDDFT) and Ehrenfest molecular dynamics (EMD) simulations, confirms this hypothesis. Furthermore, our detailed theoretical analysis reveals that the CT process along the polymer chain can only be initiated upon the resonant excitation of the S 1s⁻¹σ* state, whereas the resonant excitation of the S 1s⁻¹π* state does not lead to electron delocalisation. The electron dynamics simulations show that CT occurs on a sub-femtosecond time scale upon creation of the S 1s core hole, which compares reasonably well with the experimental estimate. This detailed mechanistic insight in the ultrafast electron/nuclear dynamics in core-level excitation in complex extended systems is made possible by an efficient implementation of RT-TDDFT in the CP2K software.¹⁶

2 Experiment

The experiments were carried out at the SOLEIL French national synchrotron facility using the high-resolution HAXPES station for hard X-ray photoemission spectroscopy¹⁷ located at the GALAXIES beamline.¹⁸ Linearly polarised light was provided by a U20 undulator followed by a Si(111) double-crystal monochromator. Electrons were detected by a large-acceptance angle EW4000 Scienta hemispherical analyser, the lens axis of which was parallel to the polarisation vector of the incident beam. A 200 eV pass energy and a 0.3 mm width curved slit were used for the measurements. The spectrometer resolution was determined at ∼180 meV while the beamline photon bandwidth δE was ∼225 meV at 2.5 keV photon energy. The measurements were performed at close to normal incidence of the X-ray beam with polarisation vector parallel to the sample surface. To avoid radiation damage to the samples, these were continuously moved during the measurements and filters were used, when necessary, to reduce the intensity of the X-ray beam.

The PT sample consists of a blend of polythiophene powder and graphite powder purchased from Sigma Aldrich. Use of such a blend served to tackle the space-charge build-up, which can severely alter the energy distribution of Auger lines.¹⁹ Equal amounts of polythiophene and graphite powders were ground together until a homogeneous mixture was obtained. The blend was deposited on carbon tape, covering the entire surface, and then fixed on a metal sample-holder. Additional carbon tape was fixed along the perimeter of the sample, increasing electric connectivity between the sample surface and metallic sample-holder. In order to exclude the influence of graphite on spectral features, we performed additional resonant inelastic X-ray scattering (RIXS) measurements, which are not affected by space charge effects in the samples. The RIXS spectra measured in pure PT powder and in PT mixed with graphite showed no differences.

The P3HT film was prepared by spin coating the 0.5 wt% solution of regio-regular P3HT powder (Sigma Aldrich) in CHCl₃, onto an indium-tin-oxide (ITO) substrate at ∼2000 RPM. The resulting film was placed on a metal sample holder and secured with carbon tape, also serving as an electrical conductor. More details on the samples characterisation can be found in the ESI,† Appendix A.

The presence of a good electric contact between the samples and the spectrometer in our experiment results in a common Fermi level (FL). This allows referencing the kinetic energy of electrons emitted from the samples with respect to the FL by adding the spectrometer work function ϕ_SP to the measured electron kinetic energy. Our calibration on the Au 4f_7/2 photoelectron line provides ϕ_SP = 4.9 eV. The incident photon energy was calibrated by using S K-edge X-ray absorption spectra of PT powder from ref. 14, and P3HT films from ref. 20, where the absorption spectra were obtained by recording the drain current of the samples.

Resonant Auger S KL_2,3L_2,3 electron spectra were measured at photon energies ranging from 2470 eV to 2475 eV with a step of 0.1 eV. Such a fine photon energy step, along with high statistics, allowed presenting the data in the form of 2D maps, where the Auger electron spectra are shown as a function of both the Auger electron kinetic energy and the incident photon energy.

To extract information from the Auger spectra, these were fitted using the SPANCF fitting suite for Igor Pro.²¹ For both polymers Voigt profiles were used, where both Lorentzian and Gaussian components were set as free parameters. Two Shirley backgrounds were used during the fit, to accurately account for the increased intensity at lower kinetic energies caused by inelastic scattering contribution.

3 Theory

3.1 Core-hole clock spectroscopy

The principle of the CHCS method, that we apply to reveal the CT effect, is illustrated in Fig. 1 showing the major excitation and decay events occurring in S KL_2,3L_2,3 Auger process. If the incident X-ray photon energy ħω exceeds the S 1s ionisation threshold, a 1s photoelectron (PE) is ejected into the continuum, followed by electron relaxation in the form of normal Auger decay, where one 2p electron fills the S 1s vacancy, while another 2p electron is ejected as an Auger electron (AE). In this case, the final state is dicationic with two holes (2h) in the 2p shell and the Auger electron energy is independent of the incident photon energy.

Fig. 1 Schematic of excitation and decay events upon absorption of an X-ray photon. Ionisation with emission of a photoelectron (PE) is followed by the normal Auger decay (c) with emission of an Auger electron (AE). Resonant excitation leads to resonant spectator Auger decay (a), when the spectator electron (SE) remains localised on the excited atom, or, to a CT decay channel (b), occurring in the case of delocalisation of the resonantly promoted electron to the environment. The green box represents destination environment of the delocalised electron. The spectator Auger decay leads to a monocationic final state (2h1e), whereas both the CT and the normal Auger decay channels lead to a dicationic (2h) final state. Longer vertical purple arrow in (a) indicates higher kinetic energy of the spectator Auger electron, compared to that of the normal Auger electron (c).

If the photon energy is insufficient for photo-ionisation, a core electron can be resonantly promoted to one of the unoccupied molecular orbitals (MO). In the event of delocalisation of the promoted electron to the surrounding environment, the subsequent relaxation, designated as a CT channel, is unaffected by the delocalised electron, and hence the process is similar to the normal Auger decay: the final state is also locally dicationic, while the Auger electron energy is constant and equal to the energy of the normal Auger line.

In the case where the promoted electron remains localised on the excited atom, one can talk about resonant Auger relaxation. In the resonant Auger process, the spectator Auger decay (the promoted spectator electron (SE) remains in the excited orbital) strongly dominates over the participator decay (the promoted electron participates in the relaxation process), therefore the latter process will be omitted in the following discussion.²² In the case of spectator Auger decay, the final state is monocationic (2h1e) with two holes in the 2p shell and one spectator electron. Here, under resonant Raman conditions, when the experimental resolution is smaller than the lifetime broadening of the core-excited state, and in absence of ultrafast nuclear dynamics in the molecule, a linear relation between the energy of the incident photon and the spectator Auger electron kinetic energy can be observed.²³ Due to the screening of the 2p holes by the spectator electron, the resulting spectator Auger kinetic energy is blue-shifted with respect to the normal Auger line. The presence of this so-called spectator shift is essential, since it allows separating the spectator Auger channel and the CT channel directly at the resonant excitation photon energy.

The branching ratio between the localised spectator Auger and delocalised CT channels, provides an estimate of the CT rate upon core-excitation. To determine the CT time scale τ_CT, the following relation is generally considered valid^7,8,24

where I_Spectator and I_CT correspond to the integrated intensity of a specific resonant spectator Auger channel and the corresponding CT channel, respectively, and τ_CH = 1.1 fs is the core-hole lifetime of the S 1s vacancy.²⁵

3.2 Computational methods

Kohn–Sham density functional theory (KS-DFT)^26,27 simulations have been carried out employing the Perdew–Burke–Ernzerhof (PBE)²⁸ exchange–correlation functional supplemented with the Grimmes D3²⁹ dispersion correction. The simulations have been performed using the CP2K program,³⁰ under the Gaussian and plane-wave (GPW) approach. Valence electrons were treated explicitly, and norm-conserving Goedecker–Teter–Hutter (GTH) pseudopotentials³¹ were used to account for the interaction between the valence electrons and the atomic cores. We employed double-zeta valence plus polarisation (DZVP) basis sets, and a cutoff of 1000 Ry for the auxiliary plane-wave basis set. The computational parameters used in the reported simulations have been converged with respect to the system size and the basis set size.

The simulations for P3HT were carried out with a regio-regular model adapted from ref. 33, shown in Fig. 2. According to the experimental conditions, the lamella sheets are positioned in the XZ plane parallel to the sample surface. The model contains two layers of 2 × 2 units, corresponding to a simulation cell with size of 30.52 × 15.02 × 15.93 ų, for which periodic boundary conditions have been applied to all three directions. In one unit, the polymer chains are laterally shifted in the XZ plane by 1.3 Å with respect to each other, as Fig. 2(b) shows. The stacking of polymer chains is then ABAB along the y direction. The calculated geometry of the system was fully relaxed until the maximum force component was smaller than 1.0 × 10⁻⁴ Ha bohr⁻¹. Electronic structure calculations were performed at 0 K temperature and at the Gamma point of the supercells.

Fig. 2 Ball and stick illustration of the employed P3HT simulation cell: (a) and (b) bottom, (c) side, and (d) diagonal views. The XZ plane is parallel to the sample surface. Colour code: brown for carbon, yellow for sulfur, green for chlorine (Z + 1 approximation), light pink for hydrogen. In panel (b), different polymer layers are depicted in pink and green to show the lateral displacement between the chains when stacked. All the structures' rendering were generated using the VESTA³² software.

Although the simulations for the measurements of PT powder could not be performed due to the lack of crystalline structure in the sample, we have explored theoretically a PT film constructed by removing the hydrocarbon side chains from the P3HT model, followed by full relaxation of the system's geometry.

To initialise the electronic structure in the 1s⁻¹π* core-excited state, we made use of the Z + 1 approximation, in which the potential of the core-excited sulfur atom is replaced by that of the fully relaxed chlorine atom. The additional electron behaves as an electron promoted to a π* MO, which splits out from the π* band after creation of the core hole. To address the 1s⁻¹σ* excited state, we modified the initial occupation of the orbitals, by removing the electron from the π* and occupying the higher-lying split-out σ* MO localised at the excited ring.

Starting from electronic configurations in the Z + 1 approximation corresponding to 1s⁻¹π* and 1s⁻¹σ* core-excited states, the electron dynamics has been propagated using the RT-TDDFT³⁴ approach, in which the electronic wavefunctions are propagated in real-time and are not associated with energy levels. The nuclei were kept at the ground-state optimised coordinates throughout the entire propagation. By means of RT-TDDFT, we are able to address the dynamical rearrangement of the electronic charge, which is taking place within a few femtoseconds upon the formation of the S 1s core hole. Hence, the electronic wavefunctions of the 1s⁻¹π* and 1s⁻¹σ* states were propagated for 20 fs, using a time step of 0.5 attosecond (as). The evolution of the electronic charge distribution has been monitored by plotting its running changes at time intervals of 5 as. Moreover, we applied the Bader population analysis to the time dependent charge density,³⁵ to reveal the regions of charge accumulation and charge depletion during the relaxation.

4 Results and discussion

4.1 Experimental data analysis

Experimental resonant Auger S KL_2,3L_2,3 spectra for P3HT thin film and PT powder are shown in Fig. 3 as 2D maps, where the resonant Auger electron spectra are plotted as a function of both the electron kinetic energy and incident photon energy. The logarithmic colour scale represents intensity normalised to the background.

Fig. 3 2D maps of S KL_2,3L_2,3 Auger spectra recorded in PT powder (a) and P3HT thin film (b). Transitions to the and final states are indicated with black crosses. Transitions to the and states, indicated with white crosses, are labelled as π* and σ*. Blue lines and adjacent labels (A–D), indicate the corresponding resonant photon energies. Diagonal dotted lines show dispersive behaviour of resonant structures. Purple stadium shapes indicate the region where the CT feature is most prominent. The maps are normalised to the background. The colour-coded intensities are on a logarithmic scale.

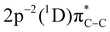The most intense features in the maps (indicated with white crosses) correspond to the spectator Auger transitions from the first two core-excited states and to the and 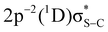final states, respectively (labelled as π* and σ*). The attribution of the states is based on earlier investigations in thiophene.³⁶ The white dotted diagonal lines highlight the dependence of the resonant Auger kinetic energy on the photon energy, typically observed in Raman conditions. Horizontal blue lines with adjacent labels (A–D) indicate the corresponding resonant photon energies. The features indicated with black crosses correspond to the transitions to the and final states. The ³P multiplet structures are forbidden due to angular momentum and parity conservation rules and are absent in the figure due to their low intensity.

Both 2D maps contain a feature on the low-energy side of the 2p⁻²(¹D)σ* line, which is marked with purple stadium shapes and labelled CT. At the top of the maps, at the photon energies above 2474 eV, one can see contributions of the Auger lines corresponding to the excitation to high-energy delocalised states. Upon further increase of the photon energy beyond the ionisation threshold located at ∼2478 eV, these features evolve into normal Auger lines.³⁷

We underline a qualitatively similar manifestation of the CT channel in both polymers in Fig. 3, which likely indicates the similarity of the CT mechanism in the powder and the thin film polymer forms. This goes in contrast to the conclusions of ref. 14, where the absence of CT in PT powder was probably due to insufficient statistics of the measurements.

Remarkably, in both polymers the CT feature is most intense at the photon energies around ∼2473.5 eV, i.e. close to the resonant excitation energy of the 1s⁻¹σ* state. As introduced above, the blue shift of the spectator Auger electron kinetic energy relative to the normal Auger line allows us to separate the delocalised CT channel from the localised resonant channel at the resonant photon energy. Indeed, at the photon energy of 2473.3 eV, the resonant Auger electrons resulting from the spectator Auger transition to the 2p⁻²(¹D)σ* state have kinetic energy of around 2116 eV. The CT channel, instead, is observed at the kinetic energy around 2113 eV. The 3 eV difference represents the spectator shift caused by the screening of the 1s and 2p core holes by the spectator electron in the σ* MO.

The spectator shift reflects the efficiency of screening of the 1s and 2p core holes by the spectator electron and therefore depends on the energy of the core-excited state with respect to the ground state. Generally, it takes the largest value for the resonant excitation to the lowest unoccupied MO and gradually decreases for higher-lying orbitals converging to zero at the ionisation threshold. On the contrary, in our case, the spectator shift of the 2p⁻²σ* line is larger than that of the 2p⁻²π* line. Indeed, the spectator shift corresponding to the 2p⁻²(¹D)π* line, is less than 1 eV at the resonant excitation photon energy (2472.5 eV) of the 1s⁻¹π* state.

This counter-intuitive behaviour has been recently observed in gas-phase thiophene.³⁸ It was demonstrated that in the process of core-excitation and Auger decay, the energy order of the first two core-excited states and the corresponding final states reverses due to the destabilisation of the conjugated π-system in the aromatic molecules. The presence of the same effect in gas-phase thiophene and solid-state thiophene-based polymers points at the general nature of the observed phenomenon for conjugated systems.

Using 2D maps as a guide, we can trace the spectator Auger and the CT channels as a function of photon energy with the help of the fitting procedure described in the Experimental section. Fig. 4 shows least-squares fit analyses of the spectra at the resonant photon energies indicated in Fig. 3 by labels A–D and horizontal blue lines.

Fig. 4 S KL_2,3L_2,3 Auger spectra of PT powder (a), (b) and P3HT thin film (c), (d) at resonant excitation energies of the S 1s⁻¹σ* (a), (c) and S 1s⁻¹π* (b), (d) states. The fitted lines correspond to the resonant spectator Auger transitions to the 2p⁻²σ* (magenta) and 2p⁻²π* (purple) final states. Green and orange show the CT channel and a shake-up from an occupied band to an unoccupied MO, respectively.

For both samples, at ħω = 2473.3 eV (Fig. 4, panels (a) and (c)) corresponding to the resonant excitation photon energy of the 1s⁻¹σ* state, the spectra are dominated by the resonant spectator Auger transition to the 2p⁻²σ* final state at a kinetic energy ∼2116 eV (magenta). The shoulder on the low-energy side of the dominant line contains the contributions from the resonant spectator transition to the 2p⁻²π* final state (purple) and the CT channel at a kinetic energy ∼2113 eV (green).

Around ħω = 2472.5 eV (Fig. 4, panels (b) and (d)), corresponding to the resonant excitation photon energy of the 1s⁻¹π* state, the 2p⁻²π* line at a kinetic energy ∼2114 eV (purple) is predominant, accompanied by a less intense 2p⁻²σ* line to the higher kinetic energy side (magenta) and a weak shoulder to the low-energy side at a kinetic energy of ∼2112 eV (orange).

The reason for using different colour coding for the green and orange lines in Fig. 4 becomes clear when considering dispersion, or kinetic energy position of the spectral features of interest as a function of the incident photon energy presented in Fig. 5. It is readily apparent that both spectator channels follow a dispersive energy trend in PT (Fig. 5(a)) and P3HT (Fig. 5(b)).

Fig. 5 Kinetic energy position of Auger electron lines in PT powder (a) and P3HT thin film (b) as a function of photon energy. Grey vertical lines indicate the resonant excitation photon energies for the 1s⁻¹π* and 1s⁻¹σ* states. Resonant spectator channels 2p⁻²σ* (magenta) and 2p⁻²π* (purple) show a quasi-linear photon energy dependence. Dashed horizontal line highlights the constant kinetic energy of the CT channel (green). Dispersive low-energy peak observed at the photon energies close to the resonant excitation of the 1s⁻¹π* state (orange) is attributed to a shake-up process. The systematic error from the fitting procedure is within the size of the marker.

In contrast to the dispersive resonant spectator channels, the kinetic energy of the Auger electrons ejected as a result of electron delocalisation is expected to be independent of the incident photon energy. We use this property as a fingerprint to identify the origin of the peaks observed in the spectra on the low-energy side of the resonant spectator features. In PT and P3HT, at ħω ≥ 2473 eV, close to the resonant excitation energy of the S 1s⁻¹σ* state, the position of the low-energy peak stays constant, which is the hallmark behaviour of electron delocalisation. Therefore, we attribute this peak to CT corresponding to electron delocalisation from the resonantly excited 1s⁻¹σ* state.

At photon energies ħω ≤ 2473 eV, close to the excitation energy of the S 1s⁻¹π* resonant state, the kinetic energy of the low-energy peak strongly depends on the photon energy. At these photon energies the intense resonant 2p⁻²π* line strongly overlaps with the weak low-energy peak (see Fig. 4, panels (b) and (d)), which reduces fitting accuracy. Nevertheless, a clear dependence of the peak kinetic energy on the photon energy eliminates its possible attribution to the CT process. Its origin may possibly be attributed to shake-up of an electron from an occupied band to an unoccupied MO during the Auger decay as was previously observed in gas-phase systems.³⁹

According to eqn (1), from the integrated intensities of the 2p⁻²σ* lines and of the CT lines, resulting from the fits in Fig. 4(a) and (c), we can estimate the CT time τ_CT at the resonant excitation energy of the S 1s⁻¹σ* state. The obtained τ_CT values are ∼3 fs and ∼9 fs for PT powder and P3HT film, respectively. Note that the 9 fs estimate of τ_CT obtained for P3HT film is comparable with the values reported in earlier studies on PT and P3HT thin films.^15,40,41 A three times shorter CT time estimated for PT powder indicates a stronger coupling between the resonantly excited S 1s⁻¹σ* state, the source orbital of the CT process, to the conduction band of the polymer, serving as the receiver for the delocalised electron.

We would like to underline that the accuracy of the reported CT times depends on the fitting uncertainties related to the choice of such fitting parameters as shapes, widths and asymmetry of the spectral lines, the shape and the level of background as well as correlation of the fitting parameters for a sequence of spectra. We estimate this uncertainty to be around 20%. Furthermore, in the case when the spectral lines strongly overlap and are affected by the background, the CT times obtained with eqn (1) have to be taken with extra caution.

4.2 Computational analysis

The ultrafast dynamics of the electronic structure induced by the creation of a core hole upon absorption of resonant or non-resonant X-ray radiation, can be simulated by RT-TDDFT. The initial electronic structure of the S 1s⁻¹π* and 1s⁻¹σ* core-excited states is constructed as described in the Computational methods section. It is worth mentioning that we assume the presence of the core hole only at one thiophene ring in the simulation box. This induces symmetry breaking and the localisation of some low-lying empty states around the excited ring, which split out of the corresponding band. Under these conditions, the 1s⁻¹π* and 1s⁻¹σ* states, occupied by the excited electron, are easily identified as the most localised, but are not necessarily the lowest in energy. Such split-out states are also referred to as core-exciton states in the literature.⁸

To illustrate the energy levels of the split-out states with respect to the unoccupied π* and σ* bands, Fig. 6 shows the density of states (DOS) projected on the angular momentum components p_y (π-orbital character), and s + p_x + p_z (σ-orbital character), and on the carbon and sulfur/chlorine atoms that compose the excited and a reference thiophene rings. The latter was chosen to be the most distant ring from the excited one. Here, we want to emphasise the energy level relaxation around the excited ring. In particular, when the excitation to the π* band (II in Fig. 6(a)) occurs, the energy of the split-out 1s⁻¹π* state (III in Fig. 6(a)) falls below any other unoccupied states. This is not the case for the excitation into the σ* band (IV in Fig. 6(b)), since despite the relaxation, the split-out 1s⁻¹σ* state (V in Fig. 6(b)) still remains above the unoccupied π* band (II in Fig. 6(a)). This implies a possibility of CT only from the S 1s⁻¹σ* state.

Fig. 6 DOS computed for P3HT projected on the carbon and sulfur/chlorine atoms of the excited and reference rings, and on the angular momentum components (a) p_y (π-orbital character) and (b) s + p_x + p_z (σ-orbital character). The energy of states is shown relative to the Fermi level. At the reference ring, the projected DOS in the ground state (grey area) and in a core-excited state (blue line) are nearly identical. The roman numerals label the occupied π band (I), the first unoccupied π* band (II) and the unoccupied σ* band (IV). At the excited ring, the projected DOS in a core-excited state (red) contains the split-out π* MO (III) and the split-out σ* MO (V).

The CT mechanism can be further inferred by considering the spatial distribution of the split-out π* and σ* orbitals upon creation of the 1s⁻¹σ* core-hole state. In the XY view, Fig. 7(a) and (c), the excited thiophene ring is located in the bottom right section of the plane, while in the XZ view, Fig. 7(b) and (d), it is located in the top right section. One can see from Fig. 7(a) and (c) that both the split-out σ* orbital and the split-out π* orbital (as well as the orbitals in the unoccupied π* band) are limited to the polymer chain containing the excited thiophene ring. In addition, Fig. 7(b) shows that the split-out π* orbital significantly extends along the polymer chain containing the excited thiophene ring, whereas the split-out σ* orbital is localised on the excited thiophene ring only (Fig. 7(d)). The spatial distributions provide qualitative information about the states, in that an apparent overlap between the σ* orbital and the unoccupied π* band can be observed. This overlap might favour the flow of electronic charge along the polymer chains.

Fig. 7 XY and XZ views of the spatial distribution of the split-out π* (a), (b) and σ* (c), (d) orbitals after creation of the 1s⁻¹σ* state in P3HT. The π* orbital significantly extends along the polymer chain, whereas the σ* orbital is spatially localised mainly on the excited thiophene ring. The red and green coloured lobes depict the orbital amplitude and represent the different phases of the wavefunction. The surfaces were plotted with an isovalue of 9.5 × 10⁻³a₀^−3/2.

By running the real-time propagation of the electronic density for a few femtoseconds, it is possible to monitor whether and how the electronic distribution around the excited ring evolves. To illustrate the electron dynamics responsible for CT in P3HT film and estimate the time scale of this process, we have extracted the spatial electron density distributions every 5 attoseconds along the first few femtoseconds of propagation. Fig. 8(a)–(c) shows the electronic density differences computed at intervals of 5 as, at 5, 15, and 30 as of propagation of the 1s⁻¹σ* state. In the case of Fig. 8(c), for instance, we plot the difference between the electronic charge density obtained at times t = 25 as and t = 30 as, with the subtraction performed point by point. Depending on the values of the density at every point in space at both instants of time, we get positive or negative values for the difference, which represent gain or loss of electronic charge, shown in Fig. 8 in blue and red, respectively.

Fig. 8 Electron density differences in P3HT film computed at time intervals of 5 as, at (a) 5 as, (b) 15 as, (c) 30 as, (d) 0.25 fs, (e) 0.5 fs, and (f) 1 fs of simulation. The electronic dynamics is limited only to the stack of polymer chains containing the excited thiophene ring. Electron accumulation regions are shown in blue, whereas electron depletion regions are shown in red. The surfaces were plotted with an isovalue of 6.0 × 10⁻⁵a₀⁻³.

We observe that, already on this time scale, a significant evolution of the electron density occurs from the excited thiophene ring along the polymer chain (right-hand side of panels (a)–(c) in Fig. 8). Furthermore, from the left-hand side of panels (a)–(c), we can conclude that the net amount of electron density propagating across the polymer chains is negligible. The electron density differences computed at 0.25, 0.5, and 1 fs, shown in Fig. 8(d)–(f), demonstrate that the dynamical electronic rearrangement slows down with time, reaching a final state within the first 0.5 fs of simulation.

One useful tool to extract quantitative information from the electronic distribution is the population analysis performed according to the Bader formalism.³⁵ In particular, we have calculated the total charge assigned to the excited ring, as well as the population on the neighbouring rings along the chain and in the layers above and below the excited ring.

The variation of the computed populations Δq over the first 3 fs of the propagation of the 1s⁻¹π* and 1s⁻¹σ* state are shown in Fig. 9(a) and (b), respectively, with positive (negative) values indicating electron accumulation (depletion). The Bader charge analysis indeed confirms that upon promotion of the core electron to the π* band, the population of all the selected rings remains unchanged (Fig. 9(a)).

Fig. 9 Bader charge analysis of the selected rings in P3HT for the first 3 fs of propagation in the core-excited states (a) 1s⁻¹π* and (b) 1s⁻¹σ*. The grey line denotes Δq = 0. Negative (positive) values indicate electron depletion (accumulation).

For the 1s⁻¹σ* state the situation is different. Upon promotion of the core-excited electron to the σ* band and propagation of the corresponding electronic wavefunction, we indeed reveal a propensity for charge transfer. The populations of the excited ring (purple) and of the adjacent rings in the same chain (blue) present a significant change at the very beginning of the propagation, which is then stabilised in less than a femtosecond (Fig. 9(b)). About 0.40 electrons are transferred from the excited ring to the neighbours along the same polymer chain. The variation of population on the rings in the layers above and below the excited ring (red) is negligible.

Note that in simulations employing real electromagnetic pulses to tackle electronic excitation processes, oscillations in the Bader charges are understood as an effect of the coherent superposition of excited states.⁴² In this study, however, the beating pattern present in Fig. 9(b) should be rather interpreted as an artefact intrinsic to the method chosen to create the core-excited 1s⁻¹σ* state in the Z + 1 approximation. As described in the section on computational methods, the 1s⁻¹σ* state is created by transferring an electron from the π* orbital to the σ* orbital. This manipulation creates an artificial superposition between the 1s⁻¹π* and 1s⁻¹σ* states leading to fast oscillations in the Bader population analysis.

Similar results were also obtained for a PT film. The Bader charge analysis performed for the first 2 fs of real-time propagation, shows no change in population in the selected thiophene rings for the 1s⁻¹π* state. On the other hand, for 1s⁻¹σ* state, exchange of population can be observed mainly between the excited ring and the adjacent rings along the chain (see ESI,† Appendix C). The similarity of the results obtained for P3HT and PT show that the hydrocarbon side chains present in P3HT do not appear to modify the mechanism behind the CT processes for this type of polymer films.

The Bader charge analysis presented in Fig. 9 and the qualitative analysis provided by the electronic density differences presented in Fig. 8 provide an estimate of CT time occurring along the polymer chain in the core-excited 1s⁻¹σ* state on the order of 1 fs. This estimate is significantly shorter compared to the experimental values of ∼9 fs and ∼3 fs for P3HT and PT samples, respectively, obtained using eqn (1). There are several possible reasons for this discrepancy. A possible effect of nuclear motion has been ruled out by the Ehrenfest molecular dynamics simulations (see ESI,† Appendix B). Sensitivity to potential surface effects and defects can also be safely excluded, since in the hard X-ray regime used in our study, the X-ray attenuation length in the sample is on the order of tens of microns, which largely exceeds the sample thickness of ∼30 nm (see ESI,† Appendix A). However, the simulations cannot fully account for such experimental parameters as possible defects in the crystalline structure of the P3HT film and thermal effects. Furthermore, as mentioned above, the accuracy of the experimental CT time estimates provided by eqn (1) is limited due to a strong overlap of the spectral features and a significant background, preventing from a reliable fitting of the peak areas.

Nevertheless, despite the quantitative variance between the experimental and computational estimates of CT time scales, our simulations provide a solid theoretical foundation for the experimental observations. Considering the density of states in the core-excited states, the spatial distribution of the relevant orbitals and the evolution of the electronic density on the femtosecond time scale, the simulations have unambiguously revealed the mechanism of CT in the studied polymer systems in agreement with the insights inferred from the experimental data.

5 Conclusions

Our joint experimental and theoretical study has demonstrated the presence of ultrafast CT in organic conjugated thiophene-based polymers induced by resonant hard X-ray excitation at the sulfur K-edge. Comparing the experimental evidence of CT in polymer powders and thin films and following the results of real-time propagation TDDFT simulations, we have established that intra-chain electron delocalisation is the dominant mechanism of CT, whereas inter-chain electron delocalisation is negligible in the studied systems. This main conclusion of our work is sketched in Fig. 10.

Fig. 10 Sketch of the excited thiophene ring (purple) and its nearest neighbours along the chain (blue) and in the layers above and below (red) in P3HT film. The green arrows show that only the intra-chain CT is possible.

Furthermore, we have shown that intra-chain electron delocalisation can be exclusively induced upon resonant excitation of S 1s⁻¹σ* state, whereas resonant excitation of the S 1s⁻¹π* state does not lead to electron delocalisation. Therefore, our approach demonstrates a capacity to not only initialise and monitor ultrafast electron dynamics in extended systems by resonant element-specific core–shell excitation, but also provides a control over electron delocalisation by a selective excitation of a specific resonance in the excited atom.

This opens perspectives for the forthcoming studies on intra-molecular conductivity in organic molecules including technologically and biologically relevant systems. A striking resemblance between the polymeric structures containing π-stacked arrays and the DNA double helical structure with π-stacked arrays of bases implies a manifestation of common mechanisms responsible for electric conduction in these systems. Thus, further investigation of CT in biological samples can provide a better understanding of the mechanisms behind molecular damage induced by X-ray radiation.

The insights into the CT mechanisms in complex systems provided by the CHCS approach owing to its site-specific nature, augmented by the high-level computational analysis, can be taken further towards the emerging field of time-resolved attosecond X-ray spectroscopy. As an example of time-resolved X-ray induced CT, proton transfer was demonstrated to occur within several femtoseconds in the course of isomerisation of an acetylene molecule ionised at the carbon 1s shell.⁴³ Taking a step towards potential applications, very recently, proton transfer and the coupled dynamics of the electronic structure in urea solutions have been demonstrated using the element and site selectivity of X-ray absorption spectroscopy in the water window.⁴⁴ Availability of higher photon energies for time-resolved experiments at XFEL facilities will allow probing deeper shells of such elements as magnesium or manganese, whose ionic form plays a vital role in the catalytic activity of DNA polymerase.^45,46

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Experiments were performed on the GALAXIES beamline at SOLEIL Synchrotron, France (proposals 20180196, 99210051 & 20201715). We are grateful to the SOLEIL staff for their smooth operation of the facility. T. M. gratefully acknowledges useful discussions with Prof. Maria Luiza Rocco. N. V., T. M., and M. O. acknowledge funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. [860553]. J. B. M. and T. M. acknowledge financial support from the French Agence Nationale de la Recherche (ANR) through the ATTOMEMUCHO project (ANR-16-CE30-0001). F. B. N. acknowledges the Graduate Campus of the University of Zurich for the GRC Travel Grant. M. O. acknowledges financial support from the Swedish Research Council (VR contract 2021-04521). The authors are thankful for the generous allocation of computing resources from the Swiss National Supercomputing Center (CSCS) under Projects s965 and ch12, and both CSCS and the Alfred Werner-Legat for the computational resources under Project uzh35.

References

1. V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, John Wiley Sons, Hoboken, NJ, 1999.
2. H. J. Wörner, C. A. Arrell, N. Banerji, A. Cannizzo, M. Chergui, A. K. Das, P. Hamm, U. Keller, P. M. Kraus, E. Liberatore, P. Lopez-Tarifa, M. Lucchini, M. Meuwly, C. Milne, J.-E. Moser, U. Rothlisberger, G. Smolentsev, J. Teuscher, J. A. van Bokhoven and O. Wenger, Charge migration and charge transfer in molecular systems, Struct. Dyn., 2017, 4, 061508.
3. S. Serkez, G. Geloni, S. Tomin, G. Feng, E. V. Gryzlova, A. N. G. Grzhimailo and M. Meyer, Overview of options for generating high-brightness attosecond X-ray pulses at free-electron lasers and applications at the European XFEL, J. Opt., 2018, 20, 024005.
4. N. Hartmann, G. Hartmann, R. Heider, M. S. Wagner, M. Ilchen, J. Buck, A. O. Lindahl, C. Benko, J. Grünert, J. Krzywinski, J. Liu, A. A. Lutman, A. Marinelli, T. Maxwell, A. A. Miahnahri, S. P. Moeller, M. Planas, J. Robinson, A. K. Kazansky, N. M. Kabachnik, J. Viefhaus, T. Feurer, R. Kienberger, R. N. Coffee and W. Helml, Attosecond time-energy structure of X-ray free-electron laser pulses, Nat. Photonics, 2018, 12, 215–220.
5. J. Li, J. Lu, A. Chew, S. Han, J. Li, Y. Wu, H. Wang, S. Ghimire and Z. Chang, Attosecond science based on high harmonic generation from gases and solids, Nat. Commun., 2020, 11, 2748.
6. O. Björneholm, A. Nilsson, A. Sandell, B. Hernnäs and N. Mårtensson, Determination of time scales for charge-transfer screening in physisorbed molecules, Phys. Rev. Lett., 1992, 68, 1892–1895.
7. P. A. Brühwiler, O. Karis and N. Mårtensson, Charge-transfer dynamics studied using resonant core spectroscopies, Rev. Mod. Phys., 2002, 74, 703–740.
8. D. Menzel, Ultrafast charge transfer at surfaces accessed by core electron spectroscopies, Chem. Soc. Rev., 2008, 37, 2212.
9. H. Ikeura-Sekiguchi and T. Sekiguchi, Attosecond Electron Delocalization in the Conduction Band through the Phosphate Backbone of Genomic DNA, Phys. Rev. Lett., 2007, 99, 228102.
10. J. C. Genereux and J. K. Barton, Mechanisms for DNA Charge Transport, Chem. Rev., 2010, 110, 1642–1662.
11. T. J. Zwang, E. C. M. Tse and J. K. Barton, Sensing DNA through DNA Charge Transport, ACS Chem. Biol., 2018, 13, 1799–1809.
12. M. Jaiswal and R. Menon, Polymer electronic materials: a review of charge transport, Polym. Int., 2006, 55, 1371–1384.
13. D. Garratt, L. Misiekis, D. Wood, E. W. Larsen, M. Matthews, O. Alexander, P. Ye, S. Jarosch, C. Ferchaud, C. Strüber, A. S. Johnson, A. A. Bakulin, T. J. Penfold and J. P. Marangos, Direct observation of ultrafast exciton localization in an organic semiconductor with soft X-ray transient absorption spectroscopy, Nat. Commun., 2022, 13, 3414.
14. H. Ikeura-Sekiguchi and T. Sekiguchi, Unoccupied electronic states in polythiophene as probed by XAS and RAS: unoccupied electronic states in polythiophene as probed by XAS, Surf. Interface Anal., 2008, 40, 673–675.
15. C. Arantes, B. G. A. L. Borges, B. Beck, G. Araújo, L. S. Roman and M. L. M. Rocco, Femtosecond Electron Delocalization in Poly(thiophene) Probed by Resonant Auger Spectroscopy, J. Phys. Chem. C, 2013, 117, 8208–8213.
16. S. Andermatt, J. Cha, F. Schiffmann and J. VandeVondele, Combining Linear-Scaling DFT with Subsystem DFT in Born–Oppenheimer and Ehrenfest Molecular Dynamics Simulations: From Molecules to a Virus in Solution, J. Chem. Theory Comput., 2016, 12, 3214–3227.
17. D. Céolin, J. Ablett, D. Prieur, T. Moreno, J.-P. Rueff, T. Marchenko, L. Journel, R. Guillemin, B. Pilette, T. Marin and M. Simon, Hard X-ray photoelectron spectroscopy on the GALAXIES beamline at the SOLEIL synchrotron, J. Electron Spectrosc. Relat. Phenom., 2013, 190, 188–192.
18. J.-P. Rueff, J. M. Ablett, D. Céolin, D. Prieur, T. Moreno, V. Balédent, B. Lassalle-Kaiser, J. E. Rault, M. Simon and A. Shukla, The GALAXIES beamline at the SOLEIL synchrotron: inelastic X-ray scattering and photoelectron spectroscopy in the hard X-ray range, J. Synchrotron Radiat., 2015, 22, 175–179.
19. G. Vereecke and P. G. Rouxhet, Surface charging of insulating samples in X-ray photoelectron spectroscopy, Surf. Interface Anal., 1998, 26, 490–497.
20. H. Ikeura-Sekiguchi and T. Sekiguchi, Molecular ordering effect of regioregular poly(3-hexylthiophene) using sulfur K-edge X-ray absorption spectroscopy, Jpn. J. Appl. Phys., 2014, 53, 02BB07.
21. E. Kukk, Spectrum Analysis by Curve Fitting (SPANCF) Macro Package for Igor Pro, 2009, https://www.geocities.ws/ekukk/intro.htm.
22. K. Yoshii, Y. Baba and T. Sasaki, Resonant Auger Electron Spectra at Si-, P-, S-, and Cl-1s Thresholds of Condensed Molecules, Phys. Status Solidi B, 1998, 206, 811–822.
23. F. Gel’mukhanov and H. Ågren, Raman, non-Raman, and anti-Raman dispersion in resonant X-ray scattering spectra of molecules, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 3960–3970.
24. W. Wurth and D. Menzel, Ultrafast electron dynamics at surfaces probed by resonant Auger spectroscopy, Chem. Phys., 2000, 251, 141–149.
25. M. O. Krause and J. H. Oliver, Natural widths of atomic K and L levels, K alpha X-ray lines and several K L L Auger lines, J. Phys. Chem. Ref. Data, 1979, 8, 329–338.
26. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871.
27. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
30. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: an electronic structure and molecular dynamics software package – Quickstep: efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103.
31. S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
32. K. Momma and F. Izumi, VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
33. Z.-F. Yao, Q.-Y. Li, H.-T. Wu, Y.-F. Ding, Z.-Y. Wang, Y. Lu, J.-Y. Wang and J. Pei, Building crystal structures of conjugated polymers through X-ray diffraction and molecular modeling, SmartMat, 2021, 2, 378–387.
34. K. Yabana and G. F. Bertsch, Time-dependent local-density approximation in real time, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4484–4487.
35. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204.
36. A. P. Hitchcock, J. A. Horsley and J. Stöhr, Inner shell excitation of thiophene and thiolane: gas, solid, and monolayer states, J. Chem. Phys., 1986, 85, 4835–4848.
37. N. Velasquez, O. Travnikova, R. Guillemin, I. Ismail, L. Journel, J. B. Martins, D. Koulentianos, D. Céolin, L. Fillaud, M. L. M. Rocco, R. Püttner, M. N. Piancastelli, M. Simon, S. Sheinerman, L. Gerchikov and T. Marchenko, Generalization of the post-collision interaction effect from gas-phase to solid-state systems demonstrated in thiophene and its polymers, Phys. Rev. Res., 2023, 5, 013048.
38. J. B. Martins, C. E. V. de Moura, G. Goldsztejn, O. Travnikova, R. Guillemin, I. Ismail, L. Journel, D. Koulentianos, M. Barbatti, A. F. Lago, D. Céolin, M. L. M. Rocco, R. Püttner, M. N. Piancastelli, M. Simon and T. Marchenko, Electron delocalisation in conjugated sulfur heterocycles probed by resonant Auger spectroscopy, Phys. Chem. Chem. Phys., 2022, 24, 8477–8487.
39. R. Püttner, P. Holzhey, M. Hrast, M. Žitnik, G. Goldsztejn, T. Marchenko, R. Guillemin, L. Journel, D. Koulentianos, O. Travnikova, M. Zmerli, D. Céolin, Y. Azuma, S. Kosugi, A. F. Lago, M. N. Piancastelli and M. Simon, Argon K L L Auger spectrum: initial states, core-hole lifetimes, shake, and knock-down processes, Phys. Rev. A, 2020, 102, 052832.
40. Y. Garcia-Basabe, B. Borges, D. Silva, A. Macedo, L. Micaroni, L. Roman and M. Rocco, The interplay of electronic structure, molecular orientation and charge transport in organic semiconductors: poly(thiophene) and poly(bithiophene), Org. Electron., 2013, 14, 2980–2986.
41. Y. Garcia-Basabe, D. Ceolin, A. J. G. Zarbin, L. S. Roman and M. L. M. Rocco, Ultrafast interface charge transfer dynamics on P3HT/MWCNT nanocomposites probed by resonant Auger spectroscopy, RSC Adv., 2018, 8, 26416–26422.
42. M. Jacobs, J. Krumland and C. Cocchi, Laser-Controlled Charge Transfer in a Two-Dimensional Organic/Inorganic Optical Coherent Nanojunction, ACS Appl. Nano Mater., 2022, 5, 5187–5195.
43. C. E. Liekhus-Schmaltz, I. Tenney, T. Osipov, A. Sanchez-Gonzalez, N. Berrah, R. Boll, C. Bomme, C. Bostedt, J. D. Bozek, S. Carron, R. Coffee, J. Devin, B. Erk, K. R. Ferguson, R. W. Field, L. Foucar, L. J. Frasinski, J. M. Glownia, M. Gühr, A. Kamalov, J. Krzywinski, H. Li, J. P. Marangos, T. J. Martinez, B. K. McFarland, S. Miyabe, B. Murphy, A. Natan, D. Rolles, A. Rudenko, M. Siano, E. R. Simpson, L. Spector, M. Swiggers, D. Walke, S. Wang, T. Weber, P. H. Bucksbaum and V. S. Petrovic, Ultrafast isomerization initiated by X-ray core ionization, Nat. Commun., 2015, 6, 8199.
44. Z. Yin, Y.-P. Chang, T. Balčiūnas, Y. Shakya, A. Djorović, G. Gaulier, G. Fazio, R. Santra, L. Inhester, J.-P. Wolf and H. J. Wörner, Femtosecond proton transfer in urea solutions probed by X-ray spectroscopy, Nature, 2023, 619, 749–754.
45. S. Xia, M. Wang, G. Blaha, W. H. Konigsberg and J. Wang, Structural Insights into Complete Metal Ion Coordination from Ternary Complexes of B Family RB69 DNA Polymerase, Biochem., 2011, 50, 9114–9124.
46. A. K. Vashishtha, J. Wang and W. H. Konigsberg, Different Divalent Cations Alter the Kinetics and Fidelity of DNA Polymerases, J. Biol. Chem., 2016, 291, 20869–20875.

---

Footnotes

† Electronic supplementary information (ESI) available: Sample characterisation details. Computational details on Ehrenfest molecular dynamics in P3HT film. Details on RT-TDDFT simulations in PT film. See DOI: https://doi.org/10.1039/d3cp04303g

‡ Present address: X-ray Science Division, Argonne National Laboratory, 9700 S. Cass Ave, Lemont, IL 60439, USA.

---