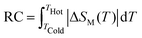Influence of heat sintering on the physical properties of bulk La_0.67Ca_0.33MnO₃ perovskite manganite: role of oxygen in tuning the magnetocaloric response

Abstract

The effect of heat treatments on bulk poly-crystalline La_0.67Ca_0.33MnO₃ perovskite manganite is presented, to explore the possible enhancement in magnetocaloric performance. Samples were prepared via conventional solid-state reaction route with annealing and sintering at various temperatures. Detailed measurements of temperature-dependent and field-dependent magnetization were carried out to estimate the Curie point and order of magnetic transition. The increased sintering temperature results in a steep transition near the T_C, and establishes the magnetic sensitivity as well as the active zone for substantial magnetocaloric performance, at about 168.2% for the LCM9 (sintered at 900 °C) sample. The cause for the significant improvement in the magnetic and magnetocaloric response is brought to light using detailed X-ray photoelectron spectroscopy (XPS) analysis, highlighting the role of oxygen in modifying the Mn³⁺/Mn⁴⁺ charge ratio. The maximum value of the isothermal magnetic entropy change for the optimized sample is found to be 6.4 J kg⁻¹ K⁻¹, achieved at 269 K, while temperature-averaged entropy change (TEC) values, TEC(ΔT_H–C = 3 K) and TEC(ΔT_H–C = 5 K), of 6 J kg⁻¹ K⁻¹ and 5.2 J kg⁻¹ K⁻¹, respectively, were obtained with a low magnetic field change of 20 kOe. The obtained isothermal entropy change at low field for the optimized La_0.67Ca_0.33MnO₃ sample is higher than that of pure Gd and most oxide-based materials. The relative cooling power (RCP) value is around 93 J kg⁻¹ (ΔH = 20 kOe). The order of the phase transition is examined with universal scaling; the scaled entropy change curves confirm the collapse onto a single curve for LCM9, asserting second-order character, whereas the breakdown of the curve with a dispersion relation (d) of 101.1% at Θ = −5 confirms the onset of intrinsic first-order nature in the case of the high-temperature-sintered samples. Calorimetry measurements show thermal hysteresis of 2.4 K and 7.1 K for LCM11 (sintered at 1100 °C) at ramp rates of 5 K min⁻¹ and 10 K min⁻¹, respectively, confirming the first-order nature of the magnetic transition.

---

1 Introduction

An efficient and eco-friendly technology, magnetic refrigeration (MR) is a relatively novel technique that utilizes magnetically ordered materials. MR works on the principles of the magnetocaloric effect (MCE) and has attracted great attention ever since the discovery of adiabatic cooling with paramagnetic salts.¹ The MCE is an intrinsic magneto-thermodynamic phenomenon in which absorption/release of heat in a magnetic material is observed upon changes in external magnetic field, induced through the coupling of the spin system.² The MCE is more pronounced in a material that exhibits large changes in magnetic entropy, which means it is more susceptible to changes in magnetic order when subjected to an external magnetic field. As a result, such materials exhibit large changes in temperature near the transition. The discovery of ferromagnetism in gadolinium metal (Gd) in 1935 by Urbain et al. makes Gd the first magnetocaloric material with a Curie temperature that is close to room temperature.³ Later, work in 1976 by Brown,⁴ who introduced the idea of near-room-temperature MR utilizing the MCE, suggested Gd could be the benchmark material for such applications. A few examples for this class of materials with a giant MCE are Gd₅Si₂Ge₂,^5,6 Fe–Rh alloys,^7,8 La(Fe,Si)₁₃-based alloys,^9,10 MnAs Heusler alloys^11–13 and RE_1−xA_xMn_1−yTM_yO₃ (RE – rare earth metal, A – divalent/monovalent ion, TM – transition metal) perovskite manganites.^14–19

Among perovskite manganites, lanthanum-based mixed-valence manganites with the general formula La_1−xA_xMnO₃ (A is mostly a divalent ion, Ca, Ba or Sr) show a variety of fascinating properties, like colossal magnetoresistance (CMR),^20–22 charge ordering (CO),^23,24 phase separation (PS),^25,26 the magnetocaloric effect (MCE),^1,27–30etc. For (La,Ca)MnO₃, both end members LaMnO₃ and CaMnO₃ are typical antiferromagnets with T_N close to 140 K and 130 K, respectively.³¹ Upon substitution of a divalent cation at the A-site, the system becomes mixed valent [La_1−xA_x(Mn_1−x³⁺Mn_x⁴⁺)O₃] with generation of Mn³⁺/Mn⁴⁺ charged species.³² Similar charge control can be achieved via monovalent substitution [La_1−xA_x (Mn_1−2x³⁺Mn_2x⁴⁺)O₃] at the La site.³³ The mixed valence of Mn³⁺ (t³_2g e¹_g) and Mn⁴⁺ (t³_2g e⁰_g) results in strong hybridization with oxygen 2p states, delocalizing the e_g electrons, which mediate the ferromagnetic interactions between the localized t_2g spins. As a result of these competitive interactions, various intriguing properties have been observed in mixed-valence manganites.

The polycrystalline La_1−xCa_xMnO₃ represent a class of materials that emerged as suitable candidates for magnetic refrigeration technology, as they exhibit a sharp drop in magnetization across the magnetic transition region.³⁴ The nature of the ferromagnetic (FM)–paramagnetic (PM) transition is most interesting for the La_1−xCa_xMnO₃ system. Only a narrow range of substitution between x ≈ 0.2–0.4 will result in a first-order phase transition (FOPT), whereas x ≤ 0.2 results in a continuous second-order phase transition (SOPT) and x ≥ 0.4 results in a continuous transition with a tricritical point. The sharp drop in magnetization at low magnetizing intensities near the transition region is a more important concern for obtaining a large magnetocaloric effect. In the present investigation, a typical value of x = 0.33 is chosen (La_0.67Ca_0.33MnO₃) because of the elusive nature of the FM–PM transition, with claims of it being first-order, with a strong volume anomaly near the transition region,³⁵ small thermal hysteresis in temperature-dependent magnetization and negative slopes observed in isothermal magnetization plots,³⁴ and shifts in heat capacity/asymmetric growth of the magnetic entropy change with field,³⁶ or being second order.³⁷ However, finite size effects,³⁸ external pressure^39,40 and a high field⁴¹ can also cause crossover in the nature of the transition. For instance, previous work by other groups^38,42 investigated the effect of size reduction on x = 0.33 composition; the intrinsic FOPT becomes continuous second-order upon size reduction, with the size threshold lying between 50 and 100 nm.

Thereby, it is hypothesized that keeping all intrinsic and extrinsic parameters unaltered, the nature of the phase transition shall differ with annealing temperature, which controls the grain size with simultaneous variation in the Mn ratio (Mn³⁺/Mn⁴⁺) via oxygen non-stoichiometry. Also, this study realizes the optimized conditions to obtain a sharp drop in magnetization at the Curie point, associated with the intrinsic first-order nature. Most importantly, the magnetocaloric phenomena linked to the nature of the phase transition are explored and eventually the optimum magnetocaloric performance, especially at low fields with La_0.67Ca_0.33MnO₃ perovskite manganites, is presented.

2 Experimental details

2.1 Sample synthesis

Polycrystalline samples with a composition of La_0.67Ca_0.33MnO₃ were synthesized via conventional solid-state reaction method. The starting oxide materials, namely La₂O₃ (pre-heated at 500 °C for 6 hours due to its hygroscopic nature), CaCO₃ and MnO₂ with a purity of 99.99% (Sigma Aldrich) were taken in stoichiometric quantities, mixed with iso-propyl alcohol, and stirred continuously using a magnetic stirrer for about 6 hours. The dried powders were subjected to grinding for about 4 hours in an agate mortar. Subsequent calcinations with intermediate grinding were carried out. The resultant powders were cold pressed to form pellets and sintered at different sintering temperatures (T_S) in intervals of 100 °C, from 900 °C to 1200 °C. Based on the T_S, the samples were named LCM9 (900 °C), LCM10 (1000 °C), LCM11 (1100 °C) and LCM12 (1200 °C). The duration of the soaking temperature was 30 hours followed by natural cooling to room temperature.

2.2 Characterization

The structure and phase purity were checked via room temperature X-ray diffraction (RT-XRD) measurements on finely ground powder samples using a Bruker D8 Advance X-ray diffractometer (Cu-K_α radiation, λ = 0.154 nm). The scan range was 20°–80° with a step size of 0.02°. Field emission scanning electron microscopy (FESEM) and Energy dispersive spectroscopy (EDS) were performed using an Oxford Zeiss Sigma under various magnifications. The Fourier transform infrared (FTIR) absorption measurements were carried out using a Bruker Vertex-70 spectrometer in the far-IR region, from 50–680 cm⁻¹. High-density polyethylene (HDPE) polymer is taken as the background, and the finely ground powders were mixed with iso-propyl alcohol and coated on HDPE to record the IR absorbance signals. X-ray photoelectron spectroscopy (XPS) measurements were performed using a SPECS (Germany) X-ray photoelectron spectroscope with Al-K_α radiation. Temperature-dependent magnetization measurements (M vs. T) at 100 Oe magnetic field using various protocols in the temperature range of 200–300 K and isothermal magnetization measurements (M vs. H) under magnetic fields ranging from 0–50 kOe were carried out using a physical property measurement system (PPMS). Differential scanning calorimetry (DSC) curves were collected during cooling and warming cycles using a Mettler Toledo DSC1 STAR^e system in the temperature range of 245–285 K.

3 Results and discussion

3.1 Structure and morphology

The RT-XRD patterns of samples with different T_S are shown in Fig. 1a. The patterns show sharp diffraction peaks with improvement in the signal-to-noise ratio with increasing T_S, indicating the samples are well-crystallized. The growth of the perovskite form with subsequent increases in sintering temperature can be found in the ESI† (Fig. S1). The normalized intensity as a function of 2θ − 2θ₀, where 2θ₀ is the (121) intensity maximum, shows a decrease in the full width at half maximum (FWHM) and a shift in the major peak towards higher 2θ angles is also observed. These findings indicate better crystallization, volume contraction and grain growth (Fig. 1b and c).⁴³ In principle, the diffraction lines measured for a sample are a convolution of a structural line onto the instrumental broadening; therefore, the intrinsic widths associated with instrumental broadening were corrected using the standard sample Al₂O₃. According to Caglioti's equation, FWHM² = U tan² θ + V tan θ + W, where U, V and W describe the shape parameters. The value of b = 0.05° is obtained for the intrinsic width associated with instrumental broadening. This enables the estimation of average crystallite size (D) from the XRD peaks using Scherrer's equation, given by D = kλ/β cos θ, where k is dimensionless constant, λ is the wavelength of X-ray, θ is diffraction angle and β = B − b (B is FWHM of sample peak and b is the instrumental broadening). A sudden decrease in D, eventually leading to saturation, is observed with the T_S.

Fig. 1 [a] The Rietveld refinement of the XRD patterns of the prepared samples; the observed data, calculated data, deviation, and Bragg positions are indicated by black dots, red lines, blue lines, and olive-colored bars, respectively. The crystal structure obtained from crystallographic information file of LCM11 is shown inset. [b] The shift of the main (121) peak with T_S. [c] The reduction in FWHM with T_S. [d] The average grain size obtained from the FESEM micrographs.

The structure, phase purity, unit-cell parameters, bond length and bond angles were determined with the help of the Rietveld refinement method using FullProf Suite.⁴⁴ The initialization and steps followed in the refinement can be found in the ESI.† The refined patterns are shown in Fig. 1a, overlaying the observed (Y_obs) data on calculated (Y_calc) data. The agreement in Y_obs and Y_calc is established based on the criteria of R-factors (R_p, R_wp, R_exp and Bragg-R) and χ² values. The samples were found to have an orthorhombic structure with the Pnma space group without any impurity phase. The obtained parameters are tabulated in Table 1. The unit-cell parameters change significantly when T_S is changed from 900 °C to 1000 °C. The lattice parameters a and b are unchanged, whereas c is found to decrease, reflecting similar changes in the unit-cell volume. Keeping the elemental composition intact throughout the sintering temperature range, this perhaps indicates a change in the Mn³⁺/Mn⁴⁺ charge ratio in the given perovskite due to changes in oxygen stoichiometry. The volume contraction could be a result of an increase in Mn⁴⁺, which has a smaller size compared to its counterpart Mn³⁺ ions. However, changes in unit-cell volume, MnO₆ octahedral tilt, average 〈Mn–O–Mn〉 bond angle and average 〈Mn–O〉 are not observed after 1000 °C. Since the bond length and bond angles are the crucial factors in controlling the exchange interaction in perovskite manganites, similar variations shall be reflected in physical properties such as magnetism.

Table 1 The structural parameters obtained from Rietveld refinement, and the T_C, θ_P, Curie constant C and effective paramagnetic moment μ^exp_eff obtained from Curie–Weiss fitting in the high temperature regime

Sample	La0.67Ca0.33MnO3
Sample code	LCM9	LCM10	LCM11	LCM12
Structure	Orthorhombic
Space group	Pnma
a (Å)	5.459	5.456	5.455	5.454
b (Å)	7.709	7.708	7.707	7.707
c (Å)	5.568	5.469	5.469	5.471
Unit-cell volume (Å)^3	230.150	229.998	229.926	229.967
〈Mn–O–Mn〉 (°)	160.37	161.18	161.74	160.89
〈Mn–O〉 (Å)	1.955	1.956	1.956	1.958
MnO6 tilt (°)	10.169	9.31	9.63	10.31
R p	9.86	8.63	9.33	9.45
R wp	13.7	12.9	13.6	13.7
R exp	11.84	11.96	12	12.53
Bragg R-factor	3.9	3.02	3.52	4.25
χ ^2	1.34	1.17	1.28	1.19
T C (K)	270.9	270.4	268.1	267.5
θ p (K)	269.6	271.9	268.4	268.2
Curie constant C	4.275	4.305	4.830	5.822
μ ^expeff (μB) (μ^theff = 4.85 μB)	5.84	5.86	6.21	6.85

---

Fig. 2 shows FESEM micrographs of the prepared samples. The average grain size is found to increase with T_S, with an apparent reduction in the grain boundaries, and the grain distribution has become compact. The average grain size has improved from 0.03 μm² to 6.02 μm². The sintered samples showed an exponential grain growth with increasing sintering temperature (Fig. 1d). This observation agrees well with the mechanism of grain growth depending on the reaction rate, which is an exponential function of the sintering temperature.⁴⁵ The grain size of the prepared specimens shows a log-normal distribution, given by the probability distribution function

where d represents the collected values of the grain size. The ω and μ are the dimensionless parameters of the log-normal distribution function, where ω represents the scale (also called the standard deviation) and μ is the shape parameter of the distribution (the detailed FESEM analysis can be found in the ESI†). The elemental composition is verified using EDS measurements (Fig. S4, ESI†). The measurements were carried out at different points on the specimen. The nominal and observed compositions are in good agreement within the experimental errors, retaining stoichiometry irrespective of T_S.

Fig. 2 The FESEM images of LCM9, LCM10, LCM11 and LCM12 samples at a scale of 1 μm. (Insets: The histograms show log-normal distributions.)

3.2 FTIR spectroscopy

The orthorhombic perovskite structure with the Pnma space group has 3 IR-active modes in the range of 50–680 cm⁻¹ (the far-IR regime). Fig. 3a shows the FTIR absorbance spectra of all specimens. The IR spectra consist of: (1) a band due to Mn–O bond stretching (ν_s) around 590 cm⁻¹, involving the internal motion of Mn ions against the MnO₆ octahedron; (2) a bending (ν_b) mode around 380 cm⁻¹, which is sensitive to the Mn–O–Mn bond angle; and (3) an external mode (ν_l) around 180 cm⁻¹, related to vibrational motion of the A-site ions against the MnO₆ octahedra.^46,47 The bands around 590 cm⁻¹ and 180 cm⁻¹ are approximately found to be at the same wavenumber in the different samples, whereas the band centred around 380 cm⁻¹ is found to shift towards higher wavenumbers with increasing T_S (Fig. 3b) This is perhaps due to the large degree of freedom for Mn–O–Mn bond bending compared to Mn–O bond stretching in the octahedral environment. The percentage change observed in the shift towards higher wavenumbers is less than 2%. This concurs with the structural attributes of the specimens, where dormant changes in cell parameters are observed, except from LCM9 to LCM10. Overall, the FTIR results directly probe the functional groups present in the specimens, confirming the perovskite structure of the manganites.

Fig. 3 [a] The FTIR absorption spectra and [b] the variation in bending mode ν_b with T_S for LCM9, LCM10, LCM11 and LCM12 samples.

3.3 X-ray photoelectron spectroscopy

XPS is a conventional tool utilized for ascertaining the surface structure and composition. Fig. 4 shows the survey spectra, which reveal prominent La 3d (La 3d_3/2, La 3d_5/2), Ca 2p (Ca 2p_1/2, Ca 2p_3/2), Mn 2p (Mn 2p_1/2, Mn 2p_3/2) and O 1s along with C 1s peaks. Thus, the survey spectra confirm the existence of La, Ca, Mn, and O elements in all samples. The spectra also contain Augur peaks related to Mn (LMM) and O (KLL), with binding energy values of 972.6 and 901.4 eV, respectively.

Fig. 4 The XPS survey spectra for LCM9, LCM10, LCM11, and LCM12 samples.

The core O 1s spectra (Fig. 5a) exhibit an asymmetric peak with a shoulder in LCM9, LCM10, and LCM12. A nearly symmetric peak is observed in LCM11. The O 1s spectrum was fitted using three distinct components that were found in the ranges of 528.38–528.84 eV, 530.52–531.40 eV and, 532.62–533.42 eV after the Shirley background was removed. The characteristics of the O 1s spectra show chemical shifts in the oxygen core levels brought on by various chemical environments (i.e., oxygen bonding with Mn, La/Ca and other functional groups). The O 1s spectral interpretation is bit challenging due to the presence of several overlapping components. Early on, similar spectra were seen for other perovskite-type oxides, although the interpretations were ambiguous and contradictory.^48–52 Some of the authors refer to oxygen bonding with each of the other elements of the compound or defects. Since the lower-binding-energy feature most closely approaches the binding energy of the O 1s core level in MnO, which is between 528.38–528.84 eV, we may infer that this peak is associated with strong covalent Mn–O bonding. On the other hand, the peak between 530.52–531.40 eV can be attributed to a layer comprising La/Ca–O or a combination of both, since ionic bonds (La/Ca–O) have a higher binding energy than covalent Mn–O bonds. According to Chu et al.,⁵³ further deconvolution of component La/Ca–O (between 530.52–531.40 eV) into two sub-components, individually corresponding to La–O and Ca–O, is not conceivable due to the spectrometer's limited energy resolution mixed with sample effects. The fact that La/Ca–O contributes significantly to LCM12 compared to the other components shows that the surface is made up of a La/Ca–O bonding environment. Thus, the intensity of Mn–O in LCM12 is comparatively lower than that in other specimens, indicating that the sample contains an abundance of oxygen and is dominated by the surface effects.⁵⁴ The higher binding energy peak (marked as O^#) between 532.62–533.42 eV might be the result of surface species like carbonyl groups or crystal lattice defects. It is argued that elements located at the outermost surface have larger binding energies than their bulk-bound counterparts, which means that surface sites often display less stability than bulk sites due to the abrupt termination of the bulk lattice structure.⁵⁵

Fig. 5 [a] Core level oxygen O1s, [b] carbon C 1s and [c] Ca 2p spectra for LCM9, LCM10, LCM11, and LCM12 samples.

Furthermore, the C 1s core spectra are examined (Fig. 5b), which deconvolute into three distinct components for LCM9 to LCM11 and four for LCM12. The major peak of C 1s can be assigned to adventitious carbon at 284.6 eV (C=C) and serves as a reference for the correction of spectra against charging effects. The peak distribution near 285.96–286.98 eV can be assigned to C–O bonds. Finally, surface carbonates are responsible for a third component between 288.10–288.47 eV (C=O), which is in support of the O 1s third component peak between 532.62–533.42 eV. The surface carbonates (purple line) are most intense for LCM12 when compared to other specimens. Evidently, another peak at 290.82 eV (orange line; marked with ♦) is observed in LCM12 and may indicate the presence of another polymorph of carbonates.⁵⁵

The Ca 2p core level spectra (Fig. 5c) display spin–orbit doublets with 2p_3/2 and 2p_1/2 peaks. The spectra are well fitted by four components: two major peaks (blue lines), corresponding to the Ca 2p_3/2 and Ca 2p_1/2 levels of the solid phase; and two other additional peaks (olive-colored lines), which may come from a small fraction of surface oxide and carbonate species.⁵⁵ In comparison to the other specimens, the LCM11 has the least contribution from surface oxide and carbonate species. However, it is clear that the primary lines in LCM12 have been shifted towards higher binding energies. This might be brought about by the segregation of Ca ions at the oxide surface, which could lead to the formation of CaCO₃ and/or CaO. Upon high temperature sintering, small quantities of extra oxygen are introduced into the system, where this appears to be accommodated by introducing A/B site vacancies in the structure.⁵⁶ Thus, it is more evident that LCM12 contains an abundance of oxygen clusters, due to which some Ca has segregated to the surface of the sample. These findings from the O 1s and C 1s core level spectra are consistent. The existence of carbonyl group contributions and their bonding with C=O (referred to as surface carbonates) were evidenced by the O 1s and C 1s core level spectra. Furthermore, in the case of LCM12, the carbonate groups – in particular, CaCO₃ – provide strong evidence that Ca segregated from the A site of the perovskite. Overall, it has been shown that differences in the electron densities surrounding the oxygen anions in the Mn–O bonds have an impact on the binding energies of the Mn 2p_3/2 and Mn 2p_1/2 orbitals in the perovskites.

The Mn 2p XPS spectra (Fig. 6) show a spin–orbit splitting between the Mn 2p_3/2 and Mn 2p_1/2 peaks, with an energy separation (given in Table 2). The energy separation in the metallic state of Mn is typically 11.05 eV,⁵⁷ whereas a higher energy separation value implies the occurrence of a Mn oxidative state. In addition, the difference between the binding energies of Mn 2p_3/2 and O 1s is found to be 111.38 eV (for LCM9) to 113.21 eV (for LCM12). This is direct evidence of the evolution of Mn⁴⁺ ion species over Mn³⁺.⁵⁸ The core spectra of Mn 2p_3/2 and Mn 2p_1/2 are deconvoluted into two peaks, unveiling the existence of mixed-valence Mn states (Mn³⁺ and Mn⁴⁺), which appear after the divalent substitution at the A-site of perovskite manganites. The corresponding binding energies for the said two peaks are tabulated in Table 2. The relative fractions of Mn³⁺ and Mn⁴⁺ ions are calculated by using the areas under the corresponding peaks. Ideally, for an x = 0.33 system, the theoretical Mn³⁺/Mn⁴⁺ ratio is 2.03 (Mn³⁺ : Mn⁴⁺ = 67 : 33). However, the values obtained are found to be 2.26, 2.11, 2.04, and 1.84 for LCM9 to LCM12, respectively. This indicates that for LCM9, the specimen is Mn³⁺ rich, whereas for LCM12, the specimen finds Mn⁴⁺ abundance, and for LCM11, the specimen is nearly stoichiometric with a 67 : 33 charge ratio. The larger Mn³⁺/Mn⁴⁺ and Mn⁴⁺/Mn³⁺ ratios at the extreme ends of the series compared to the stoichiometric compound (Mn³⁺/Mn⁴⁺ = 2.030) are indicative of oxygen off-stoichiometry (perhaps a deficiency or excess). The oxygen off-stoichiometry at low/high T_S is supported by the observed asymmetric/shoulder peak in the oxygen O 1s spectra. The rise in Mn³⁺ and Mn⁴⁺ above a nominal value originates from oxygen vacancies/excess,⁵⁹ which can alter the octahedral symmetry.⁶⁰ The overall change in this ratio severely influences the double-exchange interaction via Mn³⁺–O²⁻–Mn⁴⁺ bridges, which further modifies the transport and magnetic properties.

Fig. 6 The Mn 2p core level spectra for the samples LCM9, LCM10, LCM11 and LCM12.

Table 2 The Mn 2p core level spectral deconvolution fitting parameters

Sample	Core spectra	Spin–orbit split	Peak position eV	Difference eV	Mn states	Peak position eV	Area under curve	Mn^3+/Mn^4+ (nominal 2.03)
LCM9	Mn 2p	Mn 2p3/2	641.98	11.58	Mn^3+	641.02	33278.3	2.26
					Mn^4+	643.09	14702.7
		Mn 2p1/2	653.56		Mn^3+	652.53	14506.02
					Mn^4+	654.66	6416.5
LCM10	Mn 2p	Mn 2p3/2	642.13	11.65	Mn^3+	641.23	46583.2	2.11
					Mn^4+	643.24	22031.7
		Mn 2p1/2	653.78		Mn^3+	652.87	24642.2
					Mn^4+	654.84	11634.8
LCM11	Mn 2p	Mn 2p3/2	642.21	11.68	Mn^3+	641.3	43177.4	2.04
					Mn^4+	643.46	21134.4
		Mn 2p1/2	653.89		Mn^3+	652.96	22174.3
					Mn^4+	655.13	10856.2
LCM12	Mn 2p	Mn 2p3/2	642.56	11.75	Mn^3+	641.43	41486.8	1.84
					Mn^4+	643.52	22514.6
		Mn 2p1/2	654.31		Mn^3+	653.02	21337.5
					Mn^4+	655.27	11542.1

---

3.4 Magnetization

The temperature-dependent magnetization curves M(T) under zero field-cooled warming (ZFCW), field-cooled cooling (FC) and field-cooled warming (FCW) protocols at 100 Oe magnetic field are shown in Fig. 7. The curves show a typical magnetic transition from the PM to FM state with decreasing temperature, occurring at the Curie temperature (T_C). The minimum of the derivative of M(T) (dM/dT) on the temperature axis marks the T_C. The observed values of T_C are 270.9 K, 270.4 K, 268.1 K, and 267.5 K for samples LCM9, LCM10, LCM11, and LCM12, respectively. A marginal decrease in T_C of 1.2% from LCM9 to LCM12 is observed. Generally, the transport and magnetic properties are strongly coupled, and they are sensitive to the changes in bond lengths 〈Mn–O〉 and bond angles 〈Mn–O–Mn〉 in an octahedral environment,⁶¹ resulting in variation of the metal to insulator transition (T_MI) and T_C. The former is an extrinsic property and depends on parameters such as grain morphology alongside the bond lengths and bond angles. But T_C, being an intrinsic property, is not affected by T_S-assisted grain growth.

Fig. 7 The temperature-dependent magnetization (M–T) curves under 100 Oe magnetic field in ZFCW, FCC and FCW modes. The insets show the Curie point (dM/dT vs. T).

Bifurcation between ZFCW and FCC magnetization below T_C is seen with further decrease in temperature due to magnetic inhomogeneity. This is a characteristic property observed in manganites, where the magnitude of magnetization in ZFCW is always less than in FCC, attributed to the gradual freezing of magnetic moments in randomly distributed clusters, resulting in incomplete magnetization rather than long-range FM coupling.⁶² The M–T curve of sample LCM9 has concomitant transition broadening (FWHM ∼ 15.5 K) when compared with the other samples. This is due to enhanced grain boundary density at low sintering temperature, where each grain surface has different oxygen stoichiometry causing magnetic disorder, or in other words, the disorder can arise in perovskite manganites due to the surface termination of the crystal structure.⁶³ This fact is established through XPS characterization, which is a surface-sensitive technique. Sample LCM9 has shown a deviation from oxygen stoichiometry, as indicated by an asymmetric peak in the O 1s spectra and consequent variation in the Mn³⁺/Mn⁴⁺ ratio. The onset of disappearance of these disorders is believed to happen upon annealing, where oxygen vacancies at grain boundaries are suspended, resulting in enhancement of the grain size.⁶⁴ This is clearly established through XPS analysis on high-temperature-sintered samples. The oxygen vacancies have significantly reduced, turning LCM11 into a stoichiometric specimen. Interestingly, the presence of thermal hysteresis (<2 K) between FCC and FCW cycles is observed prominently in higher-temperature-sintered samples, which appears to be a signature of a weak FOPT.

To confirm the magnetic ground state and hence to estimate the effective paramagnetic moments and Curie–Weiss temperature (θ_P), the high temperature paramagnetic regimes after T_C are fitted with the Curie–Weiss (CW) law, given by χ = C/(T − θ_P) where C is the Curie constant, defined as C = N_Aμ_B² (μ_eff)²/(3K_B), where N_A = 6.023 × 10²³ mol⁻¹, μ_B = 9.274 × 10²¹ emu, K_B = 1.38 × 10¹⁶ erg K⁻¹ and μ_eff is the effective paramagnetic moment. The linear fit to the inverse susceptibility curve is shown in Fig. 8. The slope gives C and θ_P is obtained from the x intercept. The positive θ_P obtained from the fit concludes a dominant FM correlation between spins. Based on the assumption that the orbital moment is fully quenched (L⃑ = 0) by an internal crystal field effect,⁶⁵ we have calculated the theoretical value of the effective paramagnetic moment μ_eff by considering spin momentum (S⃑ ≠ 0). The μ_eff is given by , where the Lande g-factor g = 2, S = 3/2 for Mn⁴⁺ (t³_2g e⁰_g), S = 2 for Mn³⁺ (t³_2g e¹_g) and μ_eff (Mn³⁺) = 4.90 μ_B and μ_eff (Mn⁴⁺) = 3.87 μ_B.

Fig. 8 The temperature-dependent inverse susceptibility. The solid red lines are the Curie–Weiss fits to the high temperature data. (Inset of LCM9: log(χ⁻¹) vs. log(T/T^R_C − 1); solid lines represent the linear fitting to both the PM and GP regimes using the power law.)

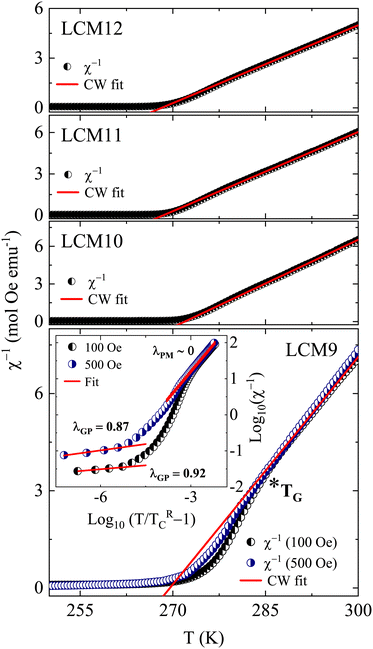
For the La_0.67Ca_0.33MnO₃ system, the total contribution from Mn³⁺ and Mn⁴⁺ ions is given by (μ^th_eff)² = 0.67μ_eff² (Mn³⁺) + 0.33μ_eff² (Mn⁴⁺) = 4.85 μ_B. The obtained values of the effective paramagnetic moments are higher than 4.85 μ_B, as tabulated in Table 1. This could be due to the contribution from FM clusters containing more than one Mn ion above the transition temperature. The spontaneous formation of magnetic clusters above T_C was detected in a small-angle neutron scattering experiment conducted on La_0.70Ca_0.30MnO₃ samples by De Teresa.⁶⁶ Thereby, these kinds of FM clusters in the PM matrix have larger effective spins, which results in higher values of μ^exp_eff than μ^th_eff. A downturn in the inverse susceptibility curve is noticed for sample LCM9 (before approaching T_C from high temperature) along with divergence from CW law, suggesting the presence of short-range FM interactions and thus a Griffiths phase (GP)-like singularity⁶⁷ in specimen LCM9. The downturn occurring at ∼285 K is referred to as the Griffiths temperature (T_G). Above T_G, χ⁻¹ exhibits pure PM behavior. The GP is formed at a characteristic freezing temperature where a short-range FM correlation exists within the cluster, which sets the PM regime and contributes to the increase in magnetic moments in the PM region. The GP singularity present between T_C and T_G is characterized by a power law, given by χ⁻¹ ∝ (T − T^R_C)^(1−λ), where λ is the magnetic susceptibility exponent and T^R_C is the critical temperature of random ferromagnetic clusters where susceptibility tends to diverge (χ → ∞). The choice of T^R_C is very crucial and is obtained using a method followed by Jiang et al.,⁶⁸ in which T^R_C is recognized as the temperature for which fitting data in the PM regime yields λ_PM ∼ 0.

In order to verify the presence of a GP in LCM9, the temperature-dependent magnetization at 500 Oe is measured. Fig. 8 illustrates the clear suppression of χ⁻¹ deviation at H = 500 Oe. This can be ascribed to the polarization of spins occurring beyond the clusters⁶⁹ and, therefore, indicates the presence of a GP-like singularity. Furthermore, a plot of log(χ⁻¹) versus log(T/T^R_C − 1) resembles a straight-line fit and is displayed in the inset of LCM9 in Fig. 8. The obtained values of λ_PM = 0.001 (for 100 Oe) and 0.004 (for 500 Oe) in the PM regime are close to ideal value of ‘0’, whereas in the GP region, the λ_GP values are 0.92 and 0.87 for 100 and 500 Oe, respectively. The obtained values of λ_GP agree well with the expected range of 0 < λ < 1. Hence, the value of λ_GP and its suppression with an increase in field validates the GP-like singularity present in LCM9. Consequently, LCM9 has no long-range ordering due to disordered spins at the surface and random magnetic interactions due to uneven distribution of grains. However, the downturn behavior in the inverse susceptibility was not seen for the rest of the samples, even though they have higher μ^exp_eff values. But the difference between T_C and θ_P decreased with T_S, which is a clue that the magnetic inhomogeneity has decreased when compared with the LCM9 sample.

To get deeper insights into the magnetic transition and variation of the magnetocaloric properties, magnetic isotherms were collected in the vicinity of the magnetic transition region for all the samples and are displayed in Fig. 9. The isotherms were collected in 2 K intervals across the transition region and 4 K away from it. The isotherms below T_C display an abrupt change in magnetization, showing a tendency towards saturation that confirms the FM behavior. Above T_C, the magnetization changes are gradual, showing linearity far away from T_C that confirms a typical PM behavior. Further, the magnitude of magnetization has increased with T_S. The findings can be rationalised by the argument that, with an increase in T_S, the oxygen off-stoichiometry at the grain surface and boundary vanishes, resulting in a homogenous, stoichiometric La_0.67Ca_0.33MnO₃ compound. Among the La_1−xCa_xMnO₃ compounds, the 67 : 33 specimen has an optimal Mn³⁺/Mn⁴⁺ ratio to have the maximum T_C in this family, or in other words, the said concentration would facilitate Zener double-exchange easily compared to the other concentrations. Variation in oxygen content would cause deviation of this ratio, resulting in a larger number of Mn³⁺ ions which are Jahn–Teller active. The oxygen vacancies are proven to break the octahedral symmetry, thereby reducing the energy of the e_g orbital and causing a strong electron–lattice interaction. This localizes the e_g electrons available for hopping, eventually suppressing ferromagnetic double-exchange (DE) interactions. Reduced DE interactions are responsible for large reductions in magnetic moment and hence the magnetization.⁶⁰ This is established clearly through the oxygen vacancies/excess observed in XPS studies. We infer that the effects of oxygen off-stoichiometry are more pronounced in LCM9 (oxygen-deficient) and LCM12 (oxygen-excess).

Fig. 9 The field-dependent isothermal magnetization curves (M vs. H) of samples LCM9, LCM10, LCM11 and LCM12 in the vicinity of the magnetic transition.

Apart from the said features, interestingly, prominent S-shaped M(H) curves are observed for the high-temperature-sintered samples. This feature is observed over a certain temperature range above T_C, indicative of a metamagnetic phase transition in the PM state of the sample. It has been proven that the magnetic transition at low field is accompanied by an abrupt decrease in unit-cell volume without a change in the crystal symmetry.^35,70 Furthermore, the observation of a change in unit-cell volume in response to an applied magnetic field may suggest the presence of magnetic polarons. These magnetic polarons have been confirmed to exist in the PM regime (T = 1.8T_C) by a small-angle neutron scattering experiment.⁶⁶ At H = 0, these are non-interacting; magnetic polarons begin to interact as H grows at a fixed temperature (close to but above T_C). At a critical value of magnetic field, the magnetic polarons grow and combine to form larger ferromagnetic clusters.⁷¹ Therefore, a gradual increase in magnetization is observed at lower fields, followed by a rapid increase above a certain critical magnetic field, reaching saturation at higher fields.

To determine the nature of the transition with an increase in T_S, Arrott plots were constructed for all isotherms and are shown in Fig. 10. According to the Banerjee criterion, the slope of M²vs. H/M distinguishes the order of the transition. From a thermodynamic point of view, a positive slope represents a second-order transition and a negative slope represents a FOPT. The slopes of the M² (H/M) curves of LCM9 at temperatures T > 277 K (T < 277 K) are negative (positive) at low fields; these features indicate a combination of first- and second-order characters. For the higher-temperature-sintered samples, significant negative slopes are observed in the M² (H/M) curves, which are consistent with previous observations for bulk La_0.67Ca_0.33MnO₃.³⁴ Bui et al.⁷² investigated the coexistence of several isostructural oxygen-deficient phases and its impact on the nature of the magnetic transition of the La_0.67Ca_0.33MnO₃ compound. They found that oxygen-deficiency led to magnetic inhomogeneity, resulting in the appearance of a Griffiths phase and causing a first- to second-order phase transformation. Earlier, work by Park et al.⁷³ found that the magnetism in perovskite manganites at the surface boundary is significantly different from that of the bulk. Thus, the outer surface layer has a probability to suppress the bulk properties and is likely to undergo an SOPT or weak FOPT. These studies are in line with the effects of oxygen off-stoichiometry causing a partial second-order nature in a typical first-order material, La_0.67Ca_0.33MnO₃ (LCM9).

Fig. 10 The plot of M²vs. H/M for samples LCM9, LCM10, LCM11 and LCM12.

3.5 Magnetocaloric effect

The MCE of a material is characterized by its isothermal magnetic entropy change (−ΔS_M) or the adiabatic temperature change (ΔT_ad) when the magnetic field H is changed from 0 to a maximum value H_max. The MCE can be indirectly determined with the help of Maxwell's relation.⁷⁴ The isothermal change in the magnetic entropy −ΔS_M can by determined from magnetization data by collecting the isothermal magnetization curves across the magnetic transition. The relation is given by
The numerical approximation of the Maxwell equation for discrete field and temperature intervals is given by,
where M_i and M_i+1 are the experimental magnetization values measured at temperatures T_i and T_i+1 respectively, under a magnetic field of H_i or H_i+1.

The magnitude of the magnetic entropy change exhibits a sharp peak near the magnetic transition temperature due to a considerable change in magnetization and the change in −ΔS_M with the field has a linear relationship. The change in isothermal entropy is always negative for a material that shows a peak at the T_C. Fig. 11 shows −ΔS_M for field variations of 10 to 50 kOe with an increment of 10 kOe. The maximum −ΔS_M is observed for LCM11 over the other samples, with peak values of 4.77 J kg⁻¹ K⁻¹, 6.39 J kg⁻¹ K⁻¹, 7.36 J kg⁻¹ K⁻¹, 8.16 J kg⁻¹ K⁻¹ and 8.83 J kg⁻¹ K⁻¹ for field changes of 10 kOe, 20 kOe, 30 kOe, 40 kOe and 50 kOe, respectively. For a low field change of 20 kOe, the peak −ΔS_M values are 3.80 J kg⁻¹ K⁻¹, 5.45 J kg⁻¹ K⁻¹, 6.39 J kg⁻¹ K⁻¹, and 5.46 J kg⁻¹ K⁻¹ for LCM9, LCM10, LCM11 and LCM12 samples, respectively. The −ΔS_M value is found to increase from sample LCM9 to LCM11 and then decreases at LCM12, having similar values to LCM10. We assert that the role of oxygen non-stoichiometry at the grain surface in modifying the magnetic properties will also be reflected in the MCE properties in an analogous way.

Fig. 11 The isothermal magnetic entropy change vs. temperature under various magnetic field changes for samples LCM9, LCM10, LCM11 and LCM12, obtained from Maxwell's equation.

Though −ΔS^max_M is a physical parameter which characterizes the magnetocaloric attributes of a specimen, nevertheless, the value of adiabatic temperature change (ΔT_ad) is meaningful quantity to quote the applicability of a material as a magnetic refrigerant.⁷⁵

where ΔS_M(T₀,H) is the isothermal magnetic entropy change and C_P(T₀,H) is the specific heat of the sample at T₀. By considering that the molar heat capacity value of manganites is 110 J mol⁻¹ K⁻¹, near room temperature the heat capacity is estimated to be 526 J kg⁻¹ K⁻¹.⁷⁵ The approximate ΔT_ad values are found to be 2.4 K, 2.9 K and 3.2 K for the field changes of 10 kOe, 15 kOe and 20 kOe, respectively. The observed ΔT_ad value for Gd is 2.6 K for a field change of 10 kOe.⁷⁶ This approximated value is high compared to those of most reported oxide-based materials.

In addition, the relative cooling power (RCP) is commonly used as a criterion for assessing a magnetocaloric material in terms of its efficiency, as a product of the peak entropy change and the temperature range in which the value of the peak entropy change becomes half of the maximum, also called the full width at half maximum (δT_FWHM) of ΔS^max_M.¹¹⁰ It is expressed by

RCP = |ΔS^max_M| × δT_FWHM

The RCP factors are calculated for all the samples, and increase monotonously with H, a similar relation to that of −ΔS_M with applied magnetic field. The obtained values of −ΔS^max_M and RCP for the prepared samples at various magnetic fields are tabulated in Table 3; this also covers a review of materials with magnetocaloric properties, where the review is categorized among existing prototype materials like intermetallic alloys, the 67 : 33 (Mn³⁺ : Mn⁴⁺) composition of ABO₃, and some divalent substituted (La, Ca/Sr/Ba)MnO₃ systems.

Table 3 Categorized review and comparison of existing materials showing magnetocaloric properties

Type	Composition	T C/T^peak (K)	ΔH (kOe)	−ΔS^maxM (J kg^−1 K^−1)	−ΔS^maxM/ΔH (J kg^−1 K^−1 kOe)	RCP (J kg^−1)	Ref.
a Approximate values.
Prototypes	Gd	294	20	5.3	26.5	212^a	76
			50	10.2	20.4	410
	Gd5Ge2Si2	275	50	18.5	37	535	77
	Fe49Rh51	316.58	20	−13.2	66	153.4	8
	La(Fe0.9Si0.1)13	184	20	28	140	532^a	10
	MnAs	318	20	31	155	124	12
			50	38	76	418
	LaFe11.2Co0.7Si1.1	274	20	12	60	216^a	9
			50	20.3	40.6	585^a
(La, Ca)MnO3	La0.5Ca0.5MnO3	220	20	1.13	5.65	67.8	78
	La0.55Ca0.45MnO3	238	15	1.9	12.66	68	17
	La0.60Ca0.40MnO3	263	30	5	16.66	135	79
	La0.65Ca0.35MnO3	235	20	1.06	5.3	52	80
	La0.70Ca0.30MnO3	216	20	7.3	36.5	124.1	81
	La0.70Ca0.30MnO3	227	10	1.95	19.5	49	82
	La0.70Ca0.30MnO3	251	10	5.71	57.1	40	83
			50	7.52	15.04	218
	La0.70Ca0.30MnO3	272	10	3.36	33.6	33.6	84
	La0.72Ca0.28MnO3	268	20	5.5	27.5	88	85
	La0.75Ca0.25MnO3	224	15	4.70	31.33	99	86
	La0.75Ca0.25MnO3	268	50	6.25	12.5	198	87
	La0.80Ca0.20MnO3	230	15	5.50	36.66	72	17
(La, Sr)MnO3	La0.5Sr0.5MnO3	340	30	0.63	2.1	—	88
	La0.60Ca0.40MnO3	365	20	0.97	4.85	98	89
			50	2.14	4.28	264
	La0.70Sr0.30MnO3	370	20	1.10	5.5	49	90
	La0.75Sr0.25MnO3	340	15	1.5	10	65	91
	LaLa0.80Sr0.20MnO3	309	10	1.42	14.2	52.7	92
	La0.70Sr0.30MnO3	369	10	1.14	11.4	46.4
	La0.80Sr0.20MnO3	330	20	1.65	8.25	103.2	93
	La0.65Sr0.35MnO3	305	10	2.12	21.2	106	94
(La, Ba)MnO3	La0.6Ba0.4MnO3	333	25	1.19	4.76	79.3	95
	La0.7Ba0.3MnO3	342	25	2.06	8.24	124
	La0.7Ba0.3MnO3	332	20	3.08	15.4	46.2^a	96
	La0.7Ba0.3MnO3	322	18	2.1	11.66	40.2^a	97
ABO3 (67 : 33) family	La0.67Ca0.33MnO3	267	15	4.3	28.66	47	17
	La0.67Ca0.33MnO3	260	15	3.7	24.66	46.25^a	98
	La0.67Ca0.33MnO3	260	10	5	50	35	42
	La0.67Ca0.33MnO3	260	10	1.10	11	36.3^a	99
	La0.67Ca0.33MnO3	278	20	4.33	21.65	86.6^a	100
	La0.67Ca0.33MnO3	252	10	2.3	23	49	101
			20	4.1	20.5	91
			50	6.8	13.6	247
	La0.67Sr0.33MnO3	370	20	2.68	13.4	85	102
			50	5.15	10.3	252
	La0.67Sr0.33MnO3	377	20	2.02	10.1	92.9^a	100
	La0.67Sr0.33MnO3	354	50	2.49	4.98	225	103
	La0.67Ba0.33MnO3	292	50	1.48	2.96	161	104
	La0.67Ba0.33MnO3	337	10	2.7	27	68	105
	La0.67Ba0.33MnO3	350	20	1.72	8.6	92.8^a	100
	Pr0.67Sr0.33MnO3	290	20	3.5	17.5	79.2	106
	Pr0.67Pb0.33MnO3	360	20	2.33	11.65	106.2	107
	La0.67Pb0.33MnO3	358	20	2.54	12.7	134.6	108
	Pr0.67Ba0.33MnO3	188	10	2.32	23.2	49	109
			40	550	13.75	225
Prepared samples	La0.67Ca0.33MnO3 (LCM9)	268	20	3.80	19	75	Our results
			50	6.45	12.9	210
	La0.67Ca0.33MnO3 (LCM10)	271	20	5.45	27.25	82
			50	7.51	15.02	225
	La0.67Ca0.33MnO3 (LCM11)	269	10	4.77	47.7	42
			15	5.72	38.13	67
			18	6.14	34.11	80
			20	6.39	31.95	93
			50	8.83	17.66	276
	La0.67Ca0.33MnO3 (LCM12)	269	20	5.46	27.3	84
			50	7.71	15.42	254

---

Refrigerant capacity (RC) is used as another parameter to assess magnetocaloric properties. It describes the thermal efficiency of a magnetocaloric material in terms of energy transfer between two reservoirs in one cycle. It is given by following relation:

The RC value tends to zero when T_Cold = T_Hot, which increases with decreasing T_Cold when RC is plotted against T_Cold (figure not shown here). The value of RC increases from 193.5 J kg⁻¹ to 235.1 J kg⁻¹ for a field change from 10 to 50 kOe in the case of the LCM11 specimen.

3.6 Temperature-averaged entropy change

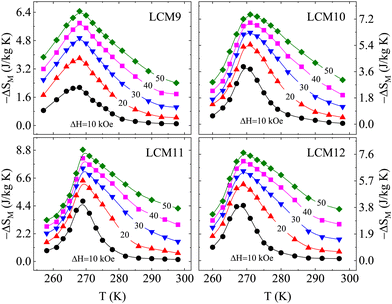
To probe the effectiveness of a refrigerant material, a material-based figure of merit, the temperature-averaged entropy change (TEC), is suggested¹¹¹ based on the temperature span for which the material can, or is intended to, provide the maximum isothermal change in entropy. Thereby, this could address how large the caloric effect is over a useful temperature range. It is expressed as
where ΔT_H–C is the temperature difference between the cold and hot reservoirs, and T_mid is the temperature that maximizes the TEC(ΔT_H–C) value. The TECs were obtained for fixed values of ΔT_H–C = 3 K, 5 K, 10 K, 15 K and 20 K. Fig. 12 shows the variation in TECs with field change for different ΔT_H–C values, where the value decreases when increasing the temperature span ΔT_H–C for all the samples, which elucidates the effectiveness of the −ΔS_M. The TECs at ΔT_H–C (3, 20 K) are denoted as TEC(3) and TEC(20), respectively, for clarity. Sample LCM9 has TEC(3) = 3.75 J kg⁻¹ K⁻¹ and 6.33 J kg⁻¹ K⁻¹ at ΔH = 20 kOe and 50 kOe, respectively, which drop to 2.93 J kg⁻¹ K⁻¹ and 5.5 J kg⁻¹ K⁻¹ for ΔT_H–C = 20 K with similar field changes, respectively. The percentage changes over ΔT_H–C = 3 K → ΔT_H–C = 20 K are 21.8% and 13.2% at fields of 20 and 50 kOe, respectively. Since anomalous changes were observed for LCM11, similar analysis was carried out at ΔT_H–C values of 3 and 20 K. The TEC(3) values at 20 kOe and 50 kOe are 6.06 J kg⁻¹ K⁻¹ and 8.39 J kg⁻¹ K⁻¹, respectively, whereas the TEC(20) values with similar field changes are 4.14 J kg⁻¹ K⁻¹ and 6.50 J kg⁻¹ K⁻¹, respectively. The effectiveness in terms of TEC from ΔT_H–C =3 K → ΔT_H–C =20 K is changed by 31.6% and 22.5% at 20 kOe and 50 kOe, respectively. The larger the TEC at wider ΔT_H–C, the better the performance. The TEC values are found to be high at a narrow ΔT_H–C = 3 K. However, the percentage drop in TEC at ΔT_H–C = 20 K does not follow an exponential pattern (Fig. 13b). This suggests a broad spread of performance of our material. Also, we have listed the TEC(3) values with a 10 kOe field change for existing prototype materials in Table 4. The optimized LCM11 has shown a 46% higher value than gadolinium's TEC(3). The obtained TEC(3) remains substantial, providing further support for the suitability of these materials for use in magnetic refrigeration technology.

So far, −ΔS_M was discussed here when the field changes from 0 → H_max. Since we have confirmed the FOPT features and large MCE of our optimal LCM11, it was further examined for its MCE under a reduction in field from H_max → 0 to ensure the repeatability. The value of −ΔS_M is changed from 5.7 J kg⁻¹ K⁻¹ (0 → 15 kOe) to 5.3 J kg⁻¹ K⁻¹ (15 → 0 kOe), as shown in the Fig. 13a for comparison. This small discrepancy further confirms the magnetic hysteresis present. But authors have pointed out that such hysteresis could also be a field-sweep-dependent case³⁷ and using an infinitely slow sweep rate during isothermal measurements resulted in no intrinsic hysteresis. Moore¹¹² demonstrated that heat exchange dynamics may lead to a significantly sweep-rate-dependent magnetic hysteresis. However, during isothermal measurements, the stability of temperature during the magnetic field sweep was maintained up to the first decimal digit. So, we claim that hysteresis may be arising from the intrinsic first-order nature rather than the uncertainties in the field sweep.

Fig. 12 The magnetic field dependence of the temperature-averaged entropy change at ΔT_H–C = 3 K, 5 K, 10 K, 15 K and 20 K temperature increases for samples LCM9, LCM10, LCM11 and LCM12.

Fig. 13 [a] The −ΔS_M (J kg⁻¹ K⁻¹) vs. T (K) curve obtained at a field change of 15 kOe. The −ΔS_M is calculated under field sweeps from 0 → 15 kOe and 15 → 0 kOe. [b] TEC performance with various temperature increases, ΔT_H–C, for LCM11.

Table 4 Summary of temperature-averaged entropy changes (TECs) for temperature increases (ΔT_H–C) of 3 K and 10 K with a 10 kOe magnetic field change

Material	TEC(3)	TEC(10)	Ref.
Gd	3.05	2.91	111
Gd5Ge2Si2	9.91	6.89
La(Fe0.88Si0.12)13	17.36	9.11
LaFe11Co0.8Si1.2	3.37	3.24
FeRh	11.09	9.08
La0.813K0.16Mn0.987O3	1.49	1.47
La0.67Ca0.33MnO3	4.45	3.51	Our result

---

Like the TEC, the normalized refrigerant capacity (NRC) is another tool to identify a material's utility for cooling performance. It is defined as a function of ΔT_H–C = T_Hot − T_Cold:

where Δμ₀H is the change in magnetic field.

Fig. 14 shows the variation of the NRC as a function of temperature increase. The results show that the NRC increases with increasing ΔT_H–C, which is an attractive feature of our material for the applicability in the field of magnetic refrigeration technology.

Fig. 14 The normalized refrigerant capacity (NRC) as a function of temperature increase (ΔT_H–C) for samples LCM9, LCM10, LCM11 and LCM12.

3.7 Universal behavior

A decade ago, Franco et al.¹¹³ proposed the universality of the magnetic entropy change; since then it has been a key tool to distinguish the order of the phase transition.¹¹⁴ According to the studies, the rescaled magnetic entropy changes for different applied magnetic fields collapse onto a single curve for materials with a second-order transition. However, the breakdown of the universal curve below T_C is an attribute of materials with a FOPT. In this context, a phenomenological curve is constructed for all the samples by normalizing the magnetic entropy change |ΔS_M| with respect to its peak value of entropy change |ΔS_M|^max, which is field-dependent, i.e., ΔS′ = |ΔS_M|/|ΔS_M|^max. The temperature axis is rescaled to Θ = ±1 using two reference points, T_r1 and T_r2, above and below the T_C, respectively. It is given by
When the normalized magnetic entropy change ΔS′ is plotted against the re-scaled temperature axis Θ (Fig. 15), one can say a material exhibits a universal class if the experimental |ΔS_M| curve falls as two branches, below and above T_C. The combination of both collapses them into a single master curve. The breakdown of universality is seen below T_C in the case of all samples except LCM9. This deviation confirms the FOPT associated with LCM10, LCM11 and LCM12. A similar breakdown is reported for La_0.67Ca_0.33MnO₃ elsewhere.¹¹⁴ If the phenomenological curves collapse into a single master curve, like for LCM9, one can make extrapolations of the entropy change in any temperature range or magnetic field without prior knowledge of critical exponents¹¹⁵ using an inverse transformation (IT). In the IT process, the averaged curves are fitted with Lorentz's function, given by
where, a, b and c are the free parameters that describe the shape of the magnetic entropy change. The low-field data provide information on the tails of the curve, whereas the high field data provide information about the magnitude of the ΔS_M. The inverse transformed magnetic entropy change for LCM9 is shown in Fig. 15. (inset in LCM9). The agreement between the experimental data obtained from Maxwell's relations and predicted data from back-transformation is remarkable and proves the validity of universality in SOPT materials.

Fig. 15 The magnetocaloric universal curves of samples LCM9, LCM10, LCM11 and LCM12 under different external magnetic fields. Inset in LCM9: experimental (solid dots) magnetic entropy changes obtained from Maxwell's equation and predictions using the universal curve (red lines).

Further, to validate the second-order character of LCM9 and first-order features of LCM11, the dispersion parameter, d (%) is estimated at an arbitrary Θ below T_C. It is given by the expression

where W is the vertical spread or width of each scaled curve relative to its mean value at a chosen Θ value. The approximate d of the scaled entropy change at Θ = −5 is found to be 26.6% for LCM9, holding the condition for a second-order nature, whereas it is 101.1% for LCM11, which supports the breakdown below T_C and confirms the FOPT.¹¹⁴

Irrespective of the negative slope observed in Arrott plots, the asymmetry observed in the −ΔS_M curve, the hysteresis observed in the isothermal magnetic entropy change and the breakdown of universality at a typical temperature of 1100 °C (LCM11) doesn't experimentally substantiate the FOPT. DSC is one of the direct measurements that validate a FOPT.

3.8 Differential scanning calorimetry (DSC)

Fig. 16 depicts the DSC curves of the LCM11 specimen. The measurements were carried out at ramp rates of +5 K min⁻¹ (−5 K min⁻¹) and +10 K min⁻¹ (−10 K min⁻¹) during warming (cooling) in a temperature range of between 245 K and 285 K. There is a sharp endothermic peak at 264.7 K during warming and a sharp exothermic peak at 262.3 K during cooling under the ramp rate of +5(−5) K min⁻¹, with a thermal hysteresis of 2.4 K near the Curie temperature T_C.

Fig. 16 The DSC curves of the LCM11 specimen under 5 K min⁻¹ and 10 K min⁻¹ ramp rates.

The transition latent heats are calculated using the area under the curve (heat flow vs. time, figure not shown here) which are 4.74 J g⁻¹ and −4.80 J g⁻¹, respectively, for the warming and cooling curves. Interestingly, with a 10 K min⁻¹ ramp rate, the hysteresis between the peaks was found to be 7.1 K. The FOPT is bound to display a systematic hysteresis upon an increase in the ramp rate due to a pronounced shift of the cooling curve to the lower temperature. The significant increase in the hysteresis upon a change in ramp rate, observed for LCM11, validates the FOPT.

Thus, the large magnetization with an improvement in magnetic sensitivity, the metamagnetic transition due the first-order crossover of the magnetic ground state, the consequent sizable entropy change, and the excellent figure-of-merit (TEC) seen for LCM11 (due to its apt charge ratio, Mn³⁺/Mn⁴⁺ = 2.04) makes it an optimal candidate amongst the other three specimens for magnetic refrigeration applications. The entropy changes can be realized even at low external fields, and those being attainable using a permanent magnet makes this candidate attractive towards cooling technology.

4 Conclusions

We have performed a detailed study on the structural, magnetic and magnetocaloric properties of La_0.67Ca_0.33MnO₃ sintered at different temperatures. The samples crystallized in the orthorhombic structure with the Pnma space group. The samples are stoichiometric with the desired elemental composition. The surface morphology indicates grain growth from 0.03 μm² (LCM9) to 6.02 μm² (LCM12), showing exponential grain growth with increasing T_S. The samples have active phonon modes in the far-IR regime, which are characteristics of the MnO₆ octahedral environment of the perovskite structure. The effect of sintering temperature has manifested in producing a series of specimens with oxygen deficiency to oxygen excess, achieving an optimal candidate at 1100 °C. Such variation in oxygen content has affected the Mn³⁺/Mn⁴⁺ charge ratio and consequent magnetic and magnetocaloric properties. The temperature-dependent magnetization reveals a growing sharpness of the magnetic transition with T_S. Consequently, the maximum isothermal changes in magnetic entropy of 5.7 J kg⁻¹ K⁻¹ and 6.4 J kg⁻¹ K⁻¹ are observed for LCM11 under the applied field changes of 15 kOe and 20 kOe, respectively. Meanwhile, the relative cooling power is 93 J kg⁻¹. The −ΔS^max_M value is almost retained even when the field sweep is reversed from 15 to 0 kOe, with a value of 5.4 J kg⁻¹ K⁻¹. The temperature-averaged entropy change at a 3 K temperature lift, TEC(3), is 146% of that of pure Gd at a 10 kOe field change. Overall, these exceptional results are attributes of a progressive change in the order of the magnetic transition due to the variation in oxygen content upon heat sintering. In the present study, the change in oxygen internal pressure is a root cause that governs the enhancement in the magnetocaloric response.

Author contributions

Pramod R Nadig: conceptualization, methodology, formal analysis, investigation and writing – original draft. M. S. Murari: data curation. Mamatha D. Daivajna: supervision, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. R. Nadig is thankful to the UGC-DAE Consortium for Scientific Research, Indore Centre, India for funding the study under the grant CSR-IC-TIMR-06/CRS-273/2017-18/1279. The authors are thankful to Dr Mahesha M. G. (MIT, Manipal) and the Manipal Academy of Higher Education for providing synthesis facilities; Dr Mukul Gupta and Layanta Behera (UGC-DAE CSR, Indore) for providing XRD measurements; AIRF, Jawaharlal Nehru University, New Delhi for providing magnetization measurements; Saroj Jha for the constant support in carrying out characterization; Dr Uday Deshpande, Sachin Kumar, and Parveen Garg (UGC-DAE CSR, Indore) for providing FTIR and XPS measurements and insights on XPS analysis; and Dr R. J. Choudhary and Suresh Bharadwaj (UGC-DAE CSR, Indore) for providing DSC measurements. Lozil Denzil Mendonca is acknowledged for the insights on magnetic analysis and grammar/language corrections. The authors further extend their gratefulness to Dr Rajeev Rawat (UGC-DAE CSR, Indore) and Dr Olivier Toulemonde (CNRS, Univ. Bordeaux, France) for the helpful suggestions.

Notes and references

1. V. Franco, J. S. Blaázquez, B. Ingale and A. Conde, Annu. Rev. Mater. Res., 2012, 42, 305–342.
2. A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications, CRC Press, 1st edn, 2003.
3. A. Kitanovski, Adv. Energy Mater., 2020, 10, 1903741.
4. G. V. Brown, J. Appl. Phys., 1976, 47, 3673–3680.
5. V. K. Pecharsky and A. Gschneidner K., Jr., Phys. Rev. Lett., 1997, 78, 4494–4497.
6. A. O. Pecharsky, K. A. Gschneidner and V. Pecharsky, J. Appl. Phys., 2003, 93, 4722–4728.
7. M. P. Annaorazov, S. A. Nikitin, A. L. Tyurin, K. A. Asatryan and A. K. Dovletov, J. Appl. Phys., 1996, 79, 1689–1695.
8. A. Chirkova, K. P. Skokov, L. Schultz, N. V. Baranov, O. Gutfleisch and T. G. Woodcock, Acta Mater., 2016, 106, 15–21.
9. F. Hu, B. Shen, J. Sun, G.-J. Wang and Z. Cheng, Appl. Phys. Lett., 2002, 80, 826–828.
10. S. Fujieda, A. Fujita and K. Fukamichi, Appl. Phys. Lett., 2002, 81, 1276–1278.
11. H. Wada and Y. Tanabe, Appl. Phys. Lett., 2001, 79, 3302–3304.
12. M. Balli, D. Fruchart, D. Gignoux, C. Dupuis, A. Kedous-Lebouc and R. Zach, J. Appl. Phys., 2003, 103, 103908.
13. E. Bruück, M. Ilyn, A. M. Tishin and O. Tegus, J. Magn. Magn. Mater., 2005, 290–291, 8–13.
14. A. R. Dinesen, S. Linderoth and S. Mørup, J. Phys.: Condens. Matter, 2005, 17, 6257.
15. M.-H. Phan, S.-C. Yu, N. H. Hur and Y.-H. Jeong, J. Appl. Phys., 2004, 96, 1154–1158.
16. M.-H. Phan, S.-C. Yu and N. H. Hur, Appl. Phys. Lett., 2005, 86, 072504.
17. Z. B. Guo, Y. W. Du, J. S. Zhu, H. Huang, W. P. Ding and D. Feng, Phys. Rev. Lett., 1997, 78, 1142–1145.
18. A. G. Gamzatov, A. B. Batdalov, N. Z. Abdulkadirova, A. M. Aliev, V. V. Khovaylo, T. D. Thanh, N. T. Dung and S.-C. Yu, J. Alloys Compd., 2023, 964, 171330.
19. Z. Xie, Z. Zou, X. Jiang and W. Zhang, Ceram. Int., 2023, 49, 32663–32678.
20. R. Mahendiran, R. Mahesh, A. K. Raychaudhuri and C. N. R. Rao, Solid State Commun., 1995, 94, 515–518.
21. C. N. R. Rao and A. K. Cheetham, Science, 1996, 272, 369–370.
22. C. N. R. Rao, A. K. Cheetham and R. Mahesh, Chem. Mater., 1996, 8, 2421–2432.
23. C. N. R. Rao, A. Arulraj, P. N. Santosh and A. K. Cheetham, Chem. Mater., 1998, 10, 2714–2722.
24. C. N. R. Rao, A. Arulraj, A. K. Cheetham and B. Raveau, J. Phys.: Condens. Matter, 2000, 12, R83.
25. G. Allodi, R. De Renzi, G. Guidi, F. Licci and M. W. Pieper, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 6036–6046.
26. S. Yunoki, J. Hu, A. L. Malvezzi, A. Moreo, N. Furukawa and E. Dagotto, Phys. Rev. Lett., 1998, 80, 845–848.
27. A. Barman, S. Kar-Narayan and D. Mukherjee, Adv. Mater. Interfaces, 2019, 6, 1900291.
28. M.-H. Phan and S.-C. Yu, J. Magn. Magn. Mater., 2007, 308, 325–340.
29. L. D. Mendonca, M. S. Murari and M. D. Daivajna, Phys. Chem. Chem. Phys., 2022, 24, 13171–13188.
30. Z. M. Wang, G. Ni, Q. Y. Xu, H. Sang and Y. W. Du, J. Appl. Phys., 2001, 90, 5689–5691.
31. E. O. Wollan and W. C. Koehler, Phys. Rev., 1955, 100, 545–563.
32. J. M. D. Coey, M. Viret and S. von Molnaár, Adv. Phys., 1999, 48, 167–293.
33. M. B. Salamon and M. Jaime, Rev. Mod. Phys., 2001, 73, 583–628.
34. J. Mira, J. Rivas, F. Rivadulla, C. Vaázquez-Vaázquez and M. A. Loópez-Quintela, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2998–3001.
35. C. A. Ramos, H. R. Salva, R. D. Sanchez, M. Tovar, F. Rivadulla, J. Mira, J. Rivas, A. M. Lopez-Quintela, L. Hueso, M. Saint-Paul, P. Lejay and Y. Tokura, J. Magn. Magn. Mater., 2001, 226–230, 582–584.
36. H. N. Bez, K. K. Nielsen, A. Smith and C. R. H. Bahl, J. Magn. Magn. Mater., 2016, 416, 429–433.
37. K. Morrison, A. Berenov and L. F. Cohen, MRS Online Proc. Libr., 2011, 1310, 205.
38. T. Sarkar, A. K. Raychaudhuri, A. K. Bera and S. M. Yusuf, New J. Phys., 2010, 12, 123026.
39. R. Thiyagarajan, S. E. Muthu, S. K. Barik, R. Mahendiran and S. Arumugam, J. Appl. Phys., 2013, 113, 023904.
40. R. Thiyagarajan, S. E. Muthu, K. Manikandan and S. Arumugam, J. Magn. Magn. Mater., 2016, 398, 116–120.
41. S. K. Giri and T. K. Nath, J. Appl. Phys., 2013, 113, 17D706.
42. L. E. Hueso, P. Sande, D. R. Migueéns, J. Rivas, F. Rivadulla and M. A. Loópez-Quintela, J. Appl. Phys., 2002, 91, 9943–9947.
43. R. Rai, A. Valente, M. Andrei, L. Kholkin and I. Coondoo, Adv. Mater. Lett., 2013, 4, 354–358.
44. T. Roisnel and J. Rodriguez-Carvajal, WinPLOTR: a Windows tool for powder diffraction patterns analysis Materials Science Forum, inProceedings of the Seventh European Powder Diffraction Conference(EPDIC 7), ed. R. Delhez and E. J.Mittenmeijer, 2000, pp. 118–123.
45. K. Witte, W. Bodnar, N. Schell, G. Fulda and E. Burkel, J. Alloys Compd., 2017, 724, 728–734.
46. K. H. Kim, J. Y. Gu, H. S. Choi, G. W. Park and T. W. Noh, Phys. Rev. Lett., 1996, 77, 1877–1880.
47. Y. Regaieg, M. Koubaa, W. C. Koubaa, A. Cheikhrouhou, L. Sicard, S. Ammar-Merah and F. Herbst, Mater. Chem. Phys., 2012, 132, 839–845.
48. P. Decorse, E. Quenneville, S. Poulin, M. Meunier, A. Yelon and F. Morin, J. Vac. Sci. Technol., A, 2001, 19, 910–915.
49. S. Ponce, M. A. Penña and J. L. G. Fierro, Appl. Catal., B, 2000, 24, 193–205.
50. J. Choi, J. Zhang, S.-H. Liou, P. A. Dowben and E. W. Plummer, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 13453–13459.
51. E. Beyreuther, S. Grafstroöm, L. M. Eng, C. Thiele and K. Doörr, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155425.
52. R. Dudric, A. Vladescu, V. Rednic, M. Neumann, I. G. Deac and R. Tetean, J. Mol. Struct., 2014, 1073, 66–70.
53. M.-W. Chu, M. Ganne, M. T. Caldes and L. Brohan, J. Appl. Phys., 2002, 91, 3178–3187.
54. R. K. Dokala, S. Das, D. C. Joshi, S. Ghosh, Z. Yan, Y. Qi, S. Das and S. Thota, J. Appl. Phys., 2020, 127, 175303.
55. G. Kozhina, V. Mitrofanov, O. Fedorova, A. Fetisov, A. Murzakaev and S. Estemirova, J. Alloys Compd., 2021, 864, 158816.
56. Q. Huang, A. Santoro, J. W. Lynn, R. W. Erwin, J. A. Borchers, J. L. Peng and R. L. Greene, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 14987–14999.
57. J. F. Moulder, W. F. Stickle, P. E. Sobol, K. D. Bomben and J. Chastain, Handbook of X-ray electron spectroscopy, Perkin-Elmer Corporation, Physical Electronics Division, Eden Prairie, United States of America, 1992, pp. 72–73.
58. P. Decorse, G. Caboche and L.-C. Dufour, Solid State Ionics, 1999, 117, 161–169.
59. U. Shankar and A. K. Singh, J. Phys. Chem. C, 2015, 119, 28620–28630.
60. H. Guo, J.-o Wang, X. He, Z. Yang, Q. Zhang, K.-j Jin, C. Ge, R. Zhao, L. Gu, Y. Feng, W. Zhou, X. Li, Q. Wan, M. He, C. Hong, Z. Guo, C. Wang, H. Lu, K. Ibrahim, S. Meng, H. Yang and G. Yang, Adv. Mater. Interfaces, 2016, 3, 1500753.
61. A. Dutta, N. Gayathri and R. Ranganathan, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 054432.
62. P. A. Sharma, S. B. Kim, T. Y. Koo, S. Guha and S.-W. Cheong, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224416.
63. H. Y. Hwang and S.-W. Cheong, Nature, 1997, 389, 942–944.
64. S. B. Kansara, D. Dhruv, Z. Joshi, D. D. Pandya, S. Rayaprol, P. S. Solanki, D. G. Kuberkar and N. A. Shah, Appl. Surf. Sci., 2015, 356, 1272–1281.
65. S. de Brion, F. Ciorcas, G. Chouteau, P. Lejay, P. Radaelli and C. Chaillout, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1304–1310.
66. J. M. De Teresa, M. R. Ibarra, P. A. Algarabel, C. Ritter, C. Marquina, J. Blasco, J. García, A. del Moral and Z. Arnold, Nature, 1997, 386, 256–259.
67. M. B. Salamon and S. H. Chun, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 014411.
68. W. Jiang, X. Zhou, G. Williams, Y. Mukovskii and K. Glazyrin, Phys. Rev. Lett., 2007, 99, 177203.
69. J. Deisenhofer, D. Braak, H.-A. Krug von Nidda, J. Hemberger, R. M. Eremina, V. A. Ivanshin, A. M. Balbashov, G. Jug, A. Loidl, T. Kimura and Y. Tokura, Phys. Rev. Lett., 2005, 95, 257202.
70. J. M. De Teresa, M. R. Ibarra, J. Blasco, J. García, C. Marquina, P. A. Algarabel, Z. Arnold, K. Kamenev, C. Ritter and R. von Helmolt, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1187–1193.
71. S. K. Barik, M. Aparnadevi, A. Rebello, V. B. Naik and R. Mahendiran, J. Appl. Phys., 2012, 111, 07D726.
72. D. T. Bui, T. A. Ho, N. N. Hoang, T. L. Phan, B. W. Lee, N. T. Dang, D. T. Khan, L. V. Truong-Son, D. N. Petrov, B. T. Huy and D. S. Yang, Mater. Trans., 2023, 64, 2070–2076.
73. J.-H. Park, E. Vescovo, H.-J. Kim, C. Kwon, R. Ramesh and T. Venkatesan, Phys. Rev. Lett., 1998, 81, 1953–1956.
74. V. K. Pecharsky, K. A. Gschneidner, A. O. Pecharsky and A. M. Tishin, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 144406.
75. V. K. Pecharsky and K. A. Gschneidner, J. Appl. Phys., 2001, 90, 4614–4622.
76. S. Y. Dan'kov, A. M. Tishin, V. K. Pecharsky and K. A. Gschneidner, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3478–3490.
77. V. K. Pecharsky and K. A. Gschneidner, Wiley Online Library, 2007.
78. A. Krichene, W. Boujelben and A. Cheikhrouhou, J. Alloys Compd., 2013, 550, 75–82.
79. X. Bohigas, J. Tejada, M. L. Mar'nez-Sarrioón, S. Tripp and R. Black, J. Magn. Magn. Mater., 2000, 208, 85–92.
80. V. M. Andrade, R. J. C. Vivas, S. S. Pedro, J. C. G. Tedesco, A. L. Rossi, A. A. Coelho, D. L. Rocco and M. S. Reis, Acta Mater., 2016, 102, 49–55.
81. A. N. Ulyanov, J. S. Kim, G. M. Shin, Y. M. Kang and S. I. Yoo, J. Phys. D: Appl. Phys., 2007, 40, 123.
82. S.-B. Tian, M.-H. Phan, S.-C. Yu and N. H. Hur, Phys. B, 2003, 327, 221–224.
83. J. C. Debnath, R. Zeng, J. H. Kim and S. X. Dou, J. Magn. Magn. Mater., 2011, 323, 138–143.
84. C. F. Pena, M. E. Soffner, A. M. Mansanares, J. A. Sampaio, F. C. G. Gandra, E. C. da Silva and H. Vargas, Phys.B, 2017, 523, 39–44.
85. H. Terashita, J. J. Garbe and J. J. Neumeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094403.
86. Z. B. Guo, J. R. Zhang, H. Huang, W. P. Ding and Y. W. Du, Appl. Phys. Lett., 1997, 70, 904–905.
87. S. Bouzidi, M. A. Gdaiem, S. Rebaoui, J. Dhahri and E. K. Hlil, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 1–16.
88. X. Zhang, J. Fan, L. Xu, D. Hu, W. Zhang and Y. Zhu, Ceram. Int., 2016, 42, 1476–1481.
89. M. Jeddi, H. Gharsallah, M. Bejar, M. Bekri, E. Dhahri and E. K. Hlil, RSC Adv., 2018, 8, 9430–9439.
90. R. Cherif, S. Zouari, M. Ellouze, E. K. Hlil and F. Elhalouani, Eur. Phys. J. Plus, 2014, 129, 1–8.
91. Z. B. Guo, W. Yang, Y. T. Shen and Y. W. Du, Solid State Commun., 1998, 105, 89–92.
92. Y. S. Jeong, M. S. Anwar, F. Ahmed, S. R. Lee and B. H. Koo, Appl. Mech. Mater., 2013, 378, 225–229.
93. Z. Xie, Z. Zou, Z. Mao, X. Jiang and W. Zhang, J. Mater. Res. Technol., 2022, 21, 2778–2796.
94. M. H. Phan, S. B. Tian, D. Q. Hoang, S. C. Yu, C. Nguyen and A. N. Ulyanov, J. Magn. Magn. Mater., 2003, 258–259, 309–311.
95. I. Hussain, M. S. Anwar, E. Kim, B. H. Koo and C. G. Lee, Korean J. Mater. Res., 2016, 26, 623–627.
96. B. Kurniawan, S. Winarsih, C. Kurniawan, M. R. Ramadhan and F. Ruli, AIP Conf.: Proc., 2017, 1862, 030061.
97. P. Zhang, T. L. Phan and S. C. Yu, J. Supercond. Novel Magn., 2012, 25, 2727–2730.
98. J. Mira, J. Rivas, L. E. Hueso, F. Rivadulla and M. A. Loópez Quintela, J. Appl. Phys., 2002, 91, 8903–8905.
99. X. X. Zhang, J. Tejada, Y. Xin, G. F. Sun, K. W. Wong and X. Bohigas, Appl. Phys. Lett., 1996, 69, 3596–3598.
100. Y. Xu, M. Meier, P. Das, M. R. Koblischka and U. Hartmann, Cryst. Eng., 2002, 5, 383–389.
101. Y. Regaieg, F. Ayadi, J. Monnier, S. Reguer, M. Koubaa, A. Cheikhrouhou, S. Nowak, L. Sicard and S. Ammar-Merah, Mater. Res. Express, 2014, 1, 046105.
102. A. Rostamnejadi, M. Venkatesan, P. Kameli, H. Salamati and J. M. D. Coey, J. Magn. Magn. Mater., 2011, 323, 2214–2218.
103. G. F. Wang, L. R. Li, Z. R. Zhao, X. Q. Yu and X. F. Zhang, Ceram. Int., 2014, 40, 16449–16454.
104. D. T. Morelli, A. M. Mance, J. V. Mantese and A. L. Micheli, J. Appl. Phys., 1996, 79, 373–375.
105. W. Zhong, W. Chen, C. T. Au and Y. W. Du, J. Magn. Magn. Mater., 2003, 261, 238–243.
106. W. Mabrouki, A. Krichene, N. Chniba Boudjada and W. Boujelben, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 182.
107. M. Hsini, S. Khadhraoui, N. Zaidi and Z. A. Alrowaili, J. Supercond. Novel Magn., 2018, 31, 3717–3722.
108. S. K. ÇÇetin, M. Acet, M. Guünes, A. Ekicibil and M. Farle, J. Alloys Compd., 2015, 650, 285–294.
109. A. Varvescu and I. G. Deac, Phys. B, 2015, 470–471, 96–101.
110. K. A. Gschneidner and V. K. Pecharsky, Annu. Rev. Mater. Sci., 2000, 30, 387–429.
111. L. D. Griffith, Y. Mudryk, J. Slaughter and V. K. Pecharsky, J. Appl. Phys., 2018, 123, 034902.
112. J. D. Moore, K. Morrison, K. G. Sandeman, M. Katter and L. F. Cohen, Appl. Phys. Lett., 2009, 95, 252504.
113. V. Franco, J. S. Blaázquez and A. Conde, Appl. Phys. Lett., 2006, 89, 222512.
114. C. M. Bonilla, J. Herrero-Albillos, F. Bartolomeé, L. M. García, M. Parra-Borderías and V. Franco, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 224424.
115. V. M. Prida, V. Franco, V. Vega, J. L. Saánchez-Llamazares, J. J. Sunñol, A. Conde and B. Hernando, J. Alloys Compd., 2011, 509, 190–194.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04185a

---