Open Access Article
Open Access ArticleElectron transfer reaction of TEMPO-based organic radical batteries in different solvent environments: comparing quantum and classical approaches†
Souvik
Mitra
 a,
Andreas
Heuer
a,
Andreas
Heuer
 ab and
Diddo
Diddens
ab and
Diddo
Diddens
 *b
*b
aInstitute of Physical Chemistry, University of Münster, Corrensstraße 28/30, 48149 Münster, Germany
bHelmholtz-Institute Münster (IEK-12), Forschungszentrum Jülich GmbH, Corrensstraße 46, 48149 Münster, Germany. E-mail: d.diddens@fz-juelich.de
First published on 21st December 2023
Abstract
In this study, we delve into the complex electron transfer reactions associated with the redox-active (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO), a common component in organic radical batteries (ORBs). Our approach estimates quantum electron-transfer (ET) energies using Density Functional Theory (DFT) calculations by sampling from structures simulated classically. This work presents a comparative study of reorganization energies in ET reactions across different solvents. Furthermore, we investigate how changes in the electrolyte environment can modify the reorganization energy and, consequently, impact ET dynamics. We also explore the relationship between classical and quantum vertical energies using linear regression models. Importantly, this comparison between quantum and classical vertical energies underscores the role of quantum effects, like charge delocalization, in offering added stabilization post-redox reactions. These effects are not adequately represented by the classical vertical energy distribution. Our study shows that, although we find a significant correlation between the vertical energies computed by DFT and the classical force field, the regression parameters depend on the solvent, highlighting that classical methods should be benchmarked by DFT before applying them to novel electrolyte materials.
Introduction
Emerging research in the field of energy storage has been highlighting the pivotal role of organic radical batteries (ORBs)1,2 due to their potential for high power density and fast charge/discharge rates. Uniquely, these ORBs present a promising alternative to conventional lithium-ion batteries, given their cost-effective and environmentally friendly aspects, derived primarily from the use of abundant and non-toxic organic materials. Among various organic radicals, 2,2,6,6-tetramethylpiperidin-1-oxyl (TEMPO) stands out due to its promising role as a redox-active group in polymer electrodes for ORBs,3 showcasing unique electron transfer (ET) mechanisms characterized by diffusive charge transport behavior. In this context, Marcus theory,4,5 a widely employed method for understanding the dynamics of ET reactions in redox systems, is often utilized.Within the semi-classical framework of Marcus theory,5,6 electron transfer reactions are described in terms of the polarization of the solvent induced by the charges carried by the donor and acceptor solute (in complex solvent systems, other effects such as charge transfer and hydrogen bonding can facilitate electron transfer). According to this theory, the solvation effect is represented by two intersecting free energy surfaces, known as diabatic states, which correspond to the reactant and product states involved in the ET process. The occurrence of electron transfer is facilitated by the presence of significant thermal fluctuations, allowing the system, initially situated near the minimum of one diabatic state, to reach the transition state denoted by the point at which the reactant and product states intersect, where electron can tunnel from the initial diabatic state to the final diabatic state, with the probability governed by the Landau–Zener formula.7 Subsequent to the electron hopping event, the system experiences a relaxation phase characterized by the reorientation of surrounding solvent molecules and the structural optimization of the solute entities. The energy associated with this intricate process is defined as the reorganization energy, a fundamental factor in the dynamics of ET reactions within these redox systems.
In the original conception of Marcus theory,6 polarization was represented as the linear response of a dielectric continuum. As a result, the impact of the solvent could be encapsulated in a singular parameter. Apart from the assumption of linear response not only legitimizes the quadratic dependency of free energy surfaces on the reaction coordinate, Marcus theory also postulates identical curvatures for the resulting parabolas of the two free energy surfaces. A microscopic characterization of the polarization order parameter was notably introduced by Warshel et al.,8 who incorporated the vertical energy gap as a reaction coordinate for ET reactions. This vertical energy gap serves as a quantitative indicator of the electron's energy preference for the donor site over the acceptor site, offering greater insight into the mechanisms of ET reactions. Their work is of significant importance as the choice of vertical energy gap as reaction coordinate in their study reveals that, under the linear response assumption, the reorganization energy of ET reactions is inversely proportional to the curvature of the resulting free energy parabolas.
The quantum mechanically calculated vertical energy gap encompasses the electron's delocalization in the donor orbital and the subsequent electronic relaxation following ET phenomena, which are not accounted for by the classically calculated vertical energy. The change in the shape of the free energy profiles, when utilizing the quantum vertical energy gap as a reaction coordinate, compared to the classical solvent electrostatic potential, was demonstrated by Blumberger et al.9 in their study on aqueous Ru2+ solutions using density functional theory (DFT) based molecular dynamics (MD) simulations. In their study, it was shown that in the absence of this orbital delocalization information, the classical vertical energy gap leads to a reduced curvature in the free energy parabola and consequently an increase in reorganization energy compared to its quantum counterpart.
Both ab initio MD (AIMD)10 and hybrid quantum/classical (QM/MM)11 approaches, although capturing quantum effects, are constrained by relatively short time trajectories on the order of a few picoseconds. The time trajectories in these systems can be significantly shorter than (1) the average time between two ETs and (2) the typical relaxation time of the local molecular environment, the latter of which leads to insufficient statistical sampling. Moreover, challenges are often posed in accurately predicting smooth distributions due to the scarcity of structures derived from these short time trajectories. In contrast, classical MD12 simulations, while potentially lacking certain quantum mechanical information, offer the advantage of encompassing significantly longer trajectories. By employing reliable force fields, a wider range of structural variations can be explored, and well-defined free energy profiles can be generated.
As part of this work, to calculate quantum vertical energy, density functional theory (DFT) calculations were performed on a small subset of the structures generated using classical MD simulation. In this way, we guarantee sufficient sampling of local solvation environments, while still obtaining additional information about the orbital energies of the transferred electron or about electronic polarization effects. Oxidation of TEMPO radical (TEMPO.) and reduction of TEMPO cation (TEMPO+) in water13 were considered to verify our method.
The second part of this work explored how changes in the electrolyte environment can impact the reorganization energies of ET reactions. In our study, the commonly employed electrolyte ethyl carbonate(EC)/ethyl methyl carbonate(EMC)/LiPF6, recently also utilized in ORBs,2,14–18 was chosen to investigate the influence of the electrolyte environment on the ET reaction dynamics. With regard to battery applications, we observe a significant impact of the electrolyte composition on the reorganization energy and hence, the estimated electron hopping rate. Notably, these findings suggest that it is important to adjust the solvent composition in order to optimize the electron hopping rate.
Finally, we will attempt to establish a relation between classical and quantum ET distributions using linear regression models. Furthermore, we explore the possibility of calculating ET reorganization energies directly through classical simulations. Although the quantum and classical energies are strongly linearly correlated for a given solvent, the predictive power of classical simulations appears to be limited.
Theory and methods
Marcus theory
Marcus introduced intersecting diabatic free energy surfaces for the reactant state (R) and the product state (P) to describe a homogeneous ET reaction.6 In his study, Marcus employed the semi-classical approximation to separate the ET rate into two components: the electronic coupling parameter and the Franck–Condon factor.9,19,20 The Franck–Condon factor, representing the probability of nuclear reorganization in the ET process, can be studied independently of the electronic coupling. This assumption in Marcus theory allows for the decomposition of the overall diabatic states for a homogeneous ET reaction into the energy surfaces of the oxidation (ox) and reduction (red) processes separately.These free energy surfaces, denoted as AM (where M refers to ox or red), are assumed to have a quadratic behavior with respect to a reaction coordinate denoted as x:
 | (1) |
The reorganization free energy, a central concept in Marcus theory, is derived from the free energy profiles. Although in the original work, λ was defined for the overall forward and backward ET reactions, for a homogeneous ET reaction it can be defined separately for the oxidation and reduction states as follows:
| λox = Aox(xred) − Aox(xox) | (2a) |
| λred = Ared(xox) − Ared(xred) | (2b) |
To describe ET reactions, it is necessary to establish an appropriate reaction coordinate as the reorganization energy, λM, relies on the choice of a suitable reaction coordinate. In their work, Warshel et al.8 incorporated the complete microscopic configuration of the system, denoted as RN (i.e., the coordinates of all N atoms in the system), into x by selecting the vertical energy (ΔE(RN)). For oxidation and reduction processes, the vertical energies are given by:
| ΔEox(RN) = Eox(RN) − Ered(RN) | (3a) |
| ΔEred(RN) = Ered(RN) − Eox(RN) | (3b) |
AM(ΔEM) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PM(ΔEM) + const PM(ΔEM) + const | (4a) |
| PM(ΔEM) = 〈δΔEM〉M | (4b) |
Based on the definition, the diabatic free energies for the same structure, as they correspond to no change in entropy, satisfy the following relationship:
| Aox(ΔE) − Ared(ΔE) = ΔEox | (5a) |
| Ared(ΔE) − Aox(ΔE) = ΔEred | (5b) |
By selecting ΔE as the coordinate, eqn (2a) and (2b) can be rewritten as:
| λox = Aox(ΔEminred) − Aox(ΔEminox) | (6a) |
| λred = Ared(ΔEminox) − Ared(ΔEminred) | (6b) |
Here, ΔEminM refers to the energy minimum of the diabatic state M.
Under the quadratic approximation of the free energy with respect to ΔEM as the coordinate, the probability distribution PM(ΔEM) can be assumed to follow a Gaussian distribution:
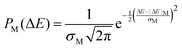 | (7) |
Here, σM denotes the standard deviation of the distribution. Manipulating the properties of diabatic free energy states (eqn (5a), (5b), (6a), (6b)) in combination with the quadratic approximation (eqn (1)), the relation between λM and the spring constant kM can be expressed as:
 | (8) |
Now, as kM can be derived from the second derivative of the free energy parabola, which can be obtained from eqn (7) and (4a), it gives a relationship with σM:
 | (9) |
 | (10) |
MD simulations
To validate our proposed method, oxidation of TEMPO. and reduction of TEMPO+ were considered. To implement this, two distinct simulations were conducted, one with TEMPO. and another with TEMPO+. Each simulation involved 66 water molecules, allowing for a comprehensive assessment of our method's performance on both species.Classical MD simulations were performed using GROMACS 2019.22 To obtain a DFT-compatible box size for future quantum calculations, a small simulation cell was considered for MD simulations. The initial configurations in a 1.7 × 1.7 × 1.7 nm3 simulation cell, were constructed using PACKMOL,23 which avoids repulsive potentials by keeping a safe inter-atomic distance. Periodic boundaries in all three Cartesian coordinates were considered. Prior to the equilibration run, a short initial MD run was performed to obtain a dense system as well as removing any unrealistic or high-energy configurations that may have arisen during the initialization of the system, for 2 ns with a 0.5 fs time step. To efficiently densify the system, the pressure was set to 100 bar for this relaxation step, ensuring a more compact and stable arrangement of the molecular components. In this relaxation step, both temperature and pressure were controlled with a Berendsen thermostat and a Berendsen barostat,12,24 respectively, both with time constants of 1.0 ps. The reference temperature was taken as 298.15 K. The Coulombic interactions were handled using a particle–particle particle–mesh (PPPM) solver with a cutoff of 0.6 nm, which was also applied to the Lennard-Jones interactions. This short cutoff was compatible with the NPT simulation performed in such a small simulation box. Following the relaxation step, dense systems with dimensions of approximately 1.3 nm were obtained. For the equilibration step, NVT simulations for both oxidation and reduction processes were performed for 20 ns with 1 fs time step with the dense systems obtained after the relaxation step. In this case, temperature were controlled with a Nosé–Hoover thermostat with time constants of 1.0 ps. The rest of the parameters were the same as the relaxation step. Finally for the collection of data, a 100 ns simulation with the exact same parameters as used for the equilibration step was run for each of the two systems.
The OPLS all-atom force field25 was used for all the MD simulations. The atomic site charges on both TEMPO radical and cation were calculated from the electrostatic potential (ESP) fit (Fig. S1, ESI†). Gaussian1626 was used to calculate the ESP charges using MP2 theory27 with pVDZ basis set.28
For the second part of our work, the same simulation setup was replicated by replacing water with 10 EC molecules and 5 EMC molecules to recreate the electrolyte environment. Additionally, simulations were conducted by introducing 1 LiPF6 salt ion pair to the system. These variations in the simulation setup allowed us to investigate the influence of different electrolyte components on the system's behavior and further validate our method.
Vertical energy calculations
From the equilibrium trajectory of the Classical MD simulation of TEMPO. (TEMPO+) in water, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames were taken at intervals of 2 ps. From each frame, potential energies were calculated both before and after altering the TEMPO radical (cation) to its corresponding cation (radical) form without changing the atomic coordinates. The classical vertical energies were then determined by computing the energy difference between these two states.
000 frames were taken at intervals of 2 ps. From each frame, potential energies were calculated both before and after altering the TEMPO radical (cation) to its corresponding cation (radical) form without changing the atomic coordinates. The classical vertical energies were then determined by computing the energy difference between these two states.
For the calculation of quantum vertical energies, a subset of 195 frames was selected from the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-frame trajectory. The selection of these 195 structures was made at intervals of 400 ps. For each of these 195 MD frames, single point energies were computed using the DFT method in Vienna ab initio simulation package (VASP),29 which is based on the plane wave pseudo-potential method. Core states were treated with the Projected Augmented Wave (PAW) technique.30 For the exchange–correlation (XC) functional, the generalized gradient approximation (GGA) was employed, specifically adopting the Perdew–Burke–Ernzerhof (PBE) parametrization.31 The cutoff energy for the plane waves was set to 520 eV. For Brillouin zone integration, a Γ-centered 1 × 1 × 1 Monkhorst–Pack grid and Gaussian smearing with a width of 0.01 eV were employed. The threshold for the self-consistency criterion in solving the Kohn–Sham equations was set at 10−5 eV.
000-frame trajectory. The selection of these 195 structures was made at intervals of 400 ps. For each of these 195 MD frames, single point energies were computed using the DFT method in Vienna ab initio simulation package (VASP),29 which is based on the plane wave pseudo-potential method. Core states were treated with the Projected Augmented Wave (PAW) technique.30 For the exchange–correlation (XC) functional, the generalized gradient approximation (GGA) was employed, specifically adopting the Perdew–Burke–Ernzerhof (PBE) parametrization.31 The cutoff energy for the plane waves was set to 520 eV. For Brillouin zone integration, a Γ-centered 1 × 1 × 1 Monkhorst–Pack grid and Gaussian smearing with a width of 0.01 eV were employed. The threshold for the self-consistency criterion in solving the Kohn–Sham equations was set at 10−5 eV.
All the input files for the quantum calculation in VASP are available in Zenodo.32
The quantum vertical energies were derived from the energy difference between these two states. To assess the impact of the DFT functionals33,34 on the vertical energies, we performed comparison calculations for 3 randomly chosen structures (shown in ESI,† Table S1). These calculations show that the choice of the functional has a marginal influence on the vertical energies. Note that for both the classical and quantum energies, the presence of a net TEMPO charge results in self-interactions, and there may be differences due to the various implementations in Gromacs and VASP. However, since our main interest lies in determining the reorganization energy (λ) from the width of the vertical energy distribution (σ), any potential shift due to these technical factors should be similar across all frames, making it an uncritical factor in our analysis.
Similar calculations were performed to calculate the classical and quantum vertical energies for TEMPO in EC/EMC and EC/EMC/LiPF6 mixture. In these systems, classical vertical energies were calculated for 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures, while quantum vertical energies were calculated for 95 structures.
000 structures, while quantum vertical energies were calculated for 95 structures.
Linear regression model
In order to establish the relationship between the quantum results and their classical counterpart, linear regression analysis was performed:| YQi = aXCi + b + εi | (11) |
Results and discussion
Quantum vertical energy distribution for TEMPO in water
The vertical energy correlation time was found to be 4 to 5 ps for both oxidation of TEMPO. and reduction of TEMPO+ in water (Fig. 1). Here, correlation time is calculated (using exponential fitting: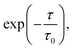 where τ and τ0 are time and correlation time, respectively) as the time at which the correlation function drops to 1/e. This implies that it takes this amount of time to obtain statistically uncorrelated structures. Consequently, unlike classical MD, methods such as AIMD, or hybrid QM/MM methods cannot produce a large number of statistically uncorrelated structures and as a result calculating a clear vertical energy distribution is not possible with such methods. This motivated the sampling of configurations by classical MD, followed by single-point DFT calculations as described in the Methods section.
where τ and τ0 are time and correlation time, respectively) as the time at which the correlation function drops to 1/e. This implies that it takes this amount of time to obtain statistically uncorrelated structures. Consequently, unlike classical MD, methods such as AIMD, or hybrid QM/MM methods cannot produce a large number of statistically uncorrelated structures and as a result calculating a clear vertical energy distribution is not possible with such methods. This motivated the sampling of configurations by classical MD, followed by single-point DFT calculations as described in the Methods section.
 | ||
Fig. 1 Vertical energy correlation,  for (a) oxidation of TEMPO. and (b) reduction of TEMPO+ in water. Correlation times are shown by the red dotted lines. for (a) oxidation of TEMPO. and (b) reduction of TEMPO+ in water. Correlation times are shown by the red dotted lines. | ||
Distributions that are approximately Gaussian were observed for quantum vertical energies calculated from 195 statistically uncorrelated structures (see Fig. 2a and b). From the direct calculation of the second moment, σQM and eqn (10), λQM were found to be 0.63 eV and 0.7 eV for M = ox and M = red, respectively, at a temperature of 298.15 K.
 | ||
| Fig. 2 Quantum vertical energy distribution (a) for the oxidation of TEMPO. in water and (b) for the reduction of TEMPO+ in water. | ||
The deviation in λQ for the oxidation and reduction processes can be attributed to the different charge states of the solute and the varying orientations of the surrounding solvent molecules.
Below, we present a table comparing the values of λQM for both the oxidation of TEMPO and the reduction of TEMPO+ across three different solvents.
In the next section, we will discuss the quantum vertical energies obtained for the oxidation of TEMPO. and the reduction of TEMPO+ in EC/EMC mixture both in the presence and absence of salt LiPF6.
Impact of electrolyte environment on ET characteristics
As mentioned in the introduction, carbonate electrolytes, usually applied in commercial lithium ion batteries, have recently also been employed in ORBs,2,14–18 which are promising as next-generation energy storages. Therefore, in this section, quantum vertical energy distributions for TEMPO dissolved in carbonate mixtures, both with and without lithium salt, were calculated. For each of these cases, 95 statistically uncorrelated structures were chosen.In Table 1, while all λQM values fall within the same range, we note a deviation in λQox and λQred for non-aqueous solvents similar to the aqueous case, presumably due to slight differences in the solvation shells of TEMPO and TEMPO+.
| Solvent | Redox step | λ QM (eV) |
|---|---|---|
| Water | Oxidation | 0.63 |
| Reduction | 0.7 | |
| EC/EMC mixture | Oxidation | 0.5 |
| Reduction | 0.77 | |
| EC/EMC/LiPF6 mixture | Oxidation | 0.7 |
| Reduction | 1.02 |
Interestingly, the oxidation process of TEMPO. in the presence of EC and EMC solvents revealed a significant increase in σQox, leading to a corresponding increase in λQox, when a single LiPF6 was added to the binary solvent (see Fig. S2a and c, ESI†). In particular, a 40% increase in λQox was observed when going from the binary EC/EMC mixture to the EC/EMC/LiPF6 electrolyte (Table 1).
Similar to the oxidation process, reduction processes of TEMPO+ to its radical in the presence of EC and EMC solvents, showed a significant increase in σQred when a single LiPF6 was added (see Fig. S2b and d, ESI†). A 32% increase in λQred was observed when going from the binary EC/EMC mixture to the EC/EMC/LiPF6 electrolyte (Table 1).
In the presence of salt, an increase in reorganization energy for both the oxidation and reduction processes occurs, as Li+ prefers coordination with solvent molecules, resulting in increased rigidity35,36 of the solvent and making it less likely to reorient during the charge transfer reaction. This coordination is justified by the radial distribution function (RDF) plots included in the ESI† (see Fig. S11 and S12).
Experimental calculations of reorganization energies in aqueous13 and non-aqueous solvents37 have been found to yield values similar to those observed in our study. Experiments indicate that reorganization energy plays a crucial role in charge hopping in organic electrodes,15,16,38 and it has also been observed that the composition of the electrolyte can heavily influence the reorganization energy.14,37
In the framework of Marcus theory,6 the activation energy (Ea) for electron transfer between a donor and an acceptor is determined by the reorganization energy, as expressed by the equation  . Here, ΔG0 and λ represent the standard Gibbs free energy change and the reorganization energy for the reaction, respectively. Considering the case of charge transfer events between a TEMPO radical and a TEMPO cation, where ΔG0 can be considered as zero, it is observed that the activation energy increases with an increase in λ. Consequently, this relationship implies that charge transfer events of this nature in the system are inversely related to the reorganization energy. Our study reveals that the addition of salt leads to an increase in reorganization energy, thereby suggesting a decrease in charge transfer events between a TEMPO radical and a TEMPO cation.
. Here, ΔG0 and λ represent the standard Gibbs free energy change and the reorganization energy for the reaction, respectively. Considering the case of charge transfer events between a TEMPO radical and a TEMPO cation, where ΔG0 can be considered as zero, it is observed that the activation energy increases with an increase in λ. Consequently, this relationship implies that charge transfer events of this nature in the system are inversely related to the reorganization energy. Our study reveals that the addition of salt leads to an increase in reorganization energy, thereby suggesting a decrease in charge transfer events between a TEMPO radical and a TEMPO cation.
In total, our results demonstrate that the reorganization energy may strongly depend on the local environment. Specifically, it demonstrates that the addition of ions increases the reorganization energy for both the oxidation and reduction processes by providing additional stability to the redox center. This will especially be the case for multicomponent systems employed in ORBs.2 Therefore, these considerations will be important for the directed optimization of ORB cathode materials. Tuning the electrolyte composition can also optimize electron transfer dynamics in the organic radical electrode. For instance, it's plausible that various types of salts influence the stability trends of both the oxidised and neutral states of redox centers, subsequently impacting the dynamics of the ET reaction.
Correlation between quantum and classical vertical energies
Having observed that the electrolyte environment is crucial to describe the vertical energy distribution, one might wonder in how far these effects are already contained in the classical force field employed in the MD simulations. To elucidate this, we first determined the correlation between quantum and classical vertical energies for the oxidation of TEMPO. and reduction of TEMPO+ for different solvents from their scatter plots (see Fig. 3 and Fig. S6, ESI†). Moderate but significant correlations are expressed by correlation coefficients in the range from 0.5 to 0.7.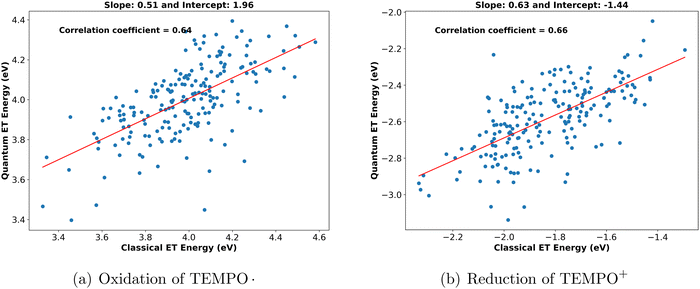 | ||
| Fig. 3 Scatter plots between classical and quantum vertical energies for (a) oxidation of TEMPO. and (b) reduction of TEMPO+ in water. | ||
In the ESI,† we show that not only the vertical energies (i.e. energy difference between both diabatic states) of the classical and the quantum mechanical model are correlated, but also the individual diabatic energies (see Fig. S3 and S4, ESI†). Moreover, when fitting a straight line to the data, we note that the residuals of both diabatic states are correlated as well (Fig. S3c and S4c, ESI†).
We derived a statistical relation (eqn (S8), ESI†) to relate the correlation of classical and quantum vertical energies to the underlying correlation of the residuals of both diabatic states. Remarkably, although the correlation in Fig. 3 appears rather moderate, it can only be achieved when the correlation of residuals for both diabatic states is extremely good, with correlation coefficients of about 0.93.
Therefore, one might be tempted that quantum vertical energies can be predicted solely from the classical vertical energies without conducting any quantum calculations. However, as we will demonstrate in the subsequent section, this is not the case.
Establishing relation between σC and σQ from Linear regression
As observed in Fig. 3 and Fig. S6 (ESI†), the relation between classical and quantum vertical energies can be reasonably well described by a linear relation (eqn (11)). Similarly, from the standard deviation (σCM) of classical vertical energies and the standard deviation of the error term, standard deviation (σQM) of Quantum vertical energies of state M (here, M = ox, red), relevant for the calculation of λQM, can be predicted based on eqn (11), which follows:
of the error term, standard deviation (σQM) of Quantum vertical energies of state M (here, M = ox, red), relevant for the calculation of λQM, can be predicted based on eqn (11), which follows: | (12) |
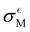 represent the slope and standard deviation of the error term from the scatter plot of quantum and classical vertical energies, respectively (see Fig. 3 and Fig. S6, ESI†).
represent the slope and standard deviation of the error term from the scatter plot of quantum and classical vertical energies, respectively (see Fig. 3 and Fig. S6, ESI†).
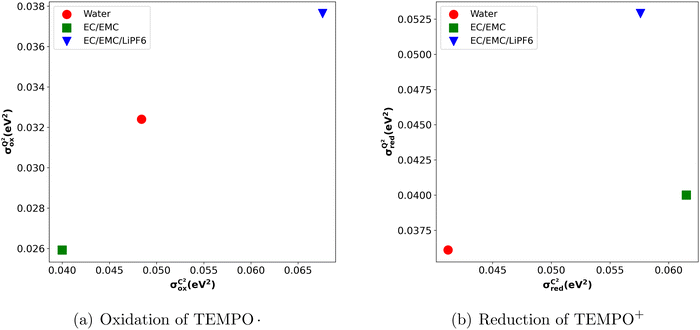
Below, we present a table comparing the values of σQM, aM, σCM and  for both the oxidation of TEMPO and the reduction of TEMPO+ across three different solvents.
for both the oxidation of TEMPO and the reduction of TEMPO+ across three different solvents.
From Table 2, it becomes evident that both aM and 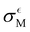 are not constant values, indicating that they are dependent on the system under consideration (naively one might assume that solely σCM depends on the system). Hence, one cannot generally predict σQM only from σCM without performing any quantum calculations.
are not constant values, indicating that they are dependent on the system under consideration (naively one might assume that solely σCM depends on the system). Hence, one cannot generally predict σQM only from σCM without performing any quantum calculations.
 for the oxidation of TEMPO as well as the reduction of TEMPO+ in three different solvents
for the oxidation of TEMPO as well as the reduction of TEMPO+ in three different solvents
If the classically obtained standard deviation σCM were identical to the quantum value σQM, classical simulations would offer a highly efficient alternative to quantum calculations. However, as seen from Table 2, this is not the case. Classical simulations might still have predictive power for the impact of the solvent if σCM and σQM were directly correlated when comparing results across different solvents. Unfortunately, Fig. 4 shows that, in the case of reduction reactions, the data are not correlated. This suggests that the apparent correlation observed in oxidation reactions may merely be a result of the small sample size. The absence of this correlation is directly tied to the significant variation in the slope aM for different solvents.
These variations in values may at least partly arise from the variation in polarization effects induced by the presence of different solvents. In this context, it's worth noting that our OPLS all-atom force field25 does not account for the polarization effect. Therefore, using a polarizable force field39 might result in uniform aM and  .
.
Another interesting observation of our study is that we noticed a lower value of σQM compared to σCM (Fig. 4). This decrease in σQM (and consequently in λQM) when compared to its classical counterpart aligns with the idea that charge delocalization due to quantum effects offers additional stabilization of the post-redox reaction state.9 This induced stabilization cannot be accounted for in the classical vertical energy distribution, as it does not consider charge delocalization or electronic polarization.
Conclusions
In this work, we studied the reorganization energies of TEMPO radicals via sampling the vertical energies by both classical MD simulations and DFT calculations. In conclusion, from our work it has been observed that the vertical energy correlation time is around 4–5 picoseconds. This suggests that generating a large dataset of uncorrelated structures using AIMD10 or hybrid QM/MM11 methods is challenging for such systems. Additionally, our research has provided insights into how the electrolyte environment influences the reorganization energy and consequently impacts ET dynamics. In particular, our study demonstrates that the addition of salt increases the reorganization energy, as the increased rigidity of the solvent reduces its likelihood of reorientation during the charge transfer reaction.Our statistical analysis shows that the quantum and classical vertical energies exhibit a good correlation, but this correlation is system-dependent. As a result, one cannot predict σQM solely from σCM. The inclusion of the polarization effect into the classical force field39 might make this prediction feasible. Nevertheless, classical MD simulations can be utilized to efficiently sample structures, which then can be subjected to quantum calculations.
A crucial observation from our study is the decrease in the quantum reorganization energy, λQM, compared to its classical counterpart, λCM. This observation aligns with the theory9 that charge delocalization, which is a quantum effect, provides additional stabilization after redox reactions.
This research has advanced our understanding of reorganization energies on single TEMPO molecules, thereby paving the way to predict local reorganization energies within an organic electrode filled with multiple redox centers. This understanding is a significant stride towards unraveling the complex ET mechanisms inside ORBs.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
SM, AH and DD acknowledge funding by Deutsche Forschungsgemeinschaft [Priority Program SPP 2248 “Polymer-based Batteries” (project number 441255373)]. I am also grateful to Sukanya Majumdar for her continuous support.References
- K. Nakahara, K. Oyaizu and H. Nishide, Organic Radical Battery Approaching Practical Use, Chem. Lett., 2011, 40, 222–227 CrossRef CAS.
- D. T. Daniel, S. Oevermann, S. Mitra, K. Rudolf, A. Heuer, R.-A. Eichel, M. Winter, D. Diddens, G. Brunklaus and J. Granwehr, Multimodal investigation of electronic transport in PTMA and its impact on organic radical battery performance, Sci. Rep., 2023, 13, 10934 CrossRef CAS PubMed.
- L. Wylie, T. Blesch, R. Freeman, K. Hatakeyama-Sato, K. Oyaizu, M. Yoshizawa-Fujita and E. I. Izgorodina, Reversible Reduction of the TEMPO Radical: One Step Closer to an All-Organic Redox Flow Battery, ACS Sustainable Chem. Eng., 2020, 8, 17988–17996 CrossRef CAS.
- J. Blumberger, Recent Advances in the Theory and Molecular Simulation of Biological Electron Transfer Reactions, Chem. Rev., 2015, 115, 11191–11238 CrossRef CAS PubMed.
- R. A. Marcus, Electron Transfer Reactions in Chemistry: Theory and Experiment (Nobel Lecture), Angew. Chem., Int. Ed. Engl., 1993, 32, 1111–1121 CrossRef.
- R. A. Marcus, On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. II. Applications to Data on the Rates of Isotopic Exchange Reactions, J. Chem. Phys., 2004, 26, 867–871 CrossRef.
- C. Zener and R. H. Fowler, Non-adiabatic crossing of energy levels, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed.
- J. K. Hwang and A. Warshel, Microscopic examination of free-energy relationships for electron transfer in polar solvents, J. Am. Chem. Soc., 1987, 109, 715–720 CrossRef CAS.
- J. Blumberger and M. Sprik, Quantum versus classical electron transfer energy as reaction coordinate for the aqueous Ru2+/Ru3+ redox reaction, Theor. Chem. Acc., 2006, 115, 113–126 Search PubMed.
- J. Blumberger and M. Sprik, Ab Initio Molecular Dynamics Simulation of the Aqueous Ru2+/Ru3+ Redox Reaction: The Marcus Perspective, J. Phys. Chem. B, 2005, 109, 6793–6804 CrossRef CAS PubMed , PMID: 16851765.
- M. I. G. Nicholson, P. R. Bueno and G. T. Feliciano, Ab Initio QM/MM Simulation of Ferrocene Homogeneous Electron-Transfer Reaction, J. Phys. Chem. A, 2021, 125, 25–33 CrossRef CAS PubMed , PMID: 33382268.
- D. Rapaport, The Art of Molecular Dynamics Simulation, Cambridge University Press, 2004 Search PubMed.
- H. O. Finklea and N. Madhiri, Reorganization energies of TEMPO/TEMPO+ in water, J. Electroanal. Chem., 2008, 621, 129–133 CrossRef CAS , Special Issue in Honor of Professor Israel Rubinstein.
- S. Wang, F. Li, A. D. Easley and J. L. Lutkenhaus, Real-time insight into the doping mechanism of redox-active organic radical polymers, Nat. Mater., 2019, 18, 69–75 CrossRef CAS PubMed.
- S. Iwasa, T. Nishi and S. Nakamura, Enhancement of rapid charging capability of organic radical battery using ethylene carbonate-based electrolyte containing LiFSI, J. Power Sources, 2018, 402, 157–162 CrossRef CAS.
- K. Nakahara, K. Oyaizu and H. Nishide, Electrolyte anion-assisted charge transportation in poly(oxoammonium cation/nitroxyl radical) redox gels, J. Mater. Chem. A, 2012, 22, 13669–13673 RSC.
- T. W. Kemper, T. Gennett and R. E. Larsen, Molecular Dynamics Simulation Study of Solvent and State of Charge Effects on Solid-Phase Structure and Counterion Binding in a Nitroxide Radical Containing Polymer Energy Storage Material, J. Phys. Chem. C, 2016, 120, 25639–25646 CrossRef CAS.
- K. Nakahara, J. Iriyama, S. Iwasa, M. Suguro, M. Satoh and E. J. Cairns, Cell properties for modified PTMA cathodes of organic radical batteries, J. Power Sources, 2007, 165, 398–402 CrossRef CAS.
- K. Ando, Quantum energy gap law of outer-sphere electron transfer reactions: a molecular dynamics study on aqueous solution, J. Chem. Phys., 1997, 106, 116–126 CrossRef CAS.
- K. Ando, Solvent nuclear quantum effects in electron transfer reactions. III. Metal ions in water. Solute size and ligand effects, J. Chem. Phys., 2001, 114, 9470–9477 CrossRef CAS.
- D. McQuarrie, Statistical Thermodynamics, University Science Books, 1973 Search PubMed.
- M. Abraham, et al.GROMACS 2023 Manual. 2023 Search PubMed.
- L. Martınez, R. Andrade, E. G. Birgin and J. M. Martınez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- M. J. Frisch et al. Gaussian-16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- P. Atkins and R. Friedman, Molecular Quantum Mechanics, OUP, Oxford, 2011 Search PubMed.
- J. Dunning and H. Thom, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Mitra, All input files for quantum calculations in VASP, 2023 DOI:10.5281/zenodo.8252154.
- A. P. Bartok and J. R. Yates, Regularized SCAN functional, J. Chem. Phys., 2019, 150, 161101 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Li, J. Owrutsky, M. Sarisky, J. P. Culver, A. Yodh and R. M. Hochstrasser, Vibrational and rotational relaxation times of solvated molecular ions, J. Chem. Phys., 1993, 98, 5499–5507 CrossRef CAS.
- M. T. Ong, O. Verners, E. W. Draeger, A. C. T. van Duin, V. Lordi and J. E. Pask, Lithium Ion Solvation and Diffusion in Bulk Organic Electrolytes from First-Principles and Classical Reactive Molecular Dynamics. The, J. Phys. Chem. B, 2015, 119, 1535–1545 CrossRef CAS PubMed , PMID: 25523643.
- C. Karlsson, T. Suga and H. Nishide, Quantifying TEMPO Redox Polymer Charge Transport toward the Organic Radical Battery, ACS Appl. Mater. Interfaces, 2017, 9, 10692–10698 CrossRef CAS PubMed , PMID: 28282111.
- K. Zhang, Y. Xie, B. B. Noble, M. J. Monteiro, J. L. Lutkenhaus, K. Oyaizu and Z. Jia, Unravelling kinetic and mass transport effects on two-electron storage in radical polymer batteries, J. Mater. Chem. A, 2021, 9, 13071–13079 RSC.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. J. MacKerell, B. Roux and C. Schroder, Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed , PMID: 31141351.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04111e |
| This journal is © the Owner Societies 2024 |