Pressure effects on both fluorescent emission and charge transport properties of organic semiconductors: a computational study†
Yi
Zeng
a,
Wen
Shi
 b,
Qian
Peng
c,
Yingli
Niu
d,
Zhiying
Ma
b,
Qian
Peng
c,
Yingli
Niu
d,
Zhiying
Ma
 e and
Xiaoyan
Zheng
e and
Xiaoyan
Zheng
 *a
*a
aKey Laboratory of Cluster Science of Ministry of Education, Beijing Key laboratory of Photoelectronic/Electro-photonic Conversion Materials, School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing, 100081, China. E-mail: xiaoyanzheng@bit.edu.cn
bSchool of Chemistry, Sun Yat-Sen University, Guangzhou, 510006, China
cKey Laboratory of Organic Solids, Beijing National Laboratory for Molecular Science (BNLMS), Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China
dSchool of Science, Beijing Jiaotong University, Beijing 100044, China
eEngineering Research Center for Nanomaterials, Henan University, Kaifeng 475004, China
First published on 5th December 2023
Abstract
External pressure can regulate the photophysical property and charge transport performance of organic semiconductors, however, the underlying mechanism at the microscopic level is still elusive. Using thermal vibrational correlation function coupled quantum mechanics/molecular mechanics and full quantum charge transfer rate theory, we systematically explore the influence of pressure on fluorescence emission and charge transport behaviours of representative cyclooctatetrathiophene (COTh). It is found that, upon pressurization, the intramolecular configurations of COTh became more twisted, leading to the blue-shifted emission. The fluorescence quantum efficiency (FQE) of COTh crystals decreases monotonically in a wide pressure range of 0–4.38 GPa, because the increase of intermolecular electronic energy transfer rate constant (keet) is larger than the decrease of internal conversion rate constant (kic), and the variation of keet is dominant. The decrease in kic is attributed to the decreasing reorganization energy, reflecting the suppression of the low-frequency flipping vibrations of four thiophene rings and the high-frequency stretching vibrations of central cyclooctatetraene, while the keet increase is due to the simultaneous increase in exciton coupling and spectra overlap. Moreover, we predicted that the hole mobility of COTh increases monotonically by nearly an order of magnitude from 0.39 to 3.00 cm2 V−1 s−1 upon compression, because of the increase in transfer integral and the decrease of charged reorganization energy. Furthermore, its hole mobility exhibits obvious anisotropy. Our work systematically builds the external pressure, molecular packing, luminescence and transport properties relationships of organic semiconductors and provides theoretical guidance for the rational design of pressure responsive organic semiconductors with excellent photoelectric performance.
1. Introduction
Organic semiconductors with perfect luminescent performance have attracted much attention due to their flexibility in molecular structure, tunability in material function as well as their potential applications in organic photovoltaic cells (OPVs), organic light-emitting diodes (OLEDs) and organic effect transistors (OFETs), and so on.1–4 External stimuli applied to organic materials, such as pressure, polarity, temperature and pH, can manipulate the intramolecular conformations and intermolecular packing of organic semiconductors in solid states simultaneously, and thus regulate their performance in terms of photoelectric properties.5–7 Isostatic pressure with equal pressure in every direction has emerged as an effective means of modulating the photoelectric properties of organic semiconductors.8–10 For example, upon compression, the fluorescence intensity of 2,3,4,5-tetraphenylfuran decreased continuously and was accompanied by redshifted spectra, due to the enhanced intermolecular π–π interactions.11 In contrast, the fluorescence quantum efficiency (FQE, ΦF) of hexaphenylsilole (HPS) presented a conspicuous enhancement upon pressurization in the pressure range of 1 to 104 atm, while the emission wavelength was almost unchanged.12 Moreover, the cocrystals of perylene and 1,2,4,5-tetracyanobenzene demonstrate a continuous pressure-induced emission enhancement up to 3 GPa, along with the blue shifted emission upon tetrahydrofuran insertion.13 In the case of cyclooctatetrathiophene (COTh) crystals with excellent hole transport capability,14,15 the fluorescence intensity diminishes monotonously upon compression with isostatic pressure from 0 to 7 GPa, accompanied by the blue-shifted emission from 540 to 520 nm.16 While the FQE of 2,6-diphenylanthracene (DPA) crystals was almost constant during pressurization, and the hole mobility doubled.17 Most recently, the mechanoelectric response of single-crystal rubrene was widely explored through experiment and theoretical calculations, however, some conflicting results about either the magnitude or the direction of the strain mostly affecting the charge mobility have been reported in the literature.18–23 The pressure effects on the physical properties of organic semiconductors are highly complex and system-dependent, due to the unclear relationship between the deformation applied and performances of materials. Under external pressure, most organic compounds exhibit redshifted emission and decreased fluorescence intensity, while the occurrence of blue-shifted spectra and weakened fluorescence is rare. Unraveling the relationship between external pressure, molecular packing and photoelectric properties are key to the rational design of pressure-responsive organic semiconductors, but it is still a big challenge through experiment due to the limited temporal and spatial resolutions on current experimental techniques. Investigation of the pressure effects on the photoelectric properties of organic semiconductors at the microscopic level using a multiscale modeling protocol is an effective way.Theoretically, the pressure effects on optical properties or charge transport of organic semiconductors have also been investigated.24–27 Shuai et al. proposed that the increase of FQE of HPS upon pressurization is attributed to the suppression of the low-frequency electron–vibration couplings.25 Shuai et al. also reported that pressurization improved the hole mobility of a naphthalene crystal by hindering the electron–phonon coupling strength.26 Hu et al. demonstrated that the hole mobility of DPA improved upon pressurization because of the increase of transfer integrals and the reduction of charged reorganization energy, while their radiative and non-radiative decay rate constants were immune to external pressures.28 Our group proposed that the non-monotonical variations of FQE with pressure in 1,2,3,4-tetraphenyl-1,3-cyclopentadiene are attributed to the competition between electron–vibration coupling and nonadiabatic electronic coupling.29 We also discovered that the piezochromic behavior of organic fluorophores can be manipulated by the conformational flexibility of the organic compounds and the FQE of organic molecules with a flexible backbone are more sensitive to external pressures than those of the rigid ones.30 However, the underlying mechanism of the simultaneous fluorescence quenching and blue-shifted emission upon pressurization of COTh in experiment,16 as well as the pressure effects on the hole transport properties of COTh at the microscopic level, are still elusive.
In this work, we take COTh as an example (Fig. 1a and Fig. S2, ESI†) to systematically explore the intrinsic mechanism of responsive behaviors of fluorescent and charge transport properties to isostatic pressure using the multiscale modeling protocol. The quantum mechanics/molecular mechanics (QM/MM) model31,32 coupled with thermal vibrational correlation function (TVCF) rate formalism were used to calculate the photophysical properties of COTh crystals under different external pressures. The calculation of charge transport properties of COTh were realized by full quantum charge transfer rate theory based on a quantum nuclear tunneling model. It is found that pressurization quenches the fluorescence emission of COTh, but is beneficial to its hole transport behavior. Upon compression, the FQE of COTh crystals decreased monotonously in the pressure range of 0–4.38 GPa due to the surge of intermolecular electronic energy transfer induced by the reduction of intermolecular distances. The intramolecular configurations of COTh become more distorted after pressurization, leading to the continuous blue shift of the fluorescence emission. In addition, we predict that the hole mobility of COTh increased by nearly one order of magnitude with increasing pressures from 0 to 4.86 GPa, because of the simultaneously increased transfer integral and the decreased charge reorganization energy. And the hole transport of COTh at different pressures exhibits obvious anisotropy. This investigation systematically reveals the pressure effects on both fluorescent emission and charge transport properties of organic semiconductors, and provides a theoretical foundation for the rational utilization of pressure to optimize the photoelectric properties of organic semiconductors.
 | ||
| Fig. 1 (a) Chemical structure of COTh with some key structure parameters in the backbone labelled. (b) The QM/MM model of the COTh crystal. | ||
2. Computational details
2.1 Prediction of the crystal structures of COTh at different pressures
To study the pressure effects on the fluorescent and charge transport properties of the COTh system, the crystal structures of COTh under different external pressures were first simulated and predicted based on the experimental crystal structure obtained under a normal temperature and pressure environment16 (ambient conditions) by PBE functional with Grimme's D3 correction33 in the Vienna Ab initio Simulation Package (VASP).34 Computationally, the compression process upon pressure can be simplified by setting a series of scaling factors to compress the lattice volume. The atomic positions of the crystal structure of COTh obtained from experiment under the ambient conditions16 were first optimized. The corresponding pressure of the optimized crystal structure of COTh is set as a reference with 0 GPa. Both the atomic positions and lattice parameters of the compressed cell were optimized with constraint of scaled volume. A single point calculation is performed on a series of compressed crystals to obtain the specific pressure values of the environment in which these crystals are placed. During the calculations, the convergence criterion of the total energy is set to be 10−5 eV in the self-consistent field iteration. The cutoff energy for the plane-wave basis set is set to be 600 eV. The cutoff radius for pair interactions is set to be 50.2 Å. A k-mesh of 4 × 6 × 4 was used during the structural optimization, and further single-point energy calculations are performed on a k-mesh of 6 × 8 × 6. All the lattice parameters, density and volume of COTh crystals at different pressures are summarized in Table S1, see details in the ESI.†2.2 Setup of QM/MM models
The supercell with a size of 3 × 3 × 3 was constructed based on the optimized crystal structure of COTh at each external pressure to set up the QM/MM model. The QM/MM calculation was performed using a two-layer ONIOM model in the Gaussian 16 package.35 The QM/MM model contains 54 COTh molecules, one COTh at the center is selected as the high-layer (QM region), and the others are set as the low-layer (MM region) (Fig. 1b). During geometry optimization of COTh at the ground (S0) and the first excited (S1) states, only the QM molecule was allowed to relax and the others were frozen. For accuracy, seven density functionals: B3LYP,33 CAM-B3LYP,36 M06, M06-2X,37 M05-2X, BMK38 and ωB97XD with the 6-31G** basis set were used to calculate the vertical excitation energy (ΔEvert) of COTh crystals at both S0 and S1, see details in Table S2 (ESI†). It is found that the excitation energy (2.31 eV) at S1 calculated at the BMK/6-31G** level was optimal and was close to the experimental value (2.38 eV).16 Therefore, all the following QM/MM calculations on the photophysical properties of COTh aggregates at different pressures were performed at the BMK/6-31G** level in the QM region, while the MM part was dealt with using the universal force field.39 The partial charge of each atom in COTh aggregates was assigned by the restrained electrostatic potential fitting approach. Electrostatic interactions between the QM and MM regions were calculated using an electrostatic charge embedding scheme.40 The optimization and harmonic vibrational frequency analyses of the COTh crystals at different pressures were all performed in the QM region of the ONIOM models, at the same time, and all atoms in the MM region were fixed. The harmonic vibrational frequency analysis was performed to ensure the optimized configurations of COTh crystals at S0 and S1 have no imaginary frequencies. There is no symmetry constraint during the optimization.2.3 The rate constants of the key channels of excited states
To evaluate the optical properties of crystals more intuitively, we need to calculate the radiation and non-radiation attenuation rates and the fluorescence quantum yield. According to Einstein's spontaneous radiation relationship, the radiative rate constant (kr) calculation formula can be expressed using the following formula: | (1) |
Based on the Fermi golden rule, the internal conversion (IC) rate constant (kic) can be written as:41
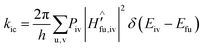 | (2) |
In most organic molecules, the ISC rate constant (kisc) can be ignored, because the spin–orbital coupling (SOC) for the π → π* electrons transition is small. The expression of the IC process is:
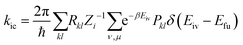 | (3) |
 | (4) |
Rkl = 〈Φf|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) fk|Φi〉〈Φi| fk|Φi〉〈Φi|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) fl|Φf〉 fl|Φf〉 | (5) |
 | (6) |
Electronic energy transfer (EET) described energy transfer between two chromophores, which is one of the non-radiative decay channels of the excited state.47 The EET is incoherent (Markovian) and irreversible,48,49 and it can influence the population of the excited state and should be considered in the calculation of fluorescence quantum yield. The EET rate constant (keet) was estimated using the following formula:
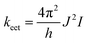 | (7) |
Based on the optimized geometric structures of COTh at both S0 and S1, as well as their electronic structures information obtained from the QM/MM model, the kr, kic and I were further calculated through the TVCF protocol in the MOMAP program42–44,46,50 The J was calculated by the Gaussian 16 program.35
2.4 Hole mobility calculations
For calculation of the hole transport properties, the geometric structures of COTh in both neutral and cationic states were optimized at the B3P86/6-31+G** level, and the vibrational frequency analysis was also performed to guarantee no imaginary frequency using the Gaussian 16 program.35 The hopping mechanism was chosen to model the hole transport processes of COTh crystals. In the hopping model, the reorganization energies of the charged molecule (λcharge) and intermolecular transfer integral (V) are two key factors affecting the rate constant of the charge transport process. Here the λcharge assessed by normal mode analysis51,52 were close to those of the adiabatic potential energy surface method53,54 (see Table S12, ESI†), indicating that the harmonic oscillator approximation is reasonable. V was calculated using the site-energy overlap correction method.55 Then the hopping rate is described by the full-quantum charge transfer rate,41,56 which can reflect the quantum nuclear tunneling effect. The hole mobilities were obtained using the Einstein relationship through evaluating a diffusion process. The diffusion process was driven by a random walk algorithm56,57 through Monte Carlo simulation in the MOMAP program (Fig. S1, ESI†).50 See more details of the hole mobility calculation in the ESI.†3. Results and discussions
3.1 Pressurization effects on intermolecular interactions
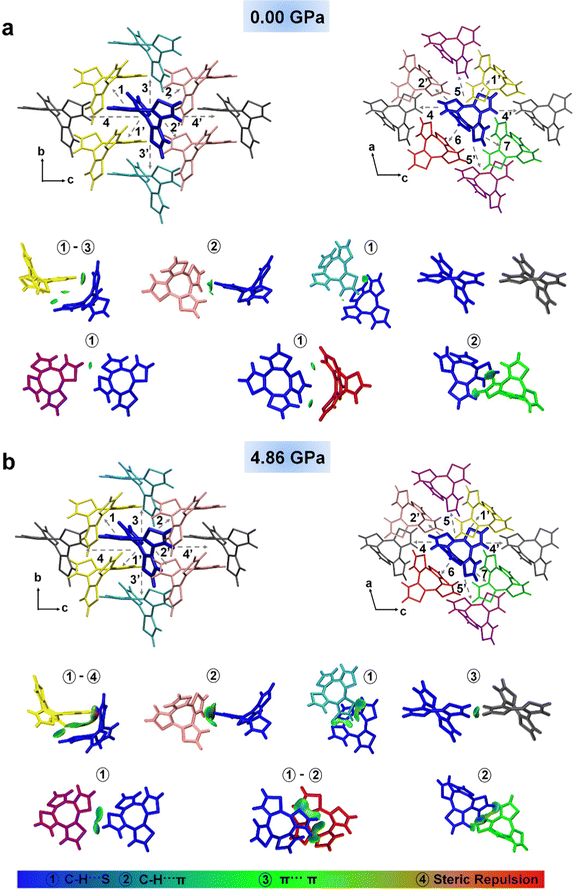
The photophysical properties of organic fluorophores in the crystalline state are closely related to the intermolecular packing and intramolecular configuration, which are key to exploring the influence of external pressure on the crystalline structures of COTh. Through analysis of the simulated COTh crystals under different pressures, we found that the unit-cell volume continuously decreased upon pressurization (Fig. 2a). The lattice constants b and c all decreased monotonically in the whole pressure range, while the a-axis firstly reduced in the pressure range of 0 to 4.38 GPa and then slightly increased as the pressure beyond 4.38 GPa. The compression rate of the b-axes is obviously greater than those of the a- and c-axes (Fig. 2b), leading to COTh molecules in the crystals being more parallel to the ac plane. Moreover, the calculated elastic constant along the b-axis of COTh crystals is also smaller than those of the a- and c-axes (Table S3, ESI†), indicating the most flexible packing along the b-axis. The compression rates of a-, b- and c-axes with pressure are significantly different before and after 4.38 GPa. The main reason for these difference in pressure responsiveness is that the molecular arrangement in the unit cell is relatively loose and the intermolecular distance is relatively large at the initial pressurization, and only small external pressure leads to a great change in the lattice axis, however, when the pressure reaches a certain extent (over 4.38 GPa), the molecular packing becomes very tight due to the sharp reduction in intermolecular distance, and the compression of the lattice axis is close to the limit. As a result, the compression effect on the lattice axes is not obvious in the high pressure region. In addition, the compression exhibited anisotropy, reflected by the small compression rate of the a-axis compared with those of the b- and c-axes. Beyond 4.38 GPa, the a-axis has almost no compressible space, resulting in a slight increase in a-axis, but the volume of the unit cell still decreases, because the reductions in the b- and c-axes are larger than the increase in the a-axis. The intermolecular centroid distance of two neighboring COTh inside the unit cell was also sharply reduced upon compression (Fig. 2c and d). We define two pairwise distances of representative carbon atoms on the opposite thiophene rings of the COTh molecule, labelled as d1 and d2. We found that upon compression, d2 changed slightly and d1 was significantly shortened, which made the intramolecular configuration of COTh more distorted (Fig. 2e and f).As shown in Fig. 3, for COTh at each external pressure, the central QM molecule (blue) and its surrounding neighbors (MM region) were labelled with different colours, and the COTh molecules in the same colour have the same centroid distance to the central COTh molecule, so the 14 neighbouring molecules around the QM molecule can actually be divided into seven representative pairs. The intermolecular interactions for seven COTh dimers under different external pressures were characterized by the independent gradient model (IGM) analysis;58,59 the types of intermolecular interactions were labelled by different numbers, with the ①–④ representing C–H⋯S (blue region), C–H⋯π (blue region), π⋯π (green region) and steric repulsion interaction (red region), respectively. In IGM analysis, the more broadened the distribution and concentrated the color region is, the stronger the intermolecular interaction is, and the strength of intermolecular interactions is negatively correlated with the intermolecular distances within a certain range. Comparing Fig. 3a and b, it can be seen that from 0 to 4.86 GPa, the intermolecular distances of representative COTh pairs in the crystalline state decrease (Table S4, ESI†), the corresponding intermolecular C−H···S and C−H···π interactions (blue region) of twelve COTh dimers (1(1′)–3(3′) and 5(5′)–7(7′)) were all largely enhanced, and steric repulsion of the dimer 1(1′) and π–π interactions of the dimer 4(4′) also increased (Fig. 3).
3.2 Pressure effects on geometrical and electronic structures
The intramolecular configuration and electronic properties of COTh aggregates at different pressures were analysed. The selected key structural parameters, including bond length, bond angle and dihedral angles of COTh at both S0 and S1, and their structural modification (Δ|S0 − S1|) under different pressures are shown in Table 1 and Table S5 (ESI†). The optimized geometry of COTh at S0 under ambient conditions is close to the X-ray crystalline structure in the experiment16 (Table S5, ESI†), confirming the reliability of our QM/MM protocol. It is found that, upon excitation, the bond lengths of COTh tend to equalize, with the length of double bonds (B1, B3, B5, B7) increasing and the length of single bonds (B2, B4, B6, B8) decreasing simultaneously (Table 1). And the bond lengths of COTh continuously decreased with increasing pressure. While the bond angles are immune to environments and are basically unchanged upon either excitation or compression (Table S5, ESI†). Upon excitation, the key dihedral angles (D1, D2, D3, D4) of COTh at different pressures are all decreased (Table 1 and Table S5, ESI†), indicating that the four thiophene rings of the saddle-type COTh undergo the flipping motions by photoexcitation. The intramolecular configuration could be effectively modulated by the external pressures and the dihedral angles D2 and D4 change by 10° with external pressure from 0 to 4.86 GPa (Table 1). In addition, the structural modifications Δ|S0 − S1| of bond length and four key dihedral angles (D1–D4) decreased monotonically upon compression (Table 1), implying that the stretching vibrations of 8-member rings and the flipping motions of the four thiophene rings may be suppressed.| 0 GPa | 4.86 GPa | |||||
|---|---|---|---|---|---|---|
| S0 | S1 | |Δ(S1 − S0)| | S0 | S1 | |Δ(S1 − S0)| | |
| B1 | 1.38 | 1.44 | 0.06 | 1.37 | 1.43 | 0.05 |
| B2 | 1.47 | 1.41 | 0.06 | 1.45 | 1.39 | 0.05 |
| B3 | 1.38 | 1.44 | 0.05 | 1.38 | 1.43 | 0.05 |
| B4 | 1.48 | 1.43 | 0.06 | 1.47 | 1.42 | 0.05 |
| B5 | 1.38 | 1.44 | 0.05 | 1.37 | 1.42 | 0.05 |
| B6 | 1.47 | 1.41 | 0.06 | 1.45 | 1.40 | 0.05 |
| B7 | 1.38 | 1.44 | 0.06 | 1.37 | 1.42 | 0.05 |
| B8 | 1.48 | 1.43 | 0.05 | 1.45 | 1.41 | 0.05 |
| D1 | −48.6 | −36.5 | 12.1 | −46.5 | −39.7 | 6.8 |
| D2 | 44.7 | 34.1 | 10.7 | 53.1 | 45.2 | 7.8 |
| D3 | −48.1 | −36.7 | 11.4 | −49.3 | −43.3 | 6.0 |
| D4 | 42.0 | 31.5 | 10.6 | 32.1 | 27.7 | 4.4 |
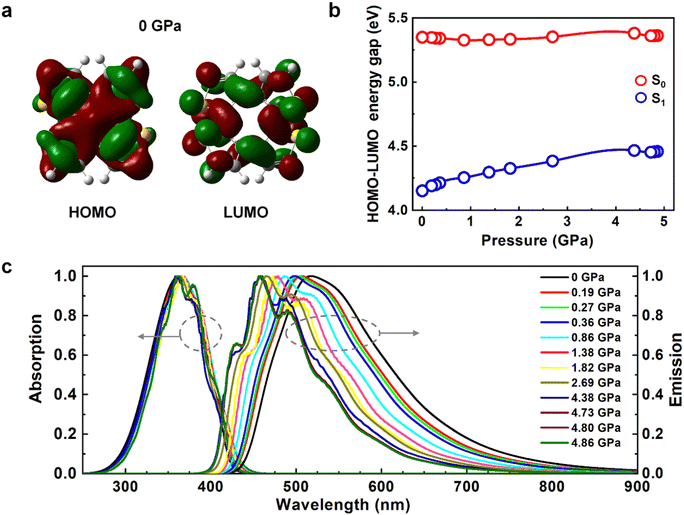
The electronic structures and fluorescent spectra of COTh crystals at different pressures were further analysed. The transition orbitals of COTh at S1 at different pressures were dominant by HOMO → LUMO with a π → π* feature, see Table S6 (ESI†). Both the HOMO and LUMO were nearly delocalized on the whole backbone of COTh (see Fig. 4a and Fig. S3, ESI†). Upon compression, the HOMO–LUMO energy gaps of COTh crystals at S0 were almost constant and thus the absorption spectra are basically unchanged (Fig. 4b and c), while the HOMO–LUMO energy gaps at S1 increase from 4.15 to 4.46 eV monotonically (Fig. 4b and c), consistent with the blue-shifted emission with increasing pressure in experiments.16 The blue-shifted emission of COTh crystals was attributed to the more twisted intramolecular conformations upon pressurization, supported by the change of D2 from 44.7° at 0 GPa to 53.1° at 4.86 GPa. The more twisted conformation of COTh upon compression leads to the change in HOMO and LUMO energy levels with pressure at S0/S1 (Fig. S4, ESI†). For crystalline COTh at different external pressures, the transition orbitals at S0/S1 were dominant by HOMO → LUMO (Table S6, ESI†), therefore, the variation of absorption and emission spectra of COTh were closely related to the change of HOMO–LUMO energy gaps. At S0, both the energy levels of HOMO and LUMO increased with pressure, and the change of HOMO and LUMO are similar (Fig. S4, ESI†), leading to the almost constant HOMO–LUMO energy gap of COTh at different external pressures (Fig. 4b). At S1, the energy level of HOMO slightly decreased, while those of LUMO significantly increased (Fig. S4, ESI†), leading to the increased HOMO–LUMO energy gap of COTh with pressure (Fig. 4b). Thus, the absorption spectra are basically unchanged, while the emission spectra blue-shifted with increasing pressure. In addition, the characteristic vibrational peaks of both absorption and emission spectra become more obvious upon compression (Fig. 4c), because of the enhanced intermolecular interactions (Fig. 3). The stronger intermolecular interactions and the more twisted structures upon pressurization are responsible for the blue-shift emission observed in experiment.16
3.3 Pressure effects on fluorescence quantum efficiency
Upon compression, the fluorescence emission of COTh crystals weakened in the experiment.16 To quantitatively characterize the fluorescence changes, the FQE (ΦF) of COTh at different pressures was calculated by ΦF = kr/(kr + kic + keet). Here the kisc can be ignored, because of the negligible spin–orbit coupling constants (about 1 cm−1, Table S7, ESI†) between S1 and triplet excited states for COTh. Therefore, the FQEs of COTh crystals are governed by competition among kr, kic and keet. The increases of kr, or the reduction of kic and keet can aggrandize FQE. Notably, the FQE of COTh dropped sharply in the pressure range of 0 to 4.38 GPa, and then increased slightly over 4.38 GPa (Fig. 5a), which is roughly consistent with the weakened fluorescence intensity observed in experiment.16Upon pressurization, kr increased slightly (Fig. 5b and Table S8, ESI†), because of the increasing of both ΔEvert and f (Table S6, ESI†), while the kic underwent a continuous reduction (Fig. 5b). For keet, it increases in the pressure range of 0 to 4.38 GPa and shows a significant decline with pressure over 4.38 GPa (Fig. 5b). At the initial stage (0–0.36 GPa), the three decay rate constants kr, kic and keet were almost in the same order of magnitude (Table S8, ESI†), and the increase of keet was slightly quicker than both the kic decrease and the kr increase, leading to the mild decrease of FQE (Fig. 5b). After further compression from 0.36 to 4.38 GPa, the keet were always two or three orders of magnitude larger than kic (Table S8, ESI†), thus keet dominated the FQE, leading to the sharp decrease of FQE in the pressure range of 0.36 to 4.38 GPa (Fig. 5a). When the pressure was over 4.38 GPa, keet decreased rapidly (Fig. 5b), thus the FQE of COTh crystals slightly increased (Fig. 5a).
The kic is determined by the reorganization energy (λ), which quantitively characterizes the strength of the electron-vibration coupling. As shown in Fig. 5c, the λtotal (total reorganization energy), λgs and λes (reorganization energy at the S0 and S1, respectively) all decrease monotonously upon compression (Fig. 5c and Table S9, ESI†). As shown in Fig. S5 (ESI†), the reduction of λgs with pressure was mainly contributed by the suppression of the flipping vibrations of four thiophene rings in the low-frequency region (<300 cm−1) and the stretching vibrations of central cyclooctatetraene in the high-frequency region (>1500 cm−1). Further projecting λgs onto the internal coordinates, we found that the decrease of λgs with pressure was dominated by the λdihedral and λbond, because they both declined sharply first and then stabilized, whereas the λangle is almost unchanged (Fig. S6, ESI†), consistent with the analysis of the normal mode and the changes of geometrical configurations above (Fig. S5, Table 1 and Table S5, ESI†).
According to eqn (7), keet is influenced by two parameters: exciton coupling constant (J)60 and spectral overlap (I). J is determined by the intermolecular distance and transition dipole moment. Here Jmax represents the J with the largest value among all calculated COTh dimers defined in Fig. 3. Upon pressurization, the J (including Jmax) along all directions increase (Fig. 5d and Table S10, ESI†), because of the shortened intermolecular distances (Table S4, ESI†). As for I, it firstly increases (0 to 4.38 GPa) and then decreases (>4.38 GPa). It is noted that the trend of I with pressure is similar to that of keet (Fig. 5b and d). Therefore, both the increase of J and I contribute to the increase of keet in the pressure range from 0 to 4.38 GPa (Fig. 5b and d). Then the decrease of keet over 4.38 GPa is influenced by the decreased I, because the reduction in I is much larger than the slightly increase of J (Fig. 5d).
3.4 Pressure effects on hole transport mobility
The external pressure not only influences the fluorescent emission properties of COTh, but also affects its performance on hole transport. Two key factors, transfer integral (V) and charged reorganization energy (λcharge), affecting the hole mobility of COTh were calculated. V represents the degree of electronic coupling between the neighbouring COTh molecules and is closely related to their relative positions. V is molecular packing dependent and is positively correlated to the hole mobility. For each COTh crystal, 14 pairwise neighbouring COTh molecules with relatively close distances were extracted to calculate V (Fig. 3). It is obvious that the V of COTh along all pathways increase upon compression (Fig. 6a and Table S11, ESI†), on account of the reduction of the intermolecular distances and the enhancement of intermolecular interactions of COTh dimers (Fig. 3 and Table S4, ESI†). It needs to be mentioned that the V of two pathways from central COTh to its two neighbours (labelled with the same colors as in Fig. 3) are the same, therefore, the transport pathways along the seven pairs of COTh dimers 1–7 were equivalent to those of 1′–7′ dimers, see Fig. 6a. It is obvious that V of COTh along pathways 1 and 1′ were larger than others (Fig. 6a), due to the shortest intermolecular distances (Table S4, ESI†). At the same time, the V along pathways of 1 and 1′ were the most sensitive to external pressures, and the corresponding V increased from 41.1 to 70.4 meV with pressure increasing from 0 to 4.86 GPa (Fig. 6a and Table S11, ESI†).Besides V, λcharge associated with the geometric change from neutral to cationic states is the other important parameter influencing the hole transport process. It is found that λcharge is in the range of 250–330 meV (Table S12, ESI†). From 0 to 4.86 GPa, λcharge reduced by about 60 meV (Fig. 6b and Table S12, ESI†), which indicates the suppression of the structural deformations between neutral states and the cationic states upon compression. The increase of V and the decrease of λcharge were both beneficial to the hole transport mobility. As shown in Fig. 6c, the mobility of COTh along a, b and c-directions was increased with pressure, with the average hole mobility significantly increasing about one order of magnitude from 0.39 to 3.00 cm2 V−1 s−1. The hole mobility along the a-axis is lower than that in both b and c directions, reflecting the anisotropic hole transport properties of COTh crystals (Fig. 6c). The anisotropy of hole mobility in the aob, boc and aoc planes were also characterized (Fig. 6d–f), and it was found that the hole mobility of COTh in the boc plane is less anisotropic, and the hole mobilities in aob and aoc planes are more anisotropic. Furthermore, the hole mobilities of COTh in three different planes are all enhanced with pressure. Therefore, the compression is beneficial for the improvement of the hole transport properties of the COTh crystal.
4. Conclusions
In conclusion, we used a thermal vibration correlation function formalism coupled quantum mechanism/molecular mechanism and full quantum charge transfer rate theory to explore the pressure effect on the optical properties and hole mobility of COTh crystals. Our results revealed that the volume of the unit cell decreases and the corresponding intermolecular distances are shortened upon compression, which induced the enhancement of intramolecular interactions. The COTh exhibits blue-shifted emission spectra upon compression due to the more distorted intramolecular configuration. The FQE of COTh crystals decreases sharply in the low-pressure region (<4.38 GPa) and then slightly increases when the extra pressure is beyond 4.38 GPa, which is roughly consistent with fluorescence quenching behavior in the experiment. At the initial pressure range (0–0.36 GPa), the slight decrease in FQE with pressure is attributed to the increase of keet which is larger than both the reduction of kic and the increase of kr. The decrease of kic is due to the reduction in reorganization energy induced by the limitation of the low-frequency flipping vibrations of four thiophene rings and the high-frequency stretching vibrations of central cyclooctatetraene. With further compression (0.36–4.38 GPa), the keet is always two or three orders of magnitude larger than kic and kr. Thus, the variation of keet determines the change of FQE. The surge of keet results in a sharp drop in FQE in the pressure range of 0.36 to 4.38 GPa. The increase in keet is attributed to the simultaneous increase of exciton coupling and spectra overlap. Due to the reduction of keet in the high pressure region (>4.38 GPa), the FQE of COTh crystals increases slightly. Fortunately, the pressurization has a positive effect on the charge transport properties of the COTh crystal. We predict that, upon compression, the hole mobility of COTh increases by nearly an order of magnitude, from 0.39 to 3.00 cm2 V−1 s−1. The increase of hole mobility is the combined contribution of an increase in the transfer integral and decrease in the charged reorganization energy. In addition, the charge transport of COTh is anisotropic. The hole mobility of COTh along the a-direction is significantly less than that along the b- and c-directions, which makes the hole mobilities in the aob and aoc planes more anisotropic. Our research provides theoretical support for understanding the influence of pressure on the fluorescent and charge transport properties. Pressurization can optimize the charge transport of organic semiconductors, but their optical properties may be inhibited and the high-performance organic materials with the combination of excellent mobility and optical properties are far from being rationally designed. The construction of multicomponent compounds, such as heterojunctions and cocrystals, may be a promising strategy for improving both the transport and luminescence properties of organic semiconductors.Conflicts of interest
The authors declare that they have no conflicts of interest.Acknowledgements
We are thankful for the financial support from the National Natural Science Foundation of China (Grants 22173006, Grants 21803007), Beijing Natural Science Foundation Municipality (Grants 2222027) and the Open Fund of Guangdong Provincial Key Laboratory of Luminescence from Molecular Aggregates (South China University of Technology, 2019B030301003).References
- C. W. Tang and S. A. VanSlyke, Appl. Phys. Lett., 1987, 51, 913–915 CrossRef.
- S. Reineke, F. Lindner, G. Schwartz, N. Seidler, K. Walzer, B. Lüssem and K. Leo, Nature, 2009, 459, 234–238 CrossRef PubMed.
- A. Dadvand, A. Moiseev, K. Sawabe, E. Sun, B. Djukic, I. Chung, T. Takenobu, F. Rosei and D. Perepichka, Angew. Chem., Int. Ed., 2012, 51, 3837–3841 CrossRef PubMed.
- H. Ju, K. Wang, J. Zhang, H. Geng, Z. Liu, G. Zhang, Y. Zhao and D. Zhang, Chem. Mater., 2017, 29, 3580–3588 CrossRef.
- P. Heremans, A. K. Tripathi, A. de Jamblinne de Meux, E. C. P. Smits, B. Hou, G. Pourtois and G. H. Gelinck, Adv. Mater., 2016, 28, 4266–4282 CrossRef PubMed.
- J. Zhang, B. He, Y. Hu, P. Alam, H. Zhang, J. W. Y. Lam and B. Z. Tang, Adv. Mater., 2021, 33, 2008071 CrossRef PubMed.
- D. J. Lipomi, H. Chong, M. Vosgueritchian, J. Mei and Z. Bao, Sol. Energy Mater. Sol. Cells, 2012, 107, 355–365 CrossRef.
- Y. Gu, K. Wang, Y. Dai, G. Xiao, Y. Ma, Y. Qiao and B. Zou, J. Phys. Chem. Lett., 2017, 8, 4191–4196 CrossRef PubMed.
- K. Takashi, I. Hiroo and M. Shigeru, Bull. Chem. Soc. Jpn., 1967, 40, 1055–1058 CrossRef.
- Y. Yang, Y. Gu, Z. Ma, Y. Zhang, W. Xu, L. Xu, K. Wang, B. Zou and H. Wang, Dyes Pigm., 2021, 184, 108803 CrossRef.
- Y. Gu, N. Li, G. Shao, K. Wang and B. Zou, J. Phys. Chem. Lett., 2020, 11, 678–682 CrossRef.
- X. Fan, J. Sun, F. Wang, Z. Chu, P. Wang, Y. Dong, R. Hu, B. Z. Tang and D. Zou, Chem. Commun., 2008, 2989–2991 RSC.
- C. Zhai, X. Yin, S. Niu, M. Yao, S. Hu, J. Dong, Y. Shang, Z. Wang, Q. Li, B. Sundqvist and B. Liu, Nat. Commun., 2021, 12, 4084 CrossRef PubMed.
- K. Y. Chernichenko, V. V. Sumerin, R. V. Shpanchenko, E. S. Balenkova and V. G. Nenajdenko, Angew. Chem., Int. Ed., 2006, 45, 7367–7370 CrossRef.
- X.-D. Tang, Y. Liao, H.-Z. Gao, Y. Geng and Z.-M. Su, J. Mater. Chem., 2012, 22, 6907–6918 RSC.
- Z. Zhao, X. Zheng, L. Du, Y. Xiong, W. He, X. Gao, C. Li, Y. Liu, B. Xu, J. Zhang, F. Song, Y. Yu, X. Zhao, Y. Cai, X. He, R. T. K. Kwok, J. W. Y. Lam, X. Huang, D. Lee Phillips, H. Wang and B. Z. Tang, Nat. Commun., 2019, 10, 2952 CrossRef PubMed.
- K. Chaitanya and X.-H. Ju, J. Mater. Res., 2016, 31, 3731–3744 CrossRef.
- M. A. Reyes-Martinez, A. J. Crosby and A. L. Briseno, Nat. Commun., 2015, 6, 6948 CrossRef PubMed.
- M. Matta, M. J. Pereira, S. M. Gali, D. Thuau, Y. Olivier, A. Briseno, I. Dufour, C. Ayela, G. Wantz and L. Muccioli, Mater. Horiz., 2018, 5, 41–50 RSC.
- M. T. Ruggiero, S. Ciuchi, S. Fratini and G. D’Avino, J. Phys. Chem. C, 2019, 123, 15897–15907 CrossRef.
- J. Elsner, S. Giannini and J. Blumberger, J. Phys. Chem. Lett., 2021, 12, 5857–5863 CrossRef PubMed.
- A. Landi, A. Peluso and A. Troisi, Adv. Mater., 2021, 33, 2008049 CrossRef.
- H. H. Choi, H. T. Yi, J. Tsurumi, J. J. Kim, A. L. Briseno, S. Watanabe, J. Takeya, K. Cho and V. Podzorov, Adv. Sci., 2020, 7, 1901824 CrossRef.
- Y. Sun, H. Geng, Q. Peng and Z. Shuai, ChemPhysChem, 2020, 21, 952–957 CrossRef PubMed.
- T. Zhang, W. Shi, D. Wang, S. Zhuo, Q. Peng and Z. Shuai, J. Mater. Chem. C, 2019, 7, 1388 RSC.
- L. J. Wang, Q. K. Li and Z. Shuai, J. Chem. Phys., 2008, 128, 194706 CrossRef CAS PubMed.
- X. Zheng, H. Geng, Y. Yi, Q. Li, Y. Jiang, D. Wang and Z. Shuai, Adv. Funct. Mater., 2014, 24, 5531–5540 CrossRef.
- X. Lu, Y. Sun, Z. Zhang, Z. Shuai and W. Hu, Chin. Chem. Lett., 2021, 32, 1233–1236 CrossRef.
- Y. Zeng, Y. Niu, Q. Peng and X. Zheng, J. Phys. Chem. A, 2022, 126, 4147–4155 CrossRef.
- J. Zhao, Y. Zeng and X. Zheng, Chem. Mater., 2022, 34, 10711–10720 CrossRef.
- X. Zheng, Q. Peng, L. Zhu, Y. Xie, X. Huang and Z. Shuai, Nanoscale, 2016, 8, 15173–15180 RSC.
- X. Zheng, D. Wang, W. Xu, S. Cao, Q. Peng and B. Z. Tang, Mater. Horiz., 2019, 6, 2016–2023 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. D. Boese and J. M. L. Martin, J. Phys. Chem., 2004, 121, 3405–3416 Search PubMed.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- S. H. Lin, C. H. Chang, K. K. Liang, R. Chang, Y. J. Shiu, J. M. Zhang, T. S. Yang, M. Hayashi and F. C. Hsu, Advances in Chemical Physics, 2002, pp. 1–88 DOI:10.1002/0471264318.ch1.
- Q. Peng, Y. Yi, Z. Shuai and J. Shao, J. Chem. Phys., 2007, 126, 114302 CrossRef.
- Y. Niu, Q. Peng and Z. Shuai, Sci. China, Ser. B: Chem., 2008, 51, 1153–1158 CrossRef.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef PubMed.
- Q. Peng, Y. Niu, Q. Shi, X. Gao and Z. Shuai, J. Chem. Theory Comput., 2013, 9, 1132–1143 CrossRef PubMed.
- Z. Shuai and Q. Peng, Phys. Rep., 2014, 537, 123–156 CrossRef.
- L. Wu, C. Huang, B. P. Emery, A. C. Sedgwick, S. D. Bull, X.-P. He, H. Tian, J. Yoon, J. L. Sessler and T. D. James, Chem. Soc. Rev., 2020, 49, 5110–5139 RSC.
- L.-Y. Hsu, W. Ding and G. C. Schatz, J. Phys. Chem. Lett., 2017, 8, 2357–2367 CrossRef CAS.
- G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87 CrossRef CAS PubMed.
- Y. Niu, W. Li, Q. Peng, H. Geng, Y. Yi, L. Wang, G. Nan, D. Wang and Z. Shuai, Mol. Phys., 2018, 116, 1078–1090 CrossRef CAS.
- O. Kwon, V. Coropceanu, N. E. Gruhn, J. C. Durivage, J. G. Laquindanum, H. E. Katz, J. Cornil and J. L. Brédas, J. Chem. Phys., 2004, 120, 8186–8194 CrossRef CAS.
- R. S. Sánchez-Carrera, V. Coropceanu, D. A. da Silva Filho, R. Friedlein, W. Osikowicz, R. Murdey, C. Suess, W. R. Salaneck and J.-L. Brédas, J. Phys. Chem. B, 2006, 110, 18904–18911 CrossRef.
- M. Malagoli and J. L. Brédas, Chem. Phys. Lett., 2000, 327, 13–17 CrossRef CAS.
- V. Lemaur, D. A. da Silva Filho, V. Coropceanu, M. Lehmann, Y. Geerts, J. Piris, M. G. Debije, A. M. van de Craats, K. Senthilkumar, L. D. A. Siebbeles, J. M. Warman, J.-L. Brédas and J. Cornil, J. Am. Chem. Soc., 2004, 126, 3271–3279 CrossRef CAS.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef PubMed.
- G. Nan, X. Yang, L. Wang, Z. Shuai and Y. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115203 CrossRef.
- H. Geng, Q. Peng, L. Wang, H. Li, Y. Liao, Z. Ma and Z. Shuai, Adv. Mater., 2012, 24, 3568–3572 CrossRef.
- C. Lefebvre, G. Rubez, H. Khartabil, J.-C. Boisson, J. Contreras-García and E. Hénon, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936 RSC.
- T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539–555 CrossRef.
- C.-P. Hsu, Z.-Q. You and H.-C. Chen, J. Phys. Chem. C, 2008, 112, 1204–1212 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03852a |
| This journal is © the Owner Societies 2024 |