 Open Access Article
Open Access ArticleNature of ultrafast dynamics in the lowest-lying singlet excited state of [Ru(bpy)3]2+†
Chenyu
Zeng
,
Yaqi
Li
,
Hangjing
Zheng
,
Mingxing
Ren
,
Wei
Wu
and
Zhenhua
Chen
 *
*
State Key Laboratory of Physical Chemistry of Solid Surfaces, Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen, Fujian 361005, China. E-mail: zhhchen@xmu.edu.cn
First published on 2nd February 2024
Abstract
This work presents mechanisms to rationalize the nature of ultrafast photochemical and photophysical processes on the first singlet metal–ligand charge transfer state (1MLCT1) of the [Ru(bpy)3]2+ complex. The 1MLCT1 state is the lowest-lying singlet excited state and the most important intermediate in the early evolution of photoexcited [Ru(bpy)3]2+*. The results obtained from simple but interpretable theoretical models show that the 1MLCT1 state can be very quickly formed via both direct photo-excitation and internal conversions and then can efficiently relax to its equilibrium geometry in ca. 5 fs. The interligand electron transfer (ILET) on the potential energy surface of the 1MLCT1 state is also extremely fast, with a rate constant of ca. 1.38 × 1013 s−1. The ultrafast ILET implies that the excited electron can dynamically delocalize over the three bpy ligands, despite the fact that the excited electron may be localized on either one of the three ligands at the equilibrium geometries of the three symmetric equivalent minima. Since rapid ILET essentially suggests delocalization, the long-standing controversy in inorganic photophysics—whether the excited electron is localized or delocalized—may therefore be calmed down to some extent.
Introduction
In light harvesting, the photosensitizer is crucially important for transferring the photo-excited electrons to the catalytic center.1–3 The rapidly growing development of homogeneous photocatalysis mainly relies on the application of photosensitizers, such as organic dyes,4,5 and transition metal complexes.6,7 These compounds have attracted widespread attention for their high activity in UV-visible driven photocatalytic reactions, because their excited states are long-lived and effective in energy.8–10 Ru(II) polypyridine complexes are currently one of the most investigated compounds in coordination chemistry, due to their excellent properties. Moreover, their ligands are modifiable, allowing for the adjustment of the properties of both the ground and excited states.11 Among these compounds, [Ru(bpy)3]2+ is a prototype and has been widely used in many fields, i.e. photovoltaics, photocatalysis and photodynamic therapy, because of its unique photoreactivity.12–15 After the initial adsorption of a photon of visible light, the molecule is excited to a metal–ligand charge transfer (MLCT) state, in which one electron is excited from one d orbital of the central metal to one ligand's π* orbital compared to the ground state.16,17 The photoexcited [Ru(bpy)3]2+* in the MLCT states may act as both a better oxidant and a better reductant than in its ground state.11 These MLCT states can participate in intermolecular electron and energy transfer reactions, and the released electron and energy can be captured by acceptors for further reactions.18 Recently, the electronic structure of the excited states of [Ru(bpy)3]2+ is still a hot topic.19–22In particular, whether the excited electron in the lowest MLCT state of the system is localized on a single ligand or delocalized on multiple ligands is still a controversy, and it is relevant to interligand electron transfer (ILET). Moreover, because this issue may determine the intermolecular electron transfer rate,18,23,24 when the [Ru(bpy)3]2+ complex interacts with acceptors, the ILET also plays an important role in this complex.23 Solvent dependence of MLCT transition25,26 and Stark effect spectra27 investigations have shown that the initially prepared 1MLCT state is highly dipolar,27 which implies that the Franck–Condon (FC) state is localized.25 The time-resolved resonance Raman spectroscopy results imply that the excited electron of the MLCT state is localized on a single bipyridine ligand.26,28–30 X-ray absorption spectra further supported this viewpoint by analyzing the correlation between the electronic structure and the geometric distortion of the MLCT state.31 Moreover, transient absorption anisotropy spectra suggested that the electron is localized immediately after excitation.23 However, femtosecond time-resolved absorption anisotropy measurements imply that the initial photoinduced MLCT state is delocalized, and followed by localization.32 Furthermore, other time-resolved spectroscopy experiments and time-dependent density functional theory (TDDFT) computations suggest that the excited electron is delocalized over the three ligands, and therefore there is no ILET.33–37 Besides, several femtosecond time-resolved spectroscopy measurements reveal that the lifetime of the 1MLCT state of the [Ru(bpy)3]2+ complex is extremely short (about 40 fs),38,39 and the intersystem crossing (ISC) occurs in only about 30 fs with a quantum yield very much close to unity.32,34,39–43 The aforementioned experimental and theoretical works are quite extensive and in-depth; nevertheless, there is still no clear consensus on whether the excited electron in this system is localized or delocalized. By exploring the nature of the electronic structure of the excited states of the system, we aim to provide a comprehensive explanation for the formation and the ILET of the lowest-lying 1MLCT1 excited state.
Results and discussion
The theoretical study of this work focuses on the formation and transformation processes of the lowest-lying 1MLCT1 state for the [Ru(bpy)3]2+ complex. In photochemical reactions, the lowest-lying singlet excited state in general may form either by direct excitation or by internal conversion (IC). The rate of direct excitation is very fast and often on a timescale of several femtoseconds. Meanwhile, the rate of IC is relatively slower and might be affected by various factors such as intersections of potential energy surfaces (PESs) and the solvent effect, etc. Fig. 1 shows the state correlation diagram for the three lowest-lying 1MLCT states. Notably, the intersection of energy levels of these states indicates that there is a three-state conical intersection (CI) somewhere along the continuous changing of the molecular geometry from the ground state equilibrium configuration to the minimum energy geometry of the 1MLCT1 state with D3 symmetry constraint. Since the intersection geometry is close to the ground state equilibrium one, the 1MLCT1 state has close energies at these geometries. In general, when there is a three-state CI, there will be a two-state CI in its branching space.44–46 Based on Longuet-Higgins’ geometric phase-change rule,47 the phase analysis of the three low-lying 1MLCT states was carried out around the minimum and transition state geometries of the 1MLCT1 state, see Fig. S3 in the ESI† for more details. It demonstrates that the 1MLCT1 state itself has no intersection with the other two states, but there is a two-state CI between the 1MLCT2 and 1MLCT3 states, and the intersection geometry is close to the just mentioned D3 constrained geometry. Since a CI and its near region is usually a very efficient path for a non-radiative transition, especially when the CI is geometrically close to the FC point, the rate of IC can be quite fast. This is indeed the case here for low-lying 1MLCT states of [Ru(bpy)3]2+. It is worth mentioning here that it cannot be directly deduced from Fig. 1 whether the initially excited 1MLCT state is localized or delocalized. However, one can infer that these 1MLCT states with close energies may convert into each other. Therefore, according to Kasha's rule, these 1MLCT states can quickly evolve to the S1 state. Naturally after that, the vibrational relaxation of the S1 state on its potential energy surface can occur, no matter what geometries the S1 state is in, whether it is the FC point or the D3 or other low-symmetry geometries in close proximity to it, regardless of what kinds of electronic structure characteristics the S1 state has at these geometries, i.e. whether the excited electron is localized or delocalized. Therefore, one may infer that the system would quickly transfer to the lowest-lying 1MLCT1 state even if it is initially excited to other 1MLCTn states.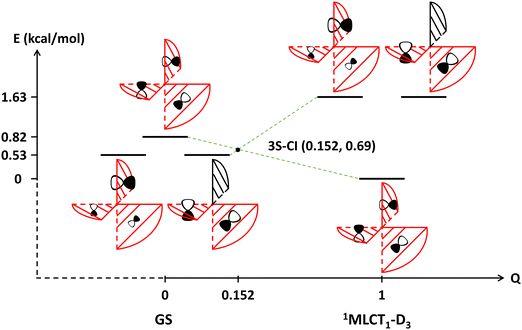 | ||
| Fig. 1 The state correlation diagram for the first three lowest-lying 1MLCT states between and at the ground state equilibrium geometry and the D3 symmetry constrained minimum energy geometry of the 1MLCT1 state for the [Ru(bpy)3]2+ complex. The reaction coordinates of the starting and ending points, at which the geometries are labelled beneath the coordinates, are set as 0 and 1, respectively. The coordinates of other points are obtained by a linear combination of the two terminal points. The energies marked on the vertical axis are presented relative to the energy of the 1MLCT1 state (−1579.36971998 Eh) at the D3 constrained geometry. All energies were calculated by the TD-PBE0 method. A schematic illustration of the adiabatic states is given in Fig. S2 (ESI†). | ||
Now, we estimate how much time is needed for the 1MLCT1 state to reach its equilibrium geometry after the initial excitation by means of a vibrational relaxation. In general, there are so many paths for the vibrational relaxation that it is difficult to accurately calculate the time required. As a rough approximation, the vibrational relaxation in this work is defined as the relaxation of the 1MLCT1 state from the FC point to the equilibrium geometry along the most relevant vibrational mode. This is fundamentally different from the vibrational energy relaxation process in which the population distribution of molecules in quantum states of high energy level returns to its thermal equilibrium status, i.e. the Maxwell–Boltzmann distribution. The initially formed 1MLCT1 state, whether by direct photo-excitation or by IC from other states, is in higher vibrational states and not at its equilibrium geometry, and so it may relax to the low-lying vibrational states at its equilibrium geometry. The time of vibrational energy relaxation might be influenced by several factors such as vibrational frequency, geometric distortion, solvent effect, etc. Meanwhile, for the vibrational relaxation from the FC point to the 1MLCT1 state equilibrium geometry, the main change in the molecular geometry is observed on the bpy ligand where the excited electron resides, as shown in Fig. 2. The largest change comes from the bridged C–C bond length, by ca. 0.051 Å, which is further used as a measure of the vibrational relaxation distance. From Fig. 2, one may also observe that the corresponding Ru–N bond lengths decrease by 0.013 Å after the electron transfer, possibly due to the enhancement of electrostatic attraction between the central metal and the ligand. Presumably, this would further affect the hybridization of the central-metal orbitals on the two Ru–N bonds along the lines and result in a similar degree of elongation in the corresponding bond length. The ground state and the 1MLCT1 state are so close in their equilibrium geometries that the latter can be reached in an extremely short time period of about 5 fs only via the relaxation on the most relevant vibrational mode; see ESI† for deduction details. This is also consistent with the fact that the vibrational relaxation from the FC point to the equilibrium geometry just comprises one-fourth of the full vibration period, about 20 fs estimated from the vibrational frequency, 4.98 × 1013 s−1. We shall note again that the vibrational relaxation in this work is not the full vibrational energy relaxation which is a more commonly used concept. The full vibrational energy relaxation, including the thermal equilibrium of the MLCT state and the response of the solvent, was found to need a much longer time.48 The vibrational relaxation time is even shorter when the initial 1MLCT1 state is obtained from an IC process, considering that the three-state CI point is closer to the 1MLCT1 state equilibrium geometry than the FC point. Thus, the initially formed 1MLCT1 state can reach the equilibrium geometry rapidly through intramolecular vibration relaxation, whether it is obtained by direct excitation or by IC. Apart from the close proximity of the 1MLCT1 state equilibrium geometry to the FC point, the fast nuclear vibration on the relevant mode is another factor that accounts for the fast relaxation of the 1MLCT1 state. Furthermore, since the 1MLCT1 state has three equivalent minima that are symmetrically distributed around the FC point, the vibrational relaxations to these three minima can occur equally along the three directions and shall take the same amount of time. These theoretical results may provide a reasonable explanation for the long-standing controversy in inorganic photophysics regarding whether the excited electron in the initial 1MLCT state is localized23,26,28–32 or delocalized,32–37 since a slight geometric distortion at the FC point may lead to immediate localization of the excited electron on one bpy ligand.
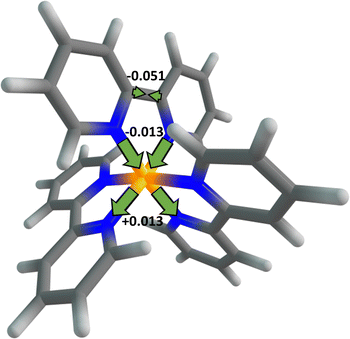 | ||
| Fig. 2 Schematic representation of the distortions of the main geometric parameters upon the vibrational relaxation of the 1MLCT1 state. The values are given in Å. | ||
In the evolution of the 1MLCT1 state, there are several competitive reaction pathways, including ILET, ISC and fluorescence. The ILET reaction occurs remaining on the PES of the 1MLCT1 state. To analyze whether the ILET reaction is adiabatic or nonadiabatic, a diabatic representation is applied. The diabatic wave functions are constructed from localized orbitals obtained from a unitary transformation of the CASSCF orbitals by using a similar procedure of Hiberty and coworkers.49 The obtained diabatic states exhibit the properties that the excited electron is localized on one ligand, and their electronic structure characteristics are essentially preserved during the whole ILET process. A merit of using the diabatic representation is that the classical valence bond (VB) interpretation,50 in particular Shaik's diagram methods,51–53 might be adopted because for electron transfer, VB structures and diabatic states are highly relevant even though not the same.54,55 Although the ligands are close in space, we found that the ILET reaction has a significant probability, about 84% from the Landau–Zener formula,56,57 to occur in a nonadiabatic manner, see ESI† for deduction details. The primary reason for this is that the electronic coupling is small, ca. 0.54 kcal mol−1, reflecting that the interaction between the reactant and the product diabatic states (Φda and Φdb in Fig. 3) is weak. Because π* molecular orbitals on two ligands are about perpendicular to each other, the electronic coupling is not originated from the direct interaction between the ligand orbitals but mainly from the metal–ligand interaction since a direct exchange interaction is quite operative for the metal center with a hole. It can also be seen from Fig. S4 (ESI†) that the localized ligand orbitals πla*, πlb* and πlc* in fact have a nonnegligible component of d orbitals of the center metal. In terms of the nonadiabaticity of the ILET reaction, the coupling is quite weak. However, its effect on the ILET rate might be significant since it can reduce further the reaction barrier to a quite small value.
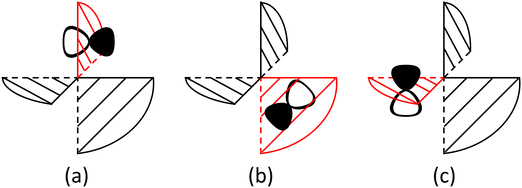 | ||
Fig. 3 Diagrammatic representation of the diabatic MLCT states. The excited electron is localized on the ligand colored as red. The localized π* orbitals, namely πla*, πlb* and πlc*, are respectively represented by the three p-type orbitals, each of which is perpendicular to its ligand plane. These orbitals are drawn in Fig. S4 (ESI†). Each sub-diagram denominates one diabatic state, namely that (a) 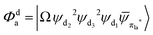 , (b) , (b) 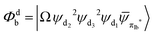 and (c) and (c) 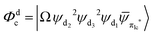 , where Ω denotes the remaining inner double occupied orbitals. Each diabatic state has a positive phase as the black part of the p-type orbital in each diagramma is in the same direction as the positive axis parallel to it. , where Ω denotes the remaining inner double occupied orbitals. Each diabatic state has a positive phase as the black part of the p-type orbital in each diagramma is in the same direction as the positive axis parallel to it. | ||
The ILET rate constant, ket, is calculated from the classical transition state formalism,57–60
ket = υeffκel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔG*/kBT), exp(−ΔG*/kBT), | (1) |
Apart from ILET, the evolution of the 1MLCT1 state also involves other processes, such as ISC, fluorescence emission and intermolecular electron transfer, etc. Most of these processes can cause the quenching of the 1MLCT1 state. Although the fluorescence emission is symmetry allowed, its transition probability is quite small due to a small transition dipole moment. In several elaborately designed experimental works,32,34,41,61 it was observed that the ISC process41 with a time constant of about 30 fs is the most competitive to ILET, and the transformation to the lowest-lying 3MLCT state is completed within a time scale of 300 fs.32,34 Because of the ultrafast ISC together with the long lifetime of the 3MLCT state, [Ru(bpy)3]2+ and its derivative complexes have wide applications in photoelectricity and photocatalysis.62,63 Meanwhile, the mechanisms of these processes have not been fully exploited and thus thorough investigations and analyses remain necessary in the future.
Conclusions
In summary, this work explains the mechanisms of the rapid formation and transformation of the 1MLCT1 state during ultrafast evolution processes of photo-excited [Ru(bpy)3]2+*, by using theoretical computations and wave function analysis. There are several findings that may have theoretical significance. Firstly, the PESs of the low-lying 1MLCT states have a variety of inter-crossings, such as the three-state and two-state CIs, around the ground state equilibrium geometry. Therefore, according to Kasha's rule, the high-lying 1MLCTn states can quickly transfer to the lowest-lying 1MLCT1 state via IC processes. Secondly, the initial 1MLCT1 state, whether it is formed by direct photo-excitation or by ICs, can reach the three minima of the 1MLCT1 state rapidly by intramolecular vibrational relaxation. Thirdly, the ILET of the 1MLCT1 state is predominantly nonadiabatic, and it is ultrafast. These theoretical discoveries naturally lead us to an alternative interpretation that the excited electron is dynamically delocalized over all three ligands. This viewpoint of dynamical delocalization may calm down to a certain extent the long-standing controversy over whether the excited electron is localized or delocalized. In brief, the 1MLCT1 state plays a vital role as an intermediate state in the early evolution of the photo-excited [Ru(bpy)3]2+*. From the formation to the quenching of the 1MLCT1 state, various interesting photochemical and photophysical processes can take place on its PES. Considering the explicit and intuitive explanations for several unusual and intriguing experimental phenomena procured by these theoretical explorations, we expect that this work would provide some valuable information for future experimental studies, such as spectral analysis and measurements of quantum yield.Computational methods
All geometry optimizations were performed using the PBE0 hybrid functional64 with D3 dispersion correction65 and def2-TZVP(Ru), 6-31G*(C/H/N) basis sets.66–69 The effective core potential (ECP) used by the def2-TZVP basis sets for Ru element takes relativistic effects into account. Frequency calculations were carried out at the same theoretical level. In addition, thermodynamic corrections were obtained from TDDFT frequency calculations.To facilitate the analysis of the wave functions, the complete active space self-consistent field (CASSCF) and the restricted active space configuration interaction (RASCI) calculations were performed.70,71 The CASSCF computation involves a minimum active space denoted as CASSCF(6,6) of distributing six active electrons on the six active orbitals, including three metal central dπ and three ligand π* orbitals. In RASCI, the active orbitals are partitioned into three sets, viz. in RAS1 orbitals are doubly occupied except for a maximum number of holes; in RAS2 orbitals can take all possible occupations; and in RAS3 orbitals are unoccupied except for a maximum number of electrons. Here, the RAS2 orbital subspace consists of all six active orbitals in CASSCF(6,6), while the RAS1 and RAS3 subspaces include three ligand π orbitals and two metal dσ* orbitals, respectively. Adding these subspaces together gives RASCI(12,11) of distributing twelve electrons in eleven orbitals. The maximum values of holes and electrons, respectively, in RAS1 and RAS3 were set to 2. These active orbitals are given in Fig. S5 (ESI†). All these orbitals are optimized with state-average (SA) CASSCF(6,6), involving ten roots, all of which are 1MLCT states except for the ground state. Relative energies of the first three 1MLCT1–3 states obtained at the RASCI(12,11) and CASSCF(12,11) levels are presented in Table S6 of the ESI.† The results show that RASCI is an acceptable approximation to CASSCF, especially when the latter is difficult to converge in the orbital optimization.
To incorporate the dynamical electronic correlation, the multi-state second-order multiconfigurational perturbation theory calculations based on the SA-CASSCF(6,6) and the RASCI(12,11) reference functions, namely CASPT272,73 and RASPT2,74,75 respectively, were performed. Table S6 of the ESI† reports also CASPT2 computations with SA-CASSCF(12,11) wave functions as a reference. The results show that the latter CASPT2 predicts the same energetic orders as RASPT2 for 1MLCT states at the ground state geometry.
For single-point energy calculations, several methods were used, including TDDFT, CASSCF, CASPT2, RASCI, and RASPT2. In addition, slightly larger basis sets, namely def2-TZVP(Ru), 6-311G*(C/N) and 6-31G**(H),68,69 combined with Cholesky decomposition76 with a threshold value of 10−8, were used. The results of TDDFT with the Douglas–Kroll–Hess approach77,78 shown that the performance of the ECP basis set is consistent with that of Sapporo-DKH3-TZP-2012(Ru)79 all-electron basis sets.80 All CASPT2 and RASPT2 calculations simultaneously involve four states, i.e. the ground state and the first three 1MLCT states, and used an imaginary level-shift81 of 0.1 Eh and an ionization potential-electron affinity (IPEA)82 of 1 Eh.
All TDDFT calculations were carried out with the Gaussian 16 package,83 while multiconfigurational calculations were performed with the Open-Molcas package.84
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has been supported by the Natural Science Foundation of China (no. 22173073).References
- K. E. Dalle, J. Warnan, J. J. Leung, B. Reuillard, I. S. Karmel and E. Reisner, Electro- and Solar-Driven Fuel Synthesis with First Row Transition Metal Complexes, Chem. Rev., 2019, 119, 2752–2875 CrossRef CAS PubMed.
- S. H. Lee, D. S. Choi, S. K. Kuk and C. B. Park, Photobiocatalysis: Activating Redox Enzymes by Direct or Indirect Transfer of Photoinduced Electrons, Angew. Chem., Int. Ed., 2018, 57, 7958–7985 CrossRef CAS PubMed.
- M. Nippe, R. S. Khnayzer, J. A. Panetier, D. Z. Zee, B. S. Olaiya, M. Head-Gordon, C. J. Chang, F. N. Castellano and J. R. Long, Catalytic proton reduction with transition metal complexes of the redox-active ligand bpy2PYMe, Chem. Sci., 2013, 4, 3934–3945 RSC.
- L. L. Li and E. W. Diau, Porphyrin-sensitized solar cells, Chem. Soc. Rev., 2013, 42, 291–304 RSC.
- N. A. Romero and D. A. Nicewicz, Organic Photoredox Catalysis, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS PubMed.
- C. K. Prier, D. A. Rankic and D. W. MacMillan, Visible light photoredox catalysis with transition metal complexes: applications in organic synthesis, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- L. Schmid, F. Glaser, R. Schaer and O. S. Wenger, High Triplet Energy Iridium(III) Isocyanoborato Complex for Photochemical Upconversion, Photoredox and Energy Transfer Catalysis, J. Am. Chem. Soc., 2022, 144, 963–976 CrossRef CAS PubMed.
- D. M. Arias-Rotondo and J. K. McCusker, The photophysics of photoredox catalysis: a roadmap for catalyst design, Chem. Soc. Rev., 2016, 45, 5803–5820 RSC.
- X. Zhao, J. Liu, J. Fan, H. Chao and X. Peng, Recent progress in photosensitizers for overcoming the challenges of photodynamic therapy: from molecular design to application, Chem. Soc. Rev., 2021, 50, 4185–4219 RSC.
- L. Li, S. Zhang, L. Xu, J. Wang, L.-X. Shi, Z.-N. Chen, M. Hong and J. Luo, Effective visible-light driven CO2 photoreduction via a promising bifunctional iridium coordination polymer, Chem. Sci., 2014, 5, 3808–3813 RSC.
- D. M. Arias-Rotondo, The fruit fly of photophysics, Nat. Chem., 2022, 14, 716 CrossRef CAS PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Dye-sensitized solar cells, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- T. P. Yoon, M. A. Ischay and J. Du, Visible light photocatalysis as a greener approach to photochemical synthesis, Nat. Chem., 2010, 2, 527–532 CrossRef CAS PubMed.
- T. R. Blum, Z. D. Miller, D. M. Bates, I. A. Guzei and T. P. Yoon, Enantioselective photochemistry through Lewis acid-catalyzed triplet energy transfer, Science, 2016, 354, 1391–1395 CrossRef CAS PubMed.
- F. Heinemann, J. Karges and G. Gasser, Critical Overview of the Use of Ru(II) Polypyridyl Complexes as Photosensitizers in One-Photon and Two-Photon Photodynamic Therapy, Acc. Chem. Res., 2017, 50, 2727–2736 CrossRef CAS PubMed.
- K. Kalyanasundaram, Photophysics, Photochemistry and Solar-Energy Conversion with Tris(Bipyridyl)Ruthenium(II) and Its Analogs, Coord. Chem. Rev., 1982, 46, 159–244 CrossRef CAS.
- A. J. Atkins and L. Gonzalez, Trajectory Surface-Hopping Dynamics Including Intersystem Crossing in [Ru(bpy)3]2+, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS PubMed.
- G. Alcover-Fortuny, J. Wu, R. Caballol and C. de Graaf, Quantum Chemical Study of the Interligand Electron Transfer in Ru Polypyridyl Complexes, J. Phys. Chem. A, 2018, 122, 1114–1123 CrossRef CAS PubMed.
- F. Alary, M. Boggio-Pasqua, J. L. Heully, C. J. Marsden and P. Vicendo, Theoretical characterization of the lowest triplet excited states of the tris-(1,4,5,8-tetraazaphenanthrene) ruthenium dication complex, Inorg. Chem., 2008, 47, 5259–5266 CrossRef CAS PubMed.
- E. Badaeva, V. V. Albert, S. Kilina, A. Koposov, M. Sykora and S. Tretiak, Effect of deprotonation on absorption and emission spectra of Ru(II)-bpy complexes functionalized with carboxyl groups, Phys. Chem. Chem. Phys., 2010, 12, 8902–8913 RSC.
- T. Sato, S. Nozawa, A. Tomita, M. Hoshino, S. Y. Koshihara, H. Fujii and S. Adachi, Coordination and Electronic Structure of Ruthenium(II)-tris-2,2'-bipyridine in the Triplet Metal-to-Ligand Charge-Transfer Excited State Observed by Picosecond Time-Resolved Ru K-Edge XAFS, J. Phys. Chem. C, 2012, 116, 14232–14236 CrossRef CAS.
- R. M. Jay, S. Eckert, B. E. Van Kuiken, M. Ochmann, M. Hantschmann, A. A. Cordones, H. Cho, K. Hong, R. Ma, J. H. Lee, G. L. Dakovski, J. J. Turner, M. P. Minitti, W. Quevedo, A. Pietzsch, M. Beye, T. K. Kim, R. W. Schoenlein, P. Wernet, A. Fohlisch and N. Huse, Following Metal-to-Ligand Charge-Transfer Dynamics with Ligand and Spin Specificity Using Femtosecond Resonant Inelastic X-ray Scattering at the Nitrogen K-Edge, J. Phys. Chem. Lett., 2021, 12, 6676–6683 CrossRef CAS PubMed.
- S. Wallin, J. Davidsson, J. Modin and L. Hammarstrom, Femtosecond transient absorption anisotropy study on [Ru(bpy)3]2+ and [Ru(bpy)(py)4]2+. Ultrafast interligand randomization of the MLCT state, J. Phys. Chem. A, 2005, 109, 4697–4704 CrossRef CAS PubMed.
- B. P. Rimgard, J. Fohlinger, J. Petersson, M. Lundberg, B. Zietz, A. M. Woys, S. A. Miller, M. R. Wasielewski and L. Hammarstrom, Ultrafast interligand electron transfer in cis-[Ru(4,4'-dicarboxylate-2,2 '-bipyridine)2(NCS)2]4− and implications for electron injection limitations in dye sensitized solar cells, Chem. Sci., 2018, 9, 7958–7967 RSC.
- P. Y. Chen and T. J. Meyer, Medium effects on charge transfer in metal complexes, Chem. Rev., 1998, 98, 1439–1477 CrossRef CAS PubMed.
- E. M. Kober, B. P. Sullivan and T. J. Meyer, Solvent Dependence of Metal-to-Ligand Charge-Transfer Transitions - Evidence for Initial Electron Localization in MLCT Excited-States of 2,2'-Bipyridine Complexes of Ruthenium(II) and Osmium(II), Inorg. Chem., 1984, 23, 2098–2104 CrossRef CAS.
- D. H. Oh and S. G. Boxer, Stark-effect spectra of [Ru(diimine)3]2+ complexes, J. Am. Chem. Soc., 1989, 111, 1130–1131 CrossRef CAS.
- P. G. Bradley, N. Kress, B. A. Hornberger, R. F. Dallinger and W. H. Woodruff, Vibrational Spectroscopy of the Electronically Excited-State.5. Time-Resolved Resonance Raman-Study of Tris(Bipyridine)Ruthenium(II) and Related Complexes - Definitive Evidence for the Localized MLCT State, J. Am. Chem. Soc., 1981, 103, 7441–7446 CrossRef CAS.
- M. Förster and R. E. Hester, Resonance Raman investigation of electronically excited Ru(bipyridine)32+ using a cw laser, Chem. Phys. Lett., 1981, 81, 42–47 CrossRef.
- W. K. Smothers and M. S. Wrighton, Raman-Spectroscopy of Electronic Excited Organometallic Complexes – a Comparison of the Metal to 2,2'-Bipyridine Charge-Transfer State of Fac-(2,2'-Bipyridine) Tricarbonylhalorhenium and Tris(2,2'-Bipyridine)Ruthenium(II), J. Am. Chem. Soc., 1983, 105, 1067–1069 CrossRef CAS.
- W. Gawelda, M. Johnson, F. M. F. de Groot, R. Abela, C. Bressler and M. Chergui, Electronic and Molecular Structure of Photoexcited [Ru(bpy)3]2+ Probed by Picosecond X-ray Absorption Spectroscopy, J. Am. Chem. Soc., 2006, 128, 5001–5009 CrossRef CAS PubMed.
- A. T. Yeh, C. V. Shank and J. K. McCusker, Ultrafast electron localization dynamics following photo-induced charge transfer, Science, 2000, 289, 935–938 CrossRef CAS PubMed.
- J. Ferguson and E. R. Krausz, The assignment of the luminescent states of Ru(bpy)32+. MCPL and time-resolved luminescence at 2.0 K, Chem. Phys. Lett., 1982, 93, 21–25 CrossRef CAS.
- N. H. Damrauer, G. Cerullo, A. Yeh, T. R. Boussie, C. V. Shank and J. K. McCusker, Femtosecond Dynamics of Excited-State Evolution in, Science, 1997, 275, 54–57 CrossRef CAS PubMed.
- J. K. McCusker, Femtosecond absorption spectroscopy of transition metal charge-transfer complexes, Acc. Chem. Res., 2003, 36, 876–887 CrossRef CAS PubMed.
- F. Alary, J.-L. Heully, L. Bijeire and P. Vicendo, Is the 3MLCT the only photoreactive state of polypyridyl complexes?, Inorg. Chem., 2007, 46, 3154–3165 CrossRef CAS PubMed.
- J. L. Heully, F. Alary and M. Boggio-Pasqua, Spin-orbit effects on the photophysical properties of Ru(bpy)32+, J. Chem. Phys., 2009, 131, 184308 CrossRef PubMed.
- A. C. Bhasikuttan, M. Suzuki, S. Nakashima and T. Okada, Ultrafast fluorescence detection in tris(2,2'-bipyridine)ruthenium(II) complex in solution: relaxation dynamics involving higher excited states, J. Am. Chem. Soc., 2002, 124, 8398–8405 CrossRef CAS PubMed.
- O. Bräm, F. Messina, A. M. El-Zohry, A. Cannizzo and M. Chergui, Polychromatic femtosecond fluorescence studies of metal-polypyridine complexes in solution, Chem. Phys., 2012, 393, 51–57 CrossRef.
- A. Cannizzo, F. van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Broadband femtosecond fluorescence spectroscopy of [Ru(bpy)3]2+, Angew. Chem., Int. Ed., 2006, 45, 3174–3176 CrossRef CAS PubMed.
- M. Chergui, Ultrafast photophysics of transition metal complexes, Acc. Chem. Res., 2015, 48, 801–808 CrossRef CAS PubMed.
- A. W. Adamson and J. N. Demas, New photosensitizer. Tris (2, 2'-bipyridine) ruthenium (II) chloride, J. Am. Chem. Soc., 1971, 93, 1800–1801 CrossRef CAS.
- J. Demas and D. Taylor, On the intersystem crossing yields in ruthenium (II) and osmium (II) photosensitizers, Inorg. Chem., 1979, 18, 3177–3179 CrossRef CAS.
- M. S. Schuurman and D. R. Yarkony, On the characterization of three-state conical intersections using a group homomorphism approach: the two-state degeneracy spaces, J. Phys. Chem. B, 2006, 110, 19031–19039 CrossRef CAS PubMed.
- J. D. Coe, M. T. Ong, B. G. Levine and T. J. Martinez, On the extent and connectivity of conical intersection seams and the effects of three-state intersections, J. Phys. Chem. A, 2008, 112, 12559–12567 CrossRef CAS PubMed.
- S. Matsika and D. R. Yarkony, Beyond two-state conical intersections. Three-state conical intersections in low symmetry molecules: the allyl radical, J. Am. Chem. Soc., 2003, 125, 10672–10676 CrossRef CAS PubMed.
- H. C. Longuet-Higgins, The intersection of potential energy surfaces in polyatomic molecules, Proc. Math. Phys. Eng. Sci., 1975, 344, 147–156 CAS.
- J. V. Caspar and T. J. Meyer, Photochemistry of Ru (bpy)32+. Solvent effects, J. Am. Chem. Soc., 1983, 105, 5583–5590 CrossRef CAS.
- P. Hiberty and C. Leforestier, Expansion of molecular orbital wave functions into valence bond wave functions. A simplified procedure, J. Am. Chem. Soc., 1978, 100, 2012–2017 CrossRef CAS.
- W. Wu, P. Su, S. Shaik and P. C. Hiberty, Classical valence bond approach by modern methods, Chem. Rev., 2011, 111, 7557–7593 CrossRef CAS PubMed.
- S. S. Shaik, What happens to molecules as they react? A valence bond approach to reactivity, J. Am. Chem. Soc., 1981, 103, 3692–3701 CrossRef CAS.
- S. Shaik and A. Shurki, Valence Bond Diagrams and Chemical Reactivity, Angew. Chem., Int. Ed., 1999, 38, 586–625 CrossRef PubMed.
- D. Usharani, W. Lai, C. Li, H. Chen, D. Danovich and S. Shaik, A tutorial for understanding chemical reactivity through the valence bond approach, Chem. Soc. Rev., 2014, 43, 4968–4988 RSC.
- X. Lin, X. Liu, F. Ying, Z. Chen and W. Wu, Explicit construction of diabatic state and its application to the direct evaluation of electronic coupling, J. Chem. Phys., 2018, 149, 044112 CrossRef PubMed.
- M. Ren, B. Ma, Z. Chen and W. Wu, Two-Dimensional Analysis of the Diabatic Transition of a General Vectorial Physical Observable Based on Adiabatic-to-Diabatic Transformation, J. Phys. Chem. Lett., 2019, 10, 5868–5872 CrossRef CAS PubMed.
- C. Zener, Non-adiabatic crossing of energy levels, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed.
- M. D. Newton and N. Sutin, Electron-Transfer Reactions in Condensed Phases, Annu. Rev. Phys. Chem., 1984, 35, 437–480 CrossRef CAS.
- N. S. Hush, Homogeneous and heterogeneous optical and thermal electron transfer, Electrochim. Acta, 1968, 13, 1005–1023 CrossRef CAS.
- R. A. Marcus and N. Sutin, Electron Transfers in Chemistry and Biology, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- C. Creutz, Mixed-Valence Complexes of D5-D6 Metal Centers, Prog. Inorg. Chem., 1983, 30, 1–73 CrossRef CAS.
- W. Henry, C. G. Coates, C. Brady, K. L. Ronayne, P. Matousek, M. Towrie, S. W. Botchway, A. W. Parker, J. G. Vos, W. R. Browne and J. J. McGarvey, The early picosecond photophysics of Ru(II) polypyridyl complexes: a tale of two timescales, J. Phys. Chem. A, 2008, 112, 4537–4544 CrossRef CAS PubMed.
- A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. Belser and A. V. Von Zelewsky, Ru (II) polypyridine complexes: photophysics, photochemistry, eletrochemistry, and chemiluminescence, Coord. Chem. Rev., 1988, 84, 85–277 CrossRef CAS.
- P. Müller and K. Brettel, [Ru (bpy)3]2+ as a reference in transient absorption spectroscopy: differential absorption coefficients for formation of the long-lived 3MLCT excited state, Photochem. Photobiol. Sci., 2012, 11, 632–636 CrossRef PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- P. Siegbahn, A. Heiberg, B. Roos and B. Levy, A comparison of the super-CI and the Newton-Raphson scheme in the complete active space SCF method, Phys. Scr., 1980, 21, 323 CrossRef CAS.
- P. A. Malmqvist, A. Rendell and B. O. Roos, The Restricted Active Space Self-Consistent-Field Method, Implemented with a Split Graph Unitary-Group Approach, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, Second-order perturbation theory with a CASSCF reference function, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P. Å. Malmqvist and B. O. Roos, Second-order perturbation theory with a complete active space self-consistent field reference function, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- P. Celani and H. J. Werner, Multireference perturbation theory for large restricted and selected active space reference wave functions, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- P. Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, The restricted active space followed by second-order perturbation theory method: Theory and application to the study of CuO2 and Cu2O2 systems, J. Chem. Phys., 2008, 128, 204109 CrossRef PubMed.
- F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, Cholesky decomposition-based multiconfiguration second-order perturbation theory (CD-CASPT2): application to the spin-state energetics of CoIII (diiminato)(NPh), J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS PubMed.
- M. Barysz and A. J. Sadlej, Two-component methods of relativistic quantum chemistry: from the Douglas-Kroll approximation to the exact two-component formalism, THEOCHEM, 2001, 573, 181–200 CrossRef CAS.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, Parallel Douglas-Kroll energy and gradients in NWChem: Estimating scalar relativistic effects using Douglas-Kroll contracted basis sets, J. Chem. Phys., 2001, 114, 48–53 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- At the ground state equilibrium geometry, the excitation energies for the 1MLCT1-3 states are 63.3, 63.3 and 63.6 kcal mol−1 respectively with pseudopotential basis sets; meanwhile these values become 62.8, 62.8 and 63.3 kcal mol−1 respectively with all-electron basis sets.
- N. Forsberg and P. A. Malmqvist, Multiconfiguration perturbation theory with imaginary level shift, Chem. Phys. Lett., 1997, 274, 196–204 CrossRef CAS.
- G. Ghigo, B. O. Roos and P. A. Malmqvist, A modified definition of the zeroth-order Hamiltonian in multiconfigurational perturbation theory (CASPT2), Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- I. Fdez Galvan, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. Gonzalez, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovacevic, E. Kallman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sorensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesolowski, P. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03806h |
| This journal is © the Owner Societies 2024 |
