DFT+U and quantum Monte Carlo study of electronic and optical properties of AgNiO₂ and AgNi_1−xCo_xO₂ delafossite

Abstract

As the only semimetallic d¹⁰-based delafossite, AgNiO₂ has received a great deal of attention due to both its unique semimetallicity and its antiferromagnetism in the NiO₂ layer that is coupled with a lattice distortion. In contrast, other delafossites such as AgCoO₂ are insulating. Here we study how the electronic structure of AgNi_1−xCo_xO₂ alloys vary with Ni/Co concentration, in order to investigate the electronic properties and phase stability of the intermetallics. While the electronic and magnetic structure of delafossites have been studied using density functional theory (DFT), earlier studies have not included corrections for strong on-site Coulomb interactions. In order to treat these interactions accurately, in this study we use Quantum Monte Carlo (QMC) simulations to obtain accurate estimates for the electronic and magnetic properties of AgNiO₂. By comparison to DFT results we show that these electron correlations are critical to account for. We show that Co doping on the magnetic Ni sites results in a metal–insulator transition near x ∼0.33, and reentrant behavior near x ∼ 0.66.

---

1 Introduction

Delafossites are minerals with the generic formula ABO₂, where A is a monovalent and B is a trivalent metal, and the structure consists of layers of the metal A cations interspersed between layers of BO₂ that are arranged in edge-sharing BO₆ octahedra, as seen in Fig. 1. A particular feature of delafossites is that the cation A is bonded vertically (along the c axis) to oxygen atoms in planes above and below. Recently, delafossites have attracted a great deal of attention because of their interesting properties that arise as a consequence of interplay between the metal A and the BO₂ layers. Since the discovery of the naturally occurring delafossite form of CuFeO₂,¹ various types of delafossites have been synthesized and studied extensively in order to understand what gives rise to the wide ranges of electronic properties for different combinations of A and B elements.^2–10 The monovalent A site is usually occupied by d⁹ or d¹⁰ noble metals or transition metal atoms. Most of the d⁹ and d¹⁰ delafossites, such as PdCoO₂ and PtCoO₂, exhibit a large electrical conductivity, but a much wider range of electronic properties, including metallic, semiconducting, and insulating, has been observed in d¹⁰ A-site compounds, and it appears that the B-site component is the dominating factor in the resulting electronic and optical properties.^11–13

Fig. 1 (a) Side and (b) top view of 2H-AgNiO₂ structure. There are two different Ni sites, Ni1 with very small magnetic moments as Ni^3.5+/d^6.5 state, and Ni2 with large magnetic moments as Ni²⁺/d⁸ state; the Ni2 sites form a triangular planar antiferromagnet.

Delafossites with d¹⁰ cations (A = Ag and Cu) have reported to possess wide direct electronic band gaps and p-type behavior, which makes them interesting for potential future applications of p-type transparent materials.^7,14–18 Among d¹⁰-based delafossites AgBO₂ and CuBO₂, the Ni B-site compound AgNiO₂ is known to possess rather unique electronic and magnetic properties: while most of the d¹⁰-based delafossites exhibit insulating or semiconducting behavior, only AgNiO₂ exhibits metallic features in 2H polytype of hexagonal space group of P6₃/mmc.^11,19,20 According to previous studies on 2H-AgNiO₂, its ideal P6₃/mmc crystal structure is transformed into the P6₃22 structure because of lattice distortions induced by strong antiferromagnetic (AFM) interactions in the NiO₂ layers of AgNiO₂.^11,21 Interestingly, the lattice distortion in AFM 2H-AgNiO₂ is not the well-known Jahn–Teller distortion, but a charge-ordering distortion induced by charge transfer on e_g states on the Ni sites. This leads to two different Ni sites, Ni1 with small magnetic moments (Ni^3.5+), and Ni2 sites with large magnetic moments (Ni²⁺); the Ni2 sites form a triangular antiferromagnet within the Ni ab-plane. This leads to charge disproportionation on the Ni sites and AFM 2H-AgNiO₂ is consequently interpreted as a strongly charge-ordered system. Moreover, because of the insulating properties of AgCoO₂ while AgNiO₂ exhibits a semimetallic phase, the existence of a metal–insulator transition has been predicted on AgNi_1−xCo_xO₂ structures wherein the NiO₂ layers in AgNiO₂ are mixed with CoO₂ layers of the insulating AgCoO₂.²²

In addition to experimental investigations, there have been a few reports from studies using density functional theory (DFT) to study AFM 2H-AgNiO₂, in particular to address the magnetic order that has been observed experimentally.^11,23 A fundamental question that can be raised in this context is to what extent electronic correlations play a role in the magnetic ordering in delafossites in general, and in AgNiO₂ in particular; linked to this is the well-known broader issue of how to accurately account for electronic correlations within DFT. This is an important question for the delafossites as they contain 3d, 4d, 4f, and 5f metals with highly localized electrons bound to oxygen. It is therefore important to accurately assess the effects of electronic correlations on delafossites, and also to devise computational schemes that allow for including correlations at a known level of accuracy. One such scheme is DFT+U, in which a Hubbard U term is added to selected localized orbitals to approximately account for on-site Coulomb correlations.^24,25 While the actual value of U can be used as a fitting variable, there are nowadays methods to self-consistently calculate U, reducing empiricism. Nevertheless, an on-site Coulomb interaction Hubbard U has not been considered at all in previous DFT studies of 2H-AgNiO₂, mainly because it has been predicted that the effect of U is small in metallic 2H-AgNiO₂.¹¹ Furthermore, a previous DFT study for 3R-AgNiO₂ concluded that projected density of state from local spin density approximation (LSDA) is in better agreement with corresponding experimental partial spectral weight (PSW) distributions than LSDA+U.²⁶ Therefore, appropriate values of U for 2H-AgNiO₂ have not been studied systematically. Previous studies have utilized the local density approximation (LDA) or the generalized gradient approximation (GGA) without any attempt to correct for on-site correlations with a Hubbard U have been used.^11,12,21,26

The main motivation for our work is to accurately assess the effect of electronic correlations on the electronic and magnetic properties of 2H-AgNiO₂, and also on intermetallic phases AgNi_1−xCo_xO₂ as well as their stability. In our work, we use quantum Monte Carlo (QMC) methods, specifically real-space variational Monte Carlo (VMC) and diffusion Monte Carlo (DMC). QMC methods are computationally expensive but highly-accurate stochastic wavefunction methods that fully incorporate electronic many-body effects.^27,28 Weak through strong electronic correlations are well described. The total energy obeys a variational principle allowing the effect of different choices for the input trail wavefunctions to be assessed. QMC methods have provided accurate ground state properties for strongly-correlated transition metal oxides, including VO₂, AFM NiO, and various alloys.^29–34 In this study, we use QMC to obtain accurate ground state properties of 2H-AgNiO₂. In addition, we study various structures of phases of the mixtures AgNi_1−xCo_xO₂ to assess their phase stability and electronic properties. Our results show that large concentrations of substitutional Co in AgNi_1−xCo_xO₂, x ≥ 0.33, lead to an opening of an electronic band gap and stable formation energies. This suggests an interesting way to generate a metal-insulating transition concomitant with a magnetic transition, different from, e.g., metal-insulating transitions in more classical correlated oxides, such as VO₂.^35–37

2 Methods

We used DMC within the fixed-node approximation as implemented in the QMCPACK code.³⁸ Single Slater-determinant wavefunctions were used as trial wavefunctions in the QMC algorithm, with up to three-body Jastrow correlation coefficients in order to incorporate electron–ion, electron–electron, and electron–electron–ion correlations. Cut-offs for the one- and two-body Jastrows were set as the Wigner–Seitz radius of the given supercell while a maximum of 5.0 bohr was used as the cut-off for the three-body term. Single-particle orbitals in the QMC trial wavefunctions were generated by solving the Kohn–Sham equations using DFT. All DFT calculations in this study were performed with a plane-wave basis set with a 700 Ry kinetic-energy cut-off and 8 × 8 × 8 k-point grids using the QUANTUM ESPRESSO code.³⁹ Kohn–Sham orbitals in the Slater determinant were generated using Perdew–Burke–Ernzerhof (PBE) parametrization⁴⁰ of the generalized gradient approximation (GGA) exchange–correlation (XC) functional. First-order Methfessel–Paxton scheme was applied as smearing method with 0.001 Ry smearing parameter for Brillouin zone integration.⁴¹ In order to account for on-site Coulomb interactions of strongly localized d orbital in Ni, we used a Hubbard “U” for the Hubbard correction within the DFT+U formalism.^24,25 Norm-conserving pseudopotentials for Ni and O in this study were the same as used in a previous QMC study of AFM NiO.³² The Ag and Co pseudopotentials were correlation-consistent effective-core potentials (ccECPs) wherein fully-correlated all-electron calculations – primarily coupled-cluster calculations – were used as references for the parameterization of the ECPs.^42–45 Because ccECP pseudopotentials are hard-core and therefore require large kinetic-energy cut-off, 700 Ry kinetic-energy, for Ag, we applied the hybrid orbital representation that combines a local atomic basis set and B-splines in order to reduce memory requirements of the QMC.⁴⁶ DMC calculations were done using 0.005 Ha⁻¹ time steps within the non-local T-move approximation⁴⁷ In order to reduce one-body finite-size effects from the periodic boundary conditions applied in the DMC calculations, we employed twist-averaged boundary conditions⁴⁸ with up to a maximum of 64 twists for the AgNiO₂ supercells.

Two-body finite-size effects were reduced using the modified periodic Coulomb interaction⁴⁹ and Chiesa's kinetic energy correction.⁵⁰ In addition to those finite-size corrections, we estimated twist-averaged DMC energies at different sizes of supercells, 48, 96, and 144 atoms cells, and extrapolated the energies to the bulk limit in order to further reduce two-body finite size effects.

3 Results

3.1 Properties of pure 2H-AgNiO₂

Previous DFT studies of AgNiO₂ delafossites assumed that on-site Coulomb interactions were not important and so did not use DFT+U.^11,21 One of the aims of our work is to examine the role of on-site Coulomb interactions in detail in order to ascertain their importance. Because there are no previously reported values for an optimal value of U, U_opt, we first estimated U_opt. We used a procedure established in previous works^32,51–54 that has proven to be a reliable and unbiased way to estimate U_opt for transition-metal oxides. In this procedure, we minimize the DMC total energy of the PBE+U trial wavefunction as a function of U. Because the DMC total energy obeys a variational principle, this energy will exhibit a minimum. Specifically, in DMC, the minimization of the energy with respect to U is a one-parameter optimization of the many-body wavefunction nodal surface. For simplicity we assume the same U value for all Ni atoms, regardless of their local charge states. Fig. 2 shows the DMC total energy for the AFM AgNiO₂ unit cell as function of the value of U in the PBE+U trial wavefunction. Using a quartic fit, we estimated an optimal U value of U_opt = 4.4(1) eV for Ni, which is close to the DMC U_opt = 4.7(2) eV found in AFM NiO.³² We use the value of U = 4.4 eV obtained from DMC for all subsequent PBE+U calculations in this study.

Fig. 2 DMC total energy of AgNiO₂ as function of Hubbard U in the PBE+U trial wavefunction.

To investigate how varied p−d hybridization within the DFT+U scheme may change the electronic properties of AgNiO₂, we first compare the electron density-of-states (DOS) obtained using PBE and PBE+U. As expected, the DOS for 2H-AgNiO₂ clearly exhibits metallic features with filled states at the Fermi level both for PBE and PBE+U (Fig. 3). Under hole doping, PBE predicts preservation of the metallic state for all doping levels. In contrast, PBE+U predicts a gap opening about 0.5 eV below the Fermi level, raising the possibility of a metal–insulator transition in 2H-AgNiO₂ under hole doping. In addition, we confirmed that the Hubbard U leads to more semimetallic electronic properties of AgNiO₂ as the conduction band minimum in PBE+U is closer to the Fermi level with lower DOS than in PBE. This suggests that localized Ni 3d orbitals induce a semimetallic nature in AgNiO₂, and that AgNiO₂ possesses an intriguing potential of tuning the band gap to a semiconductor or insulator.

Fig. 3 Projected density of states of AFM 2H-AgNiO₂ from (a) PBE and (b) PBE+U, with U = 4.4 eV.

For further analyses of the effects of U on semimetallic AgNiO₂, we compared total charge and spin densities obtained from PBE and PBE+U. Fig. 4(a) and (b) show significant differences in both charge and spin densities between PBE+U and PBE near the Ni sites – accumulation and depletion can be found near the Ni sites in both the charge and spin density differences. The charge density differences between PBE+U and PBE induced by the Hubbard U are mainly located on the octahedral NiO₆ structures, with no significant changes near the Ag sites. Within the NiO₂ layers, there is a rather pronounced charge density redistribution induced by Hubbard U on the Ni–O bond. This shows that the Hubbard U strongly affects the p−d hybridization of the Ni–O bonds, even though AgNiO₂ is in a semimetallic phase. Among the Ni sites, there is a large charge accumulation on the Ni²⁺ sites (Ni2) that also possess large magnetic moments. This indicates that there is discrepancy between the magnetic moments obtained by PBE and PBE+U, as the Hubbard U affects the magnetic moment on Ni. In addition to the charge density difference, we can also see that PBE underestimates the spin density on Ni sites relative to PBE+U (see Fig. 4), which is analogous to results obtained in an earlier DMC study of AFM NiO,³² although the spin density difference is smaller for AgNiO₂ than for insulating NiO. As assumed, it is clear that influence of the Hubbard U is not as large in semimetallic AgNiO₂ compared to its effect in insulating NiO; however, we conclude that the existence of localized 3d orbitals is still leads to moderate effects in AgNiO₂ because of the large density differences between PBE and PBE+U.

Fig. 4 (a) Charge and (b) spin density difference between PBE+U and PBE of a NiO₂ layer of AgNiO₂, those between DMC and PBE ((c) and (d)), and between DMC and PBE+U ((e) and (f)). The density differences are projected onto the (010) plane and in units of Å⁻³.

In order to further accurately assess the electronic properties of 2H-AgNiO₂, we performed DMC calculations of AgNiO₂ using a PBE+U trial wavefunction with the optimal value of U. We estimated the cohesive energy of AgNiO₂ by computing E(AgNiO₂) − E(Ag) − E(Ni) − 2E(O), where E(AgNiO₂), E(Ag), E(Ni), E(O) are the DMC total energy of AgNiO₂ and that of atomic Ag, Ni, and O, respectively. The computed DMC AgNiO₂ cohesive energy with full incorporation of the finite-size analysis is 14.23(3) eV per f.u., which is significantly smaller than the PBE result of 15.21 eV per f.u. but consistent with PBE+U one of 14.21 eV per f.u. Significantly larger PBE cohesive energy than DMC seems to be related with overestimation of NiO cohesive energy compared to corresponding experimental result within PBE functionals.³² Although experimental values of the AgNiO₂ cohesive energy are not available to the best of our knowledge, the large differences in cohesive energy clearly shows a large discrepancy between the DMC, DFT, and DFT+U schemes in dealing with the electronic structure of AgNiO₂. The charge density difference between DMC and PBE+U, ρ(DMC) − ρ(PBE+U), shows a charge density accumulation on Ni–O complexes in DMC relative to PBE+U, somewhat similar to the charge density difference ρ(PBE+U) − ρ(PBE), but the charge accumulation in ρ(DMC) − ρ(PBE+U) is concentrated on specific Ni–O pairs in the yz plane, while density difference ρ(PBE+U) − ρ(PBE) is more spread out over the entire NiO₆ layer. From this anisotropic density accumulation in DMC relative to PBE+U, we suspect there is a similar symmetry-breaking in the Ni–O bonds to that already seen in DMC studies of NiO and HfO₂.^32,55 In Fig. 4(d) and (f), we see strong spin accumulation and depletion only on the AFM Ni sites. This tells us that magnetic moment on the Ni sites is significantly underestimated in both PBE and PBE+U compared to DMC. In order to compare the DMC and DFT magnetic moments, we computed the magnetic moments on Ni sites as function of U. Fig. 5 shows that the DFT magnetic moment increases monotonically on the AFM Ni sites Ni2 as U increases. However, even at large values of U, up to 6 eV where PBE+U magnetic moment shows the largest value, the PBE+U moment is still smaller than DMC magnetic moment. The estimated DMC magnetic moment on the AFM Ni sites is 1.71(1) μ_B, which is slightly larger but in the good agreement with the reported local magnetization of Ni, 1.552(7) μ_B.⁵⁶ We see that PBE+U magnetic moment shows empirically closest result with the experimental one in U ∼ 2 eV with 1.58 μ_B while PBE without U exhibits smaller value of 1.46 μ_B. From this analysis, we conclude that the Hubbard U significantly affects the band gap and magnetic moment of 2H-AgNiO₂, and the addition of a Hubbard U is necessary in order to achieve reasonably accurate magnetic moment and charge density within DFT.

Fig. 5 Magnetic moments of (a) Ni1 and (b) Ni2 sites as function of U obtained using PBE+U (black squares) and DMC (red circle).

3.2 Moderate Co doping: metal–insulator transition for x = 0.33

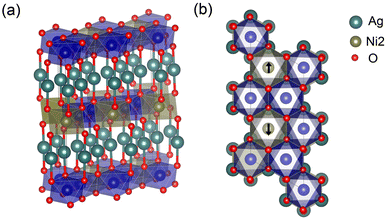
The PBE+U and DMC results for AgNiO₂ described in the previous section indicate the possibility of a metal–insulator transition based on the observations both in PBE+U and DMC of a small of electron density from states in the conduction band just below the Fermi level. This suggests that the introduction of dopants or other defects into stoichiometric AgNiO₂ may provide a path to move the conduction band minimum above the Fermi level. Various transition-metal doped delafossites have in fact been studied previously as transition-metal doping has been known to enhance p-type semiconductor properties. Among various transition metal candidates, we consider here Co as a dopant and investigate how Co doping influences the electronic properties and band gap opening in 2H-AgNiO₂. When studying these intermetallics, it is crucial first to obtain an accurate structure as the equilibrium structure and geometry vary with the concentration of dopants and with their locations, and the electronic structure in turn depends strongly on the geometry of the structure. We attempted to obtain a good quality lattice structure for AgNi_1−xCo_xO₂ by considering both the pure AgNiO₂ geometry but with dopants on Ni1 sites, and a fully relaxed structure within DFT+U framework. To compare these two geometries and to choose an energetically stable geometry for the intermetallic, we estimated the DMC total energy for these structures. The result is that the pure 2H-AgNiO₂ structure with Co on the Ni1 sites exhibits a lower FN-DMC energy than the fully relaxed structure. Therefore, we used the pure 2H-AgNiO₂ as a structure for the intermetallic AgNi_1−xCo_xO₂. Details in FN-energy comparison between different geometries are in ESI.† In order to optimize the trial wavefunction for AgNi_1−xCo_xO₂, we determined an optimal U-value of 4.0(1) eV for the Co dopants by minimizing the DMC total energy for the 2H-AgCoO₂ structure (see ESI†). Among potentially available Co concentrations of AgNi_1−xCo_xO₂, we first considered AgNi_0.66Co_0.33O₂ structure. Although the existence of MIT can be expected on AgNi_0.66Co_0.33O₂ since it is experimentally reported on x ∼ 0.3,²² the energetic stability of phases that result from random Co substitutions at various Co concentration is unclear. In order to investigate the relative stability of various random phases and the dependencies of their electronic and optical properties on substitutional sites, we considered additional phases of AgNi_0.66Co_0.33O₂ wherein four Ni²⁺ Ni1 sites out of a total of eight are replaced by Co dopants. We did not consider substitution of Co on the AFM Ni2 sites because calculations showed that this leads to a collapse of the magnetic order and an energetically unstable structure of the mixture. Because there are too many AgNi_0.66Co_0.33O₂ configurations with four Co atoms on eight possible sites to make comprehensive DMC calculations practical, we selected only four different phases, shown in Fig. 6. Other various phases with larger sizes of cell can be found on ESI.†

Fig. 6 Upper and lower Co-doped NiO₂ layers for four different phases of AgNi_0.66Co_0.33O₂. The blue spheres indicate Co dopants.

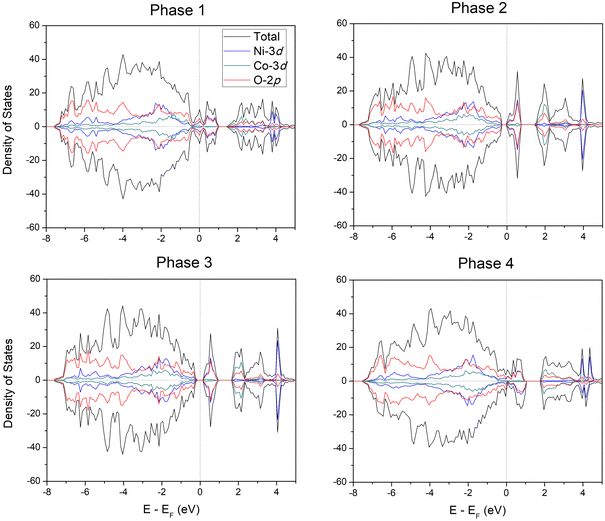
We first compute the PBE+U density-of-states of these four phases in order to compare their optical properties. As can be seen in Fig. 7, the optical properties of the AgNi_0.66Co_0.33O₂ mixture depends strongly on which of the Ni1 sites are substituted with Co. Phases 1 and 4 show completely closed band gaps and metallic densities-of-states; however, phases 2 and 3 exhibit open band gaps. Because of the completely different electronic properties of the four phases, with phases 1 and 4 metallic and phase 2 and 3 semiconductor-like, and the very large differences in densities-of-states near the Fermi level, we conclude that the electronic and optical properties vary strongly with the specific sites used for Co-substitution, and the detailed properties of AgNi_0.66Co_0.33O₂ can potentially be controlled by selectively choosing the sites for substitution.

Fig. 7 Projected density-of-states for four different phases of AgNi_0.66Co_0.33O₂.

Because there are many possible metallic and semiconducting phases of AgNi_0.66Co_0.33O₂, it is important to find the most stable one. We estimated the DMC total energy of four candidates based on symmetry. Fig. 8 shows the PBE+U and the DMC total energy differences between the four phases with the energy (PBE+U and DMC, respectively) of phase 1 as reference at zero total energy. As can be seen in the figure, the semiconducting phases 2 and 3 have lower DMC total energy than the metallic phases 1 and 4, indicating that the semiconducting phases are more energetically favored and stable than metallic ones for the AgNi_0.66Co_0.33O₂ mixture. There is a large DMC energy difference between the metallic phases 1 and 4 in DMC and a smaller PBE+U energy difference, but a relatively small energy difference between phases 2 and 3 both for PBE+U and DMC. The much smaller PBE+U energy difference between the metallic and semiconducting phases than the DMC energy difference, about 0.05 eV per f.u. and 0.21(1) eV per f.u., respectively, strongly suggests that the semiconducting phases driven by Co-substitution are due to electron correlations between the Co and Ni sites, effects that are well accounted for in DMC but not as accurately in DFT or DFT+U. From lower PBE+U and DMC total energies on semiconducting phases than semimetallic ones confirmed the existence of MIT, transiting favored phase from semimetallic on pristine AgNiO₂ to semiconducting phase on AgNi_0.66Co_0.33O₂. In addition, since coexistence of semimetallic and semiconducting phase is observed at the concentration of x = 0.33, we assume that the critical Co concentration of MIT is located nearby x = 0.33, which is consistent with the experimental measurement of MIT on x = 0.3.²² In further calculations at x = 0.33 in larger cells (96 and 144 atom cells, see ESI†), we see largely the same behavior, with a coexistence of locally gapped and ungapped phases. However, the expanded results also show that the ungapped phases are characterized by low density of states at the Fermi level. These findings are interesting because the experimental thermal behavior of the thermoelectric power²² also suggested the presence of a residual finite density of states at the Fermi level for this concentration.

Fig. 8 PBE+U and DMC relative energy between four different phases of AgNi_0.66Co_0.33O₂.

On the other hand, we see the metallic phase in higher Co concentration on the single NiO₆ layer than x = 0.33 as seen in both phases 1 and 4. Since the varied structure are in-layer density fluctuations and each of these contain a layer at higher Co concentration, these results leads us to suspect the existence of reentrant phase to the metallic phase on high Co concentration over x = 0.33.

3.3 High Co doping: AgNi_0.33Co_0.66O₂

In order to investigate optical properties on high Co concentration for AgNi_1−xCo_xO₂, we additionally considered high Co concentration of x = 0.66, substituting all non-magnetic Ni1 sites in a hexagonal pattern (see Fig. 9). This x = 0.66 seems a hypothetical structure at a concentration where no experimental result for the electronic and optical properties has been reported.

Fig. 9 (a) Side and (b) top view of AgNi_0.33Co_0.66O₂ cell. Blue atoms represent Co.

The PBE+U density-of-states of AgNi_0.33Co_0.66O₂ (see Fig. 10(a)) shows that Co-doping moves the valence band edge very close to the Fermi level, and at the conduction band edge, 3d-Co states have fully replaced d-Ni ones. Although the valence band edge still lies above Fermi level, the closeness of the band edge to the Fermi levels suggests that Co-substitution on the Ni^3.5+ Ni1 sites results in the electronic properties of AgNi_0.33Co_0.66O₂ moving from those of a semimetal closer to those of an insulator.

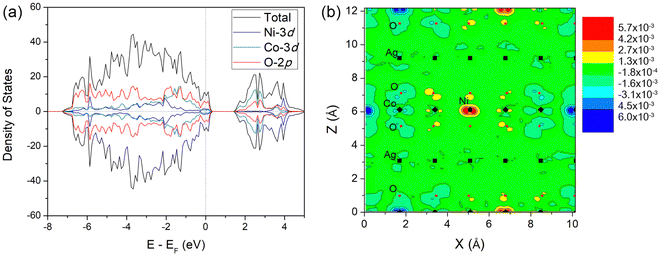Fig. 10 (a) PBE+U projected density-of-states of AgNi_0.33Co_0.66O₂, and (b) DMC spin density difference between AgNiO₂ and AgNi_0.33Co_0.66O₂.

Fig. 3(b) shows the DMC spin density difference between AgNi_0.33Co_0.66O₂ and AgNiO₂. The figure shows a density changes on the AFM Ni sites Ni2, but density change is opposite in sign to the induced AFM magnetic moments. This tells us that the magnetic moments on Ni sites on AgNi_0.33Co_0.66O₂ are smaller than in pristine AgNiO₂, and this is confirmed by a DMC estimate of the magnetic moment of 1.52(1) μ_B for AgNi_0.33Co_0.66O₂, which is smaller than the moment of 1.71(1) μ_B for the same Ni2 sites in AgNiO₂.

These results suggest that reentrance to the metallic phase can be possible at high Co doping. This behavior is also consistent with phase 1 and 4 in Fig. 6 for AgNi_0.66Co_0.33O₂, and confirms that reentrance to the metallic phase from insulator can be possible in high Co concentration.

3.4 Stability of AgNi_1−xCo_xO₂

The thermodynamic stability of the AgNiO₂ delafossite and its doped variants depends strongly on their formation energies. In order to estimate optimal conditions for formation of AgNi_1−xCo_xO₂, we calculated the enthalpy of formation for AgNiO₂ and its doped variants under different growth conditions. The enthalpy of formation of AgNiO₂ can be estimated by computing where μ_X indicates the chemical potential for given atom X. In order to prevent formation of competing phases and phase separation or decomposition of AgNiO₂, these chemical potentials should be constrained as follows:One phase boundary to AFM Co₃O₄ is avoided by respecting a constraint on Co-doping in AgNi_1−xCo_xO₂. We computed the enthalpy of formation for AgNiO₂, its decompositions, and Co₃O₄ using DFT+U reference energies for solid Ag, Ni, Co, and for gas-phase molecular O₂. We did not try to estimate DMC formation energies because of previously reported difficulties in computing an accurate reference energy for ferromagnetic bulk Ni using a single Slater-determinant trial wavefunction.³²

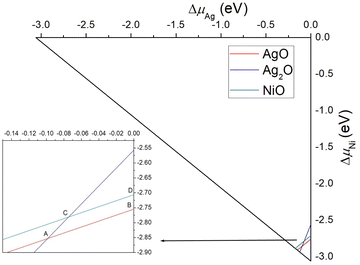
Based on the computed ΔH_f using PBE+U, the phase diagram of AgNiO₂ can be illustrated as a function of the allowed ranges of the chemical potentials of Ag, Ni, and O, given the constraints on them, as shown in Fig. 11.^57,58 Within the boundaries given by the constraints on the enthalpy of formation of AgO, Ag₂O, and NiO, we obtained the following chemical potentials of (Δμ_Ag, Δμ_Ni, Δμ_O) under different growth conditions: Ag-poor:Ni-poor:O-rich A(−0.10, −2.85, −0.05), Ag-rich:Ni-poor:O-poor B(0.00, −2.75, −0.15), Ag-poor:Ni-rich:O-rich C(−0.08, −2.78, −0.10), and Ag-rich:Ni-rich:O-poor D(0.00, −2.71, −0.17). Using these chemical potentials, the formation energy of a Co defect is given by

where E_{AgNi1−xCoxO2}, E_AgNiO2, n_i, and E_i are the total energy of AgNi_1−xCo_xO₂ and AgNiO₂, the number of added (n_i < 0) and removed (n_i > 0) atoms for substitutions, and the reference energy from the standard solid or gas-phase reference states for the constituent elements, respectively.

Fig. 11 Illustration of the accessible chemical potential range for AgNiO₂ from PBE+U.

Table 1 summarizes the computed formation energies of Co dopants in AgNi_0.66Co_0.33O₂ and AgNi_0.33Co_0.66O₂. As is seen in the table, PBE+U predicts spontaneous formation of Co-defects for all phases and growth conditions for which the formation energy of the defect is negative. It has previous been reported that PBE+U tends to underestimate the formation energy of defects in transition metal oxide systems,^32,55,59,60 so spontaneous defect formation may not occur. The PBE+U results lead us to confirm that the Ag-rich:Ni-poor:O-poor growth condition is the most favorable one for pure AgNiO₂ and AgNi_1−xCo_xO₂ with the lowest formation energy within the given constraints. Although PBE+U does not provide quantitatively accurate formation energies for Co doping, a qualitative comparison between various growth conditions does give guidelines for the best growth conditions for synthesizing AgNiO₂ and AgNi_1−xCo_xO₂.

Table 1 PBE+U formation energies in eV for AgNi_1−xCo_xO₂ under different growth conditions

	AgNi0.33Co0.66O2	AgNi0.66Co0.33O2
		Phase 1	Phase 2	Phase 3	Phase 4
Ag-poor:Ni-poor:O-rich	−0.13	−0.97	−1.02	−1.02	−0.99
Ag-rich:Ni-poor:O-poor	−0.16	−0.98	−1.03	−1.03	−1.00
Ag-poor:Ni-rich:O-rich	−0.13	−0.97	−1.02	−1.02	−0.99
Ag-rich:Ni-rich-O-poor	−0.15	−0.98	−1.02	−1.03	−1.00

---

In order to compare stability of AgNi_1−xCo_xO₂ with the binary oxides, we compute PBE+U formation energy against elemental solids and binary oxides under stoichiometric conditions. In Table 2, we see large formation energy gap of ∼8 eV between one relative with elemental solids and the binaries. With comparison of formation energies Tables 1 and 2, we see that formation energies of AgNi_1−xCo_xO₂ under the chemical potential constraints are significantly closer to formation energies from the binary oxides than those from the elemental solids in Table 2, which tells us formation of AgNi_1−xCo_xO₂ is almost energetically consistent with the ideal formation against binary oxides. In addition, smaller formation energies in x = 0.66 than x = 0.33 in all growth conditions lead us to conclude relative difficulty of AgNi_0.33Co_0.66O₂ synthesis.

Table 2 PBE+U formation energies in eV for AgNi_1−xCo_xO₂ against elemental solids (gaseous oxygen) and binary oxides under stoichiometric conditions

	x = 0.66	x = 0.33
		Phase 1	Phase 2	Phase 3	Phase 4
Elemental	−3.58	−4.22	−4.27	−4.27	−4.25
Binary	−0.09	−0.87	−0.92	−0.92	−0.89

---

4 Conclusions

We have performed DMC calculations on the AFM AgNiO₂ delafossite in order to obtain accurate electronic properties and magnetic moments. We found that the addition of Hubbard U to the DFT scheme dramatically changes the electronic and magnetic properties of AgNiO₂. Using DFT+U with the U value optimized using DMC, we confirmed that AgNiO₂ has a semimetallic nature induced by strong p−d hybridization in AFM NiO₂ layer. Our PBE+U and DMC studies of AgNi_1−xCo_xO₂ shows a metal–insulator transition at x ∼ 0.33 by Co substitution on the non-magnetic Ni1 sites, which is in good agreement with the experimental result. In addition to the semiconducting phase in AgNi_0.66Co_0.33O₂, it is found that the coexistence of metallic phase when more than x = 0.33 of Co dopant is substituted in the single layer of NiO₂ in AgNi_0.66Co_0.33O₂, leading to possible existence of the reentrance of metallic phase in high Co concentration. This reentrant behavior in AgNi_1−xCo_xO₂ is confirmed in high Co concentration of AgNi_0.33Co_0.66O₂ where semimetallic nature is discovered in the PBE+U result. PBE+U formation energies revealed that AgNi_0.66Co_0.33O₂ possesses the lowest formation energy under oxygen-rich conditions, which suggests a path for synthesizing the AgNi_0.66Co_0.33O₂ mixture. Our works clearly shows the difficulty in using PBE+U to quantitatively estimate formation energies of Co-doping in AgNiO₂ because of the poor description of the 3d orbitals in Ni and Co. More accurate electronic structure methods than existing DFT approximations are needed for accurate prediction of electronic and magnetic properties of defective delafossites.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, as part of the Computational Materials Sciences Program and Center for Predictive Simulation of Functional Materials. An award of computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under contract DE-AC02-06CH11357 and resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725.

Notes and references

1. A. Pabst, Am. Mineral., 1946, 31, 539–546.
2. R. D. Shannon, D. B. Rogers and C. T. Prewitt, Inorg. Chem., 1971, 10, 713–718.
3. C. T. Prewitt, R. D. Shannon and D. B. Rogers, Inorg. Chem., 1971, 10, 719.
4. D. B. Rogers, R. D. Shannon, C. T. Prewitt and J. L. Gillson, Inorg. Chem., 1971, 10, 723.
5. F. A. Benko and F. P. Koffyberg, J. Phys. Chem. Solids, 1984, 45, 57.
6. F. A. Benko and F. P. Koffyberg, J. Phys. Chem. Solids, 1987, 48, 431.
7. H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, Nature, 1997, 389, 939.
8. H.-J. Noh, J. Jeong, J. Jeong, E.-J. Cho, S. B. Kim, K. Kim, B. I. Min and H.-D. Kim, Phys. Rev. Lett., 2009, 102, 256404.
9. P. Kushiwaha, V. Sunko, P. J. W. Moll, L. Bawden, J. M. Riley, N. Nandi, H. Rosner, M. P. Schmidt, F. Arnold, E. Hassinger, T. K. Kim, M. Hoesch, A. P. Mackenzie and P. D. C. King, Sci. Adv., 2015, 1, e1500692.
10. J. M. Ok, M. Brahlek, W. S. Choi, K. M. Roccapriore, M. F. Chisholm, S. Kim, C. Sohn, E. Skoropata, S. Yoon, J. S. Kim and H. N. Lee, APL Mater., 2020, 8, 051104.
11. E. Wawrzyńska, R. Coldea, E. M. Wheeler, I. I. Mazin, M. D. Johannes, T. Sörgel, M. Jansen, R. M. Ibberson and P. G. Radaelli, Phys. Rev. Lett., 2007, 99, 157204.
12. J.-S. Kang, S. S. Lee, G. Kim, H. J. Lee, H. K. Song, Y. J. Shin, S. W. Han, C. Hwang, M. C. Jung, H. J. Shin, B. H. Kim, S. K. Kwon and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195122.
13. S. Seki, Y. Onose and Y. Tokura, Phys. Rev. Lett., 2008, 101, 067204.
14. K. Ueda, T. Hase, H. Yanagi, H. Kawazoe and H. Hosono, J. Appl. Phys., 2001, 88, 1790.
15. H. Yanagi, T. Hase, S. Ibuki, K. Ueda and H. Hosono, J. Appl. Phys., 2001, 78, 1583.
16. M. Snure and A. Tiwari, Appl. Phys. Lett., 2007, 91, 092123.
17. D. O. Scanlon, A. Walsh and G. W. Watson, Chem. Mater., 2009, 21, 4568.
18. S. Santra, N. S. Das and K. K. Chattopadhyay, Mater. Lett., 2013, 92, 198.
19. A. Wichainchai, P. Dordor, J. P. Doumerc, E. Marquestaut, E. Pouchard, P. Hagenmuller and A. Ammar, J. Solid State Chem., 1988, 74, 126.
20. A. I. Coldea, L. Seabra, A. McCollam, A. Carrington, L. Malone, A. F. Bangura, D. Vignoless, P. G. van Rhee, R. D. McDonald, T. Sörgel, M. Jansen, N. Shannon and R. Coldea, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 907, 020401.
21. E. Wawrzyńska, R. Coldea, E. M. Wheeler, T. Sörgel, M. Jansen, R. M. Ibberson, P. G. Radaelli and M. M. Koza, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094439.
22. Y. Shin, J. Doumerc, P. Dordor, M. Pouchard and P. Hagenmuller, J. Solid State Chem., 1993, 107, 194–200.
23. W. E. Pickett, Y. Quan and V. Pardo, J. Phys.: Condens. Matter, 2014, 26, 274203.
24. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943.
25. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
26. M. D. Johannes, S. Strelvsov, I. I. Mazin and D. I. Kohmskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 180404.
27. P. J. Reynolds, D. M. Ceperley, B. J. Alder and W. A. Lester, J. Chem. Phys., 1982, 77, 5593–5603.
28. W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal, Rev. Mod. Phys., 2001, 73, 33–83.
29. H. Zheng and L. K. Wagner, Phys. Rev. Lett., 2015, 114, 176401.
30. C. Mitra, J. T. Krogel, J. A. Santana and F. A. Reboredo, J. Chem. Phys., 2015, 143, 164710.
31. J. Trail, B. Monserrat, P. L. Ríos, R. Maezono and R. J. Needs, Phys. Rev. B, 2017, 95, 121108.
32. H. Shin, Y. Luo, P. Ganesh, J. Balachandran, J. T. Krogel, P. R. C. Kent, A. Benali and O. Heinonen, Phys. Rev. Materials, 2017, 1, 173603.
33. I. Kylänpää, Y. Luo, O. Heinonen, P. R. C. Kent and J. T. Krogel, Phys. Rev. B, 2019, 99, 075154.
34. D. Wines, K. Saritas and C. Ataca, J. Chem. Phys., 2021, 155, 194112.
35. F. J. Morin, Phys. Rev. Lett., 1959, 3, 34.
36. A. Tseleve, I. A. Luk'yanchuk, I. N. Ivanov, J. D. Budai, J. Z. Tischler, E. Strelcov, A. Kolmakov and S. V. Kalinin, Nano Lett., 2010, 10, 4409.
37. M. A. Huber, M. Plankl, M. Eisele, R. E. Marvel, F. Sandner, T. Korn, C. Schüller, R. F. H. Jr., R. Huber and T. L. Cocker, Nano Lett., 2016, 16, 1421.
38. J. Kim, A. Baczewski, T. Beaudet, A. Benali, C. Bennett, M. Berrill, N. Blunt, E. J. L. Borda, M. Casula, D. Ceperley, S. Chiesa, B. K. Clark, R. Clay, K. Delaney, M. Dewing, K. Esler, H. Hao, O. Heinonen, P. R. C. Kent, J. T. Krogel, I. Kylanpaa, Y. W. Li, M. G. Lopez, Y. Luo, F. Malone, R. Martin, A. Mathuriya, J. McMinis, C. Melton, L. Mitas, M. A. Morales, E. Neuscamman, W. Parker, S. Flores, N. A. Romero, B. Rubenstein, J. Shea, H. Shin, L. Shulenburger, A. Tillack, J. Townsend, N. Tubman, B. van der Goetz, J. Vincent, D. C. Yang, Y. Yang, S. Zhang and L. Zhao, J. Phys.: Condens. Matter, 2018, 30, 195901.
39. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. M. Samos, N. Mazari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 77, 3865.
41. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616.
42. M. C. Bennett, C. A. Melton, A. Annaberdiyev, G. Wang, L. Shulenburger and L. Mitas, J. Chem. Phys., 2017, 147, 224106.
43. M. C. Bennett, G. Wang, A. Annaberdiyev, C. A. Melton, L. Shulenburger and L. Mitas, J. Chem. Phys., 2018, 149, 104108.
44. A. Annaberdiyev, G. Wang, C. A. Melton, M. C. Bennett, L. Shulenburger and L. Mitas, J. Chem. Phys., 2018, 149, 134108.
45. G. Wang, A. Annaberdiyev, C. A. Melton, M. C. Bennett, L. Shulenburger and L. Mitas, J. Chem. Phys., 2019, 151, 144110.
46. Y. Luo, K. P. Esler, P. R. C. Kent and L. Shulenburger, J. Chem. Phys., 2018, 149, 084107.
47. M. Casula, S. Moroni, S. Sorella and C. Filippi, J. Chem. Phys., 2010, 132, 154113.
48. C. Lin, F. H. Zong and D. M. Ceperley, Phys. Rev. E, 2001, 64, 016702.
49. N. D. Drummond, R. J. Needs, A. Sorouri and W. M. C. Foulkes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125106.
50. S. Chiesa, D. M. Ceperley, R. M. Martin and M. Holzmann, Phys. Rev. Lett., 2006, 97, 076404.
51. K. Foyevstova, J. T. Krogel, J. Kim, P. R. C. Kent, E. Dagotto and F. A. Reboredo, Phys. Rev. X, 2014, 4, 031003.
52. Y. Luo, A. Benali, L. Shulenburger, J. T. Krogel, O. Heinonen and P. R. C. Kent, New J. Phys., 2016, 18, 113049.
53. H. Shin, A. Benali, Y. Luo, E. Crabb, A. Lopez-Bezanilla, L. E. Ratcliff, A. M. Jokisaari and O. Heinonen, Phys. Rev. Mater., 2018, 2, 075001.
54. K. Saritas, J. T. Krogel, S. Okamoto, H. N. Lee and F. A. Reboredo, Phys. Rev. Mater., 2019, 3, 124414.
55. R. Chimata, H. Shin, A. Benali and O. Heinonen, Phys. Rev. Mater., 2019, 3, 075005.
56. E. M. Wheeler, R. Coldea, E. Wawrzyńska, T. Sörgel, M. Jansen, M. M. Koza, J. Taylor, P. Adroguer and N. Shannon, Phys. Rev. B, 2009, 79, 104421.
57. C. Persson, Y.-J. Zhao, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035211.
58. A. Walsh, Y. Yan, M. M. Al-Jassim and S. H. Wei, J. Phys. Chem. C, 2008, 125, 12044.
59. J. Santana, J. T. Krogel, J. Kim, P. R. C. Kent and F. A. Reboredo, J. Chem. Phys., 2015, 142, 164705.
60. T. Ichibha, K. Saritas, J. T. Krogel, Y. Luo, P. R. C. Kent and F. A. Reboredo, Sci. Rep., 2023, 13, 6703.

---

Footnotes

† Electronic supplementary information (ESI) available: Geometry for AgNi_1−xCo_xO₂, U scanning for AgCoO₂. See DOI: https://doi.org/10.1039/d3cp03477a

‡ Present address: Seagate Technology, Computer Ave. 7801, Bloomington, MN 55435, USA.

---