Electronic band structure change with structural transition of buckled Au₂X monolayers induced by strain

Abstract

This study investigates the strain-induced structural transitions of η ↔ θ and the changes in electronic band structures of Au₂X (X = S, Se, Te, Si, Ge) and Au₄SSe. We focus on Au₂S monolayers, which can form multiple meta-stable monolayers theoretically, including η-Au₂S, a buckled penta-monolayer composed of a square Au lattice and S adatoms. The θ-Au₂S is regarded as a distorted structure of η-Au₂S. Based on density functional theory (DFT) calculations using a generalized gradient approximation, the conduction and the valence bands of θ-Au₂S intersect at the Γ point, leading to linear dispersion, whereas η-Au₂S has a band gap of 1.02 eV. The conduction band minimum depends on the specific Au–Au bond distance, while the valence band maximum depends on both Au–S and Au–Au interactions. The band gap undergoes significant changes during the η ↔ θ phase transition of Au₂S induced by applying tensile or compressive in-plane biaxial strain to the lattice. Moreover, substituting S atoms with other elements alters the electronic band structures, resulting in a variety of physical properties without disrupting the fundamental Au lattice network. Therefore, the family of Au₂X monolayers holds potential as materials for atomic scale network devices.

---

1 Introduction

In recent years, many new structures of AB₂-type 2D materials, such as transition metal dichalcogenides, have been proposed theoretically by high-throughput density functional theory (DFT) calculations,^1,2 and experimental material synthesis for database construction has also been actively carried out.³ In our previous study, we performed high-throughput first-principles electronic structure calculations for AB₂-type 2D materials based on DFT to construct a structure map which not only assembles families of 1T and 1H structures, such as the well-known transition metal dichalcogenides, but also highlights intriguing structural trends through the periodic table.^4,5

In that study, we also found some characteristic monolayers (see Fig. 10 in ref. 4), for example, Au₂S [P42₁2 (90)], Au₂B [P4/mbm (127)], and GeC₂ [P42₁m (113)], which can be classified into a group of penta-monolayers. Here, the compound name and space group are described to represent a specific phase of monolayers. The difference among these three monolayers is how their structures are buckled. The Au₂B [P4/mbm (127)] is a planar structure, while S atoms in the Au₂S [P42₁2 (90)] are buckled as shown in Fig. 1(b). The GeC₂ [P42₁m (113)] is in the same space group of buckled pentagonal monolayers as PdSe₂, which has already been synthesized experimentally.⁶ The top view of Au₂S [P42₁2 (90)] and Au₂B [P4/mbm (127)] are similar pentagonal monolayers. A different perspective reveals that their structures consist of triangular and square Au lattice networks and S or B adatoms. For Au₂S, there were some reports where Au₂S has several phases.^7–9 In particular, a structure of Au₂S [P4/nmm (129)], which consists of the square Au lattice networks and S adatoms as shown in Fig. 1(a), is comprehended as a distorted structure of Au₂S [P42₁2 (90)]. The geometrical structure of Au₂S [P42₁2 (90)] and Au₂S [P4/nmm (129)] have already been reported in the study about Cu₂S.^10,11 However, since Au₂S [P42₁2 (90)] and Au₂S [P4/nmm (129)] are not the most stable structure, researchers have not given a detailed analysis of the electronic structure of them. Although the most stable structure discussed in ref. 8 is ι-Au₂S, whose energy is smaller than Au₂S [P42₁2 (90)] and Au₂S [P4/nmm (129)], the structure is buckled too largely to be synthesized on a substrate. Therefore, we focus on the features of the metastable states, Au₂S [P42₁2 (90)] and Au₂S [P4/nmm (129)].

Fig. 1 Structures of η-Au₂S (a) and θ-Au₂S (b).

In this work, we discuss how structures (phases) and electronic band structures of Au₂S change under strain and adatom substitution, when Au₂S is considered as a monolayer consisting of Au lattice networks with S adatoms. For simplicity, Au₂S [P42₁2 (90)] and Au₂S [P4/nmm (129)] are denoted as buckled-η-Au₂S and buckled-θ-Au₂S, or more simply η-Au₂S and θ-Au₂S, respectively. This paper is organized as follows. In Section 2, computational details of DFT calculations and phonon calculations are outlined. In Section 3.1, geometrical structures and stability of η- and θ-Au₂S monolayers are discussed with a focus on η ↔ θ phase transitions. In Section 3.2, we focus on the electronic band structures of Au₂S, and investigate what the origin of the band gap is and how we can control the band gap. In Section 4.1, geometrical structures and stability of η- and θ-Au₂X (X = Se, Te, Si, Ge) monolayers are discussed in comparison to those of Au₂S. Moreover, as an example of the partially atom-substituted monolayers, we discuss η- and θ-Au₄SSe monolayers from the viewpoint of controlling the stability of the phase. The electronic band structures of Au₂X monolayers are investigated in Section 4.2. The last section is devoted to the conclusions and perspectives.

2 Computational details

The first-principles calculations based on DFT were carried out for Au₂X (X = S, Se, Te, Si, Ge) type monolayers of θ- and η-phase. The DFT calculations within a generalized gradient approximation (GGA)^12,13 were performed for the geometry relaxations and variable cell optimizations using the OpenMX code¹⁴ based on norm-conserving pseudopotentials generated with multireference energies¹⁵ and optimized pseudoatomic basis functions.¹⁶ The basis sets we used are listed in Table 1. For example, Au7.0-s3p2d2f1 means that three, two, two, and one optimized radial functions were allocated for the s, p, d, and f orbitals, respectively for Au atoms, and the cutoff radius of 7 Bohr was chosen. The qualities of basis functions and fully relativistic pseudopotentials were carefully benchmarked by the delta gauge method¹⁷ to ensure accuracy of our calculations. An electronic temperature of 700 K is used to count the number of electrons by the Fermi–Dirac function. The regular mesh of 240 Ry in real space was used for the numerical integration and for the solution of the Poisson equation.¹⁸ A 5 × 5 × 1 mesh of k points was adopted. Cell vectors and internal coordinates are simultaneously optimized without any constraint by using a combination scheme of the rational function (RF) method¹⁹ and the direct inversion iterative sub-space (DIIS) method²⁰ with a BFGS update^21–24 for the approximate Hessian. The force on each atom was relaxed to be less than 0.0003 Hartree/Bohr. We put four Au atoms and two Si atoms in a square unit cell to form buckled-η-phase and buckled-θ-phase as initial structures. The convergence of energy and lattice length for the number of k-mesh and energy cutoff are confirmed as shown in Tables S1 and S2 in ESI.† Calculations of phonon band structures were carried out based on the partition method proposed in ref. 25. The partition method is a method for partitioning the interatomic force constants around the supercell boundary for obtaining the better interpolated phonon dispersion of a periodic system even for the small supercell force-constant calculations. For the force calculations for estimating force constants, we used 2 × 2 supercell structures with 0.01 Å displaced configurations. We applied the r⁻⁴ weight for atoms in the region 0.4r_inner < r < r_outer to obtain proper results.

Table 1 List of basis sets

S7.0-s2p2d1f1	Se7.0-s3p2d2	Te7.0-s3p2d2f1
Si7.0-s2p2d1	Ge7.0-s3p2d2	Au7.0-s3p2d2f1

---

3 Au₂S monolayers

3.1 Structure and stability

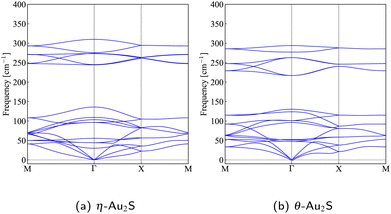
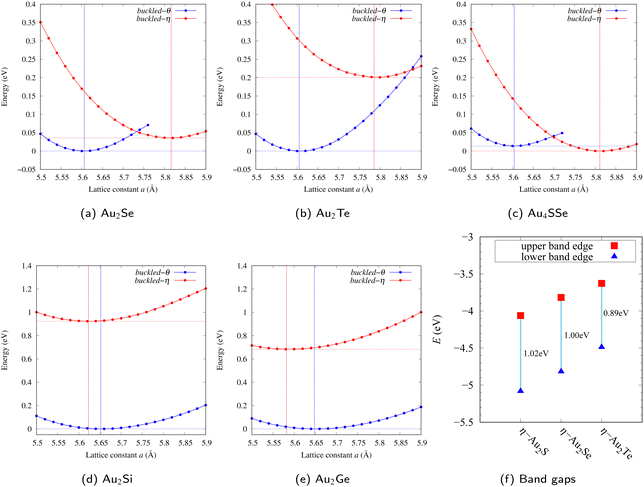
The structures of η- and θ-Au₂S monolayers obtained by the geometry optimization are shown in Fig. 1. Four Au atoms in η-phase form four square lattice in a unit cell. Two S atoms located h Å away from the center of two of the square, either up or down. The height h = 1.35 Å of η-Au₂S is a little bit shorter than h = 1.41 Å of θ-Au₂S. In the θ-Au₂S, two squares are distorted, and the distorted angle θ ≈ 60°. Therefore, each distorted square lattice forms two almost equilateral triangles. The lattice constant a = 5.613 Å of θ-Au₂S is shorter than a = 5.805 Å of η-Au₂S.

The stability of these Au₂S monolayers can be discussed by phonon dispersion in Fig. 2. Generally speaking, a imaginary frequency in a phonon band indicates a negative curvature of the potential energy surface, which means that the structure is unstable or including anharmonic contributions. The imaginary frequency in Fig. 2(b) is negligibly small enough to be considered as numerical error of force constants calculations. These phonon bands are consistent with other previous research,⁸ but our results around the Γ point are improved by the partition method.²⁵ In addition, the energy curves for lattice constants in Fig. 3 give us another insight for stability of Au₂S. The potential curve of θ-Au₂S is so shallow that a phase transition from θ-phase to η-phase is easily induced by stretching the lattice constants. The opposite concept is also true that the η-phase can cause phase transition to the θ-phase by bi-axial compression to the lattice. Such compression might be induced by lattice matching with a substrate or boundary matching with other monolayers. These kinds of interactions with other stable materials can stabilize unstable monolayers. Silicene on Ag surface^26,27 and silicene on ZrB₂²⁸ are good examples for monolayers stabilized on the surface. Therefore, it cannot be said that the θ-Au₂S is sufficiently stable as a free-standing monolayer, but it may be possible to exist on a substrate.

Fig. 2 Phonon band of η- and θ-Au₂S monolayers. (a) η-Au₂S, (b) θ-Au₂S.

Fig. 3 Energy curve of Au₂S monolayers. The red (blue) line represents the energy curve of η-phase (θ-phase).

The nudged elastic band (NEB) calculation²⁹ for Au₂S is also performed at the lattice constant a = 5.62 Å, which is close to the most stable state of θ-Au₂S. Since the energy barrier from η-phase to θ-phase is very small as shown in Fig. 4, it is concluded that the phase transition of η → θ can occur easily by applying the compressive strain of about 3.5% of the lattice constants.

Fig. 4 The change of total energy of Au₂S as a function of the distance (Bohr) from the θ-Au₂S to η-Au₂S and the corresponding geometrical structures. The NEB calculations were performed with the lattice constant a = 5.62 Å. Each number in the plot area represents the index of the NEB images.

3.2 Electronic band structure

Electronic band structures and the DOS of η- and θ-Au₂S monolayers are shown in Fig. 5(a) and 6(a). The η-Au₂S has a direct band gap of 1.02 eV at Γ point, whereas the band gap is closed for the θ-Au₂S. This kind of band gap modulation in the electronic bands of η- and θ-Cu₂S by using uniaxial and biaxial stress has been reported previously.^8,10,11,30 In ref. 11, based on the partial DOS analysis, the researchers have revealed that the valence band maximum (VBM) of θ-Cu₂S is dominantly contributed by the hybridization of p_x, p_y atomic orbitals of S atoms and d_xy atomic orbitals of Cu atoms, whereas the conduction band minimum (CBM) of θ-Cu₂S is mainly from the p_x, p_y atomic orbitals of Cu atoms.

Fig. 5 (a) Electronic band and the DOS of η-Au₂S. The y axis is taken so that the Fermi energy is zero. (b)–(f) Weight of the electronic band of Au and S atoms of η-Au₂S. The weight is projected on s, p and d type functions.

Fig. 6 (a) Electronic band and the DOS of θ-Au₂S. The y axis is taken so that the Fermi energy is zero. (b)–(f) Weight of the electronic band of Au and S atoms of θ-Au₂S. The weight is projected on s, p and d type functions.

Here, we discuss more details of the origins of the modulations of VBM and CBM around the Γ point. At first, we calculated the weight of each contribution of pseudo-atomic orbital in band structures of η- and θ-Au₂S as shown in Fig. 5(b)–(f) and 6(b)–(f) based on the ref. 31. Additionally, the partial density of states (PDOS) are shown in Fig. S2 and S3 in ESI.† Here, we denote the contribution from s type functions of Au atoms as Au-s. We also denote the valence (conduction) bands as VB1 (CB1), VB2 (CB2), and so on, in order of proximity to the Fermi level. From Fig. 5 for η-Au₂S, it is obvious that the VB1 and VB2 have large contributions from both Au-d and S-p_x,p_y. In addition, CB1 has contributions from Au-p_x,p_y, forming bonds between Au atoms arranged in a square lattice. In contrast, CB2 have contributions from Au-s, d and S-p_z, forming a flat band. The shape of VB1 and CB2 of θ-phase in Fig. 6 are similar to those of η-phase. However, two bands of VB2 and CB1 of θ-phase are hybridized and forming a crossing linear dispersion whose main contributions are Au-p_x,p_y, Au-d, and S-p_x,p_y. Here, we note that the crossing linear dispersion split a little bit when the spin–orbit interaction is included (see Fig. S1 in ESI†).

Fig. 7(a) and (b) show band structures of η- and θ-Au₂S for various heights (h + Δh Å) of S atoms with fixed positions of Au atoms. The band energy of CB1 at the Γ point remains almost unchanged when Δh is varied, since the main contributions of the CB1 are only p_x and p_y of fixed Au atoms. In contrast, the band energies of VB2, VB1 and CB2, including contributions from S atoms, decrease as the S atoms move away from the Au atomic layer. Therefore, it reveals that the CBM depends on the bond distance of Au–Au, not on the interaction between Au and S atoms. On the other hand, the VBM largely depends on the interaction between Au and S atoms. Note that the cases of Δh = 0.4, 0.6 of η-phase are not included in the above discussion to avoid the ambiguity, since the order of the bands is swapped in the cases of Δh = 0.4, 0.6 of η-phase. The flat band, whose energy decreases as Δh is increased, is a band derived from the S-p_z isolation state. It is characteristic that the flatness remains even when Δh is decreased.

Fig. 7 Band structures of (a) η- and (b) θ-Au₂S for various heights (h + Δh Å) of S atoms with fixed positions of Au atoms. (c) Band structures for some NEB images in Fig. 4. The image 0 and 9 represent the θ- and η-Au₂S, respectively. The θ (deg) represents the angle of Au atoms as shown in the Fig. 1, and d is the Au–Au bond distance in each structure.

Fig. 7(c) shows band structures of transition states from θ-phase to η-phase calculated by using structures obtained by the NEB calculation (Fig. 4). The images 0 and 9 represent the θ-phase and η-phase, respectively. The Au–Au bond distance d (see Fig. 1) increases in the transition from θ-phase to η-phase. Moreover, as the Au–Au bond distance d increases, the band energy of CB1, which consists of Au-p_x,p_y, increases. Although energies of the other bands, CB2, VB1 and VB2, also increase, the energy shifts are smaller than that of CB1.

To summarize the above discussions on Fig. 7, the CBM can be controlled by the change of Au–Au bond length d induced by strain and θ ↔ η phase transition, whereas the VBM can be controlled by interaction between the Au layer and attached S atoms.

4 Au₂X monolayers

4.1 Structure and stability

Total energies, cohesive energies, and structural parameters defined in Fig. 1 for η- and θ-Au₂X (X = S, Se, Te, Si, Ge), are listed in Table 2. The lattice constants a of all the θ-phase structures in the Table 2 are about 5.6 Å. The lattice constants a of the η-phase structures are about 5.8 Å for chalcogenides and about 5.6 Å for Si, Ge compounds. This means that lattice constants of these structures are almost independent of the species of atoms attached to the above and below the Au atomic layer. On the other hand, the heights h of X atoms are consistent with the trend in the length of the covalent bond radius.³² Since the angle θ and the Au–Au bond length d defined in Fig. 1 can be measures of the strength of the interaction between Au atoms, Table 2 indicates that θ-Au₂S, θ-Au₂Se and θ-Au₂Te might have stronger Au–Au interactions in that order.

Table 2 Properties of Au₂X. Lattice constant a, X atom's height h, angle θ, and Au–Au bond length d are defined in Fig. 1. The relative energy E_rel represents the energy difference from the energy of η-phase

Name	E rel (eV)	E coh,system (eV)	E coh,bulk (eV)	a (Å)	Height h (Å)	Angle θ (deg)	d (Å)
η-Au2S	0.0000	3.062	2.978	5.805	1.35	89.97	4.10
θ-Au2S	0.0697	3.051	2.978	5.613	1.41	62.73	3.01
η-Au2Se	0.0000	2.966	3.033	5.816	1.56	90.01	4.11
θ-Au2Se	−0.0354	2.972	3.033	5.606	1.61	60.72	2.93
η-Au2Te	0.0000	2.866	2.969	5.786	1.87	90.02	4.09
θ-Au2Te	−0.2005	2.900	2.969	5.605	1.88	58.70	2.85
η-Au2Si	0.0000	3.111	3.723	5.623	1.54	90.03	3.98
θ-Au2Si	−0.9233	3.265	3.723	5.652	1.32	54.30	2.71
η-Au2Ge	0.0000	2.940	3.418	5.582	1.76	89.97	3.95
θ-Au2Ge	−0.6835	3.054	3.418	5.648	1.52	54.32	2.71

---

The cohesive energies of monolayers and bulks in Table 2 are defined as

E_coh,system = (4 × E_Au-atom+ 2 × E_X-atom – E_{Au2X-monolayer})/6,

E_coh,bulk = {4(E_Au-atom − E_Au-bulk/N_Au-bulk) + 2(E_X-atom − E_coh,X-bulk/N_X-bulk)}/6,

where E_Au-atom and E_X-atom are the total energies of Au single atom and X single atom, respectively. E_Au-bulk and E_X-bulk are the total energies of bulk of Au and X, in which the number of the atoms in a unit cell is N. In our results, only η- and θ-Au₂S satisfy the condition E_coh,bulk < E_coh,system, which is one of the measures of stability. Therefore, η- and θ-Au₂S might be good candidates of stable monolayers. However, it cannot be said that the other monolayers do not exist as a stabilized monolayer, since these kinds of monolayers might be synthesized on a substrate.

From Fig. S6 and S7 in ESI,† the phonon bands of Au₂X monolayers around zero energy have a similar shape to Au₂S except for η-Au₂Si and η-Au₂Ge, which have large imaginary frequencies indicating instability. It is also clear from the energy curve in Fig. 8 that Au₂Si, Au₂Ge, Au₂Se, and Au₂Te prefer to be θ-phase, whereas Au₂S prefers to be η-phase. In other words, the type of more stable phase can be changed by controlling the species of atoms adsorbed on the Au lattice.

Fig. 8 Energy curves of η- and θ-Au₂X (X = Se, Te, Si, Ge) and Au₄SSe monolayers (a)–(e). The red (blue) line represents the energy curve of η-phase (θ-phase). Band gaps at the Γ point of Au₂X (X = S, Se, Te) (f). The red squares and the blue triangles represent CBM and VBM, respectively.

As an example of controlling the stability of the phase, we calculated energy curves of η- and θ-Au₄SSe, whose structure is generated by replacing a half of S atoms in Au₂S to Se atoms, as shown in Fig. 8(c). The θ-phase, which is unstable in Au₂S, stabilizes and the energy of the most stable state approaches that of the η-phase. It means that the η ↔ θ phase transition of Au₄SSe can be easily induced by tensile and compressive strain of about 3.5% of the lattice constants. Therefore, by partially substituting S atoms, it might be possible to create devices with partially different mechanical and physical properties in a single monolayer.

4.2 Electronic band structure

Electronic band structures and the DOSs of θ-Au₂X (X = Se, Te) and η- and θ-Au₂Si are shown in Fig. 9 and Fig. S10 (ESI†), respectively. The electronic band structures of the other Au₂X are shown in the ESI.† The shape of CB2, CB1, VB1, and VB2 of θ-Au₂Se is similar to θ-Au₂S. However, VB2 of θ-Au₂Te is a little bit away from the Fermi level. Therefore, though the band gap of θ-Au₂Te is closing, it does not exist a linear dispersion, which is seen in θ-Au₂S and θ-Au₂Se. The shape of the band structure of η-Au₂X (X = S, Se, Te) is almost identical, and their band gaps are shown in Fig. 8(f). In contrast, there is no band gap in η-Au₂Si and η-Au₂Ge. The shapes of the band structures of η- and θ-Au₂Si are totally different from those of Au₂X (X = S, Se, Te), since the Fermi level is lower in Au₂Si than in Au₂S. The linear dispersion and the flat band of η-Au₂Si on about 0.5 eV at the Γ point have the similar origin to the VB1, VB2 and CB1 of η-Au₂S. This means that the replacement of X atoms affects the change of the Fermi level, resulting in a drastic change of the band structure.

Fig. 9 Electronic band structures and the DOSs of θ-Au₂X (X = Se, Te) monolayers.

Finally, electronic band structures and the DOSs of η- and θ-Au₄SSe, are shown in Fig. 10. The band structure of Au₄SSe is almost identical to that of Au₂S and Au₂Se, since the number of valence electron in Au₄SSe is the same as that of Au₂S and Au₂Se. Therefore, Au₄SSe has a band structure similar to Au₂S and Au₂Se, and is equally stable in the η- and θ-phases.

Fig. 10 Electronic band structures and the DOSs of Au₄SSe monolayers.

5 Conclusions and perspectives

In this paper, we have analyzed the η ↔ θ phase transition and the change of electronic band structures of Au₂S induced by strain. We have pointed out that about 3.5% compressive biaxial strain on η-Au₂S, which is induced, e.g., by lattice matching with a substrate, can cause a transition to θ-Au₂S. It has also shown that the direct band gap of 1.02 eV in η-Au₂S disappears by this η ↔ θ phase transition. Therefore, it has revealed that the band gap and the phase of Au₂S can be controlled by strain. In addition, we have investigated the origin of band modulations around the Γ point. We have concluded that the band energy of CB1, which corresponds to CBM, is independent of the interaction between Au and S atoms, while the increase of the Au–Au bond distance d contributes significantly to the increase of the band energy of CB1. We also have found that the band energy of VB1, which corresponds to VBM, depends on both Au–S and Au–Au interactions. In particular, the band energy of VB1 decreases as the interaction between Au atoms and S atoms decreases. In the θ-Au₂S, CB1 and VB2 intersect on the Γ point, creating linear dispersion. These perspectives are significant for band gap engineering.

In the latter section, we have investigated η- and θ-Au₂X (X = Se, Te, Si, Ge) and Au₄SSe. Au₂Se and Au₂Te differ from Au₂S in that the θ-phase is more stable than the η-phase, although the electronic band structures are similar to those of Au₂S. The energy curve of Au₄SSe has revealed that we can modify the electronic state to be equally stable in the θ and η phases by replacing some of the S atoms to Se atoms. The electronic band structure of Au₂Si have revealed that the Fermi level can be shifted by replacing S atoms with Si atoms, which have different valence electron numbers, resulting in changing from semiconductor to metal. This means that, by replacing S atoms in a part of η-Au₂S that we want to give conductivity with other atoms, electronic circuits can be constructed on a single monolayer.

Thus, this family of Au₂X type monolayers has a potential to acquire a diversity of physical quantities by replacing the X element without breaking the basic Au lattice network. The family of Au₂X type monolayers may be a candidate of materials of atomic scale network devices.

Author contributions

Masahiro Fukuda: conceptualization, investigation, software, visualization, writing – original draft, writing – review & editing. Taisuke Ozaki: supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computation in this work has been done using the facilities of the Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo. The authors acknowledge financial support from JSPS KAKENHI Grant Number 20H00328. We thank Prof. Chi-Cheng Lee for helpful advises on phonon calculations based on the partition method.

References

1. M. Ashton, J. Paul, S. B. Sinnott and R. G. Hennig, Phys. Rev. Lett., 2017, 118, 106101.
2. S. Haastrup, M. Strange, M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. Torelli, P. M. Larsen, A. C. Riis-Jensen, J. Gath, K. W. Jacobsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, 2D Mater., 2018, 5, 042002.
3. J. Zhou, J. Lin, X. Huang, Y. Zhou, Y. Chen, J. Xia, H. Wang, Y. Xie, H. Yu, J. Lei, D. Wu, F. Liu, Q. Fu, Q. Zeng, C.-H. Hsu, C. Yang, L. Lu, T. Yu, Z. Shen, H. Lin, B. I. Yakobson, Q. Liu, K. Suenaga, G. Liu and Z. Liu, Nature, 2018, 556, 355–359.
4. M. Fukuda, J. Zhang, Y.-T. Lee and T. Ozaki, Mater. Adv., 2021, 2, 4392–4413.
5. Our AB₂ structure map and database are available on the interactive website, https://www.openmx-square.org/2d-ab2/.
6. A. D. Oyedele, S. Yang, L. Liang, A. A. Puretzky, K. Wang, J. Zhang, P. Yu, P. R. Pudasaini, A. W. Ghosh, Z. Liu, C. M. Rouleau, B. G. Sumpter, M. F. Chisholm, W. Zhou, P. D. Rack, D. B. Geohegan and K. Xiao, J. Am. Chem. Soc., 2017, 139, 14090–14097.
7. A. Taheri, S. Pisana and C. V. Singh, Nanoscale Adv., 2022, 4, 2873–2883.
8. L. Gao, Y.-F. Zhang and S. Du, Nano Res., 2021, 14, 2826–2830.
9. Q. Wu, W. W. Xu, D. Lin, J. Wang and X. C. Zeng, J. Phys. Chem. Lett., 2019, 10, 3773–3778.
10. H. Zhu, S. Li, W. Xia, Y. Wang and L. Shi, Solid State Commun., 2019, 302, 113704.
11. X. Chen, D. Wang, X. Liu, L. Li and B. Sanyal, J. Phys. Chem. Lett., 2020, 11, 2925–2933.
12. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
13. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
14. T. Ozaki, et al., OpenMX package, https://www.openmx-square.org/.
15. I. Morrison, D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 6728–6731.
16. T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108.
17. K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
18. T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045121.
19. A. Banerjee, N. Adams, J. Simons and R. Shepard, J. Phys. Chem., 1985, 89, 52–57.
20. P. Csaszar and P. Pulay, J. Mol. Struct., 1984, 114, 31–34.
21. C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90.
22. R. Fletcher, Comput. J., 1970, 13, 317–322.
23. D. Goldfarb, Math. Comput., 1970, 24, 23–26.
24. D. F. Shanno, Math. Comput., 1970, 24, 647–656.
25. C.-C. Lee, C.-E. Hsu and H.-C. Hsueh, J. Phys.: Condens. Matter, 2020, 33, 055902.
26. J. Gao and J. Zhao, Sci. Rep., 2012, 2, 861.
27. L. Feng, K. Yabuoshi, Y. Sugimoto, J. Onoda, M. Fukuda and T. Ozaki, Phys. Rev. B, 2018, 98, 195311.
28. A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501.
29. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985.
30. Y. Guo, Q. Wu, Y. Li, N. Lu, K. Mao, Y. Bai, J. Zhao, J. Wang and X. C. Zeng, Nanoscale Horiz., 2019, 4, 223–230.
31. C.-C. Lee, Y. Yamada-Takamura and T. Ozaki, J. Phys.: Condens. Matter, 2013, 25, 345501.
32. P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186–197.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03135g

---