Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles evaluation of dopant impact on structural deformability and processability of Li7La3Zr2O12†
A.
Dive
 *,
K.
Kim
*,
K.
Kim
 ,
S.
Kang
,
L. F.
Wan
,
S.
Kang
,
L. F.
Wan
 * and
B. C.
Wood
*
* and
B. C.
Wood
*
Laboratory for Energy Applications for the Future (LEAF), Materials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94551-0808, USA. E-mail: aniruddha.dive@wsu.edu; wan6@llnl.gov
First published on 12th July 2023
Abstract
Li7La3Zr2O12 (LLZO) and related ceramic solid electrolytes feature excellent stability and reasonable ionic conductivity, but processing remains challenging. High-temperature co-sintering is required for successful integration with the electrode, which is energetically costly and can lead to unacceptable cathode degradation. The introduction of dopants can promote lower-temperature processing by improving deformability and disrupting lattice integrity; however, an unbiased, systematic study correlating these properties to the dopant chemistry and composition is lacking. Here, we rely on a set of static and dynamic metrics derived from first-principles simulations to estimate the impact of doping on LLZO processability by quantifying LLZO structural deformability. We considered three distinct dopants (Al, Ba, and Ta) as representatives of substitutional incorporation on Li, La, and Zr sites. Our descriptors indicate that doping in general positively impacts lattice deformability, although significant sensitivities to dopant identity and concentration are observed. Amongst the tested dopants, Al doping (on the Li site) appears to have the greatest impact, as signaled across nearly the entire set of computed features. We suggest that these proxy descriptors, once properly calibrated against well-controlled experiments, could enable the use of first-principles simulations to computationally screen new ceramic electrolyte compositions with improved processability.
Introduction
Ever-growing energy demands and the impetus for clean energy continue to drive the development of advanced, reliable, and economical energy storage technologies.1–3 Conventional lithium-ion battery technology, despite its dominance in both small portable electronics and large-scale applications such as electric vehicles, is fast approaching its theoretical limits for energy density and manufacturing efficiency. In addition, safety issues associated with the use of organic liquid electrolytes continue to be a concern. All-solid-state battery (ASSB) technology,4–6 on the other hand, can be a promising alternative given its potential to achieve high energy density while reducing the fabrication cost and safety concerns.7–10 However, current ASSB technology faces several challenges, notably the development of favourable solid-state electrolytes (SSEs), to achieve decent electrochemical performance. An ideal SSE should exhibit high ionic conductivity, a wide electrochemical window, excellent stability against the electrodes, and a flexible mechanical response at the interface to accommodate volume changes of the electrodes during cycling. In addition, large-scale deployment requires cost-effective processing routes for SSEs and ASSBs.A wide range of material classes (e.g., polymers, ceramics, glasses etc.) has been explored over the past decades as potential candidates for SSEs, but none of them can simultaneously meet the abovementioned requirements for optimal performance. For example, inorganic sulfide-based SSEs, such as Li10GeP2S12 (LGPS) and Li6PS5X (X = Cl, Br, I),11–14 possess superior ionic conductivity in the range of 10−3–10−2 S cm−1 at room temperature but are chemically reactive with lithium metal and are not air stable,15–18 which presents practical challenges for handling and large-scale fabrication. In contrast, oxide-based SSEs, such as the garnet-type Li7La3Zr2O12 (LLZO), show improved chemical stability against the environment and common electrodes, including Li metal anodes,19–21 as well as tunable conductivity over a wide range of compositions.22–26 The highest Li-ion conductivity has been observed for the cubic phase of Li7−xLa3Zr2O12, although at room temperature it transforms into the thermodynamically more stable tetragonal phase with two orders of magnitude lower conductivity (∼10−6 S cm−1).27,28 Previous experimental efforts have been focused on stabilizing the cubic phase of LLZO, either by controlled synthesis at elevated temperatures19,29,30 or via elemental doping31–33 to achieve high Li-ion conductivity. Several dopants, such as Al, Ta, and Ga, have been successfully incorporated into the LLZO lattice that result in bulk conductivities of ∼10−4 S cm−1.34–39
Apart from the high ionic conductivities required for the SSEs, good physical contact between the SSEs and the electrodes needs to be realized to ensure sufficient Li-ion transport at their interfaces. In this regard, co-sintering can be an effective and economical approach for large-scale processing of the ASSB. However, due to the rigid ceramic nature of oxide-based SSEs, such as LLZO, ultra-high sintering temperatures (>1000 °C) are usually required to reach proper densification, at which point common cathode materials, such as LiCoO2, may already be decomposed. Ideally, the sintering temperature of oxide-based SSEs ought to be lowered to below 900 °C to prevent or minimize interfacial reactions while ensuring good physical contacts at the SSE-cathode interfaces. Experiments have reported that doping LLZO with Al, Ga, or Ta can lower its sintering temperature by as much as 250 °C.34,35,40,41 Despite these advances, most of these experiments were limited to single dopant compositions, and they adopted a variety of sintering approaches, e.g., conventional sintering, hot pressing, microwave assisted sintering, spark plasma sintering and field assisted sintering.42–48 Hence, a more systematic study of the impact of dopant chemistry and concentration on the sintering behaviour of LLZO would provide significant benefit.
In principle, atomistic simulations based on density functional theory (DFT) offer a way of systematically exploring dopant activity and comparing impacts in an unbiased way. However, the connection to processability is not straightforward, and the wide disparity in time and length scales make direct first-principles simulations of sintering unmanageable. Here, we instead introduce several metrics associated with lattice deformability that can be computed directly from DFT. Because local deformation is precursory to sintering, these metrics are expected to track with experimental trends in sintering temperature and densification kinetics during processing. Specifically, both static and dynamic metrics—including elastic constants, energy penalties for bulk and surface structural disordering, structural fluctuations of local building blocks, thermal vibrations of atoms, and surface energies—are combined to unravel the local correlation between structure, chemistry, and mechanics upon varying the choice of dopants and doping level. We also discuss impacts on ionic conductivity, which must be balanced against the benefits for processing. We suggest that these metrics can be used as descriptors to select suitable dopants and concentrations for optimizing LLZO processing conditions, particularly when calibrated and validated against well-controlled experiments.
Methods
The unit cell of cubic LLZO is comprised of interconnected LaO8 and ZrO6 polyhedra as shown in Fig. 1, with Li ions partially occupying the interstitial 24d (tetrahedral) and 96h (octahedral) sites.49 In this work, we consider three doping levels of three dopants, Al, Ba and Ta, distinct by their preference for occupying Li, La and Zr sites, respectively, in cubic LLZO as summarized in Table 1. The computational details on obtaining ground state for different doped LLZO compositions are provided in the ESI.† We note that the highest dopant levels can be difficult to achieve through experimental synthesis; however, trends obtained from the three dopant levels that we explore can be interpolated to draw conclusions for intermediate dopant concentrations.| Dopant type | Composition | Doping site |
|---|---|---|
| Undoped reference | Li7La3Zr2O12 | N/A |
| Al3+ | Al0.25Li6.25La3Zr2O12 | Li (24d and 96h) |
| Al0.50Li5.5La3Zr2O12 | ||
| Al0.75Li4.75La3Zr2O12 | ||
| Ba2+ | Li7.25La2.75Ba0.25Zr2O12 | La |
| Li7.5La2.5Ba0.50Zr2O12 | ||
| Li7.75La2.25Ba0.75Zr2O12 | ||
| Ta5+ | Li6.75La3Zr1.75Ta0.25O12 | Zr |
| Li6.5La3Zr1.5Ta0.50O12 | ||
| Li6.25La3Zr1.25Ta0.75O12 |
Properties of these nine doped LLZO systems were compared with those of undoped LLZO. The bulk mechanical properties were calculated by performing static DFT calculations at 0 K. We employed the generalized gradient approximation (GGA) with the projector-augmented wave (PAW)50 pseudopotentials implemented in the Vienna Ab Initio Simulation Package (VASP).51–53 The selected plane-wave cutoff was 530 eV with a Monkhorst-Pack k-point sampling using 3 × 3 × 3 grid. The DFT energies and atomic forces were converged to within 0.01 meV per atom and 10−2 eV Å−1, respectively. To calculate the dynamic properties, ab initio molecular dynamics (AIMD) simulations were performed to compute the amorphization energy and thermally activated atomic displacements and structural fluctuations. The amorphization energy of LLZO phase X was calculated following eqn (1):
| Eamorphization(X) = Edisordered(X) − Ecrystaline(X) | (1) |
A lower plane-wave cutoff of 400 eV with Γ-centered k-point mesh was selected for computational efficiency with similar DFT accuracy. All the AIMD simulations were perfomed under NVT ensemble during equilibration as well as production runs. The equilibration runs were performed for 10 ps followed by production runs of 60 ps, from which the dynamic property data were computed: mean square displacement (MSD) and the local distortion of building blocks. The MSD data were used to compute the Lindemann ratio, and the local distortion of building blocks was determined by calculating the continuous shape measure54 (CSM) of the LaO8 and ZrO6 polyhedra throughout the dynamics run. The details of the MSD plots, Lindemann ratio calculations, and CSM calculations are provided in the ESI.†
Surface energies and surface disordering energies were computed starting from the symmetric Li-rich Li7.5La3Zr2O12 slab model. Charge balance was retained by removing atoms, which results in Li7La3Zr2O12 stoichiometry. Additional details of constructing the slab models are provided in the ESI.† The surface energy was evaluated as
 | (2) |
 | (3) |
Results
Impact on bulk properties
We start by computing the elastic moduli as the first estimate of potential impact of dopants on the overall mechanical strength of the LLZO lattice. As shown in Fig. 2(a and b), our calculated bulk and shear moduli for undoped LLZO agree well with existing literature (B = 116.7 GPa and G = 63.7 GPa).55–57 For Al, Ba and Ta doping, we observe a continuous drop in the bulk and shear moduli with increase in doping concentration. Overall, when dopants are incorporated into the LLZO lattice, our calculations predict generally lowered elastic moduli than undoped LLZO, suggesting a softer lattice response and hence easier deformability of LLZO to external mechanical stress during sintering. | ||
| Fig. 2 The computed (a) bulk moduli, (b) shear moduli, and (c) amorphization energy per f.u. of undoped and doped LLZO. | ||
Another parameter that informs the ease of bulk deformability is the amorphization energy, defined as the energy difference between the amorphous and crystalline phases of the material. As the amorphization energy quantifies the energy penalty for disordering from the ordered crystalline state, lower values indicate easier symmetry breaking and atomic rearrangement. Such rearrangements are experienced locally at surfaces and interfaces during high-temperature sintering. Fig. 2(c) compares the amorphization energy of doped LLZO with the undoped phase. The results show that Al doping in AlxLi7−3xLa3Zr2O12 can gradually lower the amorphization energy by as much as 1 eV per formula unit at x = 0.75. A high doping level of Ba also shows some effectiveness in reducing the amorphization energy, although lower doping levels of Ba as well as Ta doping are less impactful. The overall trend for the observed variations in amorphization energy upon doping roughly agrees with the results obtained for the elastic moduli: any type of doping chemistry or substituting site can relax the overall lattice resistance to disordering, whether induced by external mechanical stress or internal distortions at high temperatures.
Besides the static metrics presented in Fig. 2, we performed AIMD at 1200 K and 1500 K to capture thermal vibrations of atoms and distortions of building blocks, namely LaO8 and ZrO6 polyhedra. Dynamic variations of atomic displacements and shapes of polyhedra are of interest particularly in the vicinity of dopant sites that may act as hotspots to promote structural deformation or pre-melting at higher temperatures. It is worth noting that 1200 K and 1500 K approach the experimentally reported sintering temperature (1650 K–1800 K), and thus enable direct analysis of dynamic properties at simulation-accessible timescales. From the AIMD trajectories, the MSD of individual La and Zr ions were extracted to calculate the Lindemann ratio. According to Lindemann's criterion, melting occurs when the average amplitude of thermal vibrations of atoms exceeds 10% of the interatomic distance (e.g., a Lindemann ratio of 0.1). Due to the volume constraint in the NVT ensemble, melting is generally suppressed in our simulations, but the value is nonetheless a suitable and easily calculable metric informing the degree of local bond deformation. In Fig. 3(a, b), we present the calculated Lindemann's ratio for La and Zr in doped LLZO at 1200 K (dashed lines) and 1500 K (solid lines). For Ba- and Ta-doped LLZO, since the Ba and Ta ions substitute La and Zr ions, the Ba MSD is included in the La MSD for Ba-doped LLZO, and the Ta MSD in the Zr MSD for Ta-doped LLZO respectively. We observe that La ions exhibit higher Lindemann's ratios compared to Zr ions, suggesting weaker La–O bonds which may serve as the first sign of melting or deformation in the bulk lattice. As the temperature increases from 1200 K to 1500 K, the Lindemann ratio increases, which is expected as the temperature approaches closer to the melting temperature. On the contrary, at 1200 K, Ta doping seem to have negligible impact on the Zr Lindemann ratio whereas Al and Ba doping result in small increase in Lindemann ratio with increase in doping concentrations. With increase in temperature, at 1500 K, there are two factors that contribute towards distinctive Zr Lindemann ratio trends: (a) elevated temperatures introduce a degree of anharmonicity for the atomic vibrations which increases the Lindemann ratio and (b) increased interactions with more mobile neighboring LaO8 polyhedra (being relatively weaker vibrates with greater amplitude as evident from higher Lindemann ratio). These factors are more dominant at high temperatures closer to melting temperature and therefore we observe distinct trend at high temperature as compared to 1200 K where the Zr–O bonds are is quite stable. The distinct trends at high temperature suggest distinct response of dopants on the Zr Lindemann ratio at high temperatures wherein localized pre-melting/melting could be initiated. This supports our claim that Zr Lindemann ratio especially at temperatures closer to melting temperatures could be a probable descriptor for determining the ease of sintering. Overall, for all dopants, higher doping levels increase the La and Zr Lindemann ratios, indicating enhanced local fluctuations in the La–O and Zr–O bond environments. Such increased bond deformation at high temperatures suggests possible pre-melting of the LLZO lattice on doping.
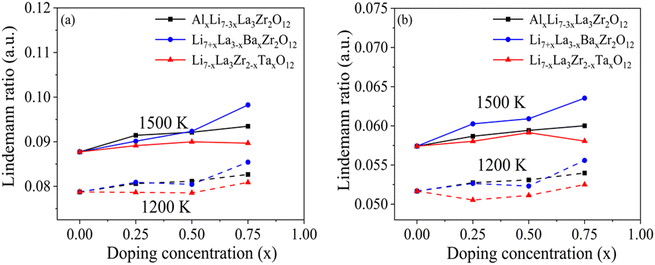 | ||
| Fig. 3 The computed Lindemann ratio averaged over (a) La and (b) Zr atoms at 1200 K and 1500 K for undoped and doped cubic LLZO. | ||
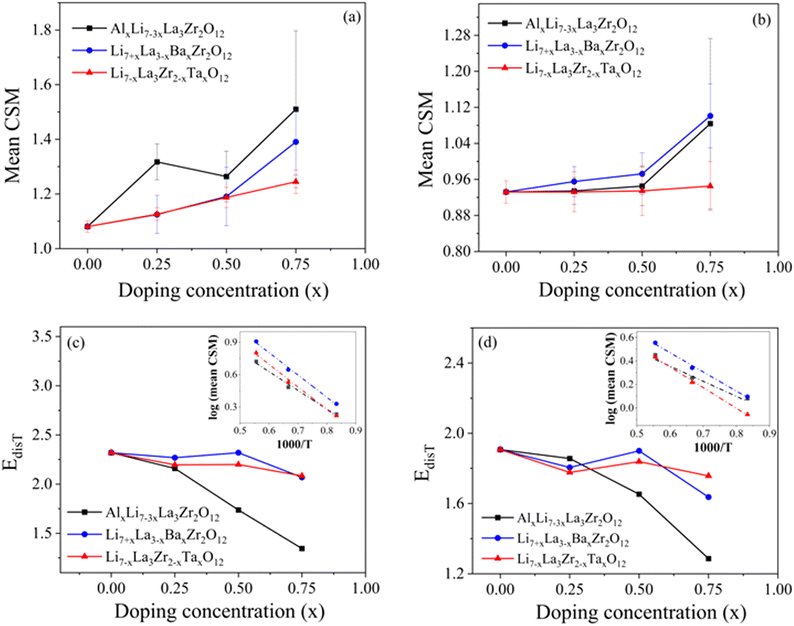
To assess the impact of dopants on the local environments in LLZO, we further expanded our scope from the La–O and Zr–O bonds represented by the Lindemann ratio to the LLZO structure building blocks: LaO8 and ZrO6 polyhedra. The ground-state structure of LLZO consists of perfect LaO8 and ZrO6 polyhedra (Fig. 1). At elevated temperatures and in the presence of dopants (The difference in the electronegativties of the dopant atoms could influence the nature of bonding between dopant and nearby oxygen atoms causing possible localized distortions within the crystal structure), the shapes of these LaO8 and ZrO6 polyhedra distort, which can be correlated to local disordering and, ultimately, materials processability. Therefore, using the AIMD trajectories at 1200 K, we computed the continuous shape measure (CSM) to probe local symmetry distortions of the LaO8 and ZrO6 polyhedra. A zero CSM value indicates a perfect match to an ideal reference polyhedral symmetry, which is extracted from the ground-state structure of undoped cubic LLZO structure at 0 K, whereas higher values correspond to greater distortions. Fig. 4(a and b) displays the mean CSM values averaged over the number of LaO8 and ZrO6 polyhedra in the simulation box. For undoped LLZO, the temperature-induced mean CSM values are 1.08 for LaO8 polyhedra and 0.93 for ZrO6 polyhedra at 1200 K respectively. Like the Lindemann ratio, the weaker La–O bonds amplify the local distortion of LaO8 polyhedra, raising their CSM values as compared to those for ZrO6. Doping increases the mean CSM values for LaO8 polyhedra, implying the dopants easily break the structural symmetry by perturbing local bond environments in building blocks. With increase in temperature from 1200 K to 1800 K, the CSM values for LaO8 as well as ZrO6 polyhedra increase (as shown in Fig. S9 and S10 in ESI†), which corresponds to highly distorted polyhedral units in the lattice. These highly distorted polyhedral units would ultimately be destroyed as melting starts. Therefore, along with the mean extent of polyhedral distortions, the relative ease of thermally amplifying such distortions would also signal lattice deformability and processability. To quantify this ease of temperature-induced polyhedral distortion, we introduce a thermal distortion energy (EdisT) associated with the polyhedral building units. The mean CSM for both LaO8 and ZrO6 polyhedra follow an exponential relationship with temperature (T) (check Fig. S9 and S10 in the ESI†). EdisT is therefore calculated by determining the slope of the log (mean CSM) versus inverse temperature (1000/T; see inset in Fig. 4(c and d)). EdisT provides an estimate of relative ease of inducing thermal distortions of polyhedral unit in the LLZO lattice. While it is difficult to correlate the absolute values of EdisT to measurable physical properties, they are beneficial in evaluating the amount of thermal energy necessary to meaningfully distort the polyhedral building units. Lower EdisT values correspond to lower barriers for polyhedral distortions, and hence to easier sintering of the LLZO lattice.
Fig. 4 shows the computed EdisT for (c) LaO8 and (d) ZrO6 polyhedra in undoped and doped LLZO. Al doping seems to highly effective in lowering EdisT for both LaO8 as well as ZrO6 polyhedra as compared to other dopants. In conjunction with relatively higher mean CSM as observed in Fig. 4(a and b), we conclude that Al doping produces larger intrinsic polyhedral distortions in the LLZO lattice, as well as higher thermal sensitivity to further distortion. This points towards earlier onset of sintering and premelting. The high relative impact of Al in determining polyhedral distortions and deformability is not obvious, given that Al substitutes on the Li site and therefore is not directly involved in the formation of LaO8 or ZrO6; nevertheless, it highlights the close coupling between the conduction cations and the broader lattice moieties.
Impact on surface properties
Apart from metrics associated with bulk LLZO properties, we further proceeded to investigate surface-dependent metrics. This choice was motivated by an understanding that solid-state sintering is driven by a reduction in surface area upon fusion and densification.58,59 As a first step, we calculated the surface energies for six low-index LLZO surfaces with different terminations: (100) Li, (110) Li, (111) Li, (110) La, (111) Zr, and (110) O (in this notation, the terminating species follows the surface orientation). Increased surface energies indicate reduced surface stability, implying higher driving force for deformation and reconstruction during thermal processing. Results are presented in Fig. 5(a–c). Here, significant differences are found among the three tested dopants. Al doping is found to increase the surface energies almost monotonically, whereas Ba doping shows the opposite trend. On the other hand, Ta doping has negligible impact on the surface energies across the entire doping concentration. We again conclude that Al doping has the largest impact on surface destabilization, which should translate to easier surface deformability. | ||
| Fig. 5 The calculated surface energies for (a) Li7−3xAlxLa3Zr2O12, (b) La7+xLa3−xBaxZr2O12 and (c) Li7−xLa3Zr2−xTaxO12. | ||
As in the bulk case, it is further desirable to augment the surface energy calculations with another metric that more directly captures the dynamic atomic rearrangements on surface.
Accordingly, we introduce the concept of surface disordering energy, defined as the energy difference between a disordered and a structured surface configuration (analogous to the bulk amorphization energy). It was previously shown by Canepa et al.60 that the (100) Li surface of LLZO is the most stable surface at high temperatures, making it a reasonable starting point for surface disordering energy calculations. In addition, we also calculated surface disordering energies for the (111) Zr surface to represent a class of high-energy surfaces. Fig. 6 displays the surface disordering energies for Al, Ta and Ba doped (100) Li and (111) Zr surfaces as a function of doping level. For undoped LLZO, the (100) Li surface shows higher surface disordering energy (11.85 J m−2) compared to the (111) Zr surface (2.13 J m−2), which is expected given that the higher stability of the (100) Li surface also implies resistance to disorder and deformation. When dopants are incorporated, the disordering energy of the (100) Li surface gradually decreases with increasing doping level up to x = 0.75, indicating doping can facilitate surface rearrangement or reconstruction and thus boost surface diffusion for sintering at elevated temperatures. On the other hand, doping has little effect on the disordering energy of the (111) Zr surface, presumably due to the intrinsic instability of the surface.
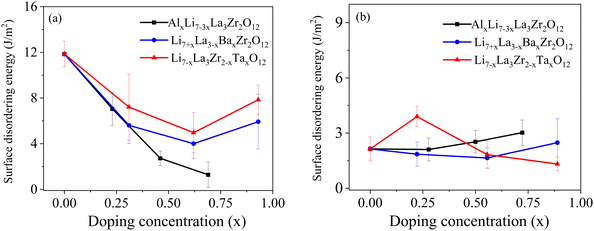 | ||
| Fig. 6 The calculated surface disordering energies for (a) the (100) Li surface and (b) the (111) Zr surface for different doped LLZO compositions. | ||
Discussion
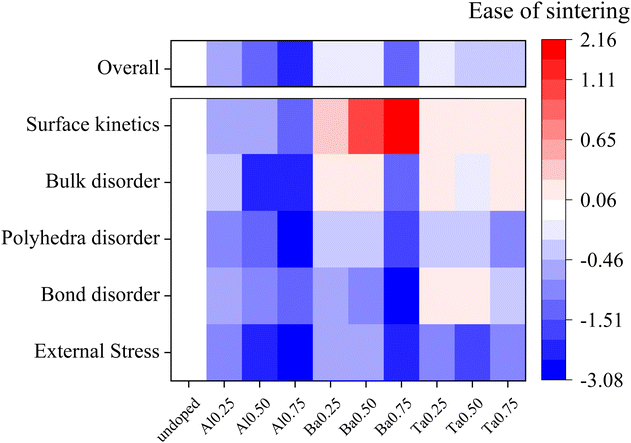
The computed results in Fig. 2–6 encompass bulk static descriptors (elastic moduli and amorphization energy) measuring the energy cost for overall lattice distortion; bulk dynamical descriptors (Lindemann's ratio and CSM) measuring the deformability of local bonds and LaO8/ZrO6 building blocks; and surface static descriptors (surface energy and surface disordering energy) measuring the energy cost for surface reconstruction and deformation. Although it is challenging to establish a direct relationship to the sintering rates of doped LLZO compositions, these metrics encode the atomistic impact of doping on the deformability of LLZO and can therefore provide a useful guide to estimate of how doping could potentially impact the sinterability of doped LLZO compositions.For further analysis, we regroup our distinct calculated metrics into five major descriptor categories based on the physical property that is being assessed: (a) external stress: a measure of ease of LLZO lattice deformability under external stress, calculated based on the bulk and shear moduli; (b) bond disorder: a measure of ease of localized bond vibration amplitude and breaking, calculated based on the Lindemann Ratio for La and Zr; (c) polyhedral disorder: a measure of temperature-induced distortions in building blocks of LLZO lattice, calculated based on the mean CSM and EdisT values for LaO8 and ZrO6; (d) bulk disorder: a measure of ease of overall lattice disordering, calculated based on the amorphization energies; (e) surface kinetics: a measure of kinetics of surface-controlled processes during sintering, calculated based on the surface energies and surface disordering energies.
Together, these five proposed descriptors effectively characterize different thermal and processing conditions encountered during sintering and therefore can be leveraged to quantify the sinterability of doped LLZO. The external stress descriptor captures the response to mechanical stresses experienced during sintering. The three disorder descriptors capture various impacts of temperature on the lattice deformability from the atomic scale (bond disorder) to the local building block (polyhedral disorder) to the bulk lattice (bulk disorder). Lastly, the surface kinetics descriptor characterizes the surface-controlled processes explored during sintering.
Fig. 7 collects these descriptors into a continuous and quantifiable “Ease of sintering,” which describes how doping impacts each descriptor with reference to the undoped system. The Ease of sintering is a unitless entity calculated as:
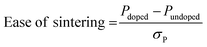 | (4) |
From Fig. 7, we can visually observe how distinct dopant species and doping levels have different impacts on each of the descriptors. Based on the Overall descriptor, we see that doping in general is beneficial towards improving the material deformability and should thereby assist in lowering the sintering temperature of LLZO. Amongst the different dopants, Al doping has a relatively larger impact on the LLZO deformability as compared to other dopants. Digging deeper into the five descriptor categorizations, we first note that all dopants seem to improve the LLZO lattice deformability under external stress as compared to the undoped LLZO. Next, in terms of temperature-induced disordering, Al doping seems to impact in broad extent from an atomic level up to bulk lattice, represented by Bond, Polyhedra and Bulk disorder descriptors, whereas the other dopants have mixed results. Similarly, Al doping seems to be most efficient in accelerating the surface kinetics. Additional computational screening may reveal whether the apparently beneficial effects of Al doping are connected to the dopant element itself or to the substitution site, although this is difficult to discern in the current study.
It is worth emphasizing that our deformability descriptors vary in terms of their apparent sensitivity to dopant species and concentration. This reflects the fact that our metrics target slightly different physical contributions. We suggest that the most effective predictive model should incorporate several individual descriptors, much as our Overall descriptor attempts to do. Well-controlled experiments could provide the necessary benchmark calibration and validation data to establish quantitative relations between predicted structural deformability descriptors and actual sintering temperature or densification kinetics of doped LLZO. Proper calibration could allow suitable weighting factors for the various descriptors to be determined and applied for efficiently screening additional dopants and their subsequent impact on densification kinetics, sintering temperature, and surface premelting.
Finally, it must be cautioned that introduction of dopants, though generally beneficial for sintering and processability, may cause unwanted disruption of local Li+ mobility. This can occur either by disrupting well-defined conduction channels that are necessary for maintaining good ionic conductivity,61–63 or by altering Li+ site occupancies as an intrinsic means of mitigating local charge redistribution and perturbing the potential energy landscape without rearrangement of the entire lattice. To understand the additional impact of doping on the Li+ mobility, we calculated the activation energies for diffusion through pristine and doped cubic LLZO, as reported in Table 2. Our calculated activation energy of 0.27 eV for pristine cubic LLZO matches closely to previously reported values from experiments as well as theory. The activation energy was calculated from the Li+ diffusivity using the Arrhenius relationship. Additional details are provided in the ESI.†
Overall, doping shows a consistent increase in the activation energy with doping concentration for all the distinct dopants. Hence, while doping positively impacts the LLZO deformability, thereby improving the processability of these solid electrolytes, the negative impact on the Li+ conductivity cannot be neglected. Ideally, a delicate balance between improved processability and suitably retained Li+ conductivity needs to be ensured for rational design.
Conclusions
Our study represents an initial step towards rapid computational evaluation of the processability of LLZO solid electrolytes, as well as related ceramics. Rather than simulating sintering directly, we adopt an approach that examines effects of chemical modification on lattice deformability based on a series of static and dynamic metrics that can readily computed from first principles. Together, we suggest that these metrics comprise a systematic, unbiased evaluation of the impact of doping on the deformability of LLZO solid electrolytes, with direct implications for promoting low-temperature processing. The metrics were further grouped into categories representing different physical contributions, which we suggest as suitable descriptors: (a) external stress, (b) bond disorder, (c) polyhedra disorder, (d) bulk disorder and (e) surface kinetics. These descriptors, which have dual benefits of continuous valuation and rigorous physical definition, are proposed as a new means of quantifying the impact of doping on sinterability, and should relate to both sintering temperature and densification kinetics.The approach was applied to evaluate the impact of three dopants (Al, Ba, and Ta) at distinct dopant sites (Li, La, and Zr, respectively). Overall, doping seems to be helpful towards improving the LLZO lattice deformability; however, the dopants were shown to differ significantly in terms of overall benefit and sensitivity to dopant concentration. Among our tested set of dopants, Al seems to have the most significant and consistent impact on majority of our descriptors, which suggests improved deformability of Al-doped LLZO solid electrolytes compared to the other cases. Although the current analysis is semi-quantitative at best, we further propose that our descriptors could eventually be used for quantitative prediction of the actual sintering temperature or densification rate. This would require careful calibration against well-controlled experiments, based on which individual descriptor weights could be optimized. The resulting computational engine could enable rapid screening of additional dopant compositions and concentrations towards higher efficiency, lower-cost processing via co-sintering of the ceramic electrolyte and cathode.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract Number DE-AC52-07NA27344. Funding was provided by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Vehicle Technologies Office. An award of computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. Additional computational resources were provided by the Department of Energy's Office of Energy Efficiency and Renewable Energy located at the National Renewable Energy Laboratory. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights.References
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
- M. M. Rahman, A. O. Oni, E. Gemechu and A. Kumar, Energy Convers. Manage., 2020, 223, 113295 CrossRef CAS.
- D. Q. Oliveira, O. R. Saavedra, K. Santos-Pereira, J. D. F. Pereira, D. S. Cosme, L. S. Veras, R. G. Bento and V. B. Riboldi, Energy Syst., 2021, 1–30 Search PubMed.
- S. H. Jung, U. H. Kim, J. H. Kim, S. Jun, C. S. Yoon, Y. S. Jung and Y. K. Sun, Adv. Energy Mater., 2020, 10, 1903360 CrossRef CAS.
- A. Banerjee, X. Wang, C. Fang, E. A. Wu and Y. S. Meng, Chem. Rev., 2020, 120, 6878 CrossRef CAS PubMed.
- C. Li, Z.-y Wang, Z.-j He, Y.-j Li, J. Mao, K.-h Dai, C. Yan and J.-c Zheng, Sustainable Mater. Technol., 2021, 29, e00297 CrossRef CAS.
- K. Takada, Acta Mater., 2013, 61, 759 CrossRef CAS.
- C. Sun, J. Liu, Y. Gong, D. P. Wilkinson and J. Zhang, Nano Energy, 2017, 33, 363 CrossRef CAS.
- K. B. Hatzell, X. C. Chen, C. L. Cobb, N. P. Dasgupta, M. B. Dixit, L. E. Marbella, M. T. McDowell, P. P. Mukherjee, A. Verma, V. Viswanathan, A. S. Westover and W. G. Zeier, ACS Energy Lett., 2020, 5, 922–934 CrossRef CAS.
- H. Liu, X. B. Cheng, J. Q. Huang, H. Yuan, Y. Lu, C. Yan, G. L. Zhu, R. Xu, C. Z. Zhao, L. P. Hou, C. He, S. Kaskel and Q. Zhang, ACS Energy Lett., 2020, 5, 833 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed.
- S. Banerjee, X. Zhang and L. W. Wang, Chem. Mater., 2019, 31, 7265 CrossRef CAS.
- A. Kuhn, V. Duppel and B. V. Lotsch, Energy Environ. Sci., 2013, 6, 3548–3552 RSC.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- Y. Zhu and Y. Mo, Angew. Chem., Int. Ed., 2020, 59, 17472–17476 CrossRef CAS.
- B. Chen, J. Ju, J. Ma, J. Zhang, R. Xiao, G. Cui and L. Chen, Phys. Chem. Chem. Phys., 2017, 19, 31436 RSC.
- S. K. Jung, H. Gwon, S. S. Lee, H. Kim, J. C. Lee, J. G. Chung, S. Y. Park, Y. Aihara and D. Im, J. Mater. Chem. A, 2019, 7, 22967 RSC.
- P. Hu, Y. Zhang, X. Chi, K. Kumar Rao, F. Hao, H. Dong, F. Guo, Y. Ren, L. C. Grabow and Y. Yao, ACS Appl. Mater. Interfaces, 2019, 11, 9672 CrossRef CAS PubMed.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778 CrossRef CAS PubMed.
- R. Sudo, Y. Nakata, K. Ishiguro, M. Matsui, A. Hirano, Y. Takeda, O. Yamamoto and N. Imanishi, Solid State Ionics, 2014, 262, 151 CrossRef CAS.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714 RSC.
- Y. Li, J. T. Han, C. A. Wang, H. Xie and J. B. Goodenough, J. Mater. Chem., 2012, 22, 15357 RSC.
- S. Ohta, T. Kobayashi and T. Asaoka, J. Power Sources, 2011, 196, 3342 CrossRef CAS.
- L. J. Miara, S. P. Ong, Y. Mo, W. D. Richards, Y. Park, J. M. Lee, H. S. Lee and G. Ceder, Chem. Mater., 2013, 25, 3048 CrossRef CAS.
- T. Zaiß, M. Ortner, R. Murugan and W. Weppner, Ionics, 2010, 16, 855 CrossRef.
- A. Ramzy and V. Thangadurai, ACS Appl. Mater. Interfaces, 2010, 2, 385 CrossRef CAS PubMed.
- M. Klenk and W. Lai, Phys. Chem. Chem. Phys., 2015, 17, 8758 RSC.
- K. Meier, T. Laino and A. Curioni, J. Phys. Chem. C, 2014, 118, 6668 CrossRef CAS.
- J. Awaka, A. Takashima, K. Kataoka, N. Kijima, Y. Idemoto and J. Akimoto, Chem. Lett., 2010, 40, 60–62 CrossRef.
- C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2011, 50, 1089 CrossRef CAS PubMed.
- S. Adams and R. P. Rao, J. Mater. Chem., 2012, 22, 1426 RSC.
- A. Dumon, M. Huang, Y. Shen and C.-W. Nan, Solid State Ionics, 2013, 243, 36–41 CrossRef CAS.
- D. Mori, K. Sugimoto, Y. Matsuda, K. Ohmori, T. Katsumata, S. Taminato, Y. Takeda, O. Yamamoto and N. Imanishi, J. Electrochem. Soc., 2018, 166, A5168–A5173 CrossRef.
- Y. Jin and P. J. McGinn, J. Power Sources, 2011, 196, 8683 CrossRef CAS.
- K. Ishiguro, H. Nemori, S. Sunahiro, Y. Nakata, R. Sudo, M. Matsui, Y. Takeda, O. Yamamoto and N. Imanishia, J. Electrochem. Soc., 2014, 161, A668 CrossRef CAS.
- J. F. Wu, E. Y. Chen, Y. Yu, L. Liu, Y. Wu, W. K. Pang, V. K. Peterson and X. Guo, ACS Appl. Mater. Interfaces, 2017, 9, 1542 CrossRef CAS PubMed.
- S. Mukhopadhyay, T. Thompson, J. Sakamoto, A. Huq, J. Wolfenstine, J. L. Allen, N. Bernstein, D. A. Stewart and M. D. Johannes, Chem. Mater., 2015, 27, 3658 CrossRef CAS.
- J. L. Allen, J. Wolfenstine, E. Rangasamy and J. Sakamoto, J. Power Sources, 2012, 206, 315 CrossRef CAS.
- E. Rangasamy, J. Wolfenstine and J. Sakamoto, Solid State Ionics, 2012, 206, 28 CrossRef CAS.
- K. Tadanaga, H. Egawa, A. Hayashi, M. Tatsumisago, J. Mosa, M. Aparicio and A. Duran, J. Power Sources, 2015, 273, 844 CrossRef CAS.
- S. Toda, K. Ishiguro, Y. Shimonishi, A. Hirano, Y. Takeda, O. Yamamoto and N. Imanishi, Solid State Ionics, 2013, 233, 102 CrossRef CAS.
- I. N. David, T. Thompson, J. Wolfenstine, J. L. Allen and J. Sakamoto, J. Am. Ceram. Soc., 2015, 98, 1209 CrossRef CAS.
- J. Xue, K. Zhang, D. Chen, J. Zeng and B. Luo, Mater. Res. Express, 2020, 7, 025518 CrossRef CAS.
- Z. Dong, C. Xu, Y. Wu, W. Tang, S. Song, J. Yao, Z. Huang, Z. Wen, L. Lu and N. Hu, Nanomaterials, 2019, 9, 721 CrossRef CAS PubMed.
- C. Li, Y. Liu, J. He and K. S. Brinkman, J. Alloys Compd., 2017, 695, 3744–3752 CrossRef CAS.
- M. Botros, R. Djenadic, O. Clemens, M. Möller and H. Hahn, J. Power Sources, 2016, 309, 108–115 CrossRef CAS.
- M. Ihrig, T. P. Mishra, W. S. Scheld, G. Häuschen, W. Rheinheimer, M. Bram, M. Finsterbusch and O. Guillon, J. Eur. Ceram. Soc., 2021, 41, 6075–6079 CrossRef CAS.
- Y. Zhang, F. Chen, R. Tu, Q. Shen and L. Zhang, J. Power Sources, 2014, 268, 960–964 CrossRef CAS.
- H. Xie, J. A. Alonso, Y. Li, M. T. Fernández-Díaz and J. B. Goodenough, Chem. Mater., 2011, 23, 3587 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. Alemany, D. Casanova, S. Alvarez, C. Dryzun and D. Avnir, Rev. Comput. Chem., 2017, 289–352 CAS.
- S. Yu, R. D. Schmidt, R. Garcia-Mendez, E. Herbert, N. J. Dudney, J. B. Wolfenstine, J. Sakamoto and D. J. Siegel, Chem. Mater., 2016, 28, 197 CrossRef CAS.
- J. Wolfenstine, J. L. Allen, J. Sakamoto, D. J. Siegel and H. Choe, Ionics, 2018, 24, 1 CrossRef.
- J. E. Ni, E. D. Case, J. S. Sakamoto, E. Rangasamy and J. B. Wolfenstine, J. Mater. Sci., 2012, 47, 7978 CrossRef CAS.
- R. Shi, M. Wood, T. W. Heo, B. C. Wood and J. Ye, J. Eur. Ceram. Soc., 2021, 41, 211–231 CrossRef CAS.
- M. Wood, X. Gao, R. Shi, T. W. Heo, J. A. Espitia, E. B. Duoss, B. C. Wood and J. Ye, J. Power Sources, 2021, 484, 229252 CrossRef CAS.
- P. Canepa, J. A. Dawson, G. Sai Gautam, J. M. Statham, S. C. Parker and M. S. Islam, Chem. Mater., 2018, 30, 3019–3027 CrossRef CAS.
- W. E. Tenhaeff, E. Rangasamy, Y. Wang, A. P. Sokolov, J. Wolfenstine, J. Sakamoto and N. J. Dudney, ChemElectroChem, 2014, 1, 375–378 CrossRef.
- S. Yu and D. J. Siegel, Chem. Mater., 2017, 29, 9639–9647 CrossRef CAS.
- T. W. Heo, A. Grieder, B. Wang, M. Wood, T. Hsu, S. A. Akhade, L. F. Wan, L.-Q. Chen, N. Adelstein and B. C. Wood, npj Comput. Mater., 2021, 7, 214 CrossRef CAS.
- C. Shao, H. Liu, Z. Yu, Z. Zheng, N. Sun and C. Diao, Solid State Ionics, 2016, 287, 13–16 CrossRef CAS.
- H. Xie, Y. Li and J. B. Goodenough, Mater. Res. Bull., 2012, 47, 1229–1232 CrossRef CAS.
- W. Xia, B. Xu, H. Duan, Y. Guo, H. Kang, H. Li and H. Liu, ACS Appl. Mater. Interfaces, 2016, 8, 5335 CrossRef CAS PubMed.
- K. Hayamizu, S. Seki and T. Haishi, J. Chem. Phys., 2017, 146, 024701 CrossRef PubMed.
- J. Sakamoto, E. Rangasamy, H. Kim, Y. Kim and J. Wolfenstine, Nanotechnology, 2013, 24, 424005 CrossRef PubMed.
- Z. F. Yow, Y. L. Oh, W. Gu, R. P. Rao and S. Adams, Solid State Ionics, 2016, 292, 122–129 CrossRef CAS.
- Y. Li, Y. Cao and X. Guo, Solid State Ionics, 2013, 253, 76–80 CrossRef CAS.
- X. Huang, Y. Lu, J. Jin, S. Gu, T. Xiu, Z. Song, M. E. Badding and Z. Wen, ACS Appl. Mater. Interfaces, 2018, 10, 17147–17155 CrossRef CAS PubMed.
- X. Huang, T. Xiu, M. E. Badding and Z. Wen, Ceram. Int., 2018, 44, 5660–5667 CrossRef CAS.
- S.-W. Baek, J.-M. Lee, T. Y. Kim, M.-S. Song and Y. Park, J. Power Sources, 2014, 249, 197–206 CrossRef CAS.
- H. Buschmann, S. Berendts, B. Mogwitz and J. Janek, J. Power Sources, 2012, 206, 236 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04382c |
| This journal is © the Owner Societies 2024 |