Open Access Article
Open Access ArticleElucidating metal–organic framework structures using synchrotron serial crystallography†
Elke
De Zitter
 *ab,
David
Perl‡
*ab,
David
Perl‡
 a,
Martin
Savko
a,
Daniel W.
Paley
c,
Alexander J.
Thom
a,
Martin
Savko
a,
Daniel W.
Paley
c,
Alexander J.
Thom
 d,
Damien
Jeangerard
a,
Aaron S.
Brewster
c,
Antoine
Tissot
d,
Christian
Serre
d and
William
Shepard
*a
d,
Damien
Jeangerard
a,
Aaron S.
Brewster
c,
Antoine
Tissot
d,
Christian
Serre
d and
William
Shepard
*a
aSynchrotron SOLEIL, 91190 Saint Aubin, France. E-mail: william.shepard@synchrotron-soleil.fr
bUniv. Grenoble Alpes, CEA, CNRS, Institut de Biologie Structurale, 38000, Grenoble, France. E-mail: elke.de-zitter@ibs.fr
cMolecular Biophysics and Integrated Bioimaging Division, Lawrence Berkeley National Laboratory, Berkeley, CA, USA
dInstitut des Matériaux Poreux de Paris, Ecole Normale Supérieure, ESPCI Paris, CNRS, PSL University, 75005, Paris, France
First published on 20th September 2024
Abstract
Metal organic frameworks (MOFs) are porous crystalline materials that display a wide variety of physical and chemical properties. Their single crystal structure determination is often challenging because in most cases micro- or nano-sized crystals spontaneously form upon MOF synthesis, which cannot be recrystallized. The production of larger single crystals for structure determination involves optimizing, and thus modifying, the conditions of synthesis, in which success cannot be guaranteed. Failure to produce crystals suitable for single-crystal X-ray diffraction leaves the 3D structure of the MOF compound unknown, and scientists must resort to more challenging structure solution methods based on X-ray powder or electron diffraction data. These laborious tasks can be avoided by using serial crystallography techniques which merge data collected on many micro-crystals. Here, we report the application of three synchrotron serial crystallography methods. We call these “mesh”, “grid” and “mesh&collect” scans. “Still” images (no rotation) are collected in the mesh scan approach, whereas small rotational wedges are collected in the grid scan method. The third protocol, mesh&collect, combines the acquisition of still images and rotational wedges. Using these means, we determine the ab initio structure of benchmark MOFs, MIL-100(Fe) and ZIF-8, that differ largely in unit cell size. These methods are expected to be widely applicable and facilitate structure determination of many MOF microcrystalline systems.
Introduction
Metal–organic frameworks (MOFs) are a class of hybrid, micro- or meso-porous materials where inorganic building blocks, or “secondary building units” (SBUs), are linked together by multi-dentate organic molecules. The inherent porosity of MOFs, as well as the structural diversity, has led to extensive studies among a wide variety of potential applications such as gas storage and separation, drug delivery systems, and even bio-sensors.1–4 For example, chemically robust MOFs have been proposed to capture and store atmospheric CO2.5,6 As such, MOFs are appealing materials for a large number of innovative applications in many emerging research fields, and their production have begun to be scaled-up to industrial proportions.7–10The function of a given MOF is directly related to its structure. It is thus of paramount importance to determine the crystal structure accurately to understand and tailor its properties towards improved performance. Single crystal X-ray diffraction (SCXRD) is the method of choice to determine accurate crystal structures, provided large enough crystals can be prepared. However, MOFs often form crystals of only several microns or smaller, due to the spontaneous formation of MOF crystalline nuclei during synthesis. This is particularly common if the ligand–SBU bond has low lability, a property desirable to make MOFs robust enough for industrial applications. Compounding the small size of the crystals, the significant void spaces filled with disordered solvent reduce diffraction intensities even further for a crystal of a given size. Not only is the selection and manual handling of micro-crystals for SCXRD analysis difficult and labor intensive, but a single micro-crystal might not provide enough diffraction signal to obtain a complete X-ray diffraction data set to atomic resolution.11 Furthermore, by their nature, MOFs cannot be recrystallized after synthesis. Thus, in order to produce crystals large enough for SCXRD studies, their synthetic protocol usually needs to be varied, tested and optimized. This is a time-consuming task without any guarantee of success, even with high-throughput methods. Importantly, it also requires the validation that the small- and large-sized crystalline samples are identical via complementary techniques (e.g. PXRD, spectroscopic methods and gas absorption experiments),12,13 which is not always the case.14
To obtain a MOF's molecular structure, researchers are forced to take often-complex alternative routes. First, the structural complexity of MOFs makes their unambiguous crystal structure determination via powder X-ray diffraction (PXRD) methods challenging, especially when impurities are present, for multiphasic samples or for compounds with large unit cells and low symmetry.12,15 Consequently, for ab initio structure determination, restrained/constrained Rietveld refinement often needs to be combined with total scattering analysis, molecular dynamics, or other characterization methods (e.g. thermogravimetric analysis, infrared spectroscopy, porosimetry and elemental analysis). Secondly, while fast progress is being made in the field of three-dimensional electron diffraction (3D-ED), it suffers from certain drawbacks. 3D-ED experiments are conducted in vacuum and vitreous ice, which both can alter the MOF sample or requires special sample preparation steps to maintain the MOF's hydration or crystallinity. Multiple scattering events restrict the thickness of the samples to below a few microns and also deteriorate the overall diffraction data quality.16 This in turn hinders symmetry assignment, prevents the straightforward resolution of the crystal structure ab initio and complicates structure refinement.17,18 Additionally, MOF crystals can suffer severe radiation damage induced by the electron beam. A third method to solve structures of micro-crystalline samples is by serial femto-second crystallography (SFX) at a X-ray free electron laser (XFEL) source.19 SFX can cover a large range of crystal sizes, allows to collect diffraction data on hydrated samples at room temperature and leads to structures less affected by radiation damage.20 Nonetheless it comes with severe limitations: XFEL beamtime is scarce, a large team of highly experienced staff is often required to successfully conduct an experiment, and data processing is complicated for samples with unknown unit cells or symmetry. Furthermore, large quantities of crystals are required when fast liquid jets are employed (e.g. gas dynamic virtual nozzle). XFELs therefore do not offer a suitable alternative for the majority of MOF research groups. Given the challenges of these alternative techniques, we believe that it is imperative to provide a complementary technique that can bridge the gap between traditional SCXRD and other diffraction methods for nano/micro-crystalline samples.
We postulate that serial synchrotron crystallography (SSX) methods have the potential to facilitate structure determination from micro-crystalline MOF samples. SSX methods are multi-crystal data collection approaches where the total radiation dose is spread over multiple crystals,21 allowing the use of higher X-ray fluxes and hence smaller crystals than for SCXRD. They have successfully been deployed to determine biological macromolecular structures from many small or radiation sensitive crystals.22–28 The use of SSX on MOF systems would allow the collection of X-ray diffraction data from MOF crystals in their originally synthesized state, thereby ensuring the consistency between characterization and structure determination experiments. Moreover, SSX methods avoid the tedious task of isolating single crystals from the bulk, while increasing the chances of data collection on the best crystals. Finally, data acquisition from multiple crystals can allow the identification and resolution of structures from mixtures of phases of the material,29 even when the deviations due to non-isomorphism are very slight.30
In this contribution, we investigate how fixed-target SSX approaches can be employed for the crystal structure determination of MOFs. We chose two well-studied MOF systems with cubic crystal symmetry as benchmarks: the mesoporous iron(III) trimesate MIL-100(Fe) (Matériaux de l'Institut Lavoisier),31 that has a relatively large unit cell length (a = 73 Å, space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), and the microporous zinc imidazolate ZIF-8 (zeolitic imidazolate framework)32,33 that has a much smaller unit cell length (a = 17 Å, space group I
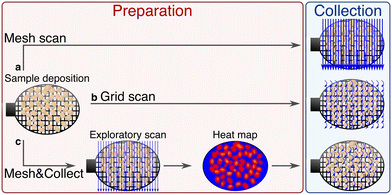
m), and the microporous zinc imidazolate ZIF-8 (zeolitic imidazolate framework)32,33 that has a much smaller unit cell length (a = 17 Å, space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m). These two MOF systems were used with three distinct fixed-target SSX data collection methods which we denote “mesh”, “grid” and “mesh&collect” scans on the PROXIMA 2A beamline at Synchrotron SOLEIL. The first method is essentially a still image data collection strategy, while the second records rotation wedges, and the third combines the still and wedge acquisition strategies. We describe the advantages and disadvantages of each data collection method and associated processing scheme, specifically in regard to MOFs. These methods can also be generalized for other small molecules and macromolecular crystalline systems.
3m). These two MOF systems were used with three distinct fixed-target SSX data collection methods which we denote “mesh”, “grid” and “mesh&collect” scans on the PROXIMA 2A beamline at Synchrotron SOLEIL. The first method is essentially a still image data collection strategy, while the second records rotation wedges, and the third combines the still and wedge acquisition strategies. We describe the advantages and disadvantages of each data collection method and associated processing scheme, specifically in regard to MOFs. These methods can also be generalized for other small molecules and macromolecular crystalline systems.
Materials and methods
Data collection and processing methods
Since the resulting X-ray diffraction data are consecutive rotational scans, full reflections are recorded.43 Therefore, standard single crystal data processing software can be used for spot finding, indexing and integrating each wedge. We developed two very similar pipelines using custom python scripts: one using XDS44via the XDSME scripts45 and the other using DIALS42via XIA2.46 The first step in both pipelines consists of consecutively processing the wedges independently, with either XDSME or XIA2, without any prior knowledge about space group or unit cell parameters. Afterwards, hierarchical cluster analysis (HCA) is performed on the ensemble of wedges, using ccCalc and ccCluster,47 clustering the wedges according to their unit cell parameters. To increase the sensitivity of the unit cell based classification for systems with high symmetry or small unit cell axes, we slightly altered the ccCluster script to use the unit cell's diagonal48 instead of the longest cell axis. Subsequently, Platon49 with the Lepage option, or alternatively iotbx.lattice_symmetry50 is run with the most abundant Bravais lattice and unit cell parameters to determine the highest possible symmetry compatible with the space group and unit cell. A suitable reference wedge can then be chosen from the HCA, Platon Lepage/iotbx.lattice_symmetry output and the data processing statistics (either CORRECT.LP (XDSME) or xia.txt (XIA2) output files). Next, the data wedges are reprocessed using the reference wedge to impose its unit cell constants and space group for consistency, as well as to avoid possible indexing ambiguities. Thereafter, a new HCA is performed, again using ccCluster, but this time the similarity between the clusters is defined by the intensity-based correlation coefficient.47 From the HCA, a threshold difference can be defined, and the wedges in the largest cluster below this threshold are merged and scaled with XSCALE.44
Details and statistics concerning data collection and refinement of each tested sample can be found in the ESI.†
Results
MIL-100(Fe) data collections, processing and refinements
We tested the above-mentioned data collection and processing strategies on two MIL-100(Fe) samples, a first one with crystal sizes between 10 and 30 μm and a second one with crystal sizes from sub-micron to 5 μm, which we denote MIL-100(Fe)10–30μm and MIL-100(Fe)1–5μm, respectively.For the MIL-100(Fe)10–30μm sample, we collected X-ray diffraction data and solved their structures with each of the three SSX methods. The main steps are graphically presented in Fig. 2–4 for the mesh, grid and mesh&collect methods, respectively.
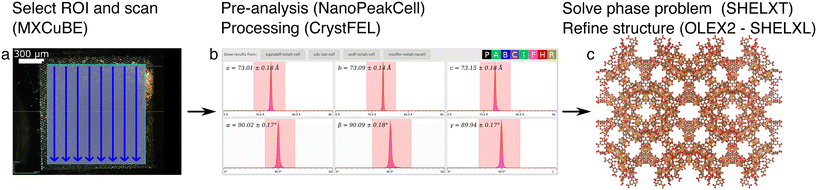
For the mesh scan approach (Fig. 2), 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 images were collected, leading to 10
639 images were collected, leading to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612 hits of which 9081 images could be processed using CrystFEL, arriving at 11
612 hits of which 9081 images could be processed using CrystFEL, arriving at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 indexed diffraction patterns.40 We tested the available scaling and merging options, being the basic Monte-Carlo method (process_hkl) and post-refinement with Partialator.51 For the latter, reflection partialities can be set to one (unity model) or can be fully modelled (xsphere model), leading to a total of three differently scaled data sets. Each of these three data sets were then used to solve the structures with SHELXT52 and subsequently refine them in OLEX2 (ref. 53) using SHELXL.54 While data were collected up to a high-resolution limit of 1 Å, proper B-factor modelling and refinement convergence could only be carried out when the data was truncated to a high resolution of 1.1 Å. A few, no and many additional restraints had to be applied for refinement with the Monte-Carlo, partialator-unity and partialor-xsphere scaled data, respectively (Tables 1 and S1†).
653 indexed diffraction patterns.40 We tested the available scaling and merging options, being the basic Monte-Carlo method (process_hkl) and post-refinement with Partialator.51 For the latter, reflection partialities can be set to one (unity model) or can be fully modelled (xsphere model), leading to a total of three differently scaled data sets. Each of these three data sets were then used to solve the structures with SHELXT52 and subsequently refine them in OLEX2 (ref. 53) using SHELXL.54 While data were collected up to a high-resolution limit of 1 Å, proper B-factor modelling and refinement convergence could only be carried out when the data was truncated to a high resolution of 1.1 Å. A few, no and many additional restraints had to be applied for refinement with the Monte-Carlo, partialator-unity and partialor-xsphere scaled data, respectively (Tables 1 and S1†).
| Sample | MIL-100(Fe)10–30μm | MIL-100(Fe)1–5μm | ZIF-825–50μm | ||||
|---|---|---|---|---|---|---|---|
| SSX method | Mesh scanb | Gridscan | Mesh&collect | Mesh scan | Mesh&collect | Mesh scan | Mesh&collect |
| a More data collection statistics and refinement statistics with and without a solvent mask can be found in the Tables S1–S4.† b Mesh scan scaling was carried out with partialator with the unity model. c Values between parentheses are for the highest resolution shell. N.A.: not applicable. N.D.: not determined. | |||||||
| CCDC code | 2353477 | 2346055 | 2353478 | 2353480 | 2353479 | 2353475 | 2353474 |
| Data collection | |||||||
|---|---|---|---|---|---|---|---|
| Rotation per wedge (°) | N.A. | 20 | 40 | N.A. | 40 | N.A. | 60 |
| No. wedges merged | N.A. | 192 | 17 | N.A. | 12 | N.A. | 5 |
| No. collected images | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 639 639 |
N.A. | N.A. | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 226 |
N.A. | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 561 |
N.A. |
| No. indexed diffraction patterns | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 653 |
N.A. | N.A. | 2356 | N.A. | 2179 | N.A. |
| Resolution range (Å) | 42.20–1.10 (1.13–1.10)c | 36.54–1.15 (1.18–1.15) | 42.08–1.06 (1.09–1.06) | 42.30–1.10 (1.13–1.10) | 42.47–1.30 (1.30–1.33) | 11.95–0.85 (0.91–0.85) | 12.01–0.94 (1.15–0.94)c |
| 〈I/σ(I)〉 | 9.03 (0.33) | 16.55 (1.72) | 24.78 (3.62) | 3.20 (0.40) | 5.43 (1.13) | 5.85 (2.37) | 64.76 (23.79) |
| R merge (%) | N.A. | 90.4 (317.6) | 36.7 (176.6) | N.A. | 72.3 (135.1) | N.A. | 5.7 (28.0) |
| R split (%) | 7.06 (58.95) | N.A. | N.A. | 17.78 (159.01) | N.A. | N.D. | N.A. |
| CC1/2 (%) | 100.00 (80.00) | 100.0 (100.0) | 99.6 (99.8) | 97.89 (53.49) | 99.2 (50.3) | 97.2 (72.8) | 99.9 (99.7) |
| Structure refinement | |||||||
|---|---|---|---|---|---|---|---|
| Space group |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
| Unit cell (Å, °) | 73.09(18); 73.09(14); 73.09(18); 90.00 | 73.099(15); 73.099(15); 73.099(15); 90.00 | 72.9(16); 72.9(16); 72.9(16); 90.00 | 73.27(18); 73.27(15); 73.27(19); 90.00 | 73.21(56); 73.21(56); 73.21(56); 90.00 | 16.9; 16.9; 16.9; 90.0 | 16.99(4); 16.99(4); 16.99(4); 90.00 |
| Data | 7027 | 6176 | 7717 | 7092 | 4287 | 341 | 618 |
| Restraints | 0 | 312 | 27 | 164 | 420 | 0 | 0 |
| Parameters | 518 | 515 | 515 | 515 | 503 | 35 | 35 |
| R 1/ωR2 (I> = 2σ(I)) (%) | 9.52/27.44 | 6.31/18.88 | 5.52/16.51 | 13.81/34.77 | 6.96/16.86 | 9.29/24.56 | 4.62/12.81 |
| R 1/ωR2 (all) (%) | 11.22/29.97 | 8.62/20.83 | 6.62/17.53 | 19.40/42.14 | 11.44/20.00 | 9.94/26.72 | 4.67/12.89 |
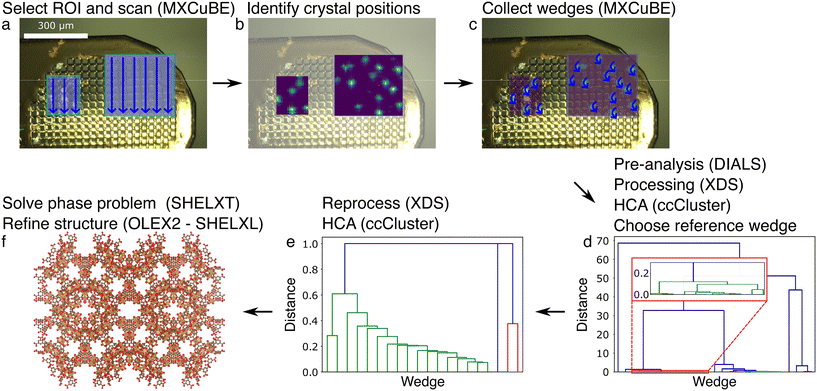
Secondly, we applied the grid scan approach on the MIL-100(Fe)10–30μm sample with the collection of 1800 wedges, each over a range of 20° (Fig. 3). 744 wedges were selected for processing based on the pre-analysiswedges. Around two thirds (512 wedges) could be processed by DIALS42 (via XIA246) in a first round of which 438 were retained after reprocessing with a reference wedge. 192 wedges were selected for merging using the HCA analysis. The phase problem was solved with SHELXT,52 and refinement carried out in OLEX253 using SHELXL.54 Many restraints had to be included during refinement using the data up to a resolution of 1.15 Å (Tables 1 and S2†).
Thirdly, we tested the mesh&collect strategy on MIL-100(Fe)10–30μm crystals (Fig. 4). From the initial mesh scan of two ROIs, 27 positions were selected, and a wedge of 40° was acquired at each position. All were successfully processed using XDS44 during the first independent processing round, but seven wedges could not be re-processed with the imposed space group or unit cell parameters. In the following HCA we selected 17 wedges for scaling and merging. The structure was then solved using SHELXT52 and refined with OLEX253 using SHELXL54 with few additional restraints (Tables 1 and S2†).
Inspired by the successful data collection and structure determination from MIL-100(Fe)10–30μm crystals, we tested if our methods would also be applicable on crystals with smaller sizes, ranging from submicron to 5 μm (MIL-100(Fe)1–5μm; Fig. S1†).
We first collected X-ray diffraction data using the mesh scan approach on MIL-100(Fe)1–5μm crystals (Fig. S2†). We collected 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 still images and all of them were directly subjected to CrystFEL40 without the hit filtering step due to difficulties to separate hits from non-hits in NanoPeakCell.38 Indexing was successful for only 1958 images giving a total of 2356 indexed diffraction patterns. The data was subsequently merged and scaled using Partialator51 with the unity model. The structure was solved and refined with all data up to 1.10 Å resolution and additional restraints (Tables 1 and S3†).
226 still images and all of them were directly subjected to CrystFEL40 without the hit filtering step due to difficulties to separate hits from non-hits in NanoPeakCell.38 Indexing was successful for only 1958 images giving a total of 2356 indexed diffraction patterns. The data was subsequently merged and scaled using Partialator51 with the unity model. The structure was solved and refined with all data up to 1.10 Å resolution and additional restraints (Tables 1 and S3†).
Secondly, we also applied the mesh&collect strategy (Fig. S3†) whereby the exploratory X-ray scan indicated 20 positions on each of which we collected a 40° wedge. Of the initial 17 successfully processed wedges, all could be reprocessed with the chosen reference wedge and 12 wedges were merged into the final data set. Refinement was carried out with data up to a high resolution of 1.3 Å and with multiple restraints as required for refinement convergence (Tables 1 and S3†).
Due to the long data collection time and difficulties encountered during structure refinement of grid scan data from MIL-100(Fe)10–30μm crystals, we did not collect data via this method on the small-sized MIL-100(Fe)1–5μm crystals.
ZIF-8 data collections, processing and refinements
We also investigated the performance of these methods on ZIF-8 crystals, another cubic MOF system but with smaller unit cell parameters – four times smaller than those for MIL-100(Fe) (a = 17 Å as compared to a = 73 Å). The ZIF-8 crystals had sizes ranging from 25 to 50 μm, and hence are denoted as ZIF-825–50μm throughout this manuscript.We first applied the mesh scan data collection approach on the ZIF-825–50μm crystals (Fig. S4†). We merged several data sets collected on different sample holders, leading to a total of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 diffraction images. We did not filter the hits from the non-hits and subjected the data directly to the cctbx.small_cell pipeline19,41 because the hit list of NanoPeakCell cannot be interpreted by cctbx.small_cell. Based on the peak locations on the diffraction images, a synthetic powder diffraction pattern could be calculated (Fig. S4†). 19 possible unit cell axes could be extracted and feed to TOPAS-Academic,55 which proposed a cubic I23 cell with a = 16.90 Å. 2179 images could subsequently indexed, integrated, scaled and merged with cctbx.xfel.small_cell_process and cctbx.xfel.merge. The structure could then be solved using SHELXS,56 and refined in SHELXL54 with the data up to a high-resolution of 0.85 Å. This first model showed some inaccurate features, but could be considered as rough model that could be used as scaling reference for a second cycle of merging with cctbx.xfel.merge. The rescaled data was then used to refine a second rough model that was re-used in a final scaling and merging cycle. The rescaled data allowed restraint-free structure refinement (Tables 1 and S4†).
561 diffraction images. We did not filter the hits from the non-hits and subjected the data directly to the cctbx.small_cell pipeline19,41 because the hit list of NanoPeakCell cannot be interpreted by cctbx.small_cell. Based on the peak locations on the diffraction images, a synthetic powder diffraction pattern could be calculated (Fig. S4†). 19 possible unit cell axes could be extracted and feed to TOPAS-Academic,55 which proposed a cubic I23 cell with a = 16.90 Å. 2179 images could subsequently indexed, integrated, scaled and merged with cctbx.xfel.small_cell_process and cctbx.xfel.merge. The structure could then be solved using SHELXS,56 and refined in SHELXL54 with the data up to a high-resolution of 0.85 Å. This first model showed some inaccurate features, but could be considered as rough model that could be used as scaling reference for a second cycle of merging with cctbx.xfel.merge. The rescaled data was then used to refine a second rough model that was re-used in a final scaling and merging cycle. The rescaled data allowed restraint-free structure refinement (Tables 1 and S4†).
We also carried out the mesh&collect data collection and processing strategy (Fig. S5†). From the initial scan, we selected 7 positions on which wedges of 60° were acquired. Five could be processed and then reprocessed with the imposed unit cell and space group parameters of the reference wedge using XDS.44 All five were subsequently merged. The structure was solved with SHELXT52 and refined with SHELXL54 in OLEX253 without additional restraints using data up to a resolution of 0.94 Å (Tables 1 and S4†).
We did not collect any data on ZIF-825–50μm crystals using the grid scan method as explained above for MIL-100(Fe)1–5μm crystals.
Discussion
We implemented and evaluated the performance of three fixed-target SSX data collection and processing strategies on MOF crystals on the micro-focused beamline PROXIMA 2A. We only used a standard goniometer environment and standard lab equipment for sample preparation.We first illustrated the considered applicability and performance of mesh scans. The data collection is very straightforward and easy to perform but requires a large sample holder with many crystals to collect thousands of diffraction images. Still images contain only partial reflections, demanding specialized processing, merging and scaling software, such as those provided by the CrystFEL40 and cctbx.xfel57 suites. The usage of pre-processing software38 to filter hits reduces the data set size and subsequent computation time. Still images originating from crystals with small unit cells and systematic absences due to crystallographic centering and symmetry elements can be difficult to index as only a few diffraction spots are collected per image. Therefore, we started to test the mesh scan strategy on MIL-100(Fe), a system with a very large unit cell (a = 73 Å). However, this was still challenging because more than 75% of the reflections are systematically absent due to its face-centered space group, yielding an effective cell length of 51 Å, and high symmetry (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Furthermore, peak finding and indexing was hampered due to the low signal-to-noise value of the diffraction peaks and simultaneous diffraction of multiple crystals (Fig. S6 and S7†). To facilitate data processing, we provided the unit cell information and lattice as prior information to CrystFEL. While known for the MIL-100(Fe) test cases, these parameters can still be obtained from a “blind” CrystFEL run or from a powder diffraction diagram. We collected and processed mesh scan data from MIL-100(Fe) crystals with sizes ranging from 10–30 μm (MIL-100(Fe)10–30μm) and submicron to 5 μm (MIL-100(Fe)1–5μm). For the first one, we tested the three possible scaling and merging algorithms that are available in CrystFEL. We found that the data set scaled using the Monte-Carlo method or post-refinement with the unity model gave the most stable structure refinements, as shown by the decent data processing statistics, good refinement R-factor values and the requirements of few refinement restraints (Table S1†). Post-refinement with full partiality modelling (xsphere) led to the rejection of many reflections, which appeared to be detrimental for structure refinement. It should be noted that the scaling and merging statistics are overall worse than what would generally be accepted in SCXRD but are comparable to macromolecular SX. Even though the signal-to-noise value in the highest resolution shell is low, we found that inclusion of data up to 1.1 Å resolution was beneficial for refinement convergence. Modelling a solvent mask to account for the presence of solvent (ethanol) leads to strongly reduced R-factors and required the use of different restraints (Table S1†). The importance of collecting, indexing and integrating many images is clearly illustrated from the mesh scan results of the MIL-100(Fe)1–5μm crystals, for which only 2179 images could be indexed, roughly 20% compared to the number of indexed images for the MIL-100(Fe)10–30μm crystals. While this data set has reasonable merging statistics, structure refinement could only converge upon the addition of many restraints (Table S3†). We reason that the small indexing rate (number of indexed images divided by number of collected images) is caused by the reduced diffraction power of the smaller crystals making it more difficult to distinguish true reflections from noise and thus to correctly find peaks (Fig. S7†).
m). Furthermore, peak finding and indexing was hampered due to the low signal-to-noise value of the diffraction peaks and simultaneous diffraction of multiple crystals (Fig. S6 and S7†). To facilitate data processing, we provided the unit cell information and lattice as prior information to CrystFEL. While known for the MIL-100(Fe) test cases, these parameters can still be obtained from a “blind” CrystFEL run or from a powder diffraction diagram. We collected and processed mesh scan data from MIL-100(Fe) crystals with sizes ranging from 10–30 μm (MIL-100(Fe)10–30μm) and submicron to 5 μm (MIL-100(Fe)1–5μm). For the first one, we tested the three possible scaling and merging algorithms that are available in CrystFEL. We found that the data set scaled using the Monte-Carlo method or post-refinement with the unity model gave the most stable structure refinements, as shown by the decent data processing statistics, good refinement R-factor values and the requirements of few refinement restraints (Table S1†). Post-refinement with full partiality modelling (xsphere) led to the rejection of many reflections, which appeared to be detrimental for structure refinement. It should be noted that the scaling and merging statistics are overall worse than what would generally be accepted in SCXRD but are comparable to macromolecular SX. Even though the signal-to-noise value in the highest resolution shell is low, we found that inclusion of data up to 1.1 Å resolution was beneficial for refinement convergence. Modelling a solvent mask to account for the presence of solvent (ethanol) leads to strongly reduced R-factors and required the use of different restraints (Table S1†). The importance of collecting, indexing and integrating many images is clearly illustrated from the mesh scan results of the MIL-100(Fe)1–5μm crystals, for which only 2179 images could be indexed, roughly 20% compared to the number of indexed images for the MIL-100(Fe)10–30μm crystals. While this data set has reasonable merging statistics, structure refinement could only converge upon the addition of many restraints (Table S3†). We reason that the small indexing rate (number of indexed images divided by number of collected images) is caused by the reduced diffraction power of the smaller crystals making it more difficult to distinguish true reflections from noise and thus to correctly find peaks (Fig. S7†).
We had even more difficulty processing the mesh scan diffraction data originating from ZIF-825–50μm. The signal-to-noise value of the diffraction data was higher than that of the two sets of MIL-100(Fe) crystals (Fig. S8†). However, the much smaller cubic unit cell (a = 17.0 Å) coupled with the systematic absences of the body-centered space group and associated symmetry operators (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) strongly reduced the number of diffraction spots. Therefore, we opted to use cctbx.small_cell.19,41 cctbx.small_cell is a program designed to treat still images with sparse patterns originating from samples with a small unit cell. After peak finding, cctbx.small_cell reconstructs a powder diffraction diagram from which the unit cell parameters can be deduced. For ZIF-825–50μm, the space group I23 with unit cell axis a = 16.90 Å could be found after restricting the search to cubic cells. The calculated powder diagram does not only allow to identify the unit cell dimensions, but also to improve the geometry description of the diffraction experiment and agreement between the different data sets. Indeed, as the data sets were collected on different dates, detector distance in each geometry file was adjusted manually to improve the agreement of the individually computed powder patterns with the reference pattern. We note that as a general practice, the detector distance should be calibrated on each day of data collection; furthermore, the most consistent results will be obtained if a complete dataset is measured in a single experiment. However, this manual correction was sufficient to index and merge all datasets. Structure solution was successful by direct methods in SHELXS.56 Other typical tools such as SHELXT were unsuccessful in this case; we surmise this difficulty was connected to the high solvent content of the crystal. SHELXS requires that space group determination is completed in a separate step. This is trivial for the previously known structure of ZIF-8, but we note that I
3m) strongly reduced the number of diffraction spots. Therefore, we opted to use cctbx.small_cell.19,41 cctbx.small_cell is a program designed to treat still images with sparse patterns originating from samples with a small unit cell. After peak finding, cctbx.small_cell reconstructs a powder diffraction diagram from which the unit cell parameters can be deduced. For ZIF-825–50μm, the space group I23 with unit cell axis a = 16.90 Å could be found after restricting the search to cubic cells. The calculated powder diagram does not only allow to identify the unit cell dimensions, but also to improve the geometry description of the diffraction experiment and agreement between the different data sets. Indeed, as the data sets were collected on different dates, detector distance in each geometry file was adjusted manually to improve the agreement of the individually computed powder patterns with the reference pattern. We note that as a general practice, the detector distance should be calibrated on each day of data collection; furthermore, the most consistent results will be obtained if a complete dataset is measured in a single experiment. However, this manual correction was sufficient to index and merge all datasets. Structure solution was successful by direct methods in SHELXS.56 Other typical tools such as SHELXT were unsuccessful in this case; we surmise this difficulty was connected to the high solvent content of the crystal. SHELXS requires that space group determination is completed in a separate step. This is trivial for the previously known structure of ZIF-8, but we note that I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m is the most common body-centered cubic space group and so a simple search by database frequency would have also given the correct answer immediately. Another important feature of cctbx.small_cell is the possibility to add a preliminary structure during scaling, allowing an iterative approach of model refinement and data re-scaling to maximize data quality. Overall, while only 2179 images of the 35
3m is the most common body-centered cubic space group and so a simple search by database frequency would have also given the correct answer immediately. Another important feature of cctbx.small_cell is the possibility to add a preliminary structure during scaling, allowing an iterative approach of model refinement and data re-scaling to maximize data quality. Overall, while only 2179 images of the 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 collected images could be indexed, the specific approaches of cctbx.small_cell permitted processing the data without prior information of the unit cell parameters and crystal system, and refining the structure without restraints.
561 collected images could be indexed, the specific approaches of cctbx.small_cell permitted processing the data without prior information of the unit cell parameters and crystal system, and refining the structure without restraints.
The grid scan strategy was successfully applied on MIL-100(Fe) crystalline slurries. As for the mesh scan method, it is easy to collect data as no assumption is made on crystal positions and their content. However, data collection with the grid scan method takes several hours for a single sample holder as a wedge is acquired at every position, irrespective of whether any crystals are present or not. Importantly, full reflections are recorded during the data collection. Peak finding, indexing and integration can thus be performed using standard rotation crystallographic software, such as XDS44 or DIALS.42 This stage also takes a long time and is thus another disadvantage concerning time and resources of the grid scan method. Indeed, hundreds to thousands of partial data sets are collected, which require large amounts of computational time for processing, even for cases where the pre-analysis selects wedges that contain diffraction data.
We only applied this strategy on the MIL-100(Fe)10–30μm crystals and solved the structure at 1.15 Å. It should be noted that many restraints were required to successfully refine the structure (Tables 1 and S2†). This is remarkable given the much better statistics and easier refinement for MIL-100(Fe)10–30μm data obtained with the mesh&collect approach. We tentatively assign these problems to the inclusion of weakly diffracting data sets (Fig. S9†) seeped through the intensity-based correlation HCA.58 However, reducing the HCA threshold, and thereby reducing the number of merged wedges and multiplicity, could not resolve this issues. Other potential factors are non-isomorphism and ambiguity in the indexing solutions, but both can be excluded. Indeed, MIL-100(Fe) is expected to be highly isomorphous, and our data processing pipeline includes a reprocessing step using a reference wedge to avoid indexing ambiguity. Optimization of the image range in a similar manner as done in the mesh&collect data processing pipeline was not included in the grid scan pipeline. Therefore, we cannot conclude if processing would have been more successful if it was carried out with an optimized image range for each wedge. Given these apparent merging issues as well as the long data collection and computation time for our non-parallel data processing pipeline, we did not apply this strategy to the other test samples in this study.
The mesh&collect method combines the rapidity of a small mesh scan with the collection of wedges to obtain full reflections. Even though the strategy demands two data acquisition steps, the total duration time of the method is generally much shorter than of both the mesh and the grid scan, for the following reasons. First, data collection is more efficient because data can be acquired on a much smaller sample holder as compared to the mesh scan, and only wedges are collected on grid points with residing crystals. Secondly, data processing is much faster, being carried out on a relatively small number of rotational data sets. A crucial point lies however in the quality and interpretation of the diffraction heat map. Indeed, a low number of reflections on still images of the initial mesh scan results in poor signal-to-noise ratios of such maps, making it difficult to distinguish between diffraction patterns from multiple and single crystals. Grid points consisting of more than one crystal will appear as the most promising, but the data will be difficult to index. Therefore, the sample should be loaded sparse enough to yield isolated single crystals. Otherwise, the heat map analysis could also be improved by taking a maximum number of spots into account, attempting to index the images on-the-fly to identify multiple lattices, or by carrying out a difference diffraction vector analysis.59 Furthermore, the success rate heavily depends on the X-ray beam and sample stability, and small beam drifts can influence the accuracy of the visited positions.
We successfully applied the mesh&collect method on MIL-100(Fe)10–30μm, MIL-100(Fe)1–5μm and ZIF-825–50μm crystals, with a resolution of 1.06, 1.30 and 0.94 Å, respectively (Tables 1 and S2–S4†). The ZIF-825–50μm structure could be refined without any restraints, while only a modest number of restraints were applied in case of the MIL-100(Fe)10–30μm crystals. A large number of restraints were required to refine the structure originating from the MIL-100(Fe)1–5μm crystals. We presume that the poorer resolution can be ascribed to the sensitivity to interpret the diffraction heat map and sample alignment, and weaker diffraction of the small crystals (Fig. S10–S12†). MIL-100(Fe)1–5μm data quality can possibly be increased by merging data from many more crystals (here we merged only 12 wedges). Also, fine tuning the X-ray beam size to the average probed crystal should increase the signal-to-noise ratio. Indeed, here crystals up to 5 μm were probed with an X-ray beam of 10 × 5 μm, hence a reduction of a factor 2 horizontally could give a noticeable background reduction.
Conclusion
We have shown how three related, complementary, fixed-target data collection and processing methods for SSX can be applied to the structure determination of two MOF model systems. For application to novel systems, one data collection method may be preferred over another depending on the sample characteristics (space group, unit cell parameters, crystal size, slurry density, etc.) and the research question.The mesh scan method consists of collecting a single still image per crystal. It is thus particularly suitable for X-ray radiation sensitive samples since the maximum dose can be applied to collect just a single image. While this method is the fastest and easiest in terms of implementation, the data processing step is more challenging and requires dedicated software. The partial reflections recorded on still images from MOFs are furthermore less abundant than those typically observed in serial macromolecular crystallography because of the smaller unit cells, higher lattice symmetries, and finer mosaicities. Software typically used for macromolecular crystallography, e.g. CrystFEL,40 can process SSX data successfully from MOF crystals, especially if the unit cell is large enough, permitting a sufficient number of spots to be observed. For small unit cell crystal systems, cctbx.small_cell19,41 can perform better as it will try all possible indexing combinations for the few spots that are present on each diffraction image.
The second and third methods, grid and mesh&collect scans, consist of the collection of rotational data wedges. The main difference between them is whether the crystals have been located prior to the collection of the wedges or not. Processing the X-ray diffraction data collected via these two approaches is much more convenient for a non-specialized crystallographer as compared to the mesh scan method. Indeed, rotational data can be processed with traditional and well-known crystallographic software, such as XDS44 or DIALS.42 The easier assignment of unit cell parameters and crystal symmetry makes these two methods also more suitable for unknown systems compared to mesh scans. The localization of crystals via an initial mesh scan makes the mesh&collect procedure faster than the grid scan method, both during data collection and processing, but relies on a very stable X-ray beam and sample position to precisely return to the locations of the identified crystals.
MOFs are mostly synthesized as small crystals, and SSX structure determination avoids the need for the synthesis of large crystals. It should be noted that SSX data collection still requires a minimal X-ray diffraction strength, which is not only related to the crystallinity of the sample, but also proportional to the size of the irradiated crystal volume. Recent and future synchrotron upgrades towards fourth generation sources will deliver increased X-ray flux densities, promising further increases in observable signal to noise on such small crystals. If the synthesized MOF crystals appear nevertheless to be too small (i.e. sub-micron) for structure determination at a synchrotron,11 then complementary techniques could be used, such as the X-ray data collection at an XFEL source19 or electron diffraction.16,18 Sample characteristics, such as the sample purity, radiation sensitivity, vacuum-resistance, presence of crystalline defects or twinning, crystal system, available quantity, etc. will determine which technique may best be applied. The high complementarity between various electron and X-ray diffraction techniques provides researchers with a variety of methods to solve the crystal structure from pristine crystals.
Serial crystallography also opens the door to time-resolved studies wherein reactions can be launched via an external trigger (e.g. light flash or temperature jump) or via the diffusion of a molecule through the crystals. Indeed, smaller crystals lead to more homogeneity in molecular diffusion and light penetration throughout crystals as compared to larger crystals. Light-induced time-resolved studies at an XFEL on MOF samples were recently demonstrated by Kang et al.60 With the possibility to also carry out experiments at synchrotrons, we believe that more studies will follow. These will allow to visualize for example the exchange between solvent and guests molecules, and the establishment of interactions between the guest and MOF that can even cause deformations of the MOF lattice.61 The rapid data collection during the mesh scan method makes it most suited for time-resolved experiments, letting the time-resolution be limited by diffusion and image acquisition time, typically up to tens of milliseconds.62 The total duration of the grid and mesh&collect experiments are much longer than mesh scans because the X-ray shutter closes between each sample translation step (moving to the next grid point or crystal). However, small wedges of data can still be acquired within a few hundreds of milliseconds or seconds. Such time scales may be adequate to observe the loading or release of guest molecules into or out of the pores of the MOF under study.
Data availability
Structures and structure factors of MIL-100(Fe) and ZIF-8 presented in Table 1 are available from the Cambridge Crystallographic Data Centre (CCDC) with deposition IDs: 2353477, 2346055, 2353478, 2353480, 2353479, 2353475 and 2353474. The raw data is available from the authors upon reasonable request.Author contributions
W. S., E. D. Z., A. T. and C. S. conceived the project and applied for financial support to Paris Ile-de-France DIM Respore. W. S., A. T. and C. S. acquired funding from the Agence National de Recherche (France). A. T., A. J. T. and C. S. provided crystalline MOF samples. E. D. Z., D. P., A. J. T. and W. S. designed and conducted experiments. E. D. Z., D. P. and D. W. P. processed X-ray diffraction data. M. S., D. J. and W. S. aided with computer programming and beamline operation. D. W. P. and A. S. B. helped with the implementation of data processing software. E. D. Z. drafted the original manuscript. E. D. Z., D. P., D. W. P., A. T., C. S. and W. S. edited the manuscript with input from all authors.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research was financed through the Paris Region DIM RESPORE (Serial-MOF project) and the Agence Nationale de la Recherche (Serial-X-Energy project ANR-19-CE29-0004). E. D. Z. thanks DIM RESPORE for a postdoctoral fellowship. D. P. and A. J. T. thank the Agence Nationale de la Recherche (ANR) for a postdoctoral fellowship. A. T. thanks Théophile Gaichies for his help in the synthesis of MIL-100(Fe) crystals. A. S. B. and D. W. P. were supported by DOE ICDI grant DE-SC0022215. E. D. Z. thanks Dr. Jacques-Philippe Colletier for encouragement. The authors thank all the staff of the PROXIMA 2A beamline at Synchrotron SOLEIL, especially Dr. Serena Sirigu for insightful discussions.References
- P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232–1268 CrossRef CAS PubMed
.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed
.
- X. Ma, M. Lepoitevin and C. Serre, Mater. Chem. Front., 2021, 5, 5573–5594 RSC
.
- L. Li, R. B. Lin, R. Krishna, H. Li, S. Xiang, H. Wu, J. Li, W. Zhou and B. Chen, Science, 2018, 362, 443–446 CrossRef CAS PubMed
.
- M. Benzaqui, M. Wahiduzzaman, H. Zhao, M. R. Hasan, T. Steenhaut, A. Saad, J. Marrot, P. Normand, J. M. Grenèche and N. Heymans,
et al.
, J. Mater. Chem. A, 2022, 10, 8535–8545 RSC
.
- S. Zhang, H. Dong, A. Lin, C. Zhang, H. Du, J. Mu, J. Han, J. Zhang and F. Wang, ACS Sustainable Chem. Eng., 2022, 10(39), 13185–13193 CrossRef CAS
.
- A. U. Czaja, N. Trukhan and U. Müller, Chem. Soc. Rev., 2009, 38, 1284–1293 RSC
.
- P. Silva, S. M. F. Vilela, J. P. C. Tomé and F. A. Almeida Paz, Chem. Soc. Rev., 2015, 44, 6774–6803 RSC
.
- X. Li, B. Wang, Y. Cao, S. Zhao, H. Wang, X. Feng, J. Zhou and X. Ma, ACS Sustainable Chem. Eng., 2019, 7, 4548–4563 CrossRef CAS
.
- J. Bin Lin, T. T. T. Nguyen, R. Vaidhyanathan, J. Burner, J. M. Taylor, H. Durekova, F. Akhtar, R. K. Mah, O. Ghaffari-Nik and S. Marx,
et al.
, Science, 2021, 374, 1464–1469 CrossRef PubMed
.
- J. M. Holton and K. A. Frankel, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 393–408 CrossRef CAS PubMed
.
- T. He, Z. Huang, S. Yuan, X. L. Lv, X. J. Kong, X. Zou, H. C. Zhou and J. R. Li, J. Am. Chem. Soc., 2020, 142, 13491–13499 CrossRef CAS PubMed
.
-
Y. Han, H. Yang and X. Guo, Synthesis Methods and Crystallization of MOFs, in Synthesis Methods and Crystallization, ed. R. Marzouki, IntechOpen, 2020, DOI:10.5772/intechopen.90435
.
- Y. Sakata, S. Furukawa, M. Kondo, K. Hirai, N. Horike, Y. Takashima, H. Uehara, N. Louvain, M. Meilikhov and T. Tsuruoka,
et al.
, Science, 2013, 339, 193–196 CrossRef CAS PubMed
.
- P. Falcaro, F. Carraro, M. D. J. Velásquez-Hernández, E. Astria, W. Liang, L. Twight, C. Parise, M. Ge, Z. Huang and R. Ricco,
et al.
, Chem. Sci., 2020, 11, 3397–3404 RSC
.
- T. Gruene and E. Mugnaioli, Chem. Rev., 2021, 121, 11823–11834 CrossRef CAS PubMed
.
- M. Ge, X. Zou and Z. Huang, Crystals, 2021, 11, 263 CrossRef CAS
.
- Z. Huang, E. S. Grape, J. Li, A. K. Inge and X. Zou, Coord. Chem. Rev., 2021, 427, 213583 CrossRef CAS
.
- E. A. Schriber, D. W. Paley, R. Bolotovsky, D. J. Rosenberg, R. G. Sierra, A. Aquila, D. Mendez, F. Poitevin, J. P. Blaschke and A. Bhowmick,
et al.
, Nature, 2022, 601, 360–365 CrossRef CAS PubMed
.
- K. Nass, Acta Crystallogr., Sect. D: Struct. Biol., 2019, 75, 211–218 CrossRef CAS PubMed
.
- K. Diederichs and M. Wang, Methods Mol. Biol., 2017, 1607, 239–272 CrossRef CAS PubMed
.
- C. Gati, G. Bourenkov, M. Klinge, D. Rehders, F. Stellato, D. Oberthür, O. Yefanov, B. P. Sommer, S. Mogk and M. Duszenko,
et al.
, IUCrJ, 2014, 1, 87–94 CrossRef CAS PubMed
.
- P. Roedig, R. Duman, J. Sanchez-Weatherby, I. Vartiainen, A. Burkhardt, M. Warmer, C. David, A. Wagner and A. Meents, J. Appl. Crystallogr., 2016, 49, 968–975 CrossRef CAS PubMed
.
- S. Botha, K. Nass, T. R. M. Barends, W. Kabsch, B. Latz, F. Dworkowski, L. Foucar, E. Panepucci, M. Wang and R. L. Shoeman,
et al.
, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 387–397 CrossRef CAS PubMed
.
- U. Zander, G. Bourenkov, A. N. Popov, D. De Sanctis, O. Svensson, A. A. Mccarthy, E. Round, V. Gordeliy, C. Mueller-Dieckmann and G. A. Leonard, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 2328–2343 CrossRef CAS PubMed
.
- C. Y. Huang, V. Olieric, P. Ma, N. Howe, L. Vogeley, X. Liu, R. Warshamanage, T. Weinert, E. Panepucci and B. Kobilka,
et al.
, Acta Crystallogr., Sect. D: Struct. Biol., 2016, 72, 93–112 CrossRef CAS PubMed
.
- R. L. Owen, D. Axford, D. A. Sherrell, A. Kuo, O. P. Ernst, E. C. Schulz, R. J. D. Miller and H. M. Mueller-Werkmeister, Acta Crystallogr., Sect. D: Struct. Biol., 2017, 73, 373–378 CrossRef CAS PubMed
.
- K. Hasegawa, K. Yamashita, T. Murai, N. Nuemket, K. Hirata, G. Ueno, H. Ago, T. Nakatsu, T. Kumasaka and M. Yamamoto, J. Synchrotron Radiat., 2017, 24, 29–41 CrossRef CAS PubMed
.
- T. Zhang, S. Jin, Y. Gu, Y. He, M. Li, Y. Li and H. Fan, IUCrJ, 2015, 2, 322–326 CrossRef CAS PubMed
.
- A. Ebrahim, M. V. Appleby, D. Axford, J. Beale, T. Moreno-Chicano, D. A. Sherrell, R. W. Strange, M. A. Hough and R. L. Owen, Acta Crystallogr., Sect. D: Struct. Biol., 2019, 75, 151–159 CrossRef CAS PubMed
.
- P. Horcajada, S. Surblé, C. Serre, D. Y. Hong, Y. K. Seo, J. S. Chang, J. M. Grenèche, I. Margiolaki and G. Férey, Chem. Commun., 2007, 2820–2822 RSC
.
- X. C. Huang, Y. Y. Lin, J. P. Zhang and X. M. Chen, Angew. Chem., Int. Ed., 2006, 45, 1557–1559 CrossRef CAS PubMed
.
- K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS PubMed
.
- P. Roedig, I. Vartiainen, R. Duman, S. Panneerselvam, N. Stübe, O. Lorbeer, M. Warmer, G. Sutton, D. I. Stuart and E. Weckert,
et al.
, Sci. Rep., 2015, 5, 10451 CrossRef CAS PubMed
.
- S. Boutet, L. Lomb, G. J. Williams, T. R. M. Barends, A. Aquila, R. B. Doak, U. Weierstall, D. P. DePonte, J. Steinbrener and R. L. Shoeman,
et al.
, Science, 2012, 337, 362–364 CrossRef CAS PubMed
.
- M. Oscarsson, A. Beteva, D. Flot, E. Gordon, M. Guijarro, G. Leonard, S. McSweeney, S. Monaco, C. Mueller-Dieckmann and M. Nanao,
et al.
, J. Synchrotron Radiat., 2019, 26, 393–405 CrossRef PubMed
.
- J. Aishima, R. L. Owen, D. Axford, E. Shepherd, G. Winter, K. Levik, P. Gibbons, A. Ashton and G. Evans, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 1032–1035 CrossRef CAS PubMed
.
- N. Coquelle, A. S. Brewster, U. Kapp, A. Shilova, B. Weinhausen, M. Burghammer and J. P. Colletier, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 1184–1196 CrossRef CAS PubMed
.
- M. Uervirojnangkoorn, O. B. Zeldin, A. Y. Lyubimov, J. Hattne, A. S. Brewster, N. K. Sauter, A. T. Brunger and W. I. Weis, eLife, 2015, 4, e05421 CrossRef PubMed
.
- T. A. White, Acta Crystallogr., Sect. D: Struct. Biol., 2019, 75, 219–233 CrossRef CAS PubMed
.
- A. S. Brewster, M. R. Sawaya, J. Rodriguez, J. Hattne, N. Echols, H. T. McFarlane, D. Cascio, P. D. Adams, D. S. Eisenberg and N. K. Sauter, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 357–366 CrossRef CAS PubMed
.
- G. Winter, D. G. Waterman, J. M. Parkhurst, A. S. Brewster, R. J. Gildea, M. Gerstel, L. Fuentes-Montero, M. Vollmar, T. Michels-Clark and I. D. Young,
et al.
, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 85–97 CrossRef CAS PubMed
.
- J. L. Wierman, O. Paré-Labrosse, A. Sarracini, J. E. Besaw, M. J. Cook, S. Oghbaey, H. Daoud, P. Mehrabi, I. Kriksunov and A. Kuo,
et al.
, IUCrJ, 2019, 6, 305–316 CrossRef CAS PubMed
.
- W. Kabsch, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 125–132 CrossRef CAS PubMed
.
- P. Legrand, GitHub Repos., 2017, https://github.com/legrandp/xdsme Search PubMed.
- G. Winter, J. Appl. Crystallogr., 2010, 43, 186–190 CrossRef CAS
.
- G. Santoni, U. Zander, C. Mueller-Dieckmann, G. Leonard and A. Popov, J. Appl. Crystallogr., 2017, 50, 1844–1851 CrossRef CAS PubMed
.
- J. Foadi, P. Aller, Y. Alguel, A. Cameron, D. Axford, R. L. Owen, W. Armour, D. G. Waterman, S. Iwata and G. Evans, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 69, 1617–1632 CrossRef CAS PubMed
.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed
.
- R. W. Grosse-Kunstleve, N. K. Sauter, N. W. Moriarty and P. D. Adams, J. Appl. Crystallogr., 2002, 35, 126–136 CrossRef CAS
.
- T. A. White, Philos. Trans. R. Soc., B, 2014, 369, 20130330 CrossRef PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed
.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS
.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
.
- A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS
.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed
.
- A. S. Brewster, D. G. Waterman, J. M. Parkhurst, R. J. Gildea, T. M. Michels-Clark, I. D. Young, H. J. Bernstein, G. Winter, G. Evans and N. K. Sauter, Computational Crystallography Newsletter, 2016, 7, 32–53 Search PubMed
.
- G. Assmann, W. Brehm and K. Diederichs, J. Appl. Crystallogr., 2016, 49, 1021–1028 CrossRef CAS PubMed
.
- I. Melnikov, O. Svensson, G. Bourenkov, G. Leonard and A. Popov, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 355–365 CrossRef CAS PubMed
.
- J. Kang, Y. Lee, S. Lee, H. Ki, J. Kim, J. Gu, Y. Cha, J. Heo, K. W. Lee and S. O. Kim,
et al.
, Nat. Chem., 2024, 16, 693–699 CrossRef CAS PubMed
.
- D. Balestri, P. P. Mazzeo, C. Carraro, N. Demitri, P. Pelagatti and A. Bacchi, Angew. Chem., Int. Ed., 2019, 58, 17342–17350 CrossRef CAS PubMed
.
- P. Mehrabi, E. C. Schulz, M. Agthe, S. Horrell, G. Bourenkov, D. von Stetten, J. P. Leimkohl, H. Schikora, T. R. Schneider and A. R. Pearson,
et al.
, Nat. Methods, 2019, 16, 979–982 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: The supporting information contains additional materials and methods concerning sample preparation and characterization, computational details and data collection, processing and refinements. Fig. S1–S15 show photographs of the crystals, data collection and processing workflows, example diffraction images. The supporting Tables S1–S4 report extensive data collection and refinement statistics. CCDC 2353477, 2346055, 2353478, 2353480, 2353479, 2353475 and 2353474. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ce00735b |
| ‡ Current address: Diamond Light Source Ltd, Harwell Science and Innovation Campus, Didcot OX11 0DE, UK. |
| This journal is © The Royal Society of Chemistry 2024 |