Matching ROY crystal structures to high-throughput PXRD

Abstract

The ability of a compound to form different crystalline structures, possessing distinct chemical and physical properties, is known as polymorphism. To identify the isolable polymorphs of a compound, extensive screening of experimental crystallization conditions is often carried out in a high-throughput fashion, where only powder X-ray diffraction (PXRD) patterns are obtainable. The room-temperature diffractograms must then be compared to low-temperature, single-crystal X-ray structures, such as from the Cambridge structural database (CSD), to identify if a particular solid form is a new or pre-existing polymorph. This comparison is problematic because the PXRD peak positions shift substantially with temperature. The variable-cell experimental powder difference (VC-xPWDF) method was recently developed to allow reliable comparison of experimental PXRD patterns to simulated diffractograms of known crystal structures. This work demonstrates the utility of VC-xPWDF to solve crystal structures from PXRD data generated during high-throughput polymorph screening for the test case of 5-methyl-2-[(2-nitrophenyl)amino]-3-thiophenecarbonitrile, also known as ROY, which is a prolific polymorph former. The method is shown to be successful for the comparison of PXRD patterns to both experimental crystal structures from the CSD and computationally generated structures obtained from a previous crystal structure prediction study. The experimental diffractogram quality was shown not to affect the results in most cases, although some errors do occur due to preferential orientation and low intensity/high baseline noise, which could potentially be reduced by additional grinding of the samples prior to making the PXRD measurements or slightly longer X-ray exposure during data collection.

---

1 Introduction

Polymorphism refers to the ability of the same material to exhibit different crystalline forms.¹ While thermodynamics dictates which polymorph is stable at a given set of conditions (e.g. temperature and pressure), the kinetics of nucleation and crystal growth influences which polymorph is actually formed for a particular set of crystallization parameters (e.g. solvent and cooling rate).^2–6 Polymorphism is particularly common for many organic compounds, where the weak intermolecular forces allow for multiple low-energy crystal structures.^7,8 As a result, polymorph control is instrumental in a variety of industries, including production of explosives, dyes, organic electronics, and especially pharmaceuticals.^9–13 Different polymorphs of a compound have different physical properties, including solubility; for a pharmaceutical, this affects its bioavailability.^14–16 Ensuring the correct polymorph is manufactured, and does not convert to a less active form over time, is vital in drug development.^5,6 Thus, theoretical and experimental screening techniques are required to identify all isolable polymorphs of pharmaceutical compounds, and these methods are seeing increased use in development of other solid-form molecular materials as well.^17–21

Crystal structure prediction (CSP) is an effective theoretical screening method that produces an energy landscape of putative crystal structures of a compound given only its molecular structure. This allows prediction of the most likely obtainable polymorphic structure(s) as the lowest-energy candidate(s).^22–27 However, CSP is based primarily on electronic energies from methods such as density-functional theory, which are only approximate and neglect thermal free-energy contributions from the lattice vibrations.^28–31 Both of these factors may lead to errors in the ranking, and extensive experimental searching for a crystal form that is actually less stable than predicted.³² Even in cases where the CSP landscape is reliable, it contains only thermodynamic data and provides an incomplete picture of crystallization that neglects the involvement of solvent, nucleation, dynamics, and kinetic factors in crystal growth.³³ As a result, one or more fairly high-energy structures on the CSP landscape may be observed experimentally, while other, lower-energy structures are not.³⁴ Hence, CSP is an excellent starting point for polymorph screening, but subsequent experimental screening is still vital in the development of new materials to be certain as to which polymorphs are actually formed. Further, differential scanning calorimetry (DSC) measurements and competitive slurry experiments are common experimental tools used to decisively determine the relative stabilities of two or more polymorphs.^35–37

High-throughput experimental screening aims to crystallize as wide a range of polymorphs as possible by using an array of different solvents and their mixtures, temperatures, and crystallization regimes, with recent studies seeking to automate this process.^38–43 The polymorphic structures obtained are typically analysed using X-ray powder diffraction (PXRD), given that high-throughput screening methods fail to produce single crystals. While PXRD is a fast and easy characterization technique, determining the crystal structure solution from the powder diffraction data is extremely challenging and not often practical. If the structure(s) of one or more polymorphs of the compound of interest have already been solved by single-crystal X-ray diffraction (SC-XRD), then they can potentially be matched to the PXRD patterns from screening studies. Similarly, if CSP has already been performed, then polymorphs identified by PXRD are likely to be represented in the landscape. However, direct comparison of experimental diffractograms to simulated diffractograms of either SC-XRD structures or in silico structures from CSP is often problematic.^44,45 This is because the PXRD peak positions are highly sensitive to the lattice parameters, which vary with temperature due to thermal expansion. SC-XRD structures are typically obtained at low temperatures of ca. 150 K, and in silico structures commonly correspond to a static lattice at 0 K, while PXRD analysis is performed under ambient conditions. The resulting shifts in PXRD peak positions make it difficult to distinguish between distinct polymorphs and redeterminations of the same form. It may, therefore, be unclear whether or not the polymorph being analyzed has already been identified.

The variable-cell experimental powder difference (VC-xPWDF) method⁴⁶ was recently proposed to allow quantitative comparison of experimental and simulated PXRD. It explores possible unit-cell bases for the candidate SC-XRD, or in silico, crystal structures, which are subsequently deformed to match the cell parameters obtained from indexing of the experimental diffractogram. VC-xPWDF then calculates the dissimilarity between the simulated and experimental powder patterns using the de Gelder cross-correlation function.⁴⁷ In this way, it accounts for the influence of anisotropic, temperature-dependent changes in the lattice parameters on the simulated diffractograms. The development of VC-xPWDF allows for efficient and reliable matching of experimental and simulated PXRD to identify the polymorphic structures formed. In its initial application, VC-xPWDF successfully identified the polymorphs of seven small organic molecules through comparison of moderate-to-low quality PXRD data to both SC-XRD and CSP structures.⁴⁶

It should be noted that the FIt with DEviating Lattice parameters (FIDEL) method^48,49 is another, highly successful approach to quantitative comparison of experimental and simulated PXRD. FIDEL is also based on the de Gelder cross-correlation function⁴⁷ but, unlike VC-xPWDF, does not require viable unit-cell parameters from indexing. Instead, FIDEL performs a global optimization where the unit-cell dimensions and atomic positions of the known crystal structure are modified to maximize similarity of its simulated diffractogram to the experimental PXRD pattern. While the freedom from indexing is a significant advantage, the global optimization approach means that FIDEL is more computationally expensive than VC-xPWDF and is susceptible to converging to a local minimum with mis-aligned peak positions, which can cause the algorithm to miss matching crystal structures in some cases.⁴⁶ Additionally, the FIDEL method is not currently implemented in freely distributed software, while VC-xPWDF is available through the open-source critic2 program.⁵⁰

This work presents an assessment of the effectiveness of VC-xPWDF when used in conjunction with PXRD data from high-throughput polymorph screening. Specifically, we apply VC-xPWDF to identify forms of 5-methyl-2-[(2-nitrophenyl)amino]-3-thiophenecarbonitrile—known as ROY due to its red, orange, and yellow polymorphs^51–60—crystallized in a previous high-throughput screening study.⁴² ROY offers a good benchmark for this investigation due to its 13 known polymorphs—12 with available SC-XRD structures—and the fact that it is well characterized from both the experimental and theoretical standpoints.^52,60–62 The low-quality experimental PXRD were compared to SC-XRD data of known ROY polymorphs in the CSD to determine if the correct matching form can be unambiguously identified. Additional comparisons were made between the experimental PXRD and in silico structures predicted in a recent CSP study of ROY.⁶²

2 Data

All experimental PXRD data used herein were obtained from the ESI† of ref. 42. In that work, Rosso et al. performed two high-throughput crystallization studies of ROY, each using a 96-well plate. The first of these was a screening array, which involved 96 different neat solvents or solvent mixtures. These experiments generally yielded polycrystalline samples of small particles. The second was a loading study that involved 12 replicated crystallizations with four different amounts (0.5, 1, 2, and 4 mg) of ROY and either isopropanol/water or tert-amyl alcohol/heptane solvent mixtures, which consistently yielded larger crystals. This loading study produced higher crystallinity samples, according to the metric used, four of which were selected in this work as the representative forms for the experimental data (vide infra). Overall, the crystallizations led to many instances of four different ROY polymorphs, denoted R (red), Y (yellow), OP (orange plates), and ON (orange needles), according to their crystalline appearance.

Not all of the samples in the work of Rosso et al. yielded crystals and some of the resulting PXRD patterns had extremely low intensity peaks. The overall crystallinity of the samples was previously defined from the diffractograms as 100 times the ratio of the crystalline peak area to the total pattern area. In our study, we only considered PXRD patterns with crystallinity values of ≥4.5; patterns with a crystallinity index lower than this were omitted due to the indistinguishably of peaks from the noise. This left us with 29 PXRD patterns from the screening array and 48 PXRD patterns from the loading array, for a total data set of 77 diffractograms. To refer to the various experimental diffractograms, we use the same numbering as in the ESI of ref. 42, but with either a leading L to indicate the loading array or a leading S to indicate the screening array. The other letter (A–H) and number (01–12) indicate the row/column position of a particular sample within the 96 wells of the array.

A set of SC-XRD structures of ROY, spanning all 12 polymorphs for which this data is available, was assembled from the Cambridge structural database (CSD) for comparison with the experimental PXRD patterns. As the CSD contains many determinations of some polymorphs under differing conditions, a single representative structure was taken for each form. Our set of representative structures, listed in Table 1, was selected to coincide with that used in ref. 62.

Table 1 VC-xPWDF scores for comparison of the four exemplar PXRD patterns with experimental crystal structures obtained from the CSD. The lowest score obtained for each pattern is highlighted. One particular crystal structure, indicated by the given refcode, was selected to represent each known ROY polymorph. The relative electronic energies of each polymorph, ΔE in kJ mol⁻¹ per molecule and obtained from Beran's previous CSP study,⁶² are also shown

---

Finally, a set of 264 in silico crystal structures was taken from a CSP landscape for ROY computed by Beran and coworkers.⁶² In that study, two million candidate structures were initially generated for Z′ = 1 using CrystalPredictor⁶³ with most intramolecular degrees of freedom constrained. Duplicates were removed and the geometries of the 1000 lowest-energy structures were fully relaxed using a distributed multipole force field⁶⁴ with CrystalOptimizer.⁶⁵ Following this, all structures within a 10 kJ mol⁻¹ energy threshold, relative to the global minimum, were fully relaxed with dispersion-corrected, plane-wave density-functional theory (DFT) with the B86bPBE functional^66,67 and exchange-dipole moment (XDM) dispersion correction^68–70 using Quantum ESPRESSO.⁷¹ The three experimentally known ROY polymorphs with Z′ = 2 were added to the data set. A monomer energy correction was applied by performing SCS-MP2D calculations⁷² on isolated molecules excised from the crystal structures using psi4.⁷³

3 Computational methods

The raw PXRD patterns were taken from the ESI of ref. 42 and analysed using the GSAS-II program⁷⁴ with the data cropped to span 5° ≤ 2θ ≤ 30° followed by background subtraction. The 19–23 most intense peaks, depending on the diffractogram, were selected manually for indexing analysis. Indexing was then performed using all methods available in CRYSFIRE2020;⁷⁵ the result that yielded the best figure of merit was selected as the final lattice parameters.

All VC-xPWDF comparisons were carried out using the critic2 program.⁵⁰ The algorithm⁴⁶ works by constructing all possible cell definitions of the candidate crystal structure such that its lattice parameters are within 30% of the cell lengths, and 20° of the angles of the indexed experimental PXRD. The lattice vectors of the candidate cell are then overwritten by those of the indexed cell. The diffractogram of the deformed candidate cell of the crystal structure is simulated using Cu K_α1 radiation (λ = 1.54036 Å) matching the X-ray wavelength used in the ROY screening experiments.⁴² The simulated and experimental PXRD are then compared using de Gelder's triangle-weighted cross-correlation function⁴⁷ with a triangle width of 1°. VC-xPWDF evaluates the powder difference, so a value of zero indicates identical structures, while a value of one indicates maximum dissimilarity. The lowest powder difference obtained for any of the possible candidate cell definitions is taken as the final VC-xPWDF score.

4 Results and discussion

4.1 Clustering and indexing

We begin by manually clustering the experimental diffractograms, although this process could, in principle, be automated. Clustering resulted in clear identification of 4 unique polymorphs, each represented by a set of similar diffractograms, as shown in Fig. 1. One exemplar PXRD from each cluster was then selected for indexing; these were patterns LG06, LG08, LG10, and LH05. The diffractograms selected were those that displayed the highest crystallinity, except for one cluster where the case exhibiting the second highest crystallinity (viz. 17.8 for LG10 vs. 18.5 for LH06) was chosen since indexing of that pattern resulted in a significantly higher figure of merit (FoM, 16 vs. 8). The indexed lattice parameters for the four exemplars are collected in Table 2. These lattice parameters were then taken to be representative values for that polymorph, and used in subsequent VC-xPWDF comparisons for all diffractograms within the corresponding cluster.

Fig. 1 Overlay of experimental diffractograms showing the results of manual clustering. The diffractogram selected for indexing from each cluster is shown in black, with the other patterns in grey.

Table 2 Experimental crystallinity, number of peaks used for indexing, figure of merit (FoM) from indexing, and indexed lattice parameters (angstroms and degrees) for the four experimental diffractograms selected as the best representatives of each cluster

Label	Crystallinity	N peaks	FoM	a	b	c	α	β	γ
LG06	15.9	23	16.2	3.9619	16.4658	18.7191	90	90	93.966
LG08	18.2	21	15.1	7.5143	7.8180	11.9392	75.574	77.726	63.725
LG10	17.8	20	16.0	7.9915	11.7043	13.3244	90	90	104.659
LH05	16.1	19	18.0	8.5089	8.5357	16.5484	90	90	92.304

---

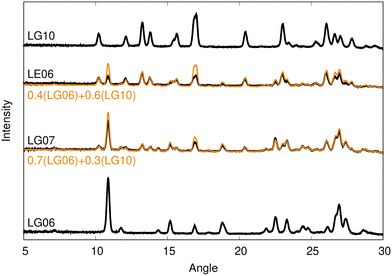
Only two diffractograms, shown in Fig. 2, could not be grouped into any of the four clusters. While an unusual PXRD may indicate formation of an unknown polymorph, consideration of these two diffractograms revealed them to be well represented by linear combinations of the LG06 and LG10 patterns with differing coefficients, implying that they are both mixtures of two polymorphs. As such, we will not consider the patterns for these two mixtures further and all subsequent analysis will focus on structure solution of the four distinct polymorphs identified from the clustering.

Fig. 2 Experimental diffractograms of the two mixtures (LG07 and LE06). Each can be well reproduced by a linear combination (shown in orange) of the LG06 and LG10 diffractograms, with differing weights.

4.2 Comparison to CSD structures

4.2.1 Exemplar cases. To identify the crystal forms matching each of our clusters, we first consider only the four exemplar diffractograms listed in Table 2. These four PXRD were compared to simulated diffractograms for the 12 representative experimental SC-XRD crystal structures from the CSD. The experimental diffractograms were processed by truncating the angle range to 5–30° and performing background subtraction only. The indexed unit-cell parameters shown in Table 2 were used as input to VC-xPWDF, along with the processed diffractograms and experimental .cif files. The final VC-xPWDF scores for all comparisons are collected in Table 1. These results show that only one low VC-xPWDF score (<0.1), indicative of a structural match,⁴⁶ is obtained for each diffractogram. This leads to a clear assignment of the experimental PXRD to particular polymorphs (LG06 = ON, LG08 = R, LG10 = OP, and LH05 = Y). This assignment is confirmed by considering overlays of the PXRD patterns with simulated diffractograms from the matching crystal structures, as shown in Fig. 3.

Fig. 3 Overlays of the four exemplar experimental PXRD patterns (black) with simulated diffractograms of their matching polymorph's CSD structure after variable-cell correction with VC-xPWDF (green).

Our results allow us to attribute all samples within a particular PXRD cluster to the polymorph matching its exemplar. All crystallization experiments were performed by dissolution at 50 °C followed by cooling to 20 °C,⁴² and the relative free energies of the observed ROY polymorphs are well known in this temperature range.⁵² Interestingly, the most stable Y polymorph (LH05 cluster) forms relatively rarely, in only 7 of the 77 cases considered from the crystallization study.⁴² Forming in 62 of the cases, the OP and ON polymorphs (LG06 and LB10 clusters) are effectively degenerate in this temperature range and slightly less stable than the Y polymorph, lying only 0.2 kJ mol⁻¹ higher in free energy.⁵² While this is a small free-energy difference, the much greater prevalence of the OP and ON forms implies that kinetic effects favour their formation over the more thermodynamically stable Y polymorph. Finally, the R polymorph is the least stable of the three observed forms (0.6 kJ mol⁻¹ higher than Y in free energy⁵²) at the ambient temperature conditions of the crystallization experiments, which is consistent with it only being generated 6 times (LG08 cluster).⁴²

The ability to assign the PXRD to the structures observed in the CSP landscape and assess the propensity of the formation of certain forms provides an additional level of understanding of the polymorphic landscape. While the OP and ON forms are still less stable than Y according to experimental determinations,⁵² the free energy difference is much smaller than implied by relative electronic energies from CSP (see Table 1), and kinetics will play a roll in their preferential formation over the Y polymorph. Conversely, the apparent stability of R (and any other forms between Y and OP/ON) from the CSP landscape⁶² is eliminated with the addition of entropy contributions, and a lower number of occurrences is expected according to thermodynamic arguments.

4.2.2 Lower crystallinity cases. To assess the requisite level of crystallinity needed for reliable VC-xPWDF comparison, further calculations were performed for the full set of 75 experimental PXRD patterns (mixtures excluded). VC-xPWDF was used to compare all diffractograms against the representative set of 12 experimental cifs using the appropriate indexed lattice constants given in Table 2. For each diffractogram, the lowest VC-xPWDF score among the 12 comparisons was identified. The data are summarized by the scatter plot of VC-xPWDF score vs. crystallinity index in Fig. 4.

Fig. 4 Scatter plot showing the minimum VC-xPWDF score obtained for comparison of each of the 75 experimental diffractograms to 12 CSD reference structures, as a function of the sample crystallinity. Data points are coloured according to the identity of the corresponding polymorph in cases were VC-xPWDF correctly identified the structural match. Cases where a lower VC-xPWDF score was obtained for some other, non-matching polymorph are coloured black and the PXRD data label given. The grey shaded region corresponds to VC-xPWDF scores <0.1, which we view as being indicative of a good structural match.

Overall, the lowest VC-xPWDF score successfully identified the CSD structure of the matching polymorph for 71/75 diffractograms. Additionally, VC-xPWDF provided the correct structure assignment in all cases with scores ≤0.1, which we view as a good cutoff for a likely match. VC-xPWDF also correctly matched all PXRD with crystallinity ≥7, although the method chosen to calculate the crystallinity index may not be the best descriptor of diffractogram quality. In ref. 42, the crystallinity was determined from the experimental diffractograms as 100 times the ratio of crystalline peak area to total pattern area, which does not account for preferred orientation. Many structures with low crystallinity values between 4.5 and 7 were correctly matched to CSP structures with VC-xPWDF scores of ≤0.2. On the other hand, one structure (LD09) with a moderate crystallinity of 6.4 gave a minimum VC-xPWDF score of 0.494 and a missed match.

To investigate the origins of the four matches missed by VC-xPWDF, we plot overlays of these experimental PXRD with the simulated diffractogram of the correct matching polymorph in Fig. 5. The upper left panel shows the result for the largest outlier in Fig. 4, which was the case of LD09; based on clustering, this sample should contain the R polymorph. The diffractogram overlay in Fig. 5 reveals that the issue here is preferential orientation, with one peak in the experimental PXRD having an anomalously high intensity compared to the others. This leads to low intensity overlap with all remaining peaks and a high VC-xPWDF score for comparison with the R polymorph (0.506), and indeed with all other reference SC-XRD structures. The upper right panel in Fig. 5 shows the result for LA01, which has a crystallinity of only 4.7. Here, the lowest VC-xPWDF score is obtained for the Y04 form (0.181), as opposed to the OP form (0.310) that is the matching polymorph for the corresponding cluster of diffractograms. The PXRD overlay again indicates issues with preferential orientation. While less severe than for LD09, there remains one peak in the experimental PXRD that is anomalously high relative to the others. Coincidentally, the most intense peak in the simulated diffractogram of the Y04 polymorph appears at a similar angle (see the ESI†), explaining why it provides a lower VC-xPWDF score in this case. In the experimental study by Rosso et al.,⁴² they note that all samples “were subjected to grinding by a magnetic stir bar to minimise preferential orientation errors”. However, this seems to have been insufficient for two of the samples from the loading study, and additional grinding before acquiring the PXRD patterns is recommended.

Fig. 5 Overlays of four experimental PXRD patterns (black) with simulated diffractograms of their matching polymorph's CSD structure after variable-cell correction with VC-xPWDF. These are the four cases for which VC-xPWDF was not able to predict the correct structural match, due to either preferential orientation (top row) or excessive noise in the experimental diffractogram (bottom row). Overlays with the (incorrect) best VC-xPWDF match are shown in the ESI.†

PXRD overlays for the other two missed matches are shown in the lower two panels of Fig. 5. These occur for samples LF12 and LH02, both of which should correspond to the OP polymorph based on the diffractogram clustering. Here, overlays of the experimental and simulated diffractograms display evident visual matches, so it is unclear why a lower VC-xPWDF score is not obtained for the OP structure. In both these cases, the lowest VC-xPWDF scores are obtained for comparison with the Y04 polymorph (viz. 0.200 and 0.160 for LF12 and LH02, respectively), despite the obvious visual differences in their diffractograms (see the ESI†). The next-lowest scores are obtained for comparison with the OP polymorph (viz. 0.221 and 0.177 for LF12 and LH02, respectively). We conjecture that the issue here is the high level of baseline noise in the experimental diffractograms, as evidenced by the low crystallinity. It is likely that higher levels of overlap with the noise are enough to bias the VC-xPWDF scores away from the correct match.

4.3 Comparison to CSP structures

In practical cases of polymorph screening, it is unlikely that the system under study will be as well characterized as ROY, with solved SC-XRD structures already available for 12 of 13 observed polymorphs. The more likely event is that screening uncovers one or more new polymorphs of a compound, but without yielding a sufficiently large single crystal for SC-XRD. The most efficient route to structure solution may then be through comparison to putative, in silico, crystal structures generated via CSP. To highlight the viability of this approach, VC-xPWDF is used to compare the four indexed, experimental PXRD (Table 2) to 264 DFT-optimized crystal structures of ROY.

Typically, the results of CSP are represented visually in the form of a crystal-energy landscape, which is a scatter plot with each point representing a candidate crystal structure. The ordinate is the energy of each structure, relative to the global minimum, while the abscissa is often the density of the crystal. Fig. 6 shows CSP landscapes where the abscissa is instead the computed VC-xPWDF score obtained from comparison of the candidate crystal structures with one of the four indexed PXRD patterns (LG06, LG08, LG10, or LH05). The most likely matches to the experimental diffractograms should be structures with both low energies and low VC-xPWDF scores, appearing near the bottom left corner of each plot.

Fig. 6 CSP landscapes for ROY, using the relative energies computed in ref. 62. For each plot, the abscissa is the VC-xPWDF score obtained from comparison of each candidate crystal structure with the indicated experimental PXRD pattern. Black points correspond to the 13 known ROY polymorphs (including the proposed structure for RPL⁶⁰), while the grey points indicate putative structures generated from CSP. The circled points correspond to the matching polymorph for each diffractogram.

The results in Fig. 6 show that the lowest VC-xPWDF scores are obtained for the ON form for LG06, the R form for LG08, the OP form for LG10, and the Y form for LH05. This exactly matches the results from VC-xPWDF comparison to CSD crystal structures of ROY (Table 1). The present results highlight the ability of VC-xPWDF to solve crystal structures from indexed powder data in conjunction with an appropriate set of candidate structures from CSP.

5 Conclusion

In this work, 77 experimental diffractograms were taken from a previous high-throughput polymorph screen of ROY.⁴² Clustering of the diffractograms revealed four distinct polymorphs, and two mixtures. One representative PXRD pattern with high crystallinity was selected for each polymorph and indexed; the resulting lattice parameters were used for all quantitative structure comparisons for that diffractogram cluster. The VC-xPWDF method was then used to compare the experimental PXRD patterns to simulated diffractograms of SC-XRD structures for 12 ROY polymorphs obtained from the CSD. The four exemplar PXRD patterns used for indexing were also compared to simulated diffractograms for all in silico crystal structures in the CSP landscape generated by Beran and coworkers.⁶²

In general, the single crystal structure that yields the lowest VC-xPWDF score when compared to an experimental diffractogram is taken as the corresponding polymorph, with a score <0.1 typically indicating a good match. Using this criterion, the VC-xPWDF comparisons for the four indexed diffractograms lead to their unambiguous assignment as the yellow (Y), red (R), orange plates (OP), and orange needles (ON) forms, regardless of whether CSD or CSP reference structures were employed. We propose that CSP-type landscapes, plotting the relative energies of candidate crystal structures vs. the VC-xPWDF scores, should be a convenient aid to structure solution from powder data.

VC-xPWDF also typically predicted the correct polymorph match to CSD structures, based on agreement with the exemplar result for a corresponding cluster, for lower-crystallinity diffractograms. However, as the crystallinity decreases, the VC-xPWDF scores for the best matching polymorph typically increase, frequently surpassing the recommended 0.1 threshold⁴⁶ for a good match. There were also four cases where VC-xPWDF assigned the best match to an incorrect polymorph, either due to substantial preferred orientation of the sample or to excessive baseline noise. In the latter situation, there was only a very small difference between the lowest and second-lowest VC-xPWDF scores, and plotting overlays of the simulated and experimental diffractograms clearly revealed the correct structural match.

Given the above results, it can be suggested that there is a minimum quality for the diffractogram that must be met to use VC-xPWDF. However, one missed match occurred for a relatively high crystallinity sample due to preferred orientation, while many samples with lower crystallinity were perfectly amenable to VC-xPWDF analysis. This prompts consideration as to how diffractogram quality is determined given that the error in identification is often due to the problem of preferred orientation rather than aspects commonly attributed to the crystallinity of the sample itself (e.g. baseline, signal to noise, etc.). In cases with several candidate structures yielding similar VC-xPWDF scores, visual inspection of PXRD data should be considered to ensure correct identification of the polymorphic forms. Issues with preferred orientation could potentially be reduced by additional grinding of the samples prior to PXRD data collection.

Finally, this work demonstrates a bridge between CSP and experimental polymorph screening, allowing us to assign structures to observed forms and understand their propensity for crystallization. From comparison of the VC-xPWDF assigned structures with the experimental free energies,⁵² it is clear that kinetics plays a role in explaining the high formation propensity of the ON and OP polymorphs. These are by far the most prevalent forms identified from the polymorph screen, despite having effectively degenerate free energies that are slightly higher than that of the Y form, which is thermodynamically favoured. On the other hand, the low crystallization propensity of the R polymorph, and lack of any less-stable forms, is consistent with the relative free energies over the experimental temperature range.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada, and by the Royal Society through a Wolfson Visiting Fellowship to ERJ.

References

1. J. Haleblian and J. W. McCrone, J. Pharm. Sci., 1969, 58, 911.
2. J. Bernstein, Polymorphism in molecular crystals 2e, International Union of Crystal, 2020, vol. 30.
3. J. R. Davey, N. Blagden, S. Righini, H. Alison and E. S. Ferrari, J. Phys. Chem., 2002, 106, 1954.
4. Y. Gui, C. Huang, C. Shi, T. Stelzer, G. G. Z. Zhang and L. Yu, J. Chem. Phys., 2022, 156, 144504.
5. J. D. Dunitz and J. Bernstein, Acc. Chem. Res., 1995, 28, 193–200.
6. D.-K. Bučar, R. W. Lancaster and J. Bernstein, Angew. Chem., Int. Ed., 2015, 54, 6972–6993.
7. G. P. Stahly, Cryst. Growth Des., 2007, 7, 1007–1026.
8. A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635.
9. R. Bu, H. Li and C. Zhang, Cryst. Growth Des., 2020, 20, 3561–3576.
10. Z. Hao and A. Iqbal, Chem. Soc. Rev., 1997, 26, 203–213.
11. Y. Yang, B. Rice, X. Shi, J. R. Brandt, R. Correa da Costa, G. J. Hedley, D.-M. Smilgies, J. M. Frost, I. D. W. Samuel, A. Otero-de-la-Roza, E. R. Johnson, K. E. Jelfs, J. Nelson, A. J. Campbell and M. J. Fuchter, ACS Nano, 2017, 11, 8329–8338.
12. J. Yang, C. T. Hu, X. Zhu, Q. Zhu, M. D. Ward and B. Kahr, Angew. Chem., Int. Ed., 2017, 56, 10165–10169.
13. S. R. Chemburkar, J. Bauer, K. Deming, H. Spiwek, K. Patel, J. Morris, R. Henry, S. Spanton, W. Dziki, W. Porter, J. Quick, P. Bauer, J. Donaubauer, B. A. Narayanan, M. Soldani, D. Riley and K. McFarland, Org. Process Res. Dev., 2000, 4, 413–417.
14. H. Park, J.-S. Kim, S. Hong, E.-S. Ha, H. Nie, Q. T. Zhou and M.-S. Kim, J. Pharm. Invest., 2022, 52, 175–194.
15. D. Singhai and W. Curatolo, Adv. Drug Delivery Rev., 2004, 56, 335–347.
16. N. Blagden, M. de Matas, P. T. Gavan and P. York, Adv. Drug Delivery Rev., 2007, 59, 617–630.
17. A. Y. Lee, D. Erdemir and A. S. Myerson, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 259–280.
18. S. L. Price and S. M. Reutzel-Edens, Drug Discovery Today, 2016, 21, 912–923.
19. S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Chem. Commun., 2016, 52, 7065–7077.
20. J. Nyman and S. M. Reutzel-Edens, Faraday Discuss., 2018, 211, 459–476.
21. A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664.
22. J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz and A. Gavezzotti, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2000, 58, 647–661.
23. W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko and P. Erk, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 647–661.
24. G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter and R. G. Della Valle, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 511–527.
25. G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk and H. L. Ammon, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125.
26. D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich and S. X. M. Boerrigter, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551.
27. A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole and K. Cosburn, et al. , Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459.
28. J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165.
29. J. Nyman and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 31132–31143.
30. J. Hoja and A. Tkatchenko, Faraday Discuss., 2018, 211, 253–274.
31. J. Hoja, H. Y. Ko, M. A. Neumann, R. Car, R. A. Distasio and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338.
32. R. M. Bhardwaj, J. A. McMahon, J. Nyman, L. S. Price, S. Konar, I. D. H. Oswald, C. R. Pulham, S. L. Price and S. M. Reutzel-Edens, J. Am. Chem. Soc., 2019, 141, 13887–13897.
33. S. L. Price, Faraday Discuss., 2018, 211, 9–30.
34. M. A. Neumann and J. van de Streek, Faraday Discuss., 2018, 211, 441–458.
35. S. Reutzel-Edens, Curr. Opin. Drug Discovery Dev., 2006, 9, 806–815.
36. K. Park, J. M. B. Evans and A. S. Myerson, Cryst. Growth Des., 2003, 3, 991–995.
37. P. G. Royall, A. K. Kett and R. J. Cameron, Int. J. Pharm., 2008, 350, 48–52.
38. A. J. Alvarez, A. Singh and A. S. Myerson, Cryst. Growth Des., 2009, 9, 4181–4188.
39. A. M. Campeta, B. P. Chekal, Y. A. Abramov, P. A. Meenan, M. J. Henson, B. Shi, R. A. Singer and K. R. Horspool, J. Pharm. Sci., 2010, 99, 3874–3886.
40. R. Storey, R. Docherty, P. Higginson, C. Dallman, C. Gilmore, G. Barr and W. Dong, Crystallogr. Rev., 2014, 10, 45–56.
41. J. A. Selekman, D. Roberts, V. Rosso, J. Qiu, J. Nolfo, Q. Gao and J. Janey, Org. Process Res. Dev., 2016, 20, 70–75.
42. V. W. Rosso, Z. Yin, H. Abourahma, A. Furman, S. Sharif, A. Werneth, J. M. Stevens, F. Roberts, D. Aulakh, R. Sommer and A. A. Sarjeant, Org. Process Res. Dev., 2023, 27, 1437–1444.
43. A. M. Lunt, H. Fakhruldeen, G. Pizzuto, L. Longley, A. White, N. Rankin, R. Clowes, B. Alston, L. Gigli and G. M. Day, et al. , Chem. Sci., 2024, 15, 2456–2463.
44. J. van de Streek and S. Motherwell, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 504–510.
45. M. Zilka, D. V. Dudenko, C. E. Hughes, P. A. Williams, S. Sturniolo, W. T. Franks, C. J. Pickard, J. R. Yates, K. D. Harris and S. P. Brown, Phys. Chem. Chem. Phys., 2017, 19, 25949–25960.
46. R. A. Mayo, K. M. Marczenko and E. R. Johnson, Chem. Sci., 2023, 14, 4777–4785.
47. R. de Gelder, R. Wehrens and J. A. Hageman, J. Comput. Chem., 2001, 22, 273–289.
48. S. Habermehl, P. Mörschel, P. Eisenbrandt, S. M. Hammer and M. U. Schmidt, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 347–359.
49. S. Habermehl, C. Schlesinger and M. U. Schmidt, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2022, 78, 195–213.
50. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
51. G. Stephenson, T. Borchardt, S. Byrn, J. Bowyer, C. Bunnell, S. Snorek and L. Yu, J. Pharm. Sci., 1995, 84, 1385–1386.
52. L. Yu, G. A. Stephenson, C. A. Mitchell, C. A. Bunnell, S. V. Snorek, J. J. Bowyer, T. B. Borchardt, J. G. Stowell and S. R. Byrn, J. Am. Chem. Soc., 2000, 122, 585–591.
53. S. Chen, I. A. Guzei and L. Yu, J. Am. Chem. Soc., 2005, 127, 9881–9885.
54. M. Tan, A. G. Shtukenberg, S. Zhu, W. Xu, E. Dooryhee, S. M. Nichols, M. D. Ward, B. Kahr and Q. Zhu, Faraday Discuss., 2018, 211, 477–491.
55. K. S. Gushurst, J. Nyman and S. X. M. Boerrigter, CrystEngComm, 2019, 21, 1363–1368.
56. A. R. Tyler, R. Ragbirsingh, C. J. McMonagle, P. G. Waddell, S. E. Heaps, J. W. Steed, P. Thaw, M. J. Hall and M. R. Probert, Chem, 2020, 6, 1755–1765.
57. A. Lévesque, T. Maris and J. D. Wuest, J. Am. Chem. Soc., 2020, 142, 11873–11883.
58. X. Li, X. Ou, H. Rong, S. Huang, J. Nyman, L. Yu and M. Lu, Cryst. Growth Des., 2020, 20, 7093–7097.
59. C. A. Mitchell, L. Yu and M. D. Ward, J. Am. Chem. Soc., 2001, 123, 10830–10839.
60. J. Nyman, L. Yu and S. M. Reutzel-Edens, CrystEngComm, 2019, 21, 2080–2088.
61. L. Yu, Acc. Chem. Res., 2010, 43, 1257–1266.
62. G. J. O. Beran, I. J. Sugden, C. Greenwell, D. H. Bowskill, C. C. Pantelides and C. S. Adjiman, Chem. Sci., 2022, 13, 1288–1297.
63. M. Habgood, I. J. Sugden, A. V. Kazantsev, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2015, 11, 1957–1969.
64. S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490.
65. A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2011, 7, 1998–2016.
66. A. D. Becke, J. Chem. Phys., 1986, 85, 7184.
67. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
68. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
69. E. R. Johnson, in Non-covalent Interactions in Quantum Chemistry and Physics, ed. A. Otero-de-la-Roza and G. A. DiLabio, Elsevier, 2017, ch. 5, pp. 169–194.
70. A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 136, 174109.
71. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
72. C. Greenwell, J. Řezáč and G. J. O. Beran, Phys. Chem. Chem. Phys., 2022, 24, 3695–3712.
73. R. M. Parrish, L. A. Burns, D. G. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio and R. M. Richard, et al. , J. Chem. Theory Comput., 2017, 13, 3185–3197.
74. B. H. Toby, R. B. Von Dreele, P. Juhás, B. Kiefer and T. Proffen, GSAS-II: the GenX of crystallography software?, Software, 2013, Available at: https://subversion.xray.aps.anl.gov/trac/pyGSAS.
75. R. B. Shirley, CRYSFIRE2020 (Version 1.0), Software, 2020, Available at: http://www.icdd.com/.

---

Footnote

† Electronic supplementary information (ESI) available: PXRD overlays of missed matches, tables of VC-xPWDF scores, and processed experimental diffractograms. See DOI: https://doi.org/10.1039/d4ce00700j

---