Symthons reveal how fluorine disrupts π–π stacking in halobenzene crystal structures

Abstract

Symmetry-forming closest approaches of aromatic rings; ‘Symthons’, are usually the strongest interactions in halobenzene crystal structures. Where they combine to create π–π stacking, they are as strong as hydrogen bonds. This π–π stacking is disrupted when fluorine is present, as revealed in this analysis of all 290 closest aromatic approaches in the crystal structures of halobenzenes. Closest aromatic approaches involving fluorine show fewer examples of ‘Symthon I’ π–π stacking, and more examples of offset translations with larger displacements. Edge⋯face approaches are also more common in the presence of fluorine, frequently accommodating fluorine atoms in the ‘edges’. Some edge⋯face approaches do not embody any symmetry. These findings are consistent with lower melting points and favourable connections between fluorine and positively charged carbon atoms.

---

Introduction

This is the third paper in a series interrogating all halobenzene crystal structures. The first study¹ dealt with halobenzenes containing either chlorine or bromine or iodine and was followed by a second study² covering ‘mixed’ halobenzenes containing more than one of these three halogens. These two studies introduced the concept of “Symthons”. Here, “Symthons” are close intermolecular approaches with defined geometry and symmetry that are building blocks for crystallisation. These are distinct from the commonly used term, “synthons” which refer to molecular fragments that are building blocks for chemical synthesis and which give rise to the notion of “supramolecular synthons” as building blocks for molecular aggregation in the form of dimers, trimers, tetramers etc., that may exist in liquids, solutions, amorphous solids or crystals.

This study focuses on closest aromatic approaches such as ‘π–π stacking’. Graphite³ was the first example of a crystal structure containing π–π stacks. The unit cell for platinum phthalocyanines followed,⁴ featuring a short unit cell repeat of b = 3.81 Å. The corresponding crystal structure⁵ confirmed that this translational symmetry was embodied in the overlap of successive identical aromatic rings in a similar manner to graphite. Kitaigorodskii⁶ rationalised these type of approaches as featuring one or two carbon atoms sitting in the ‘hollows’ above and below the centroids of neighbouring atomic rings, citing graphite and C₆Cl₆ as examples. This inspired the aforementioned investigations^1,2 of similar approaches in the crystal structures of halobenzenes without fluorine. A specific subset of π–π stacks was found in 110 out of 176 closest aromatic approaches in this dataset, being particularly favoured for molecules containing more than two (N > 2) halogen substituents. These approaches all had interplanar separations (s) in the range 3.3–3.9 Å, displacements (d) in the range 1.4–2.5 Å and embodied translational symmetry. This defined ‘Symthon I’, further characterised by short crystallographic repeats in the range 3.8–4.3 Å.

Those studies^1,2 also revealed that benzene and some halobenzenes with one or two halogen substituents (N ≤ 2) showed a strong preference for edge⋯face approaches embodying screw and/or glide symmetry, with centroid⋯edge C connections in the range 3.4–3.8 Å and neighbouring face C⋯edge C connections in the range 3.5 to 4.1 Å, defined as ‘Symthon II’. A minority of face–face approaches showed inversion rather than translational symmetry, with the same range of interplanar separations, (s) as Symthon I but with displacements (d) ranging from 0.4 to 2.5 Å, defined as Symthon III. Together these three Symthons (Fig. 1a–c) accounted for 84% (147/176) of the closest approaches in the halobenzene dataset.² Three variants of these Symthons were also identified - offset translations, halogen edge-face and offset inversions – as illustrated schematically in Fig. 1d–f. The symmetries embodied in these variants are preserved, but the aromatic rings are further apart, typically because halogen atoms (indicated by filled circles in Fig. 1d–f) now occupy hollows above and/or below each aromatic ring. For convenience, these findings are represented schematically here in Fig. 6(left).

Fig. 1 Schematic approaches between halobenzenes. Filled circles indicate halogen atoms occupying ‘hollows’.

Offset translations are also common in several phthalocyanines, including those of hydrogen, copper and nickel, accounting for short crystallographic repeats in the range b = 4.7–4.8 Å.⁴ The overlap in these crystal structures is between C₆ aromatic rings in one molecule and fused heterocycles in neighbouring layers. Larger displacements were also reported⁷ in solution complexes and crystal structures of porphyrins. Computations showed that these larger displacements were consistent with minimising unfavourable approaches of nitrogen atoms carrying partial negative charges. A surprising claim that ‘aromaticity is not required for aromatic interactions’ was based on extensive computations of mono- and 1,4 di-substituted benzenes.⁸ Separately,⁹ ‘edge⋯face’ approaches in benzene and C₆F₆ were contrasted with ‘parallel stacks’ in benzene/C₆F₆ cocrystals and cocrystals of pentafluorobenzenes with other halogen-free phenyl rings.

In the work reported here, attention is focussed on fluorobenzenes and halofluorobenzenes which are of potential interest as synthetic precursors to active pharmaceutical ingredients such as paliperidone, ticagrelor, rosuvastatin and olaparib, all of which contain partially fluorinated aromatic rings. The Crystal Structure Database (CSD) reveals a number of relevant crystal structures. For example, the crystal structures of seven fluorobenzenes have been studied in detail.¹⁰ Three further fluorobenzene crystal structures were determined later by the same group^11–13 and in a separate study¹⁴ the crystal structures of all nine di-substituted halofluorobenzenes (N = 2) were reported and discussed. For many of these fluorinated materials their sub-ambient melting necessitated crystallisation in situ in a diffractometer on a cryo-stage. The structural bases of polymorphism in C₆HF₅ (ref. 15) and 1-dibromo-2,3,5-trifluorobenzene¹⁶ have also been reported. In all of these studies, discussion of the crystal structures has focused on individual or paired C–H⋯F connections, rather than the broader examination of closest approaches and their embodied symmetries (“Symthons”) deployed in this study.

In related work, a study of C₆F₆ revealed a high-pressure polymorph.¹⁷ Separately, four polymorphs of a benzene : C₆F₆ cocrystal have been investigated.¹⁸ 1,3-Dibromo-2-chloro-5-fluorobenzene was molecule XIII in the 4th Crystal Structure Prediction “blind test”¹⁹ – in which four participants predicted the crystal structure correctly. There are several other crystal structures of halobenzenes with fluorine in the CSD that were determined to confirm molecular structure as part of synthetic chemistry investigations. Many other structures appear in specialist journals (Acta Cryst. E) or as communications directly to the CSD. In such cases, there are no accompanying discussions of the key intermolecular interactions in these structures.

A computational study²⁰ using electrostatic potential (ESP) mapping and DFT-D3 routines gave calculated energies for different interaction geometries in benzene and three hexahalobenzenes. Edge⋯face energies were in the range −8 to −14 kJ mol⁻¹ for all four compounds, whereas face⋯face interactions energies increased sharply from −13 kJ mol⁻¹ for C₆F₆ to −48 kJ mol⁻¹ for C₆Cl₆ and −59 kJ mol⁻¹ for C₆Br₆. These strong face⋯face approaches in C₆Cl₆ and C₆Br₆ are Symthon I. The calculations indicate that face⋯face approaches in C₆F₆ are much weaker, comparable with edge⋯face approaches in benzene and in C₆F₆. The calculated electrostatic potential maps²⁰ show that the ‘hollows' above each aromatic rings are weakly positively charged in C₆Cl₆ and C₆Br₆, strongly positive in C₆F₆, and negative in benzene. They also show “σ-holes” in the halogen atoms in C₆Cl₆ and C₆Br₆, but not in C₆F₆. In a more recent study²¹ of five fluorobenzenes, the stabilising contribution of entropy from C–H⋯F bonds was reported to provide an additional 10–15 kJ mol⁻¹ of stabilisation energy.

The melting points of chlorobenzenes and bromobenzenes increase approximately linearly with N, the number of halogen substituents: +36 °C per chlorine atom and +52 °C per bromine atom – see ESI† for details.²² In contrast, the melting points of fluorobenzenes show no systematic increase with N; all are liquid at room temperature with melting points in the range −59 to + 4 °C.²² These differences can hardly be due to interactions that only occur in the presence of fluorine atoms; they rather suggest stronger interactions that do not incorporate fluorine atoms.

To explore this possibility in a little more detail Table 1 was constructed to compare relevant general information about carbon, fluorine, chlorine and hydrogen atoms and bonds. These data were extracted from the Mercury software²³ and the references cited therein.^24,25 The ranges of Gasteiger charges are for the halobenzene molecules in this study. The optimum separations were calculated from the parameters and formulae in the CSD Materials/calculations/UNI option within Mercury.

Table 1 Elemental data extracted from mercury

Element	Chlorine	Carbon	Fluorine	Hydrogen
Z	17	6	9	1
Atomic radius (Å)	1.75	1.70	1.47	1.20
X⋯X optimum (Å)	3.83	3.89	3.20	3.41
C⋯X optimum (Å)	3.83	3.89	3.51	3.30
C–X bond length(Å)	1.72	1.38	1.35	0.95
Gasteiger charges	−0.08	−0.06/+0.20	−0.20/0.21	+0.06/7

---

Fluorine is smaller than carbon and other halogens, with shorter C⋯F bond lengths and optimum separations. Fluorine is also more negatively charged than chlorine and other halogen substituents. It follows that carbon atoms in C–F bonds have positive (Gasteiger) charges as high as +0.20. This suggests that fluorine atoms (F^δ−) may prefer short connections to carbon atoms carrying positive partial charges (C^δ+), which could be accommodated in ‘halogen edge’ approaches as shown in Fig. 1e. Favourable (C^δ+⋯C^δ−) short connections between non-centrosymmetric molecules could be accommodated by Symthon III. Symthon I involves short C^δ+⋯C^δ+ and F^δ−⋯F^δ− connections, so might be expected to be less popular in structures of the fluorobenzenes. This is consistent with the lower calculated interaction energies for face⋯face interactions of C₆F₆.²⁰ These considerations are combined in the hypothesis that the Symthon I type of π–π stacking, which dominates crystal structures of halobenzenes without fluorine, will be disrupted in the presence of fluorine.

Methods

The methodology of this study was similar to that used for halobenzenes without fluorine.^1,2 The CSD was interrogated to create a dataset of all halobenzene crystal structures containing fluorine. These were analysed to identify the closest approaches on each aromatic face. The symmetry and geometry of each approach were classified and compared with those of halobenzenes without fluorine.

The CSD was searched using Conquest Version 2023.1.0 and CSD Version 5.44 (April 2023 update). 104 entries were found that contained exactly six carbon atoms in an aromatic ring, between one and six fluorine atoms and no oxygen or nitrogen atoms. Structures containing other non-halogen heteroatoms, entries lacking atomic coordinates and duplicates (including 18 duplicates for C₆F₆) were removed manually. This left 42 ‘best representative’²⁶ crystal structures. A complete list, together with their REFCODES and molecular formulae, is included in the ESI.

The closest approaches to each crystallographically independent aromatic ring in each crystal structure were analysed as in the previous studies.^1,2 The closest heavy atom on each side of each aromatic ring to its centroid, ©, was identified. In this dataset this heavy atom was invariably either a carbon atom in an aromatic ring, or a halogen atom directly attached to an aromatic ring. Centroid⋯heavy atom (©⋯X) connections were all <4.2 Å, (<4.0 Å in the absence of iodine) consistent with the proposal of Kitaigorodskii⁶ that the ‘hollows’ above and below each aromatic ring are attractive locations for atoms from other molecules to occupy. The angle between the two aromatic rings was determined and used to classify the approach on that aromatic face as either edge⋯face (25–86°) or face⋯face (0–5°). The symmetry relationship between the two molecules was also recorded as either translation, inversion, glide, screw, rotation or asymmetric, as was the corresponding multiplicity, (M). Asymmetric approaches do not embody any crystallographic symmetry as they occur between molecules within the asymmetric unit. The short crystallographic repeats embodied in these approaches, either individually (for translation), or in pairs (for inversion, screw and glide symmetries), were noted.

Approach geometries were analysed as in the previous studies.^1,2 Parallel face⋯face approaches were characterised by the interplanar separation, (s) and the displacement, (d) – as illustrated in Fig. 2 for 1-fluoro-4-iodobenzene in FACQEF01. In Fig. 2 the atoms occupying the ‘hollows’ above and below each aromatic ring are fluorine and iodine; centroid (©)⋯halogen distances are ©⋯I = 3.824 Å and ©⋯F = 3.744 Å. The interplanar separation (s) is 3.722 Å, typical for iodobenzenes. The aromatic rings do not overlap; the displacement (d) is 3.176 Å in the direction of the C–I and C–F bonds. The approach embodies translational symmetry, giving the shortest crystallographic repeat of c = 4.893 Å; it is classified here as an ‘offset translation’ (Fig. 1d). This molecule prefers to crystallise using this close approach rather than an ‘offset inversion’ (Fig. 1f) in which both hollows are occupied by the same type of halogen atom.

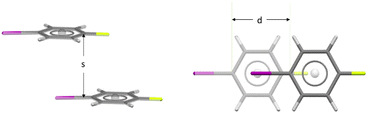Fig. 2 The closest aromatic approach in 1-fluoro-4-iodobenzene (FACQEF01), viewed approximately parallel to the molecular planes (left) and exactly perpendicular to the molecular planes (right).

Each edge⋯face approach was characterised by two short connections, as shown in Fig. 3(left) for 1,2-difluorobenzene in FACFOE. This approach embodies 2-fold screw symmetry. The geometry is characterised by the shortest ©⋯C connection of 3.676 Å and the shortest neighbouring C⋯C connection of 3.826 Å. This approach is an example of Symthon II, as shown in Fig. 1b. The edge in this approach extends to includes the fluorine atom labelled F1 which is attached to the second edge carbon atom. In some edge⋯face approaches the closest heavy (non-hydrogen) atom to the centroid, ©, is a halogen atom, which increases the separation between the aromatic rings. This is exemplified by 1,2,3,4-tetrafluorobenzene in ZELDOJ, as shown in Fig. 3(right). This approach also embodies 2-fold screw symmetry; its geometry is characterised by the shortest C⋯© connection of 4.392 Å and the shortest neighbouring C⋯C connection of 4.221 Å. The second carbon atom in the edge is attached to a second fluorine atom, so that this ‘edge’ C–C bond is also approximately parallel to the aromatic ‘face’.

Fig. 3 Close approaches in FACFOE (left) and ZELDOJ (right).

Hence this approach is an example of a ‘halogen edge⋯face’ approach, as depicted in Fig. 1e. The first test of this methodology was to ascertain how many of the closest approaches in halobenzene crystal structures with fluorine can be described using the six types of close approach displayed in Fig. 1.

To support this geometric methodology, interaction energies were calculated for a subset of halobenzene interactions using CrystalExplorer version 21.5. with default CE-B3LYP energy models and Tonto B3LYP/6-31G(d,p) electron densities.^27–31 This methodology was unsuitable for molecules containing iodine atoms or halogen disorder. Crystal structures were exported from the CSD as ‘.cifs’ and opened with the CrystalExplorer software. This automatically recalculates the position of hydrogen atoms so that C–H bond lengths are 1.083 Å. Interactions energies were calculated for up to 14 nearest neighbours of each crystallographically independent molecule in unmixed halobenzenes containing either fluorine or chlorine or bromine. The strongest and next strongest interactions on each aromatic face were identified and compared with the closest approaches identified by the geometric methods described above.

Results

The results of energy calculations for Symthons and next closest interactions in fluorobenzenes and chlorobenzenes are presented graphically in Fig. 4. Full details are given in the ESI,† including the data for bromobenzenes, which are qualitatively similar to chlorobenzenes, with larger interaction energies for Symthon I. Symthons were the strongest intermolecular interactions in 79 out of 86 closest aromatic approaches, with five of the seven exceptions being asymmetric approaches. The dramatic difference in behaviour between fluorobenzenes and chlorobenzenes is immediately apparent from inspection of Fig. 4 and will be discussed in more detail below.

Fig. 4 Symthon interaction energies in crystal structures of fluorobenzenes (top) and chlorobenzenes (bottom).

The database search results are summarised in Table 2, alongside comparable data for halobenzenes without fluorine.² Some halobenzenes exhibit polymorphism, giving more crystal structures than molecules. Some crystal structures have Z′ > 1, and each molecule has two faces, giving more than double the number of closest approaches. Details are given in the ESI.†

Table 2 The Halobenzene crystal structure dataset

	Without fluorine^2	With fluorine	Total
Molecules	57	36	93
Crystal structures	69	42	111
Closest aromatic approaches	176	114	290

---

Thus the full halobenzene crystal structure dataset comprises halobenzenes without fluorine, as studied previously,² alongside halobenzenes with fluorine as added here. There are a total of 290 closest aromatic approaches in the dataset, which is a complete dataset of all known closest aromatic approaches in halobenzene crystal structures. These 290 approaches with and without fluorine are now analysed according to their geometry and symmetry, before discussing links with number, disposition and type of halogen substituents in more detail.

Edge⋯face or face⋯face?

Fig. 5 displays the prevalence of ‘edge⋯face’ and ‘face⋯face’ closest aromatic approaches as a function of number of halogen substituents, N. In the presence of Fluorine, edge⋯face approaches occur for N = 1,2, 4,5 and 6, whereas in the absence of fluorine edge⋯face approaches are restricted to N ≤ 3.²Fig. 5 summarises 288 approaches – only the two approaches from BARBOL (1,3,5-trichloro-2,4,6-trifluorobenzene) could not be classified as either edge⋯face or face⋯face, as discussed further in the ESI.†

Fig. 5 Distribution of edge⋯face and face⋯face approaches in all halobenzenes as a function of N (= number of substituents).

Symmetries of closest aromatic approaches

The symmetries embodied in 290 closest aromatic approaches are displayed schematically in Fig. 6. Each coloured cell represents the symmetry of the closest approach on one aromatic face. The approaches occur in pairs, which are represented above/below each other in Fig. 6, and mostly embody identical symmetries. The crystal structures are arranged in order of increasing number of halogen substituents (N) from top to bottom. The central column gives the pattern of halogen substitution. The approaches with fluorine are presented to the right of the central column, for comparison with approaches without fluorine, including benzene (N = 0), as reported previously² and shown here on the left.

Fig. 6 Schematic representation of 290 closest aromatic approaches in halobenzene crystal structures, by degree and pattern of halogen substitution. Element symbols (I, Br, Cl, F) indicate where halogen atoms occupy hollows.

Where halogen atoms occupy hollows above/below aromatic rings, they are identified. This includes both approaches in FACQEF01 (Fig. 2) and one approach in ZELDOJ (Fig. 3, right).

Comparison of the left (without fluorine) and right (with fluorine) sides of Fig. 6 illustrate the effects of fluorine. The dominance of translation (grey), particularly where N = 2 and N = 6, is disrupted with fluorine. Inversions (yellow) occur for all values of N ≥ 2 instead of being confined principally to N = 3. Edge⋯face approaches appear for all values of N except N = 3, instead of being confined to N ≤ 3. Halogen atoms occupy hollows more frequently in the presence of fluorine. The unusual behaviour of 1,2,3-trihalobenzenes without fluorine cannot be investigated further at present, due to a lack of data on analogues with fluorine. The biggest impact of fluorine is to reduce the popularity of translation, which is now probed in more details by examining the geometries of these approaches.

Symthon I and offset translations

In Fig. 7, the geometries of 46 closest aromatic approaches with fluorine are compared with 112 closest aromatic approaches without fluorine that also embody translational symmetry. The impact of fluorine is dramatic. With fluorine, displacements (d) are more widely distributed over the range 1.3–4.8 Å. Almost one-half (22/46) of the approaches with fluorine have (d) > 2.7 Å, which means there is no overlap of the aromatic rings. These are the ‘offset translations’ illustrated in Fig. 1d. The example shown in Fig. 2 has the geometry circled in Fig. 7, which allows fluorine and iodine atoms to occupy ‘hollows’ in neighbouring aromatic rings. This is a common feature of almost all (21/22) of these offset translations, which allows them to be recognised in Fig. 6. This corresponds sharply with the behaviour of halobenzenes without fluorine – all but two of the 112 closest aromatic approaches embodying translation in that dataset had geometries within the shaded box, consistent with Symthon I.

Fig. 7 Interplanar separations (s) and displacements (d) for closest aromatic approaches embodying translational symmetry. The shaded box denotes the redefined Symthon I.

The shaded box in Fig. 7 presents a minor revision of the geometrical definition of Symthon I.² The lower limit for interplanar separations, (s), has been reduced from 3.4 Å to 3.3 Å to accommodate approaches involving smaller fluorine atoms. The upper limit for displacements, (d), has been increased from 2.5 Å to 2.7 Å to include all approaches in which the aromatic rings overlap, however slightly. Further details are given in the ESI.†

The dramatic effect of fluorine on increasing displacements in closest aromatic approaches embodying translational symmetry prompted a similar analysis of approaches with and without fluorine that embody inversion symmetry.

Symthon III and offset inversions

Fig. 8 shows the impact of fluorine on the geometries of approaches embodying inversion symmetry. Symthon III has been redefined in the same way as Symthon I to accommodate smaller interplanar separations in the presence of fluorine. 24 closest aromatic approaches with fluorine are compared with 20 closest aromatic approaches without fluorine. There is a tendency to larger values of (d) in the presence of fluorine atoms, although this effect is less dramatic than that shown in Fig. 7 for translations, only affecting seven of out of 24 approaches. All seven approaches feature a halogen atom occupying the hollow of an aromatic ring, allowing them to be identified in Fig. 6.

Fig. 8 Interplanar separations and displacements for approaches embodying inversion symmetry. The shaded box denotes Symthon III.

Edge⋯face approaches

Fig. 9 shows the geometries of 39 edge⋯face approaches with fluorine, compared with 30 edge⋯face approaches without fluorine.² These approaches fall into two groups defined by their ©⋯C separations. 22 approaches in the first group have ©⋯C < 4.2 Å, as illustrated in Fig. 3(left) for 1,2-difluorobenzene in FACFOE. All but two of these 22 approaches have geometry consistent with Symthon II, falling within the green shaded area in Fig. 9. These approaches only occur for molecules with one or two halogen substituents (N ≤ 2), as was also found for edge⋯face approaches without fluorine.² Ten of the twenty edge⋯face approaches with Symthon II geometry also embody the screw and/or glide symmetry associated with Symthon II; the other ten edge⋯face approaches with this geometry are asymmetric. There are fifteen edge⋯face approaches with ©⋯C in the range 4.2–4.8 Å, including the approach in ZELDOJ (©⋯C = 4.392 Å) displayed in Fig. 3(right). This range of ©⋯C separations arises when a fluorine atom occupies the hollow of an aromatic ring. These approaches only occur for N ≥ 4.

Fig. 9 Edge⋯face approaches. The green shaded area corresponds to Symthon II. The diagonal line indicates the idealised edge⋯face geometry. Approaches within the ellipse are ‘fluorine edges’.

Summary of results

As noted in the introduction, three Symthons (Fig. 1a–c) were effective in describing most of the close approaches in halobenzenes without fluorine and three further Symthon derivatives (Fig. 1d–f) were also found. The distribution of these three Symthons and their three derivatives across 290 close asymmetric approaches of all halobenzenes is summarised in Table 3. The data are presented as percentages, to aid comparison between approaches with and without fluorine. Symthons and their derivatives account for 79% of the 114 approaches with fluorine, whereas the three Symthons counted for 84% of the 176 close approaches without fluorine. Of the remaining 21% of approaches with fluorine, 9% (10) are asymmetric edge⋯face approaches with Symthon II geometries, and 12% (14) shows other symmetries and/or geometries, as detailed in the ESI.†

Table 3 Impact of fluorine on distribution of Symthons and their derivatives

Close interactions	‘With fluorine’	‘Without fluorine’
Symthon I	21%	63%
Symthon II	9%	10%
Symthon III	15%	11%
Offset translation	19%	1%
Offset inversion	6%	1%
Halogen edge⋯face	9%	1%

---

Discussion

The CrystalExplorer results in Fig. 4 are broadly consistent with the previous calculations by other methods²⁰ in showing that face⋯face interactions in some halobenzenes can be up to eight times stronger than corresponding edge⋯face interactions energies. The calculations show that Symthons are generally the strongest intermolecular interactions in halobenzene crystal structures. The seven exceptions occur in FACMOL (once), TCBENZ (twice), and HFBENZ02 (four times). These three crystal structures have Z′ > 1, and five of these seven interactions are asymmetric, hinting at metastability – further details are in the ESI.†

The interaction energies of Symthon I in chlorobenzenes (Fig. 4) show a linear increase of ∼4 kJ mol⁻¹ for each additional chlorine atom from N = 2 to N = 6, and a corresponding increase of ∼6.8 kJ mol⁻¹ for each bromine atom (see ESI†). These increases correspond to the linear increases of melting point with N (see ESI†). The next strongest interactions are all in the range −5 to −13 kJ mol⁻¹ and show no systematic dependency on N. This suggests that the increase in melting points with N is specifically owing to Symthon I. The very different melting behaviour of fluorobenzenes (see ESI†) is consistent with the disruption of Symthon I in the presence of fluorine.

The interaction energies for chlorobenzenes and bromobenzenes adopting Symthon I show very little variation between isomers. It is noteworthy that mixed halobenzenes also prefer Symthon I with almost ubiquitous chlorine/bromine disorder. The number and type of halogen atoms present in Symthon I matters, but not their disposition. As expected, dispersive and repulsive terms dominate Symthon I interaction energies calculated in this study, with much smaller contributions from electrostatic and polarisation terms.

Symthon III interaction energies are in the range −17 to −37 kJ mol⁻¹, compared with −16 to −48 kJ mol⁻¹ for Symthon I. Hence these interactions are similar to, or stronger than typical hydrogen bonds. Edge⋯face interactions are generally weaker, in the range −10 to −17 kJ mol⁻¹; as noted previously¹ these interactions may have the advantage of a multiplicity of four rather than two, accounting for their prevalence when N = 0 or 1. The next strongest interactions are in the range −5 to −13 kJ mol⁻¹, including ‘edge⋯edge’ interactions containing pairs of C–H⋯halogen and/or halogen⋯halogen connections.^10,20,21

The hypothesis that fluorine disrupts the π–π stacking which dominated closest aromatic approaches in its absence is largely confirmed by the reduced popularity of Symthon I, as shown in Table 3. Whereas Symthon I readily accommodates up to six chlorine bromine and/or iodine atoms, it accommodates a maximum of four fluorine atoms only once (CUWYUP, Fig. 10, right) and three fluorine atoms only twice (XAJNUT02, not shown and XAJNUT, Fig. 10, middle). SOXLEX01 (Fig. 10, left) also contains Symthon I and shares the same 1,2,3,5-tetrahalogen substitution pattern. No other type of approach with fluorine replaces the dominant position vacated by Symthon I.

Fig. 10 Symthon I in SOXLEX01, XAJNUT and CUWYUP.

No centrosymmetric molecules with fluorine adopt Symthon I. The closest approaches of centrosymmetric halobenzenes are summarised in Table 4 – noting that approaches embodying inversion are not accessible for centrosymmetric molecules. These molecules do not have a net dipole yet show a strong preference for offset translations.

Table 4 Centrosymmetric halobenzenes containing fluorine

X	Y	Crystal structure	Closest approach
a GEHMIT and GEHMEP display Cl/Br and Cl/I disorder to allow these two non-centrosymmetric molecules to occupy inversion centres.
H	F	FACGEV	Symthon II
F	I	ZZZAVM01	Halogen edge⋯face
F	H	FACJAU	Offset translation
I	F	PERCUM	Offset translation
F	I	ZZZAVM02	Offset translation
F	B	ZZZAVJ01	Offset translation
F	Cl/l	GEHMIT^a	Offset translation
F	Br/l	GEHMEP^a	Offset translation
F	F	HFBENZ02	Other
F	F	HFBENZ15	Skew

---

Non-centrosymmetric molecules have a reduced tendency (10/34 approaches) to take part in offset translations, and this tendency is weaker still for offset inversions (7/24 approaches). In both offset translations and offset inversions, it is the heaviest halogen atoms that occupy the hollows of neighbouring aromatic rings, while the fluorine atoms ignore each other. In other words, inserting fluorine atoms into halobenzenes creates “slippy” face⋯face approaches.

As was noted previously,² most (14/22) examples of inversion approaches without fluorine occurred in 1,2,3-trihalobenzenes. There are only two examples of approaches of 1,2,3-trihalobenzenes with fluorine. Excluding these polar molecules from both datasets reveals that otherwise inversions are more likely (24/112 = 21%) with fluorine than without fluorine (8/152= 5%).

For edge⋯face approaches, it is not surprising that Symthon II geometries also predominate in molecules containing fluorine with N ≤ 2. However, nine of these twenty approaches are asymmetric, with a halogen atom attached to the second edge carbon, in the “F1” position as shown in Fig. 3(left). It appears that halogen atoms in this position make these approaches less likely to be symmetric – “clumsy” from a crystal packing perspective. It is also not surprising that halogen edges were only found in the presence of fluorine for N ≥ 4. However, there is only one example of paired symmetry-forming halogen edges (ZZZAVM01, see Table 4). The range of geometries for halogen edges, outlined by the ellipse in Fig. 9, is larger than that for Symthon II, suggesting that ‘fluorine edges’ are less specific geometrically - ‘floppy’ – and therefore less effective than Symthon II at creating long-range order.

The datasets with and without fluorine contain sufficient approaches for meaningful comparisons for even values of N (N = 2, 4, 6). For N = 2, 44 closest aromatic approaches with fluorine include fourteen examples of Symthon I, eight of Symthon II, three of Symthon III, five offset translations, one offset inversion, ten asymmetric edge⋯face approaches and three distorted edge⋯face approaches. This diversity contrasts with the behaviour of 30 closest aromatic approaches of di-halobenzenes without fluorine, which display a simple dichotomy between 22 Symthon I's and eight Symthon II's. It appears that Symthon I and Symthon II are weakened to similar extents in the presence of fluorine, so that they remain competitive with each other, but also compete with other geometries, as well as approaches embodying inversion symmetry. Five of the twelve crystal structures with fluorine have Z′ = 2, 3 or 5, providing further evidence that these molecules have so many similar options to choose from that they struggle to crystallise simply. This may also be related to the difficulties of growing crystals at sub-ambient temperatures – a challenge for any attempts to identify more stable polymorphs.

Seventeen of the eighteen closest aromatic approaches containing fluorine with N = 4 are face⋯face, and eight of these are Symthon I. This compares with the forty closest aromatic approaches without fluorine for N = 4, all of which are face⋯face and thirty-two of which are Symthon I. It seems that combinations of Symthon II and fluorine edge⋯face approaches do not offer better alternatives to face⋯face approaches for N = 4. It may be the very disparate geometries of Symthon II and fluorine edge approaches, as shown by the green shaded area and the ellipse in Fig. 9, create difficulties in packing. CUWYUP (Fig. 10, right) may be an example of these difficulties – the molecule crystallises using Symthon I instead, with a very low melting point (−48 °C).

For the closest aromatic approaches with N = 6 there is a stark contrast between the dominance of Symthon I (36/40 approaches) without fluorine and the diversity with fluorine. There is a pattern to this diversity, which is not apparent in Fig. 6, relating to the number of fluorine atoms in each molecule. Symthons I and III accommodate 1–3 fluorine atoms. Symthon derivatives accommodate 3–5 fluorine atoms, including most of the molecules in Table 4 and one of the polymorphs of C₆F₅I (ZAHGAQ01), which has unusual interplanar separations (s = 3.26, 4.15 Å). The other polymorph, (ZAHGAQ01), has Z′ = 2 and contains two asymmetric edge⋯face approaches. C₆F₆ avoids Symthons and their derivatives completely in all six close approaches of its two polymorphs. The similar melting points of C₆F₆ (4 °C)²² and C₆H₆ (5 °C)²² conceal the contrast between the elegant simplicity of close approaches in BENZEN (Symthon II pair) and the clumsiness of HFBENZ02 (Z′ = 1.5, one pair of related asymmetric fluorine edges, one different asymmetric fluorine edge, one distorted ‘T’ fluorine edge approach embodying 2-fold screw symmetry). The other polymorph of C₆F₆ (HFBENZ15) only exists at high pressures and contains a pair of skew approaches which look like a failed attempt to crystallise using Symthon I. This suggests that C₆F₆ is simply reluctant to crystallise at all. The fact that three out of four close approaches in HFBENZ02 are asymmetric suggests similarity to an amorphous alternative - in which all approaches are asymmetric.

Although not part of this dataset, benzene and C₆F₆ form a 1 : 1 co-crystal. The melting point is 25 °C, 20° higher than either benzene or C₆F₆.^9,18 The closest approach in one of the polymorphs of this cocrystal (BICVUE03) is shown in Fig. 11. Both molecules lie on 2-fold rotation axes, so that the approaches above and below each molecule are equivalent. The aromatic planes are ‘skew’ with an interplanar angle of 2.7°. The displacement (d) is 0.910 Å, similar to that observed in inversion approaches (Fig. 8) and showing carbon atoms from one aromatic ring occupying hollows in neighbouring atomic rings - consistent with Kitaigorodskii's insight.⁶ However, there can be no embodied symmetry in this approach between two different molecules.

Fig. 11 Face⋯face approach in BICVUE03, viewed perpendicular to the C₆F₆ plane.

The combination of this approach with the symmetry-related approach with a further C₆H₆ molecule on the other face of C₆F₆ gives an aromatic stack embodying a = 7.24 Å. This analysis contrasts with a previous description of this approach as ‘parallel stacking’.⁹

Disorder was noted only three times in the presence of fluorine: Cl/Br/I disorder in GEHMIT and GEHMEP (See Table 4) and H/F disorder in NAFFIM (Z′ = 5). Only two examples of isostructures in the presence of fluorine were found: ZZZAVM02/ZZZAVJ01 (see Table 4) and FACQAB01/FACPAA01 (see ESI†), in which bromine atoms swap positions with either iodine or chlorine. This is in sharp contrast to the many examples of Cl/Br/I disorder in the isostructural series with N = 2 and N = 6 noted previously² in the absence of fluorine. This is all consistent with the interchangeability of Cl, Br and I with each other but not with fluorine. This may be understood here as Cl, Br and I preferring to be close to each other rather than to fluorine.

Alternative, simpler polymorphs based on Symthon I may exist for two crystal structures containing parallel and subtly different π–π stacks (NAFFIM: Z′ = 5, NAFDUW: Z′ = 2). Alternative simpler polymorphs based on Symthon II may exist for structures containing asymmetric edge⋯face approaches (FACPAA01 – Z′ = 3, FACQAB01 – Z′ = 3 and PUGDAX, Z′ = 2). A third, simpler polymorph may exist for C₆HF₅ containing offset inversions with more equal separations. Other 1,2,3-trihalobenzenes containing fluorine are expected to crystallise using Symthon III pairs. These suggestions could be tested computationally as well as experimentally, particularly for compounds with sub-ambient melting temperatures.

Calculated interaction energies offer a further predictive aspect. Previously¹ it was suggested that the (at that time) undetermined crystal structure of C₆HBr₅ would contain Symthon I. The linear variation of Symthon I interaction energies with N for bromobenzenes predicts a value of −39.3 kJ mol⁻¹ for this interaction of C₆HBr₅. A crystal structure for this molecule, BEBWOY was added to the CSD in 2022. It does indeed contain Symthon I, embodying b = 3.999 Å. Moreover, the calculated energy for this interaction is −38.8 kJ mol⁻¹, in close agreement with the predicted value predicted here. Further details are in the ESI.†

Similar reasoning suggests that the different versions of Symthon I shown in Fig. 10 will have interaction energies in the order of CUWYUP < XAJNUT < SOXLEX01. The calculated values are −17.5, −20.2 and −26.0 kJ mol⁻¹ respectively, as expected. This is consistent with the corresponding melting points of −48, +4 and +86 °C. There is no evidence here that the quantitative method used above for bromine atoms will also apply to fluorine atoms. This is an area for future study, for example iodobenzenes and nitrobenzenes, either unmixed or in combinations with bromine and chlorine substituents.

As suggested at the start of this study, inversions and fluorine edges become more competitive with Symthon I in the presence of fluorine. Fluorine also favours larger parallel displacements, as shown in Fig. 7, resulting in offset translations. This is consistent with their prominence in phthalocyanines and porphyrins.^5,7 These geometries favour short F^δ−⋯C^δ+ and C^δ−⋯C^δ+ connections over weaker F^δ−⋯F^δ− connections, as may be seen in the close approaches displayed in Fig. 2, 3, 10 and 11. In other words, fluorine atoms in closest aromatic approaches ignore each other when crystallising, but they do exhibit and induce close connections involving C^δ+.

Another way to assess the role of Symthons is to examine how often they generate short crystallographic repeats. As noted above, Symthon I embodies unit cell dimensions in the range 3.7–4.4 Å. The converse may also be true: any crystal structure of a simple aromatic molecule with a short repeat in this range probably contains Symthon I. For example, the CSD contains an entry for C₆Cl₅Br with a unit cell but no atomic coordinates. The unit cell has b = 3.87 Å, for which Symthon I offers the simplest explanation. Pairs of Symthon II and pairs of Symthon III generate longer translational repeats with overlapping ranges. Similar considerations apply to offset translations, pairs of offset inversions and pairs of halogen edges that embody screw and/or glide symmetry. Table 5 summarises the short crystallographic repeats in the 111 halobenzene crystal structures, showing how most of them are accounted for by Symthons and their Derivatives.

Table 5 Short unit cell dimensions

Approach	Range of unit cell dimensions (Å)	Crystal structures
Symthon I	3.7–4.4	53
Offset translation	4.4–6.0	13
2 × Symthon II	5.3–7.8	16
2 × Symthon III	7.0–8.5	8
2 × halogen edge	6.1–9.9	8
2 × offset inversion	8.8–10.6	2
Other	5.9–10.1	11
Total		111

---

The unit cell dimensions in Table 5 are generally the shortest unit cell dimensions in their crystal structure. The eight exceptions (see ESI† for details) are currently the subject of further study. The data in Table 5 illustrate how Symthons connect closest approaches in crystal structures to short crystallographic repeats. The data on Symthon I prompted a quick search of the CSD for all structures containing a C₆ ring and at least one crystallographic repeat in the range 3.7–4.4 Å. There were 8326 hits, suggesting that Symthon I is far more prevalent than in just this dataset. One area for further study is to investigate how many porphyrins and phthalocyanines crystallise in this way, or with offset translations.

This analysis has revealed several different types of “π–π stacking”, including Symthon I and offset translations with overlapping conjugated substituents. Similar offset translations give π–π stacks in which different rings overlap in fused ring systems such as phthalocyanines^4,5 and porphyrins.⁷ Paired inversion approaches create a different type of π–π stacking in which every second layer is identical, and these approaches may also be offset. Skewed aromatic planes can also create π–π stacks, either in combination with themselves (HFBENZ15) or in combination with inversions (ZELDOJ01), or for different molecules in co-crystals (BICVUE03, Fig. 11). The nomenclature developed here, based on different embodied symmetries (translation, inversions…) and displacements (overlap, offset…) offers a way to classify and understand different types of π–π stacking.

Conclusions

‘Symthons’, defined as symmetry-forming closest approaches of aromatic rings, are generally the strongest intermolecular interactions in the series of crystal structures analysed in this study. The face⋯face Symthons I and III are typically similar in strength to individual hydrogen bonds, with interaction energies ranging from −17 to −48 kJ mol⁻¹. Halobenzenes containing fluorine crystallise very differently from halobenzenes without fluorine. Symthon I, which dominates halobenzene crystal structures in the absence of fluorine, only accommodates up to four fluorine atoms. No other type of close approach achieves similar dominance in the presence of fluorine. Face⋯face approaches with fluorine display a wider range of displacements and could be described as ‘slippy’. Edge⋯face approaches with fluorine are sometimes asymmetric, so could be described as ‘clumsy’. “Fluorine edge⋯face” approaches occur for N ≥ 4; they show a wide range of geometries and are rarely paired, so could be described as ‘floppy’. These effects of fluorine are consistent with a preference for weak F^δ−⋯C^δ+ and C^δ−⋯C^δ+ connections over even weaker F^δ−⋯F^δ− connections. Despite the disruption of Symthon I in the presence of fluorine, other Symthons and their simple derivatives provide a convenient way to understand closest aromatic approaches and short crystallographic repeats in halobenzene crystal structures with and without fluorine, and to propose simpler alternatives to crystal structures with Z′ > 1. The role of edge⋯edge approaches is a topic for future research.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

SNB and RJD conceived and planned the study jointly. SNB carried out the formal analysis and wrote the first draft. SNB and RJD revised and edited subsequent drafts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Professor Paul J. Black for helpful insights and are grateful for the assistance received during reviews.

Notes and references

1. S. N. Black, Cryst. Growth Des., 2021, 21, 6981–6991.
2. S. N. Black, CrystEngComm, 2023, 25, 3079–3087.
3. O. Hassel and H. Mark, Z. Phys., 1924, 25, 317–337.
4. J. M. Robertson, R. P. Linstead and C. E. Dent, Nature, 1935, 135, 506–507.
5. J. M. Robertson and I. Woodward, J. Chem. Soc., 1940, 36–48.
6. A. I. Kitaigorodskii, Molecular crystals and molecules, Academic Press, 1973.
7. A. Hunter and J. K. M. Saunders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
8. S. E. Wheeler, Acc. Chem. Res., 2014, 46, 1029–1038.
9. L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., 2011, 50, 4808–4842.
10. R. V. Thalladi, H.-C. Weiss, D. Bläser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710.
11. M. T. Kirchner, D. Blaser, R. Boese, T. S. Thakur and G. R. Desiraju, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o2670.
12. M. T. Kirchner, D. Blaser, R. Boese, T. S. Thakur and G. R. Desiraju, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o2668.
13. T. S. Thakur, M. T. Kirchner, D. Bläser, R. Boese and G. R. Desiraju, CrystEngComm, 2010, 12, 2079–2085.
14. G. Dikundwar, R. Sathishkumar and T. N. Guru Row, Z. Kristallogr., 2014, 229, 609–624.
15. M. Bujak, H.-G. Stammler and N. W. Mitzel, Cryst. Growth Des., 2020, 20, 3217–3223.
16. M. R. Probert, Y. H. P. Chung and J. A. K. Howard, CrystEngComm, 2010, 12, 2584–2586.
17. M. Rusek, K. Kwaśna, A. Budzianowski and A. Katrusiak, J. Phys. Chem. C, 2020, 124, 99–106.
18. J. K. Cockcroft, A. Rosu-Finsen, A. N. Fitch and J. H. Williams, CrystEngComm, 2018, 20, 6677–6682.
19. G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125.
20. J. Trnka, R. Sedlak, M. Kola and P. Hobza, J. Phys. Chem. A, 2013, 117, 4331–4337.
21. C. J. G. Wilson, J. Plesniar, H. Kuhn, J. Armstrong, P. A. Wood and S. Parsons, Cryst. Growth Des., 2024, 24, 2217–2225.
22. J.-C. Bradley, A. Williams and A. Lang, Jean-Claude Bradley Open Melting Point Dataset, 2014,  DOI:10.6084/m9.figshare.1031637.v2.
23. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
24. A. Bondi, J. Phys. Chem., 1964, 441–451.
25. A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314.
26. J. van der Streek, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 567–579.
27. https://crystalexplorer.net, downloaded 21/03/2024.
28. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
29. C. F. Mackenzie, P. R. Spackman, P. Jayatilaka and M. A. Spackman, IUCrJ, 2017, 4, 575–587.
30. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11637.
31. P. C. Hariharan and J. A. People, Theor. Chim. Acta, 1973, 28, 213–221.

---

Footnote

† Electronic supplementary information (ESI) available: Refcodes linked to molecular formulae for all 42 crystal structures with fluorine, with Z′, space group and their short crystallographic repeats. Melting points of halobenzenes. CrystalExplorer dataset and full results, including bromobenzenes. Geometries (s and d) of face⋯face approaches embodying translation and inversion symmetries, with notes. Geometries (©⋯C and C⋯C) of edge⋯face approaches, with notes. Details of 14 ‘other’ approaches that are not represented in Fig. 1. Isostructures. Comparison with close approaches in ref. 21. Illustrations of ‘just overlapping’ aromatic rings in NAFFIM. Additional notes on FACMOL, TCBENZ and HFBENZ02. See DOI: https://doi.org/10.1039/d4ce00565a

---