View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/D3CE01134H (Communication) CrystEngComm, 2024, 26, 243-247

Thermodynamic stability relationship of ternary and binary cocrystals of isoniazid: why pH and coformer concentration matter†

Tatiane Cogo Machado *a, Juliana Rosa b and Thiago Caon b
aSchool of Pharmacy, Newcastle University, Newcastle upon Tyne NE1 7RU, UK. E-mail: tatiane.machado@newcastle.ac.uk
bPostgraduate Program in Pharmacy (PGFAR), Federal University of Santa Catarina, Florianopolis 88040-900, Brazil

Received 13th November 2023 , Accepted 24th November 2023

First published on 5th December 2023

Abstract

Thermodynamic stability relationships between binary and ternary cocrystals of isoniazid and their components were investigated using predictive equations based on the ionization constant (Ka) and the solubility product (Ksp). The ternary cocrystal of isoniazid exhibits multiple pHmax values and a narrow stability zone between pH 2.8 to 5.7. Ternary to binary cocrystal conversion occurs at pH < 1.8. In addition, ternary cocrystal solubility decreases with increasing coformer concentration. We expect the approach presented herein to be applicable to other ternary cocrystals to better understand the factors that can alter cocrystal solubility, which is critical during the pre-formulation stage of development, and to avoid the risk of solid phase conversion during more advanced stages.

Cocrystals can be composed of two or more molecules with different stochiometric arrangements, which can lead to multiple solids of the same drug with different physicochemical properties.1 From a drug delivery perspective, ternary cocrystals can offer an opportunity to deliver multiple drugs, opening up possibilities of combined therapies. Despite these advantages, ternary cocrystals are relatively less studied than binary cocrystals and most studies are focused on the crystal engineering of these solids.2–6 The design of the ternary cocrystals depends on the intermolecular interactions between components dictated by their supramolecular synthons, which makes their synthesis challenging.7 Furthermore, their solution chemistry can be complex, as they are composed of three different molecules with their own ionization properties.

Isoniazid (INH), an anti-tubercular drug, is well known for its tendency to form cocrystals with compounds containing carboxyl groups. Numerous multicomponent crystalline structures are reported for this drug, among them, a ternary cocrystal formed by INH, nicotinamide (NIC), and fumaric acid (FUM) in a 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 stoichiometry.8–11 Studies with INH cocrystals are well established; however, their thermodynamic solubility and stability still need to be investigated. This study attempted to explain the phase behavior of ternary and binary cocrystals of isoniazid, identifying conditions under which transformations may occur by applying the predictive solubility equations based on ionization constant (Ka) and cocrystal solubility product (Ksp).12

As cocrystal solubility is a sum of the properties of each individual component, a binary to a ternary cocrystal of the same drug can exhibit different solubilities. The cocrystals studied are composed of a basic drug (INH), an acidic coformer (FUM), and a basic coformer (NIC). Therefore, the pH is expected to be a determining factor in evaluating cocrystal solubility. Fig. 1 shows the solubility diagram for the binary 2[thin space (1/6-em)]:[thin space (1/6-em)]1 (INH–FUM) and the ternary 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 (INH–NIC–FUM) cocrystals and their respective individual components. Results demonstrate that cocrystals changed the solubility vs. pH to a “U-shaped” curve with an exponential increase above pH 4.0. Considering that NIC and INH are basic molecules, the solubility increases exponentially as pH decreases to pH values below their pKa values of 3.3 and 3.5, respectively. FUM, in turn, exhibits the opposite behaviour due to its acidic nature, with solubility increasing at pH > 2.5. The pKa values for drugs and coformers are summarised in Table 1.


image file: d3ce01134h-f1.tif
Fig. 1 Solubility of (2[thin space (1/6-em)]:[thin space (1/6-em)]1) INH–FUM, (1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1) INH–NIC–FUM and their individual components, INH, NIC, and FUM as a function of pH. Symbols represent equilibrium solubilities experimentally determined at the eutectic points. pH values correspond to equilibrium pH. The pH value at the intersection of the cocrystal and their components curves and cocrystal-cocrystal curves corresponds to pHmax or the transition point. Solubility curves were calculated from cocrystal, drug, and coformer solubility–pH dependence according to eqn (3)–(6).
Table 1 pKa values of drug and coformers
Compound Chemical structure pKa
Isoniazid image file: d3ce01134h-u1.tif 3.5 (ref. 13) and 11.1 (ref. 13)
Fumaric acid image file: d3ce01134h-u2.tif 2.7 (ref. 14) and 4.2 (ref. 14)
Nicotinamide image file: d3ce01134h-u3.tif 3.3 (ref. 15)

Symbols in the solubility curves represent equilibrium solubilities experimentally obtained from eutectic measurements in buffer solutions of different pH values (pH 1.2 to 7.4). The self-buffering effect of the basic and acidic cocrystal components caused the pH at cocrystal equilibrium solubility to fall within a narrow range (3.03–3.36). In this study, eutectic points were achieved using two solid phases in excess, cocrystal and the less soluble coformer (FUM), and equilibrating them with the solution. Cocrystal solubility was then calculated from total concentrations at the eutectic point as described in the ESI† and the following equations:

For 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 cocrystal

 
image file: d3ce01134h-t1.tif(1)
For 2[thin space (1/6-em)]:[thin space (1/6-em)]1 cocrystal
 
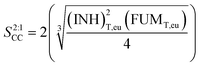image file: d3ce01134h-t2.tif(2)

Multiple transition points at corresponding pHmax values are shown in Table 2, which were obtained from the intersection of both cocrystals and their component solubility curves. This means that cocrystals exhibit different stability domains and are not thermodinamically stable over all the studied pH ranges. Close attention must be paid to the narrow pH region in which cocrystals are stable and not subject to conversions to drugs or coformers. There is a narrow stability zone (between pH 2.8 to 5.7) where the ternary cocrystal is stable, which means that no conversion can occur in those pH conditions. INH–NIC–FUM can be converted to INH–FUM at pH values below 1.8, as it is more soluble than INH–FUM. This is due to the presence of NIC. NIC is about 8000 times more soluble than FUM at pH 1.8. Above pH 1.8, binary cocrystals become more soluble than the ternary ones due to FUM's solubility behaviour, which exponentially increases with pH. Ternary cocrystal is expected to be converted to INH at a pH above 5.7, NIC at a pH above 6.5, and FUM at a pH below 2.8. The binary cocrystal is expected to convert to INH at pH above 4.8 and to FUM at pH below 3.4.

Table 2 Multiple pHmax for binary and ternary cocrystals of INH
Cocrystal pHmaxa
CC–INH CC–FUM CC–NIC CC–CC
a Obtained from the intersection of cocrystals (CC) and components (INH, FUM, NIC) solubility curves and from the intersection of binary and ternary cocrystal solubility curves in Fig. 1.
INH–FUM 4.8 3.4 — 1.8
INH–NIC–FUM 5.7 2.8 6.5 1.8

This analysis was possible by applying equations based on cocrystal dissociation equilibria, ionization of its components by Henderson–Hasselbalch theory, and the mass balance to predict the cocrystal solubility–pH dependence. The equations used in this work allow for the calculation of the solubility at other pH values. They are well recognized for binary cocrystals with different ionization properties and stoichiometries.16–19 However, to our knowledge equations of this nature have not been reported for ternary cocrystals. This motivated us to develop them for the 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 INH–NIC–FUM cocrystal.

INH is a weak base and its solubility as a function of pH is described by:

 
SINH,T = SINH,0(1 + 10pKa,INH−pH)(3)
where SINH,0 corresponds to the solubility of INH under nonionizing conditions (1.298 M). Only pKa1 (3.5) was considered for these calculations, as pKa2 (11.1) is irrelevant for the studied pH range. The same eqn (3) was used to obtain the NIC solubility curve, as NIC is also a basic molecule.

FUM is a diprotic acid and its solubility as a function of pH is described by:

 
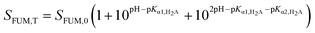image file: d3ce01134h-t3.tif(4)

Cocrystal solubility is the sum of all the cocrystal component species in the solution that are in equilibrium with the cocrystal. Theoretical solubility–pH relationships for INH cocrystals can therefore be derived, by considering ionization of components and the solubility product, Ksp. Derivations of the equations are detailed in the ESI.† In summary, the solubility expression is then obtained by considering the mass balance of each cocrystal component (ionized and unionized species). The solubility equation for INH–NIC–FUM, a 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 cocrystal of a basic drug, basic coformer and diprotic acid coformer becomes:

 
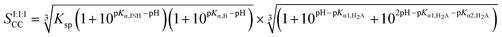image file: d3ce01134h-t4.tif(5)
For the 2[thin space (1/6-em)]:[thin space (1/6-em)]1 INH–FUM cocrystal, the solubility equation becomes:
 
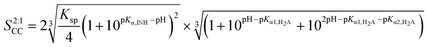image file: d3ce01134h-t5.tif(6)
The above equations are expressed in terms of moles of the drug. Ksp values of cocrystals used in these equations are shown in Table 3 and were determined from the measured equilibrium concentrations of cocrystal components at the eutectic point and the following equations:

Table 3 K sp, pKsp, and intrinsic solubility values for 2[thin space (1/6-em)]:[thin space (1/6-em)]1 INH–FUM and 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 INH–NIC–FUM cocrystals
Cocrystal K sp (M3) pKsp (−log Ksp) S 0 (M)
a Calculated from the equilibrium solubility measured at cocrystal/coformer eutectic points described in ESI.† b Cocrystal intrinsic solubility obtained from image file: d3ce01134h-t6.tif.
INH–FUM 1.65 (±0.10) × 10−3 2.78 0.12
INH–NIC–FUM 8.16 (±1.11) × 10−5 4.09 0.05

For the 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 cocrystal

 
Ksp = [INH]aq[NIC]aq[FUM]aq(7)
For the 2[thin space (1/6-em)]:[thin space (1/6-em)]1 cocrystal
 
Ksp = [INH]2aq[FUM]aq(8)
where [INH]aq, [NIC]aq, and [FUM]aq represent the molar concentration of nonionized species in solution.

INH–FUM intrinsic solubility is higher than INH–NIC–FUM and this is also expressed by its higher Ksp value (Table 3). The low values of Ksp make the use of pKsp = −log Ksp more reasonable. Higher pKsp values refer to the lower Ksp values.

The same cocrystals were investigated by Aitipamula et al. (2013)10 under a solubility experiment at an initial pH of 7.5. Their results demonstrated that both cocrystals were less soluble than the drug INH. In fact, the solubility data in this study refers to the maximum drug concentration (Cmax) from cocrystal dissolution as there is no evidence of equilibrium conditions. Drug concentration reported is a kinetic property and does not reflect the cocrystal equilibrium solubility, which is obtained from drug and coformer concentrations in equilibrium with the solution. Cocrystals are formed by components with different ionization properties and thus their solubility is not a single number as it varies with pH and concentrations of the dissolved cocrystal components. From pHmax values (Table 2), it is possible to determine the transition points where INH–FUM and INH–NIC–FUM become more soluble than INH, that is pH > 4.8 and pH > 5.7, respectively. This elucidates the importance of considering the equilibrium conditions to understand cocrystal solubility behaviour.

The influence of the solution composition on the 1[thin space (1/6-em)]:[thin space (1/6-em)]1[thin space (1/6-em)]:[thin space (1/6-em)]1 cocrystal conversion to 2[thin space (1/6-em)]:[thin space (1/6-em)]1 was also examined by plotting the solution concentrations of cocrystals components (without considering ionization) in equilibrium with the cocrystal according to the experimental Ksp from Table 2. The phase stability of the ternary cocrystal is dependent on NIC concentrations in the solution. Variations in NIC concentration in the solution appeared to change the transition point between both cocrystals. An increase in NIC concentration in the solution from 0.01 M to 0.05 M (Fig. 2a and b) showed a significant impact on the behaviour of the ternary cocrystal, which became the less soluble phase in the conditions examined. Curves in Fig. 2 were calculated using the Kspeqn (7) and (8). In essence, the decrease of the cocrystal solubility with the increase in the coformer concentration is expected to be based on the Ksp behavior.20,21


image file: d3ce01134h-f2.tif
Fig. 2 Solution concentrations (M) of the cocrystal components (INZ and FUM) in the presence of (a) 0.01 M and (b) 0.05 M of nicotinamide in solution. A higher concentration of NIC decreases ternary cocrystal solubility.

The influence of the coformer concentration on cocrystal solubility and dissolution behaviour is still poorly explored in this field. In previous work, we demonstrated the effects of the coformer on altering the driving force for cocrystal dissolution and drug precipitation.22 This knowledge is important as the coformer impurities may eventually result from cocrystal synthesis. Once the coformer can potentially be added to a cocrystal formulation as a strategy to reduce cocrystal conversion to the drug, this information is also helpful during the formulation development.22

In conclusion, the thermodynamic relationships presented in this work allow us to estimate the change in solubility and stability as a function of pH for cocrystals containing two and three components. Cocrystal pHmax is key to determining the risk of cocrystal conversions. The relative stability between both cocrystals as well as cocrystals and their constituents is also shown to be highly dependent on both pH and coformer concentration. The use of the equations and diagrams presented here provides important information to avoid undesirable solid phase transformations during cocrystal development and formulation. As demonstrated, INH–NIC–FUM can be converted to INH–FUM at pH < 1.8, which can decrease INH solubility 2 times. Formulation strategies, such as the use of excipients to modulate microenvironment pH, a gastro-resistant coating, or the addition of a coformer (NIC) to reduce ternary cocrystal solubility, could be considered in this case. For cocrystals to potentially become pharmaceutical products, it is crucial to understand their solubility and stability behaviour, which can be achieved using the approach presented here.

Conflicts of interest

There are no conflicts to declare.

References

  1. B. Saikia, D. Pathak and B. Sarma, Variable stoichiometry cocrystals: Occurrence and significance, CrystEngComm, 2021, 23, 4583–4606 RSC.
  2. C. Ortiz-De León and L. R. MacGillivray, Clues from cocrystals: a ternary solid, polymorphism, and rare supramolecular isomerism involving resveratrol and 5-fluorouracil, Chem. Commun., 2021, 57, 3809–3811 RSC.
  3. L. Song, K. Robeyns, N. Tumanov, J. Wouters and T. Leyssens, Combining API in a dual-drug ternary cocrystal approach, Chem. Commun., 2020, 56, 13229–13232 RSC.
  4. J. Zhang, et al. Vibrational spectroscopic detection and analysis of isoniazid-nicotinamide-succinic acid ternary cocrystal, Spectrochim. Acta, Part A, 2023, 295, 122623 CrossRef CAS PubMed.
  5. S. Allu, A. Garai, V. V. Chernyshev and A. K. Nangia, Synthesis of Ternary Cocrystals, Salts, and Hydrates of Acefylline with Enhanced Dissolution and High Permeability, Cryst. Growth Des., 2022, 22, 4165–4181 CrossRef CAS.
  6. G. Bolla and A. Nangia, Binary and ternary cocrystals of sulfa drug acetazolamide with pyridine carboxamides and cyclic amides, IUCrJ, 2016, 3, 152–160 CrossRef CAS PubMed.
  7. D. A. Adsmond, A. S. Sinha, U. B. R. Khandavilli, A. R. Maguire and S. E. Lawrence, Design and Synthesis of Ternary Cocrystals Using Carboxyphenols and Two Complementary Acceptor Compounds, Cryst. Growth Des., 2016, 16, 59–69 CrossRef CAS.
  8. E. Batisai, Multicomponent crystals of anti-tuberculosis drugs: a mini-review, RSC Adv., 2020, 10, 37134–37141 RSC.
  9. L. F. Diniz, et al. Novel Isoniazid cocrystals with aromatic carboxylic acids: Crystal engineering, spectroscopy and thermochemical investigations, J. Mol. Struct., 2018, 1153, 58–68 CrossRef CAS.
  10. S. Aitipamula, A. B. H. Wong, P. S. Chow and R. B. H. Tan, Novel solid forms of the anti-tuberculosis drug, Isoniazid: Ternary and polymorphic cocrystals, CrystEngComm, 2013, 15, 5877–5887 RSC.
  11. J. Rosa, et al. Isoniazid-Resveratrol Cocrystal: A Novel Alternative for Topical Treatment of Cutaneous Tuberculosis, Cryst. Growth Des., 2019, 19, 5029–5036 CrossRef CAS.
  12. S. J. Bethune, N. Huang, A. Jayasankar and N. Rodríguez-Hornedo, Understanding and predicting the effect of cocrystal components and pH on cocrystal solubility, Cryst. Growth Des., 2009, 9, 3976–3988 CrossRef CAS.
  13. C. Ràfols, et al. Acidity and hydrophobicity of several new potential antitubercular drugs: Isoniazid and benzimidazole derivatives, J. Chem. Eng. Data, 2012, 57, 330–338 CrossRef.
  14. A. Avdeef, pKa determination. In Avdeef, Alex. Absorption and drug development: solubility, permeability and charge state, Wiley, 2012 Search PubMed.
  15. M. Williams, The Merck Index: an Encyclopedia of Chemicals, Drugs, and Biologicals, Merck Inc. Drug Development Research, 14th edn, 2006, vol. 67 Search PubMed.
  16. D. J. Good and N. Rodríguez-Hornedo, Cocrystal eutectic constants and prediction of solubility behavior, Cryst. Growth Des., 2010, 10, 1028–1032 CrossRef CAS.
  17. G. Kuminek, et al. How cocrystals of weakly basic drugs and acidic coformers might modulate solubility and stability, Chem. Commun., 2016, 52, 5832–5835 RSC.
  18. T. C. Machado, G. Kuminek, S. G. Cardoso and N. Rodríguez-Hornedo, The role of pH and dose/solubility ratio on cocrystal dissolution, drug supersaturation and precipitation, Eur. J. Pharm. Sci., 2020, 152, 105422 CrossRef CAS PubMed.
  19. G. Kuminek, K. L. Cavanagh, M. F. M. Da Piedade and N. Rodríguez-Hornedo, Posaconazole Cocrystal with Superior Solubility and Dissolution Behavior, Cryst. Growth Des., 2019, 19, 6592–6602 CrossRef CAS.
  20. D. J. Good and N. Rodríguez-Hornedo, Solubility advantage of pharmaceutical cocrystals, Cryst. Growth Des., 2009, 9, 2253–2264 CrossRef.
  21. S. J. Nehm, B. Rodríguez-Spong and N. Rodríguez-Hornedo, Phase solubility diagrams of cocrystals are explained by solubility product and solution complexation, Cryst. Growth Des., 2006, 6, 592–600 CrossRef CAS.
  22. T. Cogo Machado, O. N. Kavanagh, S. Gonçalves Cardoso and N. Rodríguez-Hornedo, Synchronization of Cocrystal Dissolution and Drug Precipitation to Sustain Drug Supersaturation, Mol. Pharmaceutics, 2022, 19, 2765–2775 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available: Solubility equations and experimental data. See DOI: https://doi.org/10.1039/d3ce01134h
This journal is © The Royal Society of Chemistry 2024
Click here to see how this site uses Cookies. View our privacy policy here.