Open Access Article
Open Access ArticleLocalization effect for doping and collaborative diffusion in Er3+:YAG melt†
Feng
Liu
 a,
Xianjie
Zhang
b,
Kunfeng
Chen
a,
Xianjie
Zhang
b,
Kunfeng
Chen
 c,
Chao
Peng
a,
Guilin
Zhuang
c,
Chao
Peng
a,
Guilin
Zhuang
 b and
Dongfeng
Xue
b and
Dongfeng
Xue
 *a
*a
aMultiscale Crystal Materials Research Center, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China. E-mail: df.xue@siat.ac.cn
bInstitute of Industrial Catalysis, State Key Laboratory Breeding Base of GreenChemical Synthesis Technology, College of Chemical Engineering, Zhejiang University of Technology, Hangzhou 310032, P.R. China
cState Key Laboratory of Crystal Materials, Institute of Novel Semiconductors, Shandong University, Jinan 250100, China
First published on 12th December 2023
Abstract
Coordination geometry variations of cations in yttrium aluminium garnet (YAG) melt system doped with various Er3+ concentrations were quantitatively simulated at the classical molecular dynamic level. Our calculated radial distribution functions were discussed upon different ionic pairs, mean square displacement, and diffusion coefficient of ions, on which we clarified two important aspects, namely structure and dynamic properties in YAG melts with intermediate-range order (IRO). Our results show that Er3+ doping affects microscopic dynamic melt structures only in a confined scale localizing in the first nearest neighbour of Er3+ and O2−. Furthermore, such a localization effect is not varied with Er3+ concentration and system temperature. In the present melt system, Y3+, Al3+, and Er3+ cations with intrinsic differences (such as mass and electronegativity scales) were found to follow the same diffusion process in this system, which is mainly caused by the wholly collective rearrangement of the network-forming structure. In this Er3+:YAG melt system, there is an equivalence within both structure and dynamics for Er3+ and Y3+, which cannot be affected by the system temperature and Er3+ concentration, ascribing to the origin of the segregation coefficient of Er3+ in YAG to be equal to 1.
Introduction
Yttrium aluminum garnet (YAG, Y3Al5O12), which has a wide optical transparency, low internal stress, high hardness, chemical resistance, and heat resistance, and lacking birefringence (unlike sapphire),1–3 is a valuable material for high-energy/high-power laser systems,4 phosphors,5 and scintillation materials.6The melt method, such as the Czochralski method, is commonly used to grow YAG single crystals. In order to obtain high-quality YAG crystals by controlling the crystallization kinetics process, YAG melt has attracted the attention of scientists.7–11 At the micro-scale, the effect of temperature on the bond length between cations and anions is very small.7,11,12 Under the subcooled state, the bond lengths of Al–O and Y–O in the melts are shorter than those in the crystal,7 and the situation above the melting point is the same.11 The coordination numbers both of Al3+ and Y3+ in the melts are lower than those in the crystal.11–13 Actually, the decrease in the coordination number is related to the change in the cation coordination structure after melting. In the melted YAG, there are various AlOn coordination structures, such as AlO3 (3.6%), AlO4 (65%), and AlO5 (28.2%),13 and there is not only the YO6 coordination structure but also other coordination structures, such as YO5 (12.8%), YO6 (36.6%), YO7 (34.4%), and YO8 (13.7%).13 Our recent simulation results also have demonstrated that indeed there are various cation coordination structures.14 It is more important that the connected mode between the cation coordination structure has a significant impact on the phase transition or the state of the melt. Due to the similarity between the local structure of the cationic polyhedral connections in the YAG melt and that in YAP (YAlO3), the YAP phase appears during the cooling process in YAG melt,9,14 which will bring out the inclusions in the YAG crystals and reduce the quality of the crystal. Similarly, the connection between cations can affect the properties of the melt. For example, in the Y2O3–Al2O3 system, the connection mode of the Y3+ polyhedron can induce liquid–liquid phase transitions between low-density and high-density melts.15–17
Because pure YAG cannot be used as a working medium, doping with active ions is a common way to utilize YAG. Er3+ has abundant energy levels and at room temperature it can emit lasers of 0.86, 1.64, 1.78, and 2.94 μm when stimulated. The Er3+:YAG solid laser plays an irreplaceable role in ophthalmic surgery. There is a significant difference in the properties of Er3+ and Y3+ in the YAG melt doped with Er3+, but the segregation coefficient of Er3+ in YAG is 1. Besides, as the radius of Er3+ is close to that of Y3+ and the Er3+ valence state is the same as that of Y3+,18,19 other reasons should be more important for the microstructure and dynamics. The influence of doping Er3+ on the basic physical properties of YAG melt is a valuable issue in the preparation of Er3+:YAG crystal.
In this work, we researched the Er3+:YAG melt using molecular dynamics simulations. We found that there is a certain equivalence in the structural and dynamics behaviour of Er3+ and Y3+ in the YAG melt doped with different concentrations of Er3+, which may be one of the reasons why the segregation coefficient of Er3+ in YAG is equal to 1. In addition, the relaxation of the network structure, rather than the mass of the ions themselves, affects the diffusion of cations in the melt.
Computational details
In our works, the Buckingham and Coulomb potential model, as shown in the following formula, was used to describe the pair interaction between the ions. | (1) |
| Pairs | A (eV) | ρ | C | B (eV) | n |
|---|---|---|---|---|---|
| Er–O | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934.851 934.851 |
0.195478 | 47.651 | 469.722 | 2.714 |
| Y–O | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 526.977 526.977 |
0.211377 | 50.477 | 253.661 | 2.842 |
| Al–O | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.417 201.417 |
0.195628 | 31.997 | 43.488 | 3.435 |
| O–O | 1844.7458 | 0.343645 | 192.58 | 39.112 | 3.814 |
Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)22 has been used to simulate the YAG melt with periodic boundaries. The Nosé–Hoover method23,24 was used for canonical (nvt), isothermal-isobaric (npt) ensemble simulation, and the particle–particle algorithm25 was used to calculate the Coulomb interaction with a precision of 10−6. The time step in all simulations is 1 fs. The pure YAG melt systems include 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 ions (the quantity of each kind of ion conforms to the stoichiometric ratio), and the Er3+ doping systems were created by replacing Y3+ according to nine concentrations of Er3+ (3 at%, 6 at%, 9 at%, 12 at%, 15 at%, 20 at%, 30 at%, 40 at%, and 50 at%). Each system was relaxed sufficiently with 500 picoseconds under npt ensemble at temperatures from 2000 to 3200 K with the interval of 200 K, and then simulated under nvt ensemble to collect data for analysis.
240 ions (the quantity of each kind of ion conforms to the stoichiometric ratio), and the Er3+ doping systems were created by replacing Y3+ according to nine concentrations of Er3+ (3 at%, 6 at%, 9 at%, 12 at%, 15 at%, 20 at%, 30 at%, 40 at%, and 50 at%). Each system was relaxed sufficiently with 500 picoseconds under npt ensemble at temperatures from 2000 to 3200 K with the interval of 200 K, and then simulated under nvt ensemble to collect data for analysis.
Results and discussion
A. Effects on structure
It is necessary to have a clear understanding of the YAG melt structure before discussing the dynamic properties of the melt. YAG melt also belongs to the network-forming systems connected by cationic polyhedra and has an IRO, which has been proved in our previous studies.14 In most of the metal oxide melts, coordination units (MOn, M = cations) are formed among the cations, and oxygen ions act as the basic structural unit.26 Effects of doping Er3+ into YAG on the coordination unit between cation-anions (Al–O and Y–O pairs) are inconspicuous. The radial distribution functions (RDF) between the Al and O ions and Y and O ions were calculated using the following formula: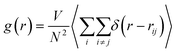 | (2) |
The results for 3200 K systems with various concentrations are taken as an example, as shown in Fig. 1. The RDF for pure YAG melt and YAG melt doping Er3+ is almost the same. Therefore, doping of Er3+ did not change the coordination units (AlOn and YOn) in YAG. The position (r) corresponding to the first peak in the RDF is the bond length between the two ions. So, the doping concentration also does not change the bond length of the Al–O and Y–O bonds. Although it is difficult to show RDF in all systems with different temperatures, this feature exists for the systems at all temperatures and doping concentrations we simulated, and the RDF between Al–O and Y–O pairs in systems with temperatures of 2000 and 2600 K are shown in Fig. S1 and S2, respectively, in the ESI.†
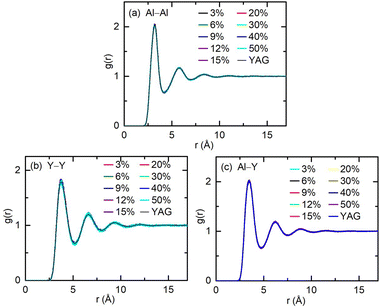
Er3+ doping does not change the relative structure between the ionic coordination units (polyhedrons) in the YAG melts. The RDF between different cation pairs (Al–Al, Y–Y, and Al–Y) were calculated, as shown in Fig. 2. Compared with the RDF for the Al–Al pairs in the pure and Er3+-doped YAG melt, it is clear that the amplitude for each peak and undulating contour for the RDF is not affected by doping, and fluctuations in the longer distance beyond the first peak is also preserved, which means that doping with Er3+ did not affect the relative connection between the AlOn coordination unit, and IRO values are also not affected by Er3+. The situation for the Y–Y and Al–Y cation pairs is similar to that of Al–Al cation pairs. Cations in the melt coordinated with O2− form the polyhedron, these polyhedrons are connected with each other by corner, edge, and face sharing O2−.14 Doping Er3+ into the YAG melt does not impact the connection between cation polyhedrons, and does not enhance or weaken the IRO, which stem from the equivalence between Er3+ and Y3+. This feature is not affected by temperature and doping concentrations, and the RDF between Al–Al, Al–Y, and Y–Y pairs in systems with temperatures of 2000 and 2600 K is shown in Fig. S3 and S4, respectively, in the ESI.† The reasons why doping of Er3+ does not impact the original network in the melts will be discussed in the next.
The actions of Er3+ on the connection between cations units in YAG melt is equivalent to that of Y3+, in other words, the structural association between Er3+ and other cations is the same as that between Y3+ and other cations in the Er3+:YAG melts. The RDF between Al–Y, Al–Er, Y–Y, and Y–Er cation pairs was calculated. The results for the systems at 3200 K with various doping concentrations are shown in Fig. 3 and 4. As shown in Fig. 3, RDF for Al–Y and Al–Er pairs are overlapping completely, which indicates that the structural association for Al–Y pairs and Al–Er pairs are equivalent. As shown in Fig. 4, the situation for Y–Y and Y–Er pairs is the same as that with Al–Y and Al–Er pairs. Therefore, in terms of the structural association between Er3+ and other cations, Er3+ is identical to Y3+, which may result from very little difference between the ionic radii of Er3+ (1.004 Å) and Y3+ (1.015 Å).27,28 This equivalence is universal at different temperatures (the RDF between Al–Y, Al–Er, Y–Y, and Y–Er cation pairs in the systems with temperature 2000 and 2600 K is shown in Fig. S5–S8 in the ESI†).
Currently, there are two main reasons for the segregation coefficient of Er3+ in YAG to be 1. One is that the ion radius of Er3+ is close to that of Y3+,18 and the other is that the valence state of Er3+ is the same as that of Y3+.19 Er3+ does not alter the original network structure of YAG, and in the melt structure, Er3+ is almost equivalent to Y3+. Therefore, Er3+ can completely replace Y3+ in any proportion of the melt without changing the melt structure. Segregation is determined by the free energy of the doped ions in crystals and melts. If the difference between Er3+ and Y3+ in the crystal is ignored, the equivalence of the two ions in the melt has a decisive impact on the segregation coefficient. So, the equivalence between Er3+ and Y3+ is the fundamental reason why the segregation coefficient of Er3+ in YAG is equal to 1.
The equivalence between the Er3+ and Y3+ is reflected in IRO. The short-range order is different between these two cations, in which the coordination units of Er3+ are a little different from that of Y3+. RDF for Er–O and Y–O pairs in the 3200 K systems with various doping concentrations is shown in Fig. 5, and RDF for Er–O and Y–O pairs in the 2000 and 2600 K systems are shown in Fig. S9 and S10, respectively, in the ESI.† Beyond the first peak, RDF for Er–O and Y–O pairs coincided wholly, while the biggest discrepancy occurred in the first peak. The intensity of the first peak in Er–O RDF is greater than that in Y–O RDF, which indicates that the strength of the pair correlation between the Er3+ and O2− is stronger than that between Y3+ and O2−. The coordination number (CN) for Er3+ and Y3+ was calculated with the formula,  , where ρ and g(r) are the densities of O2− and RDF, respectively. The coordination numbers for Y3+ and Er3+ are close to each other in systems with different temperatures and doping concentrations, as shown in Fig. S11(d).† So, the peak intensity of Er–O RDF is higher than that of Y–O RDF, which means that within the coordination structure, the strength of Er–O bond is stronger than that of Y–O, which is the only difference between their local coordination structure. The stronger Er–O bond may be caused by the ion electronegativity for Er3+ (1.438), which is greater than that of Y3+ (1.340),29 and the ability for Er3+ to attract the negatively charged oxygen ion is stronger than that of Y3+. The entire peak of Er–O RDF tends towards the direction of smaller r, as shown in Fig. S11(a)–(c).† Therefore, the local coordination structure between the Er3+ and Y3+ is closed, and Er3+ slightly has more coordination numbers than Y3+ at high temperatures.
, where ρ and g(r) are the densities of O2− and RDF, respectively. The coordination numbers for Y3+ and Er3+ are close to each other in systems with different temperatures and doping concentrations, as shown in Fig. S11(d).† So, the peak intensity of Er–O RDF is higher than that of Y–O RDF, which means that within the coordination structure, the strength of Er–O bond is stronger than that of Y–O, which is the only difference between their local coordination structure. The stronger Er–O bond may be caused by the ion electronegativity for Er3+ (1.438), which is greater than that of Y3+ (1.340),29 and the ability for Er3+ to attract the negatively charged oxygen ion is stronger than that of Y3+. The entire peak of Er–O RDF tends towards the direction of smaller r, as shown in Fig. S11(a)–(c).† Therefore, the local coordination structure between the Er3+ and Y3+ is closed, and Er3+ slightly has more coordination numbers than Y3+ at high temperatures.
B. Diffusions of ions
In the melt of YAG, the mean squared displacement (MSD) can be divided into three regimes: ballistic, sub-diffusion, and diffusion, which is similar to that of the Al2O3 melt.30 MSD was calculated using the following formula:| MSD(Δt) = 〈(rt+Δt − rt)2〉 | (3) |
In the first one, ballistic regime, ions move near the equilibrium position under the action of inertia, as shown in Fig. 6. The moving of ions in this stage belongs to the vibration around the equilibrium position, and the running time is very short (about 100 fs). As shown in Fig. 6(c) and (d), the running times for Er3+ and Y3+ in the ballistic regime are approximately equal, and this feature is not affected by temperature or concentration (MSD for ions in the YAG melts doping with 3 and 15 at% Er3+ are shown in Fig. S11 and S12 in the ESI†). If the vibration was treated as a harmonic motion, as shown in the illustration of Fig. 6(b), the running time, 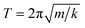 , is proportional to
, is proportional to 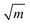 , where k is related to the stiffness coefficient of the spring and m represents the mass of ions. Therefore, the running time of the Er3+ is 1.4 times that of Y3+, which obviously contradicts the current results. Based on the pattern for the coordination structure of cations, the contradictory is attributed to the different coordination environments of Y3+ and Er3+. Because Er–O bond is stronger than the Y–O bond, the total interaction between Er3+ and O2− is stronger than that between Y3+ and O2− (as discussed preceding on the melt structure, other aspects for Er3+ and Y3+ are equal in the regime beyond the first peak). The stiffness coefficient k for Er3+ should be larger than that of Y3+, which can counteract the effect of the mass.
, where k is related to the stiffness coefficient of the spring and m represents the mass of ions. Therefore, the running time of the Er3+ is 1.4 times that of Y3+, which obviously contradicts the current results. Based on the pattern for the coordination structure of cations, the contradictory is attributed to the different coordination environments of Y3+ and Er3+. Because Er–O bond is stronger than the Y–O bond, the total interaction between Er3+ and O2− is stronger than that between Y3+ and O2− (as discussed preceding on the melt structure, other aspects for Er3+ and Y3+ are equal in the regime beyond the first peak). The stiffness coefficient k for Er3+ should be larger than that of Y3+, which can counteract the effect of the mass.
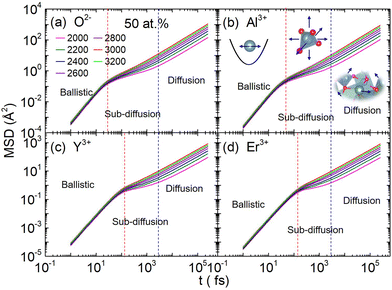 | ||
| Fig. 6 (a)–(d) respectively represent the function of mean square displacement with time for O2−, Al3+, Y3+, and Er3+, which include three different dynamic stages in Er:YAG (50 at%) melt at different temperature. Additionally, the function of mean square displacement with time in other systems with 3 and 15 at% doping concentration is shown in Fig. S11 and S12.† The mean squared displacement (MSD) can be divided into three regimes: ballistic, sub-diffusion, and diffusion, and the schematic diagram of each stage is shown in the illustration in (b). | ||
In the second one, sub-diffusive regime, ions move within a local range under the caging effects. Cations in the YAG melt form a coordination structure (polyhedron) with neighbour O2−, and the cations are located inside the polyhedron14 which is like a cage. The situation for anions is similar, but surrounded by cations. The displacement of ions at this stage mainly stems from the collective movement of the entire cage. Because the entire cage is embedded in the network structure of melts, the displacement is very small, and MSD shows as a plateau. As shown in Fig. 6(c) and (d), the length of the sub-diffusion regime of Y3+ and Er3+ are the same, which means the dynamic characteristics presented by these two cages corresponding to Y3+ and Er3+ embedded in the entire network structure are consistent. Additionally, the structural environment of the Y3+ and Er3+ in the first nearest neighbour is different, while the structural environment outside the first nearest neighbour is consistent. So, it can be inferred that the sub-diffusion behaviours are determined by the structure relaxation beyond the first nearest neighbour.
In the third one, diffusion regime, the imprisoned ions are released by the rearrangement of surrounding ions. The diffusion of ions mainly comes from this stage, and the self-diffusion coefficient is equal to the slope of MSD divided by 6. The relationship between the diffusion coefficient and temperature is shown in Fig. 7. At each doping concentration, the diffusion coefficient of anions is the largest. It is surprising that the diffusion coefficient of the cations is approximately close to each other, but their relative atomic masses are very different (Al: 26.982, Y: 88.906, and Er:167.26). Obviously, the diffusion of cations in these systems is neither determined by the mass of cations nor affected by the coordination unit, because the mass and the coordination unit for each kind of cation is much different.14 The collaborative rearrangement between the neighbouring cation polyhedrons led to the diffusion of ions. On the one hand, the starting time of diffusion for each kind of ion is basically the same, as shown in the blue dashed line in Fig. 6. On the other hand, the diffusion barrier of cations is also basically the same, as shown in Fig. 8. These two aspects can prove this conjecture. The YAG melt consists of coordination units (AlOn and YOn), which are connected with each other by sharing oxygen ions and forming the network structure.14 Equal barriers for each kind of cation mean the difficulty for rearrangement of the network structure near the cation coordination polyhedron is the same. This indirectly proves that the collaborative relaxation of the medium-range structures affects ion diffusion. On the other side, if the melt structure is divided into two parts, one is the first nearest neighbour and the other is the network structure outside the nearest neighbour, and doping of Er3+ only changes the neighbour structure between Er3+ and O2−, without affecting the entire networking structures beyond the first neighbour. Doping Er3+ into the YAG melt also did not change the diffusion properties of Al3+ and Y3+, and the diffusion properties of Er3+ are the same with those of Y3+, which indicate that the diffusion of cations in this kind of network-forming systems is controlled by the collaborative rearrangement of the overall network structure. We speculate that during this rearrangement process, O2− are exchanged between polyhedrons, and the position of the polyhedron changes at the same time, causing all ions to move simultaneously throughout the rearrangement.
Furthermore, the oxide functional crystals play an indispensable role in medical treatment,31 radiation detection,32 solid-state laser,4 and semiconductor fields.33 However, it is still very difficult to prepare large-sized and high-quality oxide functional crystals.34 One key reason is that its growth mechanism is not well understood. Crystals are formed by the solidification of atoms transported from liquid to solid by the solid–liquid interface. Although a kinetic mechanism for crystal growth was proposed based on atomic diffusion at the atomic scale,35–37 this kind of monatomic mechanism has not yet been accurately used to describe the growth process of the complex systems such as oxides.38 The collaborative rearrangement that happened near the interface may be the main dynamic process. The equivalence between Er3+ and Y3+ in the melt structure, as well as the unique diffusion behaviour in this system are the possible reasons why Er3+ ions only replace the position of Y3+ during the crystallization process. Preparation of high-quality Er3+:YAG crystals will promote the application of solid-state lasers.39–41
Conclusions
Although the properties of Er3+ are significantly different from those of Al3+ and Y3+, the effect of E3+ doping on the melt structure in YAG melt is localized in the first nearest neighbour of the coordination structure between Er3+ and O2−, and doping Er3+ does not change the original network-forming structure characteristics between the cations. The localization effect for doping Er3+ is independent of the doping concentration and the temperature of the systems. The diffusion coefficients of different ions are almost the same in each system with different doping concentrations of Er3+ and different temperatures above or near melting points. Real diffusion of ions in the Er3+:YAG melt is caused by the overall collaborative rearrangement of the overall structure in the network-forming systems. In terms of the structure and dynamics properties, Er3+ is equivalent to Y3+ in the YAG melt at different temperatures and doping concentrations, which may be the microscopic reason for the segregation coefficient of Er3+ to be 1 in YAG.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by the National Natural Science Foundation of China for Youth (52202012), Key projects of the National Natural Science Foundation of China (51832007), International (regional) cooperation and exchange projects (52220105010), 2021 Sino-German Cooperation and Exchange Program of the Sino-German Science Center of the National Natural Science Foundation (M-0755), Major basic research project of Shandong Natural Science Foundation (ZR2020ZD35).References
- A. M. Hofmeister and K. R. Campbell, J. Appl. Phys., 1992, 72(2), 638–646 CrossRef.
- R. D. Shannon, M. A. Subramanian and T. H. Allik, et al. , J. Appl. Phys., 1990, 67(8), 3798–3802 CrossRef.
- P. R. Stoddart, P. E. Ngoepe and P. M. Mjwara, et al. , J. Appl. Phys., 1993, 73(11), 7298–7301 CrossRef.
- B. Ma, W. Zhang and H. Luo, et al. , Opt. Mater., 2023, 143, 114218 CrossRef.
- L. Lv, J. He and Q. Xiao, et al. , Ceram. Int., 2023, 49(17, Part A), 28457–28464 CrossRef.
- V. Laguta, M. Buryi and V. Babin, et al. , J. Mater. Chem. C, 2023, 11(4), 1346–1359 RSC.
- J. K. R. Weber, S. Krishnan and S. Ansell, et al. , Phys. Rev. Lett., 2000, 84(16), 3622–3625 CrossRef.
- B. R. Johnson and W. M. Kriven, J. Mater. Res., 2001, 16(6), 1795–1805 CrossRef.
- K. Nagashio, J. Sasaki and K. Kuribayashi, Mater. Trans., 2004, 45(8), 2723–2727 CrossRef CAS.
- M. Wilson and P. F. McMillan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(5), 054206 CrossRef.
- V. Cristiglio, L. Hennet and G. J. Cuello, et al. , J. Phys.: Condens. Matter, 2007, 19(41), 415105 CrossRef CAS PubMed.
- L. Hennet, S. Krishnan and I. Pozdnyakova, et al. , Pure Appl. Chem., 2007, 79(10), 1643–1652 CrossRef CAS.
- V. Cristiglio, L. Hennet and G. J. Cuello, et al. , J. Non-Cryst. Solids, 2007, 353(18–21), 1789–1792 CrossRef CAS.
- X. Zhang, F. Liu and K. Chen, et al. , CrystEngComm, 2023, 25(16), 2410–2417 RSC.
- M. C. Wilding, M. Wilson and P. F. McMillan, Philos. Trans. R. Soc. London, 2005, 363(1827), 589–607 CAS.
- G. N. Greaves, M. C. Wilding and D. Langstaff, et al. , J. Non-Cryst. Solids, 2011, 357(2), 435–441 CrossRef CAS.
- P. F. McMillan, M. Wilson and M. C. Wilding, et al. , J. Phys.: Condens. Matter, 2007, 19(41), 415101 CrossRef.
- D. Zhou, X. Xu and C. Xia, et al. , J. Opt. Soc. Am. B, 2011, 28(10), 2543–2548 CrossRef CAS.
- S. Bera, P. Ohodnicki and K. Collins, et al. , J. Cryst. Growth, 2020, 547, 125801 CrossRef CAS.
- J. Du and A. N. Cormack, J. Non-Cryst. Solids, 2005, 351(27), 2263–2276 CrossRef CAS.
- J. C. Du, J. Am. Ceram. Soc., 2009, 92(1), 87–95 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- W. G. Hoover, A. J. C. Ladd and B. Moran, Phys. Rev. Lett., 1982, 48(26), 1818–1820 CrossRef CAS.
- S. Nosé, Mol. Phys., 1984, 52(2), 255–268 CrossRef.
- J. W. Eastwood, R. W. Hockney and D. Lawrence, Comput. Phys. Commun., 1980, 19(2), 215–261 CrossRef CAS.
- L. B. Skinner, C. J. Benmore and J. K. R. Weber, et al. , Phys. Rev. Lett., 2014, 112(15), 157801 CrossRef CAS.
- J. Kimpton, T. H. Randle and J. Drennan, Solid State Ionics, 2002, 149(1), 89–98 CrossRef CAS.
- Y. Q. Jia, J. Solid State Chem., 1991, 95(1), 184–187 CrossRef CAS.
- K. Li and D. Xue, J. Phys. Chem. A, 2006, 110(39), 11332–11337 CrossRef CAS PubMed.
- N. T. T. Ha, N. V. Hong and P. K. Hung, Indian J. Phys., 2019, 93(8), 971–978 CrossRef CAS.
- T. C. D. Carrieri, P. M. de Freitas and R. S. Navarro, et al. , Lasers Med. Sci., 2007, 22(3), 165–170 CrossRef.
- Z. Luchuan, X. Chao and C. Yongkang, et al., Luminescence and Scintillation Characteristics of Lyso:Ce Dosimeter for Low Dose X-Ray, Proc. SPIE, 2022, 123210R Search PubMed.
- C. J. Ou, K. P. Chang and M. W. Tasi, et al. , IEEE Photonics J., 2022, 14(6), 1–9 Search PubMed.
- F. Liu, K. Chen and D. Xue, Innovation, 2023, 4(4), 100458 Search PubMed.
- J. Q. Broughton, G. H. Gilmer and K. A. Jackson, Phys. Rev. Lett., 1982, 49(20), 1496 CrossRef CAS.
- G. Sun, J. Xu and P. Harrowell, Nat. Mater., 2018, 17(10), 881–886 CrossRef CAS PubMed.
- Q. Gao, J. D. Ai and S. X. Tang, et al. , Nat. Mater., 2021, 20(10), 1431–1439 CrossRef CAS.
- F. Liu, K. Chen and C. Peng, et al. , J. Appl. Phys., 2023, 133(17), 175301 CrossRef CAS.
- X. Zang, Z. Liu and Y. Xu, et al. , Sci. China: Technol. Sci., 2023, 66 DOI:10.1007/s11431-023-2420-x.
- G. Zhao, G. Wang and Y. Li, et al. , Sci. China: Technol. Sci., 2023, 66 DOI:10.1007/s11431-022-2327-8.
- J. Tan, Y. Lyu and J. Zhang, et al. , Sci. China: Technol. Sci., 2023, 66, 3439–3449 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ce01081c |
| This journal is © The Royal Society of Chemistry 2024 |