Crystal growth of ternary metal sulfides from an open melt: Ba₂MnS₃

Abstract

We present the growth and characterization of sizable single crystals of the transition metal sulfide Ba₂MnS₃ by the floating-zone technique. Notably, to the best of our knowledge, this method marks the first instance of sulfide melt growth in an open atmosphere, prompting us to detail modifications to our halogen image furnace to eliminate oxygen from the growth atmosphere. This advance is expected to prove valuable for cultivating substantial crystals of other sulfide materials. We present a detailed study of Ba₂MnS₃. Through single crystal X-ray and neutron diffraction, we confirm Ba₂MnS₃ adopts the orthorhombic space group Pnma with unit cell parameters of a = 8.88960 (10) Å, b = 4.33630 (10) Å, c = 17.2210 (2) Å, and V = 663.835 (19) ų at 300 K. By means of magnetometry and specific heat capacity, we identify an antiferromagnetic ground state, with two transitions at 19.6 and 21.1 K. Finally, we elucidate the magnetic ground state through single crystal neutron diffraction, demonstrating the system is described by the magnetic propagation vector k = (0, 1/2, 0) and belongs to the P_b2₁/n magnetic space group.

---

1 Introduction

Ternary transition metal sulfides are a diverse group of functional materials with promising properties.^1–4 Compared to their oxide counterparts, these sulfides exhibit greater covalency and atomic overlap due to the diffuse nature of sulfur's orbitals, which is, in part, attributed to its lower electronegativity.⁵ This leads to complementary properties, such as increased hole mobility and smaller electronic band gaps, making transition metal sulfides attractive candidates for p-type semiconductors, thermoelectric materials, and photovoltaics.^6–12 Another significant aspect of sulfides lies in their structural chemistry. The presence of larger sulfur ions, with a radii of ∼1.8 Å, stabilizes metal sulfides with lower coordination values and lower symmetry structures. Consequently, cubic structures like perovskite and pyrochlore, governed by tolerance factors between 0.9 and 1, are rarely observed in metal sulfides unless large cations can be used to compensate for the extended sulfur ion. Instead, these materials often adopt low-dimensional motifs, particularly layered structures.¹³ The prevalence of layered structures is notable because they offer potential applications in various fields. For instance, layered structures are crucial in the realm of batteries as potential cathodic materials due to their ability to facilitate cation intercalation.^14–16 In thermoelectrics, layered structures are valued for their high electrical conductivity within the layers and low thermal conductivity between them, resulting in enhanced ZT values.^17,18 Furthermore, layered materials are fundamental to the study of magnetism in low-dimensional systems, enabling the formation of exotic magnetic states.^19–22

Despite their potential, transition metal sulfide materials receive less attention compared to their oxide counterparts partly due to synthetic challenges associated with their air-sensitive chemistry. Investigations often encounter issues with small crystal sizes, which hinder the comprehensive elucidation of bulk properties. To address this, we have developed a modified floating zone setup that allows for the growth of large single crystals of transition metal sulfides. Transition metal chalcogenides containing a 1D chain structural motif often exhibit interesting physical phenomena. For example, Ba₂CoS₃ is a highly correlated material which antiferromagnetically orders at 1.5 K and exhibits metallic-like behaviour and negative magnetoresistance, making it the first 1-D sulfide containing Co²⁺ to do so.^23,24 In addition, Ba₂MnSe₃ also exhibits low dimensional magnetism as indicated by the on set of short-range magnetic correlations at high temperatures.²⁵ It has also recently been reported that Ba₂MnSe₃ exhibits low thermal conductivity over a broad temperature range.²⁶ Given the unconventional properties which emerge from this structural motif, our selected material to showcase the capabilities of this innovative synthetic methodology is Ba₂MnS₃, a quasi-1D chain magnet with an undetermined magnetic ground state.

Existing DC magnetisation measurements and elastic neutron scattering studies conducted on powder samples suggest antiferromagnetic behavior at 4 K, but no observed Néel transition temperature above this was identified.²⁷ Moreover, the magnetic structure remains unresolved, as powder measurements could not differentiate between various models.²⁷ The magnetization measurements exhibit an interesting characteristic: a high-temperature turnover around 110 K, indicating the presence of frustrated spin fluctuations and low-dimensional magnetism.^28,29

Notably, the proposed models both describe Ba₂MnS₃ as a 1D chain antiferromagnet with undetermined wave vectors. Additionally, magnetic susceptibility measurements on powders suggest that the magnetic moment of the Mn²⁺ ion is S = 2, which is lower than the expected . However, further confirmation is required to validate this observation. If accurate, the reduced magnetic moment could be attributed to the increased covalency of the Mn–S bond resulting from the low electronegativity of sulfur.^30,31 Herein, we reexamine the magnetic susceptibility of the Ba₂MnS₃, noting two magnetic transitions are present at 19.6 K and 21.1 K. These observations are confirmed via specific heat capacity measurements. Finally, we report the magnetic ground state structure of Ba₂MnS₃.

2 Materials and methods

2.1 Polycrstalline powder

Polycrystalline powder samples of Ba₂MnS₃ were prepared by a solid-state reaction method. Commercial MnS and BaS (Sigma Aldrich) powders were first purified by baking under flowing 5% H₂ gas at 950 °C for 18 hours. In particular, as-purchased BaS had a significant impurity phase of BaS₂ that decomposed on heating. Stoichiometric amounts of the purified reagents were ground in a mortar and pestle, pelletised and baked at 950 °C in 5% H₂ gas for 18 hours. The rod for the image furnace growth was prepared from these precursors and baked at similar conditions for 2 hours in an alumina boat.

2.2 Preparation of single crystals

Utilizing the optical floating zone technique, we successfully synthesized single crystals employing a four-mirror mirror furnace manufactured by Crystal Systems Corporation—more precisely, the FZ-T-4000-H model. Two necessary upgrades were introduced to this furnace. Firstly, the conventional single O-ring sealing system employed for the rotating shaft and the growth chamber was replaced with a dual-seal cavity arrangement, significantly reducing the oxygen infiltration rate into the growth chamber. Using a custom-made stainless steel mount, a second O-ring was installed 2 cm above/below the standard O-ring. Argon flowed through the cavity between the O-rings, out through a pipe, and into the main chamber. Hence, leaks through the first O-ring seal resulted in argon, not oxygen, entering the chamber. To quantify and monitor the effectiveness of this enhanced sealing configuration, we integrated a Cambridge Sensotec oxygen sensor into our experimental setup. Through continuous monitoring over an extended period involving the rotation and translation of the shaft, our observations indicated the absence of any appreciable influx of oxygen into the growth chamber.

Secondly, we implemented a novel oxygen scrubbing technology to purify the argon gas before it entered the chamber. This technology involves an oxygen pump designed as a reverse-operating homemade zirconia oxygen sensor. It consists of a yttria-stabilized zirconia membrane as an ionic conductor between two sealed gas reservoirs. One reservoir contains air, while the other serves as the inlet for argon gas. The membrane is equipped with platinum paint electrodes and heated to temperatures exceeding 600 °C. As the argon flows over the electrodes, a 2 V potential difference is applied across the membrane, causing oxygen contaminants in the argon to be conducted across the membrane and into the air reservoir. This method allows us to achieve significantly lower oxygen levels inside the growth chamber, with many orders of magnitude reduction. However, it should be noted that accurately measuring the partial oxygen pressure at such low values poses difficulties as the calibration via the Nernst equation is difficult. Recently, a commercial version of this technology produced by Canon Machinary Inc. has become available, offering more detailed information on the technique and its implementation.³²

The image furnace utilized four 500 W halogen lamps. Initial melt tests of Ba₂MnS₃ pellets revealed incongruent melting, resulting in a liquid phase composed of a mixture of BaMnS₂, Ba₂MnS₃ and BaS. A travelling solvent method was employed to address this issue using a starting pellet of BaMnS₂. The growth and feed speeds were 0.2 mm h⁻¹, with the rod and crystal rotating in counter motion at 30 rpm. The ultra-clean argon gas pressure was 1.2 bar. The growth was stable with approximately 1200 W of lamp power. This approach allowed us to establish a stable melt zone for approximately ten days. Fig. 1a depicts the crystal rod. The ingot contained multiple crystals, with the largest one weighing 0.8 g. SEM-EDS was conducted on specific sections using a Jeol JSM-6610LV equipped with an Oxford Instruments Xmaxn 80T X-ray detector to analyse the ingot. Before the analysis, the crystals were coated with a 10 nm Au layer for grounding.

Fig. 1 (a) Image of Ba₂MnS₃ sample from optical floating zone crystal growth. (b) Polished face of the single crystal. (c) Predicted and observed Laue diffraction pattern of the (001) plane.

The observed ratio of elements was determined to have an uncertainty of 2% atomic ratio. Results gave the atomic ratio Ba : Mn : S to be 2 : 0.99 : 2.90. While trace amounts of oxygen were detected, it was challenging to determine whether this was native to the crystal. We note the crystals remained stable in ambient air for several months, displaying no signs of decomposition.

X-ray Laue was employed for alignment and cutting, and a wire saw was used. Some oxygen contamination likely occurred on the crystal surfaces during processing, possibly leading to the formation of MnO. It should be mentioned that a tiny amount of MnO (less than 0.1%) was observed at 120 K in the magnetization data. We believe this MnO contamination is surface-related, as the magnetic signal decreased upon annealing in 5% H₂. Lastly, through neutron diffraction, we confirmed that all measured samples were indeed single crystals.

2.3 Single crystal X-ray diffraction

Single crystal X-ray diffraction (SC-XRD) measurements were performed at 300, 250, 200 and 150 K using a XtaLAB Synergy, Dualflex, HyPix diffractometer equipped with a monochromatic Mo Kα radiation (λ = 0.71073 Å). An absorption correction was applied using CrysalisPro. This was done based on face-indexing and Gaussian integration. The linear absorption coefficient (μ) was found to be 14.64 mm⁻¹. Data were collected on 3 samples to check reproducibility and estimate sample-to-sample variations; no significant variations in the structural parameters within 4 standard deviations were observed. Each crystal that was measured was cut from the bulk crystal grown using the floating zone technique described above. The structures were refined by a full-matrix least-squares technique based on F² using Jana2006.³³ See Fig. S1, Tables S1 and S2† for the |F_cal |²vs. |F_obs|² plot, refinement summary and refined atomic positions and atomic displacement parameters.

2.4 Magnetic susceptibility and specific heat measurements

Measurements of the magnetization were made using a Quantum Design MPMS XL-7. Three single-domain samples, confirmed by neutron diffraction, were aligned to the a, b and c axis using a Laue camera to within 1° and cut by wire saw. For the magnetic susceptibility and specific heat measurements the crystals were mounted utilising GE varnish and Apiezon N grease respectively. These were chosen as they have good thermal conductance at low temperatures and are not expected to induce significant strain in the crystal. Care was taken to avoid contact with water or acids, and the crystals were cleaned in toluene. Specific heat capacity measurements were performed on a Quantum Design PPMS measurement system between 1.8 and 300 K.

2.5 Neutron diffraction

Neutron diffraction experiments were performed at the Single Crystal Diffractometer (SXD) beamline at ISIS, where the time-of-flight Laue technique is used to access large three-dimensional (3D) volumes of reciprocal space in a single measurement.³⁴ Data was collected on two cylindrical crystals. The first was 1.4 cm × 0.13 cm². Data was collected using 5 orientations at 300 K for 2 hours, 100 K for 2 hours, 4 K for 21 hours. Additional data was collected at 25 K for 8 hours using 4 orientations. Temperature sweeps were conducted between 6–25 K at a fixed crystal orientation. A summary of the structure refinement, refined atomic positions and refined atomic displacement parameters can be seen in Tables 1–3, respectively. The second crystal was 0.3 cm × 0.15 cm². Data was collected using 5 rotational angles at 4 K for 10 hours and 25 K for 2 hours. See Fig. S2† for the |F_cal|²vs. |F_obs|² plots for the second Ba₂MnS₃ crystal and Table S3† for refined atomic positions and atomic displacement parameters of the second Ba₂MnS₃ crystal. An absorption correction was applied using SXD2001. This utilised the cylindrical shape of the crystal in conjunction with Gaussian integration. The linear absorption coefficient is wavelength-dependent.

Table 1 Results of the structure refinement of Ba₂MnS₃ using single-crystal neutron diffraction data

Formula	Ba2MnS3
Formula weight	425.79
T (K)	300
Crystal system	Orthorhombic
Space group	Pnma (no. 62)
a (Å)	8.88960 (10)
b (Å)	4.33630 (10)
c (Å)	17.2210 (2)
V (Å^3)	663.835 (19)
Z	4
No. of measured reflections	3724
R obs (%)	6.44
wR2obs (%)	9.70
GOFobs (%)	1.91

---

Table 2 Refined atomic positions derived from the single crystal neutron diffraction data of Ba₂MnS₃ collected at 300 K

Site	x	y	z	U iso
Ba1	0.41841 (8)	0.75	0.28627 (3)	0.009010 (18)
Ba2	0.26145 (9)	0.75	0.54417 (3)	0.010070 (19)
Mn1	0.12509 (12)	0.25	0.36824 (4)	0.01040 (3)
S1	−0.00122 (16)	0.75	0.40045 (6)	0.01150 (3)
S2	0.37296 (16)	0.25	0.42757 (6)	0.01080 (3)
S3	0.18001 (15)	0.25	0.22867 (6)	0.01040 (3)

---

Table 3 Refined displacement parameters derived from the single crystal neutron diffraction data of Ba₂MnS₃ collected at 300 K

Site	U11	U22	U33	U12	U13	U23
Ba1	0.0090 (4)	0.0069 (2)	0.0111 (2)	0	0	0
Ba2	0.0117 (5)	0.0089 (3)	0.0096 (2)	0	0	0
Mn1	0.0092 (6)	0.0101 (4)	0.0119 (3)	0	0	0
S1	0.0136 (8)	0.0078 (4)	0.0131 (5)	0	0	0
S2	0.0104 (8)	0.0107 (5)	0.0114 (4)	0	0	0
S3	0.0103 (8)	0.0103 (5)	0.0106 (4)	0	0	0

---

3 Results and discussion

3.1 Crystal structure

Ba₂MnS₃ crystallizes in the orthorhombic space group Pnma (No. 62) having unit cell parameters of a = 8.88960 (10) Å, b = 4.33630 (10) Å, c = 17.2210 (2) Å, and V = 663.835 (19) ų at 300 K. This is consistent with previous reports of the material. Detailed crystallographic parameters can be seen in Table 1. The crystal structure is characterised by two distinct Ba sites, one Mn site and three distinct S sites, with all atoms occupying the 4c Wyckoff position. Both Ba cations sit in a seven-fold coordination environment while the Mn cation adopts a distorted tetrahedral coordination geometry as seen in Fig. 2a. The Mn–S bond lengths in the MnS₄ tetrahedra range from 2.4288 (17) Å to 2.5039 (9) Å, these lie within the expected bond length range for a Mn²⁺ ion. The Mn–S bond length associated with the bridging Mn–S–Mn connectivity is longer than that of the bridging Mn–S–Ba con- nectivity. The Ba–S bond lengths differ according to which site is being considered. The Ba1 site has bond lengths which range between 3.1729 (7) Å and 3.2735 (9) Å while the Ba2 site has bond lengths which range between 3.1170 (10) Å and 3.4026 (15) Å. These values lie within the expected bond length range for Ba²⁺ ion. As seen in Fig. 2b. the MnS₄ units are corner-sharing, forming a 1D chain motif. The two BaS₇ polyhedra are edge-sharing and appear to form an extended network. The Ba1 site binds to four [MnS₄]_∞ chains while the Ba2 site binds to two [MnS₄]_∞ chains. From an extended perspective, it becomes apparent the [MnS₄]_∞ chains propagate through the extended BaS₇ network as seen in Fig. 2c. Due to the fact that the BaS₇ polyhedra isolate the 1D chains, the inter-chain magnetic interaction is likely to be smaller than the intra-chain interaction, explaining the low ordering temperature. Moreover, due to the long Mn–Mn distance (>4 Å) it is unlikely that a direct exchange pathway would lead to the observed long-range order. As such, any magnetic ordering observed is likely to be an exchange interaction mediated via the bridging sulfur anions. The temperature-dependent single crystal X-ray diffraction reveals no structural phase transitions down to 150 K.

Fig. 2 (a) The coordination environment of the two crystallographically distinct barium sites. On the left, Ba1 coordinates to two 1D chains. On the right, Ba2 coordinates to four other 1D chains. (b) A view of the propagating 1D chains along the crystallographic b-axis. In all cases purple spheres are manganese, green are barium and yellow are sulfur. Thermal ellipsoids represented at 90% probability.

3.2 Magnetometry

The temperature (T) dependent magnetic susceptibility χ of Ba₂MnS₃ measured at an applied field of 0.1 T is shown in Fig. 3a and b. As the system is cooled, the susceptibility increases passing through a broad asymmetric maximum at ∼100 K. This feature indicates the onset of short-range correlations in the material and is a prominent feature of low dimensional magnetic materials.³⁵ At ∼20 K, the system appears to magnetically order as indicated by the weak anomaly present in the susceptibility curve representing the Néel temperature (T_N). Upon closer inspection of Fig. 3b, it becomes clear that there are two transitions present, one located at 21.1 K, indicating the onset of long-range magnetic order and another at 19.6 K. The anisotropy of the susceptibility with respect to crystalline axes indicates that the ordering is likely antiferromagnetic, with the ordering wave-vector possibly along the b-axis and the magnetic moments lying in the a–c plane. Due to the highly correlated nature of the quasi-1D chain, the Curie–Weiss temperature region is not reached up to 400 K, preventing extraction of the Curie–Weiss temperature and local magnetic moment from our data set.

Fig. 3 (a) Magnetic susceptibility parallel to the a, b, c-axis from 4–400 K. (b) Magnetic susceptibility between 5–30 K demonstrating two antiferromagnetic features between 19–21 K. (c) Specific heat capacity between 300–4 K. (d) Specific heat capacity between 18–22 K demonstrating two λ-type anomalies.

3.3 Specific heat

In order to corroborate the occurrence of long-range order, the specific heat capacity (C_p) was measured. The T-dependent C_p was measured at zero-field is shown in Fig. 3c. Given the insulating behaviour which is expected, the total specific heat C_p, can be approximated by the individual contributions of its lattice, C_p,phonon and magnetic, C_p,mag, components such that:

C_p = C_p,phonon + C_p,mag (1)

From Fig. 3c, it can be seen that at high temperatures, C_p is dominated by the contribution of phonon excitations. Only at low temperatures is any signature of magnetic order detected. As can be seen from the inset, two weak λ-type anomalies (i.e. second-order phase transition) are present at 21.1 K and 19.6 K. This matches our observations seen in the magnetic susceptibility data and indicates the onset of long-range order. These features are seen across multiple crystal samples from different crystal growth attempts and have similar magnitudes in each case. This indicates that these features are likely not due to a minor impurity phase and are instead intrinsic to the material. Due to the fact that short-range AFM correlations persist at high temperatures, the extraction of the T-dependent lattice contribution below 300 K is not possible with the available data. As such, it is not possible to reveal the T dependence of the magnetic contribution. Given that the magnetic ions all occupy the same crystallographic site, the two λ-type anomalies likely correspond to two consecutive mag- netic orderings as opposed to a two-step magnetic transition.³⁶

3.4 Neutron diffraction

In order to establish the ground state of this material, single-crystal neutron diffraction was employed. The crystallographic and magnetic structures of two single crystalline samples were measured by neutron diffraction using the SXD beamline at ISIS Neutron and Muon Source. All findings presented in the following section were consistent on both crystal samples, indicating minimal inter-sample variations. Due to time constraints, the focus of the neutron diffraction experiment was to unambiguously solve the ground state magnetic structure of the Ba₂MnS₃ instead of investigating the temperature region between the two observed transitions. It is important to note however that within the resolution of the instrument, we do not see any sign of incommensurability at intermediate temperatures however to confirm this more work is required with a better resolution and finer temperature steps. Fig. 4a and b. displays the single crystal neutron diffraction pattern of Ba₂MnS₃ in the (h, k, 0) scattering plane at T = 25 K and 4 K, above and below the ordering temperature, respectively. At 25 K, the sharp diffraction pattern observed can be attributed to nuclear reflections only.

Fig. 4 (a and b) Single crystal neutron diffraction pattern of Ba₂MnS₃ in the (h, k, 0) scattering plane at 25 K (a) and at 4 K (b). (c) Integrated intensities of the (0, −1, −3) peak as a function of temperature. (d) Nuclear |F_calc|²vs. |F_obs|² at 25 K. (e) Nuclear|F_calc|²vs.|F_obs|² at 4 K. (f) Nuclear and magnetic |F_calc|²vs. |F_obs|² at 4 K.

Upon cooling to 4 K, additional Bragg reflections emerge due to long-range magnetic order. The additional reflections can be indexed by the propagation vector k = (0, 1/2, 0). Consequently, the magnetic unit cell is obtained by doubling the chemical cell along the b axis. The temperature dependence of the integrated intensity of the (0, −1/2, −3) peak is plotted in Fig. 4c. From 25 K to 21 K, minimal intensity is observed, indicating no long-range magnetic order. Below 21 K, the intensity of the magnetic peaks increases with decreasing temperature in good agreement with the specific heat capacity and susceptibility measurements. Fig. 4d and e show nuclear refinements at 25 K and 4 K, while Fig. 4f shows the nuclear and magnetic refinement at 4 K. By examining the nuclear refinement at 25 K, it becomes apparent that there is good agreement between the calculated nuclear structure factor and the observed one as indicated by a R_obs = 6.99%. The nuclear refinement at 4 K demonstrates good agreement between the calculated nuclear structure factor and the observed one, as highlighted by R_obs = 8.8%. The R_obs value for the nuclear contribution from the nuclear and magnetic refinement is comparable to that seen in Fig. 4e. The magnetic space group P_b2₁/n (with transformation matrix {(100)(020)(001)} origin (0,0,0) with respect to the parent nuclear structure), gave the optimal fit to the data, demonstrated by the smallest R-factor. The magnetic space group generated by the action of the mY₁ irreducible representation with order parameter direction (μ, μ), the standard setting of the magnetic space groups is P_a2₁/c (with transformation matrix {(020)(00−1)(−1−20)} origin (0,0,0) with respect to the parent nuclear structure). The calculated magnetic structure factors and the observed ones are in relatively good agreement, resulting in R_obs = 11.7%. Each magnetization component was refined individually. The largest contributions were observed along the a and c axis. A negligible contribution of 0.03 (1) μ_B was observed along the b-axis. Constraining the model to the a and c axis resulted in no increase in the R-factor. The extracted magnetization component along the a axis is 3.01 (1) μ_B and 1.54 (1) μ_B along the c axis resulting in an overall observed magnetic moment of 3.38 (1) μ_B. The observed magnetic moment is reduced from what is expected for a typical 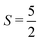system (5 μ_B). A refinement of the nuclear model in the monoclinic magnetic space groups did not highlight the presence of any additional distortions compared with the Pnma model indicating that the magnetoelestic coupling is small and below the resolution of our diffraction experiment.

The ground state magnetic structure is depicted in Fig. 5a and b. Examining the magnetic structure reveals that the moments order antiferromagnetically along the 1D chain direction. The ordering between chains is more complex. The nearest spin chains are coupled ferromagnetically; however, the next nearest spin chains are coupled antiferromagnetically. Interestingly, as seen in Fig. 5b, the magnetic moments point along the Mn1–S2 bond, the shortest bond in the MnS₄ tetrahedron, suggesting a coupling of the spin and lattice. Generally, it is expected that 3d systems would not show any form of anisotropy because of the quenching of the orbital momentum of d-electrons, presuming a high-spin configuration. In this system, a reduced magnetic moment is observed and as such, the 3d electrons might retain some orbital angular momentum, resulting in a modest spin–orbit coupling. Several scenarios might explain the observed reduced moment. The sulfides are expected to have a degree of covalency in the electronic bond between cation and anions.^37,38 Mixing the metal d-electron orbitals with the sulfur ligand orbitals can affect the diffraction intensities, altering the magnetic form factors and reducing the magnetic moment at the cation site. Hubbard and Marshall have discussed this issue for a chain of spin-only magnetic (d-orbital) and ligand (p-orbital) ions, similar to our case.³⁹ In the ionic picture, the antibonding orbitals containing the unpaired electrons are mostly d in character due to the minimal hybridisation between metal and ligand orbitals. In extended sulfur orbitals, the overlap of the sigma bond is more significant, so the antibonding orbitals are broadened to include electron density on the sulfur site. However, magnetic neutron diffraction is only sensitive to the moment on the cation; hence, the measured moment is smaller than expected. The ratio of the measured to expected moments provides an estimate of the degree of covalency. Our system's ratio is 0.67, close to that observed in NiCr₂S₄ (2 μ_B observed, 3 μ_B expected).^37,38

Fig. 5 (a) View of the magnetic unit cell demonstrating antiferromagnetic order along the 1D chain. (b) View of the magnetic moments pointing along the Mn1–S2 bond. Purple spheres are manganese and yellow are sulfur. Barium atoms are omitted for clarity.

Alternatively, the moment reduction might be related to the correlated nature of the 1D chain caused by magnetic fluctuations. For example, descloizite-type compound, SrMn(VO₄)(OH) has a 1D chain and Néel temperature of 30 K, where the observed moment was 3.4 μB, quite similar to our moment reduction.⁴⁰ The authors attribute this reduction to strong spin fluctuations due to the quasi-1D nature of the magnetic interactions. Finally, we have analysed the critical exponent of the magnetic order parameter below the Néel temperature, shown in Fig. 4c. We fitted a standard power law 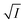∝ (T_N − T)β to the intensity of the magnetic peaks between 0.4 < T/T_N < 0.95 for ten magnetic peaks. The average β = 0.22 ± 0.03 and a T_N = 19.7 ± 0.7 K. 2D Ising and 3D Ising antiferromagnets' standard universality class is expected to have β = 0.125 and 0.35, respectively, which is markedly different to our extract value. We note it is similar to that observed in the 1D chain compound NiTe₂O₅.⁴¹ This material has a magnetic transition temperature of 30 K with β = 0.18, the origin of which is unclear. Further theoretical work on low-dimensional magnets is likely required.

4 Conclusions

To conclude, we reported the development of a novel synthetic methodology to grow large-size single crystals (>1 cm) utilising a modified optical floating zone set-up. The characterisation of Ba₂MnS₃ was targeted to demonstrate this synthetic methodology's capabilities. A reevaluation of the magnetic susceptibility revealed the presence of two transitions seen at 21.1 K and 19.6 K. Specific heat capacity measurements verified both features corresponded to magnetic transitions. Single crystal neutron diffraction revealed the magnetic Mn²⁺ ions order with a k = (0, 1/2, 0) propagation vector at 4 K. The magnetic space group that best fits the neutron diffraction data was P_b2₁/n. Here, the magnetic moments' order along the Mn1–S2 bond indicates the presence of spin–orbit coupling in the system. Some mysteries remain to be explored in this material, notably the origin of the reduced magnetic moment and the nature of the second magnetic transition at 21.1 K. Finally, we note that our demonstration of crystal growth of a ternary sulfide from an open melt could open the door to measurements on this diverse and fascinating group of materials.

Author contributions

B. J. M.: powder preparation, crystal growth, data collection, analysis of data, magnetic structure solving, writing – original draft; Z. X. C.: crystal growth; Y. L.: powder preparation, crystal growth, analysis of data; M. J. G.: neutron diffraction, analysis of data; E. N. T.: SEM-EDS; F. O.: magnetic structure solution; C. B.: analysis of data; P. M.: magnetic structure solution, supervision; R. S. P.: crystal growth, conceptualization, formal analysis, funding acquisition, supervision, writing – original draft, editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the Science and Technology Facilities Council (STFC) for access to neutron beamtime at ISIS (RB number: RB2220760-2, DOI: https://doi.org/10.5286/ISIS.E.RB2220760-2). We thank the Materials Characterisation Laboratory at ISIS Neutron and Muon Source for the time on the XtaLAB Synergy single crystal diffractometer, Quantum Design MPMS XL-7 and Quantum Design PPMS.

Notes and references

1. P. Afanasiev and I. Bezverkhyy, Appl. Catal., A, 2007, 322, 129–141.
2. G. Fu and J.-M. Lee, J. Mater. Chem. A, 2019, 7, 9386–9405.
3. J.-M. Xu, X.-C. Wang and J.-P. Cheng, ACS Omega, 2020, 5, 1305–1311.
4. S. E. Sheela, R. Sekar, D. K. Maurya, M. Paulraj and S. Angaiah, Mater. Sci. Semicond. Process., 2023, 156, 107273.
5. M. R. Harrison and M. G. Francesconi, Coord. Chem. Rev., 2011, 255, 451–458.
6. G. Brunin, F. Ricci, V.-A. Ha, G.-M. Rignanese and G. Hautier, npj Comput. Mater., 2019, 5, 63.
7. P. D'Amico, A. Calzolari, A. Ruini and A. Catellani, Sci. Rep., 2017, 7, 16805.
8. A. A. Tedstone, D. J. Lewis and P. O'Brien, Chem. Mater., 2016, 28, 1965–1974.
9. D. Zhang, X. Wang, H. Wu, Y. Huang, S. Zheng, B. Zhang, H. Fu, Z. Cheng, P. Jiang, G. Han, G. Wang, X. Zhou and X. Lu, Adv. Funct. Mater., 2023, 33, 2214163.
10. Z.-H. Ge, L.-D. Zhao, D. Wu, X. Liu, B.-P. Zhang, J.-F. Li and J. He, Mater. Today, 2016, 19, 227–239.
11. Y. Sun, X. Li, W. Qiao, L. Wu, S. Gao, H. Li, F. Liu, J. Ao and Y. Zhang, Sol. Energy Mater. Sol. Cells, 2021, 219, 110788.
12. B. Ananthoju, J. Mohapatra, M. K. Jangid, D. Bahadur, N. V. Medhekar and M. Aslam, Sci. Rep., 2016, 6, 35369.
13. W. Bronger, Angew. Chem., Int. Ed. Engl., 1981, 20, 52–62.
14. H. Shuai, R. Liu, W. Li, X. Yang, H. Lu, Y. Gao, J. Xu and K. Huang, Adv. Energy Mater., 2023, 13, 2202992.
15. J. Zhao, Y. Zhang, Y. Wang, H. Li and Y. Peng, J. Energy Chem., 2018, 27, 1536–1554.
16. Y.-P. Gao, J. Xu, K.-J. Huang, H. Lu, Y.-X. Pang and G.-Q. Li, CrystEngComm, 2021, 23, 7546–7564.
17. O. Caballero-Calero, J. R. Ares and M. Martín-González, Adv. Sustainable Syst., 2021, 5, 2100095.
18. S. Hébert, D. Berthebaud, R. Daou, Y. Bréard, D. Pelloquin, E. Guilmeau, F. Gascoin, O. Lebedev and A. Maignan, J. Phys.: Condens. Matter, 2015, 28, 013001.
19. P. Dalmas de Réotier, A. Yaouanc, D. E. MacLaughlin, S. Zhao, T. Higo, S. Nakatsuji, Y. Nambu, C. Marin, G. Lapertot, A. Amato and C. Baines, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 140407.
20. D. Reig-i Plessis and A. M. Hallas, Phys. Rev. Mater., 2021, 5, 030301.
21. J. Hemberger, T. Rudolf, H.-A. Krug von Nidda, F. Mayr, A. Pimenov, V. Tsurkan and A. Loidl, Phys. Rev. Lett., 2006, 97, 087204.
22. Z. Yue, Z. Hou, F. Yun, P. Liu, G. Yang, A. Bake, W. Zhao, D. Cortie, C. Shu, S. Hu, J. Cheng and X. Wang, J. Mater. Chem. C, 2021, 9, 8874–8881.
23. D. Headspith, P. Battle and M. Francesconi, J. Solid State Chem., 2007, 180, 2859–2863.
24. T. Baikie, V. Hardy, A. Maignan and M. G. Francesconi, Chem. Commun., 2005, 5077–5079.
25. H. Steinfink and I. E. Grey, Inorg. Chem., 1971, 10, 691–696.
26. O. P. Ojo, W. D. C. B. Gunatilleke, A. J. Biacchi, H. Wang and G. S. Nolas, Inorg. Chem., 2023, 62, 3555–3561.
27. D. A. Headspith, PhD thesis, University of Hull, 2009.
28. H. Steinfink and I. E. Grey, Inorg. Chem., 1971, 10, 691–696.
29. N. Nakayama, K. Kosuge, S. Kachi, T. Shinjo and T. Takada, J. Solid State Chem., 1980, 33, 351–356.
30. M. Wakeshima, Y. Hinatsu, K. Oikawa, Y. Shimojo and Y. Morii, J. Mater. Chem., 2000, 10, 2183–2185.
31. A. Devey and N. H. de Leeuw, Phys. Rev. B, 2010, 82, 235112.
32. C. M. Inc., https://machinery.canon/en/about/technology/future-uloce-500/, accessed September 2023.
33. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. - Cryst. Mater., 2014, 229, 345–352.
34. D. A. Keen, M. J. Gutmann and C. C. Wilson, J. Appl. Crystallogr., 2006, 39, 714–722.
35. A. D. J. Barnes, T. Baikie, V. Hardy, M.-B. Lepetit, A. Maignan, N. A. Young and M. G. Francesconi, J. Mater. Chem., 2006, 16, 3489–3502.
36. L. de Jongh and A. Miedema, Adv. Phys., 1974, 23, 1–260.
37. A. Bhutani, P. Behera, R. D. McAuliffe, H. Cao, A. Huq, M. J. Kirkham, C. R. dela Cruz, T. Woods and D. P. Shoemaker, Phys. Rev. Mater., 2019, 3, 064404.
38. A. V. Powell, D. C. Colgan and C. Ritter, J. Solid State Chem., 1999, 143, 163–173.
39. J. Hubbard and W. Marshall, Proc. Phys. Soc., London, 1965, 86, 561.
40. L. D. Sanjeewa, V. O. Garlea, M. A. McGuire, C. D. McMillen, H. Cao and J. W. Kolis, Phys. Rev. B, 2016, 93, 224407.
41. J. H. Lee, M. Kratochvílová, H. Cao, Z. Yamani, J. S. Kim, J.-G. Park, G. R. Stewart and Y. S. Oh, Phys. Rev. B, 2019, 100, 144441.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ce00977g

---