DOI:
10.1039/D4CC05336B
(Communication)
Chem. Commun., 2024,
60, 14109-14112
Supramolecular self-sorting predicted by a simple harmonic oscillator model†
Received
9th October 2024
, Accepted 25th October 2024
First published on 28th October 2024
Abstract
Macrocycles that encapsulate two guests can self-sort those into homo- and heterodimers. We report here a family of self-sorting homobimetallic Pt(II) terpyridyl acetylide dimers secured together with a pair of Cucurbit[8]uril macrocycles (CB[8]). The rigid bridging unit between both Pt centers introduces varying “hinge” angles, resulting in disparities in Pt–Pt distances in the heterodimers, and leads to recognition motif mismatch. We found that the self-sorting process can be quantified using a simple model, in which each complex behaves as a simple harmonic oscillator, whose heteroassembly tends to minimize geometry distorsions through C(aryl)–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt axis deformation.
C–Pt axis deformation.
Cucurbit[n]urils (CB[n]s) are barrel-shaped macrocycles consisting of n glycoluril units connected via methylene bridges. Their capacity to form strong inclusion complexes in aqueous media, primarily due to the release of energetically constrained water molecules, has established them as key components for self-sorting in a wide variety of chemical systems.1–7 CB[8] is capable of bringing together up to two hydrophobic guests, allowing homo/hetero pair formation.7–10 In those tertiary assemblies, cationic units on the guest tend to minimize electrostatic repulsion with the other positive guest, while maximizing attractive interaction with both carbonyl rims, resulting in head-to-tail (HT) assemblies. Nonetheless, these two driving forces might be overcome by employing square planar Pt(II)-terpyridine (tpy) complexes, wherein both extended dispersive ligand attractive forces and metallophilic interactions cooperate to exclusively afford head-to-head (HH) assemblies.11 This new arrangement has led to several applications in peptide engineering12,13 and hydrogen photoreduction.14
Homobimetallic Pt(II) acetylide complexes form quaternary assemblies upon encapsulation with two CB[8] hosts (Scheme 1). The self-sorting process can be quantified using equilibrium (1)15 and the corresponding free energy term ΔG (eqn (2)),§ where A and B are guests, AA and BB homo-quaternary complexes, AB (or BA) hetero-quaternary complexes and [AB]tot is the total concentration of hetero-complex.
| |  | (1) |
| |  | (2) |
 |
| | Scheme 1 Previously reported equilibrium between two homoquaternary inclusion complexes (HH) with tolyl and 3,5-difluorophenyl heads as recognition motifs.16 | |
The equilibrium is considered fully social when the homodimers cannot be detected by NMR spectroscopy (i.e. less than 1%); this corresponds to a −2.3 kcal mol−1 free energy term. Similarly, self-sorting is fully narcissistic when ΔG > +2.3 kcal mol−1. In the case of bimetallic Pt(II) acetylides, self-sorting properties primarily depend on (1) the relative binding free energies of the aryl head groups; and (2) the relative orientation of the bridging group.16 In order to isolate the second contribution, we use here rigid spacers to assess the importance of structural flexibility on self-sorting.
A family of five homobimetallic Pt(II)-tpy complexes 1–5 bearing distinct aromatic bridging ligands have been synthesized (Fig. 1). These species are expected to form well-defined homoquaternary assemblies whose self-sorting will be evaluated. To avoid the contribution of the aryl heads, a uniform tpy head group (3,5-difluophenyl) was utilized (see highlighted R group in Scheme 1); self-sorting is thus solely governed by interactions and angle mismatches between the central bridging units. The angle of bridging ligands (that we call “hinge” angle) is defined by two vectors extending from the quaternary carbons bearing the alkynyl moiety and the opposite quaternary (para) carbons. The range spans 64 degrees (see Fig. 1).¶ The distance between both substituted carbons in the spacer group is similar so that a good overlap is expected, with the exception of the 2,7-substituted naphthyl unit16 (complex 5, Fig. 1), whose length is significantly shorter than any other ligand. This spacer group has been studied to account for ligand length differences when the angle disparity is small (6°) in combination with complex 4. In any mixture, a tpy head group mismatch (i.e. aryl units from distinct complexes that are misaligned within the CB[8] cavity) is therefore expected. This results in the deformation of both complexes in the heteroquaternary assembly to align both pairs of head groups; the deformation would occur at the most flexible part of the molecule, i.e. the acetylide moiety.7,8,17,18 Hence, experimental free energy terms on our self-sorting scale15 provide a measurement of Pt-alkynyl flexibility.
 |
| | Fig. 1 Novel complexes (1–5) synthesized in this work along with their “hinge” angle definition.¶ Oligo(ethylene glycol) chains have been grafted to compound 1 to increase its solubility. Previously reported homobimetallic Pt-tpy complexes.16 GFN2-xTB optimized structure of assembly 3·1·CB[8]2.|| See Scheme 1 for the structure of group R. | |
Pt(II)-tpy complexes 1–4 were prepared from the corresponding diacetylide ligands, chloro-[4′-(3,5-difluoro phenyl)-2,2′:6′,2′′-terpyridine]platinum(II) chloride, copper(I) iodide and isopropyl amine.§ These complexes readily formed HH homo-quaternary assemblies 12·CB[8]2–42·CB[8]2 upon addition of 1.0 equivalent of CB[8] to their suspension in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of D2O and CD3CN (Fig. S91–S114, ESI†).§ Pairs of homoquaternary assemblies 12·CB[8]2–52·CB[8]2 were then combined in equimolar amounts, and kept at 40 °C for up to 12 days until equilibrium was reached, as shown by 1H- and 19F-NMR spectroscopy.§ All mixtures are in slow exchange regime, allowing the observation of new (integrable) signals corresponding to the heteroquaternary assemblies formed at the expense of their homoquaternary counterparts (Fig. 2 and Fig. S122–S151, ESI†).§ All heteroquaternary assemblies could also be fully characterized by high resolution mass spectrometry (HRMS).§ The observed decline in social behaviour with increasing calculated hinge angle mismatch (or dPt–Pt difference) was expected. Most mixtures self-sort narcissistically (from +0.90 to +0.02 kcal mol−1, corresponding to 18% and 49% of the heteroassembly, respectively, Table 1). A notable exception is heteroassembly 2·3·CB[8]2, that bears dibenzothiophene and fluorenone spacer groups, which is favoured over the corresponding pair of homoassemblies (free energy term −0.45 (±0.05) kcal mol−1, i.e. 68% of heterodimer, Table 1). This might suggest some favourable Coulombic interactions in the hetero-pair of central units; the low hinge angle mismatch (6°) and very short Pt–Pt distance difference (0.22 Å) are not significant enough to cause strain in the heteroassembly. On the other hand, the mixture between assemblies 42·CB[8]2 and 52·CB[8]2, which was expected to account for distinct spacer group length (dPt–Pt difference of 2.08 Å) while keeping a nearly negligible hinge angle mismatch (6°), returns a small free energy term of +0.16 (±0.01) kcal mol−1, or 43% of heteroquaternary assembly.
1 mixture of D2O and CD3CN (Fig. S91–S114, ESI†).§ Pairs of homoquaternary assemblies 12·CB[8]2–52·CB[8]2 were then combined in equimolar amounts, and kept at 40 °C for up to 12 days until equilibrium was reached, as shown by 1H- and 19F-NMR spectroscopy.§ All mixtures are in slow exchange regime, allowing the observation of new (integrable) signals corresponding to the heteroquaternary assemblies formed at the expense of their homoquaternary counterparts (Fig. 2 and Fig. S122–S151, ESI†).§ All heteroquaternary assemblies could also be fully characterized by high resolution mass spectrometry (HRMS).§ The observed decline in social behaviour with increasing calculated hinge angle mismatch (or dPt–Pt difference) was expected. Most mixtures self-sort narcissistically (from +0.90 to +0.02 kcal mol−1, corresponding to 18% and 49% of the heteroassembly, respectively, Table 1). A notable exception is heteroassembly 2·3·CB[8]2, that bears dibenzothiophene and fluorenone spacer groups, which is favoured over the corresponding pair of homoassemblies (free energy term −0.45 (±0.05) kcal mol−1, i.e. 68% of heterodimer, Table 1). This might suggest some favourable Coulombic interactions in the hetero-pair of central units; the low hinge angle mismatch (6°) and very short Pt–Pt distance difference (0.22 Å) are not significant enough to cause strain in the heteroassembly. On the other hand, the mixture between assemblies 42·CB[8]2 and 52·CB[8]2, which was expected to account for distinct spacer group length (dPt–Pt difference of 2.08 Å) while keeping a nearly negligible hinge angle mismatch (6°), returns a small free energy term of +0.16 (±0.01) kcal mol−1, or 43% of heteroquaternary assembly.
 |
| | Fig. 2 Stacked 1H-NMR (500 MHz, D2O/CD3CN 2:1) of (a) assembly 32·CB[8]2, (b) assembly 12·CB[8]2, (c) their mixture at t = 0, and (d) their mixture after 12 days. | |
Table 1 Free energy term ΔG [kcal mol−1] for the self-sorting of Pt complexes 1–5 in the presence of CB[8]. Experiments repeated in triplicate
|
|
1
|
2
|
3
|
4
|
|
2
|
+0.02 (±0.01) |
|
|
|
|
3
|
+0.07 (±0.01) |
−0.45 (±0.05) |
|
|
|
4
|
+0.90 (±0.01) |
+0.62 (±0.01) |
+0.56 (±0.02) |
|
|
5
|
|
|
|
+0.16 (±0.01) |
To rationalize these findings, we questioned whether a set of simple descriptors for each Pt complex 1–5 could be used to predict the self-sorting behaviour of any pair. To that aim, we carried out geometry optimizations with the GFN2-xTB19–21 semi-empirical method§ at various constrained Pt–Pt distances.|| Remarkably, they were found to behave as simple harmonic oscillators, as stabilities as a function of Pt–Pt distances can be fit with quadratic eqn (3), where ka is the spring constant in kcal mol−1 Å−2, a0 the optimal Pt–Pt distance, and a the Pt–Pt distance in the constrained systems (Fig. 3). The spring constants k′ were also expressed in the more commonly used mDyn Å−1 unit using eqn (4), where NA is the Avogadro constant (Table 2).
| |  | (3) |
| |  | (4) |
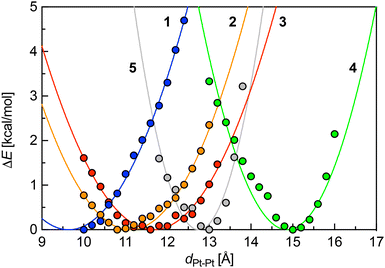 |
| | Fig. 3 Energy profiles [kcal mol−1] of Pt complexes 1–5 as a function of Pt–Pt distance [Å] (electronic component at 0 K relative to the optimized relaxed structure). | |
Table 2 Physical parameters of complexes 1–5 when treated as harmonic oscillators
|
|
Hinge angle [°] |
d
Pt–Pt [Å] |
k [kcal mol−1 Å−2] |
k′ [mDyn Å−1] |
|
1
|
62 |
10.21 |
1.22 (±0.07) |
8.5 (±0.5) × 10−3 |
|
2
|
77 |
11.23 |
1.26 (±0.05) |
8.7 (±0.4) × 10−3 |
|
3
|
83 |
11.45 |
1.16 (±0.04) |
8.0 (±0.3) × 10−3 |
|
4
|
126 |
15.24 |
2.3 (±0.2) |
1.6 (±0.1) × 10−2 |
|
5
|
120 |
13.16 |
4.6 (±0.5) |
3.2 (±0.3) × 10−2 |
As complexes 1–5 behave like simple harmonic oscillators along a Pt–Pt axis, we then questioned whether self-sorting was simply governed by the deformation of the pair of oscillators when forced to stack on top of one another upon CB[8] encapsulation of the tpy head groups. In that case, a harmonic correlation should be observed between the free energy terms of the self-sorting process and the differences in Pt–Pt distances between the complexes. Remarkably, this is indeed the case (Fig. 4, R2 = 0.997), with the exception of complex 2·3·CB[8] that self-sorts socially (Table 1, red dot in Fig. 4). One can readily notice that major mismatches in Pt–Pt distances (up to 5.0 Å) or hinge angles (up to 64°) still allow the formation of hetero-assemblies; free energy terms of the self-sorting processes do not exceed +0.90 kcal mol−1. Yet, Fig. 3 shows that compressing or expanding the Pt–Pt distance in complexes 1–5 does result in significant destabilization (0.6–2.3 kcal mol−1 for 1 Å distortions). Distortions imposed to Pt complexes to reach identical Pt–Pt distances in hetero-quaternary assemblies can be calculated using eqn (5)–(7) and the following hypothesis: the distortion energy ΔEhetero is modelled as the sum of the harmonic oscillator of both Pt complexes, where ka and kb are the spring constants (eqn (5)), a and b the Pt–Pt distances in the distorted hetero-quaternary assemblies, and a0 and b0 the distances in the optimized (relaxed) Pt complexes. With both Pt–Pt distances forced to be equal in the hetero-quaternary complexes (i.e. a = b, Fig. 5), eqn (5) and (6) afford the Pt–Pt distances that minimize the energetic penalty ΔEhetero as shown in eqn (7) (Tables 3 and 4, top half).
| | 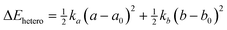 | (5) |
| | 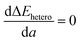 | (6) |
| |  | (7) |
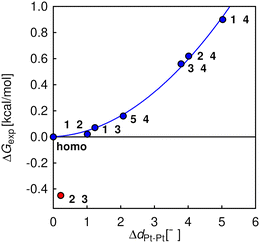 |
| | Fig. 4 Free energy terms for self-sorting processes between pairs of Pt complexes 1–5, as a function of their Pt–Pt distance mismatches. Harmonic correlation (blue line); outlier in red; “n·n” refers to all pairs of identical Pt complexes (returning ΔG = 0). | |
 |
| | Fig. 5 Extension and contraction imposed to a pair of Pt–Pt harmonic oscillators to reach even lengths. | |
Table 3 Energy penalty in kcal mol−1 required to match Pt–Pt distances in hetero-quaternary assemblies of Pt complexes 1–5 in the presence of CB[8]
|
|
1
|
2
|
3
|
4
|
|
2
|
+0.31 |
|
|
|
|
3
|
+0.48 |
+0.02 |
|
|
|
4
|
+5.31 |
+3.57 |
+2.77 |
|
|
5
|
|
|
|
+1.67 |
Table 4 Top half: proposed average Pt–Pt distortion [Å] of Pt complexes A upon quaternary CB[8]-secured complex formation with Pt complex B with identical Pt–Pt distances in the hetero-complexes, based on eqn (5)–(7). Bottom half: Proposed average Pt–Pt distortion [Å] of Pt complexes A upon quaternary CB[8]-secured complex formation with Pt complex B, based on eqn (8)–(11)
|
B
|
1
|
2
|
3
|
4
|
5
|
|
Social self-sorting observed experimentally; model not applicable.
|
|
A
|
|
|
|
|
|
|
1
|
0 |
+0.51 |
+0.60 |
+3.29 |
|
|
2
|
−0.49 |
0 |
|
+2.60 |
|
|
3
|
−0.63 |
|
0 |
+2.53 |
|
|
4
|
−1.73 |
−1.41 |
−1.26 |
0 |
−1.38 |
|
5
|
|
|
|
+0.70 |
0 |
|
|
|
1
|
0 |
+0.13 |
+0.24 |
+0.98 |
|
|
2
|
−0.13 |
0 |
|
+0.80 |
|
|
3
|
−0.25 |
|
0 |
+0.80 |
|
|
4
|
−0.52 |
−0.43 |
−0.40 |
0 |
−0.30 |
|
5
|
|
|
|
+0.15 |
0 |
The comparison of experimental self-sorting energy terms (Table 1) with the much higher calculated penalties imposed to match Pt–Pt distances in the hetero-complexes (Table 3) clearly shows that Pt–Pt distances do not need to be equal to allow hetero-quaternary assembly formation. In other terms, CB[8] encapsulation of the tpy heads remains highly favourable despite significant geometrical mismatches between the complexes. We therefore propose the following model to estimate the Pt–Pt distortions Δa and Δb in the hetero assemblies: from eqn (8) (equivalent to eqn (5), with ΔGexp being the experimental self-sorting energy term), the difference between both distortions is minimized to extract both Δa and Δb terms (eqn (9)–(11)).§Table 4 (bottom half) shows that required Pt–Pt distance distortions in the hetero assemblies are only 30 (±1)% of what they would otherwise have to be to match Pt–Pt distances (Table 4, top half, and Fig. S154 and S155, ESI†).
| |  | (8) |
| |  | (10) |
| | 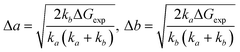 | (11) |
In summary, we showed that two CB[8] units can readily secure hetero-pairs of Pt complexes 1–5, despite major structural differences between the Pt complexes. While Pt arylacetylides are flexible along their C(aryl)–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt axis, it is the tolerance of CB[8] for the orientation and position of the encapsulated aryl tpy head groups that drives the assembly. Self-sorting can be quantified using a harmonic oscillator model based on Pt–Pt distance mismatches, predicting most self-sorting patterns. However, the model is limited, as short Pt–Pt distance mismatches may introduce favourable coulombic interactions between compatible spacer groups that promote social behaviour. Ongoing studies are addressing this limitation.
C–Pt axis, it is the tolerance of CB[8] for the orientation and position of the encapsulated aryl tpy head groups that drives the assembly. Self-sorting can be quantified using a harmonic oscillator model based on Pt–Pt distance mismatches, predicting most self-sorting patterns. However, the model is limited, as short Pt–Pt distance mismatches may introduce favourable coulombic interactions between compatible spacer groups that promote social behaviour. Ongoing studies are addressing this limitation.
We thank the Spanish Ministry of Science and Innovation (PID2021-124691NB-I00, funded by MCIN/AEI/10.13039/501100011033/FEDER, UE). EM is grateful to the National Science Foundation (grants CHE-1507321 and CHE-1905238), the American Chemical Society Petroleum Research Fund (grant 56375-ND4), the Roenigk Family Foundation and Ohio University for their continuing financial support. A. S.-M. acknowledges support from Fundación Ramón Areces for a Postdoctoral fellowship. N. A.-L. acknowledges the University of Valladolid and Santander Bank for a predoctoral contract. A. D.-V. acknowledges the Ministerio de Universidades and the European Union – NextGenerationEU for the María Zambrano contract (ADV, CONVREC-2021-264).
Data availability
All synthetic and analytical data is provided in the ESI.† All details about mathematical and computational methods, including associated coordinates are available in the ESI.†
Conflicts of interest
There are no conflicts to declare.
Notes and references
- S. Liu,
et al.
, J. Am. Chem. Soc., 2005, 127, 15959–15967 CrossRef PubMed.
- J. Lagona,
et al.
, Angew. Chem., Int. Ed., 2005, 44, 4844–4870 CrossRef PubMed.
- E. Masson,
et al.
, RSC Adv., 2012, 2, 1213–1247 RSC.
- S. J. Barrow,
et al.
, Chem. Rev., 2015, 115, 12320–12406 CrossRef PubMed.
- K. I. Assaf and W. M. Nau, Chem. Soc. Rev., 2015, 44, 394–418 RSC.
- J. Murray,
et al.
, Chem. Soc. Rev., 2017, 46, 2479–2496 RSC.
- X. Yang,
et al.
, Angew. Chem., Int. Ed., 2020, 59, 21280–21292 CrossRef.
- G. Wu,
et al.
, J. Am. Chem. Soc., 2022, 144, 14962–14975 CrossRef.
- G. Wu,
et al.
, Chem. Sci., 2020, 11, 812–825 RSC.
- G. Wu,
et al.
, Angew. Chem., Int. Ed., 2020, 59, 15963–15967 CrossRef CAS PubMed.
- K. Kotturi and E. Masson, Chem. – Eur. J., 2018, 24, 8670–8678 CrossRef CAS PubMed.
- H. Barbero,
et al.
, J. Am. Chem. Soc., 2020, 142, 867–873 CrossRef CAS PubMed.
- H. Barbero and E. Masson, Chem. Sci., 2021, 12, 9962–9968 RSC.
- R. Rabbani,
et al.
, Chem. Sci., 2021, 12, 15347–15352 RSC.
- M. Raeisi,
et al.
, J. Am. Chem. Soc., 2018, 140, 3371–3377 CrossRef CAS.
- N. A. Thompson,
et al.
, Chem. Commun., 2019, 3, 12160–12163 RSC.
- P. S. Bols and H. L. Anderson, Acc. Chem. Res., 2018, 51, 2083–2092 CrossRef PubMed.
- K. Miki and K. Ohe, Chem. – Eur. J., 2020, 26, 2529–2575 CrossRef PubMed.
- S. Grimme,
et al.
, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef.
- C. Bannwarth,
et al.
, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef PubMed.
- C. Bannwarth,
et al.
, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2021, 11, e1493 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed synthetic methods and characterization. Self-sorting process study. Computational data. See DOI: https://doi.org/10.1039/d4cc05336b |
| ‡ These two authors contributed equally to this work. |
| § See ESI† for further discussions and details. |
| ¶ According to crystal structures obtained from the Cambridge Structural Database (CSD). |
| || We must note that the Pt–Pt distances in the hetero-quaternary complexes presented herein should be seen as average distances from a large ensemble of conformers with similar energies but varying geometries; for example, the mere rotation of the CB[8]-bound aryl substituents at position 4′ of the tpy ligand clockwise or counterclockwise relative to the tpy planes yields at least 4 different hetero-quaternary assemblies with similar stabilities but different Pt–Pt distances. Reported optimized structures only represent one of these arrangements. |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Nerea
Álvarez-Llorente‡
a,
Nerea
Álvarez-Llorente‡
 b,
Eric
Masson
b,
Eric
Masson
 *c,
Alberto
Diez-Varga
*c,
Alberto
Diez-Varga
 *b and
Héctor
Barbero
*b and
Héctor
Barbero
 *b
*b
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt axis deformation.
C–Pt axis deformation.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of D2O and CD3CN (Fig. S91–S114, ESI†).§ Pairs of homoquaternary assemblies 12·CB[8]2–52·CB[8]2 were then combined in equimolar amounts, and kept at 40 °C for up to 12 days until equilibrium was reached, as shown by 1H- and 19F-NMR spectroscopy.§ All mixtures are in slow exchange regime, allowing the observation of new (integrable) signals corresponding to the heteroquaternary assemblies formed at the expense of their homoquaternary counterparts (Fig. 2 and Fig. S122–S151, ESI†).§ All heteroquaternary assemblies could also be fully characterized by high resolution mass spectrometry (HRMS).§ The observed decline in social behaviour with increasing calculated hinge angle mismatch (or dPt–Pt difference) was expected. Most mixtures self-sort narcissistically (from +0.90 to +0.02 kcal mol−1, corresponding to 18% and 49% of the heteroassembly, respectively, Table 1). A notable exception is heteroassembly 2·3·CB[8]2, that bears dibenzothiophene and fluorenone spacer groups, which is favoured over the corresponding pair of homoassemblies (free energy term −0.45 (±0.05) kcal mol−1, i.e. 68% of heterodimer, Table 1). This might suggest some favourable Coulombic interactions in the hetero-pair of central units; the low hinge angle mismatch (6°) and very short Pt–Pt distance difference (0.22 Å) are not significant enough to cause strain in the heteroassembly. On the other hand, the mixture between assemblies 42·CB[8]2 and 52·CB[8]2, which was expected to account for distinct spacer group length (dPt–Pt difference of 2.08 Å) while keeping a nearly negligible hinge angle mismatch (6°), returns a small free energy term of +0.16 (±0.01) kcal mol−1, or 43% of heteroquaternary assembly.
1 mixture of D2O and CD3CN (Fig. S91–S114, ESI†).§ Pairs of homoquaternary assemblies 12·CB[8]2–52·CB[8]2 were then combined in equimolar amounts, and kept at 40 °C for up to 12 days until equilibrium was reached, as shown by 1H- and 19F-NMR spectroscopy.§ All mixtures are in slow exchange regime, allowing the observation of new (integrable) signals corresponding to the heteroquaternary assemblies formed at the expense of their homoquaternary counterparts (Fig. 2 and Fig. S122–S151, ESI†).§ All heteroquaternary assemblies could also be fully characterized by high resolution mass spectrometry (HRMS).§ The observed decline in social behaviour with increasing calculated hinge angle mismatch (or dPt–Pt difference) was expected. Most mixtures self-sort narcissistically (from +0.90 to +0.02 kcal mol−1, corresponding to 18% and 49% of the heteroassembly, respectively, Table 1). A notable exception is heteroassembly 2·3·CB[8]2, that bears dibenzothiophene and fluorenone spacer groups, which is favoured over the corresponding pair of homoassemblies (free energy term −0.45 (±0.05) kcal mol−1, i.e. 68% of heterodimer, Table 1). This might suggest some favourable Coulombic interactions in the hetero-pair of central units; the low hinge angle mismatch (6°) and very short Pt–Pt distance difference (0.22 Å) are not significant enough to cause strain in the heteroassembly. On the other hand, the mixture between assemblies 42·CB[8]2 and 52·CB[8]2, which was expected to account for distinct spacer group length (dPt–Pt difference of 2.08 Å) while keeping a nearly negligible hinge angle mismatch (6°), returns a small free energy term of +0.16 (±0.01) kcal mol−1, or 43% of heteroquaternary assembly.



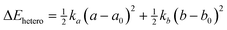
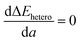




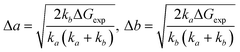
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Pt axis, it is the tolerance of CB[8] for the orientation and position of the encapsulated aryl tpy head groups that drives the assembly. Self-sorting can be quantified using a harmonic oscillator model based on Pt–Pt distance mismatches, predicting most self-sorting patterns. However, the model is limited, as short Pt–Pt distance mismatches may introduce favourable coulombic interactions between compatible spacer groups that promote social behaviour. Ongoing studies are addressing this limitation.
C–Pt axis, it is the tolerance of CB[8] for the orientation and position of the encapsulated aryl tpy head groups that drives the assembly. Self-sorting can be quantified using a harmonic oscillator model based on Pt–Pt distance mismatches, predicting most self-sorting patterns. However, the model is limited, as short Pt–Pt distance mismatches may introduce favourable coulombic interactions between compatible spacer groups that promote social behaviour. Ongoing studies are addressing this limitation.
