Sulfinfinitenes: infinitenes of fused thiophene rings

Abstract

Sulfinfinitenes, analogues of infinitene constructed from thiophene rings and assembled by applying a “cut–twist–restitch” sequence to two sulflowers, are explored through DFT calculations. The sulfinfinitene with 16 thiophene rings is only slightly more strained than the [8]sulflower, which has been synthesized, and can be considered as a promising synthetic target.

---

The synthesis of infinitene,¹ a [12]circulene twisted in a figure-of-eight loop resembling the infinity symbol, which was voted by C&EN readers as molecule of the year for 2021,² has prompted the search for other molecules constructed from fused benzene rings and displaying a similar motif. Rzeppa reported calculations on infinitene analogues with 11 and 10 benzene rings in his blog,³ but the optimised geometries of these species suggest higher levels of strain. Infinitene can be assembled by applying an imaginary “cut–twist–restitch” sequence to two coronene ([6]circulene) molecules (Scheme 1); to assemble the [11]infinitene and [10]infinitene mentioned above one would need one coronene and one corannulene ([5]circulene), or two corannulenes, respectively. The use of corannulene component(s) can be expected to produce a more strained infinitene (corannulene is bowl-shaped and more strained than coronene).

Scheme 1 Imaginary “cut–twist–restitch” assembly of infinitene from two coronene molecules.

While it is possible to consider other [m + n]infinitene analogues assembled from an [m]circulene and an [n]circulene, computational research on [n]circulenes⁴ indicates that strain increases very quickly for n < 6, and a bit slower for n > 6, with higher circulenes adopting first saddle and then helical geometries. Indeed, experimental data shows that bowl depth in a derivative of [4]circulene (quadrannulene)⁵ is higher than that in corannulene, and that [7]circulene^6–8 and a derivative of [8]circulene⁹ have saddle-shaped geometries. So, while [m + n]infinitenes with m and n outside the 5–7 range can be studied computationally, such infinitenes would be highly strained and of low synthetic feasibility. One way to reduce strain in circulene analogues is to include acene units, as in kekulene,^10,11 a close-to-planar cycloarene with 12 benzene rings. Infinitene analogues constructed from cycloarenes have been suggested and studied computationally¹² but have not been synthesized so far. The junctions in such infinitene analogues^12,13 can be different from the naphthalene junctions in [12]infinitene and calculations suggest¹³ that a [12]infinitene analogue with anthracene junctions has a lower energy than the original [12]infinitene.

Sulflowers^14–18 are heterocirculenes constructed from thiophene rings. Because of their molecular formula, (C₂S)_n, sulflowers can be considered as forms of carbon sulfide. The sulflower with 8 thiophene rings, octathio[8]circulene, has been synthesized and found to be planar, of D_8h symmetry.¹⁴ The next sulflower, nonathio[9]circulene, has not been synthesized but is predicted to be also planar, with a very similar strain energy,^14,17,18 and of D_9h symmetry.¹⁸ In this communication we explore computationally the possibility to form heteroinfinitenes by applying an imaginary “cut–twist–restitch” sequence analogous to that depicted in Scheme 1 to two sulflowers.

To guard against computational artefacts, the gas-phase ground-state geometries of [n]sulflowers with 5–10 thiophene rings, (C₂S)_n (n = 5–10), and those of the heteroinfinitenes (“sulfinfinitenes”) resulting from combining two [n]sulflowers, (C₂S)_2n, were optimized at two DFT levels of theory, B3LYP-D3(BJ)/def2-TZVP (B3LYP with Grimme's D3 dispersion corrections and Becke–Johnson damping) and M06-2X/def2-TZVP, as implemented in GAUSSIAN.¹⁹ The B3LYP-D3(BJ)/def2-TZVP optimized geometries of the [n]sulflowers with n = 6–10 are identical to those reported previously;¹⁸ we note that the lengths of the carbon-sulfur rim, carbon–carbon hub and carbon–carbon spoke bonds in the [8]sulflower of 1.752, 1.417 and 1.381 Å, respectively, provide an almost perfect match for the experimentally measured bond lengths of 1.751, 1.419 and 1.380 Å.^14,15,17 The respective M06-2X/def2-TZVP optimized bond lengths of 1.744, 1.417 and 1.371 Å show that this approach slightly underestimates the lengths of the carbon–sulfur rim and carbon–carbon spoke bonds. Apart from that, there are no major qualitative differences between the geometries and energies obtained at the two levels of theory.

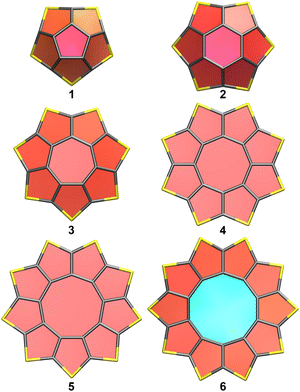
The B3LYP-D3(BJ)/def2-TZVP optimized geometries of the [n]sulflowers and [2n]sulfinfinitenes with n = 5–10 are shown in Fig. 1 and 2, respectively; the respective M06-2X/def2-TZVP optimized geometries are very similar in appearance. The junctions in all sulfinfinitenes are thieno[3,2-b]thiophene units. The individual rings have been highlighted using the PaperChain visualization algorithm²⁰ implemented in VMD²¹ which colours each ring according to the ring pucker amplitude.

Fig. 1 B3LYP-D3(BJ)/def2-TZVP optimized geometries of the [n]sulflowers with n = 5–10.

Fig. 2 B3LYP-D3(BJ)/def2-TZVP optimized geometries of the [2n]sulfinfinitenes with n = 5–10.

Looking at the sulflower series, the rings colours show that the pucker amplitudes of the individual thiophene rings decrease through 1–3 (geometries of C_5v, C_6v and C_7v symmetry, respectively), become zero in the planar 4 and 5 (geometries of D_8h and D_9h symmetry, respectively), and then increase in the nonplanar 6 [saddle-shaped geometry of C₂ or D₂ symmetry at the B3LYP-D3(BJ)/def2-TZVP or M06-2X/def2-TZVP level, respectively]. Similarly, in the sulfinfinitene series the ring pucker amplitudes decrease through 7–9, become much the same for rings in matching positions in 10 and 11, and then increase in 12. The geometries of 7 and 8 are of C₂ symmetry, and those of 9–12 are of D₂ symmetry, similarly to [12]infinitene. The changes in strain energy in the sulflower series can be quantified by calculating the energy per CS₂ unit, E(n)/n, where n is the number of CS₂ units in 1–6 (5–10, respectively).^14,17,18 An analogous quantity, E(2n)/(2n), can be calculated for each of the members of the sulfinfinitene series 7–12. The energies per CS₂ unit of 1–12 are shown in Fig. 3, relative to the lowest value of this type at each level of theory. At both levels of theory, 5 exhibits the lowest energy per CS₂ unit, with 4 coming a close second.

Fig. 3 B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP energies per CS₂ unit of the [n]sulflowers and [2n]sulfinfinitenes with n = 5–10 (1–12), relative to that of the [9]sulflower (5).

The variations in the energy per CS₂ unit show that if a [n]sulflower is nonplanar (n = 5–7, 10), the corresponding [2n]sulfinfinitene is slightly less strained; however, for planar [n]sulflowers (n = 8, 9), the corresponding [2n]sulfinfinitenes are slightly more strained. The reaction energies (ΔE) for the assembly of [16]sulfinfinitene from two [8]sulflowers through a homodesmotic scheme analogous to Scheme 1, calculated at the B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP levels, are 14.1 and 21.9 kcal mol⁻¹, respectively. These ΔE values are significantly lower than those for Scheme 1 which according to our calculations, for coronene and infinitene geometries optimized at the B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP levels, are 78.5 and 84.3 kcal mol⁻¹, respectively. The [8]sulflower is less “stiff” than coronene which helps reduce ΔE for the assembly of [16]sulfinitine. This is well-illustrated by the difference between the frequencies of the lowest a_2u normal modes of the [8]sulflower and coronene, in which the atomic displacements are similar to the initial geometry changes required for an assembly such as that shown in Scheme 1: the lowest a_2u normal mode of the [8]sulflower is ν₁, 59.6 and 59.8 cm⁻¹, at the B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP levels, respectively; the corresponding numbers for the lowest a_2u normal mode of coronene, ν₂, are higher, 124.1 and 123.9 cm⁻¹, respectively.

The HOMO–LUMO energy gaps of 1–12, which are often used as qualitative measures of reactivity, are shown in Fig. 4. The HOMO–LUMO energy gaps increase rapidly between the [5] and [8]sulflowers (1–4) and then go slightly down and stay very similar in the [9] and [10]sulflowers (5 and 6). A similar tendency is observed in the sulfinfinitene series, but the gap changes are less pronounced. This observations suggest that the [8]sulflower and the [16]sulfinfinitene are the least reactive and most stable members of the respective series. It should be noted that although the M06-2X HOMO–LUMO gaps are systematically higher than their B3LYP counterparts, the tendencies displayed by the gaps calculated with both DFT methods are very much the same. For reference, the HOMO–LUMO energy gaps in infinitene and coronene calculated at the same levels of theory as those shown in Fig. 4 are 3.18 and 4.02 eV, respectively (B3LYP), and 5.02 and 5.87 eV, respectively (M06-2X).

Fig. 4 B3LYP/def2-TZVP//B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP//M06-2X/def2-TZVP HOMO–LUMO energy gaps of the [n]sulflowers and [2n]sulfinfinitenes with n = 5–10 (1–12).

The separations between the carbon atoms from the central carbon–carbon bonds in the stacked thieno[3,2-b]thiophene junction units in [16]sulfinfinitene and [18]sulfinfinitene, 3.086 and 3.160 Å at the B3LYP-D3(BJ)/def2-TZVP level, and 3.085 and 3.147 Å at the M06-2X/def2-TZVP level, are close to the corresponding separation between the carbon atoms from the central carbon–carbon bonds in the stacked naphthalene junction units in infinitene, 2.961 and 2.966 Å at the the B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP levels, respectively (the experimentally measured separation has been reported as 2.920 Ź).

To investigate the aromaticities of the individual thiophene rings in 1–12, nucleus-independent chemical shifts (NICS)^22–24 values were obtained through B3LYP-GIAO/6-311++G(d,p) (B3LYP with gauge-including atomic orbitals) calculations at the respective B3LYP-D3(BJ)/def2-TZVP optimized geometries. According to the NICS(0) and NICS(±1) values for thiophene and the thiophene rings in 1–12 (see the ESI†), each of the thiophene rings in 1–12 is less aromatic than thiophene itself. The NICS data indicate that, in general, the aromaticities of the individual thiophene rings in the [n]sulflowers and [2n] sulfinfinitenes initially increase for 5 ≤ n ≤ 8, and then decrease for 8 ≤ n ≤ 10, in line with the behaviour of the respective energies per CS₂ unit (Fig. 3). Apart from the more highly strained 7 and 8, the variation between the NICS values for the individual thiophene rings in the sulfinfinitenes is relatively small, for example, the NICS(0) range observed in 9–12 is between −10.1 and −8.2 ppm. It should be noted that the computed ³³S isotropic shieldings included in the ESI† increase with the size of the sulflower/sulfininitene which can be attributed to the possibility to form longer conjugation pathways involving the sulfur atoms.

The results of the current calculations strongly suggest that [16]sulfinfinitene which can be formally obtained by combining two molecules of the least strained member of the sulflower series, the [8]sulflower (octathio[8]circulene),¹⁴ should be considered as a promising synthetic target. [18]sulfinfinitene and its precursor, the [9]sulflower (nonathio[9]circulene) show slightly higher strains and slightly lower HOMO–LUMO gaps and could also be of synthetic interest. We have not considered [m + n] sulfinfinitenes with different m and n values, but it can be expected that a reasonable combination, for example, [8 + 9], would have a strain energy similar to those of the [16]sulfinfinitene and [18]sulfinfinitene.

P. B. K. suggested the design and study of sulfininitenes, carried out the sulfinitene DFT calculations, and wrote the original draft. E. C. carried out the sulflower DFT calculations and calculated all NMR data. Both authors discussed the results and contributed to the final manuscript.

The authors are grateful for the support of this work by the University of York.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. M. Krzeszewski, H. Ito and K. Itami, J. Am. Chem. Soc., 2022, 144, 862–871.
2. C. H. Arnaud, 2021. https://cen.acs.org/content/cen/articles/99/i45/CENs-Year-Chemistry-2021.html#Check-out-the-molecules-of-the-year, (accessed 1 October 2024).
3. H. Rzepa, 2021. https://www.ch.imperial.ac.uk/rzepa/blog/? p = 24503, (accessed 1 October 2024).
4. H. Christoph, J. Grunenberg, H. Hopf, I. Dix, P. G. Jones, M. Scholtissek and G. Maier, Chem. – Eur. J., 2008, 14, 5604–5616.
5. B. Bharat, R. Bhola, T. Bally, A. Valente, M. K. Cyrański, Ł. Dobrzycki, S. M. Spain, P. Rempała, M. R. Chin and B. T. King, Angew. Chem., Int. Ed., 2010, 49, 399–402.
6. K. Yamamoto, T. Harada, M. Nakazaki, T. Naka, Y. Kai, S. Harada and N. Kasai, J. Am. Chem. Soc., 1983, 105, 7171–7172.
7. K. Yamamoto, T. Harada, Y. Okamoto, H. Chikamatsu, M. Nakazaki, Y. Kai, T. Nakao, M. Tanaka, S. Harada and N. Kasai, J. Am. Chem. Soc., 1988, 110, 3578–3584.
8. K. Yamamoto, H. Sonobe, H. Matsubara, M. Sato, S. Okamoto and K. Kitaura, Angew. Chem., Int. Ed. Engl., 1996, 35, 69–70.
9. C.-N. Feng, M.-Y. Kuo and Y.-T. Wu, Angew. Chem., Int. Ed., 2013, 52, 7791–7794.
10. H. A. Staab and F. Diederich, Chem. Ber., 1983, 116, 3487–3503.
11. H. A. Staab, F. Diederich, C. Krieger and D. Schweitzer, Chem. Ber., 1983, 116, 3504–3512.
12. K. Du and Y. Wang, J. Am. Chem. Soc., 2023, 145, 10763–10778.
13. S. M. Bachrach, J. Org. Chem., 2023, 88, 7962–7976.
14. K. Y. Chernichenko, V. V. Sumerin, R. V. Shpanchenko, E. S. Balenkova and V. G. Nenajdenko, Angew. Chem., Int. Ed., 2006, 45, 7367–7370.
15. O. Ivasenko, J. M. MacLeod, K. Y. Chernichenko, E. S. Balenkova, R. V. Shpanchenko, V. G. Nenajdenko, F. Rosei and D. F. Perepichka, Chem. Commun., 2009, 1192–1194.
16. G. V. Baryshnikov, R. R. Valiev, N. N. Karaush and B. F. Minaev, Phys. Chem. Chem. Phys., 2014, 16, 15367–15374.
17. N. N. Karaush-Karmazin, G. V. Baryshnikov, L. I. Valiulina, R. Valiev, H. Ågren and B. F. Minaev, New J. Chem., 2019, 43, 12178–12190.
18. E. Cummings and P. B. Karadakov, Chem. – Eur. J., 2024, 30, e202303724.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision A.03), Gaussian, Inc., Wallingford CT, 2016.
20. S. Cross, M. M. Kuttel, J. E. Stone and J. E. Gain, J. Mol. Graphics Modell., 2009, 28, 131–139.
21. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
22. P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. V. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
23. P. V. R. Schleyer, H. Jiao, N. J. R. V. E. Hommes, V. G. Malkin and O. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670.
24. H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Org. Lett., 2006, 8, 863–866.

---

Footnote

† Electronic supplementary information (ESI) available: Additional computational details; tables of NICS values and isotropic nuclear shieldings for thiophene, [n]sulflowers and [2n]sulfinfinitenes with n = 5–10; B3LYP-D3(BJ)/def2-TZVP and M06-2X/def2-TZVP optimized geometries of thiophene, [n]sulflowers and [2n]sulfinfinitenes with n = 5–10, coronene and infinitene. See DOI: https://doi.org/10.1039/d4cc05179c

---