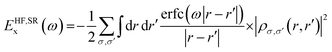Modeling-driven materials by design for conjugated polymers: insights into optoelectronic, conformational, and thermomechanical properties

Abstract

Conjugated polymers (CPs) have emerged as pivotal functional materials in the realm of flexible electronics and optoelectronic devices due to their unique blend of mechanical flexibility, solution processability, and tunable optoelectronic properties. This review synthesizes the latest molecular simulation-driven insights obtained from various multiscale modeling techniques, including quantum mechanics (QM), all-atomistic (AA) molecular dynamics (MD), coarse-grained (CG) modeling, and machine learning (ML), to elucidate the optoelectronic, structural, and thermomechanical properties of CPs. By integrating findings from our recent computational work with key experimental studies, we highlight the molecular mechanisms influencing the multifunctional performance of CPs. This comprehensive understanding aims to guide future research directions and applications in the modeling assisted design of high-performance CP-based materials and devices.

---

1. Introduction

Conjugated polymers (CPs) have emerged as critical functional materials in the realm of flexible electronics and optoelectronic devices due to their unique blend of mechanical flexibility, solution processability, and tunable optoelectronic properties.^1–4 These characteristics have driven significant research into their applications in organic field-effect transistors (OFETs),^5–8 organic photovoltaics (OPVs),^9–11 and organic light-emitting diodes (OLEDs).^12–14 Among these, donor–acceptor (D–A) CPs, which feature alternating electron-rich (donors) and electron-poor (acceptors) moieties along the polymer backbone, have been extensively studied for their superior optoelectronic properties.^15–17 Additionally, significant advancements have been made in the study of other important conjugated systems, such as porphyrin-based tapes, which have shown remarkable properties for electronic applications.^18,19 Understanding the mechanical and conformational properties of CPs at a molecular level is crucial for optimizing their performance in these applications.

Investigating CPs presents several challenges due to their diverse chemical structures, which can include various backbone configurations, side-chain lengths, and functional groups. This structural diversity leads to a wide range of thermomechanical and optoelectronic behaviors that are complex to predict and control. Experimental techniques, although valuable, often face limitations in fully capturing the dynamic and nanoscale behaviors of CPs. For instance, small-angle X-ray scattering (SAXS) and neutron scattering (SANS) are commonly used to determine chain conformation, but the presence of aggregates can complicate the interpretation of scattering profiles.^20,21 Additionally, techniques such as differential scanning calorimetry (DSC) and dynamic mechanical analysis (DMA) are employed to study thermal properties, but these methods sometimes struggle with the small sample sizes typical of CPs and their semicrystalline nature, which can obscure transitions such as the glass transition temperature (T_g).^22–25

To overcome these challenges, molecular simulations have become an indispensable tool, offering detailed molecular-level insights that complement experimental approaches. Multiscale modeling techniques, which include quantum mechanics (QM), all-atomistic (AA) molecular dynamics (MD), coarse-grained (CG) modeling, and machine learning (ML), enable the study of CPs across different length and time scales (Fig. 1). QM methods based calculations of the polymers’ electronic structure information (e.g., highest and lowest occupied molecular orbitals, band gap, electronic band structure) is needed to further understand the optoelectronic properties of CPs. For instance, Jackson et al. demonstrated that various nonbonding interactions between neighboring donor and acceptor units can improve backbone planarity.²⁶ Wang et al. utilized density functional theory (DFT) calculations of molecular orbital energies to guide the rational design of conjugated polymers for photocatalytic CO₂ reduction by analyzing molecular orbital energies, they selected polycyclic arenes and anthraquinone to construct donor–acceptor copolymers with suitable band structures.²⁷ AA-MD simulations offer insights into molecular and chain-level interactions and dynamics, which are important for exploring chain conformations and various physical properties.²⁸ For instance, Alberga et al. employed AA-MD simulations of both crystalline and amorphous phases of poly(3-hexylthiophene) (P3HT) and poly(2,5-bis(3-alkylthiophen-2-yl)thieno[3,2-b]thiophene) (PBTTT) to understand the relationship between molecular structure and charge mobility using Marcus theory.²⁹ Similarly, De Pablo et al. combined experimental SANS measurements with AA-MD simulations to accurately determine the persistence length of PTB7.³⁰ These simulations reveal the molecular structure of aggregates that contribute to complex optoelectronic phenomena, providing insights into the solution-phase conformations of CPs that are challenging to achieve through experimental methods alone. Furthermore, CG modeling simplifies complex systems, enabling the study of larger-scale phenomena and long-term behavior while retaining necessary molecular details, making CG-MD simulations particularly valuable for “bottom-up” investigations of polymer systems over extended spatiotemporal scales. By reducing degrees of freedom and eliminating non-essential atomistic details, CG-MD can explore the influences of fundamental molecular parameters on the thermomechanical behaviors of polymers with different segmental and chain structures in both bulk and confined states.^31–33 For instance, generic CG models, designed to mimic the essential structural features of diketopyrrolopyrrole (DPP)-based polymer chains, have shown that polymer chains align along the deformation axis through chain-sliding and torsional motions, increasing alignment and extension with strain.³⁴ A chemistry-specific CG model for P3HT predicted that backbone chain alignment increases with applied uniaxial strain.³⁵ These multiscale modeling techniques collectively provide a comprehensive understanding of CP behaviors across various scales.

Fig. 1 Schematics of the multiscale modeling techniques across different time and length scales of CPs material systems from quantum, all-atom, to coarse-graining. The paradigm shows the approximate ranges of time and length scales associated with each modeling technique along with relevant applications. Figure adapted from ref. 64 (copyright 2023 Elsevier).

Recently, ML algorithms have seen increasing use in developing simplified models that offer excellent predictive capabilities for polymer properties.^36–39 By deriving molecular features directly from the monomer geometry, ML models circumvent the complexity of traditional feature descriptors. For instance, ML models have effectively predicted the T_g of CPs, as demonstrated by Xie and coworkers,⁴⁰ who introduced an empirical model that predicts T_g based on the mobility of various functional groups within the repeat unit, achieving a root-mean-square error of 13 °C for 32 semi-flexible polymers. Additionally, ML techniques have been applied to enhance CG modeling by efficiently calibrating complex force fields to match properties derived from AA-MD simulations or experimental data.³⁸ This approach significantly extends the length and time scales of MD simulations, enabling more accurate predictions of thermomechanical properties across different temperatures and curing states. Integrating ML with CG modeling accelerates the materials design process, providing a powerful tool for developing new CPs with tailored properties. High-throughput experiments and simulations combined with data-driven ML approaches further enhance our ability to rapidly screen and optimize materials, significantly accelerating the discovery process. For instance, Yang et al. highlighted how ML can be utilized to predict and design properties for CPs, demonstrating the broad applicability of these techniques.⁴¹

This short review aims to summarize the recent simulation-driven insights from our research group, highlighting the main findings in the optoelectronic, structural, and thermomechanical properties of CPs. By integrating various multiscale modeling techniques, including QM, AA-MD, CG modeling, and ML, we provide a comprehensive understanding of how these properties can be optimized for flexible electronics and optoelectronic applications. Our goal is to present a multiscale modeling framework to enable fundamental understanding of the molecular mechanisms underlying CP functional behaviors, thereby offering valuable guidance for future research, design and development of advanced CP-based materials and devices. This review is organized as follows: Section 2 covers the models and methods used in our simulations, including DFT calculations, AA-MD, CG modeling, and data-driven ML approaches. Section 3 discusses the results and insights gained from these simulations, focusing on optoelectronic properties, chain conformation in solution, T_g, and mechanical properties. Finally, Section 4 concludes with a summary of our findings and perspectives on future research directions in the field of CP-based materials.

2. Models and methods

2.1 Density functional theory (DFT) calculations

To gain deeper theoretical insights at the atomistic and molecular levels, QM-based calculations of the electrical structure and optical characteristics of CPs have been extensively conducted using first-principles techniques. Notably, the Hartree–Fock (HF) technique⁴² and density functional theory (DFT)⁴³ have been employed to explore the electrical properties, charge transport kinetics, and optoelectronic features of these materials. These methods are often used to analyze the ground-state and excited-state electronic properties, band structures, band gaps, absorption spectra, and the effects of charge-carrier injection. Additionally, advanced quantum chemical methods such as the GW and mean field Hubbard models have been employed to provide detailed insights into the electronic structure of polymers.⁴⁴ DFT calculations solve the self-consistent equations of DFT within a fictitious one-electron Kohn–Sham (KS) framework and typically show good agreement with experimental data.³⁵ In simulation models, to manage computational costs while retaining accuracy, long alkyl chains are sometimes replaced with methyl groups, as charge transport primarily occurs along the polymer backbone. Geometry optimizations are typically conducted either in the gas phase without symmetry constraints or using a periodic model of an isolated polymer chain with one-dimensional periodicity along the backbone to avoid finite chain-length effects.^45,46

In our rencent DFT studies, periodic polymer chains were optimized using semi-local Perdew–Burke–Ernzerhof (PBE) functional,⁴⁷ and the projector-augmented wave (PAW)⁴⁸ to get the chain conformation into the ground state. The kinetic energy threshold was set to 400 eV. For geometry optimization, Gamma-centered 1 × 1 × 1 k-points were employed to balance computational efficiency with accuracy, given the large unit cell size (>15 Å). However, for subsequent electronic structure calculations, which are crucial for capturing the delocalized nature of CPs, we increased the k-point sampling to 16 k-points along the polymer backbone direction. This two-step approach allowed us to efficiently optimize the geometry while ensuring a more comprehensive sampling of the Brillouin zone for accurate electronic property predictions. Atomic positions were optimized using the conjugate gradient method with energy and force tolerance of 10⁻⁶ eV and 0.01 eV Å⁻¹, respectively. Then, the electronic structure was accurately calculated using the Hartree–Fock/DFT HSE06 hybrid functional.⁴⁹ Hybrid functionals are a class of approximations to the exchange–correlation energy functional in DFT that incorporate a portion of exact exchange from Hartree–Fock (HF) theory with DFT exchange and correlation. This scheme improves the accuracy of calculated molecular properties, including atomization energies, bond lengths, and vibrational frequencies, compared to pure DFT functionals. Also, the inclusion of exact exchange helps to correct the self-interaction error inherent in pure DFT functionals and improves the description of electronic localization, which is crucial for accurately predicting band gaps and electronic structures. The Heyd–Scuseria–Ernzerhof (HSE) functional, a widely used hybrid functional, employs a range-separated approach. It includes a fraction of exact Fock exchange at short range, while using pure DFT exchange at long range. The HSE exchange–correlation functional:

E^HSE_xc = αE^HF,SR_x(ω) + (1 − α)E^PBE,SR_x(ω) + E^PBE,LR_x(ω) + E^PBE_c

where α is the fraction of exact exchange, and ω is an adjustable parameter controlling the short-rangeness of the interaction. For the used HSE06, α = 1/4, and ω = 0.2. The short-range Fock exchange E^HF,SR_x(ω) is calculated as:

The long-range and remaining short-range exchange is determined from the exchange-hole formulation of PBE functionals.

All periodic structures were simulated using Vienna Ab initio Simulation Package (VASP).^50,51 While non-periodic models were simulated with the Becke's three-parameter functional B3LYP⁵² and the augmented correlation consistent triple-zeta basis set (aug-cc-pVTZ),⁵³ using Gaussian16 software package.⁵⁴ Also, the time-dependent DFT (TD-DFT) simulation were used to predict the excited states, the excitation energies and the maximal absorption wavelength. While these are commercial packages, there are several open-source alternatives available that researchers could consider, such as Quantum ESPRESSO or SIESTA, NWChem or Psi4, ABINIT, CP2K.

To study the impact of charge injection on the electrical configuration of polymers, different configurations with varying numbers of electrons were considered. The solution of the electronic structure and total energy depends on the number of electrons.⁵⁵ For the negatively charged system, DFT calculations were performed on a model with two additional electrons, while for the positively charged system (hole-injected DFT model), the model includes two fewer electrons.⁴⁵ The occupancy of molecular orbitals in the DFT periodic models was modified to simulate the promotion of electronic population from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO). This modification reflects a change in the population pattern for Kohn–Sham (KS) orbitals while maintaining a closed-shell and singlet spin configuration.

2.2 All-atomistic (AA) modeling of CPs

2.2.1 AA-MD simulations in solution states. In our recent MD studies, the initial configuration of the atomistic models for the CPs was constructed using the Materials Studio platform. The simulations utilized the general Dreiding force field, which describes all bonded (stretching, bending, and torsional) and non-bonded interactions between atoms.^56,57 This force field was chosen for its simplicity and wide applicability in studying both crystalline and amorphous phases of CPs.^58,59 To fully characterize conformational changes in dilute solution, single polymer chains were modeled, considering interactions between the polymer chain and solvent implicitly. The Lennard-Jones interaction potential was truncated and shifted to zero at r_cut = 2^1/6σ, making atom-atom interactions purely repulsive to mimic good solvent conditions, consistent with previously investigated CPs.^46,60 Electrostatic contributions were computed using the Coulombic pairwise interaction. Each polymer chain was inserted into a cubic simulation cell with dimensions significantly larger than the initial chain length. Systems were first equilibrated for 1 ns under a canonical (NVT) ensemble using a Nosé–Hoover thermostat with a damping time constant of 50 fs, applying periodic boundary conditions in all three directions with a time step of 1 fs. Following equilibration, the simulations underwent a 100 ns production run in the NVT ensemble, with data collected every 20 ps to adequately sample configurational trajectories. Six independent initial configurations were generated for each system to ensure adequate sampling and to determine averaged properties with standard deviations. All MD simulations were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS)⁶¹ software package, and atomic configurations were visualized using visual molecular dynamics (VMD) software.⁶²

2.2.2 AA-MD simulations in bulk states. Accurately modeling the thermomechanical behavior of CPs in bulk states involves detailed AA-MD simulations using specialized force fields. For the AA simulations of regio-regular poly(3-hexylthiophene) (P3HT), the Dreiding force field was employed. The initial configurations were created with the Materials Studio platform, including single P3HT chains and liquid monomer bulk systems to sample bonded and non-bonded interactions. Following energy minimization with the conjugate gradient algorithm, the system was equilibrated in the melt state at high temperatures under the isothermal–isobaric (NPT) ensemble, followed by cooling to the target temperature for sampling. Periodic boundary conditions were applied to simulate bulk behavior with an integration timestep of 1 fs, ensuring precise modeling of molecular interactions and conformations observed experimentally.⁵⁹

Additionally, the general amber force field (GAFF) was used to predict the T_g of various CPs. Initially, CP models were built and optimized, followed by atom typing and charge calculation. The bulk systems underwent equilibration under the NPT ensemble at the melt state and subsequent cooling to the target temperature. To determine T_g, the density as a function of temperature was analyzed, fitting linear lines at low-T glassy and high-T melt regimes to identify the intersection marking T_g. The AA-MD simulations further unraveled the fundamental roles of chemical building blocks in dynamical heterogeneity and local mobility of CPs. By measuring the mean-squared displacement (MSD), these measurements provided critical insights into the molecular interactions and segmental mobility that influence the mechanical performance and thermal stability of CPs.⁶³

2.3 Coarse-grained (CG) modeling of CPs

2.3.1 Generic CG modeling. Generic CG modeling provides computationally efficient approach to study the mechanical and conformational properties of CPs by simplifying complex atomistic details into larger interaction sites, or beads. This approach enables simulations of larger systems over longer timescales while maintaining the essential physical behaviors of polymers, without requiring detailed chemical specificity. Generic CG models qualitatively represent more than one type or class of materials by using simplified representations of molecules. The polymer's backbone and side-chains are typically represented by beads connected via harmonic springs to mimic bond stretching, angle bending, and torsional motions. The non-bonded interactions between these beads are described using the Lennard-Jones (LJ) potential, which effectively captures van der Waals forces. The parameters of these potentials are expressed in reduced LJ units, facilitating the study of general trends and mechanisms across different systems.⁶⁴

Simulations based on the generic CG models have been effectively employed to investigate the effect of temperature, solvent quality, and chain length on the mechanical properties and chain conformation of CPs.^34,65–68 These models simplify the representation of complex polymer architectures, allowing for detailed analysis of how side-chain length and bending rigidity influence properties such as Young's modulus, tensile strength, and ductility. The results from these simulations align well with experimental observations, providing valuable insights into the orientation and alignment of polymer chains under mechanical stress.

2.3.2 Chemistry-specific CG modeling. To achieve a more detailed understanding of CP behavior, chemistry-specific CG models are developed by systematically coarse-graining from AA models. This approach retains chemical specificity by preserving critical molecular interactions and conformations observed in AA simulations. The energy renormalization (ER) method was often employed to derive CG potentials that accurately reproduce AA simulation data, ensuring that the CG model captures the essential physics of the polymer system.^69,70 The process begins with the construction of an initial AA configuration, typically using a force field such as Dreiding or GAFF to describe bonded (bond, angle, dihedral) and non-bonded interactions. The chemistry-specific CG model was then parameterized by matching the bonded and non-bonded probability distributions from the AA simulations. This involves calculating bonded parameters (bond lengths, angles, and dihedrals) and non-bonded interactions (radial distribution functions) from the AA trajectories and fitting them to the CG potentials.

The ER approach adjusts the cohesive interaction strength and effective interaction length-scale parameters to correct deviations in activation free energies that occur upon coarse-graining. This method allows the CG model to reflect the dynamics and structural properties of the CPs accurately. By employing the ER method, the CG models maintain fidelity to the original AA model, ensuring that essential interactions and behaviors are preserved even as the model is simplified. Additionally, the ER approach allows for the creation of temperature-transferable CG models, ensuring accurate simulations across a broad range of temperatures.⁵⁹ MD simulations using these models unravel the roles of chemical building blocks in dynamical heterogeneity and local mobility of CPs, providing crucial insights for designing CP-based materials for flexible electronics and other high-performance applications.

2.4 Data-driven modeling for T_g prediction of CPs

The integration of data-driven modeling based on machine learning (ML) with MD simulations and experimental measurements provided a robust framework for predicting the T_g of CPs. This hybrid approach leveraged the strengths of each method to enhance the accuracy and reliability of T_g predictions based on chemical structure.

In this ML framework, ordinary least squares (OLS) multiple linear regression was employed to correlate the geometry of six key chemical building blocks—side-chain fraction, isolated rings, fused rings, bridged rings, halogenated atoms, and double/triple bonds—with T_g values. This model was trained on a diverse dataset comprising T_g data points from literature, experimental measurements, and MD simulations. By doing so, the ML model effectively captured the influence of these chemical features on T_g, offering a powerful predictive tool for material scientists. The dataset used in training the ML model included 154 T_g data points, allowing for the identification of patterns and relationships between chemical structure and thermal properties. The ML predictions were validated through both MD simulations and experimental techniques such as quasi-elastic neutron scattering (QENS). These validations ensured the reliability of the ML model and provided deeper insights into the segmental dynamics and local mobility of CPs.⁶³

The practical application of this ML framework was demonstrated through the accurate prediction of T_g for several high-performance CPs used in organic solar cells, such as poly[(2,6-(4,8-bis(5-(2-ethylhexyl-3-fluoro)thiophen-2-yl)-benzo[1,2-b:4,5-b0]dithiophene))-alt-(5,5-(10,30-di-2-thienyl-50,70-bis(2ethylhexyl)benzo[10,20-c:40,50-c0]dithiophene-4,8-dione))] (PM6), poly[(2,6-(4,8-bis(5-(2-ethylhexyl-3-chlore)thiophen-2-yl)-benzo[1,2-b:4,5-b0]dithiophene))-alt-(5,5-(10,30-di-2-thienyl-50,70-bis(2ethylhexyl)benzo[10,20-c:40,50-c0]dithiophene-4,8-dione))] (PM7), and PTB7 polymers. The predicted T_g values aligned closely with experimental measurements, underscoring the effectiveness of the ML approach. This predictive capability was crucial for developing CP materials with optimized thermal and mechanical properties, addressing challenges in creating stable and efficient organic electronics. Recent advancements in ML have further enhanced the prediction of electronic structures, as demonstrated by a study on polycyclic aromatic hydrocarbons (PAHs) which used guided diffusion methods for inverse molecular design, achieving accurate predictions of electronic properties.⁷¹

3. Results and discussion

3.1 Optoelectronic properties

3.1.1 First-principles studies of electronic structure and optical properties. The investigation of electronic structure and optical properties is crucial for understanding the optoelectronic performance of CPs. Alesadi et al. employed DFT to explore the effects of charge injection on the optical properties and conductivity of a diketopyrrolopyrrole (DPP)-based conjugated semiconducting polymer, PDPP3T (Fig. 2(g)).⁴⁵ Specifically, they simulated n-type (Fig. 2(b)) and p-type (Fig. 2(c)) doping through charge-carrier injection, analyzing its impact on the polymer's electronic configuration. Additionally, they examined the triplet state of the polymer model to gain insights into the excitation mechanisms of these semiconductors (Fig. 2(d)). The research focused on the response of the polymer's geometry to electronic excitation, specifically nuclear reorganization induced by promoting electrons from the HOMO to LUMO (Fig. 2(e)). This reorganization significantly influences the band gap of the polymer. The findings revealed that charge carrier injection in PDPP3T semiconducting polymers substantially affects their electronic properties, resulting in a reduced band gap and enhanced charge carrier mobility. This study suggests that manipulating charge injection could be a potent strategy to tailor the electronic performance of conjugated polymers for various technological applications. In another study, Pavlak et al. explored zinc porphene, a 2D material.⁷² They revealed its semiconductive nature, attributed to a Peierls distortion, which was accurately modeled using hybrid functionals like PBE38. This emphasizes the importance of precise electronic structure modeling. Both Alesadi and Pavlak studies highlight how structural distortions can tune electronic properties, demonstrating the broader applicability of these concepts for understanding and enhancing materials for molecular electronics and spintronics.

Fig. 2 (a) Schematic of the ground-state energy band and absorption spectra. (b) Schema of the energy band and absorption spectra due to negative type doping (electron donors). (c) Schema of the energy band and absorption spectra due to positive type doping (electron acceptors). (d) Schema of the spin polarization process and corresponding absorption spectra. (e) Portrayal of change of geometry due to excitation and optimized geometry after the excitation. (f) Schematic representation of a band structure with k-points sampling and corresponding absorption spectrum. Here, E_g, E_F, E_σ, and E_Δσ represents band gap energy, Fermi energy, and band energy gap of the excited state, respectively. (g) Top panel is the geometry-optimized structure (ground state) of the polymer model aligned in the y–z plane. Cyan, blue, gray, yellow, and red spheres represent C, N, H, S, and O atoms, respectively. Bottom panel is schematic chemical structure of the PDPP CP model employed in the simulations. Figures adapted from ref. 45 (copyright 2021 American Chemical Society). (h) HOMO for DPP:PCBM. (i) LUMO for DPP:PCBM. Shaded areas indicate the electron density. Calculations are performed via HSE06 functionals. (j) and (k) Charge carrier dynamics of the DPP:PCBM blend upon photoexcitation for three representative initial transitions which possess higher oscillator strength; HO−3 → LU+2. For all initial transitions, both excited electron and hole are located on PCBM. (j) indicates the distribution of charge as a function of energy and time, dashed and solid lines indicate expectation values for energy, calculated in an energy space distribution for conduction and valence bands, respectively. (k) represents charge density distribution as a function of time and position in the space. Electrons, equilibrium distribution, and holes are represented in yellow, green, and blue, respectively, where the offset between solid and dashed lines corresponds to the electric dipole. Figures adapted from ref. 73 (copyright 2022 American Chemical Society). (l) Top-left panel: The mechanism of molecular orbital hybridization between alternating donor unit and acceptor moiety; top-right panel: energy alignment of NDI-nT polymers; bottom panel: orbital energy alignment of DPP-nT polymers. (m) The dependence of band gap on bandwidth for DPP-nT (n = 1, 2, 3). Figures adapted from ref. 46 (copyright 2023 John Wiley and Sons). (n) Top panel: Repeating unit of a polymer chain showing the post-branching side-chain dihedral angles; bottom panel: values calculated for the dihedral angles (in degrees). (o) Schematic definition of the dihedral angles between thiophene–thiophene (ϕ_T–T) units, and isoindigo–thiophene (ϕ_I–T) units and isoindigo–isoindigo (ϕ_I–I) units. (p) DFT calculated UV-vis spectrum of IID-T2-C2C10C10 backbone with twisted T–T dihedral angles. (q) Dihedral potential for a IID-based trimer. (r) DFT calculated averaged dihedral angles ϕ_T–T and ϕ_I–T of IID-based polymers. Figures adapted from ref. 60 (copyright 2023 Royal Society of Chemistry).

In a related study, Alesadi et al. used ab initio molecular dynamics simulations to investigate photo-induced charge transfer (CT) between a diketopyrrolopyrrole-based polymer donor and two different acceptor units: non-fullerene ITIC (forming a DPP:ITIC blend) and fullerene PCBM (forming a DPP:PCBM blend).⁷³ The study employed HSE06 functionals to calculate the HOMO and LUMO orbitals for DPP:PCBM, with electron density indicated in the shaded areas (Fig. 2(h) and (i)). They analyzed representative charge carrier dynamics upon photoexcitation for specific initial electronic transitions at the blend interface with zero external electric fields. The distribution of charge as a function of energy and time is shown in Fig. 2(j), while Fig. 2(k) represents charge density distribution as a function of time and spatial position. The results demonstrated that the spatial redistribution of hole density occurs much faster than electron relaxation. At the end of the relaxation process, the hot electron relaxes on the PCBM acceptor unit, and the hot hole remains on the backbone of the DPP model. Comparing the two blends, the CT rate calculations indicated that the DPP:ITIC blend offers a better photovoltaic effect compared to the DPP:PCBM blend. This study introduced a potential computational approach to qualitatively characterize the CT performance of CP blends based on the difference between the transfer rates of electrons and holes over time. In another work, Chang et al. introduced a computationally efficient model using the effective Frenkel–Holstein (EFH) Hamiltonian to analyze donor–acceptor–donor (DAD) chromophore aggregates.⁷⁴ This model, which simplifies each chromophore to a two-level system with vibronic coupling, effectively captures the optical properties and spectral features of π-stacks with significant intermolecular charge transfer (ICT). The EFH model aligns well with experimental data from bithiophene-DPP (2T-DPP-2T) and is contrasted with other models like the essential states model (ESM). The study highlights how ICT and Coulomb coupling affect optical behavior and suggests further investigation in near-resonance regimes using more robust models.

3.1.2 Influences of segmental structures on electronic configuration and single-chain conformation. DFT calculations have been instrumental in providing critical insights into the optoelectronic properties of CPs by elucidating how the length of oligothiophene units influences the optical properties and single-chain conformation of DPP-based and NDI-based polymers.⁴⁶ DFT calculations were performed to explore the electronic features with increasing numbers of thiophene units in DPP-nT and NDI-nT polymers, aiming to understand the role of thiophene length in band gap modulation (Fig. 2(l)). Several acceptor units were analyzed to calculate their molecular orbital energy alignments, shedding light on the observed trends in conjugated polymer bandgap modulation as a function of structural modifications that highlight the role of orbital energy alignment type in determining the optoelectronic properties of D–A conjugated polymers.⁷⁵ The DFT results revealed significant differences in the nature of the orbital energy alignment between the two polymer types. For DPP-based polymers, the orbital energy alignment exhibits a sandwich-type configuration, leading to an increased band gap with longer oligothiophene chains due to bandwidth reduction (Fig. 2(m)). This reduction arises from a more localized charge density distribution and increased chain flexibility with intrachain twisting. Conversely, in NDI-based polymers, the staggered-type orbital energy alignment allows the introduction of additional thiophene units to create a new hybridized higher HOMO level, which narrows the optical band gap despite the decreased chain rigidity. This contrast highlights the critical role of orbital energy alignment in determining the optoelectronic properties of donor–acceptor CPs.

In another study, the effect of chain conformation on the optical properties of donor–acceptor CPs was investigated.⁶⁰ Specifically, chain rigidity (Fig. 2(q)), coplanarity of the polymer backbone, side-chain length, and branch points were analyzed. The study revealed the critical role of side-chain length and branch points in optical absorption, attributed to steric effects. DFT calculations demonstrated that variations in backbone planarity significantly impact optical absorption (Fig. 2(p)), with blue shifts correlating to less planar backbones. Additionally, the optical shift for IID-based polymers, which changed according to an odd–even effect of the branching point, was ascribed to changes in backbone coplanarity induced by steric hindrance from the side chains (Fig. 2(n)). Geometry-optimized structures from DFT calculations indicated that even branching positions cause the backbone to adopt a more twisted conformation, as shown in Fig. 2(r). Furthermore, DFT calculations showed that, despite their rigidity, the backbones of DPP-based and IID-based polymers are not fully planar, and their observed optical absorption shifts can be explained by local distortions in the backbone structure.⁶⁰ These DFT studies highlight the significance of single-chain conformation in determining the optoelectronic properties of CPs. By providing detailed insights into molecular interactions and conformational changes, DFT enables the rational design of CPs with optimized properties for specific optoelectronic applications.

3.2 Chain conformation in solution

3.2.1 Effects of side-chain and backbone configurations. The single-chain conformation of D–A CPs is significantly influenced by both side-chain lengths and backbone configurations, which in turn impact their optoelectronic properties. AA-MD simulations have provided detailed insights into how these molecular structures affect polymer behavior in solution. Two groups of polymers were purposefully designed to explore the influence of the side-chain and backbone structure on the single-chain conformation of DPP-based polymers (as shown in Fig. 3(a)). A 60-monomer long polymer chain model was built and simulated, considering interactions between the polymer chain and solvent implicitly, to examine the isolated-chain conformations. As illustrated in Fig. 3(b), a wave-like extended coil molecular conformation for the DPP polymer chain was observed due to flexible yet highly correlated dihedrals at various positions, demonstrating the expected behavior in a good solvent.⁷⁶ Further investigation into the trans and cis conformations along the polymer backbone revealed that trans conformations promoted a more rigid backbone structure, while cis conformations introduced flexibility. Trans conformations were associated with a more extended chain structure, contributing to higher rigidity and potentially better charge transport properties. Conversely, cis conformations, by introducing kinks and flexibility, could impact the polymer's packing and morphology, influencing its electronic performance. The simulations on DPP-based polymers with varied side-chain lengths revealed that longer side-chains led to a more rigid polymer backbone. This increased rigidity was indicated by the increased persistence length (l_p) (Fig. 3(e)) and was attributed to the reduced population of cis conformations that introduce kinks in the backbone (Fig. 3(f)). Based on DFT calculations, Fig. 3(g) shows that as the side-chain length increases, the polymer backbone becomes more twisted, indicated by the decrease in the dihedral angle ϕ_D–T from 162° to 152°. Small-angle neutron scattering (SANS) measurements supported these findings, showing a consistent increase in chain rigidity with longer side-chains.⁶⁰

Fig. 3 AA-MD simulation of single chain conformation. (a) Structure of DPP-based polymers with different side-chain lengths and varied numbers of thiophenes. (b) A snapshot of a DPP-T polymer chain simulated in a solution state. (zoom view) The enlarged inset shows the two planar conformations: trans and cis conformations for cv with different oligothiophene length. (c) Schematic definition of the dihedral angles between thiophene–thiophene units (ϕ_T–T) and DPP–thiophene units (ϕ_D–T). (d) Schematic definition of the bending angle. Grey beads denote the center-of-mass of each functional group. (e) l_p of DPP-based polymers with varied side-chain length from MD simulation. (f) Thiophene–thiophene dihedral angle distributions from AA-MD simulation. (g) DFT calculated averaged ϕ_T–T and ϕ_D–T. (h) l_p values for DPP-nT polymers with varied donor length from MD simulation. (i) Thiophene–thiophene dihedral angle distributions for DPP-nT polymers. (j) Dihedral angle between adjacent DPP cores for DPP-nT polymers. Inset shows the graphical definition of the dihedral angle between adjacent DPP cores (ϕ_D–D). Figures adapted from ref. 46 (copyright 2023 John Wiley and Sons) and ref. 60 (copyright 2023 Royal Society of Chemistry).

The backbone configuration also played a crucial role in determining chain conformation. Polymers with different backbone units exhibited distinct conformational behaviors due to varying steric hindrance and electronic effects. DPP-based polymers with longer oligothiophene units demonstrated decreased l_p (Fig. 3(h)), indicating a more flexible backbone. Longer oligothiophene units increased the population of cis conformations (Fig. 3(i)), which reduces steric hindrance and lowers l_p. Additionally, co-planar conformation between DPP cores is less favorable with increasing oligothiophene length (Fig. 3(j)), highlighting that the increased conformational freedom of longer thiophene units reduced overall chain rigidity.⁴⁶

Polymer chain conformation directly impacts optoelectronic properties. Experimental observations showed that longer side-chains lead to blue shifts in optical absorption spectra due to less planar backbone conformations.⁶⁰ Backbone structure also affects optoelectronic properties; longer oligothiophene units reduce conjugation length and alter optical absorption characteristics.⁴⁶ This alignment between AA-MD simulations and experiments underscores the importance of simulations in understanding molecular mechanisms behind optoelectronic behavior and highlights the need to carefully design side-chains and backbone structures to optimize CP-based devices.

3.2.2 Effects of solvent quality and side-chain architecture. Various solvents and solvent mixtures have been used to dissolve and process CPs,^77–79 but few studies have quantified the effect of solvent quality on the solution behavior of CPs. The impact of solvent quality and side-chain architecture on the conformation of CP chains in solution was examined using a generic CG model (Fig. 4(a) and (b)), providing valuable insights into their behavior under various conditions.

Fig. 4 (a) Schematic illustration of CG polymer model with branched side-chain, where N_bb and N_sc are the numbers of segments in the backbone and each side-chain, respectively. (b) Snapshot of a single polymer chain simulated in a solution state. (c) Evolution of persistence length L_p of the polymer chain as a function of the temperature under two distinct solvent conditions. Influence of side-chain on the location of the θ point. Normalized squared radius of gyration R_g²/(N − 1) as a function of solvent quality parameter λ for different scenarios: (d) side-chain length N_sc = 4, (e) comparison of whole chain and backbone for N_sc = 4, (f) N_sc = 3, with N_bb representing the number of monomers in each polymer chain. The location of the θ point is indicated by the black dashed line. (g) Molecular mass dependence of R_g for solvent qualities ranging from an ideal good solvent (λ = 0), θ solvent (λ = λ_θ), to a poor solvent (λ = 1). (h) Snapshot of a CP simulated using the CG model in a solution state, where schematic cylinders denote a chain of effective persistence length of segments L_{p,whole chain} and cross-sectional radius of R. (i) Comparison of the L_p between the backbone alone and the overall polymer chain. All L_p values are reported in reduced LJ units. Figures adapted from ref. 68 (copyright 2023 John Wiley and Sons) and ref. 80 (copyright 2020 American Chemical Society).

Higher temperatures and good solvents significantly impact polymer chain conformation in similar ways, both promoting extended polymer configurations. Conversely, lower temperatures and poor solvents lead to chain aggregation. As temperature increases, polymer chains become more flexible, resulting in a decrease in persistence length L_p. At lower temperatures, chains in poor solvents exhibit significant aggregation, but as temperature rises, chains show slight extension, though L_p remains low compared to good solvents (Fig. 4(c)).⁶⁸ The solvent quality parameter (λ) was adopted to describe the interaction between polymer and solvent, where a higher λ indicates a poorer solvent, enabling tuning of “solvent quality” by varying λ between particles.^81,82 In good solvents, chains exhibit increased radius of gyration (R_g) and L_p, indicating a more extended conformation. As the λ increases, indicating worse solvent quality, the R_g diminishes, reflecting the gradual compaction of the polymer coil within the solution. When λ exceeds a certain threshold, the polymer chain collapses into a compact conformation, demonstrating the impact of solvent quality on polymer chain behavior (Fig. 4(d)). For a more comprehensive analysis, R_g was calculated for both the entire polymer chain and the backbone alone, exhibiting a consistent decreasing trend (as shown in Fig. 4(e)). However, the difference in R_g between the entire chain and the backbone becomes more pronounced for shorter chain lengths, while for longer chains, the presence of side-chains has a relatively minor impact on the polymer size. Moreover, the parameter λ_θ, marking the θ solvent condition where the polymer transitions from a good solvent to a poor solvent, is defined by the crossover point where curves from different molecular masses intersect (Fig. 4(d)). Side-chain length significantly impacts λ_θ, with longer side-chains improving solubility and delaying the transition to poorer solvent conditions (Fig. 4(f)).⁶⁸ Side-chain architecture also affects λ_θ, suggesting that CPs with long, dense, and branched side-chains can achieve enhanced polymer–solvent interaction, thus enabling overall better solution dispersion.⁶⁷ These conclusions were corroborated by experimental observations, which demonstrated that side-chain modifications could significantly enhance polymer–solvent interactions, showing that polymers with longer and branched side-chains exhibited better solubility, less aggregation, and maintained extended chain conformations even in poorer solvents.⁶⁷

Additionally, the mass scaling exponent ν, defined by the power-law relationship R_g ∝ N^ν_bb, serves as a fundamental structural measure of polymer size. A higher ν suggests that the polymer expands more rapidly as it grows, while a lower ν indicates that the polymer remains relatively compact even as its length increases. The scaling exponent ν was systematically investigated under different solvent conditions (as shown in Fig. 4(g)). In good solvents, ν approximates 0.62 and remains nearly constant across varying side-chain lengths. However, in θ solvents, distinct variations in ν were observed with different side-chain lengths, showing greater sensitivity to changes in solvent quality. These findings underscore the significant influence of side-chain length and solvent quality on the scaling behavior of polymer chains in dilute solutions, emphasizing the robustness of ν as a structural descriptor in polymer science.

3.2.3 Effects of backbone rigidity. The backbone rigidity of CPs is crucial for determining their chain conformation, significantly impacting their optoelectronic properties and solution behavior. Experimental techniques such as small-angle neutron scattering (SANS) and selective deuteration have been employed to decouple the scattering contributions from CPs’ backbone and side-chains.⁸⁰ This methodology elucidates the inherent conformation of the electronically active conjugated backbone, highlighting how backbone rigidity affects electron delocalization along the chain, which is essential for optimizing the performance of CPs in optoelectronic applications. Additionally, recent studies have shown that backbone planarity can be improved by adsorption on specific surfaces, such as the adsorption of dinitrosobenzene polymer on a gold surface, which significantly narrows the band gap due to enhanced backbone planarity, as evidenced by spectroscopic ellipsometry measurements.⁸³

To explore the impact of backbone rigidity on chain conformation, CG-MD simulations were employed, offering a detailed examination of the structural properties of CPs by varying the stiffness of the polymer backbone. The stiffness of the backbone was controlled through an angular stiffness constant (k_θ) parameter, allowing the simulation of different degrees of rigidity. The CG-MD simulations revealed several key insights. Increasing backbone rigidity led to a more extended chain conformation. Specifically, for polymers with flexible backbones, the overall chain conformation, including both the backbone and side-chains, exhibited a significant increase in rigidity compared to the backbone alone (as shown in Fig. 4(h)). This was evident from the L_p measurements, which showed that the L_p of the backbone alone was significantly smaller than that of the entire chain contour. By employing a center of geometry (COG) assumption, the effective persistence length of the entire CP contour was calculated, accounting for the influence of side-chains. This approach demonstrated that the presence of side-chains significantly affects the overall chain rigidity, especially for polymers with flexible backbones.⁸⁰ As the backbone stiffness increased, the difference between the L_p of the backbone and the overall chain diminished, eventually resulting in an almost linear, rod-like configuration for the most rigid polymers (Fig. 4(i)). For semi-rigid and highly rigid backbones, the impact of side-chains on the overall chain conformation was reduced, aligning closely with experimental observations. These findings highlight the importance of considering both backbone and side-chain effects when designing CPs for specific applications, providing quantitative insights into the solution behavior of CPs and guiding the design and processing of CPs toward next-generation organic electronics.

3.3 Glass transition temperature (T_g)

3.3.1 CG modeling of effects of side-chain on T_g. The glass transition temperature (T_g) is crucial for determining the thermal and mechanical performance of CPs, especially in organic electronics where thermal stability directly impacts device performance and longevity. Experimental studies indicate that the side-chain length and structure significantly influence T_g, with longer alkyl side-chains decreasing T_g due to increased chain flexibility and reduced intermolecular interactions.^66,84 This underscores the importance of side-chain engineering in tuning the thermal properties of CPs for optimal performance.

To verify the experimental results and gain more insights, CG-MD simulations were employed to probe how side-chain length (M) and grafting density (f) influence mechanical properties and T_g.⁶⁶ A generic bead-spring CG model was used to preserve the essential structural features of the D–A CPs (Fig. 5(a)). Specifically, the CG model of each CP consists of a linear backbone chain, a side-chain branching site, and side-chains representing alkyl groups. These simulations revealed that increasing the side-chain length significantly decreased the T_g of the bulk polymers. For polymer models with a side-chain length (M) greater than three, T_g tended to plateau, indicating a reduced rate of decrease with further increases in side-chain length (Fig. 5(a)). These simulation results were consistent with experimental findings, demonstrating that longer side-chain lengths lead to a greater reduction in T_g. To further explore the influence of the side-chain group on bulk properties, the Debye–Waller factor 〈u²〉 was calculated, which measures local free volume and segmental mobility.^85,86 The simulations indicated that larger side-chain lengths exhibited higher mean-squared displacement (MSD) values, reflecting enhanced chain mobility. As the fraction of side-chain beads in the bulk polymer model increases, either by increasing side-chain length (M) or grafting density (f), 〈u²〉 also increases (as shown in Fig. 5(a)). This suggests a greater local free volume associated with segmental mobility, which significantly influences T_g. The simulation results highlight that the structure of side-chain groups is a critical parameter for controlling the T_g and mechanical properties of D–A CPs.

Fig. 5 (a) Computational molecular model of PDPPT-based polymers. Representative geometrical configuration of simulated polymers with branched side-chains. The backbone of all chains is composed of 20 CG beads (shown in gray). M represents the number of CG beads for each branched side-chain (shown in cyan). f represents the grafting density (the branching position is shown in purple). A snapshot of bulk CG polymer system. T_gversus side-chain length M for six polymers with different grafting densities f. Debye–Waller factor 〈u²〉 versus side-chain length M for polymers with different grafting densities f. Figure adapted from ref. 66 (copyright 2020 John Wiley and Sons). (b) Bulk CG of polymer with random cleaved side-chains. Representative configuration of simulated polymers with cleaved branch side-chains. Snapshot of the bulk CG polymer system. The variation of T_g as a function of the degree of cleavage ω for constant cohesive interaction strength ε₂ (red color) and variant cohesive interaction strength ε₂ (blue color). Inset shows the function of constant ε₂ and variant ε₂. Figure adapted from ref. 87 (copyright 2022 John Wiley and Sons). (c) Machine learning model. Flow chart of the integrated machine learning framework, molecular dynamics simulations, and experimental techniques to predict T_g of conjugated polymers. Figure adapted from ref. 63 (copyright 2022 Elsevier).

Building on the insights gained from examining how side-chain length affects T_g, it is equally crucial to understand the impact of side-chain cleavage. Experimental studies have demonstrated that flexible side-chains possess much faster dynamics, and the cleavage of these side-chains reduces chain dynamics, leading to a higher T_g. Controlled side-chain cleavage in polythiophenes, for instance, revealed that removing more than 95% of alkyl side-chains at 140 °C significantly raised the backbone T_g from 23 °C to 75 °C.⁸⁷ This increase in T_g was attributed to the specific interchain interactions between the residual carbonyl groups in ester groups and the hydroxyl groups of newly formed carboxylic groups. To gain deeper insights and verify experimental results, CG-MD simulations were employed to study the T_g dependence on side-chain cleavage. These simulations examined the structural properties and molecular dynamics by varying the degree of side-chain cleavage. The CG model represented the polymer backbone and side-chains, where side-chain segments were selectively removed to mimic thermal cleavage (Fig. 5(b)). The simulations revealed that increasing side-chain cleavage significantly increased T_g, agreeing well with experimental findings. The reduction of flexible side-chains was found to enhance the thermal stability of CPs by decreasing chain dynamics. The T_g enhancement trend was found to be governed by specific interchain interactions, which were captured at the molecular level.

These findings underscore the importance of considering both side-chain length and side-chain cleavage in designing CPs for specific applications, highlighting the consistency between simulation and experimental results. Such a comprehensive understanding of side-chain effects on T_g is crucial for guiding the development and processing of CPs toward next-generation organic electronics.

3.3.2 Machine learning predictions of T_g from chemical structure. Designing and predicting the T_g for CPs remains a significant challenge due to the complex architecture and diverse chemical building blocks of these materials. This complexity necessitates advanced predictive approaches to facilitate the design of new materials with desired thermal properties. To address this challenge, a predictive modeling framework was developed by integrating machine learning (ML), MD simulations, and experimental data (as shown in Fig. 5(c)).⁶³ This integrated approach aims to accurately predict the T_g of CPs, facilitating the design of new materials with desired thermal properties.

The foundation of this framework lies in the construction of an ML model using a dataset of 154 T_g values collected from both literature and experimental measurements. Simplified molecular features derived from the chemical structure of the repeat units of CPs were used to develop the model. Six key structural features were identified as the most influential: side-chain fraction, isolated rings, fused rings, bridged rings, halogenated atoms, and double/triple bonds. These features formed the basis of a multiple linear regression model, which demonstrated strong predictive capability for diverse CPs. To enhance the model's accuracy, MD simulations provided deeper insights into the role of these chemical building blocks. The simulations revealed the influence of side-chains and aromatic rings on the dynamic heterogeneity and local mobility of CPs, corroborating the ML model's predictions. By capturing the molecular-level interactions and chain dynamics, the MD simulations offered a detailed understanding of how these structural features govern T_g. This integration of ML predictions and MD insights underscores the robustness of the predictive framework.

Additionally, the integrated approach included dynamic mechanical analysis (DMA), differential scanning calorimetry (DSC) experiments, and quasi-elastic neutron scattering on CPs to improve dataset diversity and validate model predictions.⁶³ This comprehensive method highlighted that T_g is strongly governed by the chemical structure of key building blocks of CPs. Recent studies have demonstrated the use of ML for predicting the T_g of polymers, achieving significant accuracy improvements and emphasizing the importance of diverse datasets and robust feature selection.^40,88 The practical application of this combined ML and MD approach was demonstrated through accurate T_g predictions for high-performance CPs used in organic solar cells, such as PM6 and PTB7. These predictions closely aligned with experimental measurements, showcasing the model's capability to design CPs with tailored thermal properties. This integrated predictive framework underscores the importance of combining computational and experimental methods to achieve reliable material predictions.

3.4 Mechanical properties

3.4.1 Elastic and deformational behaviors of CP thin films. The mechanical properties of CPs are crucial for their application in flexible and wearable electronics. Traditionally, achieving high stretchability in CPs has focused on ensuring a low elastic modulus (E). However, recent studies have shown that the degree of entanglement, rather than softness alone, determines stretchability.⁶⁵ Experimental studies have highlighted that side-chain length and architecture significantly influence the mechanical behavior of CPs, affecting properties such as stress–strain response and E.³⁴ Understanding these structural influences is essential for designing CPs with both high mechanical performance and desirable electronic properties.

To complement the experimental investigations on thin film systems, CG-MD simulations were employed to study the mechanical behavior of CPs with varying side-chain lengths and structures (Fig. 6(a)). The simulations utilized a “bead-spring” model to capture essential structural characteristics, where a linear backbone chain with each backbone bead was connected to a side-chain to simulate the alkyl groups. In the CG-MD simulations, the elastic modulus (E) was analyzed as a function of temperature for the polymer thin film system, ranging from 0.7 T_g to 1.3 T_g (Fig. 6(b)). The results revealed a significant drop in E with increasing temperature, indicating that the material becomes less stiff as it approaches and surpasses the T_g. The inset of Fig. 6(b) illustrates the representative tensile stress–strain response of the polymer thin film at different temperatures, where E was determined by linearly fitting the stress–strain data within 3% strain, as marked by the dashed lines. These findings align well with experimental observations, demonstrating the validity of the simulation approach.⁶⁵

Fig. 6 (a) Snapshot of CG free-standing thin film. (b) Elastic modulus vs. T for polymer thin film system. Inset shows representative tensile stress–strain response of polymer thin film for different T, where the elastic modulus E was determined by linearly fitting the stress–strain data within 3% strain as marked by the dashed lines. (c) Average orientation parameter (left y-axis) and end-to-end distance (right y-axis) versus strain for two representative T. Inset shows the schematic of a single polymer chain with a defined angle between the bond orientation and tensile direction. CG-MD simulation results were expressed using the reduced LJ units. (d) Coarse-graining the all-atomistic (AA) model of P3HT to the CG model, illustrating the CG mapping scheme. The snapshot depicts a scratching test on polymer thin film, with the bottom 2 nm polymer layer treated as a rigid region (gray atoms), and the cone-shaped indenter also shown in gray. (e) Toughness (area under tensile stress curve to 250%) of P3HT with different M_w (or n) with the inset showing a snapshot of stretched P3HT thin films with different chain lengths at 135% strain. (f) Representative indentation curves of force vs. depth for P3HT thin film systems with 10 and 150 monomers per chain and with the inset showing the nanoindentation theoretical model. (g) Top view snapshots of P3HT thin film at various strains: for the 30-mer film at strains 1.2 and 1.3, cracks occur by chain pullout with decreased orientation along the tensile direction when straining ⩾1.1. For the 150-mer film at strains 0.7 and 1.3, polymer chains continuously align in the stretching direction, and the film gradually narrows. Only backbones are shown here for clarity, and chains are colored using their local ordering parameter P₂. (h) Von Mises stress distribution of atoms in P3HT thin film with 10 and 150 monomers per chain, respectively, at the final stage of scratching (scratch distances of 300 Å). The color bar below indicates the atomic Von Mises stress. (i) Snapshot of the equilibrated P3HT/graphene nanocomposite system containing 12 graphene flakes and 800 P3HT chains with 20 monomers chain. (j) Young's modulus (left y-axis) and T_g (right y-axis) vs. graphene content of P3HT/graphene nanocomposites. The experimental⁸⁹ and Halpin–Tsai predictive Young's modulus values for nanocomposites are also shown for comparison. (k) Dynamical heterogeneity of the P3HT/graphene nanocomposite at 300 K: color maps of local stiffness 1/〈u²〉 of the center of mass of the CG beads of P3HT/graphene nanocomposites with different graphene contents. (l) Tensile modulus E/E_bulkvs. 〈u²〉_bulk/〈u²〉 for all P3AT/graphene nanocomposites at different temperatures and with different graphene contents, where the dashed line indicates the linear fitting of the data. (m) Representative snapshot of amorphous morphology before and after straining to 150% (only graphene and two P3HT chains are shown for clarity). (n) Orientation parameter f of the axial and transverse components of the P3HT backbone and the graphene C–C bond during the uniaxial tension deformation at 300 K. Figures adapted from ref. 65 (copyright 2023 John Wiley and Sons), ref. 90 (copyright 2024 American Chemical Society), and ref. 91 (copyright 2023 Royal Society of Chemistry).

Experimental studies have emphasized the need for detailed insights into the mechanical and conformational properties of CPs thin films to design materials with optimal performance. To address this need, a chemistry-specific CG model was developed, derived from all-atomistic (AA) simulations of poly(3-hexylthiophene) (P3HT).⁵⁹ This approach preserves the critical molecular interactions and conformations observed experimentally, enabling systematic investigation of the mechanical behavior and conformational characteristics of free-standing CP thin films through uniaxial tension, nanoindentation, and scratching tests.

Using the chemistry-specific CG model, the mechanical properties of P3AT derivatives with different side-chain lengths were systematically explored. The simulations revealed that increasing the side-chain length generally leads to a decrease in E and tensile strength, as longer side-chains introduce more free volume and flexibility into the polymer matrix. This trend was consistent across various molecular weight (M_w), indicating that side-chain length is a significant factor in determining the mechanical behavior of CP thin films. Uniaxial tension tests further revealed that higher M_w, corresponding to longer polymer chains, resulted in elevated stress levels before fracture. As the stretching progressed, the radius of gyration (R_g) of P3HT chains exhibited a trend similar to that of stress, with R_g undergoing a decline upon film fracture. This behavior is attributed to the increased entanglement and segmental rearrangement capacity of higher M_w chains, which accommodate applied strain more effectively, preventing fracture initiation. Fig. 6(e) illustrates this trend, where the area under the stress–strain curve (indicative of material toughness) increases with M_w. The inset of Fig. 6(e) provides visual confirmation, showing that low-M_w systems tend to fracture via chain pullout, whereas high-M_w systems allow more conformational changes and segmental rearrangements within the polymer chains, accommodating the applied strain more effectively. This enhancement in ductility and toughness with increasing M_w is crucial for the performance of flexible devices.

The orientation of polymer chains during stretching was further evaluated by calculating the orientation parameter of the thin film system. This parameter, defined by the angle formed by the bond vector connecting two consecutive backbone CG beads relative to the deformation direction (inset of Fig. 6(c)), provided insights into the chain alignment. Fig. 6(c) shows clear evidence that, as the tensile strain increased, the polymer chains exhibited a greater tendency to align along the deformation axis, resulting in a higher orientation parameter and an increase in the end-to-end distance of the polymer chains. This tendency for backbone orientation under strain was observed for different temperatures (0.7 T_g and 1.3 T_g), with a Gaussian-like distribution of local orientation parameters, indicating a propensity for backbone alignment in the direction of strain. The end-to-end distance distribution exhibited a similar trend, with both the orientation parameter and end-to-end distance being nearly independent of temperature.⁶⁵ These CG-MD simulations provided valuable insights into the molecular-level mechanisms driving the mechanical behavior and chain conformation during stretching, complementing the experimental observations.

3.4.2 Interfacial characterization of CP thin films. The interfacial properties of CP thin films are equally critical for their performance in practical applications. Nanoindentation and scratching tests provide insights into the mechanical resilience and durability of CP thin films. Using the chemistry-specific CG model, nanoindentation behavior was studied for P3AT thin films. The representative force vs. indentation depth curve (Fig. 6(f)) revealed stiffening behavior with increasing M_w. Young's modulus (E), derived using the nanoindentation theoretical model, showed that E obtained from indentation is more sensitive to M_w than from tensile tests. This difference is attributed to the distinctive deformation mechanisms, where chains are more uniformly stretched under uniaxial tension and locally compressed under nanoindentation. Additionally, side-chain length significantly influenced the mechanical response; longer side-chains resulted in lower toughness and E due to the additional mobility and spatial accommodation provided by the side-chains. Despite these influences, the backbone's structural integrity remains crucial in determining the overall film properties. Transitioning to the chain conformation under mechanical stress provides essential insights into both mechanical and electronic behavior. Simulation results demonstrated that stretching promotes both chain alignment and extended conjugation lengths, enhancing the electronic properties of P3AT thin films. As shown in Fig. 6(g), chain alignment increases with applied strain, especially for high-M_w samples. For low-M_w thin films, chain pullout and fracture occur at lower strains, accompanied by a drop in orientation along the tensile direction. In contrast, high-M_w thin films exhibit continuous alignment and narrowing under higher strains, maintaining structural integrity and enhancing electronic performance.⁹⁰ This behavior underscores the importance of molecular weight in determining the mechanical response and stability of CP thin films under mechanical stress.

Furthermore, scratch testing provided additional insights into the mechanical resilience and durability of CP thin films. The simulations indicated that high-M_w thin films exhibited elevated friction forces due to chain accumulation on the indenter. The Von Mises stress distribution, depicted in Fig. 6(h), revealed that high-M_w films could better distribute and dissipate stress, contributing to their enhanced mechanical performance. This behavior is due to the sufficient chain sliding and alignment along the scratch path, which allows the material to absorb and redistribute stress more effectively. Conversely, films with longer side-chains showed lower friction coefficients, correlating with their reduced mechanical strength. The polymer chains in these films exhibited lower stress values, indicating less effective stress distribution and higher susceptibility to damage during scratching.⁹⁰ The chemistry-specific CG model effectively captured the mechanical and conformational behaviors of P3AT thin films, providing molecular-level insights consistent with experimental observations, and guiding the design of CP-based materials for flexible electronics.

3.4.3 CG modeling of thermomechanical behaviors of CP nanocomposites. The integration of graphene into CP nanocomposites is a promising strategy to enhance their mechanical properties, crucial for flexible and electronic devices. Experimental studies have shown that graphene, with its exceptional mechanical strength and electrical conductivity, can significantly improve the thermomechanical properties of CPs.^92–94 Despite these advancements, a fundamental understanding of these enhancements at the molecular level remains limited. To address this gap, a chemistry-specific P3AT CG model, informed by atomistic simulations, was employed to investigate the temperature-dependent thermomechanical properties of graphene-reinforced P3AT nanocomposites (Fig. 6(i)).^59,91

To elucidate the impact of graphene content on the mechanical performance of P3AT nanocomposites, tensile deformation simulations were conducted. As shown in Fig. 6(j), the Young's modulus of P3HT/graphene nanocomposites increases with graphene content. The comparison between the simulation results and the Halpin–Tsai predictive model^95,96 highlights the reinforcing effect of graphene. Notably, the experimental data align well with the simulation predictions, demonstrating the reliability of the CG model.⁸⁹ Additionally, the T_g also showed a positive correlation with graphene content, further reinforcing the thermal stability of the nanocomposites. The simulations revealed that higher graphene content leads to improved mechanical strength and thermal stability, making these nanocomposites suitable for advanced applications. Furthermore, to explore the impact of graphene content on dynamical heterogeneity, color maps of local stiffness 1/〈u²〉 were generated for P3HT/graphene nanocomposites at 300 K (Fig. 6(k)). The results indicate that as the graphene content increases, the local stiffness becomes more pronounced, with higher concentrations of red regions representing areas of slower molecular dynamics. This increased dynamical heterogeneity is attributed to the presence of more rigid graphene, which enhances the mechanical response of the system. The inclusion of graphene not only increases the overall stiffness of the nanocomposite but also induces significant dynamical heterogeneity, contributing to the improved mechanical properties of the material. Additionally, Fig. 6(l) illustrates the tensile modulus E/E_bulkvs. 〈u²〉_bulk/〈u²〉 for all P3AT/graphene nanocomposites at different temperatures and with varying graphene contents. The dashed line represents the linear fitting of the data, showing a clear linear relationship. This linear correlation between the tensile modulus and local stiffness highlights the fundamental role of graphene in altering the mechanical properties of CP nanocomposites. Specifically, the presence of graphene significantly increases the local molecular stiffness, as indicated by the higher values of 1/〈u²〉. This enhanced stiffness translates directly into higher tensile moduli, demonstrating that the mechanical reinforcement provided by graphene is not only due to its intrinsic strength but also due to its ability to modify the local dynamics and structural properties of the polymer matrix. The consistent increase in tensile modulus with local stiffness further underscores the effectiveness of graphene in improving the mechanical performance of CP nanocomposites.

Furthermore, the strain-induced chain conformation of P3AT/graphene nanocomposites was evaluated to understand the effects of uniaxial strain on molecular alignment. Applying uniaxial strain causes the chain segments to align along the axial direction, enhancing charge carrier mobilities in highly aligned nanofibrillar structures.⁹⁷ Representative snapshots before and after straining to 150% show significant morphological changes (Fig. 6(m)). Simulations of P3HT/graphene nanocomposites (5 wt% graphene) at 300 K demonstrated that both the P3HT backbone and graphene exhibited increasing chain alignment with rising strain along the stretching direction, while decreasing along the transverse direction (Fig. 6(n)). Due to its planar architecture and high stiffness, graphene exhibited a lower degree of alignment, which nonetheless contributes to the overall mechanical enhancement of the nanocomposite. The alignment behavior was found to be relatively insensitive to temperature and graphene content, but the longer side-chains in the P3AT system exhibited a higher tendency for alignment due to stronger segment dynamics. These findings provide a comprehensive understanding of the thermomechanical behavior of graphene-reinforced CP nanocomposites, highlighting the significant role of graphene in enhancing mechanical properties and stability. This molecular-level insight is crucial for optimizing CP nanocomposites for advanced flexible electronics and other high-performance applications.

4. Conclusion

In summary, this review underscores the significant advancements in understanding the optoelectronic, structural, and thermomechanical properties of CPs through multiscale simulations. Quantum mechanical studies have provided critical insights into the electronic structures and conformational dynamics of CPs, establishing foundational knowledge for predicting material behavior. AA-MD simulations have elucidated the intricate interplay between polymer chain morphology and optoelectronic properties, while coarse-grained models have enabled the exploration of larger-scale phenomena and long-term behavior. ML approaches have shown promise in developing predictive models for CP properties, offering an efficient route for material design and optimization. The integration of these computational techniques has not only enhanced our understanding of CPs at a molecular level but also bridged the gap between theoretical predictions and experimental observations. Moving forward, the continued development of these simulation methodologies, coupled with experimental validation, will be crucial in advancing the field of conjugated polymers. Future research should focus on refining these models to capture the complexities of CP behavior more accurately and exploring new CP architectures and compositions to meet the evolving demands of flexible and wearable electronics.

Author contributions

Conceptualization: Z. L. and W. X.; writing – original draft: Z. L., S. A. T., and W. X.; writing – review and editing: Z. L., Y. W., A. A., and W. X.; supervision: W. X.; funding acquisition: W. X. All authors read and approved the final manuscript.

Data availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.S. National Science Foundation (NSF) under award no. 2237063, 2331017, and 2119691. The authors also acknowledged the support from the Department of Aerospace Engineering and College of Engineering at Iowa State University.

References

1. R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, Nat. Mater., 2013, 12, 1038–1044.
2. J. Mei, Y. Diao, A. L. Appleton, L. Fang and Z. Bao, J. Am. Chem. Soc., 2013, 135, 6724–6746.
3. A. F. Paterson, S. Singh, K. J. Fallon, T. Hodsden, Y. Han, B. C. Schroeder, H. Bronstein, M. Heeney, I. McCulloch and T. D. Anthopoulos, Adv. Mater., 2018, 30, 1801079.
4. D. Venkateshvaran, M. Nikolka, A. Sadhanala, V. Lemaur, M. Zelazny, M. Kepa, M. Hurhangee, A. J. Kronemeijer, V. Pecunia, I. Nasrallah, I. Romanov, K. Broch, I. McCulloch, D. Emin, Y. Olivier, J. Cornil, D. Beljonne and H. Sirringhaus, Nature, 2014, 515, 384–388.
5. C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267.
6. A. Facchetti, Chem. Mater., 2011, 23, 733–758.
7. J. Mei, Y. Diao, A. L. Appleton, L. Fang and Z. Bao, J. Am. Chem. Soc., 2013, 135, 6724–6746.
8. A. J. Heeger, J. Phys. Chem. B, 2001, 105, 8475–8491.
9. G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791.
10. A. J. Moulé, J. B. Bonekamp and K. Meerholz, J. Appl. Phys., 2006, 100, 094503.
11. J. Rivnay, S. C. B. Mannsfeld, C. E. Miller, A. Salleo and M. F. Toney, Chem. Rev., 2012, 112, 5488–5519.
12. J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539–541.
13. I. F. Perepichka, D. F. Perepichka, H. Meng and F. Wudl, Adv. Mater., 2005, 17, 2281–2305.
14. H. Wu, L. Ying, W. Yang and Y. Cao, Chem. Soc. Rev., 2009, 38, 3391–3400.
15. R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, Nat. Mater., 2013, 12, 1038–1044.
16. S. Holliday, J. E. Donaghey and I. McCulloch, Chem. Mater., 2014, 26, 647–663.
17. S. Hedström, E. Wang and P. Persson, Mol. Phys., 2017, 115, 485–496.
18. I. Pozo, F. Lombardi, D. I. Alexandropoulos, F. Kong, J.-R. Deng, P. N. Hor-Ton, S. J. Coles, W. K. Myers, L. Bogani and H. L. Anderson, Conjugated Porphyrin Tapes as Quantum Mediators for Vanadyl Qubits.
19. T. Tanaka and A. Osuka, Chem. Soc. Rev., 2015, 44, 943–969.
20. C. Liu, W. Hu, H. Jiang, G. Liu, C. C. Han, H. Sirringhaus, F. Boué and D. Wang, Macromolecules, 2020, 53, 8255–8266.
21. M. Abdelsamie, T. P. Chaney, H. Yan, S. A. Schneider, I. A. Ayhan, E. D. Gomez, J. R. Reynolds and M. F. Toney, J. Mater. Chem. A, 2022, 10, 2096–2104.
22. A. Sharma, X. Pan, J. A. Campbell, M. R. Andersson and D. A. Lewis, Macromolecules, 2017, 50, 3347–3354.
23. N. Balar, J. J. Rech, R. Henry, L. Ye, H. Ade, W. You and B. T. O’Connor, Chem. Mater., 2019, 31, 5124–5132.
24. Z. Qian, Z. Cao, L. Galuska, S. Zhang, J. Xu and X. Gu, Macromol. Chem. Phys., 2019, 220, 1900062.
25. S. Savagatrup, A. D. Printz, H. Wu, K. M. Rajan, E. J. Sawyer, A. V. Zaretski, C. J. Bettinger and D. J. Lipomi, Synth. Met., 2015, 203, 208–214.
26. N. E. Jackson, B. M. Savoie, K. L. Kohlstedt, M. Olvera de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2013, 135, 10475–10483.
27. Y. Wang, G. Ji, W. Ye, F. Zhang, Y. Wang, Y. Zhao and Z. Liu, ACS Sustainable Chem. Eng., 2022, 10, 9460–9468.
28. C. M. Wolf, L. Guio, S. Scheiwiller, V. Pakhnyuk, C. Luscombe and L. D. Pozzo, ACS Polym. Au, 2021, 1, 134–152.
29. D. Alberga, A. Perrier, I. Ciofini, G. F. Mangiatordi, G. Lattanzi and C. Adamo, Phys. Chem. Chem. Phys., 2015, 17, 18742–18750.
30. D. R. Reid, N. E. Jackson, A. J. Bourque, C. R. Snyder, R. L. Jones and J. J. De Pablo, J. Phys. Chem. Lett., 2018, 9, 4802–4807.
31. W. Xia and T. Lan, Macromolecules, 2019, 52, 6547–6554.
32. Z. Li and W. Xia, Extreme Mech. Lett., 2020, 40, 100942.
33. C. Wu, R. Wu, W. Xia and L. Tam, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1779–1791.
34. S. Zhang, A. Alesadi, G. T. Mason, K. L. Chen, G. Freychet, L. Galuska, Y. H. Cheng, P. B. J. St. Onge, M. U. Ocheje, G. Ma, Z. Qian, S. Dhakal, Z. Ahmad, C. Wang, Y. C. Chiu, S. Rondeau-Gagné, W. Xia and X. Gu, Adv. Funct. Mater., 2021, 31, 2100161.
35. S. E. Root, S. Savagatrup, C. J. Pais, G. Arya and D. J. Lipomi, Macromolecules, 2016, 49, 2886–2894.
36. H. Doan Tran, C. Kim, L. Chen, A. Chandrasekaran, R. Batra, S. Venkatram, D. Kamal, J. P. Lightstone, R. Gurnani, P. Shetty, M. Ramprasad, J. Laws, M. Shelton and R. Ramprasad, J. Appl. Phys., 2020, 128, 171104.
37. N. E. Jackson, M. A. Webb and J. J. de Pablo, Curr. Opin. Chem. Eng., 2019, 23, 106–114.
38. A. Giuntoli, N. K. Hansoge, A. van Beek, Z. Meng, W. Chen and S. Keten, npj Comput. Mater., 2021, 7, 168.
39. K. N. Keya, A. Arshad, S. A. Tolba, W. Nie, A. Alesadi, L. A. Ruiz Pestana and W. Xia, in Fundamentals of Multiscale Modeling of Structural Materials, ed. W. Xia and L. A. Ruiz Pestana, Elsevier, 2023, pp. 203–236.
40. R. Xie, A. R. Weisen, Y. Lee, M. A. Aplan, A. M. Fenton, A. E. Masucci, F. Kempe, M. Sommer, C. W. Pester, R. H. Colby and E. D. Gomez, Nat. Commun., 2020, 11, 893.
41. Q. Yang, A. Vriza, C. A. Castro Rubio, H. Chan, Y. Wu and J. Xu, Chem. Mater., 2024, 36, 2602–2622.
42. D. S. Sholl and J. A. Steckel, Density functional theory: a practical introduction, John Wiley & Sons, 2022.
43. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
44. A. Honet, L. Henrard and V. Meunier, J. Phys.: Condens. Matter, 2023, 35, 485703.
45. A. Alesadi, F. Fatima, W. Xia and D. Kilin, J. Phys. Chem. B, 2021, 125, 8953–8964.
46. Z. Cao, S. A. Tolba, Z. Li, G. T. Mason, Y. Wang, C. Do, S. Rondeau-Gagné, W. Xia and X. Gu, Adv. Mater., 2023, 35, 2302178.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
48. L. Chaput, P. Pécheur and H. Scherrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045116.
49. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
50. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
51. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
52. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
53. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre and P. d’Arco, 2014.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
55. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
56. S. L. Mayo, B. D. Olafson and W. A. Goddard III, DREIDING: A Generic Force Field for Molecular Simulations, BioDesign, Inc, 1990, vol. 94.
57. L. A. Ruiz Pestana, Y. Liao, Z. Li and W. Xia, Fundamentals of Multiscale Modeling of Structural Materials, Elsevier, 2022, pp. 37–73.
58. O. Alexiadis and V. G. Mavrantzas, Macromolecules, 2013, 46, 2450–2467.
59. Y. Wang, Z. Li, K. Niu and W. Xia, Polymer, 2022, 256, 125159.
60. Z. Cao, Z. Li, S. A. Tolba, G. T. Mason, M. Xiong, M. U. Ocheje, A. Alesadi, C. Do, K. Hong, T. Lei, S. Rondeau-Gagné, W. Xia and X. Gu, J. Mater. Chem. A, 2023, 11, 12928–12940.
61. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
62. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, 1996.
63. A. Alesadi, Z. Cao, Z. Li, S. Zhang, H. Zhao, X. Gu and W. Xia, Cell Rep. Phys. Sci., 2022, 3, 100911.
64. Z. Li, Y. Wang, A. Alesadi, L. A. Ruiz Pestana and W. Xia, Fundamentals of Multiscale Modeling of Structural Materials, Elsevier, 2022, pp. 75–111.
65. Y. Wang, S. Zhang, G. Freychet, Z. Li, K. L. Chen, C. T. Liu, Z. Cao, Y. C. Chiu, W. Xia and X. Gu, Adv. Funct. Mater., 2023, 33, 2306576.
66. S. Zhang, A. Alesadi, M. Selivanova, Z. Cao, Z. Qian, S. Luo, L. Galuska, C. Teh, M. U. Ocheje, G. T. Mason, P. B. J. St. Onge, D. Zhou, S. Rondeau-Gagné, W. Xia and X. Gu, Adv. Funct. Mater., 2020, 30, 2002221.
67. G. Ma, Z. Li, L. Fang, W. Xia and X. Gu, Nanoscale, 2024, 16, 6495–6506.
68. Z. Li, Y. Wang, G. Ma, Y. Liao, X. Gu and W. Xia, J. Polym. Sci., 2024, 62, 1296–1309.
69. W. Xia, N. K. Hansoge, W.-S. Xu, F. R. Phelan, S. Keten and J. F. Douglas, Sci. Adv., 2019, 5, eaav4683.
70. W. Xia, J. Song, C. Jeong, D. D. Hsu, F. R. Phelan, J. F. Douglas and S. Keten, Macromolecules, 2017, 50, 8787–8796.
71. T. Weiss, E. Mayo Yanes, S. Chakraborty, L. Cosmo, A. M. Bronstein and R. Gershoni-Poranne, Nat. Comput. Sci., 2023, 3, 873–882.
72. I. Pavlak, L. Matasović, E. A. Buchanan, J. Michl and I. Rončević, J. Am. Chem. Soc., 2024, 146, 3992–4000.
73. A. Alesadi, W. Xia and D. Kilin, J. Phys. Chem. C, 2022, 126, 12015–12024.
74. X. Chang, M. Balooch Qarai and F. C. Spano, Chem. Mater., 2023, 35, 10018–10029.
75. K. Müllen and W. Pisula, J. Am. Chem. Soc., 2015, 137, 9503–9505.
76. B. Kuei and E. D. Gomez, Soft Matter, 2017, 13, 49–67.
77. D. Wang, Y. Yuan, Y. Mardiyati, C. Bubeck and K. Koynov, Macromolecules, 2013, 46, 6217–6224.
78. T.-Q. Nguyen, V. Doan and B. J. Schwartz, J. Chem. Phys., 1999, 110, 4068–4078.
79. Y. Xi, C. M. Wolf and L. D. Pozzo, Soft Matter, 2019, 15, 1799–1812.
80. Z. Cao, Z. Li, S. Zhang, L. Galuska, T. Li, C. Do, W. Xia, K. Hong and X. Gu, Macromolecules, 2020, 53, 11142–11152.
81. A. Chremos, P. J. Camp, E. Glynos and V. Koutsos, Soft Matter, 2010, 6, 1483–1493.
82. A. Chremos, J. F. Douglas, P. J. Basser and F. Horkay, Soft Matter, 2022, 18, 6278–6290.
83. L. Matasović, B. Panić, M. Bubaš, H. Vančik, I. Biljan and I. Rončević, J. Mater. Chem. C, 2022, 10, 5433–5446.
84. A. Sharma, X. Pan, J. M. Bjuggren, D. Gedefaw, X. Xu, R. Kroon, E. Wang, J. A. Campbell, D. A. Lewis and M. R. Andersson, Chem. Mater., 2019, 31, 6740–6749.
85. M. C. Bellissent-Funel, A. Filabozzi and S. H. Chen, Biophys. J., 1997, 72, 1792–1799.
86. F. W. Starr, S. Sastry, J. F. Douglas and S. C. Glotzer, Phys. Rev. Lett., 2002, 89, 125501.
87. H. Zhao, J. J. Shanahan, S. Samson, Z. Li, G. Ma, N. Prine, L. Galuska, Y. Wang, W. Xia, W. You and X. Gu, Macromol. Rapid Commun. DOI:10.1002/marc.202200533.
88. G. Chen, L. Tao and Y. Li, Polymers, 2021, 13, 1898.
89. Y. Kim, Y. J. Kwon, S. Ryu, C. J. Lee and J. U. Lee, Polymers, 2020, 12, 1046.
90. Y. Wang, Z. Li, K. Niu, W. Xia and A. Giuntoli, Macromolecules, 2024, 57, 5130–5142.
91. Y. Wang, Z. Li, D. Sun, N. Jiang, K. Niu, A. Giuntoli and W. Xia, Nanoscale, 2023, 15, 17124–17137.
92. C. J. Lin, C. L. Liu and W. C. Chen, J. Mater. Chem. C, 2015, 3, 4290–4296.
93. A. Yadav, A. Upadhyaya, S. K. Gupta, A. S. Verma and C. M. S. Negi, Thin Solid Films, 2019, 675, 128–135.
94. Y. Liu, W. Hao, H. Yao, S. Li, Y. Wu, J. Zhu and L. Jiang, Adv. Mater., 2017, 30, 1705377.
95. J. C. H. Affdl and J. L. Kardos, Polym. Eng. Sci., 1976, 16, 344–352.
96. A. Navidfar and L. Trabzon, Composites, Part B, 2019, 176, 107337.
97. P. H. Chu, N. Kleinhenz, N. Persson, M. McBride, J. L. Hernandez, B. Fu, G. Zhang and E. Reichmanis, Chem. Mater., 2016, 28, 9099–9109.

---