Promoting exchange coupling in (Cp^iPr₅)₂Gd₂X₃ complexes

Abstract

Introducing magnetic coupling between lanthanide ions has been shown to yield better-performing single-molecule magnets (SMMs), as exemplified by the Cp₂^iPr₅Ln₂I₃ family of compounds (Cp^iPr₅: pentaisopropylcyclopentadienyl, Ln: Gd, Tb, or Dy). This unique coupling is mediated through an unpaired electron hosted in a σ-like orbital, that results from the two 5d_z² Ln ions, and understanding these interactions holds the key to continue advancing the rational design of SMMs. Here, we focus on the Cp₂^iPr₅Gd₂I₃ spin-only system and apply a recently proposed DFT-based decomposition scheme to assess the chemical and structural factors that affect the magnetic coupling. Based on these, we propose synthetically feasible systems with increased coupling.

---

The magnetic exchange interaction (J) is a key element in the design of materials and molecules with novel magnetic properties, having been imaginatively leveraged to make advances in a range of fields, such as organic magnetism,¹ spintronics,² qubits³ and single-molecule magnets.⁴ Of particular interest to this work is the latter, whose defining feature is a capacity to retain magnetisation at the molecular level. While numerous strategies have been put forward across the years to design and synthesize these systems,⁵ the common goal still is to maximise the time a SMM retains its magnetisation, ideally at ever-increasing temperatures. This is sought after because it leads to coercive fields, which provide the SMM with magnetic bistability and the potential to be used as platforms for high-density information storage devices.⁶ A well-studied strategy over the last decade has been to force an indirect coupling between lanthanide ions through coupling with a radical moiety, resulting in Ln-radical-Ln architectures.⁴ Recently, huge coercive fields have been achieved by introducing a strong J between two axial lanthanide ions,^7,8 opening up a new and exciting avenue towards better-performing SMMs. This strong J has been realised through an exotic coupling between lanthanide ions and singly occupied σ-like orbital, constituted of the 5d_z² orbitals of both ions. This bonding interaction belongs to class III of the Robin–Day mixed-valence classification⁹ and results in an intermediate situation between a three-coupled-magnetic-centres case and Hund's rule. Given the central role that J has in improving the properties of these systems, it seems appropriate to develop an understanding of what the governing factors are, as well as proposing strategies that afford its control through chemical modifications. To that end, we apply a decomposition scheme,¹⁰ that informs of the different contributions that make up J, to the series Cp₂^iPr₅Gd₂X₃ (Cp = cyclopentadienyl, iPr = isopropyl, Gd = gadolinium, X = chlorine, bromine, iodine). We also investigate how structural variations of the parent Cp₂^iPr₅Gd₂I₃ compound⁷ impact J, establishing clear magneto-structural relationships. We focus on the Gd-derivatives because our methodology is well-defined for spin-only systems, whilst given the separate origins of Ln anisotropy and the interaction between their spin component with the unpaired electron hosted by 5d_z² orbital, we hypothesise that our findings are also of relevance across the whole series.

The present series of compounds implies three magnetic centres (labelled Gd₁, Gd₂ and σ) and their coupling is described by the Heisenberg–Dirac–van Vleck (HDvV) Hamiltonian Ĥ^HDvV = −2J_Gd1-σŜ_Gd1·Ŝ_σ − 2J_σ-Gd2Ŝ_σ·Ŝ_Gd2 − 2J_Gd1−Gd2Ŝ_Gd1·Ŝ_Gd2. Magnetic exchange coupling may be interpreted as the competition between three main physical contributions¹¹ with (i) the direct exchange J₀ corresponding to the direct exchange integral between two magnetic centres, (ii) the kinetic exchange ΔJ_KE translating the relaxation of the magnetic centres in the low spin-states and analogous to Anderson's superexchange mechanism and (iii) the spin polarisation ΔJ_SP reflecting the different responses of the non-magnetic electrons to the different spin distribution of the spin states. J₀ favours a parallel alignment of the spin of the magnetic centres while ΔJ_KE has the opposite effect. The impact of ΔJ_SP on the coupling depends on the system but is expected to be negligible in transition metal- or lanthanide-based series of compounds due to the local nature of the magnetic orbitals. Recent developments allow extracting these three contributions in density functional theory (DFT) (methodology and computational details are presented in the ESI†), and this strategy has been successfully applied to rationalise couplings in various situations.¹² In systems implying more than two magnetic centres, these three contributions are used to determine the overall coupling as J_Σ = J₀ + ΔJ_SP + ΔJ_KE.¹⁰

As a starting point, we first calculate and decompose J_Σ for the crystal structure of Cp₂^iPr₅Gd₂I₃⁷ for both the Gd–Gd (J_Gd−Gd) and Gd-σ (J_Gd-σ) interactions (Table S1, ESI†). Focusing on J_Gd−σ, since J_Gd−Gd is comparatively negligible (J_Σ = −1, J₀ = 0, ΔJ_SP = 0 and ΔJ_KE = −2 cm⁻¹), we find that the originally reported value of 333 cm⁻¹ is dominated by the direct exchange (J₀ = 350 cm⁻¹), with the remaining being a negative contribution from the kinetic exchange part (ΔJ_KE = −17 cm⁻¹) and the spin polarisation part (ΔJ_SP = 0 cm⁻¹) playing no role. This pattern can be understood given that the exchange integral informs of the spatial overlap of the interacting magnetic orbitals, which in this case is large. In what follows, we perform a series of structural distortions (Fig. 2) and chemical modifications (Fig. 3) on the parent compound, looking for the conditions that concomitantly result in a large J₀, a minimised negative contribution from ΔJ_KE and a positive one from ΔJ_SP in order to maximise J_Σ.

First, we perform a series of distortions involving the Gd–Gd distance while keeping the relative position of all other groups fixed (Table S2, ESI† and Fig. 2 left). As expected, as the distance decreases, J_Σ increases thanks to an increase in J₀ (+40 cm⁻¹) which is damped by a much faster increase of the negative, yet smaller, ΔJ_KE values (−17 to −34 cm⁻¹). Similarly, in increasing the distance between gadolinium centres, J_Σ decreases due to a reduction in J₀ and ΔJ_KE values. This analysis shows that while reducing the Gd–Gd distance introduces a rapidly growing, detrimental contribution from ΔJ_KE, its effect is masked by the exceedingly larger J₀, suggesting that chemical modifications aimed at reducing the Gd–Gd distance are an effective way to promote the overall exchange.

Whereas the analysis of linear Gd–Gd distance indicated that a preferred strategy would be to bring the lanthanide ions closer, it also showed that pushing them apart makes ΔJ_KE go towards ever smaller negative values. If this was combined with changes that did not decrease J₀, it would represent a way to increase the overall exchange in these compounds. To that end, we looked at how changing the angle between Gd ions and the centroid of the halogen ions (Fig. 1) affects the exchange interaction and its contributions – we note here that this distortion keeps the relative orientation and distance of the Cp ligands intact with respect to the gadolinium. We first performed a distortion where both Gd ions are moved symmetrically relative to the I₃ centroid. Fig. 2 (middle) shows significant variations in both J₀ and ΔJ_KE contributions. However, the values of both contributions increase in magnitude resulting in almost no variation of the total coupling J_Σ, rendering this strategy ineffective. The final structural variation focuses on symmetrically bending the angles between the Cp external ligand, its centroid (“o” on Fig. 1) and the GdI₃Gd moiety – the Cp ligand pivots around its centroid, and the centroid itself does not move. As shown Fig. 2 (right), J_Σ presents a quadratic decrease, which results from the same behaviour of the dominating direct exchange contribution. For the kinetic exchange, the magnitude also decreases but with a more linear pattern. Hence, having the Cp ligands at right angles with the GdI₃Gd moiety should be a preferable arrangement to maximise the coupling. It may be worth noting that this variation has been done on a model structure close to the X-ray one, explaining why the relative energies are not equal to zero at 90 degrees.

Fig. 1 Schematic representation of the structural and chemical modifications investigated. Blue (denoted o) and red dots represent the centroids of the Cp^iPr₅ and X₃ components, respectively. X refers to halogen atoms (X = I, Cl, F). Green dashed lines represent the distortions applied to the structure.

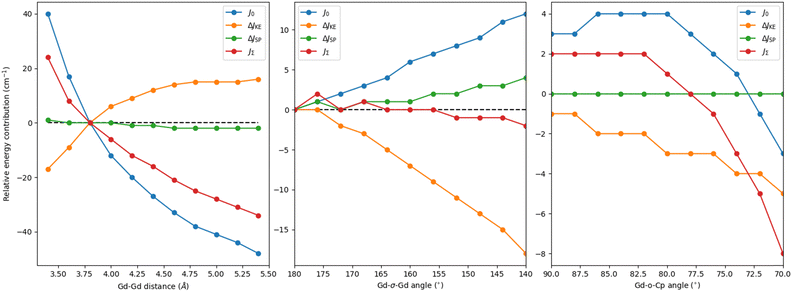Fig. 2 Energy contributions relative to the original Cp₂^iPr₅Gd₂I₃ complex as a function of the Gd–Gd distance (left), the Gd-σ-Gd angle (middle) and the Gd-o-Cp angle (right) in cm⁻¹.

Despite the strong torsions we applied to the structure, the magnetic exchange coupling between the Gd ions and the σ orbital remains rather unchanged. This may be readily explained by considering the nature of the σ centre; regardless of the torsion applied to the structure, the σ centre would be composed of the 5d_z² orbital of both Gd ions and would result in similar on-site interactions. This peculiarity motivates us to focus on how the bridging halogen triangle affects the σ-like orbital and the associated coupling.

To that end, we first performed the decomposition analysis on the series Cp₂^iPr₅Gd₂X₃ (X = F, Br, Cl), having simply substituted the original iodine atoms at the crystal structure, without geometry optimisation (Fig. 3 – constrained geometry). Here, we observe an increase of J_Σ by substituting with lighter halogen atoms. This trend results from larger direct exchange contributions while the kinetic exchange ones remain rather unchanged. One may also note the larger spin polarisation contribution going from iodine to fluorine. This may be rationalised thanks to the Mulliken spin and charge populations over the gadolinium and halogen atoms presented in Table S3 (ESI†) for X = I and F for the determinants defining the magnetic and core orbitals of the systems (ESI†). In the constrained Cp₂^iPr₅Gd₂F₃ structure, the spin population is more concentrated over the Gd and less over the halogen than in the Cp₂^iPr₅Gd₂I₃. One may readily think this would result in a greater on-site interaction, leading to larger J₀ and ΔJ_SP. It may be worth noting that despite this modification of the spin populations, the kinetic exchange contribution is not impacted.

Fig. 3 Contributions to the exchange coupling constants between Gd centre and σ centre in the constrained and relaxed Cp₂^iPr₅Gd₂X₃ (X = F, Cl, Br, I) structures.

We then performed geometry optimisations on the diamagnetic yttrium analogues and applied our decomposition analysis to those structures. We note that the fluorine substituted system could not be converged to a stationary point. This suggests that the resulting Gd–Gd environment is not capable of effectively hosting a σ-like orbital with the fluorine atoms coming too close to the yttrium during the optimisation. Fig. 3 presents the contributions of the decomposition and J_Σ for the series of optimised Cp₂^iPr₅Gd₂X₃ compounds (relaxed geometry in Fig. 3). Substituting the iodine atoms with lighter halogen atoms results in significantly stronger ferromagnetic J₀ contributions, with increases of 39 cm⁻¹ and 56 cm⁻¹ for Br and Cl atoms, respectively. The latter change represents a large modification with an increase of 15%. These chemical substitutions also provide larger ΔJ_KE in magnitude with lower values of 20 and 24 cm⁻¹ for Br and Cl atoms, respectively. Consequently, these substitutions enhance the ferromagnetic nature of the overall J_Gd-σ coupling by 23 and 14 cm⁻¹ for Cl and Br, respectively, in line with the Gd–Gd distances (Cl: 3.386, Br: 3.496 Å).

From all the structural distortions and chemical modifications investigated, it is apparent that the best strategy to promote the overall exchange in these compounds is by substituting the heavy iodide ions with smaller halogens, ideally chlorine, as very recently shown in uranium-based triangular complexes.¹³ In terms of their synthetic feasibility, we argue that the proposed derivatives are reasonable – the original synthesis⁷ relies on a salt metathesis between anhydrous GdI3 and NaCp^iPr₅ to form the iodide-bridged dimer precursor, which after reduction, via the formation of potassium iodide (KI), results in the crucial single electron bond between the metals – GdF₃,¹⁴ GdCl₃¹⁵ and GdBr₃¹⁶ are readily available starting materials, and the reduction of the associated precursor should, in principle, be thermodynamically favoured as the enthalpy of formation of KF, KCl and KBr are 56, 26 and 15 kcal mol⁻¹ higher than that of KI, respectively.

This work focuses on the Gd-based complexes and the study of lanthanide ions with stronger local anisotropy implies tedious theoretical machinery. However, due to the isotropic nature of the magnetic exchange interaction, one may reasonably expect our conclusions to hold for other lanthanide ions and that the increase in J would result in even larger coercive fields and longer relaxation times at temperatures ever closer to ambient conditions. With this, we hope to have provided compelling enough arguments for skilled chemists to take on the challenge of synthesising Dy₃Cp₂^iPr₅Cl₃ and Tb₃Cp₂^iPr₅Cl₃.

The authors thank the French GENCI/IDRIS-CINES centres for high-performance computing resources. DR thanks the Basque Government for the IT1584-22 grant. G. D. received research funding from the European Union’s 843 Horizon 2020 Research and Program under Marie Skłdowska-Curie Grant Agreement No. 899546.

Data availability

The data supporting this article have been included as part of the ESI† (geometries and results). Calculations have been performed with a homemade version of ORCA 4, of which the access is restricted, but output files and other data are available upon request from the authors.

Conflicts of interest

There are no conflicts to declare.

References

1. A. Rajca, J. Wongsriratanakul and S. Rajca, Science, 2001, 294, 1503–1505.
2. R. Gaudenzi, E. Burzuri, D. Reta, I. D. P. R. Moreira, S. T. Bromley, C. Rovira, J. Veciana and H. S. J. van der Zant, Nano Lett., 2016, 16(3), 2066.
3. M. Slota, A. Keerthi and W. K. Myers, et al. , Nature, 2018, 557, 691–695.
4. (a) S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176; (b) L. Yang, J. J. Oppenheim and M. Dinca, Dalton Trans., 2022, 51, 8583–8587; (c) N. Mavragani, A. A. Kitos, J. L. Brusso and M. Murugesu, Chem. – Eur. J., 2021, 27, 5091–5106; (d) S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144; (e) C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, J. Am. Chem. Soc., 2020, 142, 21197–21209; (f) F. Benner, L. La Droitte, O. Cador, B. Le Guennic and S. Demir, Chem. Sci., 2023, 14, 5577–5592; (g) N. Mavragani, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Inorg. Chem. Front., 2023, 10, 259–266; (h) S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549; (i) G. Huang, C. Daiguebonne, G. Calvez, Y. Suffren, O. Guillou, T. Guizouarn., B. Le Guennic, O. Cador and K. Bernot, Inorg. Chem., 2018, 57(17), 11044–11057; (j) F. Houard, A. Olivier, G. Cucinotta, O. Galangau, M. Gautier, F. Camerel, T. Guizouarn, T. Roisnel, B. Le Guennic, M. Ozerov, Y. Suffren, G. Calvez, C. Daiguebonne, O. Guillou, F. Artzner, M. Mannini and K. Bernot, J. Mater. Chem. C, 2024, 12, 3228–3237; (k) J. Jung, M. Puget, O. Cador, K. Bernot, C. J. Calzado and B. Le Guennic, Inorg. Chem., 2017, 12, 6788–6801; (l) J. Rinehart, M. Fang, W. Evans and J. R. Long, Nature, 2011, 3, 538–542.
5. J. L. Liu, Y. C. Chen and M. L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453.
6. I. Cimatti, X. Yi, R. Sessoli, M. Puget, B. L. Guennic, J. Jung, T. Guizouarn, A. Magnani, K. Bernot and M. Mannini, Appl. Surf. Sci., 2018, 432, 7–14.
7. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
8. H. Kwon, K. R. McClain, J. G. C. Kragskow, J. K. Staab, M. Ozerov, K. R. Meihaus, B. G. Harvey, E. S. Choi, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2024, 146, 18714–18721.
9. M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1967, 101, 247–422.
10. (a) G. David, G. Duplaix-Rata and B. L. Guennic, Phys. Chem. Chem. Phys., 2024, 24, 8952–8964; (b) G. David, N. Ferré and B. L. Guennic, J. Chem. Theory Comput., 2023, 19(1), 157–173; (c) G. David, G. Trinquier and J.-P. Malrieu, J. Chem. Phys., 2020, 153, 194107.
11. J.-P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Chem. Rev., 2014, 114(1), 429–492.
12. (a) G. David, F. Wennmohs, F. Neese and N. Ferré, Inorg. Chem., 2018, 57(20), 12769–12776; (b) G. Duplaix-Rata, B. L. Guennic and G. David, Phys. Chem. Chem. Phys., 2023, 25, 14170–14178; (c) S. Coetzee, M. M. Turnbull, C. P. Landee, J. C. Monroe, M. Deumal, J. J. Novoa and M. Rademeyer, Phys. Chem. Chem. Phys., 2023, 25, 9176–9187.
13. D. J. Lussier, E. Ito, K. R. McClain, P. W. Smith, H. Kwon, R. Rutkauskaite, B. G. Harvey, D. K. Shuh and J. R. Long, J. Am. Chem. Soc., 2024, 146, 21280–21295.
14. Q. Zhao, W. Lv, N. Guo, Y. C. Jia, W. Z. Lv, B. Q. Shao, M. M. Jiao and H. P. You, Dalton Trans., 2013, 42, 6902.
15. CAS number 10138-52-0.
16. CAS number 13818-75-2.

---

Footnote

† Electronic supplementary information (ESI) available: Theory part, computational details, detailed table of data and plot of the magnetic orbitals. See DOI: https://doi.org/10.1039/d4cc03025g

---