The size-dependent valence and conduction band-edge energies of Cu quantum dots

Abstract

Ultra-small metal particles having band gaps are regarded as a new class of functional materials. We investigated the size dependencies of the band-edge energies on Cu quantum-dots in the size range of 0.7–2.1 nm. The extremely high conduction band-edge energies owing to the strong quantum-size effects were observed for sizes below 1 nm.

---

A shiny luster, which originates from the light reflection by their free electrons, is one of the most common characteristics of metals.¹ The continuous energy band of metals around their Fermi level allows the presence of free electrons. When the particle sizes are reduced to a few tens of nanometers, the collective oscillation of the free electrons resonates with visible light and displays brilliant colors, which is called localized surface plasmon resonance (LSPR) (Fig. 1a).² Upon further reduction of the particle size to near their Fermi wavelength (∼0.5 nm for Au), their optical and electronic properties change dramatically.³ In this size region, the electronic structure changes from a metallic to a molecule-like state (Fig. 1c). LSPR absorption is no longer observable due to the absence of free electrons and new absorption edges that originate from the electronic transition across the energy-gap.⁴ In the earlier studies, these tiny particles, mostly called “metal clusters,” were only formed as a cluster ion beam in a vacuum chamber.^4b Since these metal clusters are formed and exist only for a short time in the chamber, their research has been limited to the field of fundamental physical chemistry.^4b,5 Recently, metal clusters were regarded as practical materials owing to the development of large-scale synthetic routes via solution processes.⁶ Thus, these tiny metal clusters are now gathering interest in the field of materials chemistry as a new class of fluorophores and photocatalysts. For example, thiol-protected Au clusters are one of the most studied species.^6a,b They show size-dependent photoluminescence in the UV and near-infrared regions. For Au, the transition from the metallic to the molecule-like state occurs at a size of ∼1.6–1.8 nm (Au₁₄₄–Au₁₈₇).⁷ Thus, the appearance of energy-gap states is not only the case for 2-dimensional clusters having a few-atoms, but also occurs for much larger 3-dimensional particles having a few tens to a few hundreds of atoms. These particles were recognized as metal quantum-dots (QDs) (Fig. 1b).^3a

Fig. 1 Schematic illustration of Cu nanoparticles (Cu NPs), Cu quantum dots (Cu QDs) and Cu clusters.

From the viewpoint of solid-state physics, the formation of electronic gap states with the size reduction of the metal particles is ascribed to quantum size effects, which have been well studied in the field of semiconductors.⁸ When the sizes of the semiconductor particles are similar to their exciton Bohr radius, their band gap energies (E_gs) increase with the size reduction. Therefore, the E_g of QDs is controlled by changing their particle sizes. Semiconductor QDs show size-dependent functionalities, such as color-tunable bright luminescence.^9–12

In the field of photocatalysis, valence and conduction band-edge energies (E_vb and E_cb) are important because the photocatalytic activity strongly depends on the alignment of their energies and the redox potential of the target reactions.^8b,13 Therefore, the photocatalytic reactivities are controllable by changing the sizes of the QDs. For example, the E_vb and E_cb of WO₃ QDs were optimized by controlling their sizes below 1 nm to improve the photocatalytic hydroxylation of benzene.¹⁴ The size dependency of E_vb and E_cb owing to the quantum size effect is theoretically calculated using an effective mass approximation (EMA) method and shows good agreement with experimental values.¹⁵

The aim of the present study is to determine the size dependency of the E_vb and E_cb of Cu QDs by using spectroscopic approaches. Different from Au and Pt, Cu has a relatively high Fermi level in its bulk state.¹⁶ Thus, Cu QDs smaller than 1 nm are excellent candidates for photocatalysts having a high E_cb level. Although the size dependency of the E_vb and E_cb of Cu QDs has been theoretically investigated,¹⁷ experimental work was lacking because of the difficulty of the size-selective synthesis. Previously, our research group found a large expansion of E_g for CuO QDs with sizes below 1 nm, which were synthesized by using pores of porous silicas (PSs) as templates.¹⁸ In the present study, we synthesized Cu QDs through the reduction of CuO QDs and then unveiled the size dependency of the E_vb, and E_cb of the Cu QDs (Fig. 1). In particular, for the 1 nm Cu QDs, an extremely high E_cb was observed, which corresponded to the high photocatalytic reduction ability of the Cu QDs expected from the theoretical study.¹⁹ Furthermore, we found that the band expansion of the metal QDs was explainable via the EMA method by taking into account the physical quantities obtained from a recent spectroscopic study of Cu.²⁰

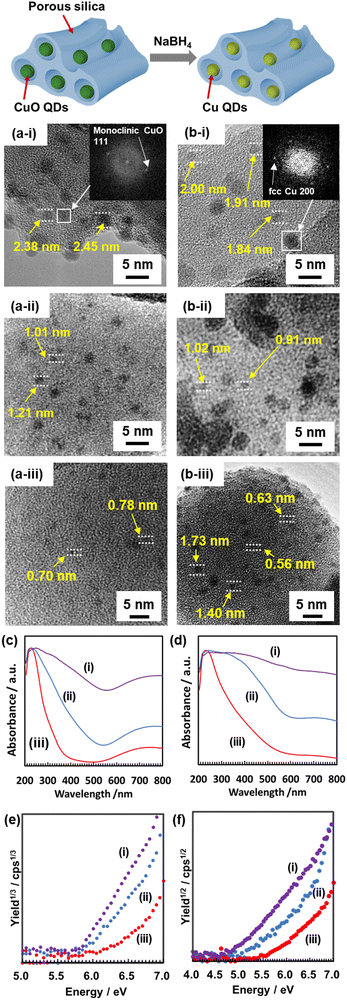
Here, four kinds of PSs with different pore sizes were used as templates for the production of CuO QDs (see Section S2 in the ESI† for the synthesis and analyses of the PSs).²¹ CuO QDs were prepared in the PSs using a simple impregnation method (see Section S3 in the ESI† for the experimental details). As shown in the typical transmission electron microscopy (TEM) images (Fig. 2a, and Fig. S3 in the ESI†), fine particles were prepared in the pores of PSs, and the particle size was well controlled in a range from 0.6 to 2.1 nm. The presence of CuO was confirmed by observing a lattice fringe image and a fast Fourier transform (FFT) pattern corresponding to the (111) plane of monoclinic CuO (inset in Fig. 2a-i). From UV-visible (UV-vis) absorption spectra, we observed a broad absorption of Cu²⁺d–d transition around 800 nm and size-dependent absorption edges around 300 to 500 nm for CuO QDs (see Fig. 2c, Fig. S8 and S9 in the ESI†). As described in our previous study,¹⁸ the band gap energy of the CuO QDs increased remarkably owing to the strong quantum size effect expressed below 2 nm. The detailed band structure analyses of the CuO QDs are described in Section 6 in the ESI.†

Fig. 2 Typical TEM images (a) and (b), UV-vis spectra (c) and (d), and PYSA (e) and (f) of CuO QDs, (a), (c) and (e) and Cu QDs (b), (d) and (f) prepared (i) in C18PS with 5 M solution, (ii) in C18PS with 0.2 M solution, and (iii) in C6PS with 0.05 M solution.

For the Cu QD preparation, a reductant solution of NaBH₄ was injected into the pores of PSs containing CuO QDs. Fig. 2b and Fig. S4 in the ESI† show typical TEM images of Cu QDs. In particular, for Cu QDs, the aggregation and growth of the particles occurred during the high magnitude TEM observations (Fig. S5 in the ESI†). We analyzed the particle size distribution profiles by deconvoluting the primal and large particles formed by electron beam exposure to determine the average size and dispersity of the primal particles from TEM images. The primal particle size of the Cu QDs was well controlled in the range from 0.7 to 2.1 nm. As shown in the inset of Fig. 2b-i, we observed a lattice fringe image and an FFT pattern corresponding to the (200) planes of fcc Cu for the sample after the reduction. This clearly indicates the successful formation of Cu QDs. The presence of Cu QDs was also confirmed by the X-ray absorption near-edge structure (XANES) spectra of the samples before and after the reduction (Fig. S7 in the ESI†). The present Cu QDs show no fluorescence due to the absence of surface passivation agents.

The UV-vis spectra indicate that the absorption energy shifts due to the quantum size effect (Fig. 2d and Fig. S10a in the ESI†). After the reduction, the absorption of the Cu²⁺d–d transition disappeared, and the absorption edges shifted to a lower-energy side. These changes in the UV-vis spectra also indicate the reduction of CuO QDs to Cu QDs. The size dependency of the band gap energies of the Cu QDs was calculated using Tauc plots²² (Fig. S10b in the ESI†) as shown in Fig. 3a. The dotted curve in Fig. 3a represents the theoretical fitting of the present experimental data using an EMA method (see Section S7 in the ESI† for detailed analyses using the EMA method). Adopting a value of μ = 1.15 m₀ as a reduced mass of Cu, the present experimental data were well fitted using the EMA method. For the 2.1 nm Cu particles, the absorption peak assigned to the LSPR was observed at 580 nm (Fig. S11 in the ESI†).²³ Based on this result, the transition from the metallic state (= LSPR active) to the semiconductor-like state occurs at around 2 nm. This threshold diameter is slightly larger than that of the thiolate-protected Au QDs (1.6–1.8 nm).⁷

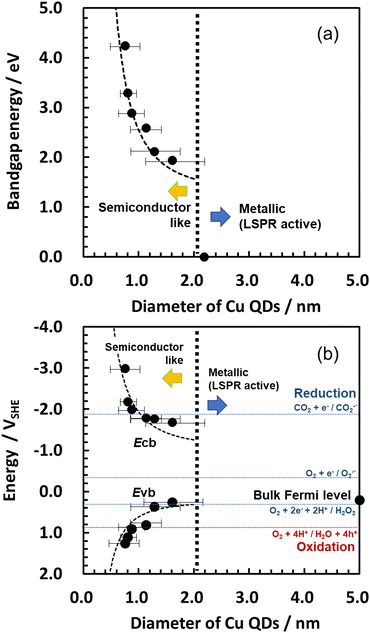Fig. 3 Size dependency of (a) E_g, (b) E_vb, and E_cb for Cu QDs. The dotted curves represent calculation data using an EMA method. Several redox potentials of photocatalytic reactions are represented with horizontal lines. The error bars represent the FWHM of the particle size distribution profiles shown in Fig. S4 (ESI†).

For the band-structure analysis of the Cu QDs, their E_vb was measured using photoemission yield spectroscopy in air (PYSA) (Fig. 2f and Fig. S13 in the ESI†) (Fig. 2e and Fig. S12 in the ESI† show the PYSA spectra for CuO QDs).²⁴ PYSA is a powerful tool for investigating the E_vb for semiconductors and the Fermi level for metals. The PYSA stimulation with very weak UV light (10–100 nW, 4.0–7.0 eV) under ambient conditions is a suitable method to determine the E_vb of QDs, which is sensitive to the measurement conditions.^24b By combining the E_g obtained from UV-vis spectra and the E_vb obtained from PYSA, the size dependency of the E_vb and E_cb of Cu QDs was obtained and is summarized in Fig. 3b (see Section S6 in the ESI† for detailed analyses). Both the E_vb and E_cb show dramatic shifts below 1 nm. The energy shift of the E_cb is larger than that of the E_vb. This is in contrast to the case of CuO QDs (Fig. S14 in the ESI†). The present experimental values were fitted via EMA separately for the E_vb and E_cb. Since the electronic configuration of a Cu atom is described as 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹ 4p⁰, the partially filled 4s orbitals mainly contribute to the occupied energy state around the Fermi level.^17b When the quantum size effect became significant, this orbital shifts to the lower-energy side and forms a valence band. On the other hand, unoccupied energy states, which are mainly formed by 4p orbitals, exist above the Fermi level. Recently, Sonoda found that the lowest unoccupied bulk electronic state of Cu lies 1.24 eV above the Fermi level (structure D in the article) by using angle-resolved two-photon photoemission spectroscopy.²⁰ This energy state shifts to the higher-energy side and constructs the conduction-band edge owing to the quantum size effect. The effective mass of the electron in this state was estimated to be 1.67 m₀. Therefore, we used the following physical quantities for the EMA fitting: E_cb(bulk) = −1.03 V_SHE, E_vb(bulk) = +0.21 V_SHE, m_e = 1.67 m₀, μ = 1.15 m₀, and m_h = 3.69 m₀ (see Section S7 in the ESI† for details of the EMA method). Using these values, the present experimental data were well fitted with EMA (Fig. 3b). Therefore, similar to the semiconductor QDs, the formation of the band gap states and their expansion due to the size reduction of metal QDs are explainable with a theory based on the quantum size effects of nanoparticles. The present results show a similar tendency with previous studies.^4b,19b

Here, the E_cb for 1 nm QDs exceeds −2.0 V_SHE and shifts to −3.0 V_SHE for 0.7 nm Cu QDs. These E_cb values are higher than those of the single-electron reduction potential of O₂ (−0.35 V_SHE)²⁵ and CO₂ (−1.90 V_SHE).²⁶ Thus, as described in the previous molecular orbital calculations, Cu QDs are efficient photocatalysts, especially for the reduction reaction. Cysteine-capped Cu₁₀ was reported to have high photocatalytic activity for the degradation of an organic dye.^19b This is probably due to the high E_cb, which produces highly active superoxide radicals. The Cu₁₀ also has high stability against aerobic oxidation owing to its low HOMO level expected in the previous study.^19b In the present study, we experimentally observed the low E_vb levels (+ 1.26 V_SHE), which were located below the reduction potential of molecular oxygen for 0.7 nm Cu QDs.²⁵ Taking the relationship between the E_vb and the particle sizes into account, oxidative stability is expected for Cu QDs smaller than 2 nm. However, the E_vb levels of the Cu QDs were only slightly lower than the oxidation potential of water.²⁵ Thus, relatively low efficiency is expected for the photocatalytic water oxidation. The construction of a Z-scheme hetero-junction²⁷ with oxide semiconductors is required for the best photocatalytic performance of the Cu QDs.

In summary, we produced Cu QDs of various sizes, ranging from 0.7 to 2.1 nm, by reducing CuO QDs synthesized in the pores of PSs. The size dependency of their E_vb and E_cb was investigated experimentally using UV-vis and PYSA techniques. We observed a significant shift in the E_vb and E_cb, which was due to strong quantum size effects when the particle sizes were below 1 nm. Since the E_cb for 0.7 nm Cu QDs exceeds the single-electron reduction potentials of O₂ and CO₂, Cu QDs would be potential candidates for efficient photocatalysts for the reduction reactions.

We thank Dr Y. Nakajima (RIKEN KEIKI Co., Ltd.) for helpful discussions and kind assistance with the PYSA experiments. We thank Dr T. Kaya (Keio University) for the TEM experiments. This work was partially supported by JSPS KAKENHI grant number JP21H01627.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. M. A. White, Physical Properties of Materials, CRC Press, Boca Raton, 2018, pp. 47.
2. K. M. Mayer and J. H. Hafner, Chem. Rev., 2011, 111, 3828.
3. (a) J. Zheng, P. R. Nicovich and R. M. Dickson, Annu. Rev. Phys. Chem., 2007, 58, 409; (b) Y. Lu and W. Chen, Chem. Soc. Rev., 2012, 41, 3594.
4. (a) W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611; (b) K. J. Taylor, C. L. Pettiette-Hall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 96, 3319.
5. (a) A. Sebetci and Z. B. Güvenç, Surf. Sci., 2003, 525, 66; (b) M. A. Tafoughalt and M. Samah, Comput. Theor. Chem., 2014, 1033, 23; (c) T. Tsuneda, J. Comput. Chem., 2019, 40, 206.
6. (a) J. Zheng, C. Zhang and R. M. Dickson, Phys. Chem. Lett., 2004, 93, 077402-1; (b) K. G. Stamplecoskie and P. V. Kamat, J. Am. Chem. Soc., 2014, 136, 11093; (c) I. Chakraborty, R. G. Bhuin, S. Bhat and T. Pradeep, Nanoscale, 2014, 6, 8561; C. Vázquez-Vázquez, M. Bañobre-López, A. Mitra, M. A. López-Quintela and J. Rivas, Langmuir, 2009, 25, 8208; (d) T. Imaoka and K. Yamamoto, Bull. Chem. Soc. Jpn., 2019, 92, 941.
7. Y. Negishi, T. Nakazaki, S. Malola, S. Takano, Y. Niihori, W. Kurashige, S. Yamazoe, T. Tsukuda and H. Hakkinen, J. Am. Chem. Soc., 2015, 137, 1206.
8. (a) F. P. García de Arquer, D. V. Talapin, V. I. Klimov, Y. Arakawa, M. Bayer and E. H. Sargent, Science, 2021, 373, eaaz8541; (b) D. Kandi, S. Martha and K. M. Parida, Int. J. Hydrogen Energy, 2017, 42, 9467.
9. M. L. Landry, T. E. Morrell, T. K. Karagounis, C. H. Hsia and C. Y. Wang, J. Chem. Educ., 2014, 91, 274.
10. M. Shen, W. Jia, Y. You, F. Li, S. Tian, J. Li, Y. Jin and D. Han, Nanoscale Res. Lett., 2013, 8, 253.
11. H. R. You, J. Y. Park, D. H. Lee, Y. Kim and J. Choi, Appl. Sci., 2020, 10, 975.
12. T. Nakotte, H. Luo and J. Pietryga, Nanomaterials, 2020, 10, 172.
13. (a) T. Inoue, A. Fujishima, S. Konishi and K. Honda, Nature, 1979, 277, 637; (b) T. Suzuki, H. Watanabe, Y. Oaki and H. Imai, Chem. Commun., 2016, 52, 6185.
14. A. Ohno, H. Watanabe, T. Matsui, S. Somekawa, M. Tomisaki, Y. Einaga, Y. Oaki and H. Imai, Catal. Sci. Technol., 2021, 11, 6537.
15. (a) L. Brus, J. Phys. Chem., 1986, 90, 2555; (b) F. Rodríguez-Mas, J. C. Ferrer, J. L. Alonso, D. Valiente and S. Fernández de Ávila, Crystals, 2020, 10, 226.
16. T. Tani, J. Soc. Photogr. Imaging Jpn., 2015, 78, 16.
17. (a) M. Kabir, A. Mookerjee and A. K. Bhattacharya, Eur. Phys. J. D, 2004, 31, 477; (b) C. G. Li, Z. G. Shen, Y. F. Hu, Y. N. Tang, W. G. Chen and B. Z. Ren, Sci. Rep., 2017, 7, 1345; (c) U. J. Rangel-Peña, R. L. Camacho-Mendoza, S. González-Montiel, L. Feria and J. Cruz-Borbolla, Clust. Sci., 2021, 32, 1155.
18. H. Tamaki, H. Watanabe, S. Kamiyama, Y. Oaki and H. Imai, Angew. Chem., Int. Ed., 2014, 53, 10706.
19. (a) S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902; (b) S. Huseyinova, J. M. B. Trillo, J. M. Ramallo-López, F. G. Requejo, D. Buceta and M. A. López-Quintela, Phys. Chem. Chem. Phys., 2023, 25, 6025.
20. Y. Sonoda, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245410.
21. H. Watanabe, K. Fujikata, Y. Oaki and H. Imai, Microporous Mesoporous Mater., 2015, 214, 41.
22. J. Tauc, Mater. Res. Bull., 1970, 5, 721.
23. P. Liu, H. Wang, X. Li, M. Rui and H. Zeng, RSC Adv., 2015, 5, 79738.
24. (a) D. Yamashita, Y. Nakajima, A. Ishizaki and M. Uda, J. Surf. Anal., 2008, 14, 433; (b) J. Jasieniak, M. Califano and S. E. Watkins, ACS Nano, 2011, 5, 5888; (c) E. O. Kane, Phys. Rev., 1962, 127, 131.
25. W. H. Koppenol, D. M. Stanbury and P. L. Bounds, Free Radical Biol. Med., 2010, 49, 317.
26. S. Lu, F. Lou and Z. Yu, Catalysts, 2022, 12, 228.
27. B.-J. Ng, L. K. Putri, X. Y. Kong, Y. W. The, P. Pasbakhsh and S.-P. Chai, Adv. Sci., 2020, 7, 1903171.

---

Footnote

† Electronic supplementary information (ESI) available: (1) Materials. (2) Preparation and characterization of porous silicas. (3) Preparation and characterization of the CuO QDs and Cu QDs. (4) Particle size analysis of the CuO QDs and Cu QDs. (5) Determination of the valence states of the CuO QDs and Cu QDs by X-ray absorption near-edge structure measurements. (6) Determination of the band structures of the CuO QDs and Cu QDs. (7) Curve fitting with effective mass approximation (EMA) for the CuO QDs and Cu QDs. See DOI: https://doi.org/10.1039/d4cc00260a

---