Open Access Article
Open Access ArticleGeminal bimetallic coordination of a carbone to main-group and transition metals†
Akachukwu D.
Obi
 a,
Chun-Lin
Deng
b,
Andrew J.
Alexis
a,
Diane A.
Dickie
a,
Chun-Lin
Deng
b,
Andrew J.
Alexis
a,
Diane A.
Dickie
 a and
Robert J.
Gilliard
Jr
*b
a and
Robert J.
Gilliard
Jr
*b
aDepartment of Chemistry, University of Virginia, 409 McCormick Road, PO Box 400319, Charlottesville, Virginia 22904, USA
bDepartment of Chemistry, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Building 18-596, Cambridge, MA 02139-4307, USA. E-mail: gilliard@mit.edu
First published on 16th January 2024
Abstract
The non-bonding carbone lone pair in geometrically-constrained antimony and bismuth carbodiphosphorane complexes readily complexed AuCl to afford rare examples of geminal bimetallic carbone coordination featuring a main-group metal.
Since the introduction of hexaphenylcarbodiphosphorane (C(PPh3)2 or CDP) by Ramirez et al. in 1961, the bonding situation of the divalent carbon center has been the subject of much debate.1 However, the turn of the century witnessed remarkable advances in the experimental and theoretical elucidation of carbones (CL2), which are now widely recognized as double Lewis bases comprised of two orthogonal (σ- and π-symmetric) lone pairs within a formally C(0) atom.2 This facilitated their increased adoption as electronically-flexible ligands, which can serve as two- or four-electron donors depending on their coordination environment.3 While the stabilization of main-group Lewis acids through only one carbone lone pair (type I) is now ubiquitous in literature, complexes involving the contribution of both lone pairs (types II and III) are sparse (Fig. 1).
Coordination type II to double Lewis acids (mononuclear centers possessing acceptor σ and π orbitals) are of fundamental importance as they represent a non-reductive approach to carbon-element multiple bonding through the formation of novel double dative C⇉E bonding.4 Achieving this bonding situation depends on both metal Lewis acidity and orbital geometry. Carbone bonding to the hardest double Lewis acid Be2+ forms predominantly C→Be σ-donation (type I) in monodentate (carbone)BeCl2 complexes,5 where further interactions (types II or III) are inhibited by unfavorable stereoelectronics. Examples of C⇉E multiple bonding in comparative p-block element complexes (E = B, Ge, Sb, Bi) were typically promoted by cationization to enhance the electrophilicity of the Lewis acid.6 The elusive C⇉Be bond was recently achieved within an ortho-beryllated carbodiphosphorane (Be(CDP)), wherein the overlap of beryllium and carbone frontier orbitals were enhanced by encapsulating the metal within the tridentate ligand.7
Heteronuclear coordination (type III) establishes the intrinsic nature of carbones as containing stereochemically active lone pairs,8 but remains underdeveloped and extremely rare among main-group elements (MGEs).9 Indeed, this contrasts the affinity of main-group Lewis acids to form bimetallic complexes with double Lewis bases such as chalcogenides via non-covalent interactions.10 Petz, Neumüller, Frenking, and coworkers reported a gem-diborylated carbone complex in 2009 in their reaction of CDP and BH3, which afforded [(CDP)(B2H5)][BH4], presumably via (CDP)(BH3)2.11 A recently isolated Li2(CDP) etherate features a bimetallic MGE carbone complex stabilized by a kinetic chelating effect,12 although quantum chemical studies were not performed for comparisons with (CDP)(BH3)2. As these instances feature small 2nd row MGEs (Li, B), we sought to investigate this bonding scenario for larger main-group Lewis acids and its implications for their reactivity profiles.
We recently discovered that ortho-bismuthination of CDP yields predominantly C→Bi σ-donor interactions,13 which contrasts C⇉Bi interactions in the simple coordination adducts.6c,d,14 The constrained carbone interaction in the former is robust and yielded air-stable complexes with enhanced activity for Bi(II)/Bi(III) redox catalysis.13,15 However, the see-saw geometry of the four-coordinate Bi(III) center is not symmetry correct for proper overlap with the carbone π lone pair. Encouraged by the robust nature of this framework, we anticipated that the non-bonding lone pair may readily complex metallic electrophiles to achieve novel bimetallic carbone coordination to heavy MGEs.11 We now report the isolation and bonding analyses of carbodiphosphorane antimony and bismuth complexes involving bis(metalated) carbone centers, obtained by reactions of geometrically constrained carbone-pnictogen complexes and AuCl.
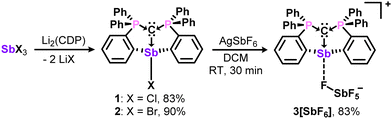
For comparisons with their bismuth analogues, the antimony complexes 1-3 were prepared in likewise manner,13 and isolated as analytically pure white solids in 83 – 90% yields (Scheme 1). Characterization by 31P{1H} and 13C{1H} NMR spectroscopy reveal upfield resonances for the phosphorous and ylidic carbon atoms, which may be diagnostic of metal Lewis acidity.16 However, 3+, like the bismuth analogue, is a weak Lewis acid and does not complex triethylphosphine oxide for quantitative analysis via the Gutmann-Beckett method. The fluoride ion affinity (FIA) values in CH2Cl2 (calculated at PW6B95-(D3BJ)/def2-TZVPP level of theory) are comparable for 3+ (156 kJ mol−1) and the Bi analogue (146 kJ mol−1), and contrasts the superacidic nature of the monodentate carbodicarbene adducts.6c
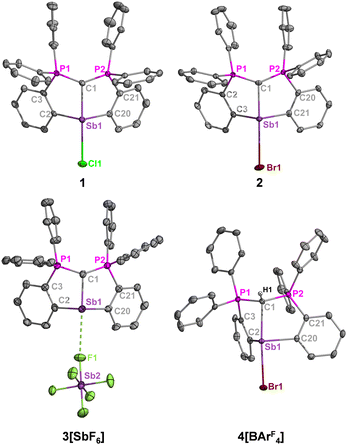
In their solid-state structures (Fig. 2), 1 and 2 feature the anticipated trans carbone-metal-halide ligation observed at bismuth, resulting in highly elongated Sb–Cl (2.8382(10) Å vs 2.39 for ∑Rcov) and Sb–Br (3.1063(10) Å vs 2.54 for ∑Rcov) bonds, which are comparable to the bismuth analogues.13 Solvent interactions through halide hydrogen bonding also contribute to the elongated metal-halide bonds. Charge separation in 3[SbF6] resulted in a downfield 31P NMR shift and shortened carboneC–Sb bond length compared to 1 and 2 (Fig. 2 caption) due to enhanced metal Lewis acidity.
Compound 3[SbF6] is further stabilized by weak cation–anion contacts. Attempts to isolate a fully charge separated complex without cation–anion contacts by the reaction of 2 and Na[BArF4] (ArF = 3,5-(CF3)2C6H3) led to the protonated adduct [H(CDP)SbBr][BArF4] (4[BArF4]) due to hydrolysis by adventitious moisture. Because the anticipated [(CDP)M][BArF4] complex was successfully isolated for bismuth under the same reaction and solvent conditions,13 it is suspected that the cationic unit in this framework is more reactive for antimony than bismuth, which is consistent with reports by Gabbai,17 Venugopal,18 and our laboratory,6c who observed higher Lewis acidity for Sb versus Bi cations with the same ligand environments. The phosphorus resonance for 4[BArF4] (δP = 28.0 ppm) is slightly upfield from 2 (δP = 31.7 ppm), but the 13C{1H} NMR spectrum reveals more dramatic differences whereby the ylidic carbon resonance for 4[BArF4] (δC = 16.3 ppm, 1JCP = 62.5 Hz) is similarly upfield from 2 (δC = 6.4 ppm, 1JCP = 99.1 Hz) but extends a much smaller 1J(13C–31P) coupling constant.
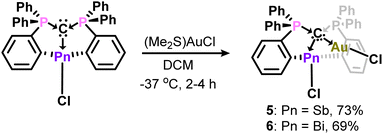
Having established structural and spectroscopic similarities between these antimony complexes and their bismuth analogues, we probed the potential for geminal bimetallic coordination at the carbone center. The reaction of 1 or (CDP)BiCl with (Me2S)AuCl readily affords the anticipated coordination adducts 5 and 6 as colorless solids (Scheme 2). Upon isolation, 5 and 6 are stable as solids for several weeks under ambient conditions, but rapidly decompose in solution (CH2Cl2) within 30–45 minutes by gradually depositing a gold film on the walls of the reaction flask. Despite their extreme sensitivity, compounds 5 and 6 were isolated in 69–73% yields as single crystals, which were grown by combining concentrated, cold DCM solutions of their respective reagents and immediately storing at −37 °C in the dark for two (6) or four (5) hours.
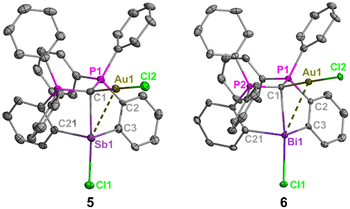
The phosphorus resonances of 5 (δP = 30.1 ppm) and 6 (δP = 32.8 ppm) suggest electronic similarities between these compounds in solution. Notably, the phosphorus resonance of 5 is comparable to that of 1 (δP = 29.5 ppm), but the formation of a new product was confirmed by unique 1H and 13C{1H} NMR resonances, combustion microanalysis, and X-ray crystallography (Fig. 3). The 1J(13C–31P) coupling constant for the ylidic carbon in 6 (50.9 Hz) is smaller than those of (CDP)BiCl (98 Hz) and [H(CDP)BiCl][BPh4] (70.7 Hz), which further highlights the diverse nature of carbone coordination in these bismuth complexes. Similar comparisons were not possible for 5, as the ylidic carbon was not observed in the 13C{1H} NMR spectrum due to its poor solubility and propensity to rapidly decompose in solution.
The carbone-pnictogen bonds of compounds 5 (2.453(6) Å) and 6 (2.574(4) Å) are elongated from their starting materials, and expectedly shorter for 5 compared to 6. Indeed, they are comparable to the carbone-pnictogen bonds of the protonated adducts (e.g., 4+ and [H(CDP)BiCl]+), suggesting similarities in the coordination mode of the carbone. The geometry about the carbone is a distorted tetrahedron, and the P1–C1–P2 bond angles (Fig. 3 caption) are comparable to 4+, as well as the gem-diborylated11 and -diaurated8b complexes. The carboneC1–Au and Au–Cl bond distances are each identical in 5 and 6, and their Au–pnictogen interactions are comparable and within the anticipated van der Waals radii for Sb–Au (rW = 3.72 Å) and Bi–Au (rW = 3.73 Å) aurophilic interactions.
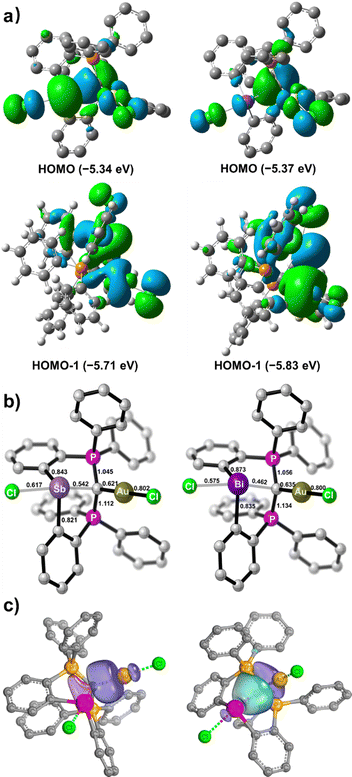
To gain more insight into the bonding nature of the bimetallic complexes 5 and 6, DFT calculations at the BP86-D3(BJ)/def2-TZVP level of theory were performed. When the implicit solvation model (PCM, DCM) was included, the optimized geometrical parameters agree with those observed for the crystal structures, as discussed in our previous report.13 The HOMOs of 5 and 6 are located on the gem-dimetalated structural units with contributions from the carbone π electron and Au d orbitals (Fig. 4a). The lone pair from the Sb(III) atom in 5 features the largest HOMO orbital coefficient (28.3%), while the lone pair of the Bi(III) atom in 6 only has a small contribution (8.6%) to its HOMO. The two-armed PPh3 in the CDP unit contribute predominantly to the energetically close-lying LUMO and LUMO+1 of 5 and 6 (Fig. S21 and S22, ESI†).
The Mayer bond indices are comparable for the C1–Au bonds in 5 (0.62) and 6 (0.64), but significantly higher for C1–Sb (0.54) than C1–Bi (0.46). These values are indicative of single dative bond characters (Fig. 4b). Intrinsic bond orbital (IBO) analyses for 5 and 6 reveal that there are one polarized 2c–2e σ-bonding feature for C1–Au, and three σ-bonds between the CDP moiety and the Sb or Bi atom (Fig. 4c and Fig. S20, ESI†). Specifically, the carbone π and σ electrons interact with the σ* orbitals of Au–Cl and Sb–Cl or Bi–Cl, respectively, which are consistent with the frontier orbital analyses (Fig. 4a). Quantum theory of atoms-in-molecules (QTAIM) analyses corroborate these observations (Tables S2 and S3, ESI†). Thus, 5 and 6 are the first examples of geminal bimetallic CDP coordination to both main-group and transition metals.
Table 1 highlights some electronic features of the carbone-gold coordination. The calculated C1–Au bond dissociation energies (in CH2Cl2) in 5 (55.6 kcal mol−1) and 6 (57.2 kcal mol−1) suggest that AuCl coordination is strongly favored and deauration is not facile. Therefore, the rapid decomposition of 5 and 6 in CH2Cl2 likely does not result from initial deauration, but may proceed through alternative pathways. The stronger C1–Au interaction in 6 is likely due to a weaker Bi–C1 interaction compared to Sb–C1.
In conclusion, we have isolated and characterized rare examples of gem-dimetalated main-group carbone complexes. This coordination mode is a fundamental feature of double Lewis bases in bonding, widely observed in chalcogenide main-group metal complexes, but hitherto unobserved in likewise manner for carbones. Therefore, these complexes further highlight the electronic flexibility of carbones at main-group metal centers, and may have significant implications for carbone-stabilized heterobimetallic reactivities.
The authors acknowledge support and funding from the David and Lucile Packard Foundation, Research Computing at the Massachusetts Institute of Technology (Supercloud), and the National Science Foundation MRI program (CHE-2018870).
Conflicts of interest
There are no conflicts to declare.Notes and references
-
(a) F. Ramirez, N. B. Desai, B. Hansen and N. McKelvie, J. Am. Chem. Soc., 1961, 83, 3539–3540 CrossRef CAS
; (b) N. D. Jones and R. G. Cavell, J. Organomet. Chem., 2005, 690, 5485–5496 CrossRef CAS
; (c) H. Schmidbaur, Angew. Chem., Int. Ed., 2007, 46, 2984–2985 CrossRef CAS PubMed
; (d) G. Frenking, B. Neumüller, W. Petz, R. Tonner and F. Öxler, Angew. Chem., Int. Ed., 2007, 46, 2986–2987 CrossRef
.
-
(a) R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Angew. Chem., Int. Ed., 2006, 45, 8038–8042 CrossRef CAS PubMed
; (b) R. Tonner and G. Frenking, Chem. – Eur. J., 2008, 14, 3260–3272 CrossRef CAS PubMed
; (c) V. H. Gessner, Modern ylide chemistry: applications in ligand design, organic and catalytic transformations, Springer, 2018 Search PubMed
; (d) A. L. Liberman-Martin, Cell Rep. Phys. Sci., 2023, 4, 101519 CrossRef CAS
; (e) R. W. A. Havenith, A. V. Cunha, J. E. M. N. Klein, F. Perolari and X. Feng, Phys. Chem. Chem. Phys., 2021, 23, 3327–3334 RSC
.
-
(a) S.-k Liu, W.-C. Chen, G. P. A. Yap and T.-G. Ong, Organometallics, 2020, 39, 4395–4401 CrossRef CAS
; (b) B. S. Aweke, C.-H. Yu, M. Zhi, W.-C. Chen, G. P. A. Yap, L. Zhao and T.-G. Ong, Angew. Chem., Int. Ed., 2022, 61, e202201884 CrossRef CAS PubMed
; (c) L. Zhao, C. Chai, W. Petz and G. Frenking, Molecules, 2020, 25, 4943–4990 CrossRef CAS PubMed
; (d) W.-C. Chen, J.-S. Shen, T. Jurca, C.-J. Peng, Y.-H. Lin, Y.-P. Wang, W.-C. Shih, G. P. A. Yap and T.-G. Ong, Angew. Chem., Int. Ed., 2015, 54, 15207–15212 CrossRef CAS PubMed
.
-
(a) M. Hermann and G. Frenking, Chem. – Eur. J., 2017, 23, 3347–3356 CrossRef CAS PubMed
; (b) M. A. L. Johansen and A. Ghosh, Nat. Chem., 2023, 15, 1042 CrossRef CAS PubMed
.
-
(a) J. E. Walley, G. Breiner, G. Wang, D. A. Dickie, A. Molino, J. L. Dutton, D. J. D. Wilson and J. R. J. Gilliard, Chem. Commun., 2019, 55, 1967–1970 RSC
; (b) W. Petz, K. Dehnicke, N. Holzmann, G. Frenking and B. Neumüller, Z. Anorg. Allg. Chem., 2011, 637, 1702–1710 CrossRef CAS
.
-
(a) S. Khan, G. Gopakumar, W. Thiel and M. Alcarazo, Angew. Chem., Int. Ed., 2013, 52, 5644–5647 CrossRef CAS PubMed
; (b) B. Inés, M. Patil, J. Carreras, R. Goddard, W. Thiel and M. Alcarazo, Angew. Chem., Int. Ed., 2011, 50, 8400–8403 CrossRef PubMed
; (c) L. S. Warring, J. E. Walley, D. A. Dickie, W. Tiznado, S. Pan and R. J. Gilliard Jr, Inorg. Chem., 2022, 61, 18640–18652 CrossRef CAS PubMed
; (d) J. Walley, L. Warring, G. Wang, D. A. Dickie, S. Pan, G. Frenking and R. J. Gilliard, Angew. Chem., Int. Ed., 2021, 60, 6682–6690 CrossRef CAS PubMed
; (e) K. K. Hollister, A. Molino, G. Breiner, J. E. Walley, K. E. Wentz, A. M. Conley, D. A. Dickie, D. J. D. Wilson and R. J. Gilliard, J. Am. Chem. Soc., 2022, 144, 590–598 CrossRef CAS PubMed
; (f) C.-L. Deng, A. D. Obi, B. Y. E. Tra, S. K. Sarkar, D. A. Dickie and R. J. Gilliard, Nat. Chem., 2023 DOI:10.1038/s41557-023-01381-0
.
- M. R. Buchner, S. Pan, C. Poggel, N. Spang, M. Müller, G. Frenking and J. Sundermeyer, Organometallics, 2020, 39, 3224–3231 CrossRef CAS
.
-
(a) C. Esterhuysen and G. Frenking, Chem. – Eur. J., 2011, 17, 9944–9956 CrossRef CAS PubMed
; (b) J. Vicente, A. R. Singhal and P. G. Jones, Organometallics, 2002, 21, 5887–5900 CrossRef CAS
; (c) M. Alcarazo, C. W. Lehmann, A. Anoop, W. Thiel and A. Fürstner, Nat. Chem., 2009, 1, 295–301 CrossRef CAS PubMed
.
- M. Fustier-Boutignon, N. Nebra and N. Mézailles, Chem. Rev., 2019, 119, 8555–8700 CrossRef CAS PubMed
.
-
(a) K. T. Mahmudov, A. V. Gurbanov, V. A. Aliyeva, M. F. C. Guedes da Silva, G. Resnati and A. J. L. Pombeiro, Coord. Chem. Rev., 2022, 464, 214556 CrossRef CAS
; (b) F. A. Devillanova and W.-W. Du Mont, Handbook of chalcogen chemistry: new perspectives in sulfur, selenium and tellurium, Royal Society of Chemistry, 2013 Search PubMed
.
- W. Petz, F. Öxler, B. Neumüller, R. Tonner and G. Frenking, Eur. J. Inorg. Chem., 2009, 4507–4517 CrossRef CAS
.
- S. C. Böttger, C. Poggel and J. Sundermeyer, Organometallics, 2020, 39, 3789–3793 CrossRef
.
- A. D. Obi, D. A. Dickie, W. Tiznado, G. Frenking, S. Pan and R. J. Gilliard Jr, Inorg. Chem., 2022, 61, 19452–19462 CrossRef CAS PubMed
.
- J. E. Münzer, N.-J. H. Kneusels, B. Weinert, B. Neumüller and I. Kuzu, Dalton Trans., 2019, 48, 11076–11085 RSC
.
- The isostructural phosphorus species was recently isolated, and enabled metallomimetic P(iii)/P(v) redox catalysis. See K. Chulsky, I. Malahov, D. Bawari and R. Dobrovetsky, Metallomimetic Chemistry of a Cationic, Geometrically Constrained Phosphine in the Catalytic Hydrodefluorination and Amination of Ar–F Bonds, J. Am. Chem. Soc., 2023, 145, 3786–3794 CrossRef CAS PubMed
.
-
(a) P. Erdmann and L. Greb, Angew. Chem., Int. Ed., 2022, 61, e202114550 CrossRef CAS PubMed
; (b) Q. Teng and H. V. Huynh, Dalton Trans., 2017, 46, 614–627 RSC
.
- G. Park, D. J. Brock, J.-P. Pellois and F. P. Gabbaï, Chemistry, 2019, 5, 2215–2227 CrossRef CAS PubMed
.
- D. Sharma, S. Balasubramaniam, S. Kumar, E. D. Jemmis and A. Venugopal, Chem. Commun., 2021, 57, 8889–8892 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, NMR spectra, crystallographic refinement details, computational details (PDF). CCDC 2312268–2312274. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cc06226k |
| This journal is © The Royal Society of Chemistry 2024 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: