Molecular baskets form inclusion complexes with phenethylamine drugs in water

Abstract

Molecular basket 1⁶⁻ comprising a nonpolar cavity and an anionic nest of six carboxylates at its rim was found to form inclusion complexes with (1R, 2S)-ephedrine, (1R, 2R)-pseudoephedrine, and (1S, 2R)-tranylcypromine. Experimental results (NMR) and theory (MM/DFT) suggest the basket encapsulates phenethylamines in unique and predictable fashion.

---

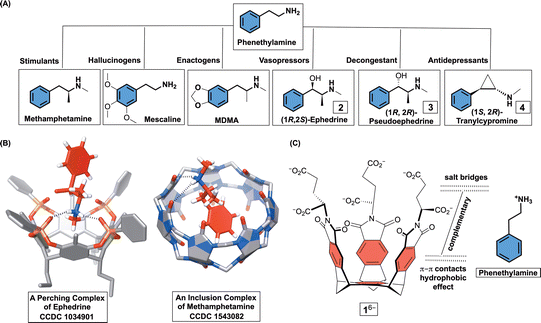
Substituted phenethylamines (Fig. 1A) are organic molecules with the 2-phenylethan-1-amine framework and a broad range of biological activities. To mention a few, phenethylamines include stimulants (e.g., methamphetamine), hallucinogens (e.g., mescaline), entactogens (e.g. MDMA), vasopressors (e.g., ephedrine), decongestants (e.g., pseudoephedrine), bronchodilators (e.g., albuterol), and antidepressants (e.g., tranylcypromine).¹ With facile access to a great number of phenethylamines,² there has been a considerable interest toward derivatizing their framework and examining potentially novel pharmacological effects.³ In this vein, development of more potent but also cheap hallucinogens and stimulants⁴ is having a negative impact on society by expanding the drug epidemic and illicit activities.⁵ Accordingly, supramolecular chemists have used macrocyclic hosts (i.e., cavitands) for examining facile detection,⁶ resolution,^1e,7 and sequestration⁸ of phenethylamine drugs. The rationale behind these studies is to use functionalized but also conformationally restricted cavitands for complementing ammonium and/or phenyl units within targeted compound. In the cases of resorcin[4]arenes^1e and cucurbit[6]urils,^1d,6c,9 the formation of perching complexes ensued in polar solvents and/or solid state with cavitands’ polar rim holding onto the ammonium site of phenethylamines via hydrogen bonding (Fig. 1B). With cucurbit[7]urils,^6a calix[4]arenes^8b β,γ-cyclodextrins,¹⁰ pillar[5]arenes,¹¹ and pillar[6]arenes,^8a the phenyl group was found to, in aqueous media, insert into each host's nonpolar cavity thereby placing the ammonium at the polar rim to form hydrogen bonds (Fig. 1B). We wondered, would molecular basket 1⁶⁻ (Fig. 1C), comprising a nonpolar cavity and an anionic nest of six carboxylates at the rim (i.e., three glutamic acid residues),¹² form an inclusion complex with positively charged phenethylamines in water? In this regard, easily accessible and enantiopure (1R, 2S)-ephedrine 2, (1R, 2R)-pseudoephedrine 3, and (1S, 2R)-tranylcypromine 4 (Fig. 1A) seemed suitable for the study. While these drugs appeared to have structural complementarity to 1⁶⁻ (Fig. 1C), we were curious about the exact mode of interaction (i.e., stoichiometry and docking geometry)¹³ as well as the stability of these complexes. In fact, host 1⁶⁻ was previously shown to form inclusion complexes with organophosphorus agents (OPs)¹⁴ and α,ω-diammonium alkanes^13,15 with millimolar (or even greater) stabilities. While nonpolar P–CH₃/P–OCH₃ groups from OPs occupy the inner space of 1⁶⁻, polar P = O units reside at the rim of binary [OPs⊂1]⁶⁻. In the case of diammonium alkanes, two RNH₃⁺ groups would form salt bridges with α- and γ-carboxylates from two molecules of 1⁶⁻ surrounding the guest to give a ternary complex.¹⁵

Fig. 1 (A) Chemical structures of selected phenethylamine drugs and their biological functions. (B) Line representations of X-ray structures of a derivative of resorcin[4]arene holding ephedrine at its top (CCDC 1034901) and cucurbit[7]uril forming an inclusion complex with methamphetamine (CCDC 1543082). (C) Chemical structures of basket 1⁶⁻ and phenethylammonium cation showing their structural and electronic complementarity.

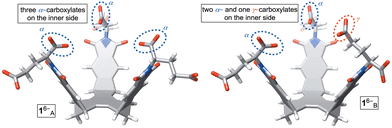
Molecular basket 1 was obtained by following an earlier described synthetic protocol.¹² This molecule can be dissolved in aqueous 30 mM phosphate buffer solution (PBS) at pH = 7.0 to give hexaanionic 1⁶⁻. At concentrations of 5.0 mM or lower, amphiphilic 1⁶⁻ was shown to be monomeric with results from DLS, UV-Vis, MS, and NMR experiments all suggesting the absence of aggregation.¹² Importantly, ¹H NMR spectrum of 1⁶⁻ (Fig. 3A) comprises a set of sharp signals corresponding to, on average, a C₃ symmetric compound. A Monte Carlo conformational search (OPLS3) in implicit water solvent showed the presence of two conformers 1_A/B⁶⁻ within 1 kcal mol⁻¹ (Fig. 2; Table S3, ESI†); each conformer was additionally optimized at a higher level of theory (DFT:B3LYP/6-31+G*). While 1_A⁶⁻ has all three α-carboxylates from glutamic acid residues pointing to the concave side of the host, 1_B⁶⁻ has one of these carboxylates at the convex face. Along with computational results, we reasoned that a rapid interconversion of 1_A⁶⁻ to 1_B⁶⁻ (Fig. 2), in addition to each molecule's conformational dynamics, contributed to the observed ¹H NMR spectrum of 1⁶⁻.

Fig. 2 Stick representations of two most stable conformers (Monte Carlo, OPLS3) of basket 1⁶⁻. Conformers 1_A⁶⁻ (top) and 1_A⁶⁻ (bottom) are energy optimized using density functional theory (B3LYP/6-31+G*).

Fig. 3 (A) ¹H NMR spectra of basket 1⁶⁻ (30 mM PBS at pH = 7.0) obtained after incremental addition of a standard solution of (1R, 2R)-pseudoephedrine 3⁺ (up to 20 molar equivalents). (B) A plot showing normalized chemical shifts of ¹H NMR resonances from basket 1⁶⁻ (Δδ) as a function of the quantity of (1R, 2R)-pseudoephedrine 3⁺ added to its aqueous solution. The data were fit to 1 : 2 binding model (supramolecular.org) with a distribution of residuals shown below.

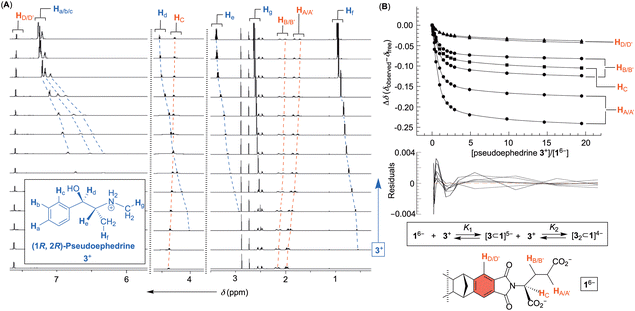
An incremental addition of a standard solution of phenethylamines 2⁺–4⁺ to 1⁶⁻ was monitored (30 mM PBS at pH = 7.0) with ¹H NMR spectroscopy (Fig. 3 and Fig. S1–S3, ESI†); each titration was repeated three times. Importantly, additions prompted a steady change (i.e., magnetic shielding) of the basket's resonances (Fig. 3A). We reasoned that noncovalent complexation ought to be taking place with the host residing in the shielding region of aromatic guests (Fig. 3B). To determine the stoichiometry of the complexation, the change in chemical shift of seven resonances from 1⁶⁻ as a function of the concentration of 2⁺–4⁺ was subjected to nonlinear regression analyses using 1 : 1, 1 : 2 and 2 : 1 binding models (Fig. S4–S6, ESI†).¹⁶ In this regard, it is important to note that ¹H NMR resonances of drugs 2⁺–4⁺ remained constant as a function of their variable concentrations (Fig. S7–S9, ESI†) so no competing dimerization or aggregation of drug molecules took place during supramolecular titrations. The curve fitting result for the titration of pseudoephedrine 3⁺ to 1⁶⁻ using 1 : 2 binding model (i.e., [3⊂1]⁵⁻ and [3₂⊂1]⁴⁻ complexes) is shown in Fig. 3B. The model is accepted given a somewhat random distribution of residuals¹⁷ and the small covariance of the fit (i.e., cov_fit = 3 × 10⁻⁴; Fig. S5, ESI†).^18,19 When the same criteria were used for evaluating the goodness of fit (GOF) for 1 : 1 and 2 : 1 binding models, we could disqualify both 1 : 1 (cov_fit = 3 × 10⁻³) and 2 : 1 complexations (cov_fit = 6 × 10⁻⁴).¹⁹ For all three drugs, the covariance of the fit slightly favoured 1 : 2 over 2 : 1 models of association (Fig. S4–S6, ESI†). Additionally, we decided to examine Akaike's information criterion (AIC).²⁰ This information-theoretic approach was recently introduced²⁰ to the field of host–guest chemistry as a superior alternative for evaluating the GOF. To calculate AIC, one needs to use the formula AIC = N ln (SSR/N) + 2k in which N is the number of fitted points, SSR is the sum of the squared residuals and k is the number of fitted parameters. The smaller the AIC the better the GOF. After computing AIC values for three independent titrations of each drug to 1⁶⁻ (Table 1 and Tables S1 and S2, ESI†), in addition to Akaike weights w_i, we compared the data. First, 1 : 1 complexations are uniformly showing the least favorable AIC scores (i.e., the most positive numbers). Between the other two models, 1 : 2 gave lower AIC values than 2 : 1 in two out of three titrations for each drug. We conclude that 1 : 2 association ought to be dominating under the experimental conditions. To corroborate statistical considerations of the fit, ESI† mass spectrometry measurements of a mixture of phenethylamine drugs 2⁺–4⁺ with basket 1⁶⁻ were taken in 1 : 10, 1 : 1, and 10 : 1 ratios (Fig. S10–S12, ESI†). At all ratios, only the presence of 1 : 1 and 1 : 2 complexes were observed. While the electrostatic repulsion between two anionic 1⁶⁻ disfavors 2 : 1 complexation, we hypothesize that 1 : 2 complex comprises the first guest occupying the cavity of 1⁶⁻ while the second one undergoes an exo-complexation.

Table 1 Akaike information criterion (AIC) scores and Akaike weights (w_i) obtained for three independent titrations in which (1R, 2R)-pseudoephedrine 3⁺ was added to basket 1⁶⁻ (Fig. 3A and Fig. S5). The data were fit to three models (1:1, 1:2, and 2:1) with AIC and w_i obtained using formulas from ref. 20

		Model 1 : 1	Model 1 : 2	Model 2 : 1
Titration I	AIC	−1039.7	−1̲1̲9̲2̲.6̲	−1113.3
	w i	4 × 10^−67	1̲	2 × 10^−26
Titration II	AIC	−1108.8	−1̲2̲3̲8̲.1̲	−1232.5
	w i	7 × 10^−57	1̲	4 × 10^−3
Titration III	AIC	−1541.3	−1619.2	−1̲9̲7̲8̲.5̲
	w i	1 × 10^−190	9 × 10^−157	1̲

---

After elucidating the binding stoichiometry, we went on to analyse the thermodynamic stability of binary [drug⊂1]⁵⁻ and ternary [drug₂⊂1]⁴⁻ complexes (Table 2; see also Fig. S4–S6, ESI†). Evidently, the formation of binary complexes dominates each equilibria with K₁ ≫ K₂. This bodes well with the earlier notion that [drug⊂1]⁵⁻ is an inclusion and more stable complex than [drug₂⊂1]⁴⁻ in which the association takes place on the basket's outer side. The stability of 1 : 1 complexes are in the millimolar range, but interestingly the affinity of tranylcypromine 4⁺ toward 1⁶⁻ is an order of magnitude greater than ephedrine 2⁺ and pseudoephedrine 3⁺.

Table 2 Experimental binding constants (K₁ and K₂) for the complexation of phenethylamine drugs 2–4⁺ to 1⁶⁻ and describing the formation of binary [2–4⊂1]⁵⁻ and ternary [(2–4)₂⊂1]⁴⁻ structures. From three independent titrations, each number is reported as mean ± standard deviation (Fig. S4–S6)

Phenethylamine drug	K 1 (M^−1)	K 2 (M^−1)
(1R, 2S)-ephedrine 2^+	7 ± 1 × 10^3	54 ± 11
(1R, 2R)-pseudoephedrine 3^+	6 ± 2 × 10^3	58 ± 11
(1S, 2R)-tranylcypromine 4^+	2 ± 1 × 10^4	39 ± 14

---

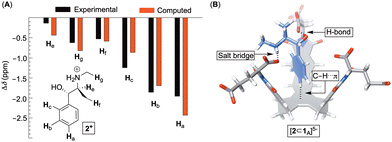
After quantifying the thermodynamic parameters characterizing the binding, we sought out to learn more about the mode of complexation and intermolecular interactions driving the association. First, the magnetic perturbation of resonances from each drug undergoing complexation show phenyls’ H_a/b/c experiencing the largest magnetic shielding (Δδ = δ_bound − δ_free, Fig. 4A; Fig. S1–S3, ESI†). Inclusion of the phenyl ring into the basket's cavity with H_a reaching for the cavity's bottom would explain the observation.¹³ Along with such docking of the aromatic, the ammonium site from 2–4⁺ ought to reside in the anionic nest (Fig. 1C). If so, what is the exact role of α- and γ-carboxylates in the complexation and what is the dominant pose of each guest with respect to the basket host? To answer these questions, we developed a computational protocol to estimate a pose which best represents the observed NMR shielding effect. First, the magnetic environments of 1_A⁶⁻ and 1_B⁶⁻ were mapped by computing nucleus independent chemical shift values (NICS) for a grid around the molecules (Fig. S14 and S15, ESI†).²¹ Next, we ran Monte-Carlo conformational searches (OPLS3) for inclusion complexes [2–4⊂1_A]⁵⁻ and [2–4⊂1_B]⁵⁻. During MC searches, we froze conformational motions of 1_A/B⁶⁻ but allowed guests to change their position and conformation, akin to docking protocols. Finally, we algorithmically assigned shielding values (Δδ_comp) for proton nuclei of all MC conformers of [2–4⊂1_A]⁵⁻ and [2–4⊂1_B]⁵⁻ using the NICS maps from 1_A⁶⁻ and 1_B⁶⁻. Having computed (Δδ_comp) and experimental (Δδ_exp) values of proton shifts, we analysed the data in two different ways. For the first approach, we determined root mean squared error 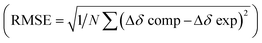for each computed pose and the pose with the lowest RMSE was assumed to be the best representation of the experimental result (Table 3, Fig. 4B; see also Fig. S19–S21, ESI†). As for the second approach, we Boltzmann weighted Δδ_comp values for each proton from all computed poses and summed each poses contribution to the ensemble average 〈Δδ_comp〉. Next, RMSEs for [2–4⊂1_A]⁵⁻ and [2–4⊂1_B]⁵⁻ were determined using the 〈Δδ_comp〉 values (Table 3). From Table 3, one notes that the ensemble of poses is, in more cases than not, giving lower RMSEs than single structures. It follows that the ensemble is more effective than a single pose at describing the experimental result. Furthermore, the values for RMSEs from complexes of 1_A⁶⁻ and 1_B⁶⁻ are comparable to indicate that both conformers likely participate in the binding; however, we noted that 1_A⁶⁻ showed a closer agreement to experimental NMR shielding values (Fig. S16–S18, ESI†). For (1R, 2S)-ephedrine 2⁺ occupying 1_A⁶⁻, RMSE values for the ensemble of poses (0.52) and a single pose (0.79) are similar (Table 3).

Fig. 4 (A) Experimental (black) and computed (red, for an ensemble of structures) chemical shift perturbations (Δδ) of ephedrine resonances within [2⊂1_A]⁵⁻. (B) A stick representation of single conformer of [2⊂1_A]⁵⁻ having the lowest RMSE.

Table 3 Root mean squared error (RMSE) data for ensemble and single poses of [2–4⊂1_A]⁵⁻ and [2–4⊂1_B]⁵⁻ complexes

Phenethylamine drug	Type	1 A ^6− (RMSE)	1 B ^6− (RMSE)
(1R, 2S)-ephedrine 2^+	Ensemble	0.52	0.43
	Single	0.79	0.89
(1R, 2R)-pseudoephedrine 3^+	Ensemble	0.86	0.88
	Single	0.65	0.70
(1S, 2R)-tranylcypromine 4^+	Ensemble	0.50	0.78
	Single	0.95	1.0

---

With an assumption that this single pose presents an average picture of the ensemble, the structure of [2⊂1_A]⁵⁻ in Fig. 4B shows ephedrine anchoring its benzene in the basket's cavity (via C–H⋯π contacts) while using hydroxyl and ammonium groups to form a hydrogen bond and salt bridge with α-carboxylates. Importantly, all of the best fit single poses of 2–4⁺ bound to 1_A/B⁶⁻ show the benzene from phenethylamines occupying the basket's cavity to contribute to non-classical hydrophobic effect²² with ΔH° < 0 (Fig. S13, ESI†) while OH and NH⁺ groups hydrogen bond/salt bridge α- and to a smaller degree γ-carboxylates (Fig. S19–S21, ESI†).

In conclusion, molecular basket 1⁶⁻ forms inclusion complexes with phenethylamines in water. The results of both experimental and computational studies suggest that the probed drug molecules anchor their phenyl ring in the basket's cavity as driven by C–H⋯π contacts and the hydrophobic effect while forming hydrogen bonds and/or salt bridges with primarily α-carboxylates at the rim. With a well characterized mode of binding, the opportunity to install alternative amino acids or peptides atop our basket scaffold is clear. In addition to the investigation of structure function relationships, further derivatization may indeed furnish a better agent for the preparation of chemosensors or sequesters of phenethylamines.

This study was financially supported with funds obtained from the National Science Foundation under CHE-2304883.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) M. D. Anglin, C. Burke, B. Perrochet, E. Stamper and S. Dawud-Noursi, J. Psychoact. Drugs, 2000, 32, 137–141; (b) G. K. Aghajanian and G. J. Marek, Neuropsychopharmacology, 1999, 21, 16S–23S; (c) D. J. Heal, J. Gosden, S. L. Smith and C. K. Atterwill, Neuropharmacology, 2023, 225, 109375; (d) O. Danylyuk, CrystEngComm, 2018, 20, 7642–7647; (e) E. Biavardi, F. Ugozzoli and C. Massera, Chem. Commun., 2015, 51, 3426–3429.
2. S. Freeman and J. F. Alder, Eur. J. Med. Chem., 2002, 37, 527–539.
3. D. E. Nichols and W. E. Fantegrossi, Emerging designer drugs, 2014, pp. 575–596.
4. M. E. Nelson, S. M. Bryant and S. E. Aks, Emerg. Med. Clin. North Am., 2014, 32, 1–28.
5. R. Gonzales, L. Mooney and R. A. Rawson, Ann. Rev. Public Health, 2010, 31, 385–398.
6. (a) Y. Jang, M. Jang, H. Kim, S. J. Lee, E. Jin, J. Y. Koo, I.-C. Hwang, Y. Kim, Y. H. Ko, I. Hwang, J. H. Oh and K. Kim, Chemistry, 2017, 3, 641–651; (b) D. King, C.-L. Deng and L. Isaacs, Tetrahedron, 2023, 145, 133607; (c) E. Biavardi, S. Federici, C. Tudisco, D. Menozzi, C. Massera, A. Sottini, G. G. Condorelli, P. Bergese and E. Dalcanale, Angew. Chem., Int. Ed., 2014, 53, 9183–9188.
7. J. Vachon, S. Harthong, E. Jeanneau, C. Aronica, N. Vanthuyne, C. Roussel and J.-P. Dutasta, Org. Biomol. Chem., 2011, 9, 5086–5091.
8. (a) A. T. Brockett, W. Xue, D. King, C.-L. Deng, C. Zhai, M. Shuster, S. Rastogi, V. Briken, M. R. Roesch and L. Isaacs, Chemistry, 2023, 9, 881–900; (b) S. Ganapati, S. D. Grabitz, S. Murkli, F. Scheffenbichler, M. I. Rudolph, P. Y. Zavalij, M. Eikermann and L. Isaacs, ChemBioChem, 2017, 18, 1583–1588.
9. O. Danylyuk, V. P. Fedin and V. Sashuk, Chem. Commun., 2013, 49, 1859–1861.
10. M. T. Garcia-Valverde, M. L. Soriano, R. Lucena and S. Cardenas, Anal. Chim. Acta, 2020, 1126, 133–143.
11. R. Zhang, Y. Ren, Q. Zhang, W. Huang, H. Bai and X. Zeng, New J. Chem., 2022, 46, 20909–20917.
12. S. E. Border, R. Z. Pavlovic, L. Zhiquan, M. J. Gunther, H. Wang, H. Cui and J. D. Badjic, Chem. – Eur. J., 2019, 25, 273–279.
13. R. Z. Pavlovic, S. E. Border, T. J. Finnegan, L. Zhiquan, M. J. Gunther, E. Munoz, C. E. Moore, C. M. Hadad and J. D. Badjic, J. Am. Chem. Soc., 2019, 141, 16600–16604.
14. S. E. Border, R. Z. Pavlovic, Z. Lei, M. J. Gunther, H. Wang, H. Cui and J. D. Badjic, Chem. Commun., 2019, 55, 1987.
15. R. Z. Pavlovic, S. E. Border, Y. Li, X. Li and J. D. Badjic, Chem. Commun., 2020, 56, 2987–2990.
16. P. Thordarson, Supramolecular Chemistry: From Molecules to Nanomaterials, 2012, vol. 2, pp. 239–274.
17. (a) F. Ulatowski, K. Dabrowa, T. Balakier and J. Jurczak, J. Org. Chem., 2016, 81, 1746–1756; (b) D. Brynn Hibbert and P. Thordarson, Chem. Commun., 2016, 52, 12792–12805.
18. J. E. A. Webb, M. J. Crossley, P. Turner and P. Thordarson, J. Am. Chem. Soc., 2007, 129, 7155–7162.
19. P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323.
20. K. Ikemoto, K. Takahashi, T. Ozawa and H. Isobe, Angew. Chem., Int. Ed., 2023, 62, e202219059.
21. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
22. L. Zhiquan, S. M. Polen, C. M. Hadad, T. V. RajanBabu and J. D. Badjic, Org. Lett., 2017, 19, 4932–4935.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc05485c

‡ These two authors contributed equally to this study.

---