Flip-flop dynamics in smectic liquid-crystal organic semiconductors revealed by molecular dynamics simulations

Abstract

Asymmetric liquid-crystal (LC) organic semiconductors, such as 2-decyl-7-(p-tolyl)-[1]benzothieno[3,2-b][1]benzothiophene (pTol-BTBT-C₁₀), exhibit high mobilities exceeding 10 cm² V⁻¹ s⁻¹. The LC phases play important roles in thermal stability and self-assembly ordering during film deposition and annealing. In this study, we show molecular dynamics simulations of pTol-BTBT-C₁₀ and reveal a unique mechanism of the molecular flip-flop motion at the smectic E/smectic B phase transition.

---

Smectic liquid crystals (SmLCs) are characterized by their layered structure, parallel orientation of molecules, and absence of long-range translational ordering within each layer. The layered structure of SmLCs was first observed using X-ray diffraction (XRD) by Maurice de Broglie and Edmont Friedel in 1923.¹ Smectic A (SmA) and smectic C (SmC) phases do not have translational ordering within each layer.² SmA and SmC phases have, respectively, normal and inclined orientations of the molecular long axis with respect to the smectic layer. The chiral smectic C (SmC) phase, which has a spontaneous electric polarization, was discovered by Meyer in the mid-1970s.³ Smectic B (SmB) and smectic E (SmE) phases have hexatic and herringbone orderings in each smectic layer, respectively.

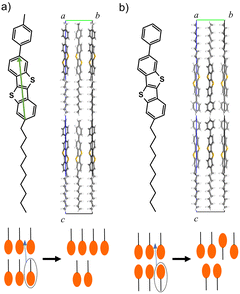
The applications of SmLCs include LC displays, optical switches, nonlinear optics, and organic semiconductors (OSCs). One of the popular SmLC OSCs is 2,7-octyl-[1]benzothieno[3,2-b][1]benzothiophene (C₈-BTBT), which exhibits a high mobility of 16 cm² V⁻¹ s⁻¹.^4,5 C₈-BTBT possesses SmA phase at 383–399 K. Since thermal stability of C₈-BTBT is relatively low (∼373 K), asymmetrically-substituted BTBT derivative, 2-decyl-7-phenyl-BTBT (Ph-BTBT-C₁₀), has been developed.^6,7 Ph-BTBT-C₁₀ possesses a SmE phase at 415–483 K and higher thermal stability (∼473 K) than C₈-BTBT. Ph-BTBT-C₁₀ exhibits a mobility of 20 cm² V⁻¹ s⁻¹, which is one of the highest mobilities among solution-processed OSCs. The high mobility is due to the self-ordering of the molecules in the SmE phase during film deposition and annealing. Other SmLC OSCs such as 2-decyl-7-(p-tolyl)-[1]benzothieno[3,2-b][1]benzothiophene (pTol-BTBT-C₁₀, 10 cm² V⁻¹ s⁻¹) also exhibit high mobilities.^8,9 Asymmetric substitution to rigid π-conjugated cores is a key technology to increase thermal stability and induce the highly ordered SmE phase for high mobility. These compounds typically undergo three phase transitions from crystal to liquid phases via SmE and SmA phases. Asymmetric SmLC OSCs exhibit unique polar or antipolar layered structures;^6–11pTol-BTBT-C₁₀ exhibits a polar structure, where all the alkyl chains have the same orientation (Fig. 1a).⁹ By contrast, Ph-BTBT-C₁₀ exhibits an antipolar structure, where the alkyl chains are oriented alternately layer by layer (Fig. 1b).^6,7,10,11 The elucidation of the mechanism of SmLC phase transitions is important for understanding the self-assembly ordering and thermal stability of OSCs. The self-assembly ordering in the SmE phase is preferable for increasing the mobility, whereas the SmA phase degrades the thermal stability.

Fig. 1 (a) Molecular and crystal structures of pTol-BTBT-C₁₀ and (b) Ph-BTBT-C₁₀. A green arrow is BTBT major axis for order parameter P₁. Bottom schematics illustrate interlayer sliding of molecules in each compound.

One of the important events involved in SmLC phase transitions is the flip-flop motion of molecules; that is, the inversion of the molecular long axis.^12,13 External electric fields induce this flip-flop motion, as utilized in ferroelectric LC displays.^14,15 However, an electric-field-free flip-flop motion has recently been observed in SmLC OSCs and is responsible for phase transitions by heating or mixing.^6,8,16,17 The interlayer sliding of molecules can cause the same transition as the flip-flop motion in antipolar layered structures, where adjacent smectic layers have opposite molecular orientations, as in Ph-BTBT-C₁₀ (Fig. 1b).¹⁸ However, interlayer sliding cannot explain the flip-flop motion in polar layered structures, where all the molecular long axes have the same orientation, as in pTol-BTBT-C₁₀ (Fig. 1a).

In this study, we performed full atomistic molecular dynamics (MD) simulations of pTol-BTBT-C₁₀, which exhibits the polar layered structure, for fully understanding LC phase transitions and molecular flip-flop dynamics. The proposed model and adopted simulation protocol reproduced SmE and SmB phases and transition temperatures that agreed well with the corresponding experimental measurements. The SmE phase possessed a rotation of molecules around their long axis and disordered alkyl chains. The SmB phase possessed interlayer diffusion and flipped molecules. The detailed analysis of the molecular trajectory near the SmE/SmB transition temperature revealed the unique mechanism of the molecular flip-flop motion.

GROMACS (ver. 2020.6) was used for MD simulations of pTol-BTBT-C₁₀. A general AMBER force field was used for all the atoms,¹⁹ and the parameters were assigned using Antechamber. All the hydrogen-atom bonds were constrained using the LINCS algorithm.²⁰ The initial crystal structure of pTol-BTBT-C₁₀ was prepared as a 6 × 7 × 12 supercell containing 512 molecules, based on a single-crystal XRD experiment. Three-dimensional periodic boundary conditions were used. The pressure was 1 atm. The temperature was increased from 340 to 525 K using the velocity rescaling algorithm at a relaxation time of 0.02 ps. The time step was set at 2 fs, and the cutoff distance of the Lennard-Jones nonbonded interactions was set at 1.2 nm. The particle mesh Ewald method (Fourier space of 0.12 nm) was used for the electrostatic interaction.²¹ First, we performed the energy minimization with the steepest descent algorithm, starting from the initial structure of the system. For the equilibrium calculation, the Berendsen weak-coupling scheme was used,²² and the box was set by anisotropic coupling at a characteristic relaxation time of 0.5 ps. During the production run, the isothermal–isobaric (NPT) simulation was performed using the Parrinello–Rahman algorithm at a characteristic relaxation time of 20 ps.²³ The box was isotropically and anisotropically scaled to and above 420 K, respectively. The simulated annealing at a rate of 0.5–2 K ns⁻¹ was used to increase temperature from one to another values. At the next temperature, the production run was performed for at least 20 ns until the mass density of the system equilibrated. The average dihedral angles were calculated for the last 2 ns at each temperature, and the radial distribution functions (RDFs) were calculated based on the last configuration at each temperature.

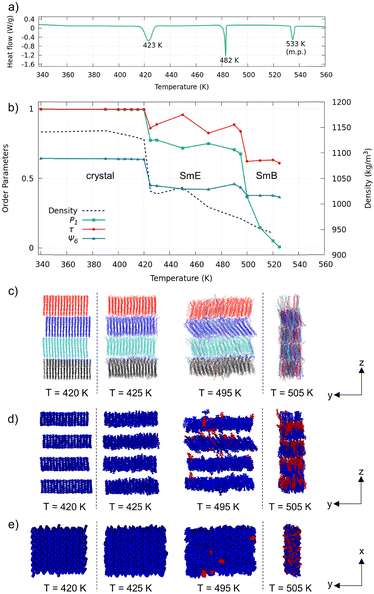
The single-crystal XRD analysis revealed that the pTol-BTBT-C₁₀ crystal possessed a polar layered herringbone structure (Fig. 1a).⁹ All the alkyl chains were oriented in the same direction. The polar structure is different from the antipolar herringbone structure of Ph-BTBT-C₁₀, where the alkyl chains are oriented alternately layer by layer (Fig. 1b). The cell parameters of pTol-BTBT-C₁₀ were a = 5.92852(18) Å, b = 7.7655(2) Å, c = 56.2232(16) Å, and α = β = γ = 90°. Because the cell parameters, a, b, and γ, along the herringbone molecular layer approximate those of Ph-BTBT-C₁₀, a = 6.0471(3) Å, b = 7.7568(4) Å, and γ = 90°, the molecular packings in each layer of both compounds are considered as being quite similar. The methyl group of pTol-BTBT-C₁₀ induced an interlayer stacking different from that of Ph-BTBT-C₁₀. The experimental differential scanning calorimetry (DSC) thermogram in Fig. 2a indicates that pTol-BTBT-C₁₀ exhibits three phase transitions at 423, 482, and 533 K, which are like those of Ph-BTBT-C₁₀.⁶

Fig. 2 (a) Experimental DSC thermogram of pTol-BTBT-C₁₀ in heating. (b) Density and order parameters, P₁, τ, and ψ₆, at different temperatures. (c) Snapshots just below and above each transition temperature colored according to initial layers. (d) Side view and (e) top view of snapshots colored according to molecular orientations (blue: same as initial orientation; red: inverted orientation). Alkyl chains were omitted for clarity.

The force field was validated first in terms of the stability of the crystal structure. The cell parameters in NPT simulation at 292 K were a = 6.38014 Å, b = 7.5608 Å, c = 55.8983 Å, α = 90.001°, β = 89.898°, and γ = 90.085°. These values are consistent with experimental ones. Simulated phase transition temperatures are also consistent with experimental ones as discussed in the next paragraph.

To investigate the phase-transition behavior, the mass density, order parameter (P₁) for the BTBT major axis, translational order parameter τ,²⁴ and hexatic order parameters ψ₆²⁵ were calculated by averaging the last 10 ns trajectory at each temperature (Fig. 2b). P₁ is defined as P₁ = 〈cos θ〉, where θ is the angle of the BTBT major axis (Fig. 1a) with respect to the z-axis normal to the smectic layers. τ was calculated for molecular mass center. ψ₆ was calculated for the six closest molecules. The density and order parameters indicate two phase transitions at 425 and 495 K. Both transition temperatures in the MD simulations are consistent with those (423 and 482 K) in the experimental DSC thermogram and validate the simulation results. The simulation was stopped at 525 K because the box size became too anisotropic. The system retained the smectic layered structure at 525 K, and the liquid-transition temperature should be above 525 K.

Fig. 2c–e displays the snapshots of the system just below and above respective phase-transition temperatures. Because the original crystal structure was retained up to 420 K, the first phase is considered as the crystal phase. The second phase at 425–495 K retained the layered herringbone structure, while the order parameters were substantially lower than those of the crystal phase. The herringbone structure and nonzero order parameters, P₁ ∼ 0.7, τ ∼ 0.9 and ψ₆ ∼ 0.4, indicate that the second phase is SmE. The third phase above 495 K still retained the layered structure, while herringbone structure was not observed. Translational order (τ ∼ 0.6) and hexatic order (ψ₆ ∼ 0.4) were present, while order parameter P₁ decreased to zero. These features indicate that the third phase is SmB.

Although the SmE phase was not observed in the previous MD study on Ph-BTBT-C₁₀,^25,26 experiments have revealed that Ph-BTBT-C₁₀ possesses both SmE and SmA phases. The simulated SmLC phase of Ph-BTBT-C₁₀ did not exhibit hexatic order and is considered as SmA. Possible reasons for the lack of the SmE phase in the previous MD study may be the different layered structures (polar/antipolar) and system sizes. pTol-BTBT-C₁₀ in this study exhibits a DSC thermogram that is quite similar to that of Ph-BTBT-C₁₀. The two SmLC phases are SmE and SmB in MD simulations.

The difference between SmE and SmB phases can be observed in the interlayer diffusion and flip-flop motion of the molecules. The molecules are colored according to their initial layers in the snapshots in Fig. 2c. The interlayer diffusion occurred at and above 495 K. Because the simulated time is as short as 10 ns, actual system should have enough interlayer diffusion at 495 K. The snapshots in Fig. 2d and e show the molecules colored according to their orientations: blue molecules have the same orientations as in the initial structure, and red molecules have the inverted orientation. The number of inverted molecules started to increase at 495 K, and approximately half the molecules were inverted at 505 K. The critical temperatures required for the interlayer diffusion and flip-flop motion of the molecules coincided.

For further investigating the SmE phase, the dihedral angles for the four carbon atoms (CH₃CH₂CH₂CH₂−) in the alkyl chain and between the BTBT and tolyl groups and the RDF for the BTBT center of mass were analyzed. The histogram of dihedral angle for the alkyl chain (Fig. S2a, ESI†) indicates that the ratio of the gauche form (∼70°) substantially increased at the crystal/SmE transition at 420–425 K and was almost constant between 425 and 525 K. The dihedral angle between the BTBT and tolyl groups (Fig. S2b, ESI†) shifted from 44 to 33° at 420 and 425 K, respectively, with negligible peak broadening. Hence, the torsional motion of the tolyl group is not responsible for the crystal/SmE transition. These results indicate that the melting of the alkyl chains at 420–425 K triggers the crystal/SmE transition and that the equilibrium angle of the tolyl group shifted owing to the relaxation of the crystal packing. This model is consistent with the experiments where the entropy changes at the crystal/SmE transition increased monotonically with increasing alkyl chain length.¹³ At 420 K, the RDF (Fig. S2c, ESI†) exhibited two sharp peaks at 5.1 and 6.5 Å, indicating the anisotropic intermolecular distances in the herringbone packing. At 425–495 K, both peaks were less pronounced, and the anisotropy was weakened. This phenomenon at the crystal/SmE transition is consistent with the XRD pattern.²⁷

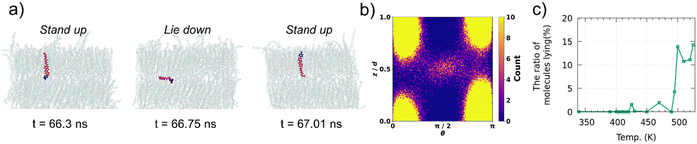
In Ph-BTBT-C₁₀ crystals, molecular flip-flop motion has been explained by the interlayer sliding of the molecules because Ph-BTBT-C₁₀ possesses the antipolar crystal structure, where the adjacent layers possess opposite orientations. However, in pTol-BTBT-C₁₀, the flip-flop motion cannot be explained by the same mechanism because pTol-BTBT-C₁₀ possesses the polar crystal structure, where all the molecules possess the same orientation. To investigate the flip-flop dynamics of the pTol-BTBT-C₁₀ molecules, the trajectories of the inverted molecules were analyzed in detail. Fig. 3a shows the trajectory of an inverted molecule; the molecule inverted when it slid out of the smectic layer, lay down in the interlayer, and then reentered the original or forward/backward layer. This molecular inversion behavior was observed within 1 ns at 510 K and, in some cases, was repeated many times. Fig. 3b shows the probability map of the molecular long axis angles θ with respect to the z-axis and z coordinates of molecular mass center in last 5 ns at 510 K. The top and bottom of the map (z/d = 0 and 1) correspond to the centers of the smectic layers and z/d = 0.5 corresponds to the interlayer. This map clearly indicates that molecules has higher probability of lying (θ = π/2) at the interlayer. Fig. 3c shows the percentages of the molecules for which the BTBT major axes possessed angles between 80 and 100° with respect to the z-axis (normal to the herringbone molecular layer) at different temperatures. The results show that 10–15% of the molecules in the system lay down in the interlayer above 495 K, whereas few molecules lay down below 495 K. To the best of our knowledge, this is the first time that this lie-down stand-up behavior has been observed for LC molecules. This unique mechanism explains the molecular inversion in polar SmLCs, which could not be explained simply by interlayer sliding. This mechanism is also consistent with the coincidence of the critical temperatures for the interlayer diffusion and flip-flop motion of the molecules because the interlayer diffusion is required for the flip-flop motion in this mechanism. This unique motion inverts the molecules and critically distinguishes the SmE and SmB LC phases.

Fig. 3 (a) Snapshots of molecule inverting at 510 K along time evolution (red: BTBT core and alkyl chain; blue: tolyl group). (b) The probability map of the molecular long axis angles θ with respect to the z-axis and z coordinates of molecular mass center at 510 K. d is the smectic layer spacing. The center of the smectic layers are located at z/d = 0 and 1. (c) Ratio of molecules lying between layers in last 10 ns of trajectory at each temperature.

We performed fully atomistic MD simulations of pTol-BTBT-C₁₀ by simulating annealing at 340–525 K for fully understanding crystal/SmE/SmB transitions and molecular flip-flop dynamics. The simulated transition temperatures agreed well with the experimentally measured ones, which validates the simulation results. The detailed analysis of the MD around the SmE/SmB transition temperature revealed the unique molecular inversion mechanism, in which molecules first lie between molecular layers and then reenter the original or forward/backward layer. The lie-down stand-up mechanism explains the molecular inversion in the SmCLs possessing polar layered structures.

This work was supported by JST CREST, grant number JPMJCR18J2, and JST, “The Establishment of University Fellowships Toward the Creation of Science Technology Innovation,” grant number JPMJFS2104. The computations were carried out using the computer resources offered under the category of “General Project by Research Institute for Information Technology,” Kyushu University.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. M. De Broglie and E. Friedel, C. R. Acad. Sci., 1923, 176, 738–740.
2. J. P. F. Lagerwall and F. Giesselmann, Chem. Phys. Chem., 2006, 7, 20–45.
3. R. B. Meyer, L. Liebert, L. Strzelecki and P. Keller, J. Phys., Lett., 1975, 36, 69–71.
4. H. Ebata, T. Izawa, E. Miyazaki, K. Takimiya, M. Ikeda, H. Kuwabara and T. Yui, J. Am. Chem. Soc., 2007, 129, 15732–15733.
5. H. Minemawari, T. Yamada, H. Matsui, J. Tsutsumi, S. Haas, R. Chiba, R. Kumai and T. Hasegawa, Nature, 2011, 475, 364–367.
6. H. Iino, T. Usui and J. I. Hanna, Nat. Commun., 2015, 6, 6828.
7. T. Hamai, S. Arai, H. Minemawari, S. Inoue, R. Kumai and T. Hasegawa, Phys. Rev. Appl., 2017, 8, 054011.
8. K. Nikaido, S. Inoue, R. Kumai, T. Higashino, S. Matsuoka, S. Arai and T. Hasegawa, Adv. Mater. Interfaces, 2022, 9, 2201789.
9. S. Inoue, T. Higashino, K. Nikaido, R. Miyata, S. Matsuoka, M. Tanaka, S. Tsuzuki, S. Horiuchi, R. Kondo, R. Sagayama and T. Hasegawa, Res. Square, 2023 DOI:10.21203/rs.3.rs-2531770/v1.
10. S. Inoue, H. Minemawari, J. Tsutsumi, M. Chikamatsu, T. Yamada, S. Horiuchi, M. Tanaka, R. Kumai, M. Yoneya and T. Hasegawa, Chem. Mater., 2015, 27, 3809–3812.
11. S. Hofer, J. Unterkofler, M. Kaltenegger, G. Schweicher, C. Ruzié, A. Tamayo, T. Salzillo, M. Mas-Torrent, A. Sanzone, L. Beverina, Y. H. Geerts and R. Resel, Chem. Mater., 2021, 33, 1455–1461.
12. J. Schacht, P. Zugenmaier, M. Buivydas, L. Komitov, B. Stebler, S. T. Lagerwall, F. Gouda and F. Horii, Phys. Rev. E, 2000, 61, 3926.
13. N. Osiecka, M. Massalska-Arodź, Z. Galewski, K. Chłędowska and A. Bąk, Phys. Rev. E, 2015, 92, 052503.
14. N. Yadav, Y. P. Panarin, J. K. Vij, W. Jiang and G. H. Mehl, J. Mol. Liq., 2023, 378, 121570.
15. N. A. Clark, X. Chen, J. E. Maclennan and M. A. Glaser, arXiv, 2023, arXiv:2208.09784v2 DOI:10.48550/arXiv.2208.09784.
16. Y. F. Wang, H. Iino and J. I. Hanna, Soft Matter, 2017, 13, 6499–6505.
17. H. Wu, H. Iino and J. I. Hanna, Chem. Lett., 2018, 47, 510–513.
18. E. Ferrari, L. Pandolfi, G. Schweicher, Y. Geerts, T. Salzillo, M. Masino and E. Venuti, Chem. Mater., 2023, 35, 5777–5783.
19. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
20. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
21. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
22. H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
23. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
24. M. T. Sims, L. C. Abbott, J. W. Goodby and J. N. Moore, Soft Matter, 2019, 15, 7722–7732.
25. A. Baggioli, M. Casalegno, G. Raos, L. Muccioli, S. Orlandi and C. Zannoni, Chem. Mater., 2019, 31, 7092–7103.
26. M. Yoneya, J. Phys. Chem. C, 2018, 122, 22225–22231.
27. S. Inoue, K. Nikaido, T. Higashino, S. Arai, M. Tanaka, R. Kumai, S. Tsuzuki, S. Horiuchi, H. Sugiyama, Y. Segawa, K. Takaba, S. Maki-Yonekura, K. Yonekura and T. Hasegawa, Chem. Mater., 2022, 34, 72–83.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc05222b

---