Dielectric behaviour of nitrogen doped perovskite SrTiO_3−δN_δ films

Abstract

Technologically important high-permittivity dielectrics are often achieved using cationic engineering of ABO₃-type perovskite para(ferro)electrics. Here, we experimentally and theoretically explore the potential of less conventional anionic engineering in ABO₃ dielectrics. We demonstrate that in an archetypal representative SrTiO₃, nitrogen substitution can occur on two distinct oxygen atomic sites, reduce crystal symmetry, and lead to significant changes in the patterns and frequencies of lattice vibrations. These phonon transformations diminish permittivity, whereas contribution from nitrogen-induced nanoregions can raise it. The effects of nitrogen are found to be especially strong in epitaxial films. We anticipate that the revealed phenomena may be relevant for a broad class of high-permittivity perovskite oxides.

---

Introduction

ABO₃-type perovskite-structure metal oxides comprise a vast class of scientifically intriguing and technologically important multifunctional materials. The crystal stability and key properties of these oxides are intrinsically related to distortions of the BO₆ octahedra. These distortions are determined by the nature of both the B- and A-site cations. Therefore, the main methods to achieve desired functional properties of these oxides are based on cationic engineering and include creation of novel A–B combinations, partial A- and/or B-cationic substitution in the basic stable perovskites, and formation of solid solutions of two or more perovskite oxides. In addition to cationic engineering, another possibility involves anionic engineering, namely: substitution of oxygen with another anion. Anionic substitution can directly affect octahedral distortions and, hence, properties of perovskites. Although this approach was implemented for selected materials, its potential is far from being understood and fully employed.¹

This work explores anionic nitrogen (N) substitution in strontium titanate SrTiO₃ (STO). STO is one of the best studied archetypal representatives of a large family of perovskite oxide ferro(para)electrics (FEs). Being an excellent platform for investigations of the fundamentals of crystal chemistry and properties and the synthesis of perovskite oxides, STO steadily attracts high research interest.^2–19 Among all perovskite oxides, FEs are the most renowned, most widely employed in electronics and photonics, as well as promising for advanced catalysis and life sciences.^20–26 FEs exhibit high dielectric permittivity and are first-rate high-permittivity dielectrics for miscellaneous modern capacitors. In FEs, the dielectric constant can reach several thousand with its maximal values in vicinity of the para-to-ferroelectric phase transition. However, often, paraelectric dielectrics are preferred. Development of high-permittivity ABO₃ dielectrics with dedicated properties (exact permittivity, thermal stability, low losses, etc.) is an important field of the present-day materials research.

Pure unstressed STO is paraelectric at all temperatures and serves as a primary high-permittivity ABO₃-type dielectric. For ABO₃ paraelectric dielectrics at low frequencies (up to gigahertz range), the dielectric permittivity ε (or static permittivity) is determined by lattice vibrations, mainly by the lowest-frequency transverse optical phonon (TO), or so-called soft mode.^27–36 In cubic STO (at the temperatures above 105 K), the soft mode (phonon frequency ω_TO) is related to bending of the Ti–O–Ti chain and dominates the dielectric response. Therein, the product [ε × (ω_TO)²] is a temperature-independent constant and the relationship [1/ε ∝ (ω_TO)²] is valid. The Cochran's behavior [(ω_TO)² ∝ (T − T₀)] is in force and the Curie–Weiss law takes the form [ε = ε_L + c_C/(T − T_C)], where ε_L, c_C, and T_C are the dielectric constant extrapolated to infinite temperature, the Curie constant, and the Curie temperature, correspondingly.

Because the Ti–O–Ti distortions and vibrations are highly sensitive to the nature of A-site cations, a partial substitution of Sr principally allows for tuning the phonons and, hence, the static dielectric permittivity in STO. An extensive search for appropriate A-site cationic substitution is ongoing. Alternatively, replacement of oxygen with nitrogen may also affect the lattice distortions and vibrations, and thus may lead to changes in the dielectric permittivity. We note that a nitrogen-induced tendency towards improved dielectric behavior of ferroelectrics was recently indicated.^37,38 Previously, we demonstrated significant changes in the electronic structure and in the optical and charge-transport properties caused by nitrogen substitution in STO.^39–41 The local structure and optical properties of nitrogen-doped STO were theoretically investigated using first-principles analysis.^41–45 However, explicit effects from nitrogen substitution on the dielectric constant in STO are unknown.

We note that in the last decades, remarkable progress in synthesis of perovskite oxide thin films has enabled control of properties by using film-substrate misfit strain.^46–49 For some strained epitaxial STO films, the soft-mode frequency was found to be relatively high.^33,34,36 Intuitively, one can anticipate that nitrogen substitution in the presence of strain may affect the dielectric permittivity in a different way compared to that for unstressed STO. A combined impact from the nitrogen substitution and lattice strain on the dielectric permittivity is completely uncharted.

Here we performed experimental and the first-principles theoretical investigations of the perovskite oxide dielectric STO, where up to 10% of oxygen atoms were replaced with nitrogen and where epitaxial lattice strain was varied. As a reference, pure unstressed STO was analysed. We experimentally found that compared to pure STO, nitrogen doping leads to diminished matrix dielectric permittivity, reduced Curie constant, and ample dipolar relaxation, which raises total permittivity. We theoretically demonstrated two distinct atomic sites for nitrogen substitution, lowering of crystal symmetry, and changes in the lattice vibrations and dielectric constant. We also established enhancement of the nitrogen-induced effects in strained epitaxial films. The unveiled nitrogen-induced complexity of the lattice vibrations may be relevant for many technologically important perovskite oxide dielectrics.

Methods

Experimental section

To experimentally establish effects of nitrogen substitution on the dielectric properties of unstressed STO as well as on those of strained STO, we studied different STO films with the same thicknesses of ∼150 nm. The regular stoichiometric films and the nitrogen-doped films were obtained in situ by controlling oxygen or nitrogen gas ambience, correspondingly, during the growth of the films by pulsed laser deposition.^{39–41,50–53} The proper cationic composition and substitution of up to 10% of oxygen atoms with nitrogen were confirmed using several techniques.^50–53

For studies of unstressed STO, the films were grown on commercial Pt-coated Si substrates.⁵³ Such films were randomly oriented polycrystalline and retained cubic perovskite structure with the lattice parameters close to that of bulk STO. The films possessed columnar microstructure, with the vertical columnar boundaries normal to the substrate surface. Additionally, unstressed (001)-oriented epitaxial films were grown on (001)-cut STO substrates [ESI,† Fig. S1]. To explore nitrogen substitution in the presence of strain, the nitrogen-doped epitaxial (001) STO films were prepared on (001)(LaAlO₃)_0.3(Sr₂AlTaO₆)_0.7 (LSAT) and (001)LaAlO₃ (LAO) substrates. These films were elongated in the out-of-plane direction (normal to the substrate surface). Compared to unstressed pure STO, the measured out-of-plane tensile strain was ∼1.4% and ∼1% in the films on LSAT and LAO, correspondingly [ESI,† Fig. S2 and S3]. Mechanisms for such strain stabilization were explored and justified before.^50,52 As a reference, also (001)-oriented epitaxial stoichiometric films, where misfit strain was fully relaxed, were obtained on LSAT and LAO substrates [ESI,† Fig. S2 and S3].

For electrical characterization, vertical electrode-STO-electrode capacitors were created. As bottom electrodes, we used thin layers of Pt on Si substrates, SrRuO₃ (SRO) on STO, and LaNiO₃ (LNO) on LSAT and LAO. The top electrode pads with diameters of 0.2–2.0 mm² were formed using a room-temperature vacuum pulsed laser deposition of Pt through a shadow mask.

The small-signal impedance of the capacitors was measured on a NOVOCONTROL Alpha-AN High-Performance Frequency Analyzer. The amplitude of the probing AC voltage was 10–3 V, the frequency range was from 1 Hz to 1 MHz, and the temperature was varied from 80 to 550 K. The control of temperature was realized using Linkam cold/hot stages. The electric field was applied, and the response was measured in the out-of-plane direction. The impedance data were processed using an equivalent-circuit model of a leaky parallel-plate thin-film ferroelectric capacitor [ESI,† Fig. S4 and expressions (S1)–(S5)]^54–56 To discard possible influence of the bottom thin-film electrodes on the measured permittivity, the electrodes’ resistance was measured separately. As a reference and for comparison, we inspected the dielectric response of bulk pure unstressed single-crystal STO.

Computational methods

Ab initio (first principles) computer simulations were performed to investigate the effect of substitutional nitrogen atoms in unstressed and epitaxially compressed STO. The structural, vibrational, and dielectric properties were examined within the linear combination of atomic orbitals (LCAO) approximation of the density functional theory (DFT), as implemented in CRYSTAL17 computer code for large scale quantum-chemical simulations.^57,58 The B1WC global hybrid DFT-HF exchange–correlation functional, which combines the Wu-Cohen WCGGA exchange functional with 16% of Hartree–Fock (HF) exchange and the Perdew–Wang PWGGA correlation functional, was employed. This functional proved its reliability in our previous simulations of perovskite solid solutions and heterostructures.^59–61 The basis sets of Gaussian type functions with Hay and Wadt small core effective core pseudopotential were used for Sr and Ti atoms,⁶² while the all-electron basis sets with additional exponents for d-shells were applied for description of oxygen⁶² and nitrogen⁶³ atoms.

At the temperatures T > 105 K, pure unstressed paraelectric STO possesses the ideal perovskite cubic structure (where each Ti atom is octahedrally coordinated to the six nearest oxygen atoms) with the centrosymmetric cubic space group Pm3̄m (SG 221). At T < 105 K, STO acquires another paraelectric tetragonal phase I4/mcm (SG 140). The corresponding crystallographic unit cell consists of 20 atoms (4 Sr atoms, 4 Ti atoms and 12 oxygen atoms), and the lattice parameters of the undistorted structure are (a = b = a₀√2, c = 2a₀), where a₀ is the lattice constant of STO in the cubic phase [Fig. 1]. The SG140 STO phase is characterized by tetragonal lattice distortion with a slight unit cell stretching and an antiphase rotation of neighbouring TiO₆ octahedra around the tetragonal z-axis. To explore possible rotations of oxygen octahedra in STO with substitutional nitrogen atom, the SG140 crystallographic structure with 20 atoms was used as the computational model. The concentration of nitrogen was 8.3% relative to the stoichiometric number of oxygen atoms.

Fig. 1 The 20-atom crystallographic unit cell of the low-temperature tetragonal phase I4/mcm (SG 140) in STO. Sr atoms are shown by green balls, Ti atoms – blue balls, oxygen atoms – red balls. The oxygen atom O1 (or axial atom) is located in the SrO plane, and the atom O5 (or equatorial atom) is located in the TiO₂ plane.

The Wyckoff positions of the 20 atoms in the unit cell of STO are Sr:4b(0, 1/2, 1/4), Ti:4c(0, 0, 0), O_I:4a(0, 0, 1/4) and O_II:8h(1/2–x, x, 0). There are two symmetrically dissimilar oxygen positions: O_I and O_II. The O_I atoms, or axial atoms, are located in the atomic SrO planes normal to z-axis [O1 in Fig. 1] and occupy fixed positions. The O_II atoms (or equatorial atoms) are located in the TiO₂ planes [O5 in Fig. 1] and take part in the rotation of the oxygen octahedra around z-axis. Because effects of nitrogen substitution for the axial O1 atoms in the SrO-planes may differ from those for the equatorial O5 atoms in the TiO₂ planes, simulations were performed for each of the two cases.

We analysed 6 different systems including unstressed STO: (1) pure, (2) with nitrogen substitution for O1 in the SrO planes, and (3) with nitrogen substitution for O5 in the TiO₂ planes; as well as epitaxially compressed STO: (4) pure, (5) with nitrogen substitution for O1 in the SrO planes, and (6) with nitrogen substitution for O5 in the TiO₂ planes. To correctly compare these systems, all calculations were carried out without any symmetry constraints (SG 1) so that the results depend only on the atomic interaction potentials.

To simulate epitaxially compressed STO, the lattice constants a = b were reduced by 1% compared to those in pure unstressed STO and remained fixed. The angles between the lattice axes were fixed at 90 degrees. The lattice constant c and positions of all atoms were allowed to relax during the full geometry optimization. This model corresponds to epitaxial (001) oriented STO film on top of cubic substrate, where the film-substrate biaxial in-plane (i.e., parallel to the substrate surface and normal to the tetragonal z-axis) lattice misfit is compressive 1%. Such strain is enabled by LSAT substrates.

Because oxygen and nitrogen are not isovalent, not all chemical bonds are closed with nitrogen substitution for oxygen, and one unpaired electron is associated with the nitrogen atom. Such system may have only one spin state with the effective spin projection S_z = 1/2. To investigate the system with uncoupled “dangling” bond, we used the unrestricted open shell DFT calculations.⁵⁸

To compare the dielectric properties of different systems, the transverse optical (TO) vibrational frequencies and vibrational contributions to the static dielectric tensor were calculated at the Γ-point (the centre of the first Brillouin zone) in the framework of the harmonic approximation.

Results and discussion

Dielectric behaviour in nitrogen doped STO films

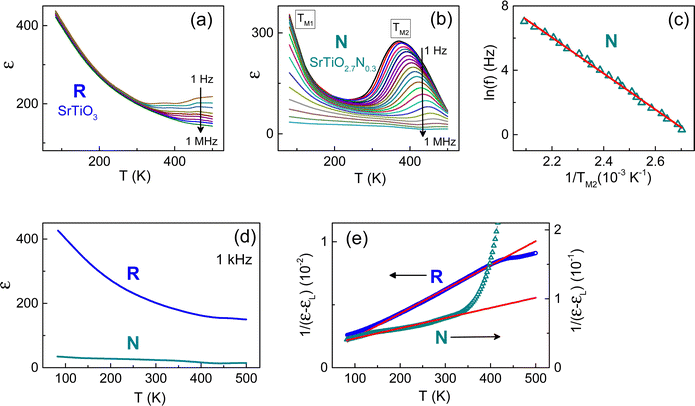
The dielectric effects from nitrogen substitution were first inspected in stress-free STO using randomly oriented polycrystalline STO films [Fig. 2]. In the reference regular stoichiometric SrTiO₃ film (R-STO), the real part of the dielectric permittivity ε monotonically increases with decreasing temperature and displays a frequency-dependent rise at high temperatures T > 400 K [Fig. 2(a)]. This behaviour is fully consistent with that in the reference R-STO crystal [ESI,† Fig. S5]. The high-temperature dispersion of ε is due to thermally activated electrical conduction, whereas intrinsic ε is frequency-independent in the R-STO film and crystal.

Fig. 2 Dielectric properties of the regular SrTiO₃ (R) and nitrogen-doped SrTiO_2.7N_0.3 (N) polycrystalline STO films. (a), (b) and (d) The real part of the dielectric permittivity ε as a function of temperature at different frequencies (a) and (b) f = 1–10⁶ Hz and (d) f = 1 kHz. In (a) and (b), arrows show directions of frequency increase. (c) The frequency-temperature relationship for the dielectric peak at T_M2 in the nitrogen-doped film. Straight line shows fit [ln(f) ∝ 1/T_M2]. (e) The modified Curie–Weiss behaviour (f = 1 kHz). Straight solid lines show fits [1/(ε − ε_L) ∝ T].

Compared to R-STO, nitrogen substitution produces dramatic changes in the dielectric response: the permittivity ε(f,T) of the nitrogen doped SrTiO_2.7N_0.3 film (N-STO) is completely altered [Fig. 2(b)]. There are two broad frequency-dependent dielectric peaks, with the peaks’ maxima at the temperatures T_M1 ∼ 100 K and T_M2 ∼ (240–460) K. Concurrently, the measured very small and frequency-dependent electrical conductivity is nearly the same in the R- and N- films [ESI,† Fig. S6] and indicates hopping of small polarons.⁴⁰

The temperature T_M1 is difficult to analyse as a function of frequency, whereas the temperature T_M2 exhibits a massive frequency dispersion. The most common Debye-type dipolar dielectric relaxation is manifested in the frequency-temperature relationship [f = f₀exp(−E₀/k_BT_M)] and the corresponding linear relationship [ln(f) = ln(f₀) − E₀/k_BT_M]. The parameters f₀ and E₀ are the eigenfrequency and activation energy, respectively, and k_B is the Boltzmann constant. Here, a good linear fit [ln(f) ∝ 1/T_M2] is obtained, with the fitted parameters being f₀ = 2.4 × 10¹¹ Hz and E₀ = 0.54 eV [Fig. 2(c)]. These observations point to giant electrical dipoles, whose electric-field induced motion is coupled with lattice vibrations. In ABO₃ perovskite oxide para(ferro)electrics, such behaviour is commonly associated with nanoregions, where the lattice strain and polarization differ from the main matrix material (see e.g., ref. 64 and references therein).

The two dielectric peaks signify coexistence of two types of nanoregions. The nanoregions may be related to lattice distortions within a few unit cells around nitrogen.⁴² Substitution of oxygen with nitrogen can lower local crystal symmetry, which stimulates local dynamical off-centre displacements of the Ti cation (pseudo-Jahn–Teller instability). Such local polar instability is not correlated throughout the whole film, leading to the formation of polar nanoregions but not a long-range ferroelectric state.⁶⁴ Our observations imply two possible distinct sites, or locations for nitrogen substitution in the lattice, and are in line with the two different locations of oxygen atoms: axial in the SrO plane and equatorial in the TiO₂ plane in the tetragonal STO [Fig. 1]. The atomic SrO and TiO₂ planes can host specific sites for nitrogen in the absence of cubic symmetry. Notably, coexistence of the distinct nitrogen sites promotes uncorrelated polar instabilities and favours polar nanoregions over ferroelectricity.

Apart from the detected dielectric response of nanoregions, there is a genuine dielectric effect from nitrogen substitution on the atomic level. This genuine matrix effect is assessed at high enough frequencies, at which the dielectric contribution of the nanoregions is negligible. Compared to R-STO, nitrogen substitution leads to a significant drop in the matrix permittivity: the permittivity of N-STO is up to three times smaller than in R-STO [Fig. 2(d)]. Furthermore, the Curie–Weiss behaviour is also affected by nitrogen [Fig. 2(e)]. The Curie constants, extracted from the linear fits [1/(ε − ε_L) ∝ T], are c_C = 1.3 × 10⁴ K in the N-STO matrix and c_C = 3.4 × 10⁴ K in the regular R-STO one. The detected decrease of both the permittivity and the Curie constant in N-STO compared to R-STO unambiguously implies intrinsic matrix phenomena induced by nitrogen substitution.

All the revealed nitrogen-induced dielectric effects, including significant decrease of the matrix permittivity, reduction of the Curie constant, and substantial dual dipolar relaxation – are better expressed in the (001)-oriented homoepitaxial N-STO film on the (001)STO substrate [Fig. 3 and ESI,† Fig. S7]. The permittivity in the regular (001)R-STO film practically coincides with those in the polycrystalline R-STO film and the reference crystal [Fig. 3(a)]. In the nitrogen-doped (001) N-STO film, the two frequency-dependent dielectric peaks are present and attest to relaxation of two distinct types of nanoregions [Fig. 3(b)]. A linear fit [ln(f) ∝ 1/T_M2] is obtained for the peak temperature T_M2, and the fitted parameters are f₀ = 9.8 × 10¹² Hz and E₀ = 0.95 eV [Fig. 3(c)]. Observations at high frequencies evidence that compared to the permittivity in the (001) R-STO film, the matrix permittivity in the (001) N-STO film is reduced by factor ∼12 [Fig. 3(d)]. The Curie constant also decreases from c_C = 5.2 × 10⁴ K in (001) R-STO to c_C = 0.7 × 10⁴ K in (001) N-STO [Fig. 3(e)].

Fig. 3 Dielectric properties of the regular SrTiO₃ (R) and nitrogen-doped SrTiO_2.7N_0.3 (N) homoepitaxial (001) STO films. (a), (b) and (d) The real part of the dielectric permittivity ε as a function of temperature at different frequencies (a) and (b) f = 1–10⁶ Hz and (d) f = 1 kHz. In (a) and (b), arrows show directions of frequency increase. (c) The frequency-temperature relationship for the dielectric peak at T_M2 in the nitrogen-doped film. Straight line shows fit [ln(f) ∝ 1/T_M2]. (e) The modified Curie–Weiss behavior (f = 1 kHz). Straight solid lines show fits [1/(ε − ε_L) ∝ T].

The obtained results [Fig. 2(d) and 3(d)] show that the nitrogen-induced suppression of the matrix permittivity is much more robust in the (001)-oriented film (by factor 12 compared to R-STO) than in the random polycrystalline one (by factor 3 compared to R-STO). We emphasize that such behaviour of (001) N-STO is not influenced by the bottom SRO electrode: similar permittivity is found in the R-STO films on Pt/Si and on SRO/STO, whereas nitrogen-induced changes of the SRO resistivity are not detected.

The experimentally observed different strengths of the matrix dielectric effect in the randomly oriented polycrystalline and in the (001) oriented epitaxial N-STO films may be related to different crystal orientations, lattice strains, and/or nitrogen distributions in these films. The macroscopic dielectric response is isotropic in random N-STO, where all components of the dielectric tensor contribute to the measured out-of-plane dielectric constant. The atomic SrO-planes and TiO₂-planes are aligned parallel to the substrate surface in the (001)-oriented perovskite STO films crystal [ESI,† Fig. S8]. In terms of the theoretical tetragonal unit cell [Fig. 1], the out-of-plane dielectric response of the (001) oriented N-STO film may then correspond to either z-component, ε_zz, of the dielectric tensor or to the other components, ε_xx and ε_yy. Importantly, epitaxial film is coherent to the underlying STO substrate and, thus, subjected to a weak biaxial in-plane compression, which arises due to nitrogen-induced lattice expansion of N-STO. In contrast, polycrystalline film is free of such lattice strain. Finally, atomic sites for nitrogen incorporation are energetically more favourable at columnar boundaries than inside crystal.⁴¹ Therefore, for the same total concentration of nitrogen in all films, the nitrogen concentration inside columns in polycrystalline films may be smaller than that inside epitaxial films.

Next, we inspected epitaxially strained films. The detected profound nitrogen-induced reduction of the matrix permittivity is found to be dramatically intensified in the presence of epitaxial lattice strain [Fig. 4]. The films are metrically tetragonal, with the out-of-plane lattice parameters c being larger than the in-plane parameters a = b. The measured average out-of-plane strain is tensile s_c ≈ 1.0% in the heteroepitaxial (001) N-STO film on LAO and s_c ≈ 1.4% in the heteroepitaxial (001) N-STO film on LSAT. It is worth noting that N substitution causes anisotropic local lattice distortions, where relative Ti–N–Ti elongation (compared to the Ti–O–Ti length) is qualitatively understandable as a dominant local distortion. Therefore, elastic tensors, associated with nitrogen substitution, are anisotropic and can differ for substitutions in different atomic planes [ESI,† Fig. S9]. As shown before,^50,52 macroscopic elastic energy of the in-plane compressed (001)-oriented epitaxial film can be minimized if the main elongation (Ti–N–Ti direction here) is aligned out-of-plane (normal to the substrate surface). Thus, the measured out-of-plane tensile strains result from the substrate-induced compressive misfit and preferential out-of-plane alignment of elastic tensors.⁵²

Fig. 4 Semi-log permittivity – temperature plots for the strained heteroepitaxial nitrogen-doped SrTiO_2.7N_0.3 films (marked by “N s_c = 1.0%” and “N s_c = 1.4%”) compared to those for the homoepitaxial nitrogen-doped SrTiO_2.7N_0.3 and regular SrTiO₃ films (marked by “N” and “R”, correspondingly). Frequency is 1 kHz.

The strained N-doped films exhibit massive orders-of-magnitude drop of the out-of-plane dielectric constant compared to that in the regular homoepitaxial film. Such a striking frustration of the dielectric constant was not reported for epitaxially strained stoichiometric films, nor for oxygen-deficient films. The nitrogen substitution plays a critical role here.

Thus, our experimental observations imply that nitrogen substitution can produce local lattice distortions, which lower the cubic symmetry of STO. The two distinct sites for nitrogen location are possible: in the SrO- and TiO₂-planes. Nitrogen substitution leads to a decrease of the matrix dielectric permittivity. The effect is overwhelming in the presence of anisotropic lattice strain. Next, we used first-principles analyses and demonstrated solid theoretical support for these suggestions as well as revealed atomistic mechanisms behind them.

Nitrogen substitution on atomic level

We theoretically analysed the crystal structure and lattice vibrations for 6 different states, including unstressed pure state, unstressed doped states with substitutions in either SrO- or TiO₂-planes, as well as biaxially in-plane compressed pure state and two doped states, correspondingly [ESI,† Table S1 and S2]. Interestingly, our calculations revealed a high localization of the unpaired spin (∼0.87 electron spin) at the nitrogen substitution atom, which has two closed and one dangling chemical bonds, with the N–Ti bond strength (characterized by the bond populations) being larger than that of O–Ti bond in a regular STO.

First, we focus on the low frequency TO vibrational modes, which determine ε_zz component of the static dielectric tensor.

For unstressed pure tetragonal STO, our previous simulations in the framework of I4/mcm (SG 140) space group revealed that Raman-inactive A_2u mode (53 cm⁻¹) gives the main contribution to ε_zz component.⁶⁵ In this mode, all atoms oscillate exclusively along z-axis, with the Ti and Sr oscillations being in phase and oxygen ones in antiphase, and with the same vibrational amplitudes for the given kind of atoms. There is only a minor difference between amplitudes for the axial and equatorial oxygen atoms. The results of calculations in the framework of SG 1, performed here, agree well with those obtained for SG 140. The structural parameters for SG1 [ESI,† Table S1] nearly coincide with those for SG 140.^61,65 For SG 1, the frequency of the mode, which gives the main dielectric contribution, is 57 cm⁻¹. The main atomic oscillations are along z-axis, in-phase for Sr and Ti and antiphase for oxygen, and with the amplitude of equatorial oxygen atoms being 2.5–3% larger than those of axial ones. Additionally, there are tiny vibrations of all atoms in xy-plane: the ratio of amplitudes along x- and y-axes to those along z-axis does not exceed 10%. Again, Sr and Ti atoms oscillate in phase, with the amplitudes along x- and y-axes being practically the same. All oxygen atoms oscillate in the xy-plane in antiphase with the Sr and Ti atoms. For axial oxygen atoms (SrO-planes), amplitudes along x- and y-axes are nearly equal. For equatorial oxygen atoms (TiO₂-planes), the motion is more complex, with the ratio of amplitudes along x and y axes within 1–2.8. The vibrations in the mode 57 cm⁻¹ are shown schematically in [ESI,† Fig. S10]. The calculated dielectric contribution from this mode is Δε_zz = 743 of the total ε_zz = 760 [ESI,† Table S2].

Compared to pure unstressed state, nitrogen substitutions for the axial oxygen atoms (SrO-planes) [Fig. 5(a)] or for the equatorial oxygen atoms (TiO₂-planes) [Fig. 5(b)] produce structural changes [Fig. 5 and Fig. S11, Table S1, ESI,†]. The main deformation is an elongation of the Ti–Ti distance. For the axial substitution, the Ti–N–Ti distance is 3.957 Å compared to the Ti–O–Ti distance of 3.887 Å, and for the equatorial substitution, the Ti–N–Ti distance is 3.965 Å compared to the Ti–O–Ti distance of 3.881 Å. The Ti–N–Ti elongation is mainly responsible for the formation of anisotropic elastic tensors, whose presence was indicated herein. Compared to pure STO, the unit cell of N-STO expands so that the chemical tensile lattice strain is (s_a = s_b ≈ 0.2%, s_c ≈ 0.7%) for N in the SrO-planes and (s_a ≈ 0.5%, s_b ≈ 0.4%, s_c ≈ 0.2%) for N in the TiO₂ planes. These results imply that the (001) N-STO films on STO are subjected to a weak in-plane compression, which is difficult to detect experimentally but whose presence may explain the above discussed difference between polycrystalline N-STO and (001) N-STO on STO.

Fig. 5 Schematic structures of unstressed nitrogen doped STO. Sr atoms are shown by green balls, Ti atoms – blue balls, oxygen atoms – red balls, nitrogen atoms – yellow balls. The nitrogen substitution is (a) axial (in the SrO plane) and (b) equatorial (in the TiO₂ plane). For structural parameters see ESI,† Table S1.

The substitutions significantly alter the very nature of the lattice vibrations. Thus, the experimentally observed nitrogen-induced dielectric effects cannot be simplistically ascribed to hardening of the same vibrational soft mode as in pure STO. The calculated frequency of the lowest-frequency mode increases from 17 cm⁻¹ in pure STO to 49 cm⁻¹ and 23 cm⁻¹ for N in the SrO- and TiO₂-planes, correspondingly. Importantly, the vibrational contributions to the component ε_zz of the static dielectric tensor are distributed among several modes in the presence of nitrogen compared to the main mode 57 cm⁻¹ in pure STO. The calculated dielectric constant ε_zz decreases from 760 in pure STO to 228 and 368 for N in the SrO- and TiO₂-planes, correspondingly.

For the axial substitution (nitrogen in the SrO-plane) [Fig. 6(a)], the largest dielectric contribution comes from the vibrational mode with the frequency 81.56 cm⁻¹. The vibrations in the mode 81.56 cm⁻¹ are shown schematically in [ESI,† Fig. S12]. In this mode, the vibrations of the nitrogen atom and all oxygen atoms along z-axis are in phase, but the amplitudes of vibrations in xy-plane exceed those along z-axis for some of oxygen atoms. The motion of Ti atoms retains a nearly uniaxial character: mainly along z-axis with relatively small components in xy-plane. Additionally, the four Ti atoms form two pairs, which oscillate along the z-axis in antiphase. The Ti2 and Ti3 atoms [see Fig. 6(a)] vibrate in phase and demonstrate the largest displacements. Examination of the chemical bonds, involved in the relative motions between atoms, reveals that the biggest contortions occur in the bonds Ti3–O1, Ti3–O6, Ti3–O8, Ti2–O7 and Ti2–O9 [see Fig. 6(a)]. The bond Ti3–O1 exhibits stretching behaviour because both atoms oscillate antiphase along the z-axis. In the Ti3–O6 and Ti3–O8 bonds, the oxygen atoms oscillate in the xy-plane in addition to their antiphase motions with the Ti atoms along the z-axis. This leads to a more complicated deformation of the bonds. The deformations of the bonds Ti2–O7 and Ti2–O9 are determined by the antiphase motions of the Ti and oxygen atoms along the z-axis, with the oxygen vibrations in the xy-plane being rather small. The calculated dielectric contribution from this mode is Δε_zz = 153 of the total ε_zz = 228 [ESI,† Table S2].

Fig. 6 Schematics of the atomic positions for (a) axial and (b) equatorial nitrogen substitution in the unit cell. Sr atoms are shown by green balls, Ti atoms – blue balls, oxygen atoms – red balls, nitrogen atoms – yellow balls.

For the equatorial substitution (nitrogen in the TiO₂ plane) [Fig. 6(b)], the calculated total dielectric constant is ε_zz = 368, whereto the largest contribution Δε_zz =176 originates from the mode with the frequency 39 cm⁻¹. The corresponding lattice vibrations are schematically presented in [ESI,† Fig. S13]. These vibrations are rather chaotic. The Sr and Ti atoms vibrate in phase along the z-axis. Concurrently, the Ti atoms oscillate in phase along all coordinate axes with commensurable amplitudes. The nitrogen and oxygen O5 atoms also vibrate in-phase along all axes. The other oxygen atoms oscillate in phase along the z-axis, but in antiphase to the nitrogen and oxygen O5. Interestingly, the oxygen atom O6 [see Fig. 6(b)] exhibits the largest amplitudes of oscillations along all axes. Therefore, the bonds between O6 and the nearest Ti1 and Ti3 atoms experience the strongest deformations, which, however, are not simply stretching because the atoms move not only in the bond direction.

Our calculations also disclosed that the nitrogen-induced effects on the dielectric components ε_xx and ε_yy are of the same character as those on the component ε_zz. For the pure unstressed tetragonal state, the mode 52.1 cm⁻¹ gives the largest contribution Δε_xx = 859 to the total ε_xx = 908, whereas the mode 52.7 cm⁻¹ gives the largest contribution Δε_yy = 837 to the total ε_yy = 888. The nitrogen substitution complicates and hardens the lattice vibrations. Compared to pure STO, the dielectric components become determined by several new modes and significantly decline, namely: to ε_xx = ε_yy = 113 for N in the SrO-planes and to ε_xx = 285, ε_yy = 307 for N in the TiO₂-planes. With respect to the experimentally observed dielectric behaviour in polycrystalline N-STO and (001) N-STO on STO, these results refute crystal orientation as critical and indicate strain as an important factor therein. The calculations confirmed the role of epitaxial strain as shown below.

Our theoretical analysis substantiated the experimentally observed frustration of the dielectric component ε_zz in the presence of biaxial in-plane compression in epitaxial N-STO films. Compared to pure unstressed STO, the calculated relative out-of-plane elongation (i.e., relative change of the lattice parameter c along the z-axis), or tensile strain s_c, is 0.85% for the in-plane compression of 1% [ESI,† Fig. S14 and Table S1]. The nitrogen substitution deforms the lattice, so that the total out-of-plane elongation is 1.7 and 2.1% for N in the SrO- and TiO₂-planes, respectively. The calculated frequency of the lowest-frequency mode further increases to 84 cm⁻¹ and 71 cm⁻¹ for N in the SrO- and TiO₂-planes, correspondingly. Again, the dielectric constant ε_zz is determined by several vibrational modes. For N in the SrO-plane, the calculated constant is ε_zz = 197, with the main contribution Δε_zz = 167 being from the relatively low-frequency mode 88 cm⁻¹. But for N in the TiO₂-plane, the vibrational contributions to the total constant ε_zz = 56 are spread over a broad frequency range, where the largest contribution Δε_zz = 23 is given by the relatively high-frequency mode 225 cm⁻¹.

From the calculated lattice strains, vibrations, and dielectric constants, we found a nearly monotonic correlation between elongation of the unit cell along the c-axis [Fig. 1], or tensile strain s_c, and the dielectric component ε_zz: the component ε_zz decreases with increasing strain s_c [ESI,† Table S3]. We emphasize that this tendency is not associated with strain-induced ferroelectric phase transition, which is expected for epitaxial films of pure STO.^66,67 The constant ε_zz can decrease due to hardening of the ferroelectric soft mode with increasing strain sc in the strain-induced ferroelectric state of pure STO films.⁶⁸ In contrast, nitrogen substitution complicates lattice vibrations, so that the matrix dielectric response of N-STO is not determined anymore by the same soft mode as in pure STO, and there is no ferroelectric state.

The first-principles calculations revealed general nitrogen-induced trends towards complicated vibrational patterns, hardening of vibrations, and, consequently, reduced matrix static dielectric constants. The calculations could not capture temperature dependence of the permittivity, nor dielectric relaxation of nanoregions, that made it difficult to directly compare the explicit theoretical and experimental magnitudes of the dielectric permittivity. Importantly, the theoretically disclosed nitrogen effects on the crystal structure, lattice vibrations, and dielectric response were found to be consistent with the relevant experimental observations. The atomistic mechanism for the nitrogen-controlled dielectric constant is thus through increased complexity and elevated frequencies (hardening) of the lattice vibrations. We expect that this mechanism may be valid for the dielectric behaviour in many perovskite oxide para(ferro)electrics.

Conclusions

We report self-consistent experimentally detected and theoretically revealed effects of nitrogen substitution on the dielectric permittivity in the archetypal perovskite oxide paraelectric SrTiO₃. By inspecting impedance as a function of temperature (T = 100–500 K) and frequency (f = 1–10⁶ Hz) in the in situ grown nitrogen doped and reference undoped polycrystalline and epitaxial films, we found that compared to pure SrTiO₃, nitrogen doping leads to a significant decrease of the matrix permittivity, reduction of the Curie constant, and substantial dual dipolar relaxation. Using first-principles analyses of nitrogen substitution, we demonstrated two distinct atomic sites for nitrogen location, lowering of crystal symmetry, changes in the pattern and frequencies of lattice vibrations, and decrease in the static dielectric constant. We also established that misfit lattice strain can enhance the nitrogen-induced effects in epitaxial films. The unveiled mechanism for the nitrogen-controlled dielectric constant through increased complexity of the lattice vibrations may be akin in many technologically important perovskite oxide para(ferro)electrics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to thank T. Kocourek (PLD) and O. Pacherova (XRD). The work was partly supported by the Czech Science Foundation (Grant No. 22-10832S) (MT), the European Structural and Investment Funds and the Ministry of Education, Youth and Sports of the Czech Republic through Programme “Research, Development and Education” (Project No. SOLID21 – CZ.02.1.01/0.0/0.0/16_019/0000760) (MT, AD), and the Czech Academy of Sciences through the program Strategy AV21“Breakthrough technologies for the future – sensing, digitization, artificial intelligence and quantum technologies” (MT, MS, AD). The financial support of M-ERA-NET HetCat project is acknowledged by LR and EK. The Institute of Solid State Physics, University of Latvia (Latvia) as the Centre of Excellence has received funding from the European Union's Horizon 2020 Frame-work Programme H2020-WIDESPREAD-01-2016-2017- Teaming Phase2 under grant agreement No. 739508, project CAMART2. The computer resources were provided by the Stuttgart Supercomputing Center (project DEFTD 12939) and Latvian Super Cluster (LASC).

References

1. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772.
2. A. Tkach, O. Okhay, I. M. Reaney and P. M. Vilarinho, J. Mater. Chem. C, 2018, 6, 2467.
3. S. Xiao, W. Gao, M. Yao, Z. Su and X. Yao, J. Mater. Chem. C, 2019, 7, 673.
4. N. Kalfagiannis, J. L. Stoner, J. Hillier, I. Vangelidis and E. Lidorikis, J. Mater. Chem. C, 2019, 7, 7851.
5. W. Pan, M. Cao, A. Jan, H. Hao, Z. Yao and H. Liu, J. Mater. Chem. C, 2020, 8, 2019.
6. A. V. Plokhikh, I. S. Golovina, M. Falmbigl, I. A. Karateev, A. L. Vasiliev, J. Lapano, R. Engel-Herbert and J. E. Spanier, J. Mater. Chem. C, 2021, 9, 13115.
7. Z. Yang, H. Du, L. Jin and D. Poelman, J. Mater. Chem. A, 2021, 9, 18026.
8. A. N. Adeyemi, A. Venkatesh, C. Xiao, Z. Zhao, Y. Li, T. Cox, D. Jing, A. J. Rossini, F. E. Osterloh and J. V. Zaikina, Mater. Adv., 2022, 3, 4736.
9. F. Zhu, Y. Gao, J. Ding and J. Qiu, J. Mater. Chem. C, 2023, 11, 10236.
10. M. Liu, Z. Cao, X. Wang, S. Mao, J. Qin, Y. Yang, Z. Rao, Y. Zhao and B. Sun, J. Mater. Chem. C, 2023, 11, 13167.
11. C.-C. Hsu, C.-W. Cheng, X.-M. Wen and M. Joodaki, J. Mater. Chem. C, 2023, 11, 10651.
12. A. A. Wilson, T. P. Shalvey, A. Kafizas, A. Mumtaz and J. R. Durrant, Sustainable Energy Fuels, 2023, 7, 5066.
13. C. Wang, Y. Li, X. Cai, D. Duan and Q. Jia, J. Mater. Chem. A, 2023, 11, 21046–21057.
14. A. Čontala, N. Daneu, S. Gupta, M. Spreitzer, A. Meden and M. M. Kržmanc, Nanoscale Adv., 2023, 5, 3005.
15. R. A. Maier, E. Cockayne, M. Donohue, G. Cibin and I. Levin, Chem. Mater., 2020, 32, 4651.
16. Z. Zhao, R. V. Goncalves, S. K. Barman, E. J. Willard, E. Byle, R. Perry, Z. Wu, M. N. Huda, A. J. Moulé and F. E. Osterloh, Energy Environ. Sci., 2019, 12, 1385.
17. Y. Zhang, W. Li, Z. Wang, Y. Qiao, Y. Yu, Y. Zhao, R. Song, H. Xia and W. Fei, J. Mater. Chem. A, 2019, 7, 17797.
18. A. R. Jayakrishnan, A. Kumar, S. Druvakumar, R. John, M. Sudeesh, V. S. Puli, J. P. B. Silva, M. J. M. Gomes and K. C. Sekhar, J. Mater. Chem. C, 2023, 11, 827.
19. Y. Fan, Z. Zhou, Y. Chen, W. Huang and X. Dong, J. Mater. Chem. C, 2020, 8, 50.
20. M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials. Clarendon Press, Oxford, 2004.
21. K. Uchino, Ferroelectric Devices, Marcel Dekker, New York, 2000.
22. J. F. Scott, Science, 2007, 315, 954.
23. Ferroelectric Materials for Energy Applications, ed. H. Huang, J. F. Scott, Wiley-VCH Verlag, Weinheim, 2018.
24. T. Mikolajick, S. Slesazeck, H. Mulaosmanovic, M. H. Park, S. Fichtner, P. D. Lomenzo, M. Hoffmann and U. Schroeder, J. Appl. Phys., 2021, 129, 100901.
25. T. L. Wan, L. Ge, Y. Pan, Q. Yuan, L. Liu, S. Sarina and L. Kou, Nanoscale, 2021, 13, 7096.
26. W. Wang, J. Li, H. Liu and S. Ge, Adv. Sci., 2021, 8, 2003074.
27. A. S. Barker and M. Tinkham, Phys. Rev., 1962, 125, 1527.
28. G. Rupprecht and R. O. Bell, Phys. Rev., 1964, 135, A748.
29. R. C. Neville, B. Hoeneisen and C. A. Mead, J. Appl. Phys., 1972, 43, 2124.
30. R. Migoni, H. Bilz and D. Bäuerle, Phys. Rev. Lett., 1976, 37, 1155.
31. K. Kamaras, K. L. Barth, F. Keilmann, R. Henn, M. Reedyk, C. Thomsen, M. Cardona, J. Kircher, P. L. Richards and J. L. Stehle, J. Appl. Phys., 1995, 78, 1235.
32. A. Bussmann-Holder, J. Phys.: Condens. Matter, 2012, 24, 273202.
33. A. A. Sirenko, C. Bernhard, A. Golnik, A. M. Clark, J. Hao, W. Si and X. X. Xi, Nature, 2000, 404, 373.
34. P. Marsik, K. Sen, J. Khmaladze, M. Yazdi-Rizi, B. P. P. Mallett and C. Bernhard, Appl. Phys. Lett., 2016, 108, 052901.
35. J. M. Edge, Y. Kedem, U. Aschauer, N. A. Spaldin and A. V. Balatsky, Phys. Rev. Lett., 2015, 115, 247002.
36. W. Peng, R. Tétot, G. Niu, E. Amzallag, B. Vilquin, J. B. Brubach and P. Roy, Sci. Rep., 2017, 7, 2160.
37. A. Mostaed, I. Bakaimi, B. Hayden, D. C. Sinclair and I. M. Reaney, Phys. Rev. Mater., 2020, 4, 094410.
38. P. Long, C. Chen, D. Pang, X. Liu and Z. Yi, J. Am. Ceram. Soc., 2019, 102, 1741.
39. M. Tyunina, O. Pacherova, N. Nepomniashchaia, V. Vetokhina, S. Cichon, T. Kocourek and A. Dejneka, Phys. Chem. Chem. Phys., 2020, 22, 24796.
40. M. Tyunina, M. Savinov and A. Dejneka, Appl. Phys. Lett., 2021, 119, 192901.
41. L. L. Rusevich, M. Tyunina, E. A. Kotomin, N. Nepomniashchaia and A. Dejneka, Sci. Rep., 2021, 11, 2334.
42. P. Reunchan, N. Umezawa, A. Janotti, J. T. Thienprasert and S. Limpijumnong, Phys. Rev. B, 2017, 95, 205204.
43. Y. Yang, W. Zheng, D. Cheng and D. Cao, Sustainable Energy Fuels, 2017, 1, 1968.
44. C. Zhang, Y. Jia, Y. Jing, Y. Yao, J. Ma and J. Sun, Phys. B, 2012, 407, 4649.
45. S. Piskunov, O. Lisovski, J. Begens, D. Bocharov, Yu. F. Zhukovskii, M. Wessel and E. Spohr, J. Phys. Chem. C, 2015, 119, 18686.
46. Epitaxial Growth of Complex Metal Oxides, ed. G. Koster, M. Huijben, G. Rijnders, Woodhead Publishing, Oxford, 2015.
47. J. L. MacManus-Driscoll, M. P. Wells, C. Yun, J.-W. Lee, C.-B. Eom and D. G. Schlom, APL Mater., 2020, 8, 040904.
48. Z. Feng, N. Charles, X. R. Wang, D. Lee, K. A. Stoerzinger, S. Muy, R. R. Rao, D. Lee, R. Jacobs, D. Morgan and Y. Shao-Horn, Mater. Today, 2019, 31, 100.
49. R. Ramesh and D. G. Schlom, Nat. Rev. Mater., 2019, 4, 257.
50. M. Tyunina, L. L. Rusevich, E. A. Kotomin, O. Pacherova, T. Kocourek and A. Dejneka, J. Mater. Chem. C, 2021, 9, 1693.
51. M. Tyunina, N. Nepomniashchaia, V. Vetokhina and A. Dejneka, APL Mater., 2021, 9, 121108.
52. M. Tyunina, J. Levoska, O. Pacherova, T. Kocourek and A. Dejneka, J. Mater. Chem. C, 2022, 10, 6770.
53. M. Tyunina, S. Cichon, N. Nepomniashchaia, T. Kocourek, P. Svora, M. Savinov, V. Vetokhina, M. Klementova and A. Dejneka, Next Mater., 2023, 1, 100003.
54. M. Tyunina and J. Levoska, Appl. Phys. Lett., 2006, 88, 262904.
55. M. Tyunina, J. Phys.: Condens. Matter, 2006, 18, 5725.
56. M. Tyunina, M. Plekh, M. Antonova and A. Kalvane, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 224105.
57. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rerat, S. Casassa, J. Baima and S. Salustro, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
58. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison and I. J. Bush, et al., CRYSTAL17 User's Manual. 2017, University of Torino, Torino.
59. L. L. Rusevich, G. Zvejnieks, E. A. Kotomin, M. Maček Kržmanc, A. Meden, Š. Kunej and I. D. Vlaicu, J. Phys. Chem. C, 2019, 123, 2031.
60. L. L. Rusevich, G. Zvejnieks and E. A. Kotomin, Solid State Ionics, 2019, 337, 76.
61. G. Zvejnieks, L. L. Rusevich, D. Gryaznov and E. A. Kotomin, Phys. Chem. Chem. Phys., 2019, 21, 23541.
62. S. Piskunov, E. Heifets, R. I. Eglitis and G. Borstel, Comput. Mater. Sci., 2004, 29, 165.
63. C. Gatti, V. R. Saunders and C. Roetti, J. Chem. Phys., 1994, 101, 10686.
64. V. Polinger and I. B. Bersuker, Phys. Rev. B, 2018, 98, 214102.
65. L. L. Rusevich, E. A. Kotomin, G. Zvejnieks and A. I. Popov, Low Temp. Phys., 2020, 46, 1185.
66. N. A. Pertsev, A. K. Tagantsev and N. Setter, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R825.
67. J. H. Haeni, et al. , Nature, 2004, 430, 758.
68. A. Antons, J. B. Neaton, K. M. Rabe and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 024102.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03757f

---