 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermoelectric properties of Pnma and R3m GeS and GeSe†
Min
Zhang
 ,
Joseph M.
Flitcroft
,
Joseph M.
Flitcroft
 ,
Sophie K.
Guillemot
,
Sophie K.
Guillemot
 and
Jonathan M.
Skelton
and
Jonathan M.
Skelton
 *
*
Department of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: jonathan.skelton@manchester.ac.uk
First published on 10th October 2023
Abstract
With ∼60% of global energy lost as heat, technologies such as thermoelectric generators (TEGs) are an important route to enhancing the efficiency of energy-intensive processes. Optimising thermoelectric (TE) materials requires balancing a set of interdependent physical properties to meet efficiency, cost and sustainability requirements, and is a complex materials-design challenge. In this study, we demonstrate a fully first-principles modelling approach to calculating the properties and thermoelectric figure of merit ZT and apply it to the orthorhombic and rhombohedral phases of GeS and GeSe. While p-doped Pnma GeS and GeSe do not match the performance of the Sn analogues, due to a smaller electrical conductivity σ and larger lattice thermal conductivity κlatt, we predict a large ZTmax = 2.12 for n-doped Pnma GeSe at 900 K, which would make it a good match for p-type SnSe in a thermoelectric couple. Moreover, with n-type doping the σ is largest along the layering direction and aligns with the minimum κlatt, and a much larger ZTmax > 3 could potentially be accessible with control over the growth direction. We also predict that p-doped R3m GeS and GeSe can achieve an industrially-viable ZT > 1, through a high σ counterbalanced by a large thermal conductivity, and experiments indicate this can be further improved by alloying. Our results therefore strongly motivate further study of the under-explored Ge chalcogenides as prospective TEs, with a particular focus on strategies for n-doping the Pnma phases.
1 Introduction
Energy underpins every aspect of modern human life. Despite substantial progress in renewable energy technologies such as wind and solar power, fossil fuels remain the leading energy resource in many countries, and demand is still increasing.1 However, fossil fuels are a finite resource, and the CO2 and other emissions from extracting and burning them have serious impacts on the climate and on human health.2 To reduce our reliance on fossil fuels, it is critical both to develop a portfolio of clean energy technologies and to improve the efficiency with which we use energy.3–7At present, around 60% of the energy consumed globally is wasted as heat,8,9 which has led to substantial interest in thermoelectric generators (TEGs) to convert heat to electricity and thereby improve the efficiency of energy-intensive processes. TEGs are solid-state devices that extract electrical energy from a temperature gradient and are easily scalable to a range of applications including in the automotive, manufacturing and power-generation industries.9 The performance of a thermoelectric material can be described by the dimensionless figure of merit ZT:9
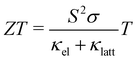 | (1) |
A wide variety of inorganic materials have been explored as thermoelectric (TE) materials, including chalcogenides,10–14 metal oxides,15–18 clathrates,19–22 and skutterudites.23–26 The current industry-standard TEs are Bi2Te3 (ZTmax ≈ 1 from 359–450 K) and PbTe (ZTmax = 2.2 at 915 K).27–29 However, Pb is toxic and Te has a low terrestrial abundance of ca. 1 ppb,30 comparable to Pt, and is required for other technologies such as photovoltaics. This makes it impractical to deploy TEGs based on either material at scale.9
Given that chalcogenides often show the required balance of favourable electrical properties and low κlatt, much research has focused on alternative compositions. The electrical properties required for a high-performance TE are similar to those needed for many other optoelectronic applications, and the Sn and Ge monochalcogenides SnS/SnSe and GeS/GeSe have both been widely explored as absorber materials for thin-film solar cells.31–36 SnSe has been identified as an extremely promising TE material with an ultra-high bulk ZTmax ≈ 2.6 at 923 K,37 a good ZT over a wide temperature range of 300–773 K,38 and an even higher polycrystalline ZTmax ≈ 3.1 at 773 K.39 SnS shows very similar structural chemistry to SnSe, and is advantageous due to the higher abundance and lower toxicity of S, but has yet to demonstrate comparable TE performance.40–42
The Ge chalcogenides exhibit similar structures and optoelectronic properties to the Sn analogues, but their TE performance is less well characterised. However, Ge is 1000× more abundant than Te and less toxic than Pb,43 making GeS and GeSe attractive as prospective TEs. A small number of computational studies have predicted the orthorhombic Pnma phase of GeSe to have a large ZTmax = 2.5 at 800 K, competitive with SnSe, and Pnma GeS to attain ZTmax = 0.73 at 700 K, close to the industry-standard ZT = 1.44,45 More recently, the R3m phase of GeSe was also reported to show a ZT > 1.46
In our previous work on the tin chalcogenides we developed a workflow for calculating the four parameters in the ZT equation (eqn (1)) from first principles, which was found to give accurate predictions for the well-characterised Pnma SnS and SnSe.11 In this work, we apply a similar approach to predict the electrical and thermal transport properties of the Pnma and R3m phases of GeS and GeSe, with good agreement to available experimental data.47–50 By considering both p- and n-type doping, we predict that n-type Pnma GeSe has the highest potential ZTmax of 2.12 at 900 K, at a realistic doping level of 6 × 1019 cm−3, which would make it a good partner for p-type SnSe in a thermoelectric couple. Moreover, the n-doped material is predicted to show the largest σ and lowest κlatt along the layered b direction, potentially yielding a much larger ZT > 3 if the growth direction can be controlled. We also predict that the R3m phases can potentially attain ZT > 1 at mid-to-high temperature, which experiments suggest can be improved by suppressing the κlatt through alloying.
2 Computational methods
Pseudopotential plane-wave density–functional theory (DFT) calculations were performed using the Vienna ab initio Simulation Package (VASP) code.51Initial crystal structures of Pnma GeS and GeSe were taken from ref. 52, and the R3m structures of the two chalcogenides were derived from the GeTe structure reported in ref. 53 by replacing the chalcogen atom. The rocksalt structure of GeSe was taken from ref. 54, and rocksalt GeS was prepared from this by substituting Se with S.
All six structures were fully optimized using a plane-wave cutoff of 550 eV and tight tolerances of 10−8 eV and 10−2 eV Å−1 on the electronic total energy and forces, respectively. The dispersion-corrected PBEsol+D3 method55,56 was chosen to model the electron exchange and correlation based on our previous work.57,58 Projector-augmented wave (PAW) pseudopotentials59,60 were used to model the ion cores with the following valence configurations: Ge 3d104s24p2; S 3s23p4; and Se 4s24p4. Γ-centred Monkhort-Pack k-point meshes with 7 × 3 × 9, 7 × 7 × 7 (7 × 7 × 2) and 10 × 10 × 10 (6 × 6 × 6) subdivisions were used to sample the Brillouin zones of the Pnma and primitive (conventional) R3m and rocksalt unit cells, respectively.
Supercell finite-displacement phonon calculations were performed using the Phonopy package,61 and the lattice thermal conductivities were computed using the Phono3py code.62 The second-order (harmonic) force constants were obtained using a displacement step of 10−2 Å with 4 × 2 × 4, 4 × 4 × 2 and 3 × 3 × 3 supercell expansions of the Pnma, R3m and rocksalt conventional cells, respectively, containing 256, 192 and 216 atoms. The third-order (anharmonic) force constants for the Pnma and R3m structures were obtained using a displacement step of 3 × 10−2 Å with 2 × 1 × 2 and 3 × 3 × 1 supercells containing 32 and 54 atoms. (As explained below, we did not attempt thermal-conductivity or electronic-structure calculations on the rocksalt structures due to the presence of imaginary modes in the phonon spectra.) During post-processing, transformation matrices were applied to the R3m and rocksalt structures to transform to the primitive cells.
To evaluate the atom-projected phonon density of states (PDoS) curves, the phonon frequencies were interpolated onto uniform Γ-centered q-point meshes with 28 × 13 × 36, 28 × 28 × 28, and 40 × 40 × 40 subdivisions for the Pnma, R3m, and rocksalt phases, respectively. The phonon dispersion curves were evaluated by interpolating the frequencies onto strings of q-points passing through the high-symmetry points in the respective Brillouin zones. Non-analytical corrections at q → Γ were included to model the splitting between the longitudinal and transverse optic modes (i.e., LO/TO splitting) using the approach in ref. 63. The required Born effective charges Z* and high-frequency dielectric constants ε∞ were computed using PBEsol+D3 and density–functional perturbation theory (DFPT).64 The κlatt was calculated within the single-mode relaxation-time approximation (SM-RTA) based on modal properties calculated on Γ-centered q-point meshes with 16 × 8 × 16 and 24 × 24 × 24 subdivisions for the Pnma and R3m phases, respectively. We found that LO/TO splitting has a negligible impact on the κlatt of the four systems (Fig. S1, ESI†).
Electronic-structure calculations were performed using the HSE06 hybrid functional65 to obtain accurate electronic bandgaps Eg and were used as the basis to model the electronic transport properties with the AMSET code.66
Uniform band structures were calculated using PBEsol+D3 and k-point meshes with two times the number of subdivisions along each reciprocal lattice vector as the meshes used for the geometry optimisations (2.5× for R3m GeS), and a scissors operator applied to increase the Eg to the HSE06 values. Four scattering mechanisms were considered to determine the electronic relaxation times, viz. acoustic deformation potential (ADP), piezoelectric (PIE), polar optical phonon (POP), and ionized impurity (IMP) scattering. The high-frequency dielectric constants ε∞ were obtained as the real part of the energy-dependent dielectric function ε(E) = εre(E) + iεim(E) at E = 0. The ε(E) were calculated using HSE06 within the independent-particle approximation, from a sum over transitions between occupied and virtual electronic states,64 and with the number of bands in the calculations increased to 2× and 3× the defaults for the Pnma and R3m phases, respectively, to ensure convergence. The static dielectric constants, elastic constants and piezoelectric moduli were obtained using the finite-difference routines in VASP with PBEsol+D3. The POP frequency was obtained from the Γ-point phonon frequencies and the Z* determined using PBEsol+D3 and DFPT.64 We note that PIE scattering is only relevant for the R3m systems, since the Pnma structure is centrosymmetric and the piezoelectric moduli vanish by symmetry.
For the HSE06 calculations, the semi-core Ge 3d electrons were subsumed into the pseudopotential cores, which we found had very little impact on the electronic-structure calculations but significantly reduced the computational cost of the hybrid calculations. Whereas the k-point meshes used for the geometry optimisations were sufficient to converge the Eg and ε∞ of the Pnma phases, explicit testing indicated that denser sampling was required in calculations on the R3m phases. For these systems, we therefore employed the non-self-consistent approach documented in previous work,67 after verifying that the Eg and ε∞ obtained using both methods and the “base” k-point meshes gave quantitatively similar results. Convergence tests and a comparison of the self-consistent and non-self-consistent HSE06 calculations can be found in Section 1 of the ESI.†
3 Results and discussion
3.1 Structures and lattice dynamics
A feature of the group IV–VI chalcogenides is the rich structural chemistry related to the stereochemical activity of the tetrel lone pairs.57,58,68 Under ambient conditions, GeS and GeSe both adopt the “pseudo 2D” layered Herzenbergite structure formed by SnS and SnSe with the orthorhombic Pnma spacegroup (Fig. 1(a)). Pnma GeSe is also known to transform to the rhombohedral phase (space group R3m; Fig. 1(b)) adopted by GeTe under low hydrostatic pressure.69 GeSe has also been proposed to form the cubic rocksalt structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; Fig. 1(c)) adopted by the Pb chalcogenides at elevated temperature and under pressure.69,70 A variety of other monochalcogenide phases are also reported,71,72 but we focus here on the Pnma, R3m and rocksalt phases.
m; Fig. 1(c)) adopted by the Pb chalcogenides at elevated temperature and under pressure.69,70 A variety of other monochalcogenide phases are also reported,71,72 but we focus here on the Pnma, R3m and rocksalt phases.
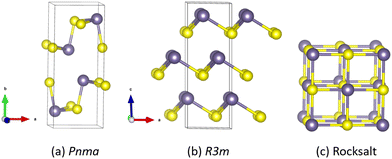 | ||
Fig. 1 Structures of the Pnma (a), R3m (b), and rocksalt (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) (c) phases of GeS and GeSe. Purple and yellow spheres denote the Ge and chalcogen atoms, respectively. The R3m and Fm m) (c) phases of GeS and GeSe. Purple and yellow spheres denote the Ge and chalcogen atoms, respectively. The R3m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures are shown in the conventional cells. These figures were generated using VESTA.74 m structures are shown in the conventional cells. These figures were generated using VESTA.74 | ||
In the high-symmetry cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure both the tetrel and chalcogen atoms occupy six-fold coordinated octahedral sites. The rhombohedral R3m structure is derived from the rocksalt structure by a small displacement of the cations from their ideal positions, which results in both atoms forming three short and three long bonds. The Pnma phase can be considered a further distortion to the rocksalt structure in which every other unit cell along the b axis is offset, resulting in a pseudo 2D layered structure in which the Ge and S atoms each form two short and one long bond. This structure enables the Ge2+ cations to have an active 4s2 lone pair, which projects into the interlayer space and supports a van der Waals interaction between adjacent layers.73
m structure both the tetrel and chalcogen atoms occupy six-fold coordinated octahedral sites. The rhombohedral R3m structure is derived from the rocksalt structure by a small displacement of the cations from their ideal positions, which results in both atoms forming three short and three long bonds. The Pnma phase can be considered a further distortion to the rocksalt structure in which every other unit cell along the b axis is offset, resulting in a pseudo 2D layered structure in which the Ge and S atoms each form two short and one long bond. This structure enables the Ge2+ cations to have an active 4s2 lone pair, which projects into the interlayer space and supports a van der Waals interaction between adjacent layers.73
The optimized lattice constants are compared to previous reports in Table S3 in the ESI.† The lattice parameters for the Pnma phases are in good agreement with previous measurements.54,75 The lattice parameters for rocksalt and R3m GeSe are underestimated by 3.5% and 2.5% compared to experiments, which we attribute to the measurements in ref. 54 and 50 being carried out at finite temperature and therefore including an appreciable amount of thermal expansion compared to our “athermal” DFT optimisations.58 There are some discrepancies between our calculations on the R3m and rocksalt phases and other theoretical work,76,77 which we attribute primarily to the tendency of the PBE functional employed in these studies to overestimate lattice constants and cell volumes compared to PBEsol+D3.
The phonon dispersion and density of states (DoS) curves of the Pnma, R3m and rocksalt phases of GeS are shown in Fig. 2. The unit cell of Pnma phase contains na = 8 atoms, and the primitive cells of the R3m and rocksalt phases contain na = 2 atoms, resulting in 3na = 24 and 3na = 6 branches at each wavevector q in the respective phonon dispersions. The phonon dispersion of Pnma GeS, with the most phonon bands, is notably more complex than those of the R3m and rocksalt phases. The lower symmetry of the R3m phase and consequent lower band degeneracy also results in a more complex phonon spectrum than for the rocksalt structure. The atom-projected DoS (PDoS) curves for Pnma and R3m GeS show that the lower- and higher-frequency modes are dominated by motions of heavier Ge and lighter S, respectively. Pnma GeS also shows a clear separation between the 12 lower- and higher-frequency modes and a prominent “phonon bandgap”. In contrast, while the PDoS of rocksalt GeS also shows a low-frequency feature dominated by Ge motion, there is considerable overlap between Ge and S at higher frequencies.
The calculated phonon spectra of the three GeSe phases (Fig. S4, ESI†) show similar features, with the notable exception that the PDoS of Pnma and R3m GeSe shows contributions from both atoms across the full range of phonon frequencies. Similarly, while there is some “splitting” in the PDoS of rocksalt GeSe, it is less prominent than in GeS. The extent of the splitting can be attributed to both the mass differences between Ge and S/Se, and to the nature of the bonding in the different structure types. Comparison of the spectra of GeS and GeSe also shows that the latter span a narrower range of frequencies, which is primarily due to the inverse relationship between frequency and atomic mass.
Whereas the phonon dispersion curves of both pairs of Pnma and R3m structures show real frequencies across the Brillouin zone, the two rocksalt structures show prominent imaginary modes at the q = Γ wavevector, indicating that the high-symmetry cubic phase is dynamically unstable. The position of the imaginary modes further indicates that the energy-lowering distortion can be represented in the primitive cell, and therefore likely corresponds to a cation off-centering to the R3m structure. This in turn suggests that the high-temperature rocksalt structure observed in experiments may be a crystallographic average over locally-distorted R3m domains. The predicted dynamical stability of Pnma GeS/GeSe and R3m GeSe is consistent with previous studies,76–78 as is the instability of rocksalt GeSe.79
There is, however, an interesting contrast with the analagous rocksalt SnS and SnSe. Rocksalt SnS is dynamically unstable under ambient conditions, but the imaginary mode lies at q = X rather than q = Γ, indicating a different type of energy-lowering distortion.57,58 In contrast to both SnS and GeSe, rocksalt SnSe is dynamically stable.58
The calculations in ref. 76 predicted R3m GeS to be dynamically unstable with a small imaginary mode along the Γ → X and Γ → L directions in the phonon dispersion. We attribute this discrepancy to an overestimation of the unit-cell volume with PBE, which has been shown in some cases to introduce unphysical imaginary modes into phonon spectra.80 Nevertheless, to rule out possible technical issues, we tested a series of second-order supercell expansions containing 300–648 atoms, but did not observe imaginary modes in any of these calculations (Fig. S5, ESI†).
Given the dynamical instability of the rocksalt structures, we focus on the Pnma and R3m phases in the remainder of this study.
3.2 Electronic transport properties
The calculated electronic band structures and density of states (DoS) curves of Pnma and R3m GeSe are presented in Fig. 3, and those of GeS are presented in Fig. S6 (ESI†). For both Pnma phases the conduction band minima (CBM) and valence band maxima (VBM) lie at different points along the Γ → X direction, resulting in indirect bandgaps of Eg = 1.32 and 1.17 eV for GeS and GeSe, respectively. The CBM and VBM of the two R3m phases are both located at the k = L wavevector, as in the rocksalt Pb and Sn chalcogenides,11,81 resulting in a direct gap of Eg = 0.3 eV for both systems. These predictions are generally in very good agreement with experimental measurements and previous calculations.49,82–85 We note, however, that previous computational studies on R3m GeS and GeSe predicted much larger Eg,77,86 which we attribute to insufficiently dense k-point meshes (cf. Table S2 and Fig. S2/S3, ESI†). The calculated bandgaps of Pnma GeS and GeSe are larger than the 0.93 and 0.82 eV predicted for Pnma SnS and SnSe in our previous work.11 On the other hand, the Eg of the R3m phases are considerably smaller than the 0.6 eV we predicted for rocksalt SnS and SnSe,11 which suggests the rhombohedral distortion in GeS and GeSe may lead to a significant narrowing of the gap.Having verified our calculated bandgaps, the electronic-structure calculations were used as the basis for electronic-transport calculations using semi-classical Boltzmann transport theory and an approximate model of the electron relaxation times.66,87
The transport properties are determined from the spectral conductivity Σ and the nth-order moments of the generalised transport coefficients  given by:66,88
given by:66,88
 | (2) |
 | (3) |
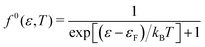 | (4) |
The εkj and νkj are obtained from a high-quality electronic-structure calculation. The electron relaxation times τkj in eqn (2) are computed from four scattering processes, viz. acoustic deformation potential (ADP), piezoelectric (PIE), polar optical phonon (POP) and ionised impurity (IMP) scattering, according to Matthiessen's Rule:
 | (5) |
With the Σ and  defined, the three electrical properties in eqn (1) can be calculated according to:
defined, the three electrical properties in eqn (1) can be calculated according to:
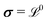 | (6) |
 | (7) |
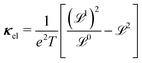 | (8) |
 for brevity.
for brevity.
The electrical properties are calculated for a set of specified temperatures and extrinsic carrier concentrations n (“doping levels”), which together determine the Fermi energy εF in eqn (3) and (4). We selected a temperature range of 300–900 K, with room temperature being the practical lower limit for most thermoelectric applications and 900 K close to the highest of the reported phase-transition temperatures of Pnma GeS and GeSe (863 and 907 K, respectively).44,70 A range of doping levels between n = 1016−1020 cm−3 was chosen to bracket the intrinsic carrier concentration of 1016 cm−3 reported for GeSe89 and the n ≈ 5 × 1019 cm−3 reported in experiments on doped SnSe.38,39,90,91 Experiments on the Ge and Se chalcogenides typically target p-type (hole) doping, which is readily achieved in SnSe e.g. by substituting Sn with Ag or Na,38,39 or by promoting Sn vacancies.90,91 However, n-type (electron) doping has also been reported for both SnS and SnSe,92,93 and has been predicted to lead to favourable properties in Pnma GeS.45 We therefore considered both types of doping. We note that the n is set by adjusting the position of the Fermi energy EF in the electronic-structure calculations, and the calculations therefore do not consider the practicality or potential effect of incorporating the defects or dopants at the concentration required to achieve a target doping level.
The σ, S, and κel are 3 × 3 tensors in which the diagonal components correspond to transport along the principal x, y and z directions. TEGs are typically based on thin films or pressed/sintered pellets composed of randomly-oriented crystal grains, and we therefore focus mainly on the scalar averages of the diagonal elements, which we denote S, σ and κel to distinguish them from the tensor quantities.
Fig. 4 compares the averaged electrical conductivity σ, absolute Seebeck coefficient |S|, thermoelectric power factor S2σ (PF) and electronic thermal conductivity κel of the four systems, for both p- and n-type doping. We first performed an analysis of the transport properties as a function of doping level at a fixed T = 800 K, chosen to be slightly below the reported phase-transition temperatures of Pnma GeS and GeSe.44,70 At this temperature, the PFs of Pnma GeS and GeSe are negligible up to n ≈ 1018 cm−3 and then increase rapidly with the doping level (Fig. 4(e)). Comparison with the Seebeck coefficient and conductivity shows that this is due to an exponential-like increase in σ at large n, which compensates a monotonic fall in the S from the peak values around n = 1017 cm−3 (Fig. 4(a) and (c)). Interestingly, the calculations predict that n-type doping leads to comparable or larger S and 2–3× larger σ than p-type doping, resulting in a much larger PF.
The narrow bandgap of the R3m phases results in large intrinsic p-type conductivity that dominates the electrical properties up to n ≈ 1017 cm−3. Above this, both the σ and S increase with larger doping levels, and the increase in the electrical conductivity results in a steep rise in the PF above n ≈ 1019 cm−3. Similar behaviour was also predicted for rocksalt SnS and SnSe in our previous work.11 The S of the R3m phases is smaller than the Pnma phases at low n but comparable at large n. The σ obtained with p-type doping is larger than in the p-doped Pnma phases over the range of n tested, resulting in a 3–4× larger PF at n = 1020 cm−3. n-type doping produces a smaller σ, comparable to the n-doped Pnma systems, and the balance of the smaller S and steeper dependence of the σ on n results in lower PFs than predicted for the n-doped Pnma systems at most doping levels.
The Pnma phases are predicted to have comparable and low κel, increasing with the conductivity to maximum values of ∼0.4 and 0.8 W m−1 K−1 for GeS and GeSe, respectively, at the largest n = 1020 cm−3 we tested (Fig. 4(g)). On the other hand, the intrinsic p-type conductivity of the R3m systems results in a much larger κel, of around 3 and 3.5 W m−1 K−1 for R3m GeS and GeSe, respectively, which reduces to 1.6–2 W m−1 K−1 at large n. This indicates a somewhat complex relationship between the carrier concentration, σ and κel in the R3m systems, but is again similar to our previous calculations on rocksalt SnS and SnSe.11
At a fixed n = 2 × 1019 cm−3, which is a conservative estimate of the achievable p-type doping levels in SnSe,38,39,90,91 the PFs of p-doped Pnma GeS and GeSe show a slow decrease, while the S2σ of the n-doped phases peak at intermediate temperature and fall at higher T (Fig. 4(f)). In both cases, this is a product of a reduction in the σ with temperature and a rise in the S (Fig. 4(b) and (d)). On the other hand, at this n the S of the two R3m phases are predicted to fall with temperature, leading to a significant drop in the PFs at higher T.
The reduction in σ with temperature predicted for the Pnma phases is typical of a degenerate semiconductor, i.e. a heavily-doped semiconductor that exhibits metallic-like behaviour, and so one might expect the electrical thermal conductivity to follow the Wiedemann–Franz law:
| κel = LσT | (9) |
We also investigated the anisoptropy in the electronic transport of the four systems (Fig. S7–S14, ESI†). The Seebeck coefficients of the Pnma phases are predicted to be relatively isotropic for n > 5 × 1017 cm−3. On the other hand, the calculations predict strong anisotropy in the σ. In the p-doped systems, the in-plane conductivity along the a and c directions is up to 2–3× higher than along the layered b direction, while, conversely, in the n-doped systems the interlayer conductivity along the b direction is more than 5× higher than along the in-plane directions. This anisotropy is reflected in the power factors, and is largely preserved across the 300–900 K temperature range with a fixed n = 2 × 1019 cm−3. In contrast to the Pnma phases, the transport in the R3m phases is relatively isotropic. The largest discrepancies are that the Seebeck coefficients of the p- and n-doped systems are smaller and larger along the c direction, respectively, but the relatively small absolute values of the S mean the anisotropy in the PFs is minimal.
Finally, we also examined the electron scattering rates for both p- and n-type doping at n = 2 × 1019 cm−3 and T = 800 K (Fig. 5 and Fig. S15–S18, ESI†). POP scattering generally dominates close to the Fermi energy, with additional contributions from PIE scattering in the R3m phases. ADP scattering becomes dominant at energies above the conduction-band minimum in the n-doped Pnma phases, and also at energies below and above the VBM/CBM in the p- and n-doped R3m phases, respectively, while for the p-doped Pnma phases IMP scattering is predicted to be significant at energies below the VBM.
 | ||
| Fig. 5 Calculated scattering rates as a function of energy for p-doped R3m GeSe at a doping level of n = 2 × 1019 cm−3 and temperature T = 800 K. | ||
The modelling approach employed here previously yielded accurate predictions for SnS and SnSe.11 While the Ge chalcogenides are not as well characterised, the present calculations appear to show similarly good agreement with available experimental measurements. The measurements on Pnma Ge0.79Ag0.01Sn0.2Se in ref. 47 obtained S ≈ 300 μV K−1 at 300 K with n ≈ 5 × 1018 cm−3, and we predict the same 300 K Seebeck coefficient with a 2× larger n = 1019 cm−3. The measurements on R3m (GeSe)0.9(AgBiTe2)0.1 in ref. 49 reported S ≈ 151 and 250 μV K−1 at room temperature and 723 K, and a PF of 1.28 mW m−1 K−2 at 627 K, all with a carrier concentration of 1.1 × 1019 cm−3. With a comparable n = 1019 cm−3 we predict a power factor of 1.47 mW m−1 K−2 at 620 K and a S = 287 and 218 μV K−1 at 300 and 720 K, which we again consider to be reasonable agreement given that the experimental sample is an alloy. (We note that our calculations predict a very similar S = 156 and 251 μV K−1 at the two temperatures with increased carrier concentrations of 8 × 1019 cm−3 and 1020 cm−3, respectively).
3.3 Lattice thermal conductivity
Within the single-mode relaxation-time approximation (SM-RTA), the macroscopic lattice thermal conductivity κlatt is calculated as a sum of contributions from microscopic phonon modes λ = qj according to:62 | (10) |
 | (11) |
The calculated scalar-averaged κlatt of the four Ge chalcogenides is shown in Fig. 6(a). Given that the ultra-low lattice thermal conductivity of SnSe is a key contributor to its high thermoelectric performance,37,94–96 we also compare our predictions to similar calculations on SnS and SnSe.97 The κlatt span a range of 0.82–1.71 W m−1 K−1 at 800 K (Table 1) and fall in the order of R3m GeSe > Pnma GeS ≈ R3m GeS > Pnma GeSe ≈ Pnma SnS > Pnma SnSe. The orthorhombic Ge chalcogenides therefore have larger κlatt than the Sn analogues, but Pnma GeSe has a κlatt comparable to SnS.
 | ||
| Fig. 6 Lattice thermal conductivity of Pnma and R3m GeS/GeSe and Pnma SnS/SnSe: averaged lattice thermal conductivity κlatt (a) and constant relaxation-time approximation (CRTA) decomposition into an averaged harmonic component κlatt/τCRTA (b) and averaged lifetime τCRTA (c) as defined in eqn (12). The data on SnS and SnSe was taken from our previous work.97 | ||
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) λ for each model. Data for Pnma SnS and SnSe from the similar calculations in ref. 97 are also given for comparison
λ for each model. Data for Pnma SnS and SnSe from the similar calculations in ref. 97 are also given for comparison
| κ latt [W m−1 K−1] | κ/τCRTA [W m−1 K−1 ps−1] | τ CRTA [ps] |
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) λ
[10−8 eV2]
λ
[10−8 eV2] |
||||
|---|---|---|---|---|---|---|---|
| κ xx | κ yy | κ zz | κ ave | ||||
| GeS (Pnma) | 0.85 | 0.50 | 2.35 | 1.23 | 0.68 | 1.80 | 3.06 |
| GeSe (Pnma) | 0.72 | 0.30 | 1.45 | 0.82 | 0.40 | 2.06 | 1.43 |
| GeS (R3m) | 1.15 | 1.15 | 1.03 | 1.11 | 2.76 | 0.40 | 7.37 |
| GeSe (R3m) | 1.83 | 1.83 | 1.47 | 1.71 | 1.29 | 1.32 | 1.87 |
| SnS (Pnma)97 | 0.71 | 0.51 | 1.20 | 0.80 | 0.75 | 1.07 | 2.62 |
| SnSe (Pnma)97 | 0.61 | 0.35 | 0.81 | 0.59 | 0.38 | 1.56 | 1.10 |
As for the electrical properties, the averaged κlatt is likely to be of most relevance to thermoelectric devices. However, Pnma SnS and SnSe both show strongly-anisotropic thermal transport,97 which is an important contributor to the “headline” ZT in single-crystal SnSe,37 so we also examined the anisotropy in the κlatt of the four systems (Table 1 and Fig. S19–S22, ESI†). The symmetry of the R3m structure is such that κxx = κyy ≠ κzz, and the independent κxx and κzz are similar and close to the average. For the Pnma structures, on the other hand, we predict strong anisotropy such that the lowest κlatt is obtained along the layered b axes (κyy) and the highest along the strongly-bonded c axes (κzz). Indeed, the anisotropy is so large that while Pnma and R3m GeS are predicted to have similar averaged κlatt of 1.23 and 1.11 W m−1 K−1, respectively, at 800 K, the κlatt of the Pnma phase is an average over three values that range from 0.50 W m−1 K−1 along the b direction to 2.35 W m−1 K−1 along the c axis.
Again as for the electrical properties, our predictions of the lattice thermal conductivity are generally in good agreement with experimental measurements and other calculations. Our predicted 300 K κlatt = 2.18 W m−1 K−1 for Pnma GeSe compares favourably to the measured values of 1.8–2.9 W m−1 K−1.47,49,50 The axial components are also similar to reported values of 2.3, 0.64–1.11 and 4.8 W m−1 K−1 along the a, b and c directions.44,50,98,99 At a higher T = 700 K, our predicted average value of 0.92 W m−1 K−1 is also comparable to the 0.85 W m−1 K−1 reported in ref. 50. We note that our calculated κlatt of Pnma GeS and GeSe are substantially larger than the minimum values of 0.52 and 0.39 W m−1 K−1 predicted by the approximate model in ref. 100, but the poor agreement with previous experimental and theoretical studies on GeSe suggest this model does not make realistic predictions. On the other hand, the predicted κlatt = 0.98 W m−1 K−1 along the b direction of Pnma GeS at T = 700 K predicted in ref. 45 is much larger than our predicted 0.56 W m−1 K−1, which we attribute to the use of PBE and a smaller 64-atom supercell to compute the force constants.
Our predicted 300 K κlatt = 4.53 W m−1 K−1 for R3m GeSe is similar to the 4.88 W m−1 K−1 obtained in previous calculations,101 whereas we attribute the lower values obtained from the calculations in ref. 77 to an overestimation of the lattice constants with PBE. We were only able to find experimental measurements on polycrystalline R3m (GeSe)0.9(AgBiSe2)0.1,46,49 which report lattice thermal conductivities of 0.74, 0.38 and 0.47 W m−1 K−1 at 300, 578 and 723 K, respectively. While these are much lower than our predicted 4.53, 2.36 and 1.95 W m−1 K−1, this can be attributed at least partially to the established impact of alloying on the κlatt.97,102–105
Having shown that our predicted κlatt are in good agreement with comparable measurements, we used the analysis techniques developed in our previous work19,23,97 to investigate the origin of the differences between the systems.
We first rewrite the κlatt as the product of a harmonic term and a weighted-average phonon lifetime τCRTA according to:
 | (12) |
In contrast, the τCRTA are strongly temperature dependent, and the sharp reduction in the phonon lifetimes with temperature, due to larger phonon occupation numbers and stronger scattering, dominates the behaviour of the κlatt once the κ/τCRTA reach the limiting values. Pnma GeS and GeSe have similar averaged lifetimes, so differences in the κlatt are due to the group velocities. R3m GeS and GeSe both have shorter τCRTA than the corresponding Pnma phases. The averaged lifetimes of GeS are shorter than those of GeSe, which compensates for the higher νλ, and, somewhat counter-intuitively, results in a smaller overall predicted κlatt for the sulphide than the selenide. The two Sn chalcogenides both have shorter averaged lifetimes than the equivalent Ge phases, resulting in smaller κlatt despite the similar κ/τCRTA. This indicates that, while the tetrel atoms have a minimal effect on the group velocities, they do have an impact on the κlatt through the phonon lifetimes.
The τCRTA can be further written as the product of a set of averaged modal (anharmonic) three-phonon interaction strengths, Pλ, and a counting function N2(q,ω) that captures the number of allowed energy- and (crystal) momentum-conserving scattering pathways (termed the “scattering phase space”).19 A comparison between systems can be made by calculating a weighted-average interaction strength, ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) , and a function
, and a function ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 that shows the size of the scattering phase space (average number of scattering pathways) as a function of phonon frequency only. Full details can be found in our previous work.19,23,97 The
2 that shows the size of the scattering phase space (average number of scattering pathways) as a function of phonon frequency only. Full details can be found in our previous work.19,23,97 The ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) were determined at 800 K as described in our previous work23,97 (Fig. S23–S26, ESI†). Scaled
were determined at 800 K as described in our previous work23,97 (Fig. S23–S26, ESI†). Scaled ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) and
and ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 that can be compared between systems are provided in Table 1 and Fig. 7 respectively. (Unscaled
2 that can be compared between systems are provided in Table 1 and Fig. 7 respectively. (Unscaled ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 for the four systems examined in this work, showing separate contributions from collision and decay pathways, are shown in Fig. S27–S30 in the ESI†).
2 for the four systems examined in this work, showing separate contributions from collision and decay pathways, are shown in Fig. S27–S30 in the ESI†).
 | ||
Fig. 7 Calculated averaged weighted joint density of states (w-JDoS) functions ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 at 800 K for the four Ge chalcogenides examined in this work compared to data on orthorhombic SnS and SnSe from ref. 97. 2 at 800 K for the four Ge chalcogenides examined in this work compared to data on orthorhombic SnS and SnSe from ref. 97. | ||
The calculated ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) of the Pnma Ge and Sn chalcogenides range from 1.10–3.06 × 10−8 eV2. The averaged interaction strengths are slightly higher in the Ge chalcogenides, and around 2× larger in the sulphides than the selenides. The calculated
of the Pnma Ge and Sn chalcogenides range from 1.10–3.06 × 10−8 eV2. The averaged interaction strengths are slightly higher in the Ge chalcogenides, and around 2× larger in the sulphides than the selenides. The calculated ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) of R3m GeSe is ∼30% larger than that of Pnma GeSe, but the averaged interaction strength in rhombohedral GeS is a much larger 2× that of Pnma GeS. Taking the
of R3m GeSe is ∼30% larger than that of Pnma GeSe, but the averaged interaction strength in rhombohedral GeS is a much larger 2× that of Pnma GeS. Taking the ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) as a measure of the intrinsic phonon anharmonicity, this analysis shows that the sulphides are more anharmonic than the selenides, the Ge chalcogenides are more anharmonic than the Sn analogues, and the R3m phases are more anharmonic than the Pnma structures.
as a measure of the intrinsic phonon anharmonicity, this analysis shows that the sulphides are more anharmonic than the selenides, the Ge chalcogenides are more anharmonic than the Sn analogues, and the R3m phases are more anharmonic than the Pnma structures.
The trends in anharmonicity are balanced by the ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2, which show that the scattering phase spaces are larger for the Sn chalcogenides than the Ge analogues, larger for the selenides than the sulphides, and larger for the Pnma phases than the R3m phases, at least at low frequencies where modes typically contribute most to the κlatt. The longer averaged lifetimes of Pnma GeSe and SnSe compared to the respective sulphides indicate that the larger
2, which show that the scattering phase spaces are larger for the Sn chalcogenides than the Ge analogues, larger for the selenides than the sulphides, and larger for the Pnma phases than the R3m phases, at least at low frequencies where modes typically contribute most to the κlatt. The longer averaged lifetimes of Pnma GeSe and SnSe compared to the respective sulphides indicate that the larger ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 do not fully compensate for the smaller
2 do not fully compensate for the smaller ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) . On the other hand, the smaller
. On the other hand, the smaller ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) of Pnma SnS and SnSe is more than compensated by the larger
of Pnma SnS and SnSe is more than compensated by the larger ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 and results in both Sn chalcogenides having shorter lifetimes than the Ge analogues. For the R3m phases, while GeSe has a larger
2 and results in both Sn chalcogenides having shorter lifetimes than the Ge analogues. For the R3m phases, while GeSe has a larger ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) 2 than GeS this does not compensate for the much larger
2 than GeS this does not compensate for the much larger ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) in the sulphide, resulting in the selenide having a ∼3.2× longer τCRTA.
in the sulphide, resulting in the selenide having a ∼3.2× longer τCRTA.
3.4 Thermoelectric figure of merit
We now combine our calculated electrical properties S, σ and κel with the calculated κlatt to obtain the figure of merit ZT as a function of doping level and temperature using eqn (1) (Fig. 8 and Fig. S31–S34, ESI†). | ||
| Fig. 8 Calculated scalar-averaged figure of merit ZT of (a) n-type Pnma GeS, (b) n-type Pnma GeSe, (c) p-type R3m GeS, and (d) p-type R3m GeSe as a function of doping level n and temperature T. | ||
As in previous sections we mainly focus on the averaged ZT. The ZTmax for the four p- and n-doped Ge chalcogenides and Pnma SnS/SnSe,11,97 at temperatures below the reported phase transition temperatures (GeS: 863 K, GeSe: 907 K, SnS: 878 K, SnSe: 750 K37,44,70,106–108), are summarised in Table 2 and S4 (ESI†).
| n [cm−3] | T [K] | ZT | σ [S cm−1] | S [μV K−1] | PF S2σ [mW m−1 K−2] | κ [W m−1 K−1] | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| κ el | κ latt | κ tot | ||||||||
| GeS (Pnma) | p-type | 1020 | 860 | 0.75 | 150 | 286 | 1.23 | 0.27 | 1.14 | 1.41 |
| n-type | 8 × 1019 | 860 | 1.33 | 415 | −260 | 2.81 | 0.67 | 1.14 | 1.81 | |
| GeSe (Pnma) | p-type | 8 × 1019 | 900 | 1.33 | 229 | 260 | 1.55 | 0.32 | 0.73 | 1.05 |
| n-type | 6 × 1019 | 900 | 2.12 | 287 | −313 | 2.81 | 0.46 | 0.73 | 1.19 | |
| GeS (R3m) | p-type | 1020 | 760 | 1.29 | 759 | 247 | 4.65 | 1.57 | 1.16 | 2.73 |
| n-type | 1020 | 660 | 1.22 | 605 | −261 | 4.11 | 0.88 | 1.34 | 2.22 | |
| GeSe (R3m) | p-type | 1020 | 740 | 1.20 | 858 | 253 | 5.49 | 1.55 | 1.85 | 3.40 |
| n-type | 1020 | 700 | 0.96 | 612 | −265 | 4.31 | 1.20 | 1.95 | 3.15 | |
| SnS (Pnma)11,97 | p-type | 3.16 × 1019 | 860 | 1.39 | 226 | 279 | 1.76 | 0.34 | 0.75 | 1.09 |
| n-type | 4 × 1019 | 860 | 1.78 | 400 | −259 | 2.68 | 0.55 | 0.75 | 1.30 | |
| SnSe (Pnma)11,97 | p-type | 3.16 × 1019 | 740 | 2.07 | 399 | 272 | 2.96 | 0.42 | 0.64 | 1.06 |
| n-type | 2 × 1019 | 740 | 2.39 | 450 | −289 | 3.75 | 0.52 | 0.64 | 1.16 | |
The ZTmax of the Pnma phases are all achieved at higher doping levels and temperatures. Higher n maximise the electrical conductivity, which dominates the power factor S2σ, while the shallow temperature dependence of the power factor S2σ and electronic thermal conductivity κel mean that the reduction in κlatt favours higher T (cf.Fig. 4 and 6(a)). In contrast, the ZTmax of the R3m phases occur at the largest n = 1020 cm−3 we tested but at lower T. In these systems, larger n maximises the S, σ and PF and reduces the κel, whereas the mid-temperature maximum in the PF and the opposing increase and decrease in the κel and κlatt, respectively, at higher temperatures produce a ZTmax between 650–750 K.
We predict all four n-doped Pnma phases, i.e. GeS/GeSe as well as SnS/SnSe, to show larger ZTmax than can be obtained with p-type doping. This is due to the anisotropy in the transport properties. With p-type doping, the σ and PFs are largest along the a and c directions but the ZT is limited by the larger κlatt along these directions. With n-type doping, the most facile electrical transport is along the layered b direction and is therefore “aligned” with the minimum in the κlatt. This results in a large ZTmax along the b direction and a larger averaged ZT than obtained with p-type doping. We discuss the anisotropy in the figure of merit of the Pnma phases below.
For Pnma SnS and SnSe, we predict n-type doping to lead to 28% and 15% larger ZTmax than p-type doping, whereas the ZTmax of Pnma GeS and GeSe are predicted to be 77% and 59% larger with n-type doping. Pnma GeSe and SnSe are predicted to have superior TE performance to the corresponding sulfides with 77% and 49% larger ZTmax with p-type doping and 59% and 34% larger ZTmax with n-type doping. This is due to a combination of a generally larger σ and comparable or larger S, leading to comparable or larger PFs, and lower total thermal conductivity.
On the other hand, p-doped R3m GeS and GeSe are predicted to show larger ZTmax than with n-type doping. R3m GeS is predicted to have an 8% higher ZTmax than R3m GeSe due to the larger predicted κlatt of the selenide outweighing the larger PF.
The predicted n required to obtain the ZTmax of SnS and SnSe are comparable to the carrier concentrations achieved in experiments,38,39,90,91 and these studies suggest the larger n required to optimise the ZT of the p-type Ge chalcogenides may also be achievable. Studies on n-doped SnS for PV applications have demonstrated n ≈ 1018 in halogen-doped single crystals and n ≈ 5 × 1018 cm−3 in Sn1−xPbxS thin films,92 while the recent study in ref. 93 achieved n ≈ 1019 cm−3 in Sn0.95Se with 1% HfCl4. We therefore tentatively suggest that the lower n required to achieve the predicted ZTmax in the n-doped chalcogenides may be achievable with further optimisation.
Of all the system considered, Pnma SnSe has the highest predicted average ZTmax of 2.07 and 2.39 with p- and n-type doping, respectively, while n-type GeSe is predicted to attain a ZTmax of 2.12 comparable to p-type SnSe. This would potentially make n-type GeSe a good match for p-type SnSe in a thermoelectric couple. Although the ZTmax of the two R3m phases are not competitive with the Pnma systems, they are predicted to attain an industrially-viable mid-to-high temperature ZT > 1, which may make them useful for some applications. It is also worth noting that the highly-anisotropic electrical and thermal transport in the Pnma phases means a larger ZTmax could be obtained if the growth direction could be controlled. For p-doped GeS, the largest ZT = 1.18 is along the layered b direction, where the κlatt is minimised, whereas in p-doped GeSe the largest ZT = 1.68 is obtained along the a direction, which balances a smaller κlatt with more favourable electrical properties. For n-type doping, the largest PF and smallest σ are both obtained along the layered b direction, producing large ZT of 1.85 and 3.03.
Interestingly, the synergy between the electrical and thermal transport with n-type doping is also predicted for the Pnma Sn chalcogenides (Table S4, ESI†). We predict ZTmax of 2.91 and 4.32 for SnS and SnSe, respectively, along the layered b axes, which are 60% and 80% larger than the averaged values of 1.78 and 2.39. (This may be compared with the p-type ZTmax of 1.56 and 2.29 along the c directions, which are both ∼10% larger than the average values of 1.39 and 2.07.) Given that successful n-type doping of both SnS and SnSe has been demonstrated, and at comparable n to what we predict is needed,93 this is also a potentially significant finding.
We briefly discuss a key approximation made in these calculations. The electrical-transport properties are calculated under the assumption that doping does not significantly change the host electronic band structure, termed the “rigid-band approximation” (RBA). While the RBA is to some extent a practical necessity, calculations on hole-doped PbTe found that the lowering of the band degeneracy with explicit doping led to a reduction in the calculated S on the order of 5–10%.109 Given the lower symmetry and band degeneracy of the Pnma and R3m phases, we might expect a smaller effect in the systems examined in the present study. We also note that the methodology we use for the electrical-transport calculations has been explicitly tested against heavily-doped systems and found to give good results.66 A further consideration is the potential impact of doping on the phonon spectrum and κlatt. While there has been little theoretical investigation of this, experiments on single-crystal SnS and SnSe with up to 3 at% doping, yielding hole concentrations on the order of 5 × 1019 cm−3, suggest a small reduction in the κlatt.38,110 The calculations would therefore overestimate the κlatt, which could partially compensate a potential overestimation of the S similar to that reported in ref. 109. Indeed, our previous work on the Sn chalcogenides, and recent work on the bismuth oxychalcogenides, suggests that the predicted ZT may benefit from a favourable cancellation of errors between the electrical and thermal transport properties.11,111 Therefore, without explicit calculations to confirm, or otherwise, we tentatively suggest that the use of the RBA should not have too large an impact on our predicted ZT.
With this in mind, our predicted ZT for GeS and GeSe are generally a good match to previous experimental and theoretical studies.44,47 In particular, measurements on Ag0.01Ge0.79Sn0.2Se reported a ZT of 0.2 at T = 700 K and n ≈ 1018 cm−3,47 and we obtain the same figure of merit with a similar n = 2 × 1018 cm−3. The authors also predicted a significant enhancement to ZT = 0.6 at a larger n ≈ 5 × 1019 cm−3, which is consistent with our predicted ZT = 0.87 with n = 4 × 1019 cm−3. Previous theoretical studies have also predicted superior TE performance for n-type doping, as found in the present study.45,99 We note, however, that our predictions show considerable quantitative differences to some previous calculations.44,45,99,112 For example, the study on Pnma GeS in ref. 45 predicted a ∼2.5× larger κlatt and 50% smaller ZT at 700 K than the present calculations, while the calculations in ref. 44 predicted a 5× larger σ, smaller κel, and 2–4× larger ZT. However, this can be put down to the considerable technical differences to the present calculations.
The comparison of our predictions for the R3m phases to experiments is rather more mixed. We predict a comparable ZT = 0.83 for GeSe at 540 K (n = 8 × 1019 cm−3) to the ZT = 0.9 at 500 K predicted in ref. 101. On the other hand, the study in ref. 77 predicted ZT > 2 at 800 K and n ≈ 1019 cm−3, whereas we predict ZT < 1 at 800 K at a larger n = 8 × 1019 cm−3 due to our higher predicted κlatt. Compared to the measurements on GeSe/AgBiSe2 alloys in ref. 46 and 49, our calculations predict that much larger n are required to obtain comparable ZT. This can be attributed in part to the high thermal conductivity predicted in these calculations, but we also find that we require a 4× larger n to reproduce the measured σ, which suggests the alloying may also impact the electrical properties. We note, however, that our calculations do reproduce the ZT = 0.84 at 720 K obtained for (GeSe)0.85(AgSbSe2)0.1548 with a reasonable n = 4 × 1019 cm−3. We therefore suggest that further characterisation of the R3m phases, to measure the properties of the pure phases and to better understand the impact of alloying on the transport properties, is warranted.
4 Conclusions
In summary, we have used a fully first-principles modelling approach to explore the potential thermoelectric performance of the Ge chalcogenides GeS and GeSe.Our calculations predict that Pnma GeS and GeSe can achieve larger ZTmax with n-type doping compared to the p-type doping typically targeted in experiments. The averaged ZTmax of 2.12 for Pnma GeSe is comparable to our predicted 2.07 for p-type Pnma SnSe and suggests n-type GeSe may make a good partner for SnSe in a thermoelectric couple. n-type doping results in the the maximum electrical conductivity and minimum κlatt being aligned along the layered b direction, and we predict a much larger ZTmax > 3 for Pnma GeSe if the growth direction can be controlled. The same appears to be true for n-type SnSe, where the average ZTmax with n-doping is predicted to be 15% larger than with p-type doping and the directional ZT along the b axis is predicted to be 4.32. Our results therefore suggest that further exploration of the Ge chalcogenides, and of the possibility of n-type doping of both the Sn and Ge chalcogenides, will be a fruitful direction for future research.
The large predicted κ of the R3m phases means the predicted ZTmax are not competitive with the Pnma structures, but p-type doping is nonetheless predicted to achieve ZT ≈ 1 between 650–750 K, which is promising and which may be useful for some applications. Given that experimental work on alloys suggests it may be possible to mitigate the large κlatt and/or to enhance the electrical properties, we also suggest these materials may warrant further investigation.
Author contributions
Conceptualisation – JMS; methodology – all authors; data curation – all authors; formal analysis and investigation – all authors; writing (original draft) – MZ and JMF; writing (review and editing) – all authors; funding acquisition – JMS. All authors have read and agreed to the published version of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge helpful comments from Prof. Nicholas Chilton on a draft version of this manuscript. MZ is supported by a China Scholarship Council (CSC) studentship (202006700004). JMS and JMF are supported by a UKRI Future Leaders Fellowship (MR/T043121/1), and JMS previously held a University of Manchester Presidential Fellowship. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431 and EP/X035859), this work used ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk). A subset of our calculations also made use of the UoM Computational Shared Facility (CSF) computing cluster, which is maintained by UoM Research IT.References
- N. Abas, A. Kalair and N. Khan, Futures, 2015, 69, 31–49 CrossRef.
- M. A. Ansari, Renewable Sustainable Energy Rev., 2022, 168, 112867 CrossRef.
- W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2021, 9, 20417–20435 RSC.
- R. Wolniak and B. Skotnicka-Zasadzień, Energies, 2022, 15, 662 CrossRef.
- B. Xu, J. Zhang, M. Egusquiza, D. Chen, F. Li, P. Behrens and E. Egusquiza, Renewable Sustainable Energy Rev., 2021, 144, 110880 CrossRef.
- X. Xu, Q. Zhou and D. Yu, Int. J. Hydrogen Energy, 2022, 47, 33677–33698 CrossRef.
- R. Zailan, J. S. Lim, Z. A. Manan, S. R. W. Alwi, B. Mohammadi-ivatloo and K. Jamaluddin, Renewable Sustainable Energy Rev., 2021, 148, 111289 CrossRef.
- A. Firth, B. Zhang and A. Yang, Appl. Energy, 2019, 235, 1314–1334 CrossRef.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- M. Rakshit, D. Jana and D. Banerjee, J. Mater. Chem. A, 2022, 10, 6872–6926 RSC.
- J. M. Flitcroft, I. Pallikara and J. M. Skelton, Solids, 2022, 3, 155–176 CrossRef.
- T.-R. Wei, P. Qiu, K. Zhao, X. Shi and L. Chen, Adv. Mater., 2023, 35, 2110236 CrossRef PubMed.
- J. M. Skelton, JPhys: Energy, 2020, 2, 025006 Search PubMed.
- T.-R. Wei, Y. Qin, T. Deng, Q. Song, B. Jiang, R. Liu, P. Qiu, X. Shi and L. Chen, Sci. China: Mater., 2018, 62, 8–24 Search PubMed.
- S. Ghosh, S. Harish, M. Ohtaki and B. B. Saha, Mater. Today Energy, 2020, 18, 100492 CrossRef.
- K. Brlec, K. B. Spooner, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2022, 10, 16813–16824 RSC.
- Y. Feng, X. Jiang, E. Ghafari, B. Kucukgok, C. Zhang, I. Ferguson and N. Lu, Adv. Compos. Hybrid Mater., 2018, 1, 114–126 CrossRef.
- S. D. Luu, T. A. Duong and T. B. Phan, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2019, 10, 023001 Search PubMed.
- B. Wei, J. M. Flitcroft and J. M. Skelton, Molecules, 2022, 27, 6431 CrossRef PubMed.
- W. R. Puspita, H. Takeya, T. Mochiku, Y. Ishikawa, S. Lee, S. Torii, M. Hagihala and T. Kamiyama, 2019 2nd International Conference on Applied Engineering (ICAE), 2019, pp. 1-5.
- H. Sato, H. Tamaki and T. Kanno, Appl. Phys. Lett., 2020, 116, 253901 CrossRef.
- B. Sun, J. Zhao, Y. Li, L. Cao, Y. Yang, X. Fan, X. Liu, C. Wang, X. Huang and X. Wang, et al. , J. Phys. Chem. C, 2020, 124, 9082–9088 CrossRef.
- J. Tang and J. M. Skelton, J. Phys.: Condens. Matter, 2021, 33, 164002 CrossRef PubMed.
- G. Rogl, F. Garmroudi, A. Riss, X. Yan, J. Sereni, E. Bauer and P. Rogl, Intermetallics, 2022, 146, 107567 CrossRef.
- A. Serrano, O. Caballero-Calero, C. Granados-Miralles, G. Gorni, C. V. Manzano, M. Rull-Bravo, A. Moure, M. Martn-González and J. F. Fernández, J. Alloys Compd., 2022, 167534 Search PubMed.
- H. Feng, Q. Deng, Y. Zhong, X. Rao, Y. Wang, J. Zhu, F. Zhang and R. Ang, J. Mater. Sci. Technol., 2023, 150, 168–174 CrossRef.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef PubMed.
- Y.-K. Zhu, P. Wu, J. Guo, Y. Zhou, X. Chong, Z.-H. Ge and J. Feng, Ceram. Int., 2020, 46, 14994–15002 CrossRef.
- H.-C. Hsieh, C.-H. Wang, W.-C. Lin, S. Chakroborty, T.-H. Lee, H.-S. Chu and A. T. Wu, J. Alloys Compd., 2017, 728, 1023–1029 CrossRef.
- N. Belzile and Y.-W. Chen, Appl. Geochem., 2015, 63, 83–92 CrossRef.
- Y. Mao, C. Xu, J. Yuan and H. Zhao, J. Mater. Chem. A, 2019, 7, 11265–11271 RSC.
- S.-C. Liu, Y. Yang, Z. Li, D.-J. Xue and J.-S. Hu, Mater. Chem. Front., 2020, 4, 775–787 RSC.
- Y. Shen, Y. Zhang, J. Huo, X. Li, Z. Yan, Y. Pan, W. Sun, N. Deng and W. Kang, J. Energy Storage, 2023, 69, 107958 CrossRef.
- V. Krishnamurthi, H. Khan, T. Ahmed, A. Zavabeti, S. A. Tawfik, S. K. Jain, M. J. Spencer, S. Balendhran, K. B. Crozier and Z. Li, et al. , Adv. Mater., 2020, 32, 2004247 CrossRef PubMed.
- I. Suzuki, S. Kawanishi, T. Omata and H. Yanagi, JPhys: Energy, 2022, 4, 042002 Search PubMed.
- M. Feng, S.-C. Liu, L. Hu, J. Wu, X. Liu, D.-J. Xue, J.-S. Hu and L.-J. Wan, J. Am. Chem. Soc., 2021, 143, 9664–9671 CrossRef PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef PubMed.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu and V. P. Dravid, et al. , Science, 2016, 351, 141–144 CrossRef PubMed.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen and J. Y. Lee, et al. , Nat. Mater., 2021, 20, 1378–1384 CrossRef PubMed.
- B. Zhou, S. Li, W. Li, J. Li, X. Zhang, S. Lin, Z. Chen and Y. Pei, ACS Appl. Mater. Interfaces, 2017, 9, 34033–34041 CrossRef PubMed.
- B. Cai, L.-D. Zhao and J.-F. Li, et al. , J. Materiomics, 2020, 6, 77–85 CrossRef.
- Y. Liu, P. D. McNaughter, F. Azough, X. Liu, J. M. Skelton, A. V. Kretinin, D. J. Lewis and R. Freer, ACS Appl. Energy Mater., 2023, 6, 4462–4474 CrossRef PubMed.
- J. Burton, F. Culkin and J. Riley, Geochim. Cosmochim. Acta, 1959, 16, 151–180 CrossRef.
- S. Hao, F. Shi, V. P. Dravid, M. G. Kanatzidis and C. Wolverton, Chem. Mater., 2016, 28, 3218–3226 CrossRef.
- M. Rakshit, S. Nath, S. Chowdhury, R. Mondal, D. Banerjee and D. Jana, Phys. Scr., 2022, 97, 125804 CrossRef.
- D. Sarkar, T. Ghosh, S. Roychowdhury, R. Arora, S. Sajan, G. Sheet, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2020, 142, 12237–12244 CrossRef PubMed.
- X. Zhang, J. Shen, S. Lin, J. Li, Z. Chen, W. Li and Y. Pei, J. Materiomics, 2016, 2, 331–337 CrossRef.
- Y. Yu, C. Zhou, T. Ghosh, C.-F. Schön, Y. Zhou, S. Wahl, M. Raghuwanshi, P. Kerres, C. Bellin and A. Shukla, et al. , Adv. Mater., 2023, 2300893 CrossRef PubMed.
- D. Sarkar, S. Roychowdhury, R. Arora, T. Ghosh, A. Vasdev, B. Joseph, G. Sheet, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2021, 60, 10350–10358 CrossRef PubMed.
- Z. Huang, S. A. Miller, B. Ge, M. Yan, S. Anand, T. Wu, P. Nan, Y. Zhu, W. Zhuang and G. J. Snyder, et al. , Angew. Chem., Int. Ed., 2017, 56, 14113–14118 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef PubMed.
- H. Wiedemeier, H. Georg and G. von Schnering, Z. Kristallogr. - Cryst. Mater., 1978, 148, 295–304 CrossRef.
- P. Bauer Pereira, I. Sergueev, S. Gorsse, J. Dadda, E. Müller and R. P. Hermann, Phys. Status Solidi B, 2013, 250, 1300–1307 CrossRef.
- H. Wiedemeier and P. Siemers, Zeitschrift für Anorganische und Allgemeine Chemie, 1975, 411, 90–96 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. M. Skelton, L. A. Burton, F. Oba and A. Walsh, J. Phys. Chem. C, 2017, 121, 6446–6454 CrossRef PubMed.
- I. Pallikara and J. M. Skelton, Phys. Chem. Chem. Phys., 2021, 23, 19219–19236 RSC.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355 CrossRef.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef PubMed.
- J. M. Skelton, D. S. Gunn, S. Metz and S. C. Parker, J. Chem. Theory Comput., 2020, 16, 3543–3557 CrossRef PubMed.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- H. Yu, D. Gao, X. Wang, X. Du, X. Lin, W. Guo, R. Zou, C. Jin, K. Li and Y. Chen, NPG Asia Mater., 2018, 10, 882–887 CrossRef.
- M. Sist, C. Gatti, P. Nørby, S. Cenedese, H. Kasai, K. Kato and B. B. Iversen, Chem. – Eur. J., 2017, 23, 6888–6895 CrossRef PubMed.
- L. Ehm, K. Knorr, P. Dera, A. Krimmel, P. Bouvier and M. Mezouar, J. Phys.: Condens. Matter, 2004, 16, 3545 CrossRef.
- S. Xie, X. Cheng, C. Hu, Y. Tao, M. Liu and Z. Qi, J. Alloys Compd., 2020, 849, 155915 CrossRef.
- M. J. Smiles, J. M. Skelton, H. Shiel, L. A. Jones, J. E. Swallow, H. J. Edwards, P. A. Murgatroyd, T. J. Featherstone, P. K. Thakur and T.-L. Lee, et al. , J. Mater. Chem. A, 2021, 9, 22440–22452 RSC.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef.
- P. Sutter, C. Argyropoulos and E. Sutter, Nano Lett., 2018, 18, 4576–4583 CrossRef PubMed.
- L. T. Nguyen and G. Makov, Cryst. Growth Des., 2022, 22, 4956–4969 CrossRef.
- K. Yuan, Z. Sun, X. Zhang, X. Gong and D. Tang, Phys. Chem. Chem. Phys., 2020, 22, 1911–1922 RSC.
- J. Yang, Q. Fan, B. Xiao and Y. Ding, Materials, 2019, 12, 3612 CrossRef PubMed.
- V. L. Deringer, R. P. Stoffel and R. Dronskowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094303 CrossRef.
- J. M. Skelton, D. Tiana, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, J. Chem. Phys., 2015, 143, 064710 CrossRef PubMed.
- J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205203 CrossRef.
- C. Kannewurf and R. Cashman, J. Phys. Chem. Solids, 1961, 22, 293–298 CrossRef.
- A. Elkorashy, J. Phys. C-Solid State Phys., 1988, 21, 2595 CrossRef.
- P. Ramasamy, D. Kwak, D.-H. Lim, H.-S. Ra and J.-S. Lee, J. Mater. Chem. C, 2016, 4, 479–485 RSC.
- P. A. Murgatroyd, M. J. Smiles, C. N. Savory, T. P. Shalvey, J. E. Swallow, N. Fleck, C. M. Robertson, F. Jackel, J. Alaria and J. D. Major, et al. , Chem. Mater., 2020, 32, 3245–3253 CrossRef PubMed.
- E. Segev, U. Argaman, R. E. Abutbul, Y. Golan and G. Makov, CrystEngComm, 2017, 19, 1751–1761 RSC.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef.
- T. Lyu, X. Li, Q. Yang, J. Cheng, Y. Zhang, C. Zhang, F. Liu, J. Li, W. Ao and H. Xie, et al. , Chem. Eng. J., 2022, 442, 136332 CrossRef.
- X. Shi, Z.-G. Chen, W. Liu, L. Yang, M. Hong, R. Moshwan, L. Huang and J. Zou, Energy Storage Mater., 2018, 10, 130–138 CrossRef.
- X. Shi, A. Wu, T. Feng, K. Zheng, W. Liu, Q. Sun, M. Hong, S. T. Pantelides, Z.-G. Chen and J. Zou, Adv. Energy Mater., 2019, 9, 1803242 CrossRef.
- I. Suzuki, S. Kawanishi, T. Omata and H. Yanagi, JPhys: Energy, 2022, 4, 042002 Search PubMed.
- X. Yang, W.-H. Gu, W.-J. Li, Y.-X. Zhang, J. Feng and Z.-H. Ge, J. Phys. Chem. Solids, 2023, 172, 111077 CrossRef.
- C. W. Li, J. Hong, A. F. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063–1069 Search PubMed.
- J. M. Skelton, L. A. Burton, S. C. Parker, A. Walsh, C.-E. Kim, A. Soon, J. Buckeridge, A. A. Sokol, C. R. A. Catlow, A. Togo and I. Tanaka, Phys. Rev. Lett., 2016, 117, 075502 CrossRef PubMed.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. Lett., 2019, 122, 075901 CrossRef PubMed.
- J. M. Skelton, J. Mater. Chem. C, 2021, 9, 11772–11787 RSC.
- K. Yuan, Z. Sun, X. Zhang and D. Tang, Sci. Rep., 2019, 9, 9490 CrossRef PubMed.
- Q. Fan, J. Yang, J. Cao and C. Liu, R. Soc. Open Sci., 2021, 8, 201980 CrossRef PubMed.
- G. Ding, G. Gao and K. Yao, Sci. Rep., 2015, 5, 9567 CrossRef PubMed.
- H. L. Kagdada, P. K. Jha, P. Spiewak, K. J. Kurzydłowski and D. K. Singh, J. Appl. Phys., 2020, 127, 175104 CrossRef.
- W. Liu, K. C. Lukas, K. McEnaney, S. Lee, Q. Zhang, C. P. Opeil, G. Chen and Z. Ren, Energy Environ. Sci., 2013, 6, 552–560 RSC.
- Y.-M. Han, J. Zhao, M. Zhou, X.-X. Jiang, H.-Q. Leng and L.-F. Li, J. Mater. Chem. A, 2015, 3, 4555–4559 RSC.
- Asfandiyar, T.-R. Wei, Z. Li, F.-H. Sun, Y. Pan, C.-F. Wu, M. U. Farooq, H. Tang, F. Li and B. Li, et al. , Sci. Rep., 2017, 7, 43262 CrossRef PubMed.
- C.-C. Lin, R. Lydia, J. H. Yun, H. S. Lee and J. S. Rhyee, Chem. Mater., 2017, 29, 5344–5352 CrossRef.
- F. Ke, J. Yang, C. Liu, Q. Wang, Y. Li, J. Zhang, L. Wu, X. Zhang, Y. Han and B. Wu, et al. , J. Phys. Chem. C, 2013, 117, 6033–6038 CrossRef.
- K. Adouby, C. Perez-Vicente, J. Jumas, R. Fourcade and A. A. Toure, Z. Kristallogr. - Cryst. Mater., 1998, 213, 343–349 CrossRef.
- T. Chattopadhyay, J. Pannetier and H. G. Von Schnering, J. Phys. Chem. Solids, 1986, 47, 879–885 CrossRef.
- M.-S. Lee and S. D. Mahanti, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165149 CrossRef.
- W. He, D. Wang, J.-F. Dong, Y. Qiu, L. Fu, Y. Feng, Y. Hao, G. Wang, J. Wang, C. Liu, J.-F. Li, J. He and L.-D. Zhao, J. Mater. Chem. A, 2018, 6, 10048–10056 RSC.
- J. Flitcroft, A. Althubiani and J. Skelton, ChemRxiv, 2023, preprint DOI:10.26434/chemrxiv-2023-lh90f.
- A. S. Chaves, D. T. Larson, E. Kaxiras and A. Antonelli, Phys. Rev. B, 2022, 105, 205201 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Impact of non-analytical corrections on the lattice thermal conductivity; comparison of electronic-structure calculations with self-consistent and non-self-consistent HSE06 and with a variety of k-point meshes; optimized lattice parameters and comparison to experimental measurements; phonon spectra of the three GeSe structures examined in this work; phonon spectra of R3m GeS obtained using different second-order supercell expansions; electronic band structure and density of states of Pnma and R3m GeS; and additional data on the electrical transport properties, lattice thermal conductivity and thermoelectric figure of merit of the four systems examined in this work, including on the anisotropy. See DOI: https://doi.org/10.1039/d3tc02938g |
| This journal is © The Royal Society of Chemistry 2023 |



