Open Access Article
Open Access ArticleThe effect of inert dopant ions on spin-crossover materials is not simply controlled by chemical pressure†
Prabir
Ghosh
a,
Christopher M.
Pask
b,
Hari Babu
Vasili
c,
Nobuto
Yoshinari
 d,
Takumi
Konno‡
d,
Takumi
Konno‡
 d,
Oscar
Cespedes
c,
Cristian
Enachescu
e,
Pradip
Chakraborty
d,
Oscar
Cespedes
c,
Cristian
Enachescu
e,
Pradip
Chakraborty
 *f and
Malcolm A.
Halcrow
*f and
Malcolm A.
Halcrow
 *b
*b
aDepartment of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur-721302, India
bSchool of Chemistry, University of Leeds, Woodhouse Lane, Leeds LS2 9JT, UK. E-mail: m.a.halcrow@leeds.ac.uk
cSchool of Physics and Astronomy, W. H. Bragg Building, University of Leeds, Leeds LS2 9JT, UK
dDepartment of Chemistry, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan
eFaculty of Physics, Alexandru Ioan Cuza University, 700506 Iasi, Romania
fDepartment of Chemistry, Indian Institute of Technology Kharagpur, Kharagpur-721302, India. E-mail: pradipc@chem.iitkgp.ac.in
First published on 30th August 2023
Abstract
[Fe(bpp)2][BF4]2 (bpp = 2,6-bis{pyrazol-1-yl}pyridine) undergoes abrupt thermal spin-crossover (SCO) at 261 K with a small 2–3 K thermal hysteresis. Different compositions of doped materials [FezZn1−z(bpp)2][BF4]2 and [FezRu1−z(bpp)2][BF4]2 (0 < z < 1) show similar broadening of the SCO transition with increased doping, but differ in their effect on the transition temperature. Doping with zinc strongly lowers T½, which is consistent with previous work. In contrast, doping with ruthenium increases T½ to a smaller degree, which cannot be explained by the chemical pressure arguments that are conventionally applied to doped SCO materials. Mechanoelastic simulations imply that different dopants exert opposite effects on the lattice elastic interactions in the material during the SCO transition. Consistent with that, the materials show a complicated dependence of the crystallographic lattice parameters and thermal expansion properties on the iron spin state, for different dopant ions. These changes correlate with small perturbations to the molecular structure of high-spin [Fe(bpp)2]2+, in the presence of dopants with different geometric preferences and conformational rigidities. We conclude the effect of isomorphous dopants on T½ reflects how the dopant influences the coordination geometry of the iron centres, as well as the chemical pressure exerted by the dopant ion size.
Introduction
Spin-crossover (SCO) materials undergo a spin state change under a physical or chemical stimulus.1–5 The electronic rearrangement is accompanied by structural changes, which impact the colour,6 volume,7 conductivity,8 permittivity9 and other materials properties of a solid sample.10–12 That switching functionality is being exploited in molecular electronics8,13 and nanoscience,5,14,15 while SCO materials are being investigated for solid state refrigeration,16–19 mechanical actuation,7,20–22 thermochromic printing23,24 and other macroscopic applications.6,25–28 Spin-transitions are also useful probes of crystal lattice dynamics, which allow the nucleation, growth and decay of new phases to be observed in real time.29,30Most of these applications require materials undergoing first order spin-transitions, which arise from an interplay between the individual switching centres and the surrounding lattice.31 Solid solutions of SCO compounds with inert isomorphous dopants have been essential for developing our understanding of that synergy. Early work on doped SCO materials showed how the strength and dimensionality of elastic interactions in a lattice controls the cooperativity of phase transformations,32,33 leading to the development of Monte Carlo methods for simulating SCO processes.34 More recently, doped SCO materials have shed light on the kinetics of spin state relaxation processes at low temperatures.33,35,36
Isomorphous M2+ dopant ions in an iron(II) SCO material [FezM1−zLn]m+ (M = Mn, Co, Ni, Zn etc.; L = a ligand) reduce the transition cooperativity as z decreases. That reflects the weakening of elastic interactions between the switching centres, as they become separated by dopant molecule spacers in the lattice.32–34 However, their effect on the transition temperature T½ is more variable. While increased fractions of Mn2+, Co2+ or Zn2+ dopant ions consistently lower T½ of an iron(II) SCO compound,32,36–51 Ni2+ dopants have a much smaller effect on T½ of the same materials (Fig. S1, ESI†).36,46–54 That is usually explained by the chemical pressure exerted by each dopant ion. The ionic radii of Mn2+ (83 pm), Co2+ (74.5 pm) and Zn2+ (74 pm) resemble high-spin Fe2+ (78 pm),55 so introducing those dopant ions into the lattice should favour the high-spin state of the SCO material. In contrast, the ionic radius of Ni2+ (69 pm) is essentially the average of high-spin (78 pm) and low-spin (61 pm) Fe2+, so doping an iron(II) lattice with Ni2+ has less effect on its internal chemical pressure.32–34 By that argument, no dopant ion should increase T½, since no common metal dications have ionic radii approaching low-spin Fe2+.56
Chakraborty and co-workers recently reported that [Fe0.65Ru0.35(ptz)6][BF4]2 (ptz = 1-propyltetrazole) exhibits T½ = 135 K,57 which is 10 K higher than for [Fe(ptz)6][BF4]2 itself.58 That was the first observation of chemical doping leading to stabilisation of the low-spin state of an SCO material. However, interpretation of that result is complicated by a crystallographic phase transition in [Fe(ptz)6][BF4]2, which is associated with the SCO event and influences T½, but is kinetically slow.59–62 Other M2+ dopant ions in [FezM1−z(ptz)6][BF4]2 affect T½ and the phase transition temperature to different degrees, such that the two processes become decoupled at higher dopant levels.63
To clarify that observation, we have investigated the [FezM1−z(bpp)2][BF4]2 system (Scheme 1; bpp = 2,6-bis{pyrazol-1-yl}pyridine). The parent complex [Fe(bpp)2][BF4]2 undergoes an abrupt spin-transition at T½ = 261 K with narrow thermal hysteresis, but without a crystallographic phase change.64 Previous studies of [FezM1−z(bpp)2][BF4]2 with M = Co2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 or Ni2+
42 or Ni2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 showed typical trends for those dopants. Analogous materials with M = Zn2+ and Ru2+ are presented here, which confirm those dopant ions have opposing effects on T½ in the [Fe(bpp)2][BF4]2 lattice.65 We show this reflects the geometric preferences and conformational flexibility of the different dopant ions, and how these perturb the local crystal lattice site structure.
54 showed typical trends for those dopants. Analogous materials with M = Zn2+ and Ru2+ are presented here, which confirm those dopant ions have opposing effects on T½ in the [Fe(bpp)2][BF4]2 lattice.65 We show this reflects the geometric preferences and conformational flexibility of the different dopant ions, and how these perturb the local crystal lattice site structure.
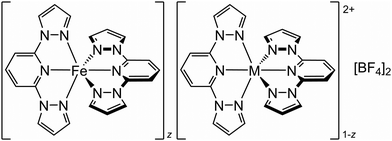 | ||
| Scheme 1 The [FezM1−z(bpp)2][BF4]2 materials referred to in this study (M2+ = Co2+, Ni2+, Zn2+ or Ru2+; 0 < z < 1). | ||
Results
The starting materials [M′(bpp)2][BF4]2 (M′ = Fe,64 Zn66 and Ru67) are crystallographically isomorphous. Co-crystallizing the iron complex with different mole ratios of the appropriate dopant from nitromethane, using diethyl ether vapour as the anti-solvent, yielded polycrystalline [FezZn1−z(bpp)2][BF4]2 (1a–1e) and [FezRu1−z(bpp)2][BF4]2 (2a–2d). Samples of 1a–1e are yellow in colour which becomes paler as z decreases, while 2a–2d become darker brown with increased ruthenium content.68 The materials are phase-pure and isomorphous with the precursor complexes by powder diffraction (Fig. S2 and S3, ESI†). EDX analysis and magnetic measurements confirm the composition of each material is consistent with the stoichiometry of its crystallisation mixture (Table 1).| z | C found (calcd) | H found (calcd) | N found (calcd) | Fe:M calculated from: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Synthesis stoichiometry | EDXa | Magnetic datab | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a Errors on the EDX data are between ±0.01–0.05 (Table S1). b Calculated assuming χMT = 3.5 cm3 mol−1 K for high-spin Fe(II), and χMT = 0 for low-spin Fe(II) and the diamagnetic dopant ions. Estimated errors on these values are ±0.02. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M = Zn | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1a | 0.89 | 40.7(40.5) | 2.73(2.78) | 21.6(21.5) | 0.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.11 0.11 |
0.90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 0.10 |
0.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.11 0.11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1b | 0.69 | 40.2(40.3) | 2.68(2.77) | 21.4(21.4) | 0.68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.32 0.32 |
0.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.30 0.30 |
0.69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.31 0.31 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1c | 0.51 | 40.1(40.2) | 2.69(2.76) | 21.1(21.3) | 0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50 0.50 |
0.55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.45 0.45 |
0.49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.51 0.51 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1d | 0.26 | 40.0(40.1) | 2.82(2.75) | 21.1(21.3) | 0.28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.72 0.72 |
0.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.76 0.76 |
0.27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.73 0.73 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1e | 0.07 | 40.2(40.0) | 2.87(2.75) | 21.0(21.2) | 0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.92 0.92 |
0.06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.94 0.94 |
0.07![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.93 0.93 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M = Ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2a | 0.88 | 39.9(40.2) | 2.97(2.76) | 20.9(21.3) | 0.88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.12 0.12 |
0.84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.16 0.16 |
0.91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.09 0.09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2b | 0.67 | 39.4(39.6) | 2.78(2.72) | 20.7(21.0) | 0.69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.31 0.31 |
0.65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35 0.35 |
0.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.33 0.33 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2c | 0.49 | 38.9(39.2) | 2.79(2.69) | 20.4(20.8) | 0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50 0.50 |
0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50 0.50 |
0.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.52 0.52 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2d | 0.14 | 38.0(38.3) | 2.48(2.63) | 19.9(20.3) | 0.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85 0.85 |
0.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.86 0.86 |
0.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.86 0.86 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
SCO in the new materials was monitored by magnetic susceptibility measurements (Fig. 1). The FeZn materials 1a–1e show the expected trend, in that increasing zinc concentration leads to broadening of the transition, while significantly lowering T½.32,40,43–49 Ruthenium doping in 2a–2d has a similar influence on the SCO cooperativity as the zinc dopant at each dopant concentration. However, the two dopant ions have opposite effects on the transition temperature, in that T½ in 2a–2d increases at higher ruthenium dopant levels (Fig. 1 and 2). The larger population of low-spin iron centres in the ruthenium-doped materials at room temperature is consistent with their brown colouration.68
 | ||
| Fig. 1 Spin-crossover in [Fe(bpp)2][BF4]2 and its solid solutions, from magnetic susceptibility data measured at a scan rate of 2 K min−1. Data are plotted as the fraction of the sample that is high-spin at each temperature (γHS), and the transition midpoint at γHS = 0.5 is marked with a dashed line. Data points from each compound are linked by spline curves for clarity, Data for [Fe(bpp)2][BF4]2 are taken from ref. 54. | ||
 | ||
| Fig. 2 Variation of T½ with composition in [FezM1−z(bpp)2][BF4]2 with different dopant ions, from magnetic susceptibility data measured at a 2 K min−1 scan rate (Fig. 1). Data for M = Ni and Co are taken from ref. 42 and 54. | ||
These trends were confirmed by differential scanning calorimetry (DSC) measurements (Fig. S6 and S7, ESI†). The transition temperatures measured by DSC and the magnetic data show minor differences, which we attribute to the different temperature ramps employed for the measurements (Table 2). However, the DSC data confirm T½ in [FezM1−z(bpp)2][BF4]2 decreases with z when M = Zn, but increases when M = Ru. ΔH and ΔS for the spin-transitions decrease more slowly with increased doping for M = Ru than for M = Zn at small dopant concentrations. DSC measurements at larger dopant levels were not achieved, because their endotherms were too weak or outside the temperature range of our calorimeter (Tmin = 190 K).
| Magnetic measurements | DSC | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T ½↓/K | T ½↑/K | T ½↑/K | ΔH/kJ mol−1 | ΔS/J mol−1 K−1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a Taken from ref. 54. b DSC endotherms for 1c and 2d were too weak to be accurately measured. c Outside the temperature range of our calorimeter. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Fe(bpp)2][BF4]2a | 261.0 | 262.5 | 263.2 | 21.8(2) | 82.9(8) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M = Zn | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1a | 251.1 | 251.3 | 255.0 | 13.3(2) | 52.2(8) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1b | 233.6 | 233.2 | 237.7 | 6.6(4) | 28(2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1c | 217.2 | 216.5 | —b | — | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1d | 193 | 193 | —c | — | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1e | 166 | — | —c | — | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M = Ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2a | 264.1 | 265.0 | 269.1 | 18.6(2) | 69.0(8) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2b | 268.5 | 269.4 | 271.0 | 11.2(3) | 41.3(11) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2c | 272.7 | 272.7 | 274.6 | 8.4(7) | 30(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2d | 279 | 279 | —b | — | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
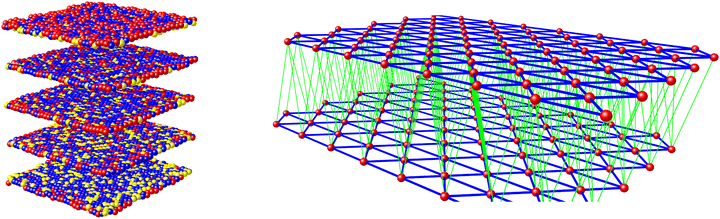
The materials’ SCO profiles were simulated using a 3D mechanoelastic approach.69–71 The sample used is a lattice of 6400 molecules, represented as balls situated at the sites of a face-centered cubic structure of five interconnected layers with open boundary conditions (Fig. 3). All the bulk molecules have twelve nearest neighbours (six on the same layer and six on the adjacent layers), which are linked by springs.
The molecules can flip between spin states according to the Monte Carlo Arrhenius probabilities (eqn (1) and (2)):34,72
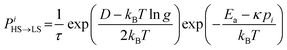 | (1) |
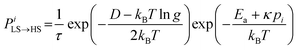 | (2) |
 | (3) |
During a Monte Carlo Step (MCS), all the molecules are checked to establish if they change state, by comparing the individual switching probability with a randomly generated number. After the completion of each MCS, the new equilibrium positions of the molecules are computed by solving differential equations considering the new molecular sizes. In this simulation we used a temperature sweep rate of 0.001 K per MCS, which is small enough to obtain a quasi-static thermal transition while minimizing kinetic effects. The radius of the molecules (including the ligand sphere) is 0.22 nm for HS and 0.20 nm for LS, with a distance of 1 nm between the centres of adjacent Fe ions.32 The scaling factor κ takes the value 1450 × 10−14 J N−1, similar to that in previous studies.73
First we determined which values of the elastic spring constant k give the best fit for the thermal transition loop from the pure iron compound, setting the experimental values for D and g (g = exp{DS/kB}). We found a value of k = 5 N m−1 within the layers in the lattice, which corresponds to a relatively high cooperativity, and ten times smaller between the layers. Recent experiments showed the stiffness of springs between molecules in different spin states can differ by 25–50%,74 but this difference does not qualitatively change the simulation results.75 Hence, to minimise the number of fitted parameters, we employed a single value of k between SCO molecules, irrespective of their state.
We introduced dopants into the system by randomly replacing fractions of SCO molecules with dopant molecules, represented as balls of a different radius. The radius of the zinc dopant molecules was set at 0.216 nm which is close to iron in its high-spin state, while the radius of the ruthenium dopant is 0.210 nm, the average of the two iron spin states in the model. Dopants are linked to neighbouring SCO molecules by different elastic constants, which depend on the state of the SCO molecules (k = kDL or k = kDH for springs linking dopants with low-spin and high-spin iron sites, respectively; Fig. 4). No other assumptions were made, and other parameters used to reproduce SCO in the pure iron compound were kept constant.
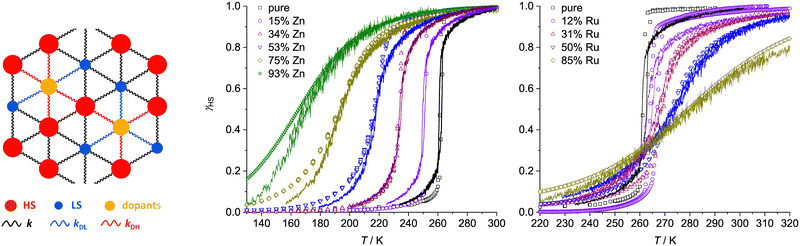 | ||
| Fig. 4 Left: Schematic of an expanded layer of the simulation system showing dopants replacing SCO molecules, and their links with SCO nearest neighbours (HS = high-spin, LS = low-spin). The experimental (data points) and simulated (lines) thermal SCO transitions in 1a–1e (centre) and 2a–2d (right). The simulations show the equilibrated spin state population at each temperature for the in silico lattice in Fig. 3, using the dopant concentration and force constant parameters described in the text.77 | ||
Fig. 4 presents simulations obtained with the following parameters: for Zn dopants, kDL = 6 N m−1 and kDH = 4 N m−1; and for Ru dopants, kDL = 3 N m−1 and kDH = 7 N m−1. This reproduces the shift of T½ to lower temperatures for Zn doping and to higher temperatures for Ru doping, as observed experimentally. That is, the Zn(II) dopant ions in 1a–1e and the Ru(II) dopants in 2a–2d exert opposite influences on the lattice energetics of SCO in [Fe(bpp)2][BF4]2.
Full crystallographic refinements were achieved from both spin states of 1c, 2c and [Fe0.5Ni0.5(bpp)2][BF4]2 (3c),54 using synchrotron radiation to maximize the resolution of the datasets. The structures were first refined as crystallographically ordered molecules, with mixed-composition metal atom sites.36,40,41,45,76 The bond lengths and angles in the low-spin crystals, and in high-spin 1c, are a good match for the weighted average values calculated from the two component molecules. However, the high-spin structures of 2c and 3c show some deviation from expectation (Table 3). Most notably, the trans-N{pyridyl}–M–N{pyridyl} angle (ϕ)78 is larger than expected by 4–5σ, and is essentially equal to that of the ruthenium or nickel dopant molecule.67,79
| 1c | 2c | 3c | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HS, 300 K | LS, 100 K | HS, 350 K | LS, 100 K | HS, 350 K | LS, 100 K | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a HS = high-spin, LS = low-spin. b γ is the average bpp ligand bite angle in the model, which is sensitive to the spin state and the composition of the metal content in the crystal. c ϕ is the trans-N{pyridyl}–M–N{pyridyl} bond angle. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M–N{pyridyl}average | 2.114(6) {2.114(6)} | 1.996(2) {1.993(4)} | 2.058(6) {2.074(5)} | 1.950(3) {1.962(4)} | 2.065(6) {2.065{3}} | 1.959(2) {1.962(3)} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M–N{pyrazolyl}average | 2.184(10) {2.183(10)} | 2.067(3) {2.069(5)} | 2.119(12) {2.137(8)} | 2.026(4) {2.034(7)} | 2.143(13) {2.144(6)} | 2.041(4) {2.049(4)} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| γ/degb | 73.8(5) {73.8(4)} | 77.19(14) {77.4(3)} | 75.8(5) {75.9(3)} | 79.03(17) {79.2(3)} | 75.2(4) {75.3(2)} | 78.38(14) {78.37(18)} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ϕ/degc | 173.8(2) {173.5(2)} | 175.47(8) {175.70(17)} | 177.6(3) {175.7(2)} | 177.94(11) {178.1(2)} | 176.6(3) {175.20(12)} | 177.32(8) {177.43(11)} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The observed ϕ should be a weighted average of the iron and dopant molecule values (eqn (4)):76
| ϕobs = zϕ{Fe} + (1 − z)ϕ{M} | (4) |
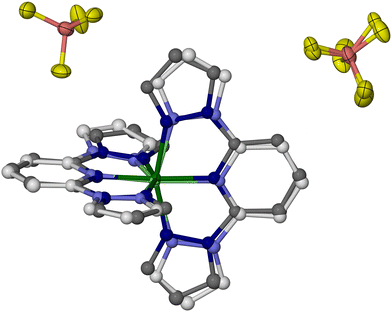
Whole molecule disorder models were constructed from the 100 K datasets of each crystal, to resolve their [Fe(bpp)2]2+ and [M(bpp)2]2+ (M = Zn, Ru or Ni) moieties. These refined without geometric restraints, although thermal parameter constraints were sometimes required between equivalent atoms in the two partial molecules. That allowed the metal composition of each crystal to be refined, which lay in the range 0.46 ≤ z ≤ 0.54. The most precise disorder refinement is for 1c (Fig. 5), because the geometry of its [Zn(bpp)2]2+ dopant is most different from the low-spin [Fe(bpp)2]2+ centres. Hence, those components are distinguished most clearly by the disorder model.
The geometries of [Fe(bpp)2]2+ and [Zn(bpp)2]2+ in 1c are identical to the single-component crystals [Fe(bpp)2][BF4]2 and [Zn(bpp)2][BF4]2, within experimental error (Table S3, ESI†). The cation disorder refinements of 2c and 3c are less accurate and deviate slightly from expectation, particularly in their Fe–N{pyridyl} and M–N{pyridyl} bond lengths which are more similar than expected (Tables S4 and S5, ESI†). The resolution of the synchrotron diffraction data may be too low to fully define the disorder in that region of the asymmetric unit.
As previously described,82 the crystals adopt a “terpyridine embrace” crystal lattice, which is often found in homoleptic complexes of 2,2′:6′,2′′-terpyridine and related ligands.83 The [M(bpp)2]2+ molecules associate into layers in the (001) crystal plane, through four-fold interdigitation of their distal pyrazolyl groups (Fig. 6 and Fig. S11, ESI†). Nearest neighbour cations within the layers are in close contact, through edge-to-face C–H⋯π and face-to-face π⋯π interactions between their pyrazolyl rings. Adjacent layers in the crystal are separated by the BF4− anions, and are not in direct van der Waals contact.
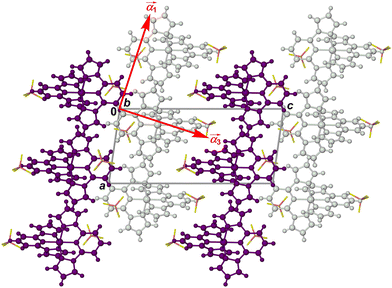 | ||
Fig. 6 Packing diagram of [Fe(bpp)2][BF4]2 at 150 K,64 viewed in the plane of the terpyridine embrace cation layers (Fig. S11, ESI†). Alternate cation layers are coloured white and purple, while the BF4− ions are de-emphasised for clarity. The red arrows show the approximate directions of the principal components of thermal expansion; the  vector is oriented along b, perpendicular to the view. vector is oriented along b, perpendicular to the view. | ||
Unit cell data were collected at 10 K intervals between 350 and 100 K, from 1c–3c and the precursor crystals [M′(bpp)2][BF4]2 (M′ = Fe, Zn, Ni and Ru; Fig. 7). The isothermal volume change during the high → low-spin transition of the iron-containing crystals (ΔVSCO) was calculated at T½ (Table 4). The magnitude of ΔVSCO shows significant variation, in the order 1c < 2c ≈ 3c < [Fe(bpp)2][BF4]2. ΔVSCO for 2c and 3c is 54–62% that of the pure iron complex, reflecting that they contain ca. 50% of the iron content in the pure iron crystal.76 Unexpectedly however, 1c shows a much smaller ΔVSCO which is ca. half that of the other solid solutions. This variation in ΔVSCO has little effect on the SCO cooperativity in 1c/2c/3c, which is very similar in each material from the magnetic susceptibility data (Fig. S21, ESI†).
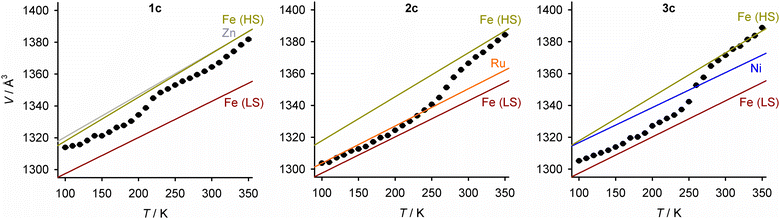 | ||
| Fig. 7 Variable temperature unit cell volumes for 1c–3c. Error bars are smaller than the symbols on the graphs. The lines show the thermal expansion linear regression fits for each [M′(bpp)2][BF4]2 component in the crystal, as a pure material (HS = high-spin, LS = low-spin; Fig. S21–S22, ESI†). | ||
| ΔaSCO/Å | ΔbSCO/Å | ΔcSCO/Å | ΔβSCO/deg | ΔabSCOa/Å | ΔVSCO/Å3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a ΔabSCO denotes the change in the area of the 2D cation layers in the unit cell during SCO, where ab is the product of the a and b unit cell dimensions. b The isothermal ΔVSCO for [Fe(bpp)2][BF4]2 at 30 K has also been measured, at −29.3(5) Å3 or 2.22%.86 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Fe(bpp)2][BF4]2 | ΔxSCO | +0.0231(6) | +0.074(2) | −0.5570(9) | +2.027(5) | 0.82(2) | −30.4(3)b | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| % | +0.27 | +0.87 | −2.93 | +2.11 | +1.14 | −2.23 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1c | ΔxSCO | +0.0153(15) | +0.0428(11) | −0.222(3) | +0.666(13) | 0.49(2) | −8.8(4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| % | +0.18 | +0.50 | −1.18 | +0.69 | +0.68 | −0.65 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2c | ΔxSCO | −0.0093(7) | +0.0103(6) | −0.1993(16) | +0.724(8) | 0.008(11) | −16.5(2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| % | −0.11 | +0.12 | −1.06 | +0.75 | +0.01 | −1.22 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3c | ΔxSCO | −0.0041(8) | +0.0213(10) | −0.264(2) | +0.800(10) | 0.146(16) | −18.8(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| % | −0.05 | +0.25 | −1.40 | +0.83 | +0.20 | −1.38 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The largest changes to the lattice during SCO involve the canting of the cation layers (the unit cell β angle), which is greater in the low-spin state; and, the spacing between them (the c dimension), which contracts in the low-spin material (Fig. 6). Both those changes contribute to the negative value of ΔVSCO, as observed (Fig. 7 and Table 4). Those parameters behave quite consistently in 1c–3c. Rather, the main differences between 1c–3c during SCO lie in the dimensions of the cation layers in the ab plane. SCO in [Fe(bpp)2][BF4]2 causes a small expansion of a and b in the low-spin state, despite the shorter distal Fe–N bond lengths in the low-spin molecule. That layer expansion is replicated in 1c, roughly proportionately with its iron concentration. In contrast, the effect of SCO on a and b in 2c and 3c is much smaller. The expansion of the cation layers during SCO in 1c partly offsets the other changes to the lattice, and is the main origin of its smaller ΔVSCO volume contraction compared to 2c and 3c.
The area of the cation layers in all the single-component [M′(bpp)2][BF4]2 lattices, as the product of a and b, shows a reasonable linear correlation with the bond angle ϕ (Fig. S23, ESI†). That is, the complex molecules pack less efficiently in two dimensions as ϕ approaches 180°, corresponding to idealised D2d molecular symmetry. That explains the expansion of a and b in the low spin states of [Fe(bpp)2][BF4]2 and 1c. The change in ab during SCO at T½ in the iron-containing compounds, ΔabSCO, decreases linearly with ΔϕSCO{Fe} for their iron centres, as estimated from eqn (4) (Fig. 8).
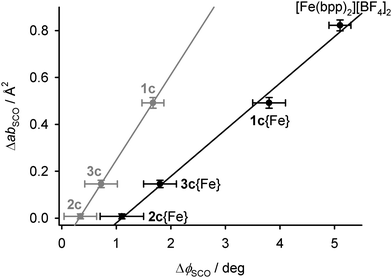 | ||
| Fig. 8 The relationship between the changes in ϕ, and the area of the 2D cation layers, during SCO in the iron-containing crystals. The black datapoints are for the iron centres in 1c–3c, calculated from eqn (4), while the grey points are directly measured values averaged between the iron and dopant complex molecules (Tables S2–S4, ESI†). Linear regression lines are included for both sets of data. | ||
The unit cell data were used to calculate linear thermal expansion coefficients (αV, eqn (5)).84,85
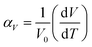 | (5) |
| α V {100 K}/106 K−1 | α TE{100 K}b/106 K−1 | α 3{100 K}/106 K−1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a HS = high-spin, LS = low-spin. b See eqn (6). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Fe(bpp)2][BF4]2, HS | 209(2) | 38(3) | 167.0(10) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Fe(bpp)2][BF4]2, LS | 160(4) | 82.0(15) | 76(2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1c, HS | 213(8) | 50(4) | 158(4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1c, LS | 140(7) | 57(3) | 80(4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2c, HS | 273(2) | 60(4) | 208(6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2c, LS | 170(5) | 90(2) | 78(2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3c, HS | 251(8) | 64(4) | 182(4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3c, LS | 173(6) | 88(3) | 81(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Zn(bpp)2][BF4]2 | 204(7) | 70(2) | 127(5) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Ru(bpp)2][BF4]2 | 180(4) | 66.3(16) | 98(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [Ni(bpp)2][BF4]2 | 168(4) | 83.1(10) | 93(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The αV{100 K} coefficients in Table 5 are typical for molecular crystals.84,85 While they show some variation, αV{100 K} for the high-spin iron-containing materials is consistently larger than for their low-spin states.76,87–89 The dopants [Ni(bpp)2][BF4]2 and [Ru(bpp)2][BF4]2 yield αV{100 K} values close to the low-spin iron crystals, whereas for [Zn(bpp)2][BF4]2 it is nearer the high-spin iron range. αV{100 K} coefficients calculated using published unit cell data from other iron(II) SCO molecular materials and their zinc(II) analogs also conform to these trends (Table S14, ESI†). In particular, αV{100K} for the zinc complexes is always 82–94% of the value for the isomorphous high-spin iron(II) complex.89
More insight is provided by the principal anisotropic components of the thermal expansion, which follow the same pattern in each crystal (Table S13, ESI†).90 The two smallest component vectors (α1 and α2 in the Table) are oriented within the cation layers in the crystal. The largest component, α3, the most deformable direction in the lattice, lies approximately perpendicular to the cation layers (Fig. 6). Since the intermolecular interactions in the lattice are weakest in that direction, these results are consistent with expectations.
The 2D thermal expansion coefficient of the terpyridine embrace cation layers, αTE, is given by the sum in eqn (6).
| αTE = α1 + α2 | (6) |
The second observation, exhibited by all the iron-containing crystals, is that α3{HS} = 2–3 × α3{LS}. That is, high → low-spin SCO makes the crystal more deformable in the plane of the terpyridine embrace layers, but more rigid when deformed perpendicular to the cation layers. That is again mirrored in the [M′(bpp)2][BF4]2 precursor crystals, where α3 follows the trend M′ = Zn > Ni ≈ Ru. Thus, crystals of the largest and most flexible zinc(II) and high-spin iron(II) complexes are most susceptible to deformation between the cation layers. Of all these parameters, α3 shows the most significant differences between the spin states, which is the origin of the consistent reduction in αV during SCO.
Discussion
Derivatives of [Fe(bpp)2][BF4]2 doped with inert metal ions, of formula [FezM1−z(bpp)2][BF4]2, have now been produced with M = Co, Ni, Zn and Ru (Fig. 2). The first three dopant ions stabilise the high-spin state of the materials, in the expected order M = Co ≈ Zn > Ni for a given composition z (Fig. S1, ESI†).32,33,48,49 In contrast, doping with Ru increases the transition temperature T½, stabilising the low-spin state. Such trends have previously been explained by chemical pressure arguments, where larger dopant ions progressively stabilise the larger high-spin form of the iron centres.32–34 While no ionic radius for Ru2+ is available,55 the relative sizes of the dopant ions can be expressed by the octahedral coordination volume (VOh91) in their isomorphous [M′(bpp)2][BF4]2 crystals. The trend in VOh runs as follows:| M′ = Fe{HS} [12.378(9) Å3] > Zn [12.251(12)] > Co [12.012(6)] |
| >Ni [11.320(5)] ≈ Ru [11.279(10)] ≫ Fe{LS} [9.620(5)] |
Mechanoelastic simulations of the SCO curves show these trends can be explained, if the [Zn(bpp)2]2+ dopant molecules in 1a–1e and the [Ru(bpp)2]2+ dopant in 2a–2d exert opposite influences on the energetics of the [FezM1−z(bpp)2][BF4]2 lattice. That is, intermolecular elastic interactions are stronger in the low-spin state of 1a–1e, and in the high-spin state of 2a–2d (Fig. 4). This is supported by a crystallographic comparison of [FezM1−z(bpp)2][BF4]2 (z ≈ 0.5; M = Zn, 1c; M = Ru, 2c; M = Ni, 3c), which implies those three dopant ions affect the iron lattice in different ways. That is clear in their lattice properties, where the isothermal volume change during SCO (ΔVSCO) in 1c is only ca half the value for 2c and 3c. The difference mostly reflects the low-spin unit cell of 1c, whose volume is significantly larger than for the other two materials (Fig. 7).
These changes in ΔVSCO are anisotropic in nature (Table 4), so they do not simply originate from the different ionic radii of the dopant metal ions. Rather, they reflect the dimensions of the cation layers, which become measurably larger during SCO in 1c but are almost unchanged in 2c and 3c (Table 4). This in turn correlates with the molecular structure changes during SCO at the iron sites in 1c–3c (Fig. 8).
Related observations can be made from the thermal expansion coefficients of each material. All the iron-containing crystals are less deformable in their low-spin states (smaller αV, Table 5), which reflects significant changes perpendicular to the cation layers during SCO. The cation layers themselves show the opposite trend, in being more deformable in the low-spin crystals than in their high-spin state (larger αTE). However that trend is less pronounced in 1c than in the other iron-containing crystals, where αTE in both spin states lies within experimental error. That is more evidence that the lattice properties of 1c are different from 2c and 3c.
At the molecular level, the crystallographic metric parameters in high-spin 2c and 3c deviate slightly from expectation, when considered as an average of their component molecules. This is most obvious in the ϕ angle, which is larger than predicted for high-spin 2c and 3c based on the structures of their pure component molecules (Table 3). In contrast ϕ for high-spin 1c, and for all of the low-spin crystals, are essentially equal to the expected values.
The plasticity of the coordination sphere in [M′(bpp)2]2+ should vary according to the d-electron configuration of M′, as M′ = Fe{HS} > Zn > Ni > Fe{LS} ≈ Ru.80 Hence, this variation in ϕ implies the molecular geometry of high-spin [Fe(bpp)2]2+ in 2c and 3c may be influenced by the presence of more rigid dopant molecules. That in turn correlates with the observed structural differences between 1c–3c during SCO, which appear to reflect the influence of ϕ on their crystal packing rather than the size of the dopant ions (Fig. 8).
T ½ in salts of [Fe(bpp)2]2+ derivatives with terpyridine embrace crystal packing correlates linearly with the change in Θ during SCO (ΔΘSCO, Fig. 9).92,93Θ is a torsion angle parameter, defined in the ESI,† which reflects the position of the metal coordination geometry along the Oh → D3h distortion pathway.91 While Θ is a function of the whole metal coordination sphere, ϕ and Θ are approximately proportional to each other when other metric parameters are unchanged.78
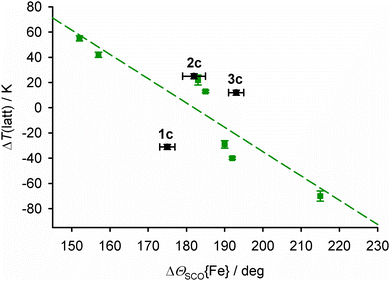 | ||
| Fig. 9 The relationship between ΔΘSCO{Fe} and the lattice contribution to T½, ΔT(latt),93 for salts of [Fe(bpp)2]2+ derivatives with terpyridine embrace crystal packing. The green data points and line show the published correlation,92 while 1c–3c are plotted in black.94 | ||
Data in Fig. 9 are plotted as ΔT(latt), which is the lattice contribution to T½ separated from the molecular ligand field component, which is estimated from solution measurements (eqn (7)).93,94
| ΔT(latt) = T½(solid) − T½(solution) | (7) |
The average ΔΘSCO for the mixed-metal sites in 1c–3c (Tables S2–S4, ESI†) bears no relation to the correlation in Fig. 9. However, ΘSCO for their iron centres can be extracted from these averaged values, by correction for Θ of the dopant molecule (eqn (8), cf.eqn (4)).
| Θobs = zΘ{Fe} + (1 − z)Θ{M} | (8) |
Lastly, since 2c and 3c both lie a similar distance above the main correlation line in Fig. 9, we conclude the higher T½ in 2c compared to 3c is also a function of ΔΘSCO; that is, how their iron coordination geometries are modified by the presence of ruthenium(II) and nickel(II) dopants.
Conclusions
The effect of dopant ions ‘M’ on SCO in [FezM1−z(bpp)2][BF4]2 is more complicated than expected, based on previous work.32–34 Most unexpectedly, T½ increases with increased ruthenium doping in [FezRu1−z(bpp)2][BF4]2 (2a–2d; Table 1). That cannot be explained from the ionic radius of Ru2+, which is too large to stabilise the low-spin state of the iron lattice. Rather, it reflects that different dopant ions cause opposite perturbations to the energetics of SCO in the host lattice (Fig. 4). Since another ruthenium-doped SCO crystal also exhibits a higher T½ than the parent iron complex,57 that might be a general observation.Crystallographic analysis of [FezM1−z(bpp)2][BF4]2 (z ≈ 0.5) with M = Zn, Ru and Ni correlates these macroscopic observations with their structures at the molecular level. Small but consistent trends in their molecular structures, unit cell parameters and thermal expansion coefficients imply the influence of zinc dopants on the materials’ structures differs from doping with nickel or ruthenium. That is clearly expressed in the structure:function correlation in Fig. 9. This shows 2c and 3c behave broadly consistently with each other, with their doped lattices stabilizing the low-spin state of the material compared to the undoped material. However 1c behaves differently, in that its zinc-doped lattice strongly stabilises the high-spin state. The structure:function properties of the two types of doped material must be considered separately.
We conclude that large dopant ions like zinc(II) in 1c indeed lower T½ as previously understood, which is reflected in its smaller ΔVSCO unit cell volume change (Fig. 7).32–34 However Fig. 8 implies the more distorted coordination geometry of the zinc(II) dopant complex, and its impact on the structure of the iron sites in the material, contributes to ΔVSCO as much as the ionic radius of the zinc(II) ion. In contrast the ruthenium(II) and nickel(II) dopants in 2c and 3c exert more moderate, and very similar, chemical pressure on the [Fe(bpp)2][BF4]2 lattice (Fig. 9). In that case, the variation of T½ with composition reflects the different influences of those two dopant ions on the molecular structure of the iron switching centres, and how that feeds through to the bulk lattice (Fig. 8 and 9).
The above implies that salts of [Fe(bpp)2]2+ derivatives with more distorted high-spin molecular geometries and a larger structure change during SCO, should be affected more strongly by ruthenium doping.96–99 Other moderately sized dopant ions whose coordination geometries impose a regular Oh symmetry preferred by low-spin iron(II) centres, should also increase T½ most effectively in doped [FezM1−zLn] lattices. Current work aims to test those predictions, and to probe the generality of our conclusions.
Finally, “molecular alloying”100 by chemical doping of different metals, ligands and/or anions into SCO materials has been used to tune T½ towards room temperature for application purposes.45,100–106 Up to now, metal doping has only been used in such materials undergoing high temperature SCO, to lower their T½ towards 300 K.102,103 This study shows how metal doping can increase T½ towards a desired range, as well as decreasing it. That could have value for adjusting solid-state refrigerants based on SCO materials, for example, to optimise their performance at room temperature.16–19 While chemical doping also quenches thermal hysteresis in cooperative SCO materials, that is beneficial for cooling applications requiring a first-order transition that is thermodynamically reversible (ie with no thermal hysteresis).107
Experimental
The precursor complexes [M′(bpp)2][BF4]2 (M′ = Fe,64 Ni,79 Zn66 and Ru67), and [Fe0.5Ni0.5(bpp)2][BF4]2 (3c),54 were prepared by the literature methods.Synthesis of [FezZn1−z(bpp)2][BF4]2 (1a–1e)
Preformed [Fe(bpp)2][BF4]2 and [Zn(bpp)2][BF4]2 were mixed in different mole ratios, to a combined mass of 0.25 g. The combined solids were stirred in nitromethane (25 cm3), until all the solid had dissolved. The solutions were concentrated to ca. 10 cm3, then filtered. Slow diffusion of diethyl ether vapour into the solutions afforded yellow polycrystalline materials, whose colour becomes paler as z decreases. Crystallised yields were in the range 80–85%. The compositions and analytical data for 1a–1e are given in Table 1.Synthesis of [FezRu1−z(bpp)2][BF4]2 (2a–2d)
Method as above, using [Ru(bpp)2][BF4]2 (Table 1). Polycrystalline 2a–2d are brown in colour, which becomes darker with increased Ru content.Single crystal structure analyses
Single crystals of 1c, 2c, 3c and the precursor complexes were grown by vapour diffusion methods as described above. Full datasets of the doped crystals were collected at station I19 of the Diamond synchrotron (λ = 0.6889 Å), while variable temperature unit cell data were measured with an Agilent SuperNova diffractometer using Mo-Kα radiation (λ = 0.7107 Å).Experimental details and refinement protocols for the full structure determinations are given in the ESI.† The structures were solved by direct methods (SHELX-TL108), and developed by full least-squares refinement on F2 (SHELXL2018109). Crystallographic figures were produced using XSEED,110 and other publication materials were prepared with OLEX2.111
Isotropic and anisotropic thermal expansion parameters at 100 K were calculated with PASCal.90 Thermal expansion coefficients at 300 K were derived from linear regression analyses of unit cell data (eqn (1)). Estimated errors on αV{300 K} are also based on the PASCal calculations.
Other measurements
All physical characterisation was performed using the same sample of each material. CHN elemental microanalyses were performed by the microanalytical service at the London Metropolitan University School of Human Sciences. Energy Dispersive X-Ray (EDX) analysis was carried out using a Jeol JSM-7610F field emission scanning electron microscope with a 15 kV applied voltage; or, with a FEI Nova NanoSEM 450 environmental microscope operating at 3 kV. X-ray powder diffraction data were obtained with a Bruker D8 Advance A25 diffractometer using Cu-Kα radiation (λ = 1.5418 Å). Differential scanning calorimetry (DSC) measurements used a TA Instruments DSC Q20 calorimeter, with heating at a rate of 10 K min−1.Magnetic susceptibility measurements were performed on a Quantum Design MPMS-2 SQUID or a MPMS-3 SQUID/VSM magnetometer, with an applied field of 5000 G and a scan rate of 2 K min−1. A diamagnetic correction for the samples was estimated from Pascal's constants;112 a diamagnetic correction for the sample holder was also applied. Processing of magnetic data and all graph plotting was performed using using SIGMAPLOT.113
Author contributions
The project was conceived and supervised by PC and MAH. PG undertook the synthesis and analytical characterisation of the new materials. HBV and NY measured the magnetic susceptibility data, using SQUID magnetometer time provided by OC and TK. CMP collected the crystallographic data, and MAH did the structure refinements and analysis. CE performed the mechanoelastic model simulations and analysed the results. MAH and CE wrote the manuscript draft, which was reviewed and edited by PC. All authors approved the final version of the publication.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Alexander Kulak and Dr Namrah Shahid (University of Leeds) for help with some measurements. PC and MAH's collaboration was funded by the Royal Society, UK (IES\R3\193172). PG gratefully acknowledges financial support by the SERB, India (PDF/2021/004430); PC by the SERB (ECR/2018/000923); and CE by the UEFISCDI, Romania (PN-III-P4-ID-PCE-2020-1946). MAH acknowledges Diamond Light Source for access to beamline I19 (CY26879), which contributed to the results presented here.Notes and references
- in Spin Crossover in Transition Metal Compounds I–III: Topics in Current Chemistry, ed. P. Gütlich and H. A. Goodwin, Springer-Verlag, Berlin, 2004, vols. 233–235 Search PubMed.
- in Spin-crossover materials – properties and applications, ed. M. A. Halcrow, John Wiley & Sons, Chichester, UK, 2013, p. 568 Search PubMed.
- J. Zarembowitch, F. Varret, A. Hauser, J. A. Real and K. Boukheddaden, C. R. Chim, 2018, 21, 1056–1059 CrossRef CAS.
- K. Senthil Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176–205 CrossRef CAS.
- G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 1703862 CrossRef PubMed.
- O. Kahn, J. Kröber and C. Jay, Adv. Mater., 1992, 4, 718–728 CrossRef CAS.
- M. D. Manrique-Juárez, S. Rat, L. Salmon, G. Molnár, C. M. Quintero, L. Nicu, H. J. Shepherd and A. Bousseksou, Coord. Chem. Rev., 2016, 308, 395–408 CrossRef.
- M. Wang, Z.-Y. Li, R. Ishikawa and M. Yamashita, Coord. Chem. Rev., 2021, 435, 213819 CrossRef CAS.
- Y. Sekine, R. Akiyoshi and S. Hayami, Coord. Chem. Rev., 2022, 469, 214663 CrossRef CAS.
- A. B. Gaspar and M. Seredyuk, Coord. Chem. Rev., 2014, 268, 41–58 CrossRef CAS.
- A. Enriquez-Cabrera, A. Rapakousiou, M. Piedrahita Bello, G. Molnár, L. Salmon and A. Bousseksou, Coord. Chem. Rev., 2020, 419, 213396 CrossRef CAS.
- M. K. Javed, A. Sulaiman, M. Yamashita and Z.-Y. Li, Coord. Chem. Rev., 2022, 467, 214625 CrossRef CAS; K. Sun, J.-P. Xue, Z.-S. Yao and J. Tao, Dalton Trans., 2022, 51, 16044–16054 RSC.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- K. Senthil Kumar and M. Ruben, Angew. Chem., Int. Ed., 2021, 60, 7502–7521 CrossRef PubMed.
- L. Kipgen, M. Bernien, F. Tuczek and W. Kuch, Adv. Mater., 2021, 33, 2008141 CrossRef CAS PubMed and 2021, 33, 2170354 (correction).
- S. P. Vallone, A. N. Tantillo, A. M. dos Santos, J. Molaison, R. Kulmaczewski, A. Chapoy, P. Ahmadi, M. A. Halcrow and K. G. Sandeman, Adv. Mater., 2019, 31, 1807334 CrossRef PubMed.
- K. Ridier, Y. Zhang, M. Piedrahita-Bello, C. M. Quintero, L. Salmon, G. Molnár, C. Bergaud and A. Bousseksou, Adv. Mater., 2020, 32, 2000987 CrossRef CAS PubMed.
- M. Romanini, Y. Wang, K. Gürpinar, G. Ornelas, P. Lloveras, Y. Zhang, W. Zheng, M. Barrio, A. Aznar, A. Gràcia-Condal, B. Emre, O. Atakol, C. Popescu, H. Zhang, Y. Long, L. Balicas, J. L. Tamarit, A. Planes, M. Shatruk and L. Mañosa, Adv. Mater., 2021, 33, 2008076 CrossRef CAS PubMed.
- J. Seo, J. D. Braun, V. M. Dev and J. A. Mason, J. Am. Chem. Soc., 2022, 144, 6493–6503 CrossRef CAS PubMed.
- M. D. Manrique-Juárez, F. Mathieu, V. Shalabaeva, J. Cacheux, S. Rat, L. Nicu, T. Leïchlé, L. Salmon, G. Molnár and A. Bousseksou, Angew. Chem., Int. Ed., 2017, 56, 8074–8078 CrossRef PubMed.
- M. D. Manrique-Juárez, F. Mathieu, A. Laborde, S. Rat, V. Shalabaeva, P. Demont, O. Thomas, L. Salmon, T. Leïchlé, L. Nicu, G. Molnár and A. Bousseksou, Adv. Funct. Mater., 2018, 28, 1801970 CrossRef.
- M. Piedrahita-Bello, J. E. Angulo-Cervera, A. Enriquez-Cabrera, G. Molnár, B. Tondu, L. Salmon and A. Bousseksou, Mater. Horiz., 2021, 8, 3055–3062 RSC.
- V. Nagy, I. Suleimanov, G. Molnár, L. Salmon, A. Bousseksou and L. Csóka, J. Mater. Chem. C, 2015, 3, 7897–7905 RSC.
- M. Piedrahita-Bello, J. E. Angulo-Cervera, R. Courson, G. Molnár, L. Malaquin, C. Thibault, B. Tondu, L. Salmon and A. Bousseksou, J. Mater. Chem. C, 2020, 8, 6001–6005 RSC.
- O. I. Kucheriv, V. V. Oliynyk, V. V. Zagorodnii, V. L. Launets and I. A. Gural'skiy, Sci. Rep., 2016, 6, 38334 CrossRef CAS PubMed.
- A. Tsukiashi, K. S. Min, H. Kitayama, H. Terasawa, S. Yoshinaga, M. Takeda, L. F. Lindoy and S. Hayami, Sci. Rep., 2018, 8, 14911 CrossRef PubMed.
- O. Calvez, H. Camon, K. Ridier, G. Molnár and O. Gauthier-Lafaye, Appl. Opt., 2022, 61, 9562–9568 CrossRef PubMed.
- E. Resines-Urien, E. Fernandez-Bartolome, A. Martinez-Martinez, A. Gamonal, L. Piñeiro-López and J. S. Costa, Chem. Soc. Rev., 2023, 52, 705–727 RSC.
- M. Chergui and E. Collet, Chem. Rev., 2017, 117, 11025–11065 CrossRef CAS PubMed.
- K. J. Gaffney, Chem. Sci., 2021, 12, 8010–8025 RSC.
- P. Guionneau, M. Marchivie and G. Chastanet, Chem. – Eur. J., 2021, 27, 1483–1486 CrossRef CAS PubMed.
- P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed., 1994, 33, 2024–2054 CrossRef.
- A. Hauser, J. Jeftić, H. Romstedt, R. Hinek and H. Spiering, Coord. Chem. Rev., 1999, 190–192, 471–491 CrossRef CAS.
- A.-I. Popa, L. Stoleriu and C. Enachescu, J. Appl. Phys., 2021, 129, 131101 CrossRef CAS.
- G. Chastanet, C. Desplanches, C. Baldé, P. Rosa, M. Marchivie and P. Guionneau, Chem. Sq., 2018, 2, 2 Search PubMed.
- X. Li, D. Zhang, Y. Qian, W. Liu, C. Mathonière, R. Clérac and X. Bao, J. Am. Chem. Soc., 2023, 145, 9564–9570 CrossRef CAS PubMed.
- J.-P. Martin, J. Zarembowitch, A. Bousseksou, A. Dworkin, J. G. Haasnoot and F. Varret, Inorg. Chem., 1994, 33, 6325–6333 CrossRef CAS.
- N. Paradis, G. Chastanet, T. Palamarciuc, P. Rosa, F. Varret, K. Boukheddaden and J.-F. Letard, J. Phys. Chem. C, 2015, 119, 20039–20050 CrossRef CAS.
- N. Paradis, G. Chastanet, F. Varret and J.-F. Letard, Eur. J. Inorg. Chem., 2013, 968–974 CrossRef CAS.
- C. Baldé, C. Desplanches, F. Le Gac, P. Guionneau and J.-F. Létard, Dalton Trans., 2014, 43, 7820–7829 RSC.
- H. Wang, C. Baldé, A. Grosjean, C. Desplanches, P. Guionneau and G. Chastanet, Dalton Trans., 2018, 47, 14741–14750 RSC.
- M. A. Halcrow and G. Chastanet, Polyhedron, 2017, 136, 5–12 CrossRef CAS.
- C. Balde, C. Desplanches, M. Grunert, Y. Wei, P. Gütlich and J.-F. Létard, Eur. J. Inorg. Chem., 2008, 5382–5389 CrossRef CAS.
- C. Baldé, C. Desplanches, A. Wattiaux, P. Guionneau, P. Gütlich and J.-F. Létard, Dalton Trans., 2008, 2702–2707 RSC.
- R. Diego, O. Roubeau and G. Aromí, Chem Sq., 2021, 5, 1 Search PubMed.
- Z. Yu, T. Kuroda-Sowa, H. Kume, T. Okubo, M. Maekawa and M. Munakata, Bull. Chem. Soc. Jpn., 2009, 82, 333–337 CrossRef CAS.
- A. Rotaru, M. M. Dîrtu, C. Enachescu, R. Tanasa, J. Linares, A. Stancu and Y. Garcia, Polyhedron, 2009, 28, 2531–2536 CrossRef CAS.
- M. S. Sylla, C. Baldé, N. Daro, C. Desplanches, M. Marchivie and G. Chastanet, Eur. J. Inorg. Chem., 2018, 297–304 CrossRef CAS.
- C. Das, S. Dey, A. Adak, C. Enachescu and P. Chakraborty, Cryst. Growth Des., 2023, 23, 3496–3508 CrossRef CAS.
- T. Tayagaki, A. Galet, G. Molnár, M. C. Muñoz, A. Zwick, K. Tanaka, J. A. Real and A. Bousseksou, J. Phys. Chem. B, 2005, 109, 14859–14867 CrossRef CAS PubMed.
- Y. Avila, R. Terrero, P. M. Crespo, L. A. Díaz-Paneque, M. González, M. Ávila and E. Reguera, Eur. J. Inorg. Chem., 2021, 3969–3980 CrossRef CAS.
- J.-P. Martin, J. Zarembowitch, A. Dworkin, J. G. Haasnoot and E. Codjovi, Inorg. Chem., 1994, 33, 2617–2623 CrossRef CAS.
- C. Baldé, C. Desplanches, J.-F. Létard and G. Chastanet, Polyhedron, 2017, 123, 138–144 CrossRef.
- C. A. Tovee, C. A. Kilner, J. A. Thomas and M. A. Halcrow, CrystEngComm, 2009, 11, 2069–2077 RSC . [Fe0.5Ni0.5(bpp)2][BF4]2 from this paper is reexamined in this study, as compound 3c.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- Low-spin states of metal complexes have been stabilised by including them in the pores of a framework lattice. The restricted pore volume of the rigid host framework exerts a localised mechanical pressure on the guest complex molecules. A. Hauser, N. Amstutz, S. Delahaye, A. Sadki, S. Schenker, R. Sieber and M. Zerara, Struct. Bonding, 2004, 106, 81–96 CrossRef CAS.
- P. Chakraborty, M. Sy, H. Fourati, T. Delgado, M. Dutta, C. Das, C. Besnard, A. Hauser, C. Enachescu and K. Boukheddaden, Phys. Chem. Chem. Phys., 2022, 24, 982–994 RSC.
- E. W. Müller, J. Ensling, H. Spiering and P. Gütlich, Inorg. Chem., 1983, 22, 2074–2078 CrossRef.
- S. Lakhloufi, P. Guionneau, M. H. Lemée-Cailleau, P. Rosa and J.-F. Létard, Phys. Rev. B, 2010, 82, 132104 CrossRef.
- J. Kusz, M. Zubko, R. B. Neder and P. Gütlich, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 40–56 CrossRef CAS PubMed.
- E. Collet, G. Azzolina, J. Jeftić and M.-H. Lemée-Cailleau, Adv. Phys.: X, 2023, 8, 2161936 Search PubMed.
- F. J. Valverde-Muñoz, R. G. Torres Ramírez, A. Ulhe, E. Trzop, M. Dutta, C. Das, P. Chakraborty and E. Collet, CrystEngComm, 2023, 25, 3588–3597 RSC.
- J. Jeftić and A. Hauser, J. Phys. Chem. B, 1997, 101, 10262–10270 CrossRef.
- J. M. Holland, J. A. McAllister, Z. Lu, C. A. Kilner, M. Thornton-Pett and M. A. Halcrow, Chem. Commun., 2001, 577–578 RSC.
- We have investigated doping [Ru(terpy)2]2+ (terpy = 2,2′:6′,2′′-terpyridine) and related molecules into the [Fe(bpp)2][BF4]2 lattice, as a potential route to emissive SCO materials. There is a more complicated relationship between composition and T½ in solid solutions of two non-isomorphous molecules. See ref. 54, and L. J. Kershaw Cook and M. A. Halcrow, Polyhedron, 2015, 87, 91–97 CrossRef CAS.
- N. K. Solanki, M. A. Leech, E. J. L. McInnes, F. E. Mabbs, J. A. K. Howard, C. A. Kilner, J. M. Rawson and M. A. Halcrow, J. Chem. Soc., Dalton Trans., 2002, 1295–1301 RSC.
- M. A. Halcrow, Chem. Commun., 2010, 46, 4761–4763 RSC.
- [Fe(bpp)2][BF4]2 is yellow in its high-spin state, and dark brown when low-spin (ref. 64). For comparison, pure [Zn(bpp)2][BF4]2 is colourless; [Ru(bpp)2][BF4]2 is yellow as a powder but forms orange single crystals; and [Ni(bpp)2][BF4]2 is blue.
- L. Stoleriu, M. Nishino, S. Miyashita, A. Stancu and C. Enachescu, Phys. Rev. B, 2017, 96, 064115 CrossRef.
- N. di Scala, N. E. Belmouri, M. A. P. Espejo and K. Boukheddaden, Phys. Rev. B, 2022, 106, 014422 CrossRef CAS.
- T. Delgado, C. Enachescu, A. Tissot, L. Guénée, A. Hauser and C. Besnard, Phys. Chem. Chem. Phys., 2018, 20, 12493–12502 RSC.
- L. Stoleriu, P. Chakraborty, A. Hauser, A. Stancu and C. Enachescu, Phys. Rev. B, 2011, 84, 134102 CrossRef.
- C. Enachescu and A. Hauser, Phys. Chem. Chem. Phys., 2016, 18, 20591–20599 RSC.
- H. Hsu, C. P. Crisostomo, W. Wang and Z. Wu, Phys. Rev. B, 2021, 103, 054401 CrossRef CAS.
- A. Railean, M. Kelai, A. Bellec, V. Repain, M. L. Boillot, T. Mallah, L. Stoleriu and C. Enachescu, Phys. Rev. B, 2023, 107, 014304 CrossRef CAS.
- J. Kusz, H. Spiering and P. Gütlich, J. Appl. Crystallogr., 2004, 37, 589–595 CrossRef CAS (ref. 114).
- Some metal ratios used in the mechanoelastic simulations in Fig. 4 are slightly different from the sample compositions z in Table 1. That is because the simulations were done before we had completed the analytical characterisation of the materials. However the differences are within the experimental error on z, and do not affect the conclusions of our study.
- L. J. Kershaw Cook, R. Mohammed, G. Sherborne, T. D. Roberts, S. Alvarez and M. A. Halcrow, Coord. Chem. Rev., 2015, 289–290, 2–12 CrossRef CAS.
- J. M. Holland, C. A. Kilner, M. Thornton-Pett and M. A. Halcrow, Polyhedron, 2001, 20, 2829–2840 CrossRef CAS.
- S. Alvarez, Chem. Rev., 2015, 115, 13447–13483 CrossRef CAS PubMed.
- S. Vela, J. J. Novoa and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2014, 16, 27012–27024 RSC . This is a computational study comparing SCO in [Fe(bpp)2][BF4]2 and [Fe(bpp)2][PF6]2. The high-spin PF6− salt crystallises in a highly distorted geometry with ϕ = 154°, and two bpp ligands canted 28° away from the perpendicular. That distorted high-spin geometry perturbs the ligand field at the iron atom, which was calculated to lower the thermodynamic T½ of [Fe(bpp)2][PF6]2 by 13 K. Hence, the much smaller changes to ϕ induced by the dopants in 2c–3c should contribute no more than 1–2 K to the higher T½ in 2c, at the molecular level.
- R. Pritchard, C. A. Kilner and M. A. Halcrow, Chem. Commun., 2007, 577–579 RSC.
- I. Dance and M. Scudder, CrystEngComm, 2009, 11, 2233–2247 RSC.
- A. van der Lee and D. G. Dumitrescu, Chem. Sci., 2021, 12, 8537–8547 RSC.
- A. D. Bond, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2021, 77, 357–364 CrossRef CAS PubMed.
- V. A. Money, I. R. Evans, M. A. Halcrow, A. E. Goeta and J. A. K. Howard, Chem. Commun., 2003, 158–159 RSC.
- L. Wiehl, G. Kiel, C. P. Köhler, H. Spiering and P. Gütlich, Inorg. Chem., 1986, 25, 1565–1571 CrossRef CAS (ref. 114).
- J. Kusz, H. Spiering and P. Gütlich, J. Appl. Cryst., 2001, 34, 229–238 CrossRef CAS (ref. 114).
- P. Guionneau, M. Marchivie, G. Bravic, J.-F. Létard and D. Chasseau, J. Mater. Chem., 2002, 12, 2546–2551 RSC.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Cryst., 2012, 45, 1321–1329 CrossRef CAS.
- P. Guionneau, M. Marchivie, G. Bravic, J.-F. Létard and D. Chasseau, Top. Curr. Chem., 2004, 234, 97–128 CrossRef CAS.
- E. Michaels, C. M. Pask, I. Capel Berdiell, H. B. Vasili, M. J. Howard, O. Cespedes and M. A. Halcrow, Cryst. Growth Des., 2022, 22, 6809–6817 CrossRef CAS.
- M. A. Halcrow, I. Capel Berdiell, C. M. Pask and R. Kulmaczewski, Inorg. Chem., 2019, 58, 9811–9821 CrossRef CAS PubMed.
- [Fe(bpp)2][BF4]2 exhibits T½ = 248 K in solution, so ΔT(latt) = T½ − 248 for 1c–3c (ref. 93).
- A multivariate structure:function analysis of SCO in salts of [Fe(bpp)2]2+ derivatives was published while this article was under review. L. Marchi, S. Fantuzzi, A. Cingolani, A. Messori, R. Mazzoni, S. Zacchini, M. Cocchi and L. Rigamonti, Dalton Trans., 2023, 52, 7684–7694 RSC.
- L. J. Kershaw Cook, F. L. Thorp-Greenwood, T. P. Comyn, O. Cespedes, G. Chastanet and M. A. Halcrow, Inorg. Chem., 2015, 54, 6319–6330 CrossRef CAS PubMed.
- I. Capel Berdiell, R. Kulmaczewski, N. Shahid, O. Cespedes and M. A. Halcrow, Chem. Commun., 2021, 57, 6566–6569 RSC.
- N. Suryadevara, A. Mizuno, L. Spieker, S. Salamon, S. Sleziona, A. Maas, E. Pollmann, B. Heinrich, M. Schleberger, H. Wende, S. K. Kuppusamy and M. Ruben, Chem. − Eur. J., 2022, 28, e202103853 CrossRef CAS PubMed.
- R. Kulmaczewski, L. J. Kershaw Cook, C. M. Pask, O. Cespedes and M. A. Halcrow, Cryst. Growth Des., 2022, 22, 1960–1971 CrossRef CAS PubMed.
- O. Kahn, L. Sommier and E. Codjovi, Chem. Mater., 1997, 9, 3199–3205 CrossRef CAS.
- J. Kröber, E. Codjovi, O. Kahn, F. Grolière and C. Jay, J. Am. Chem. Soc., 1993, 115, 9810–9811 CrossRef.
- J. R. Galán-Mascarós, E. Coronado, A. Forment-Aliaga, M. Monrabal-Capilla, E. Pinilla-Cienfuegos and M. Ceolin, Inorg. Chem., 2010, 49, 5706–5714 CrossRef PubMed.
- C. Lefter, S. Tricard, H. Peng, G. Molnár, L. Salmon, P. Demont, A. Rotaru and A. Bousseksou, J. Phys. Chem. C, 2015, 119, 8522–8529 CrossRef CAS.
- M. Piedrahita-Bello, B. Martin, L. Salmon, G. Molnár, P. Demont and A. Bousseksou, J. Mater. Chem. C, 2020, 8, 6042–6051 RSC.
- C. Bartual-Murgui, C. Perez-Padilla, S. J. Teat, O. Roubeau and G. Aromí, Inorg. Chem., 2020, 59, 12132–12142 CrossRef CAS PubMed.
- Y. Gong, Z.-H. Li, X. Yan, Y.-Q. Wang, C.-Y. Zhao, W.-K. Han, Q.-T. Hu, H.-S. Lu and Z.-G. Gu, Chem. – Eur. J., 2020, 26, 12472–12480 CrossRef CAS PubMed.
- K. G. Sandeman, APL Mater., 2016, 4, 111102 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. B: Struct. Sci., 2015, 71, 3–8 CrossRef PubMed.
- L. J. Barbour, J. Appl. Cryst., 2020, 53, 1141–1146 CrossRef CAS.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Cryst., 2009, 42, 339–341 CrossRef CAS.
- C. J. O’Connor, Prog. Inorg. Chem., 1982, 29, 203–283 CrossRef.
- SIGMAPLOT, version 8.02, SPSS Inc., 2002 Search PubMed.
- Ref. 76, 87 and 88 describe a theoretical treatment of thermal expansion in SCO crystals, based on the theory of elastic lattice interactions. The α coefficient derived in these studies is not the same as the widely used αV thermal expansion parameter in eqn (5) (ref. 84, 85 and 90).
Footnotes |
| † Electronic supplementary information (ESI) available: X-ray powder diffraction and magnetic susceptibility data; crystallographic experimental data, refinement procedures, Figures and tabulated metric parameters; calculated thermal expansion coefficients from the compounds in this work, and selected literature materials. CCDC 2261786–2261796. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc02683c |
| ‡ Current address: Department of Chemistry, Faculty of Science, National Taiwan Normal University, Taipei 11677, Taiwan. |
| This journal is © The Royal Society of Chemistry 2023 |