Open Access Article
Open Access ArticleRevealing the interplay between the structural complexity of triphenylamine redox derivatives and their charge transport processes via computational modeling†
Robert
Herzhoff
a,
Fabrizia
Negri
 b,
Klaus
Meerholz
*a and
Daniele
Fazzi
b,
Klaus
Meerholz
*a and
Daniele
Fazzi
 *b
*b
aDepartment für Chemie, Universität zu Köln, Institut für Physikalische Chemie, Köln, Nordrhein-Westfalen, Germany. E-mail: klaus.meerholz@uni-koeln.de
bUniversità di Bologna, Department of Chemistry ‘G. Ciamician’, Bologna, Italy. E-mail: daniele.fazzi@unibo.it
First published on 7th August 2023
Abstract
Triphenylamine derivatives (TPAs) are organic functional materials well known for their semiconducting charge transport and redox properties. These features characterize their applications in the field of organic electronics, for instance as hole transport layers for organic light emitting diodes (OLEDs), and perovskite-based solar cells (PSCs), as well as organic cathodes for electrochemical energy storage (EES) devices (e.g. organic batteries). Despite a large number of experimental and computational investigations, some structure–property relationships still remain elusive. Here, we explore through a bottom-up computational approach the molecular and solid state structures, as well as the charge transport processes in amorphous and single crystalline phases of four different redox active TPAs, characterized by increased molecular structure complexity. The TPAs considered feature one-, two- or four redox centers, namely (i) a single TPA unit, two TPAs linked via (ii) a flexible diphenyl bridge (TPD) or (iii) a rigid fluorene bridge (FTPD), and (iv) four TPAs connected via a spiro-center (spiro-OMeTAD). A combination of density functional theory, semiempirical and molecular dynamics methods is used to analyse the experimental crystalline structures, to generate the amorphous morphologies, and to calculate the charge transport parameters and hole mobility. Our results show that short- and long-range structural order in condensed phases is strongly influenced by the molecular architecture. Furthermore, charge transport parameters, such as site energies, reorganization energies and coupling integrals, are intimately coupled with the number of redox centers and the way they are connected. The charge transport is differently characterized depending on the degree of morphological disorder, namely reorganization energy-controlled transport in the crystalline phase and site-energy static-disorder controlled transport in the amorphous phase. The computed hole bulk mobilities for both single crystal and amorphous cases are in good agreement with the available experimental literature data.
Introduction
Triphenylamines (TPAs) are commonly used in various (opto-)electronic devices due to their good hole-transporting properties,1–4 their high redox potential vs. Li/Li+ and cycling stability,5 and their high glass transition temperature.6,7 Moreover, they are readily synthetically available, allowing for fine-tuning of their redox, spectroscopic and charge transport properties through the use of electro-active substituents.8,9TPAs are used as hole transporting layers (HTL) in organic light emitting diodes (OLEDs),4,10 organic solar cells (OSCs),11 and perovskite solar cells (PSCs),12 and as redox-active materials for rechargeable electrochemical energy storage (EES) devices, such as organic batteries and supercapacitors.9,13 Due to the popularity of such compounds in organic electronics (especially OLED applications), a significant number of experimental publications,12,14–16 as well as theoretical and computational investigations, have been reported.17–22 Fundamental charge transport parameters, such as the inner reorganization energy (λint), have been studied systematically at multiple levels of theory and relevant structural parameters have been identified.20,23,24 Charge mobilities for various triphenylamine derivatives have been computed in the amorphous phase in good agreement with experimental data.17 However, some questions concerning the relationships between the molecular structure, bulk morphology, and charge transport properties still remain to be answered. For example, it is not clear how the presence of one-, two- or more redox centers (i.e., triphenylamine units) affects the supramolecular organisation in the solid state, for both crystalline and amorphous phases, and how it impacts the charge transport parameters and the charge mobility, specifically with respect to the mixed-valence nature of multi-TPA compounds. Herein, we analyse such aspects as well as the influence of crystal packing and amorphous morphologies on the degree of charge transport isotropy/anisotropy. These issues have not been comprehensively addressed so far, in particular a systematic comparison between the computed charge transport parameters and hole mobilities in single crystalline vs. amorphous morphologies.We focus on a library of four triphenylamine derivatives showing increasing molecular structure complexity, namely triphenylamine (TPA), N,N′-bis-(3-methylphenyl)-N,N′-diphenylbenzidin (TPD), N2,N2,N7,N7-Tetrakis(4-methoxyphenyl)-9,9-dimethyl-9H-fluorene-2,7-diamine (FTPD), and N2,N2,N2′,N2′,N7,N7,N7′,N7′-Octakis(4-methoxyphenyl)-9,9′-spirobi[fluorene]-2,2′,7,7′-tetraamine (spiro-OMeTAD) (see Fig. 1). Ideally, we would have chosen identical substitution patterns for all cases (i.e. para-methoxy substituents on the peripheral aryl substituents, such as MeO-TPD); however, we were limited to the compounds for which experimental crystal structures are available in the literature. While TPA has one redox center, TPD and FTPD have two redox centers, as connected either via a flexible bridge (TPD) or by a rigid (ladder type) one (FTPD), and finally spiro-OMeTAD has four redox centers, consisting of two FTPD-subunits that are orthogonally connected via a central spiro carbon. Such increasing structural complexity impacts the inter-molecular packing and morphological properties, as well as the charge transport processes in the bulk phase. The goal of our work is to rationalize via a bottom-up molecular modeling approach the impact of different molecular structures, as characterized by various internal torsional degrees of freedom and steric demand, on both the morphological and charge-transport properties for both crystalline and amorphous states. To this end, a computational methodology was chosen that focuses on accurately describing the energetic and static disorder as well as those charge transport parameters intimately connected to the molecular structure.
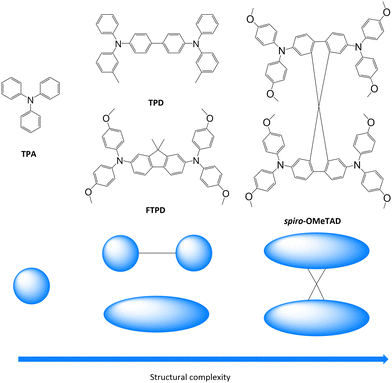 | ||
| Fig. 1 Triphenylamine derivatives investigated in this work (TPA, TPD, FTPD and spiro-OMeTAD) with simplified sketches showing their structural complexity. | ||
By combining density functional theory (DFT), molecular dynamics (MD), and kinetic Monte-Carlo (KMC) methods we simulated the molecular and bulk properties, encompassing the calculation of the charge transport parameters and charge mobility. For each species, we analysed both single crystalline (experimental (XRD)) and amorphous phases (generated via MD simulations), focusing on the impact of the structural complexity as well as the morphological and static energetic disorder on the charge transport properties. We found a subtle interplay between the molecular structure complexity (namely one-, two- and four redox centers differently linked), supramolecular organizations, and charge transport mechanisms. The molecular geometry and shape impact not only the supramolecular organization in the condensed phases but also the reorganization energy and the isotropy of charge carrier diffusion via its short- and long-range effects on the crystal packing, as well as the site energy difference distributions in the amorphous phase.
Computational methods
Single molecule equilibrium geometries
The calculations were performed at multiple computational levels. For the DFT calculations, the range separated hybrid functional with Grimme's scheme of dispersion corrections ωB97X-D,25 the hybrid B3LYP26–28 and the triple-split polarized Pople basis set 6-311G*29–31 were used. Constrained-DFT (C-DFT) schemes were applied to localize the charge on specific molecular fragments. C-DFT calculations were performed by using the Coulomb Attenuated Method (CAM-B3LYP32) with the 6-311G* basis-set. All molecular geometries optimized at the DFT level showed stable equilibrium structures (no imaginary frequencies found). Geometries were also computed at the semiempirical quantum mechanical tight-binding DFT level (SQM) by using GFN2-xTB as proposed by Grimme et al.33,34 The neutral ground state calculations were performed at the restricted DFT level while the singly charged state calculations were performed at the spin-polarized unrestricted (UDFT) level.Bulk morphologies
The single crystalline morphologies were obtained from experimental XRD-data,21,22,35,36 while the amorphous morphologies were generated via MD simulations, where a simulated annealing procedure was employed for equilibration. Details about the force field parametrization and the MD simulations can be found in the ESI.† For all compounds, systems of 1000 molecules were generated, in the case of the crystalline morphologies by expanding the experimental unit cell as a supercell.Charge transport parameters
Marcus theory37,38 provides the rates kij for the charge transfer between two sites i and j in the low electronic coupling regime as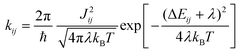 | (1) |
| λ = λint + λo | (2) |
In this work, λint was calculated at multiple levels of theory by using the adiabatic potential method.39λint is given by
| λint = (UnC − UnN) + (UcN − UcC) | (3) |
In eqn (3), U is the energy, the superscripted lower-case letters stand for the electronic state (neutral or charged) while the superscripted upper-case letters stand for the equilibrium geometry. For the outer reorganization energy λo, a constant of 50 meV was assumed.40–42
The electronic coupling Jij between two sites i and j is given by43
| Jij = 〈ϕi|Ĥ|ϕj〉 | (4) |
The site energy differences (ΔEij) for the crystalline and amorphous morphologies were calculated based on the static electrostatic interactions and induced dipoles, all based upon the atomic partial charges evaluated at the CHELPG level (ωB97X-D/6-311G*). The site energy Ei is given by46,47
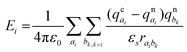 | (5) |
Charge transport simulations
The charge transport simulations (hopping regime) were performed using a kinetic Monte Carlo (KMC) approach, based on the Marcus charge transfer rates calculated viaeqn (1). The charge transport parameters, such as the coupling and the site energies, were computed separately for the entire system before each KMC run. The KMC simulations were performed under periodic boundary conditions for a single charge at a temperature of 300 K, using 1000 trajectories of 105 steps each. The diffusion coefficient (D) was obtained by a linear fit to the mean square displacements and the zero-field mobility was computed via the Einstein–Smoluchowski relationship: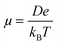 | (6) |
The KMC procedure was repeated for ten snapshots as extracted from the MD production run at a temperature of 300 K. The final hole mobilities are averaged over all KMC trajectories obtained from the ten snapshots.48 With the charge mobility being a tensor, we refer here to μ as the average value (i.e.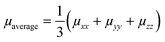 , with μii being the i,i-component of the mobility tensor, i ∈ x, y, z). For those cases where the charge transport presents a pronounced anisotropy, single values of the tensor along specific axes are specified (vide infra, Table 3). Charge transport simulations were also performed with an applied electric field of 108 V m−1. The results for these last simulations are listed in the ESI.†
, with μii being the i,i-component of the mobility tensor, i ∈ x, y, z). For those cases where the charge transport presents a pronounced anisotropy, single values of the tensor along specific axes are specified (vide infra, Table 3). Charge transport simulations were also performed with an applied electric field of 108 V m−1. The results for these last simulations are listed in the ESI.†
Software
DFT calculations were performed by combining the codes GAUSSIAN49 and ORCA,50 C-DFT was carried out by using NWChem,51 while GFN2-xTB calculations were done with xTB.33,34 MD simulations were executed with GROMACS,52–56 using an in-house re-parameterized version of the OPLS-AA force field57,58 (see the ESI† for details). The evaluation of the electronic couplings was done by using the open-source code VOTCA46 for both the crystalline and amorphous bulk morphologies. For crystalline morphologies, additionally an in-house DIPRO script interfaced with Gaussian and ORCA was also adopted. Charge transport simulations for crystalline structures were performed (and internally compared for consistency) by using two codes: an in-house code developed by Negri et al.59–61 and the open-source code VOTCA.46 Charge transport simulations for amorphous morphologies were carried out with VOTCA.Results and discussion
(1) Bulk morphologies: crystalline vs. amorphous phases
The center-of-mass (CoM) radial distribution functions (gCoM(r)) of the simulated amorphous and experimental single crystalline21,22,35,36 morphologies for each compound, as reported in Fig. 2, show clear differences that can be traced back to the molecular structure and the short-/long-range supramolecular packing.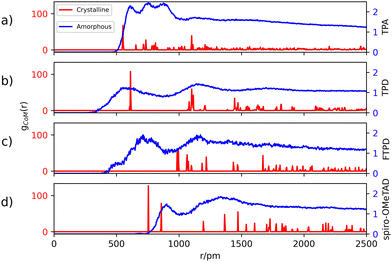 | ||
| Fig. 2 Center-of-mass (CoM) radial distribution functions gCoM(r) in the crystalline (red) and amorphous (blue) morphologies. Crystalline structures of TPA, TPD, FTPD and spiro-OMeTAD are taken from ref. 21, 22, 35, and 36, and the bulk amorphous structures are obtained from MD simulations (see details in the Computational methods section and the ESI†). Labels (a), (b), (c) and (d) refer to TPA, TPD, FTPD and spiro-OMeTAD respectively. | ||
Generally, in the amorphous phase, gCoM(r) is a continuous distribution characterized by broad bands reflecting different nearest-neighbours coordination shells and a lack of long-range structural order, while in the crystalline phase, as expected, gCoM(r) consists of narrow and well-defined peaks, according to the periodic structural order appropriate for crystals. Notably, the different molecular sizes and shapes of the TPA derivatives impact gCoM(r) of both crystalline and amorphous phases.
For TPA in the crystal phase, gCoM(r) shows an intense peak at 551 pm and many small peaks centered at well-defined distances. In the amorphous phase, gCoM(r) shows three broad bands from 600 pm to 800 pm, followed by a constant distribution at higher distances. The three bands reflect a short-range structural order, showing the formation of multiple coordination shells around each TPA. This local structural order, induced by the isotropic molecular structure (sphere-like shape) of TPA, is however lost for large distances (r > 1000 pm).
TPD, featuring two redox-centers, is characterized by a more elongated and, therefore, anisotropic molecular structure in contrast to TPA. This is also reflected in the herringbone-type packing in the crystalline phase of TPD (see the ESI†), leading to larger CoM distances and more defined coordination shells. In the amorphous phase, the gCoM(r) of TPD shows two very broad coordination shells, centered around the crystalline peaks at 600 pm and 1200 pm, with contributions falling off to smaller values than TPA (<500 pm). This is caused by a fraction of molecules that can get very close to each other affording very short CoM distances, a feature which is enabled in the amorphous phase by the elongated and flexible structure of TPD.
FTPD shows an elongated structure similar to TPD, however, it is characterised by a more rigid backbone due to the suppression of the inter-ring torsional degree of freedom via the fluorene structure. The gCoM(r) of the crystalline phase of FTPD is therefore very different from those of TPD and TPA, showing the first coordination peak at around 1000 pm. However, similarly to TPD, in the amorphous case the first coordination shell of FTPD is computed at lower values than the crystalline phase, namely at around 750 pm, showing a broad band falling off below 500 pm, thus indicating close CoM distances between the molecules. These results suggest that molecules with elongated shapes enable short range packing in the amorphous phase, a situation that is however not always observed in the crystal phase. For FTPD such short range packing in the amorphous phase stems from cross-like pair configurations (see Fig. S12, ESI†), i.e. pairs where the molecules cross along their long axes forming an X-shaped structure. This configuration enables small CoM distances.
For crystalline spiro-OMeTAD, the coordination shells are located at higher values than TPA, TPD and FTPD, thus showing the very bulky nature of the molecule. In the amorphous phase, a sharp coordination shell around 800 pm, followed by a very broad band centered at 1200 pm, is observed. Only a very small fraction of the molecules gets closer (∼650 pm) than in the crystal. Generally, the steric hindrance and the aspect ratio of the molecule prevent close contacts also in the amorphous phase, in contrast to TPD and FTPD. With respect to other TPAs, spiro-OMeTAD shows the highest CoM distance of the first gCoM(r) peak in the amorphous phase, which reflects the bulkier nature of spiro-OMeTAD as compared to the other compounds.
From the structural investigation in solid phases we can draw some partial conclusions based on the molecular structures: (i) as expected, small, sphere-like, one-redox center systems (e.g., TPA) show smaller CoM distances in the crystalline phase than the elongated and bulkier derivatives (e.g., TPD, FTPD and spiro-OMeTAD), however (ii) elongated two-redox centers derivatives (e.g., TPD and FTPD), afford short CoM distances in the amorphous phase thanks to their structural flexibility and molecular aspect ratio. Finally, (iii) sterically demanding four-redox centers compounds (e.g., spiro-OMeTAD) present the largest CoM distances in both crystalline and amorphous phases due to their bulky nature.
(2a) Charge transport parameters: hole reorganization energy
The first charge transport parameter we computed is the internal (intramolecular) reorganization energy λint. λint was calculated at multiple levels of theory (Table 1), encompassing DFT, SQM and constrained-DFT (C-DFT), by assuming the charge partitioning schemes as reported in Fig. 3. An additional calculation of λint using the BLYP35 functional, as previously introduced by Renz et al. for the quantum-chemical characterization of mixed-valence systems,62 can be found in Table S12 of the ESI.†| TPA | TPD | FTPD | spiro-OMeTAD | |
|---|---|---|---|---|
| ωB97X-D | 0.12 | 0.73 | 0.54 | 0.50 |
| ωB97X-D (fda) | 0.12 | 0.26 | 0.33 | 0.25 |
| B3LYP | 0.11 | 0.30 | 0.23 | 0.16 |
| GFN2-xTB | 0.07 | 0.09 | 0.12 | 0.08 |
| CAM-B3LYP, c0 | 0.13 | 0.67 | 0.48 | 0.53 |
| CAM-B3LYP, c1 | 0.10 | 0.10 | 0.31 | 0.24 |
| CAM-B3LYP, c2 | — | 0.60 | 0.57 | 0.46 |
| CAM-B3LYP, c3 | — | 0.20 | 0.32 | 0.30 |
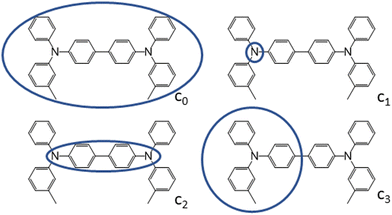 | ||
| Fig. 3 Charge constraint schemes for TPD. The circles indicate the domains where the positive charge is localized. Charge-constrain schemes for FTPD and spiro-OMeTAD are reported in the ESI.† | ||
All methods are largely consistent for TPA, leading to hole reorganization energy values around 0.1 eV, very much in accordance with the literature data.23 Moving to two- (TPD and FTPD) and four redox units (spiro-OMeTAD) all methods yield very different results. This discrepancy can be traced back to the well-known self-interaction error (SIE), which in the case of B3LYP and GFN2-xTB leads to an artificial stabilization of the charged state.63 When long range corrected schemes are taken into account (e.g. CAM-B3LYP, ωB97X-D) the reorganization energy raises up to 0.73 eV for TPD. Similar findings have been reported by Li et al.64 and by Blaskovitz et al.24 This result shows that an accurate description of the reorganization energy is not trivial. While the SIE can be mitigated by using a range-separated functional like ωB97X-D, Renz et al. reported that mixed-valence systems – very similar to TPD – are borderline cases of the Robin-Day classification, with a charged state being on the border between delocalization and partial localization.62 This circumstance has an additional impact on the final value of the reorganization energy. BLYP35, as introduced by Renz et al., resulted in similar reorganization energy values as B3LYP, showing the lowest for TPA and the highest for TPD. Here, we suggest an alternative approach to describe the reorganization energy by taking into account both the SIE and the partial localization problem.
To characterize the nature of the charged state, we devised multiple charge-constrain partitioning schemes at the C-DFT level, as reported in Fig. 3 (for the sake of simplicity only TPD is shown) and recalculated the reorganization energy accordingly. The partitioning serves to characterize the extreme cases of full delocalization (c0 and c2) versus full localization (c1 and c3). The SIE is mitigated by using the range separated CAM-B3LYP functional.
We compared the unconstrained situation (c0, normal DFT) to different charge partitioning schemes, namely the charge confined to one nitrogen atom (c1), to the central bridging unit (c2), or to one TPA-subunit (c3). Generally, the reorganization energies computed with C-DFT-schemes c1 and c3 are similar to those evaluated at the B3LYP level, while the reorganization energies computed with C-DFT-schemes c0 and c2 are similar to those calculated at the ωB97X-D level. In C-DFT-schemes c0 and c2 the charge is allowed to delocalize across the bridge and since the functional used (CAM-B3LYP) is a range-separated one, similar results as by using ωB97X-D are obtained. For the C-DFT-schemes c1 and c3 a lower reorganization energy is obtained than for c0 and c2 by avoiding the charge delocalization across the whole molecular backbone. This trend shows that the delocalization of the charge across the bridge connecting the redox centers is the main factor governing the magnitude of the reorganization energies in multi-TPA species. Still, what remains to be answered is which kind of scenario (localized or delocalized charged state), is more realistic when modeling charge transfer processes in bulk TPA-based materials, which we approach by analysing the charged state geometries.
From Fig. 4 the effects of charge delocalization become clear (data for FTPD and spiro-OMeTAD, respectively, are reported in Fig. S4 and S6 of the ESI†). In the unconstrained/delocalized schemes (i.e., c0 and c2 C-DFT, as well as normal DFT at the B3LYP and ωB97X-D levels), significant changes in the bond lengths and dihedral angles occur. Most notably, the central bond (number 5) shortens significantly, and the central dihedral angle D becomes planar (quinoid-like structure). In the constrained/localized schemes (i.e. c1, c3), the bond length changes are much less pronounced and an asymmetric change in the dihedral angles occurs, where only the dihedral angles of the charge-bearing TPA-redox subunit change significantly. Thus, a large contribution to the reorganization energy can be related to the variation of the dihedral angles.
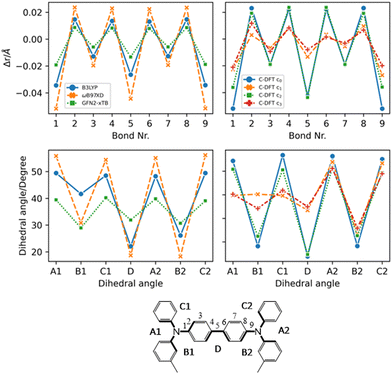 | ||
| Fig. 4 Geometric parameters of TPD in the charged state (+1) by considering different methods (DFT, C-DFT, GFN2-xTB), DFT functionals and various charge constraint (C-DFT) schemes. The two panels on the top show the bond length difference (Δr = rcharged − rneutral) patterns by moving from the neutral to the charged state. Top left panel: DFT (B3LYP vs. ωB97X-D) versus GFN2-xTB data. Top right panel: C-DFT data with different schemes. The two panels on the bottom show the dihedral angles in the charged state. Bottom left panel: DFT (B3LYP vs. ωB97X-D) versus GFN2-xTB data. Bottom right panel: C-DFT data with different charge constraint schemes. See the ESI† (Fig. S4 and S6) for the geometric parameters of the other compounds. | ||
This feature was already reported by Friedrich et al.17 Since the steric demands of the surrounding molecules in the bulk phase presumably hinder large dihedral relaxations upon charging, we recalculated the reorganization energy by fixing the dihedral angles at the values they assumed in the neutral state, similar to reports in literature.17 Very similar reorganization energies as compared to those values obtained by the C-DFT scheme c3 were computed (see the fda approach in Table 1). Therefore, either assuming a charge localization (C-DFT) or a frozen dihedral approach leads to the same effects. Constraining the dihedral angles prevents the multi-TPA compounds to assume a quinoidal structure upon charging, thus corresponding to a delocalization restraint. In this work we assume for the final calculation of the charge transfer rates and mobility the intramolecular reorganization energy as obtained by C-DFT scheme c3 for TPD, FTPD and spiro-OMeTAD and c0 (unconstrained) for TPA.
Summarizing, by constraining the charge over one TPA redox unit (c3 scheme) as suggested by chemical intuition, the reorganization energy smoothly increases from 0.10 eV for TPA, up to 0.20–0.30 eV for the two- (TPD, FTPD) and four-redox centers (spiro-OMeTDAD) cases. We believe that this trend reflects the dispersion of the hole reorganization energy by moving from one to multiple TPA centers, also mimicking the structural constraints as induced in the bulk phase by the surrounding molecules. Globally, our computational analysis shows that the hole reorganization energy in multi-redox TPA compounds is intrinsically linked to the degree of charge delocalization across units, and thus the variation of the central bond lengths and dihedral angles upon charging. The computed reorganization energies are however still approximate in nature, with the true reorganization energy lying in between the localized/frozen dihedral energies and the unconstrained calculations (e.g., using the BLYP35 functional), corresponding to a probably partially localized situation.
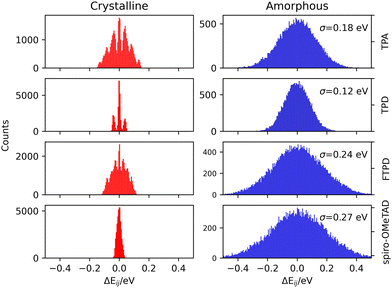
(2b) Charge transport parameters: site energy differences
The impact of morphological order becomes apparent when analysing the charge transport parameters, like the site energy difference distributions ΔEij (see eqn (1)) as shown in Fig. 5.As it can be generally expected, rather discrete ΔEij distributions are found for single crystalline phases, while the amorphous phases show much wider, Gaussian-like shapes due to the statistical distribution of conformers. The nonequivalent molecular sites of the crystalline phases are reflected in the peaks of the histograms, with each peak being slightly broadened due to the finite numerical accuracy in the calculation of the site energies. The electrostatic disorder, quantified as the standard deviation σ of the site energy difference distributions in the amorphous phase, is of a similar magnitude as the reorganization energies for each compound. This feature leads to the static disorder being the dominating parameter for hopping transport in the amorphous phase. On the other hand, the site-energy difference distributions in the crystalline phases are narrower, causing the reorganization energy to be the dominant parameter for the hopping transport in crystals. Comparable values for the static disorder have been reported by Friedrich et al.,17 Lin et al.20 and Mondal et al.19 Comparing the σ-values, molecules characterized by an increased structural complexity like FTPD and spiro-OMeTAD show increased electrostatic disorder effects in the amorphous phase when compared to TPA and TPD.
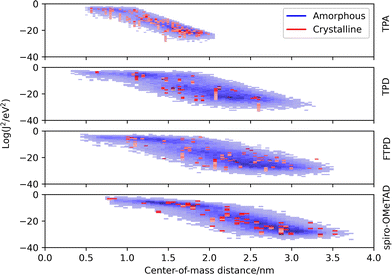
(2c) Charge transport parameters: electronic couplings
The electronic coupling distributions (Fig. 6) as computed for both crystalline and amorphous morphologies, show similar characteristics as the site energy difference distributions, being continuous in the amorphous phase and discrete in the crystalline phase. Generally, low values are obtained for the electronic coupling (largest Jij is around 20 meV), clearly supporting the observation of a disorder-controlled nature of the charge transport.Comparing the molecular classes, we notice that the coupling distribution in the TPA crystal is much more narrow than in the TPD, FTPD and spiro-OMeTAD crystals, reflecting the smaller size and sphere-like shape (isotropy) of the molecule. For TPD, FTPD and spiro-OMeTAD, broader distributions are obtained, and even at large CoM distances (>2 nm) nonzero electronic coupling is found due to the elongated or bulky shape of the molecules. In the amorphous phase, we can observe that there are two trends for the couplings, a horizontal dispersion (from roughly 0.5 to 1.5 nm) and a linear one (from 2.0 to 3.5 nm). In the first range, the couplings are almost independent from the CoM distances, indicating the interplanar distance as the determining factor for the magnitude of the coupling, while at larger CoM distances, the coupling drops approximately linearly, indicating a crossing point at which the CoM distance becomes the dominating factor ruling the strength of the electronic coupling. Considering the logarithmic scale, this linear decrease corresponds to an exponential decrease in a linear scale.
Analysis of the electronic couplings based on the experimental crystal structures
To gain an in-depth understanding about the influence of solid-state packing and molecular orientations on the electronic coupling, the crystal structures of TPA, TPD, FTPD and spiro-OMeTAD were analysed by calculating the electronic coupling using the DIPRO approach (ωB97X-D/6-311G*) for each unique molecular site and its neighbours, applying a cutoff of 1.5 nm. A detailed listing of the results and the geometric parameters can be found in the ESI† (Tables S2–S9). For TPA, TPD and FTPD three non-equivalent pairs (couplings) can be isolated, named A, B and C in Table 2. For spiro-OMeTAD only two pairs are identified (A and B).| TPA | TPD | FTPD | spiro-OMeTAD | |
|---|---|---|---|---|
| A (black-red) | 50 | 36 | 9.8 | 39 |
| B (black-green) | 40 | 11 | 9.3 | 15 |
| C (black-blue) | 36 | 8 | 9 |
From Fig. 7 and Table 2 we can observe that TPA shows the highest electronic couplings amongst the triphenylamine series. Furthermore, the highest TPA coupling (50 meV) results from an interdigitation of the amine moieties, see pair A (black-red pair). For TPA, all couplings are of the same order of magnitude, thus, an isotropic transport of the charges within the crystal is to be expected. For TPD a similar interdigitation motif as for TPA is found (pair A), resulting in a high electronic coupling (36 meV). However, in contrast to TPA, for TPD the other couplings (pairs B and C) are smaller in magnitude than pair A. Because pair A of TPD is prevalently aligned with the crystallographic axis b, charge transport is expected to occur preferably along this direction in an anisotropic way in the crystal. For the case of FTPD, lower couplings (∼10 meV) are observed when compared to the other triphenylamine compounds. This can be due to the shifted orientation of the monomers in the crystal packing, which prevents close contact between the molecular backbones (as reported in the gCoM(r), Fig. 2) and the interdigitation of the triphenylamine moieties. All FTPD couplings are very similar in magnitude, in accordance with ref. 21, making isotropic-like charge transport in the crystal probable. Finally, for spiro-OMeTAD, one can observe that pair A is more intertwined than the others, leading to higher electronic coupling (39 meV), in accordance with ref. 21, possibly resulting in an anisotropic charge diffusion as for the case of the TPD crystal.
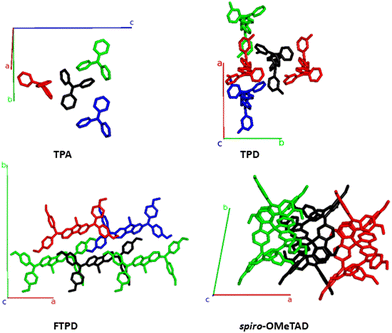 | ||
| Fig. 7 Structures featuring the largest electronic coupling (see main text) from the TPA- TPD-, FTPD- and spiro-OMeTAD crystal unit cells, also reporting the crystallographic axes. The central molecule is shown in black. The pair formed by the black and red molecules is, for each compound, the one with the highest electronic coupling, followed by the black-green and black-blue pairs, respectively (see Table 2). | ||
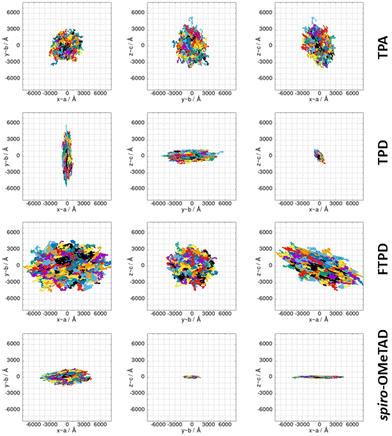
Kinetic Monte-Carlo charge transport simulations and zero-field (Brownian) hole mobilities
The computed KMC charge percolation pathways for single crystals, as reported in Fig. 8, show the expected characteristics as anticipated from the analysis of the electronic couplings. While for TPA, due to its molecular shape (sphere-like) and solid state packing, isotropic charge transport is found, other compounds show either marked anisotropic charge diffusion (TPD and spiro-OMeTAD) or weak anisotropic charge percolation (FTPD) due to different molecular aspect ratios, bridge flexibility, steric hindrance and packing motifs. In TPD, the b direction is clearly favoured over the a and c axes (Fig. 7). This preferred direction is readily explained by the orientation of the main charge transport pairs (i.e., those showing the highest Jij) along the b axis (Fig. 7 and Table 2), as favoured by the elongated molecular shape and interdigitation of the nearest neighbour TPA units. In the charge mobility simulations of single crystal FTPD, a weak anisotropy of the charge transport along the a axis is observed, due to the similar (small) magnitude of the electronic coupling in all charge transport pairs (∼9 meV, Table 2). In the charge hopping pathways of spiro-OMeTAD, the charge transport takes place mainly along the a axis due to the high coupling (39 meV) on the basis of the π–π stacking along this direction (Fig. 7).
Table 3 collects the computed zero-field (Brownian) KMC hole mobilities (that is, 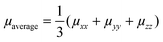 , with μii being the i,i-component of the mobility tensor, i ∈ x, y, z) for all species in their crystalline and amorphous phases. In Table 3 are also shown the experimental data available from the literature. A one-to-one comparison between the computed single crystal/amorphous charge mobility and the experimental single crystal/amorphous-films hole mobility was sometimes not possible to do. For instance, for TPA only the experimental single crystal hole mobility was found, while no data is available for amorphous films. The only case in which we could find both single crystal and amorphous measured hole mobility is spiro-OMeTAD. In the ESI† are reported the computed mobilities in the presence of an electric field (Table S10). Furthermore, we report also the μxx, μyy, and μzz components in order to highlight the isotropy vs. anisotropy of the charge transport in single crystals.
, with μii being the i,i-component of the mobility tensor, i ∈ x, y, z) for all species in their crystalline and amorphous phases. In Table 3 are also shown the experimental data available from the literature. A one-to-one comparison between the computed single crystal/amorphous charge mobility and the experimental single crystal/amorphous-films hole mobility was sometimes not possible to do. For instance, for TPA only the experimental single crystal hole mobility was found, while no data is available for amorphous films. The only case in which we could find both single crystal and amorphous measured hole mobility is spiro-OMeTAD. In the ESI† are reported the computed mobilities in the presence of an electric field (Table S10). Furthermore, we report also the μxx, μyy, and μzz components in order to highlight the isotropy vs. anisotropy of the charge transport in single crystals.
| TPA | TPD | FTPD | spiro-OMeTAD | |
|---|---|---|---|---|
| Computed (single crystal) | ||||
| μ average | 2.5 × 10−2 | 5.9 × 10−2 | 1.0 × 10−3 | 1.6 × 10−2 |
| μ xx | 2.3 × 10−2 | 7.1 × 10−3 | 1.8 × 10−3 | 4.3 × 10−2 |
| μ yy | 2.2 × 10−2 | 1.6 × 10−1 | 8.6 × 10−4 | 5.3 × 10−3 |
| μ zz | 3.1 × 10−2 | 1.1 × 10−2 | 4.5 × 10−4 | 3.4 × 10−4 |
| Computed (amorphous) | ||||
| μ average | 8.3 × 10−4 | 5.9 × 10−4 | 3.1 × 10−6 | 2.3 × 10−6 |
| Experimental data from literature | 2 × 10−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 (single crystal) 65 (single crystal) |
1 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (amorphous thin film) 1 (amorphous thin film) |
4.3 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 (semicrystalline thin film) 21 (semicrystalline thin film) |
1.30 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 (single crystal) 22 (single crystal) |
1.69 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 (amorphous thin film) 22 (amorphous thin film) |
||||
By moving from the crystalline to the amorphous phase a drop of various orders of magnitude of the charge mobility occurs, as expected due to the impact of morphological (Fig. 2) and energetic (Fig. 5) disorder. This phenomenon is, however, more drastic in the case of FTPD and spiro-OMeTAD, due to the higher σ value of the site energy difference distributions in the amorphous phase (Fig. 5). In the crystalline phase, the computed hole mobilities are generally comparable to each other (∼10−2 cm2 V−1 s−1), with the only exception of FTPD, which has a lower average mobility, probably due to the rather low values of the electronic couplings (around 9 meV), as compared to the other triphenylamines. For those cases in which the experimental single crystal hole mobility is available in the literature, that are TPA and spiro-OMeTAD (Table 3), the computed hole mobilities of single crystals are in very good agreement with the measured one. For TPD we could not find experimental data referring to single crystals, while for FTPD the experimental values refer to semi-crystalline thin films. Clearly, our simulations on a single crystal do not take into account the presence of defects (e.g., vacancies, dislocations), impurities or grain boundaries, thus overestimating the charge mobility. We note that one cannot trivially infer the magnitude of the charge mobility from the size of the area covered by the superimposed trajectories (Fig. 8) alone when comparing different compounds, since the time it took to complete the trajectories is not visible in the plots and the same number of KMC steps is performed in all cases. The anisotropy of the mobility tensors however can be clearly observed.
Comparing the results from the KMC charge transport simulations in the crystalline and amorphous morphologies (see also the ESI,† Fig. S11 and S14), besides the drop of the hole mobility from two to four orders of magnitude (which is expected for small molecules), one can also observe the loss of directional anisotropy, especially for TPD and spiro-OMeTAD, which show clear preferential charge percolation directions in single crystals. Interestingly, for these anisotropic cases (TPD and spiro-OMeTAD), the highest computed hole mobility (μyy = 1.6 × 10−1 cm2 V−1 s−1 for TPD and μxx = 4.3 × 10−2 cm2 V−1 s−1 for spiro-OMeTAD) can be one or two orders of magnitude larger than the other components of the mobility tensor. This knowledge can pave the way for exploiting morphologically controlled experimental techniques to grow the TPAs crystals along with particular directions, in order to enhance the hole mobility.
In the amorphous bulk morphology all triphenylamines show isotropic Brownian charge diffusion. This feature is related to the loss of structural order passing from the crystal to the amorphous phase, as suggested by the radial distribution function analysis (Fig. 2). TPA and TPD show the highest computed hole mobilities (8.3 and 5.9 × 10−4 cm2 V−1 s−1) in the amorphous phase, two orders of magnitudes higher than FTPD and spiro-OMeTAD (∼10−6 cm2 V−1 s−1). These differences originate from the site energy disorder (Fig. 4), which is lower for TPA and TPD (σ = 0.18 and 0.12 meV, respectively) with respect to FTPD and spiro-OMeTAD (σ = 0.24 and 0.27 meV, respectively). The broad site energy difference distributions in the amorphous phase of each species lead to charge trapping and low charge transfer rates, thus impacting the final zero-field charge mobility. A good agreement is achieved between the computed charge mobility for the amorphous phase with respect to the available experimental data, as for the cases of TPD and spiro-MeOTAD.
Conclusion
We have presented an in-depth study about the interplay between the structural complexity, the supramolecular packing in the crystalline and amorphous condensed phases, and the charge transport parameters of four triphenylamine derivatives. The influence of the molecular architecture can be observed in the radial distribution function characterising the CoM distances at short- and long-ranges, in both the crystalline and amorphous phases. In the crystal phase, small, sphere-like compounds like TPA can get very close to each other, resulting in packed structures, while elongated two-redox center (TPD, FTPD) or sterically demanding four-redox center (spiro-OMeTAD) compounds show very large CoM distances. In the amorphous phase, however, due to the favourable aspect ratio or backbone flexibility, the elongated two-redox center derivatives can afford shorter CoM distances than TPA and spiro-OMeTAD. Such a different structural order impacts the bulk charge mobility.From the calculation of the charge transport parameters, we firstly remarked the dependence of the intramolecular reorganization energy on the degree of charge delocalization in multi-redox-center TPA species. This charge delocalization is influenced by the flexibility of the molecular structure, namely the bridge connecting the redox centers. We found that reasonable reorganization energies can be computed by adopting a charge partitioning scheme (via C-DFT), which localizes the charge on single redox TPA centers. This method provides values of the internal reorganization energy very close to those obtained by the well-consolidated frozen dihedral angle approach, where torsional angles are fixed upon charging, thus avoiding the twisting which is reasonably hindered in the bulk phase.
The narrow site-energy distributions in the crystalline phase as computed for all TPAs lead to a reorganization energy controlled hopping transport regime in single crystals. In the amorphous phase, however, the charge transport is instead dominated by the static energetic disorder. Indeed, the standard deviation of the site energy difference distributions of amorphous morphologies is larger than for crystals. In particular, the structurally complex compounds like FTPD and spiro-OMeTAD show higher energetic disorder than TPA and TPD, thus leading to very low (10−6 cm2 V−1 s−1) values for the charge mobility in the amorphous phase. A detailed analysis of the crystal structures of TPAs with regard to molecular packing and electronic coupling distribution revealed the origin of the charge transport (an)isotropy in the single crystalline phases. In particular, elongated TPD or bulky spiro-OMeTAD show preferential charge diffusion along specific crystal axes, leading to strong anisotropy in hole transport. Our work shows that in crystalline phases the average mobility is very similar for all compounds; however the charge transport anisotropy leads to charge mobility differences for some directions of multiple orders of magnitude for some species, like TPD and spiro-OMeTAD. This characteristic can be potentially exploited to grow crystalline films along particular crystallographic directions, thus achieving the highest charge mobility for that compound. Generally, the computed hole mobilities are in very good agreement with the available experimental data (either measured on single crystal/semi-crystalline films, or amorphous films), corroborating our computational approach.
Author contributions
R. H. and D. F. performed the calculations and the computational analyses. R. H., D. F., K. M. and F. N. conceptualized the work. All authors contributed to rationalizing the data and writing the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
D. F. acknowledges the Deutsche Forschungsgemeinschaft (DFG) for the grant (FA 1502/1-1, years 2018-2021), the Regional Computing Centre (RRZK) of the University of Cologne for providing computing time and resources on the HPC RRZK CHEOPS, and partial funding from the National Recovery and Resilience Plan (NRRP), Mission 04 Component 2, Investment 1.5 – NextGenerationEU, Call for tender n. 3277 dated 30/12/2021, Award Number: 0001052 dated 23/06/2022. K. M., D. F. and R. H. acknowledge the excellence initiative of the University of Cologne, “Quantum Matter and Materials” (QM2), and the DFG Research Training Group 2591 “Template-designed Organic Electronics (TIDE)” for supporting their research.Notes and references
- M. Stolka, J. F. Yanus and D. M. Pai, J. Phys. Chem., 1984, 88, 4707–4714 CrossRef CAS.
- P. Cias, C. Slugovc and G. Gescheidt, J. Phys. Chem. A, 2011, 115, 14519–14525 CrossRef CAS PubMed.
- C. Adachi, K. Nagai and N. Tamoto, Appl. Phys. Lett., 1995, 66, 2679–2681 CrossRef CAS.
- Y. Shirota, J. Mater. Chem., 2005, 15, 75–93 RSC.
- J. K. Feng, Y. L. Cao, X. P. Ai and H. X. Yang, J. Power Sources, 2008, 177, 199–204 CrossRef CAS.
- H. Tanaka, S. Tokito, Y. Taga and A. Okada, Chem. Commun., 1996, 2175 RSC.
- S. Tokito, H. Tanaka, K. Noda, A. Okada and Y. Taga, Appl. Phys. Lett., 1997, 70, 1929–1931 CrossRef CAS.
- P. Agarwala and D. Kabra, J. Mater. Chem. A, 2017, 5, 1348–1373 RSC.
- P. Blanchard, C. Malacrida, C. Cabanetos, J. Roncali and S. Ludwigs, Polym. Int., 2019, 68, 589–606 CrossRef CAS.
- Y. Tao, Q. Wang, C. Yang, C. Zhong, J. Qin and D. Ma, Adv. Funct. Mater., 2010, 20, 2923–2929 CrossRef CAS.
- A. Leliège, P. Blanchard, T. Rousseau and J. Roncali, Org. Lett., 2011, 13, 3098–3101 CrossRef PubMed.
- H. Choi, J. W. Cho, M.-S. Kang and J. Ko, Chem. Commun., 2015, 51, 9305–9308 RSC.
- N. Goujon, N. Casado, N. Patil, R. Marcilla and D. Mecerreyes, Prog. Polym. Sci., 2021, 122, 101449 CrossRef CAS.
- L. Fan, Q. Liu, Z. Xu and B. Lu, ACS Energy Lett., 2017, 2, 1614–1620 CrossRef CAS.
- S. Feser and K. Meerholz, Chem. Mater., 2011, 23, 5001–5005 CrossRef CAS.
- P. Zacharias, M. C. Gather, M. Rojahn, O. Nuyken and K. Meerholz, Angew. Chem., Int. Ed., 2007, 46, 4388–4392 CrossRef CAS PubMed.
- P. Friederich, V. Meded, A. Poschlad, T. Neumann, V. Rodin, V. Stehr, F. Symalla, D. Danilov, G. Lüdemann, R. F. Fink, I. Kondov, F. von Wrochem and W. Wenzel, Adv. Funct. Mater., 2016, 26, 5757–5763 CrossRef CAS.
- K.-H. Lin, L. Paterson, F. May and D. Andrienko, npj Comput. Mater., 2021, 7, 1–7 CrossRef.
- A. Mondal, L. Paterson, J. Cho, K.-H. Lin, B. van der Zee, G.-J. A. H. Wetzelaer, A. Stankevych, A. Vakhnin, J.-J. Kim, A. Kadashchuk, P. W. M. Blom, F. May and D. Andrienko, Chem. Phys. Rev., 2021, 2, 31304 CrossRef.
- K.-H. Lin, A. Prlj, L. Yao, N. Drigo, H.-H. Cho, M. K. Nazeeruddin, K. Sivula and C. Corminboeuf, Chem. Mater., 2019, 31, 6605–6614 CrossRef CAS.
- L. Fang, A. Zheng, M. Ren, X. Xie and P. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 39001–39009 CrossRef CAS PubMed.
- D. Shi, X. Qin, Y. Li, Y. He, C. Zhong, J. Pan, H. Dong, W. Xu, T. Li, W. Hu, J.-L. Brédas and O. M. Bakr, Sci. Adv., 2016, 2, e1501491 CrossRef PubMed.
- B. C. Lin, C. P. Cheng and Z. P. M. Lao, J. Phys. Chem. A, 2003, 107, 5241–5251 CrossRef CAS.
- J. T. Blaskovits, K.-H. Lin, R. Fabregat, I. Swiderska, H. Wu and C. Corminboeuf, J. Phys. Chem. C, 2021, 125, 17355–17362 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, WIREs Comput. Mol. Sci., 2021, 11, e1493 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- K. Ramachandran, A. Raja, N. Lingamurthy, M. S. Pandian, P. Ramasamy and S. Venugopal Rao, Chem. Phys. Lett., 2020, 742, 137128 CrossRef CAS.
- Z. Zhang, E. Burkholder and J. Zubieta, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, o452–4 CrossRef PubMed.
- R. A. Marcus, Angew. Chem., Int. Ed. Engl., 1993, 32, 1111–1121 CrossRef.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS.
- S. Di Motta, E. Di Donato, F. Negri, G. Orlandi, D. Fazzi and C. Castiglioni, J. Am. Chem. Soc., 2009, 131, 6591–6598 CrossRef CAS PubMed.
- D. P. McMahon and A. Troisi, J. Phys. Chem. Lett., 2010, 1, 941–946 CrossRef CAS.
- J. E. Norton and J.-L. Brédas, J. Am. Chem. Soc., 2008, 130, 12377–12384 CrossRef CAS PubMed.
- E. F. Valeev, V. Coropceanu, D. A. Da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- B. Baumeier, J. Kirkpatrick and D. Andrienko, Phys. Chem. Chem. Phys., 2010, 12, 11103–11113 RSC.
- J. Kirkpatrick, Int. J. Quantum Chem., 2008, 108, 51–56 CrossRef CAS.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- J. Kirkpatrick, V. Marcon, K. Kremer, J. Nelson and D. Andrienko, J. Chem. Phys., 2008, 129, 94506 CrossRef PubMed.
- I. Yavuz, B. N. Martin, J. Park and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 2856–2866 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Del Martin Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317 CrossRef CAS.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- E. Di Donato, R. P. Fornari, S. Di Motta, Y. Li, Z. Wang and F. Negri, J. Phys. Chem. B, 2010, 114, 5327–5334 CrossRef CAS PubMed.
- S. Di Motta, M. Siracusa and F. Negri, J. Phys. Chem. C, 2011, 115, 20754–20764 CrossRef CAS.
- N. Gildemeister, G. Ricci, L. Böhner, J. M. Neudörfl, D. Hertel, F. Würthner, F. Negri, K. Meerholz and D. Fazzi, J. Mater. Chem. C, 2021, 9, 10851–10864 RSC.
- M. Renz, K. Theilacker, C. Lambert and M. Kaupp, J. Am. Chem. Soc., 2009, 131, 16292–16302 CrossRef CAS PubMed.
- M. Lundberg and P. E. M. Siegbahn, J. Chem. Phys., 2005, 122, 224103 CrossRef PubMed.
- Y. Li, H. Li, C. Zhong, G. Sini and J.-L. Brédas, npj Flexible Electron., 2017, 1, 1–8 CrossRef CAS.
- D. C. Hoesterey and G. M. Letson, J. Chem. Phys., 1964, 41, 675–679 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc02206d |
| This journal is © The Royal Society of Chemistry 2023 |